Parallel Parking: Optimal Entry and Minimum Slot Dimensions
Jiri Vlasak
1,2 a
, Michal Sojka
2 b
and Zden
ˇ
ek Hanz
´
alek
2 c
1
Faculty of Electrical Engineering, Czech Technical University in Prague, Czech Republic
2
Czech Institute of Informatics, Robotics and Cybernetics, Czech Technical University in Prague, Czech Republic
Keywords:
Automated Parking, Parallel Parking.
Abstract:
The problem of path planning for automated parking is usually presented as finding a collision-free path from
initial to goal positions, where three out of four parking slot edges represent obstacles. We rethink the path
planning problem for parallel parking by decomposing it into two independent parts. The topic of this paper is
finding optimal parking slot entry positions. Path planning from initial to entry position is out of scope here.
We show the relation between entry positions, parking slot dimensions, and the number of backward-forward
direction changes. This information can be used as an input to optimize other parts of the automated parking
process.
1 INTRODUCTION
Driver assistance systems experience a great expan-
sion. Proposals for automated driving are topics of
many teams of engineers and academics. One of the
basic building blocks of automated driving is the (au-
tomated) parking assistant.
A common approach to the problem of path plan-
ning for parallel parking is to geometrically com-
pute a path from the current (initial) position to
the goal position inside the parking slot. When an
optimization-based approach is used, the time or path
length between initial and goal positions is usually
minimized. But what if the given goal position is not
chosen optimally?
In this paper, we reformulate the path planning
problem of automated parking for a parallel parking
slot into the problem of finding optimal entry and goal
positions. We solve this problem for the given park-
ing slot and car dimensions using a simulation ap-
proach. A feasible path is computed by simulating
the car movement between these positions.
We show how we find the entry positions, the de-
pendency between entry positions, parking slot di-
mensions, and the number of backward-forward di-
rection changes, and how to find the minimum dimen-
sions of a parking slot for the given car. The results of
our simulations can be used as parameters in parking
a
https://orcid.org/0000-0002-6618-8152
b
https://orcid.org/0000-0002-8738-075X
c
https://orcid.org/0000-0002-8135-1296
assistant algorithms to quickly decide about the pos-
sibility of parking and simplify the navigation toward
the parking slot.
The rest of the paper is structured as follows.
We define the parallel parking problem in Section 2.
In Section 3, we describe how we find the entry
positions, how entry positions depend on direction
changes, and how we compute the minimum dimen-
sions of a parallel parking slot. In Section 4, we per-
form computational experiments and compare our re-
sults to related works. We conclude the paper in Sec-
tion 5. The source code of our algorithm is publicly
available as free and open source software
1
.
1.1 Related Works
(Blackburn, 2009) explains how to compute the mini-
mum length of a parallel parking slot, to which the car
can park in only one maneuver. In this paper, we con-
sider parallel parking slots that could be shorter and
therefore we allow multiple backward-forward direc-
tion changes.
(Zips et al., 2013) introduce two-phased constraint
optimization algorithm to plan the parking maneu-
ver for parallel, perpendicular, and angle parking slot.
During the first phase, the algorithm computes a path
from the goal position to a phase switching point,
from which the car can leave the slot. In the second
phase, the algorithm finds a path from the switching
point to the initial position. In their follow-up work
1
https://rtime.ciirc.cvut.cz/gitweb/hubacji1/bcar.git
300
Vlasak, J., Sojka, M. and Hanzálek, Z.
Parallel Parking: Optimal Entry and Minimum Slot Dimensions.
DOI: 10.5220/0011045600003191
In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 300-307
ISBN: 978-989-758-573-9; ISSN: 2184-495X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Zips et al., 2016), they present improvements to the
algorithm for a path planning outside the parking slot.
Our paper differs in the problem definition. We con-
sider the parallel parking slot – not the goal position –
as the input. Our approach guarantees the optimality
of entry positions as opposed to the phase switching
point.
(Vorobieva et al., 2015) present three algorithms
for geometric parking: (1) The algorithm for parking
in one maneuver computes path from the goal posi-
tion by simulating forward movement with the max-
imum steering. This algorithm works only for long
enough parking slots. (2) Parking in several paral-
lel trials algorithm starts by computing the path from
initial position to some position partially inside the
parking slot with the constraint of the car heading be-
ing parallel to the parking slot heading. Then, the
algorithm continues by simulating forward-backward
moves toward the parking slot with the constraint of
the car heading being parallel to the parking slot head-
ing when the car stops for the direction change. (3)
Parking algorithm called several reversed trials gen-
eralize the algorithm for parking in one maneuver. It
computes the path in the reverse order to the park-
ing process: the algorithm starts from the goal po-
sition and computes the path by simulating forward-
backward moves with the maximum steering until the
car leaves the parking slot.
(Li and Tseng, 2016) propose complete system for
automated parking. Their planning algorithm com-
putes a path for a parallel parking slot from three cir-
cle segments. The initial position is considered a part
of the input to the algorithm and only one (backward)
move is allowed.
The works above describe a geometric planner to
find a path between initial and goal position. In this
paper, we also use the geometric approach. How-
ever, we consider entry and goal positions as the re-
sult, which allows us to guarantee that the car can
park from entry positions into the parking slot with
the minimum number of backward-forward direction
changes. Path planning from initial to entry position
is out of scope this paper.
(Li et al., 2016) present dynamic optimization
framework for computing a time-optimal maneuvers
for parallel parking. They compute trajectory from
initial position to any parked position, i.e., a position
of a car when the car is completely inside the parking
slot. Compared to our approach, we do not consider
the time. However, we compute a set of entry posi-
tions and return it as the result.
To solve the path planning problem of parallel
parking for automated vehicle, (Jing et al., 2018)
introduce nonlinear programming optimization that
minimizes multiple objectives such as path length,
distance from the car front to the parking slot front,
and the distance from the car center to the parking slot
center. The initial position of the car is fixed and only
one (backward) move is allowed. In this paper, we
allow multiple backward-forward direction changes,
but we minimize their count.
2 PARALLEL PARKING
PROBLEM
We define the used terminology and the parallel park-
ing problem in this section.
2.1 Definitions
Car position is a tuple C = (x, y,θ,s,φ), where x and
y are cartesian coordinates of the rear axle center, θ is
car heading, s ∈
{
−1,+1
}
is direction of the move-
ment (backward and forward respectively), and φ ∈
[−φ
max
,+φ
max
] is car steering angle. Car positions
are subject to a discrete kinematic model (Kuwata
et al., 2009) C
k+1
= f (C
k
), k ∈ N where function f
is given by Eq. (1):
x
k+1
= x
k
+ s
k
· ∆ ·cos(θ
k
)
y
k+1
= y
k
+ s
k
· ∆ ·sin(θ
k
)
θ
k+1
= θ
k
+
s
k
· ∆
b
·tan(φ
k
),
(1)
where ∆ ∈ R
+
is a positive constant we call the
step distance.
The direction change is a change of the car move-
ment direction s. We denote Γ the number of direction
changes.
Car dimensions is a tuple D = (w,d
f
,d
r
,b,φ
max
),
where w is the width of the car, d
f
and d
r
is the dis-
tance from the rear axle center to the front, respective
back of the car, b is the wheelbase (distance between
the front and rear axle), and φ
max
is the maximum
steering angle.
Car frame F (C) is a rectangle given by car posi-
tion C and car dimensions D.
Minimum turning radius is the radius r of the cir-
cle traced by the rear axle center when the car moves
with the maximum steering. It holds that r =
b
tanφ
max
.
Curb-to-curb distance is the diameter d of the
circle traced by the outer front wheel when the car
moves with the maximum steering. It holds that
d = 2 ·
q

r +
w
2

2
+ b
2
.
Parallel Parking: Optimal Entry and Minimum Slot Dimensions
301

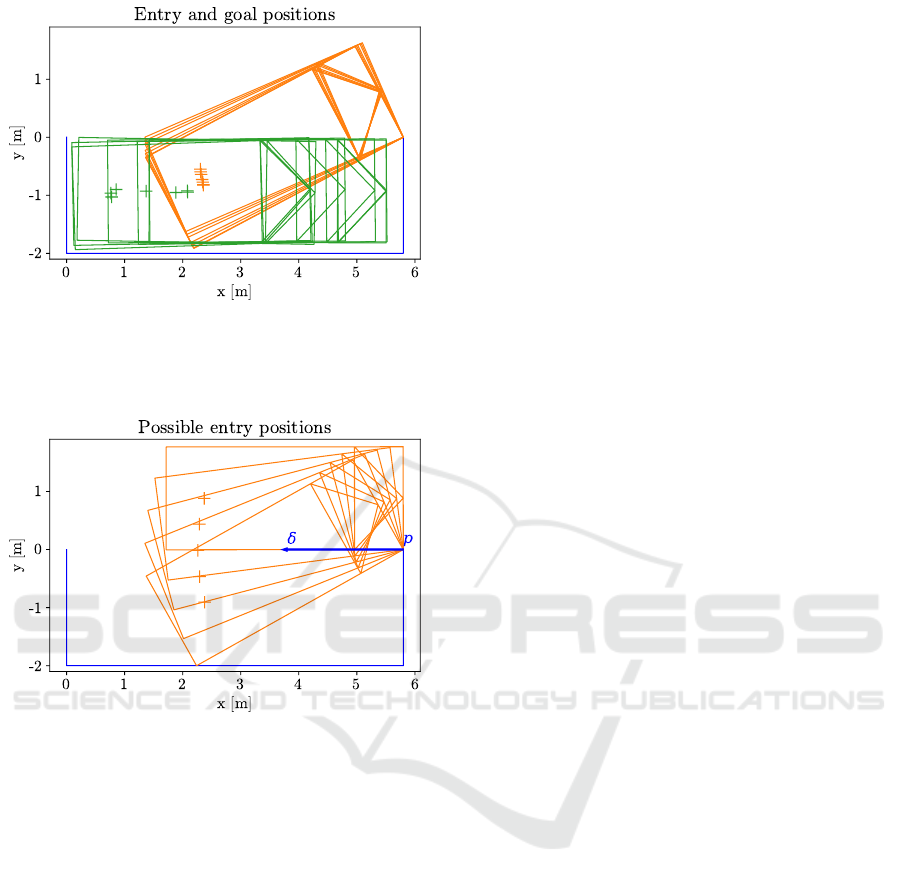
Figure 1: Orange rectangles represent an example subset
of computed entry positions, green rectangles are goal po-
sitions, and blue frame is parallel parking slot. The cross
represents the middle of the rear axle.
Figure 2: Orange rectangles represent an example subset of
possible entry positions, blue frame is parallel parking slot.
The cross represents the middle of the rear axle.
Parallel parking slot is a rectangle whose one side
(that we call entry side) is adjacent to the road. Paral-
lel parking slot is defined as a tuple P = (p,δ,W,L),
where point p ∈ R
2
is one corner of the rectangle on
the entry side, δ is the direction vector of the en-
try side relative to p, W > w is parking slot width
greater than the width of the car, and the length of
the parking slot, equal to the length of the entry side,
is L ≥ d
f
+ d
r
.
Goal position is a car position C
G
for which
F (C
G
) is completely inside the parallel parking slot
P. We can see an example of different green goal po-
sitions C
G
in Fig. 1.
Possible entry position for parallel parking slot
positioned on the right side of a road (for left-sided
parking slot the definition would be symmetric) is a
car position C
P
E
= (x,y, θ,−1,+φ
max
) with the follow-
ing properties: (i) right front corner of the car frame
F (C
P
E
) corresponds to the parking slot corner p, (ii)
the car heading is in between the angle parallel to the
entry side up to the angle perpendicular to the entry
side, i.e., δ + π ≤ θ ≤ δ + 3/2π, and (iii) car frame
F (C
P
E
) does not intersect with non-entry sides of the
parking slot. We denote C
P
E
a set of possible entry
positions and we can see an example subset of C
P
E
in
Fig. 2.
2.2 Problem Statement
The main problem we solve is:
1. Given a parallel parking slot and car dimensions,
find a set of entry positions C
E
⊂ C
P
E
from which
the car can park into the slot with the minimum
number of direction changes.
There are two additional related problems we solve
along with the main one:
2. Given a parallel parking slot, car dimensions, and
the maximum number of direction changes, what
is a set of all entry positions C
A
E
⊂ C
P
E
from which
the car can park into the slot?
3. Given the car dimensions and the maximum num-
ber of direction changes, what are the minimum
dimensions (i.e., width and length) of a parallel
parking slot the car can park into?
3 PARKING SIMULATION
ALGORITHMS
In this section, we describe our parallel parking sim-
ulation algorithm, and we show how we use it to
solve the problems from Section 2.2. In Section 3.1,
we describe our algorithm for finding entry positions
from which it is possible to park into the slot with the
minimum number of direction changes, i.e., the main
problem. In Section 3.2, we relax the condition on
the minimum number of direction changes (problem
2), and in Section 3.3 we describe how we use the al-
gorithm to find the minimum dimensions of a parallel
parking slot (problem 3).
3.1 Finding Entry Positions
Our simulation algorithm first computes the set of
possible entry positions C
P
E
. Then, the algorithm sim-
ulates backward-forward moves from each possible
entry position C
P
E
∈ C
P
E
until the car frame is com-
pletely inside the parking slot which mean the goal
position is found. We can see the pseudocode in Al-
gorithm 1. ∆
θ
is the increment to the car position
heading for the consequent possible entry positions.
VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems
302

Algorithm 1: Finding entry positions.
• Input: car dimensions D, parking slot P
• Output: entry positions C
E
1: C
0
← {C
P
E
(D,P,θ)|θ = δ + π + m · ∆
θ
,m ∈ N}
2: H ← {(C
0
,C
0
,s,φ, Γ)|C
0
∈ C
0
, s = −1, φ =
φ
max
,Γ = 0}
3: Γ
max
← ∞
4: I ←
/
0  Set of goal and entry positions
5: while I =
/
0 do
6: for (C,C
0
,s,φ, Γ) ∈ H do
7: if Γ > Γ
max
then
8: continue
9: end if
10: while F(C) not intersects with P do
11: C ← f (C,s, φ)  Simulate move
12: end while
13: if F(C) inside P then
14: I ← I ∪ (C,C
0
)
15: Γ
max
← Γ
16: else
17: H ← H ∪ (C,C
0
,−s,−φ, Γ+ 1)
18: end if
19: end for
20: end while
21: return C
E
= {C
0
|(C,C
0
) ∈ I}
3.2 Limit on the Direction Changes
Algorithm 1 finds the set of entry positions from
which it is possible to park into the parking slot with
the minimum number of direction changes. To find
all entry positions C
A
E
⊂ C
P
E
for the given maximum
number of direction changes, we provide Γ
max
as the
input to the Algorithm 1 and remove Γ
max
update in
Line 15.
By removing Γ
max
update, the computed set of en-
try positions does not need to be continuous, i.e., the
difference in headings of neighboring entry positions
could be greater than ∆
θ
. We can see such a situation
in Fig. 1, where orange rectangles represent an ex-
ample subset of computed entry positions where the
continuity is broken approximately in the middle.
3.3 Minimum Slot Dimensions
To find the minimum dimensions (i.e., width and
length) of a parallel parking slot for the given car di-
mensions and maximum number of direction changes
Γ
max
, we run Algorithm 1 for finding entry positions
repeatedly, looping over different parking slot widths
and lengths. First, we initialize the parking slot width
W = w and length L = d
f
+d
r
to match the car dimen-
sions. Then, we gradually increase the parking slot
-1
0
1
2
3
4
5
-6 -4 -2 0 2 4
Car width w [m]
Car length d
f
+ d
r
[m]
"mid-sized vehicle"
Renault ZOE
Opel Corsa
Volkswagen transporter
Mercede-Benz AMG GT
Figure 3: Car frame and the simulated path given by the
forward movement with the maximum steering angle for
“mid-sized vehicle”, Renault ZOE, Opel Corsa, Volkswa-
gen transporter, and Mercedes-Benz AMG GT.
width and length by the width step ∆
W
and the length
step ∆
L
respectively.
4 RESULTS
In this section, we present the results of the com-
putational experiments. In Section 4.1, we compare
our approach to the related works. In Section 4.2,
we show the range of all entry positions heading for
the given maximum number of direction changes. Fi-
nally, we show the minimum dimensions of a parallel
parking slot in Section 4.3.
We provide the results for five different cars. Their
dimensions are shown in Table 1. In Fig. 3, we can see
the car frames and the simulated paths given by the
forward movement with the maximum steering angle.
The width of the car is always without left and right
rear view mirrors.
4.1 Comparison to Related Works
(Zips et al., 2013) use the dimensions of the “mid-
sized vehicle” and the parallel parking slot with the
width W = 2.2 m and the length L = 5.1 m for their
simulations. There is no change to the first phase of
their algorithm in their follow-up work.
Along with the parallel parking slot and car di-
mensions, (Zips et al., 2013) are given the initial and
goal positions. There is no further information or ex-
act values provided in their simulation studies. They
need at least 12 direction changes to park in the slot.
We compute that it’s possible to park into the slot
they use with 10 direction changes for the given car
dimensions, so we conclude that the used goal posi-
tion is not optimal.
(Vorobieva et al., 2015) use the dimensions of the
Renault ZOE for their experiments. They use several
Parallel Parking: Optimal Entry and Minimum Slot Dimensions
303

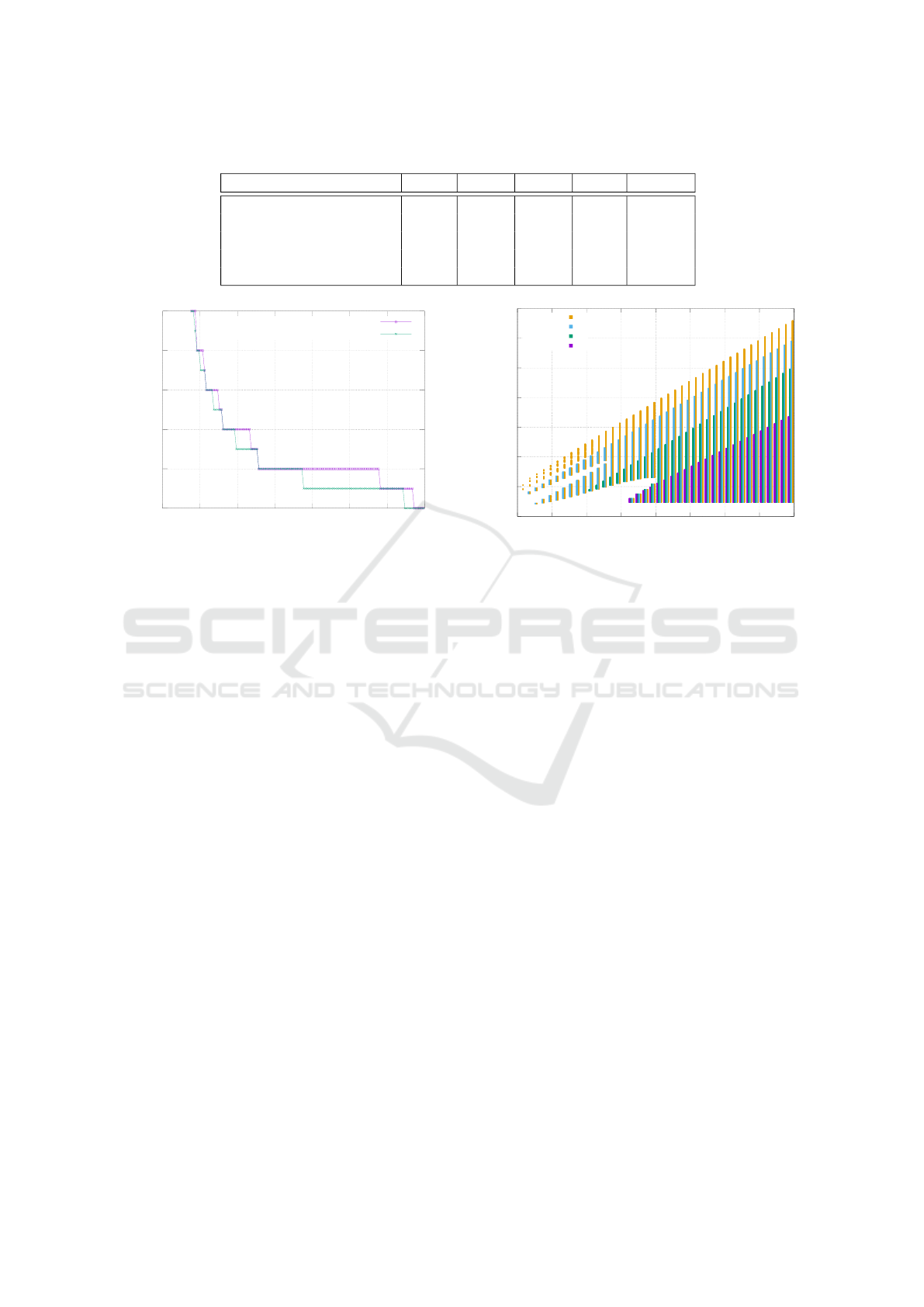
Table 1: Car dimensions used in the computations.
Car w [m] d
f
[m] d
r
[m] b [m] φ
max
[
◦
]
“mid-sized vehicle” 1.8 3.7 1.0 2.7 45
Renault ZOE 1.771 3.427 0.657 2.588 33
Opel Corsa 1.532 3.212 0.410 2.343 32
Volkswagen transporter 1.994 4.308 1.192 3.400 36
Mercedes-Benz AMG GT 1.939 3.528 1.016 2.630 32
0
2
4
6
8
10
4.4 4.6 4.8 5 5.2 5.4 5.6 5.8
Number of direction changes [-]
Parallel parking slot length [m]
Vorobieva et al., 2015
this paper
Figure 4: Comparison of direction changes for Renault
ZOE when several reversed trials method is used with goal
positions from (Vorobieva et al., 2015) or with goal posi-
tions from this paper. Goal positions from (Vorobieva et al.,
2015) has the car frame aligned with the entry and rear sides
of the parallel parking slot. The parallel parking slot has the
width W = 2.0 m and variable length of up to L = 5.8 m with
the length step of ∆
L
= 0.01m.
reversed trials method to plan a path into the parallel
parking slot.
We compare our implementation of several re-
versed trials for goal positions used in (Vorobieva
et al., 2015) with goal positions computed by our ap-
proach.
The goal position used in (Vorobieva et al., 2015)
is not explicitly stated. They assume the goal position
is known. For our computational experiments, we de-
duce the goal position from the context of the paper,
i.e. the goal position for parallel parking slot posi-
tioned on the right side of a road has the following
properties: (i) left side of the car frame given by the
goal position corresponds to parking slot entry side,
and (ii) rear side of the car frame given by the goal
position corresponds to parking slot rear side.
The parallel parking slot has the width W = 2.0m,
and we test the length of up to L = 5.8 m with the
length step of ∆
L
= 0.01 m.
In Fig. 4, we can see that when goal position
is given by our approach, it leads to less direction
changes.
(Li et al., 2016) use the dimensions of the Renault
ZOE for their simulations. The parallel parking slot
25
26
27
28
29
30
31
32
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45
Heading of entry positions [°]
Extra slot width W - w [m]
Γ
max
=10
Γ
max
=5
Γ
max
=2
Γ
max
=1
Figure 5: Entry positions heading for Renault ZOE, the par-
allel parking slot with different extra slot width W − w with
the width step of ∆
W
= 0.01m, constant extra slot length
L − d
f
− d
r
= 1.1 m, and different maximum number of di-
rection changes Γ
max
.
has the width W = 2.0m and the length L = 4.5 m.
(Li et al., 2016) need 19 direction changes for the
given parallel parking slot and car dimensions. Our
approach results in 19 direction changes for the given
values, too.
4.2 Limit on the Direction Changes
To compute the set of all entry positions for the given
maximum number of direction changes, we use the
car dimensions of the Renault ZOE.
In Fig. 5, we can see the entry positions heading
for the parallel parking slot with constant extra slot
length L − d
f
− d
r
= 1.1 m and different maximum
number of direction changes Γ
max
= 1, 2, 5, and 10
respectively.
We can see that the range of entry positions head-
ing is wider for larger extra slot width W − w and for
increasing Γ
max
. Also, we can see that the entry po-
sitions are found for narrower slots for higher Γ
max
.
Finally, the set of entry positions does not need to
be continuous, i.e., the difference between two neigh-
boring entry positions could be greater than ∆
θ
. The
range of entry positions heading then consists of the
subranges.
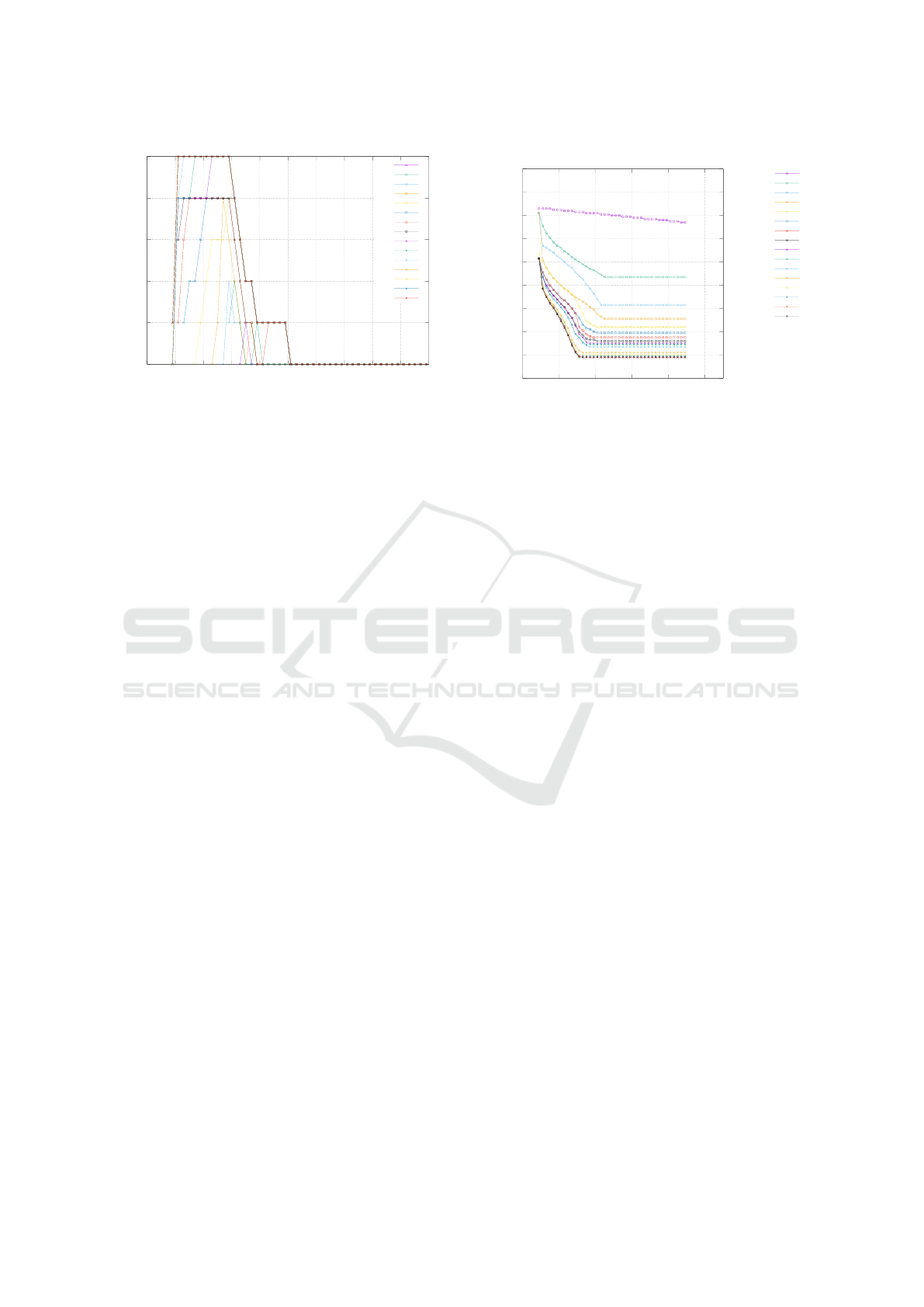
In Fig. 6, we can see the number of entry positions
VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems
304

1
2
3
4
5
6
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
Number of subranges [-]
Extra slot width W - w [m]
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
Figure 6: The number of entry positions heading subranges
for Renault ZOE, the parallel parking slot with different ex-
tra slot width W − w with the width step of ∆
W
= 0.01 m,
extra slot length L − d
f
− d
r
from 0.5m up to 1.9m with the
length step of ∆
L
= 0.1m, and constant Γ
max
= 10.
heading subranges for the parallel parking slot with
different extra slot lengths L − d
f
− d
r
from 0.5m up
to 1.9m and constant Γ
max
= 10.
We can see that there is only one range of entry po-
sitions heading for wide enough slots. The number of
subranges increases for narrower slots but decreases
again for the slots that are too narrow.
4.3 Minimum Slot Dimensions
To compute the minimum dimensions of a parallel
parking slot, we use the possible entry position head-
ing step ∆
θ
= 10
−4
rad, parking slot width step ∆
W
=
0.01m, and the length step ∆
L
= 0.01 m.
In Fig. 7, we can see the computed minimum di-
mensions of a parallel parking slot for Renault ZOE
and different maximum number of direction changes
Γ
max
.
Renault ZOE needs to perform at least Γ = 30 di-
rection changes when parking into the parallel park-
ing slot with extra slot length L − d
f
− d
r
= 0.4 m.
Also, there is a negligible improvement of 0.02m
when increasing the number of direction changes to
Γ = 100.
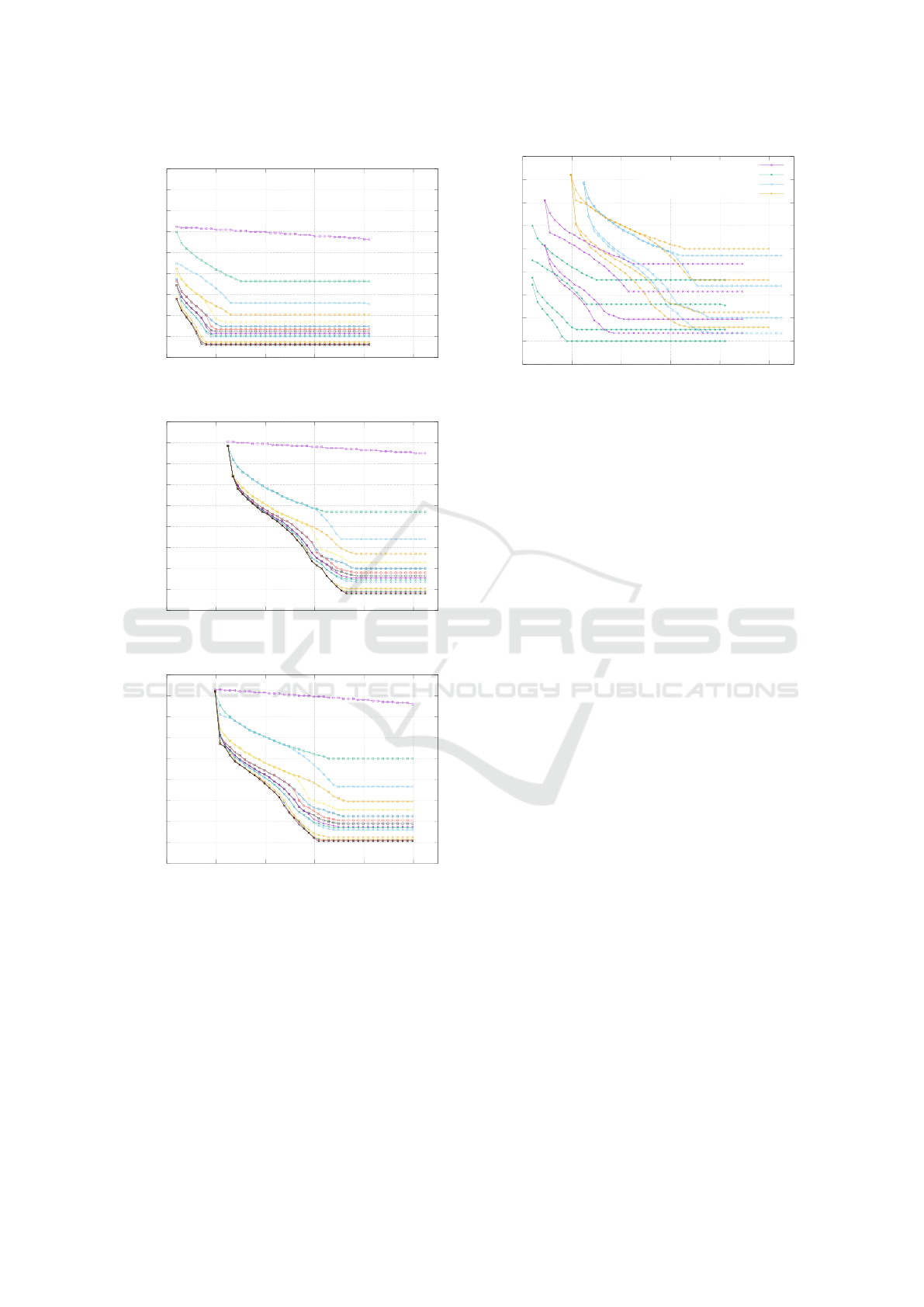
In Fig. 8, we can see the minimum dimensions of
a parallel parking slot for Opel Corsa, Volkswagen
transporter, and Mercedes-Benz AMG GT.
Opel Corsa can park into the parallel parking slot
with extra slot length of 0.4 m with Γ = 10 direc-
tion changes. Volkswagen transporter needs the same
number of direction changes Γ = 30 as the Renault
ZOE, although it requires more extra slot width. It
is not possible to park Mercedes-Benz AMG GT into
the parallel parking slot with extra slot length of 0.4m
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 0.1 0.2 0.3 0.4 0.5
Extra slot length L - d
f
- d
r
[m]
Extra slot width W - w [m]
Renault ZOE
Γ
max
=0
Γ
max
=1
Γ
max
=2
Γ
max
=3
Γ
max
=4
Γ
max
=5
Γ
max
=6
Γ
max
=7
Γ
max
=8
Γ
max
=9
Γ
max
=10
Γ
max
=20
Γ
max
=30
Γ
max
=40
Γ
max
=50
Γ
max
=100
Figure 7: Computed minimum dimensions of a parallel
parking slot for Renault ZOE and different maximum num-
ber of direction changes. The first line at the top of the graph
shows the minimum dimensions when no direction change
is allowed (Γ
max
= 0), followed by the maximum number
(Γ
max
) of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, and
100 direction changes. The width step ∆
W
= 0.01 m and the
length step ∆
L
= 0.01m.
within the reasonable number of backward-forward
direction changes.
The improvement to extra slot length for Γ > 20
is negligible, i.e., in the order of 10
−2
m. The shape
of the slot’s minimum dimensions curve depends on
whether the number of backward-forward direction
changes is even or odd.
Fig. 9 shows the minimum dimensions of a paral-
lel parking slot for all the cars. The maximum number
of direction changes shown in the figure is Γ
max
= 1,
2, 5, and 10 respectively.
5 CONCLUSION
In this paper, we re-formulate the path planning prob-
lem for parallel parking: Given a parallel parking slot
and car dimensions, we compute a set of entry po-
sitions to the parking slot from which it is possible
to park into the slot with the minimum number of
backward-forward direction changes. We also use our
approach to compute the minimum dimensions (i.e.,
width and length) of a parallel parking slot for the
given car dimensions.
Our algorithm is designed for offline use. By pre-
computing entry positions for different parallel park-
ing slots and car dimensions and using them in online
planning, we can speed up the path planning as it does
not need to plan the path inside the parking slot. Park-
ing assistants using our results can ensure that when
the automated vehicle reaches one of the entry posi-
Parallel Parking: Optimal Entry and Minimum Slot Dimensions
305

0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 0.1 0.2 0.3 0.4 0.5
Extra slot length L - d
f
- d
r
[m]
Extra slot width W - w [m]
Opel Corsa
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 0.1 0.2 0.3 0.4 0.5
Extra slot length L - d
f
- d
r
[m]
Extra slot width W - w [m]
Volkswagen transporter
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 0.1 0.2 0.3 0.4 0.5
Extra slot length L - d
f
- d
r
[m]
Extra slot width W - w [m]
Mercedes-Benz AMG GT
Figure 8: Computed minimum dimensions of a paral-
lel parking slot for Opel Corsa, Volkswagen transporter,
Mercedes-Benz AMG GT, and different maximum number
of direction changes.
tions, it can optimally park into the parallel parking
slot.
The range of entry positions from which the given
car can park optimally depends on the slot dimen-
sions. The range is wider for larger slots and a higher
number of backward-forward direction changes as
shown in Section 4.
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 0.1 0.2 0.3 0.4 0.5
Extra slot length L - d
f
- d
r
[m]
Extra slot width W - w [m]
Renault ZOE
Opel Corsa
Volkswagen transporter
Mercede-Benz AMG GT
Figure 9: Computed minimum dimensions of a parallel
parking slot for Renault ZOE, Opel Corsa, Volkswagen
transporter, and Mercedes-Benz AMG GT. The width step
∆
W
= 0.01 m and the length step ∆
L
= 0.01 m. The maxi-
mum number of direction changes is Γ
max
= 1, 2, 5, and 10
respectively.
By precomputing minimum dimensions of differ-
ent parallel parking slots, we can simplify the decision
of whether it is possible to park into the slot.
Using more than 20 direction changes does not
lead to significant reduction of the parking slot size.
The shape of the slot’s minimum dimensions curve
depends on whether the number of backward-forward
direction changes is even or odd.
ACKNOWLEDGEMENTS
Research leading to these results has received fund-
ing from the EU ECSEL Joint Undertaking and the
Ministry of Education of the Czech Republic un-
der grant agreement 826452, 8A19011, and MSMT-
24623/2019-4/11 (project Arrowhead Tools).
REFERENCES
Blackburn, S. R. (2009). The Geometry of Perfect Parking
| Department Of Mathematics, Royal Holloway, Uni-
versity of London.
Jing, W., Feng, D., Zhang, P., Zhang, S., Lin, S., and
Tang, B. (2018). A Multi-Objective Optimization-
based Path Planning Method for Parallel Parking
of Autonomous Vehicle via Nonlinear Programming.
In 2018 15th International Conference on Control,
Automation, Robotics and Vision (ICARCV), pages
1665–1670.
Kuwata, Y., Teo, J., Fiore, G., Karaman, S., Frazzoli, E., and
How, J. P. (2009). Real-time motion planning with ap-
plications to autonomous urban driving. IEEE Trans-
VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems
306

actions on Control Systems Technology, 17(5):1105–
1118.
Li, B., Wang, K., and Shao, Z. (2016). Time-Optimal Ma-
neuver Planning in Automatic Parallel Parking Us-
ing a Simultaneous Dynamic Optimization Approach.
IEEE Transactions on Intelligent Transportation Sys-
tems, 17(11):3263–3274.
Li, M. H. and Tseng, P. K. (2016). Implementation of an au-
tonomous driving system for parallel and perpendicu-
lar parking. In Proc. IEEE/SICE Int. Symp. System
Integration (SII), pages 198–203.
Vorobieva, H., Glaser, S., Minoiu-Enache, N., and Mam-
mar, S. (2015). Automatic Parallel Parking in Tiny
Spots: Path Planning and Control. IEEE, 16(1):396–
410.
Zips, P., B
¨
ock, M., and Kugi, A. (2016). Optimisation based
path planning for car parking in narrow environments.
Robotics and Autonomous Systems, 79:1–11.
Zips, P., Bock, M., and Kugi, A. (2013). A fast motion
planning algorithm for car parking based on static op-
timization. In 2013 IEEE/RSJ International Confer-
ence on Intelligent Robots and Systems, pages 2392–
2397. ISSN: 2153-0866.
Parallel Parking: Optimal Entry and Minimum Slot Dimensions
307