Comparative Analysis of Heuristic Approaches to PkC

max

Dragutin Ostoji

1 a

, Tatjana Davidovi

2 b

, Tatjana Jak

c Kr

uger

2 c

and Du

san Ramljak

3 d

Faculty of Science, Department of Mathematics and Informatics, University of Kragujevac, Serbia

Mathematical Institute, Serbian Academy of Sciences and Arts, Belgrade, Serbia

School of Professional Graduate Studies at Great Valley, The Pennsylvania State University, Malvern, PA, U.S.A.

Keywords:

Scheduling Problems, Identical Processors, Stochastic Heuristics, Solution Transformation.

Abstract:

Cloud computing, new paradigms like fog, edge computing, require revisiting scheduling and resource alloca-

tion problems. Static scheduling of independent tasks on identical processors, one of the simplest scheduling

problems, has regained importance and we aim to ﬁnd stochastic iterative heuristic algorithms to efﬁciently

deal with it. Combining various actions to deﬁne solution transformations to improve solution quality, we cre-

ated 35 heuristic algorithms. To investigate the performance of the proposed approaches, extensive numerical

experiments are performed on hard benchmark instances. Among the tested variants, we identiﬁed the best

performing ones with respect to the solution quality, running time, and stability.

1 INTRODUCTION

Driving online decision making requires generating

huge amounts of data and its expeditious analysis -

thus high performance computing resources and their

efﬁcient use are needed. This yields reconsideration

of already extensively investigated practical, usually

complex, scheduling/resource allocation problems.

We revisit a problem of scheduling independent

tasks on parallel processors (Graham, 1969; Davi-

dovi

c et al., 2012; Frachtenberg and Schwiegelshohn,

2010; Pinedo, 2012) as a result of an increased inter-

est in efﬁcient exploration of high performance com-

puting resources, cloud computing and massively par-

allel multiprocessor systems. We are considering a

case study of P||C

max

- static scheduling of indepen-

dent tasks on identical processors. The expression

static means that the number of tasks and their du-

ration (lengths, processing times) are known a pri-

ori. The problem objective is to minimize the time

required to complete the execution of all tasks, i.e.,

makespan C

max

. P||C

max

is known to be NP-hard in

a strong sense (Fanjul-Peyro and Ruiz, 2010). Nu-

merous exact (Mrad and Souayah, 2018), heuristic

(Paletta and Ruiz-Torres, 2015), and metaheuristic

https://orcid.org/0000-0001-6704-353X

https://orcid.org/0000-0001-9561-5339

https://orcid.org/0000-0001-6766-4811

https://orcid.org/0000-0001-7477-1973

(Davidovi

c et al., 2012; Alharkan et al., 2018; Laha

and Gupta, 2018; Kamaraj and Saravanan, 2019) al-

gorithms have been developed for P||C

max

To efﬁciently handle P||C

max

, we analyze stochas-

tic iterative heuristic algorithms based on random

transformations of the current solution with an aim to

improve its quality. Transformations are applied re-

peatedly until some predeﬁned stopping criterion is

met. Each transformation consists of several steps

(different actions could be performed within each).

Combining various actions, we created 35 heuristic

algorithms and compared them on hard benchmark in-

stances. The diversity in performance with respect to

the solution quality, running time, and stability can be

signiﬁcant. Our experimental evaluation enabled to

identify the best performing variants.

In the remainder of this paper: Section 2 contains

P||C

max

problem description, and a brief relevant liter-

ature overview, the proposed heuristic algorithms are

presented in section 3, the experimental evaluation in

section 4, and concluding remarks in section 5.

2 P||C

max

BACKGROUND

Let m be the total number of available identical pro-

cessors, n the number of tasks to be executed. The

P||C

max

problem consists of assigning tasks to pro-

cessors, and determining their starting times. All the

Ostoji

c, D., Davidovi

c, T., Jakši

c Krüger, T. and Ramljak, D.

Comparative Analysis of Heuristic Approaches to P||Cmax.

DOI: 10.5220/0011008500003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 259-266

ISBN: 978-989-758-548-7; ISSN: 2184-4372

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

259

tasks should be allocated for execution, each to ex-

actly one processor. Task execution is performed in

a non-preemptive way: once the task starts it will

continue without interruption until completion. We

denote by T = {1,2,...,n} a given set of indepen-

dent tasks, and by M = {1, 2,... ,m} the set of iden-

tical processors. Each processor can engage only one

task at a time. Let p

denote the processing time

of task i (i = 1,2,.. .,n), which is a priori known

and ﬁxed, and let y

( j = 1,2,. . .,m) represent the

load of processor j calculated as the sum of process-

ing times of all tasks assigned to processor j. The

goal is to ﬁnd a schedule of tasks on processors such

that the corresponding completion time of all tasks

(makespan) is minimized (Davidovi

c et al., 2012).

The makespan is usually denoted as C

max

and calcu-

lated as: C

max

= max

j∈M

). P||C

max

can be formu-

lated as integer linear program (ILP) based on the as-

signment variables (Mokotoff, 2004), on the arc-ﬂow

model (Mrad and Souayah, 2018) or in some other

ways (Unlu and Mason, 2010). Although the opti-

mality of provided solutions is guaranteed, these for-

mulations have limitations in practical use: they re-

quire a lot of time and memory, even for small-size

instances. Therefore, after brieﬂy reviewing some of

the relevant results below, we propose heuristic ap-

proaches that can be more efﬁcient in practice.

P||C

max

is by far the most studied among all com-

pletion time related criteria and an enormous body of

knowledge, technical results, and connections to real-

world problems has been accumulated in this area.

We could think of production lines where several ma-

chines with the same speed have to perform a cer-

tain amount of jobs (Mokotoff, 2004), or minimizing

the overall CPU-time for identical processors by efﬁ-

ciently assigning tasks (Graham, 1969; Frachtenberg

and Schwiegelshohn, 2010; Davidovi

c et al., 2012).

(Lawrinenko, 2017) contains an extensive sur-

vey of the P||C

max

, in-depth explanations of exact

algorithms, while (Walter and Lawrinenko, 2017)

presented a depth-ﬁrst branch-and-bound algorithm

with symmetry-breaking dominance criteria. Ex-

act algorithms state-of-the-art application (Mrad and

Souayah, 2018) presents an arc-ﬂow based ILP model

inspired by the duality between the bin-packing and

the P||C

max

and discuss the hardness of test instances

expressed by n and m ratio.

(Della Croce and Scatamacchia, 2020) revisited

Longest Processing Time (LPT (Graham, 1969)) and

derived an O(nlogn) time complexity constructive

heuristic. Two procedures of constructive heuristic

approach, (Paletta and Ruiz-Torres, 2015), are con-

structing a feasible solution, and then Many Times

Multiﬁt (MTMF) procedure tightening the initial so-

lution by iteratively using a bin-packing based pro-

cedure on different job sets. Iterative heuristic ap-

proach, (Paletta and Vocaturo, 2011), also builds upon

initially constructed feasible solution, and use local

search techniques where single jobs or sets of jobs are

exchanged between different machine pairs (i1,i2).

Approximation heuristic approach (Mnich and Wiese,

2015) show that there is an Fixed-parameter tractabil-

ity (FPT) algorithm for this problem when parameter-

ized by p

max

(the largest job processing time). Several

Efﬁcient Polynomial Time Approximation Schemes

(EPTAS) for the P||C

max

exist (Jansen et al., 2020).

Among the ﬁrst metaheuristic approaches, Tabu

Search (TS) is proposed in (Thesen, 1998). A

rather simple implementation of Variable Neighbor-

hood Search (VNS) is proposed in (Davidovi

c and

Jani

cijevi

c, 2009). The authors of (Alharkan et al.,

2018) extended its study to more general variant

of VNS, investigating the effect of including new

neighborhood structures and changing the order in

which the neighborhoods are explored. Bee Colony

Optimization (BCO) metaheuristic was developed in

(Davidovi

c et al., 2012) exploring stochastic LPT rule

to construct feasible solutions. (Laha and Gupta,

2018) improved Cuckoo Search Algorithm (CSA)

and explored LPT construction scheme, but included

the pairwise exchange neighborhood in the improve-

ment phase. Grey Wolf Optimiser (GWO) algorithm

in (Kamaraj and Saravanan, 2019) starts from ran-

domly generated population and explores GWO rules

attempting to improve selected subset of solutions.

3 THE PROPOSED HEURISTIC

ALGORITHMS FOR P||C

max

Our approach consists of building heuristics through

transformations that have a potential to improve the

quality of solutions. We present the process of build-

ing the proposed 35 variants of the heuristic algo-

rithms for P||C

max

and discuss their implementation,

including dependence on initial solution and com-

plexity of the implementation. The latter is reduced

by carefully deﬁned solution representation and per-

formed pre-processing. The variants of heuristic algo-

rithms differ by the type of transformation applied to

the given initial solution and by the way initial solu-

tion is obtained. All the variants can be described by

the steps presented in the remainder of this section.

3.1 Description of Transformations

The quality of a solution is deﬁned by C

max

that rep-

resents the execution time of the most heavily loaded

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

260

processor (k). The only way to improve the current

solution is to reduce its load by moving a task to some

other processor l. At the same time, the new load of

the processor l should not exceed the previous C

max

However, constant improvement of the solution qual-

ity could result in undesired outcome: getting stuck

in a local optimum. For P||Cmax, in majority of the

cases, the only way to improve the current solution

is to degrade its quality ﬁrst. Therefore, we deﬁne

stochastic transformations that do not necessarily im-

prove the current solution.

We deﬁne two classes of transformations depend-

ing on selection strategies for reallocation task and

destination processors for them. Transformations are

composed of steps that could be realized in differ-

ent ways, i.e., by performing different actions on

the given input solution. Different actions are coded

by different indicators combined in the input vector

Ind. Even though two classes of transformations have

some similar steps, their number is different, thus

we present two different algorithms. Each algorithm

starts with an initial solution (Sol) and performs the

corresponding transformation as it is deﬁned by the

input parameters from the Ind vector.

First class transformations’ ﬁve steps are in Algo-

rithm 1. First step of each transformation (SProc): the

most heavily loaded processor k is identiﬁed. SProc

is also the source of the task i to be moved.

Algorithm 1: Class 1 transformation.

1 Trans f orm (S ol,Ind)

2 k ← SProc(Sol,Ind)

3 i ← TaskID(Sol,Ind,k)

4 l ← DProc(Sol,Ind,k)

5 Move(Sol,k, i,l)

6 Swap(Sol,Ind, k,l)

7 return(S ol)

The second step (TaskID): selecting the task i

to be moved from processor k. Three different ac-

tions we used to perform it are 1. random selection

(denoted by MR), 2. roulette wheel with the higher

probability to select longer tasks, (marked by MRL),

3. roulette wheel with the higher probability to select

shorter tasks, (denoted by MRS).

The third step (DProc): selecting the destination

processor for task i. The ﬁve different actions are

as follows. The ﬁrst is completely random (DRand),

while the remaining four assume the roulette wheel

application involving a subset of promising proces-

sors and giving the higher probability to the less

loaded processors. In this step the following param-

eters are used: y = min

h∈[1,m]

- load of the least

loaded processor, ˆy - load of the most loaded pro-

cessor k, ¯y - constant deﬁned as average load of all

processors, and LB = d ¯ye - constant deﬁning theoret-

ically the best objective function value of P||C

max

. In

the ﬁrst roulette action (DROpt), the considered sub-

set is composed of the processors with load belong-

ing to the interval [LB,y]. The second (DRYmax)

considers the complete set of processors. The third

(DROpt1) the processor loads are limited by LB + 1

and y, while the corresponding interval for proces-

sor load in the fourth roulette action (DRUpper) is

bounded by d ¯y + 1e and y.

In the fourth step task i is moved from pro-

cessor k to processor l, performed by procedure

Move(Sol,k, i,l). The ﬁfth step, not mandatory, con-

siders the possibility of swapping tasks. More pre-

cisely, for task i that was moved from processor k to

processor l, a number of shorter tasks is reallocated

from l to k, in such a way that the load of k does not

exceed LB value. This process starts with the longest

possible task from processor l that satisﬁes the above

mentioned condition - procedure is performed as long

as possible and denoted as Swap(Sol,Ind, k,l).

Algorithm 2: Class 2 transformation.

1 Trans f orm (S ol,Ind)

2 k ← SProc(Sol,Ind)

3 l ← DProc(Sol,Ind,k)

4 Mix(Sol, k,l)

5 return(S ol)

Second class transformations contain tree steps (Al-

gorithm 2). The ﬁrst is the same as the ﬁrst step in

class 1, while the second is same as the third step in

class 1. In the third step, denoted as Mix(Sol,k,l),

tasks from processors k and l of the current solution

Sol are rearranged in a deterministic way as follows.

First, a subset of tasks with the sum of loads as close

as possible to LB is selected with the knapsack 0-1

algorithm and allocated to processor k. Then the re-

maining tasks are allocated to processors l. Table 1

summarizes both classes transformations notation.

3.2 Complexity Evaluation

To efﬁciently perform the transformations, solutions

are represented by four structures:

• tasksOnProcessor - 2D vector (k,i) representing

index of i-th task scheduled on processor k.

• tasksOnProcessorSet - k-th value of 1D vec-

tor represents set of tasks scheduled to proces-

sor k. The set is balanced binary tree, each

Comparative Analysis of Heuristic Approaches to P||Cmax

261

Table 1: Transformations nomenclature.

Step Action Indicator

SProc() deterministic

TaskID()

random MR

roulette (longest) MRL

roulette (shortes) MRS

DProc()

random DRand

roulette [LB,y] DROpt

roulette [ ˆy,y] DRYmax

roulette [LB + 1, y] DROpt1

roulette [UB( ¯y + 1),y] DRUpper

Move() deterministic

Swap()

NONE

Mix() mix

Table 2: Transformation complexity.

Indicator Time Memory

SProc O(1) O(m)

MR O(1) O(n)

MRL O(1) O(n)

MRS O(1) O(n)

DRand O(1) O(m)

DROpt O(1) O(m)

DRYmax O(1) O(m)

DROpt1 O(1) O(m)

DRUpper O(logm) O(m)

Move O(logn) O(n)

Sw O(nlog n) O(n)

mix O(n · LB + logm) O(n · LB + m)

node is 2-tuple (p

, index of task i in vector

tasksOnProcessor

). The sets are sorted in non-

decreasing order, by p

ﬁrst and then by the sec-

ond value of a tuple.

• processorLoad - 1D vector with k-th value repre-

senting the load of processor with id k. More pre-

cisely, processorLoad

∑

j∈tasksOnProcessor

• processorLoadSet - Set of processors. The set is

a balanced binary tree, where l-th node is 2-tuple

(processorLoad

, id of processor with l-th load).

3.3 Iterative Heuristics Approach

Having all the transformations characterized by ac-

tions taken to transform a solution, we deﬁned 35

heuristic algorithms for P||C

max

. Each heuristic re-

peatedly calls the corresponding transformation to

Algorithm 3: Iterative heuristic.

1 Heuristic (Sol,Ind,StopCrit)

2 BestSol ← Sol

3 while StopCrit is not met do

4 Tr ans f orm (Sol,Ind)

5 if (y(Sol) < y(BestSol)) then

6 BestSol ← Sol

7 end

8 end

9 return BestSol

modify the current solution until the stopping crite-

rion is met. After the transformation is completed,

the quality of the obtained solution is compared to

the best so far and the corresponding update is per-

formed. At the end, the best obtained solution is re-

ported. The main components of our iterative heuris-

tics approach are presented in Algorithm 3. Inputs

to our algorithm are an initial solution Sol, transfor-

mation indicator Ind, and the stopping criterion for

heuristics. The most common stopping criteria are the

maximum number of iterations n

and the maximum

allowed CPU time t

max

4 EXPERIMENTAL EVALUATION

Comparative analysis of our iterative heuristics ap-

proaches is performed in a simulator we built in C++

and compiled with gcc version 7.5.0. All the runs

were performed on Intel(R) Core(TM) i5-6400 CPU

@ 2.70GHz with 8GB RAM under Ubuntu 7.5.0-

3ubuntu1∼18.04. In the remainder of this section we

explain all details of the performed experiments.

4.1 Simulation Environment

In previous section we deﬁned 35 heuristic algorithms

for P||C

max

based on various solution transformations

performed iteratively aiming to lead towards optimal

solution. Due to the stochastic nature of proposed

transformations, all the factors inﬂuencing their vari-

ability need to be explored. We present our heuristic

algorithms effectiveness with respect to solution qual-

ity and convergence, depending on the initial solution

and number of transformations required to reach the

solution of good quality. In addition, we examined

the stability of transformations, i.e., the variations of

results depending on the random number generator

seed value initialization. Our generated testing envi-

ronment is presented in Algorithm 4.

The initial solution we obtained applying the random

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

262

Algorithm 4: Testing environment.

1 Run (n

run

,Ind)

2 for i ← 1 to n

run

3 Seed ← i

4 Sol ← Init ()

5 Heuristic(Sol,Ind,n

)

U pdate(SolBase)

6 end

7 return SolBase

and greedy approaches. The random initial solution is

determined by allocating randomly selected task i to

the randomly selected processor k. Time complexity

of this random procedure is O(nlog n + mlog m). For

greedy algorithm, we selected list scheduling proce-

dure based on LPT rule used for ordering tasks and

Earliest Start (ES) heuristic to determine the most ap-

propriate processor. This implies sorting the jobs in

non-increasing order of processing times before they

are scheduled to the least loaded processor (Graham,

1969; Davidovi

c et al., 2012). LPT+ES constructive

heuristic is in fact an approximation algorithm with

the worst-case approximation ratio 4/3 − 1/(3m). Its

time complexity is O(n log n + n log m) and it is per-

formed in preprocessing phase. Each run starts from

either different random solution or from the same

LPT+ES solution.

Testing Environment. input values for our heuris-

tics are the number of repetitions n

run

(the stopping

criterion of the corresponding test), the number of it-

erations (transformation applied) n

, and the vector

Ind containing indicators which transformation to be

considered. In each run, an initial solution of P||C

max

is generated and then the transformation deﬁned by

the vector Ind is performed repeatedly, until the stop-

ping criterion is satisﬁed, i.e., until n

run

repetitions

are completed. All obtained solutions are saved in

SolBase, together with the required number of trans-

formations and the corresponding running times.

Test Instances. We evaluated the proposed heuris-

tic algorithms on the known set Iogra of hard bench-

mark problem instances with the known optimal value

of the objective function used in (Davidovi

c et al.,

2012). The number of tasks in these instances range

is n ∈ {50, 100, 200,250} and there are 28 instances

in total. Several studies have shown that hardness

of instances increase with increasing the value of

n/m (Mrad and Souayah, 2018), but this doesn’t ap-

ply for Iogra set. In fact, for ﬁxed number of ma-

chines, the hardness of problem instances decreases

as the number of tasks increases. In addition, for ﬁxed

number of tasks the problem instances become harder

as number of machines increases, regardless the de-

crease in n/m. The hardest test instances are with 50

tasks (Jak

c Kr

uger, 2017). Therefore, comparative

analysis of heuristics is depicted on 7 test instances

with 50 tasks.

4.2 Comparative Analysis Methodology

We set n

run

= 100 to repeat algorithm’s execution for

different values of random number generator seed due

to stochastic nature of presented heuristic algorithms.

After each run we record: solution, solution’s qual-

ity, number of iterations and time required to generate

the best (optimal) solution for the ﬁrst time. In order

to capture central tendencies of these results we em-

ploy descriptive statistics such as mean, median and

the corresponding dispersion statistics. The goal is to

gauge the effectiveness of our algorithms, i.e., to esti-

mate an effort needed to reach the optimal solution.

Performance Measures. Due to high efﬁciency of

our algorithms, the dominant performance measure is

number of times the optimal solution is reached (n

opt

)

within n

run

repetitions. Other performance measures:

average solution quality, average or maximal runtime

and the corresponding number of iterations. The aver-

age quality of solutions ¯y

max

is important in case when

the optimal solution is never reached. We also em-

ploy ¯y

max

in graphical representations of our results.

An important concept for our comparison study is the

deﬁnition of poor performance. We deﬁne a trans-

formation’s poor performance if an average quality

of solutions is worse than in case of transformations

that obtained the optimum. Measure of time is im-

portant due to the fact that duration of one iteration

is different w.r.t. to type of transformation. The iter-

ation count may be misleading and overly optimistic

for methods that invoke more work within one itera-

tion. For some transformation A we determine run-

time t

as t

= max

1≥seed≥n

run

seed

, where t

seed

is the

ﬁrst-hit time of the best solution for the given seed.

Stopping Criteria Evaluation. A high value for n

might lead to a better solution quality, but for heuris-

tic approaches it is hard to predict how far from the

optimum we are. The most suitable value for n

when algorithms reach stagnation, i.e., there is no so-

lution improvements anymore. After performing ini-

tial evaluation, we set n

= 10000 as a stopping cri-

terion for empirical analysis of the proposed heuris-

tic algorithms. As each transformation needs differ-

ent time to execute n

iterations, we report the time

required to complete all of them and the number of

iterations required to ﬁnd the best reported solution.

Methodology of Selecting Good Transformations.

Our comparison study of heuristics on Iogra bench-

mark set is based on n

opt

, ¯y

max

, and t

. To represent

Comparative Analysis of Heuristic Approaches to P||Cmax

263

whether optimal solution was found and how often,

our results are two-dimensional scatter plots with n

opt

represented by the size of the circle (see Fig. 1). The

ranking procedure is performed in two phases. The

ﬁrst phase criterion awards the transformations that

reached an optimal solution within n

run

repetitions.

All such transformations are removed from the rank-

ing pool and used to deﬁne the performance of the

remaining transformations. The second phase crite-

rion awards the transformations that have a better av-

erage solution quality than the removed transforma-

tions. Whenever the heuristic algorithm achieves one

of these goals we appoint 1 to its rank. We repeat this

process for all problem instances from Iogra set.

4.3 Results

Selection of Good Heuristics. In Fig. 1 we present

scatter plot for all 70 tested variants (IR random ini-

tial solution, IL greedy initial solution) for problem

instance Iogra50 and variable number of processors.

The position of the point on the graph is determined

by number of iterations needed to either reach opti-

mum or a given average solution. Comparing heuris-

tics grouped by IR and IL, we do not detect signif-

icant changes in the performance w.r.t. average so-

lution quality and average number of iterations indi-

cating that the initial solution does not inﬂuence sig-

niﬁcantly. Obviously, the transformations positioned

at the lower left corner of graphs perform the best.

Then, we clearly demonstrate that transformations de-

picted as points in the upper left region of the plot in

Fig. 1 for instances with m ≥ 6 characterised by small

runtime and low average solution quality performed

the worst. They exhibit premature convergence prop-

erty, reaching their best solution early in the execution

stages and mainly call MRS action. Next, a group

of heuristics at the right parts of the plots in Fig. 1

(mostly Drand with MR or MRL strategies) for m ≥ 4

also performed poorly, due to the fact that the average

required number of iterations is large. Finally, from

the same ﬁgure we see that combination of DRYmax

with MR or MRL strategies perform badly.

Performance Discussion. Good heuristics are ranked

based on their performance on all testing instances.

The largest rank is appointed to all heuristics pre-

sented in Table 3. It contains the results for Iogra50

organized as follows. Each heuristic variant is iden-

tiﬁed by the acronym (ﬁrst column). The indicators

of different initial solution (IR, IL) are in the second

column and the percentage of found optimal solutions

is in the third column. The fourth column contains

¯y

max

. In the last two columns, the average number of

iterations required to obtain the best solution and the

corresponding average CPU times are given. For all

average values, standard deviations are also provided.

From Table 3 we note the following. MRL-

DROpt-Sw and MRL-DROpt1-Sw were not as suc-

cessful in ﬁnding an optimal solution as the other

three methods, but the variability of the results is low

- they produce the best average quality of solutions.

In addition, all heuristics with Mix() step belong to

the so-called good heuristics that produce optimal so-

lutions for Iogra test set in the largest percentage of

runs. Including the action Swap(), signiﬁcantly in-

creases the performance w.r.t. n

opt

. Action DProc() is

the most efﬁcient when combined with actions such

as DROpt and DRUpper.

The initial solution has signiﬁcant inﬂuence in

the case of the last two (MRL-DROpt-Sw and MRL-

DROpt1-Sw) where random initial solutions prevent

reaching the optimal solution. We can note that all

heuristics are very stable in reaching high-quality so-

lutions as the average values of ¯y

max

are close to the

optimums and the standard deviations are small (ex-

cept for heuristics that used Mix() action where in

some sporadic cases the low quality solutions are pro-

vided). Based on the average number of iterations,

it can be concluded that our selected heuristics reach

their best solutions very fast, except in some isolated

cases. This is conﬁrmed by the CPU time data pro-

vided in the last column. Our analysis shows that

the selected heuristics are very fast in providing high-

quality solutions for the hard benchmark instances of

P||C

max

and thus can be an useful tool in more general

frameworks, such as metaheuristics.

5 CONCLUSION

In this paper we proposed several stochastic iterative

heuristic algorithms to efﬁciently deal with the prob-

lem of static scheduling of independent tasks on ho-

mogeneous multiprocessors. We created 35 heuris-

tic algorithms by combining various actions to de-

ﬁne solution transformations aimed at improving so-

lution quality. Testing was performed for 2 variants

of choosing the initial solution which resulted in 70

variants to be tested. We have conducted an extensive

numerical experiments on hard benchmark instances

from the literature. Among the tested 70 variants, we

identiﬁed 10 the best performing heuristics with re-

spect to the solution quality, running time, and stabil-

ity. As the future work we plan to evaluate our heuris-

tics on other sets of test instances and to incorporate

the best performing heuristics in some metaheuristic

frameworks and examine their inﬂuence on the per-

formance of the resulting approaches.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

264

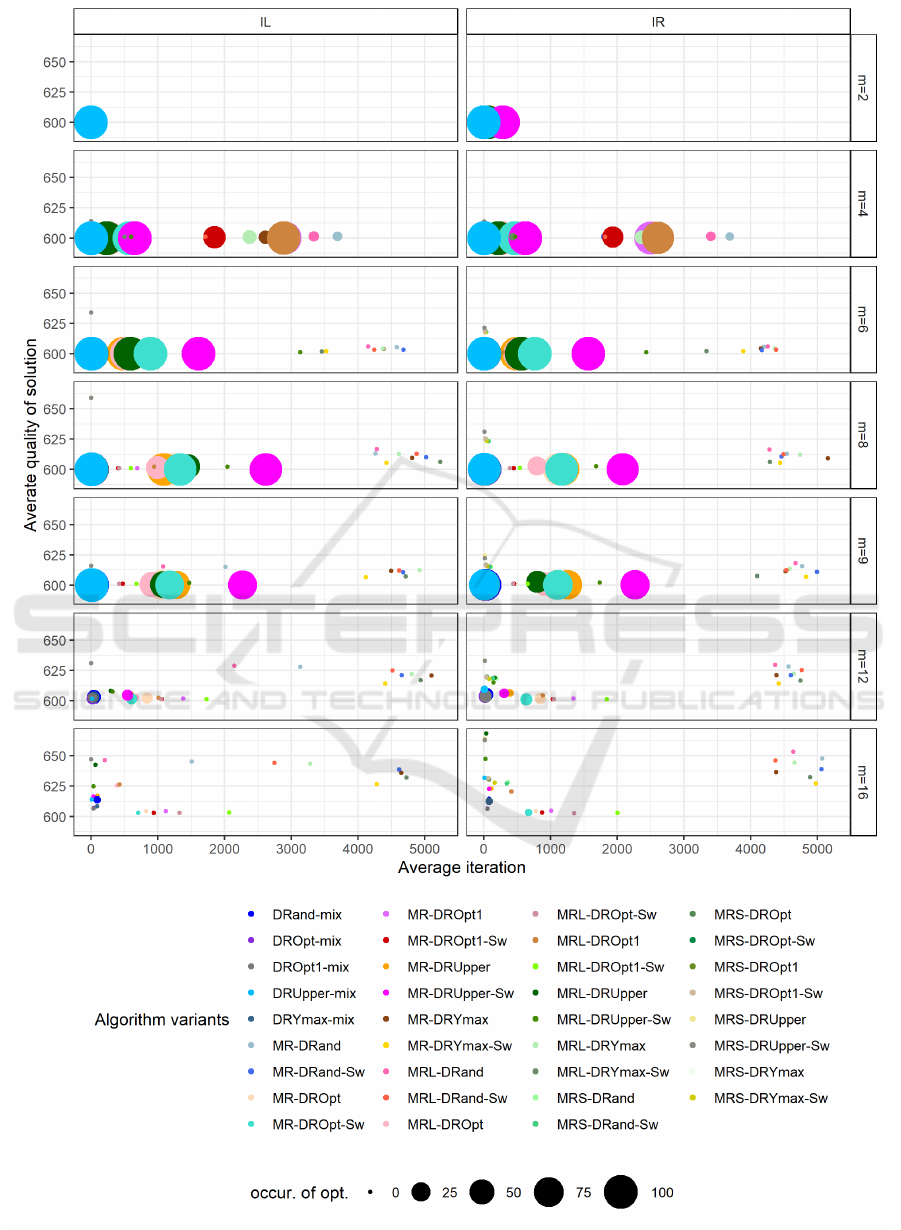
Figure 1: Results of comparisons between 35 transformations on 7 problem instances from Iogra50 set.

Comparative Analysis of Heuristic Approaches to P||Cmax

265

Table 3: 10 best heuristics on Iogra50, m = 2,4, 6,8,9, 12,16. Each average result has the standard deviation.

Heuristic Init() sum.opt[%] ¯y

max

Av. iter Av. t

[10

−3

sec]

DRand-Mix IR 70 602.91 ± 5.57 25.85 ± 27.94 0.90 ± 0.46

IL 71 602.45 ± 5.11 27.69 ± 32.08 0.98 ± 0.86

MR-DROpt-Sw IR 68.4 600.66 ± 1.16 729.38 ± 320.19 2.44 ± 2.13

IL 66.8 600.66 ± 1.08 754.44 ± 439.13 2.80 ± 2.26

DRYmax-Mix IR 68.3 602.47 ± 4.73 23.76 ± 28.53 0.80 ± 0.54

IL 70.7 601.63 ± 3.12 24.41 ± 31.14 0.71 ± 0.57

MRL-DROpt-Sw IR 0.6 601.3 ± 0.63 501.21 ± 509.95 1.59 ± 1.91

IL 14.3 601.20 ± 0.91 499.6 ± 501.94 1.18 ± 1.07

MRL-DROpt1-Sw IR 0.6 601.32 ± 0.69 762.56 ± 830.41 2.63 ± 3.35

IL 14.3 601.23 ± 0.99 771.03 ± 816.83 2.02 ± 2.41

ACKNOWLEDGEMENTS

This work was partially supported by the Science

Fund of Republic of Serbia AI4TrustBC project and

by the Serbian Ministry of Education, Science and

Technological Development, Agreement No. 451-03-

9/2021-14/200029. The authors thank Penn State GV

IT team for the support.

REFERENCES

Alharkan, I. et al. (2018). An order effect of neighborhood

structures in variable neighborhood search algorithm

for minimizing the makespan in an identical parallel

machine scheduling. Math. Problems in Engineering.

Davidovi

c, T. et al. (2012). Bee colony optimization for

scheduling independent tasks to identical processors.

Journal of Heuristics, 18(4):549–569.

Davidovi

c, T. and Jani

cijevi

c, S. (2009). VNS for schedul-

ing independent tasks on identical processor. In Proc.

36th Symp. on Operational Research, SYM-OP-IS

2009,, pages 301–304, Ivanjica.

Della Croce, F. and Scatamacchia, R. (2020). The longest

processing time rule for identical parallel machines re-

visited. Journal of Scheduling, 23(2):163–176.

Fanjul-Peyro, L. and Ruiz, R. (2010). Iterated greedy

local search methods for unrelated parallel machine

scheduling. European Journal of Operational Re-

search, 207(1):55–69.

Frachtenberg, E. and Schwiegelshohn, U. (2010). Pref-

ace. In 15th Internation Workshop, JSSPP 2010, Job

Scheduling Strategies for Parallel Processing, pages

V–VII.

Graham, R. L. (1969). Bounds on multiprocessing timing

anomalies. SIAM journal on Applied Mathematics,

17(2):416–429.

Jak

c Kr

uger, T. (2017). Development, implementation

and theoretical analysis of the bee colony optimiza-

tion meta-heuristic method. PhD thesis, Faculty of

tehnical sciences, University of Novi Sad.

Jansen, K. et al. (2020). Closing the gap for makespan

scheduling via sparsiﬁcation techniques. Mathemat-

ics of Operations Research, 45(4):1371–1392.

Kamaraj, S. and Saravanan, M. (2019). Optimisation of

identical parallel machine scheduling problem. Int.

Journal of Rapid Manufacturing, 8(1-2):123–132.

Laha, D. and Gupta, J. N. (2018). An improved cuckoo

search algorithm for scheduling jobs on identical par-

allel machines. Computers & IE, 126:348–360.

Lawrinenko, A. (2017). Identical parallel machine

scheduling problems: structural patterns, bounding

techniques and solution procedures. PhD thesis,

Friedrich-Schiller-Universit

at Jena.

Mnich, M. and Wiese, A. (2015). Scheduling and ﬁxed-

parameter tractability. Mathematical Programming,

154(1):533–562.

Mokotoff, E. (2004). An exact algorithm for the identical

parallel machine scheduling problem. European Jour-

nal of Operational Research, 152(3):758–769.

Mrad, M. and Souayah, N. (2018). An arc-ﬂow model for

the makespan minimization problem on identical par-

allel machines. IEEE Access, 6:5300–5307.

Paletta, G. and Ruiz-Torres, A. J. (2015). Partial solutions

and multiﬁt algorithm for multiprocessor scheduling.

Journal of Mathematical Modelling and Algorithms in

Operations Research, 14(2):125–143.

Paletta, G. and Vocaturo, F. (2011). A composite algorithm

for multiprocessor scheduling. Journal of Heuristics,

17(3):281–301.

Pinedo, M. L. (2012). Scheduling: theory, algorithms, and

systems. Springer Science & Business Media.

Thesen, A. (1998). Design and evaluation of a tabu search

algorithm for multiprocessor scheduling. J. Heuris-

tics, 4(2):141–160.

Unlu, Y. and Mason, S. J. (2010). Evaluation of mixed in-

teger programming formulations for non-preemptive

parallel machine scheduling problems. Computers &

Industrial Engineering, 58(4):785–800.

Walter, R. and Lawrinenko, A. (2017). Lower bounds and

algorithms for the minimum cardinality bin covering

problem. European Journal of Operational Research,

256(2):392–403.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

266