Two-phase Kernel Search: An Application to Facility Location Problems

with Incompatibilities

Renata Mansini

and Roberto Zanotti

Department of Information Engineering, University of Brescia, Italy

Keywords:

Single-source Capacitated Facility Location Problem, Multi-source Capacitated Facility Location Problem,

Incompatibilities, Kernel Search.

Abstract:

Among the most important variants of the capacitated facility location problem are those introducing side

constraints. In the present paper, we analyze the introduction of incompatibility constraints in the single- and

multi-source capacitated facility location problems. We deal with two different types of conﬂict that concern:

(i) the incompatibility among customers when jointly served by the same facility and (ii) the conﬂict among

facilities. We study their mathematical formulations and solve them by means of a two-phase variant of

the general-purpose framework Kernel Search. The method, evaluated on benchmark instances, shows to be

extremely effective getting better results than Gurobi when solving the models with a time limit of one hour.

Interesting managerial insights are also drawn on optimal solutions, when available.

1 INTRODUCTION

The problem of the facility location and customers as-

signment represents one of the main issues in the or-

ganization of distribution systems in large industrial

companies. The number and relative geographical po-

sition of selected facilities is also strongly related to

the quality of the services provided to customers. Lo-

cation models ﬁnd application in several contexts and

possibly include different side constraints as well as

single- or multi-objective functions. For a classiﬁca-

tion of facility location problems, interested readers

can refer to (Hamacher and Nickel, 1998), (Klose and

Drexl, 2005), and (Fern

andez and Landete, 2015).

In the Single-Source Capacitated Facility Loca-

tion Problem (SSCFLP), a set M = {1, ..., m} of cus-

tomers, each one with a nonnegative demand d

, i ∈

M, has to be served by a set N = 1, ..., n of suppliers

(facilities) in such a way that each customer i ∈ M is

assigned to exactly one facility j ∈ N, satisfying its

whole demand. The total amount of customers’ de-

mand allocated to a facility j cannot exceed its posi-

tive capacity s

, j ∈ N. Without loss of generality, it is

assumed that

∑

j∈N

≥

∑

i∈M

. Each facility j ∈ N

has a set-up cost f

that has to be paid if at least one

customer is served by it. Furthermore, if customer i

https://orcid.org/0000-0002-2194-0339

https://orcid.org/0000-0002-3073-4895

is assigned to facility j a proportional unitary cost c

i j

has to be paid. The problem aims to minimize the to-

tal cost of opening the facilities and supply all the cus-

tomers. The assumption that forces each customer to

be served by exactly one facility (single-source) can

be relaxed by allowing that a customer can be served

by more than one supplier (multi-source).

Despite the extensive literature existing on facility

location problems, very few contributions introduce

conﬂicts. In this paper, we study two different types

of conﬂict, both motivated by real applications: (i) in-

compatibilities among facilities; (ii) incompatibilities

among customers when served by the same facility.

We solve and compare these two different conﬂict-

based formulations by using a new variant of Kernel

Search (KS). The method belongs to the class of the

general purpose methods and can be used to solve

mixed integer linear programming problems. Initially

applied to the multidimensional knapsack problem

(Angelelli et al., 2010) and to a portfolio selection

problem (Angelelli et al., 2012), KS is based on the

sequential solution of restricted problems by means

of a mixed integer programming (MIP) solver. Re-

stricted problems are constructed by selecting prede-

ﬁned subsets of the decision variables while setting

to zero the remaining ones. The method identiﬁes

a set of more promising variables, called kernel set,

and partitions the remaining ones into groups, called

buckets. To construct the kernel set and the buck-

Mansini, R. and Zanotti, R.

Two-phase Kernel Search: An Application to Facility Location Problems with Incompatibilities.

DOI: 10.5220/0011008100003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 105-111

ISBN: 978-989-758-548-7; ISSN: 2184-4372

105

ets, variables are sorted so that the most promising

ones come ﬁrst. A variable is promising when its

likelihood to take a value different from zero in an

optimal integer solution is high. To estimate such a

value the method makes use of information provided

by the Linear Programming (LP) relaxation optimal

solution. The higher the value of a variable in the

LP relaxation, the higher the probability it will take a

positive value in the optimal integer solution as well.

Moreover, variables taking value equal to zero in the

LP relaxation are sorted in non-decreasing order of

their absolute reduced cost values. Restricted prob-

lems are constructed by iteratively considering the

variables in the kernel set plus the variables belong-

ing to the current bucket. When solving a restricted

problem, the variables belonging to the bucket that

are selected in the corresponding solution enter the

kernel set. The rationale is to adaptively change the

kernel set, hopefully identifying all the variables tak-

ing part in the optimal solution. The iterative variant

of the KS allows to work over the sequence of buckets

more than once. At each bucket iteration, the sorting

of variables, the size of the buckets, and the construc-

tion of the kernel set are possibly modiﬁed.

KS has been recently applied in different applica-

tion contexts including vehicle routing (Hanaﬁ et al.,

2020) and knapsack problems (Lamanna et al., 2022).

The main contribution of this paper is the anal-

ysis of facility location problems with conﬂicts and

their solution with a two-phase Kernel Search. Math-

ematical formulations of single- and multi-source ca-

pacitated facility location problems with both types of

incompatibilities are solved on benchmark instances.

The results found by the two-phase KS are compared

with the solutions obtained by solving the mathe-

matical formulations by means of a commercial MIP

solver (Gurobi).

The paper is organized as follows. In Section 2,

we analyze the existing literature on problems with

conﬂicts with a special focus on the facility location

ones. In Section 3, the mathematical formulation of

both single- and multi-source capacitated facility lo-

cation problems along with the introduction of incom-

patibilities constraints are provided. The solution al-

gorithm is presented in Section 4, whereas computa-

tional results on a set of benchmark instances are ana-

lyzed in Section 5. Concluding remarks are provided

in Section 6.

2 LITERATURE REVIEW

Given their practical relevance, facility location prob-

lems have been largely studied in the literature. Sev-

eral solution approaches have been proposed, both

exact and heuristic. For the SSCFLP, several suc-

cessful heuristics have been proposed as in (Ahuja

et al., 2004), (Chen and Ting, 2008), and (Ho, 2015).

A heuristic for large-scale SSCFLP is presented in

(Oliveira et al., 2020). Interesting exact approaches

have also been introduced, such as the Branch-and-

Cut-and-Price presented in (Avella and Boccia, 2009)

or the three-phase cut-and-solve algorithm in (Gade-

gaard et al., 2018). There is also a considerable

body of work on the MSCFLP. For example, we can

mention the application of Benders Decomposition in

(Fischetti et al., 2016), or the new valid inequalities

introduced in (Avella et al., 2021).

Despite the intense research effort devoted to

these problems, their variants taking into account con-

ﬂicts have received a limited attention in the litera-

ture. To the best of our knowledge, only the paper

by (Mar

ın and Pelegr

ın, 2019) deals with incompat-

ibilities in a facility location problem. In particular,

they consider the Uncapacitated Single-Source Facil-

ity Location Problem in which each customer has the

same demand. They reformulate the problem as a

set packing problem and introduce several valid in-

equalities that are exploited in a custom Branch-and-

Cut. In general, incompatibility constraints have re-

ceived a considerable amount of attention in the last

few years, and several examples can be found in the

scientiﬁc literature under different names such as neg-

ative disjunctive constraints, conﬂicts, or exclusion-

ary side constraints. For instance, there are applica-

tions in the context of transportation problems, where

pairs of suppliers are incompatible when serving the

same customer (Goossens and Spieksma, 2009), in

horizontal collaboration among carriers and shippers

where transportation lanes cannot include incompati-

ble goods such as food and chemicals (Colombi et al.,

2017), knapsack problems (Bettinelli et al., 2017),

and max-ﬂow problems (S¸uvak et al., 2020).

3 THE MATHEMATICAL

FORMULATIONS

We ﬁrst introduce the basic SSCFLP and the

MSCFLP and then describe the additional constraints

needed to formulate the incompatibility constraints.

3.1 Basic Formulation

We model the basic SSCFLP by means of two sets of

variables. In the ﬁrst set, binary variable x

i j

, i ∈ M, j ∈

N, is equal to 1 if customer i is assigned to facility j,

and zero otherwise. In the second set, binary variable

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

106

, j ∈ N, takes value equal to 1 if facility j has been

opened and zero otherwise.

(SSCFLP) min

∑

i∈M

∑

j∈N

i j

∑

j∈N

(1)

subject to:

∑

i∈M

i j

≤ s

j ∈ N (2)

∑

j∈N

i j

= 1 i ∈ M (3)

i j

∈ {0, 1} i ∈ M, j ∈ N (4)

∈ {0, 1} j ∈ N (5)

Objective function (1) minimizes the total cost as sum

of set-up and assignment costs, the latter computed by

multiplying the unitary cost for the total quantity re-

quired by a customer, i.e. , c

i j

= c

i j

, i ∈ M, j ∈ N.

Constraints (2) impose that the total demand from

customers assigned to a facility should be lower than

or equal to its capacity. Assignment Constraints (3)

establish that the demand of each customer is supplied

by exactly one facility. The remaining are binary con-

ditions on variables.

To this formulation, one can easily add the follow-

ing valid inequalities:

i j

≤ y

i ∈ M, j ∈ N (6)

∑

j∈N

≥ D j ∈ N (7)

where D =

∑

i∈M

In the multi-source variant, binary variables x

i j

are

substituted with continuous variables X

i j

to specify

quantities assigned by a facility to customers as fol-

lows:

(MSCFLP) min

∑

i∈M

∑

j∈N

i j

∑

j∈N

(8)

subject to:

∑

i∈M

i j

≤ s

j ∈ N (9)

∑

j∈N

i j

≥ d

i ∈ M (10)

i j

≥ 0 i ∈ M, j ∈ N (11)

∈ {0, 1} j ∈ N (12)

It is worth noticing that, given a set of open facili-

ties, the SSCFLP results in a set partitioning problem,

whereas the MSCFLP boils down to a transportation

problem, which can be easily solved to optimality.

3.2 Incompatibility Constraints

Nowadays, many company offer services alongside

produced items (servitization). For example, a manu-

facturer may provide equipment spare parts to cus-

tomers to ease repair and maintenance activities.

There are also more advanced kinds of servitization

that include, for instance, the provision of continu-

ous after-sales services of possibly different nature.

Customers that require advanced services are usually

more demanding than other customers. To guarantee

a high level of customer’s satisfaction, the company

prefers to impose an incompatibility among demand-

ing customers when served by the same facility. We

identify this type of conﬂict as customers incompati-

bility and indicates that, if two customers are incom-

patible, they cannot be jointly served by the same fa-

cility.

There is also another type of conﬂict related to the

geographical position of facilities. If the location of

two plants is quite close, the company might consider

the two facilities as incompatible and decide to open

only one of the two. We call this type of conﬂict fa-

cilities incompatibility.

To model incompatibilities, we deﬁne two con-

ﬂict graphs I = (M, E) with e = (i, k) ∈ E if and

only if customers i and k, i 6= k, are incompatible

and thus cannot be assigned to the same facility and

= (N, E

) with e

= ( j, q) ∈ E

if and only if facil-

ities j and q, j 6= q, are incompatible (too close) and

thus cannot be both opened.

In formulation SSCFLP, customers incompatibil-

ity can be dealt with by adding the following con-

straints:

i j

+ x

k j

≤ 1 (i, k) ∈ E (13)

The corresponding constraints in formulation

MSCFLP require the introduction of an additional set

of binary variables z

i j

, taking value 1 if customer i is

assigned to facility j and zero otherwise, as follows:

i j

≤ d

i j

i ∈ M, j ∈ N (14)

i j

+ z

k j

≤ 1 (i, k) ∈ E (15)

Facilities incompatibility are formalized in both

models SSCFLP and MSCFLP as follows:

+ y

≤ 1 ( j, q) ∈ E

. (16)

4 KERNEL SEARCH

To solve capacitated facility location problems with

incompatibilities, we have implement a solution ap-

proach based on the sequential run of two sepa-

rated KS algorithms (Two-Phase Kernel Search). The

method is partially inspired by the one proposed in

(Lamanna et al., 2022) for the solution of the mul-

tidimensional multiple-choice knapsack problem, but

Two-phase Kernel Search: An Application to Facility Location Problems with Incompatibilities

107

with some relevant differences. In that approach, the

ﬁrst phase of the method solves a KS with the aim to

collect statistics on the solved restricted problems and

use them to dynamically set the parameters value (size

of the buckets, solution time) of the second phase KS.

In our method, the ﬁrst phase is mainly focused on

ﬁnding a good feasible solution rather than in collect-

ing information, whereas the second phase works on

smaller restricted problems to reﬁne the search.

We brieﬂy describe the two phases and their

main features. The pseudocode of Two-Phase Ker-

nel Search is presented in Algorithm 1. In both

phases, the implemented Kernel Search is iterative

since buckets are scrolled more than once. The num-

ber of bucket iterations computed by each KS in the

two phases depends on the total time assigned to each

phase. Given T

max

the total time assigned to the

method as stopping rule, we have decided to allocate

a percentage γ of T

max

to the ﬁrst phase and the re-

maining (1 − γ)T

max

time to the second one.

4.1 First Phase Kernel Search

In this phase, the KS constructs a restricted number

of buckets with a quite large size (b

). Since buckets

are scrolled more than once, at each bucket iteration

their size is reduced by an amount equal to ∆

. More-

over, since restricted problems might be quite large,

a time limit t

is assigned to the solution of each of

them. When creating subproblems by using informa-

tion provided by the optimal solution of the problem

continuous relaxation (SOLVELPRELAXATION), the

method deals separately with the variables associated

with facilities (variables y) with respect to variables

for customers assignment (variables x or X according

to the variant). In particular, procedure BUILDKER-

NELSET constructs the initial kernel set by adding all

y variables, while only the x variables that have been

activated in the optimal solution of the LP relaxation

are included. The remaining x variables are equally

divided among the buckets depending on the facility

they are associated with. More precisely, facilities are

sorted in descending order of the sum of the values

taken by the associated x variables in the LP relax-

ation. All the facilities that have not been selected

in the optimal solution of the LP relaxation are then

sorted in ascending order of reduced costs. Then, a

certain number of x variables for each facility is added

to each bucket depending on the position of the cor-

responding y variable in the ranking. A higher rank-

ing corresponds to more variables added in the initial

buckets, while a low ranking will result in almost no

variables added to the initial buckets. Once the initial

number of variables to be added to the initial bucket is

established, such value linearly increases (decreases)

in the following ones (procedure BUILDBUCKETS).

For example, if we decide to create 5 buckets, the best

positioned facility will have 40% of its x variables in

the ﬁrst bucket, 30% in the second one, and so on,

with no such variables in the last one. The worst po-

sitioned facility will have the opposite distribution.

At Line 14 of Algorithm 1, the current restricted

problem (constructed by eliminating all variables

but those in the current bucket B and in the up-

dated kernel set

Λ) is solved by means of proce-

dure SOLVE(Inst,

Λ∪B, [x

∗

, y

∗

],t) that calls the MIP

solver at hand to ﬁnd an integer solution (possibly the

optimal one) within a time limit equal to t. A cut-

off constraint on the objective function value is also

added to the restricted problem formulation. Such a

cut-off is computed through the incumbent integer so-

lution [x

∗

, y

∗

] received in input. The procedure pro-

vides as output a possibly new incumbent solution

ILP

, y

ILP

] and the set of variables

S belonging to the

current bucket to be added to the kernel set (Line 18).

At each bucket iteration, the kernel set is

updated (see Line 24), by means of procedure

UPDATEKERNELSET, that takes into account the

variables of the best integer solution found so far

([x

∗

, y

∗

]), plus all the variables included in the initial

kernel set (Λ).

Notice that all the time the incumbent integer so-

lution is updated a VARIABLEFIXING procedure tries

to ﬁx at optimality as many variables as possible by

making use of the classical ﬁxing procedures based on

comparing the absolute reduced cost values to the gap

between the optimal continuous relaxation value and

the value of a feasible solution (further details about

these ﬁxing rules can be found in (Mansini and Zan-

otti, 2020)).

4.2 Second Phase Kernel Search

The second phase is focused on reﬁning the search.

The corresponding KS builds double the number of

buckets with respect to the ﬁrst phase. The result-

ing buckets have a smaller bucket size b

and are

increased by ∆

< ∆

at each bucket iteration. The

initial kernel set consists of all the variables corre-

sponding to the incumbent integer solution plus all the

variables included in the initial kernel set of the ﬁrst

phase. In this phase, when a bucket iteration ends, the

kernel set is not updated and keeps all the variables

acquired throughout the iteration.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

108

Algorithm 1: TWO-PHASE KS(Inst, T

max

1: Initialize parameters (b

, ∆

), (b

, ∆

), γ

2: ([x

, y

], r

, z

) ← SOLVELPRELAXATION(Inst)

3: Λ ← BUILDKERNELSET(Inst, [x

, y

], r

)

Λ ← Λ

5: phase

← true

6: T

max

← γ ·T

max

7: (b, ∆, t) ← (b

, ∆

)

8: ([x

∗

, y

∗

], z

∗

S, t

el a psed

) ← SOLVE(Inst, Λ, [

0],t)

9: VARIABLEFIXING(z

∗

, z

, [x

, y

], r

)

10: while t

el a psed

< T

max

11: B ← BUILDBUCKETS(N \

Λ, b)

12: for all B ∈ B do

13: t ← min(t, T

max

−t

el a psed

)

14: ([x

I LP

, y

I LP

], z

I LP

S, t

used

) ← SOLVE(Inst,

Λ ∪B, [x

∗

, y

∗

],t)

15: t

el a psed

← t

el a psed

used

16: if [x

I LP

, y

I LP

] 6= [x

∗

, y

∗

] then

17: ([x

∗

, y

∗

], z

∗

) ← ([x

I LP

, y

I LP

], z

I LP

)

18:

Λ ←

Λ ∪

19: VARIABLEFIXING(z

∗

, z

, [x

, y

], r

)

20: end if

21: end for

22: b ← b + ∆

23: if phase

= true then

24:

Λ ← UPDATEKERNELSET(Λ, [x

∗

, y

∗

])

25: end if

26: if t

el a psed

≥ T

max

and phase

= true then

27: (b, ∆,t) ← (b

, ∆

)

28: phase

← f alse

29: t ← min(t, T

max

−t

el a psed

)

30: ([x

∗

, y

∗

], z

∗

S, t

used

) ← SOLVE(Inst,

Λ, [x

∗

, y

∗

],t)

31: t

el a psed

← t

el a psed

used

32: end if

33: end while

34: return ([x

∗

, y

∗

], z

∗

)

5 COMPUTATIONAL RESULTS

The proposed algorithm has been tested on bench-

mark instances constructed by using the data set

TBED1 deﬁned in (Avella and Boccia, 2009) to which

a conﬂict graph has been added to model incompati-

bilities as in (Mar

ın and Pelegr

ın, 2019). More pre-

cisely, we have taken the ﬁrst 5 instances of the set

i300 consisting of 300 facilities and 300 customers.

The incompatibility graphs I and I

have been gener-

ated by assuming a density equal to 5%.

The two-phase KS has been coded in Java, and

computational results have been run on an Intel i7-

5930K machine running a 64-bit Windows 10 operat-

ing system, 6 cores, and 64GB of RAM. The math-

ematical formulations as well as the restricted prob-

lems in the solution algorithms have been solved by

means of Gurobi 9.1.2.

In the following, we analyze the results obtained

when solving the SSCFLP and the MSCFLP with

both types of incompatibilities. Some interesting in-

sights on the impact of the different type of conﬂicts

on the total costs are drawn by considering the opti-

mal solution of the problems without incompatibili-

ties.

5.1 Single-source CFLP with

Incompatibilities

In Table 1, we show the results obtained by the SS-

CFLP with incompatibilities among customers (C-

INC) and among facilities (F-INC). We compare the

solutions obtained by Gurobi with our Two-phase KS.

The ﬁrst has been running for one hour, whereas the

time limit for the heuristic procedure has been set to

15 minutes. Column ”Obj” reports the objective func-

tion value found by each method, ”#fac” indicates the

number of facilities opened out of the 300 available,

whereas ”ttb” provides the time to best, i.e. the time

required to ﬁnd the solution provided as output. Col-

umn ”gap(%)” provides the optimality gap achieved

by Gurobi, while column ”err(%)” provides the per-

centage error of the solution found by Two-Phase KS

with respect to the solution obtained by Gurobi. A

negative value indicates that our heuristic framework

has been able to ﬁnd a better solution value with re-

spect to Gurobi.

Interesting enough the time to best of Gurobi is

on average quite high and in some cases almost equal

to the CPU time of 1 hour indicating that these are

not easy instances to solve at optimality. On the con-

trary, column ttb for the Two-Phase KS shows that

the method is able to achieve good quality solutions

in a relatively short amount of time, since the average

value stays below 800 seconds. In general, Two-phase

KS is able to improve the solution found by Gurobi

in 8 out of 10 instances. It is quite clear that in-

stances that include F-INC are more difﬁcult to solve

for Gurobi, given the fact that the optimality gap is

relatively large (2.55% on average vs 0.68% in the

C-INC case). Frequently, Two-Phase KS is able to

improve Gurobi’s solution by a considerable margin

(-0.97% on average, which corresponds to hundreds

of units of cost). Interesting enough, in the F-INC

case, the solutions found by Two-phase KS open, on

average, slightly more facilities.

5.2 Multi-source CFLP with

Incompatibilities

Differently from the single-source variant, all the in-

stances for the MSCFLP with both types of incompat-

ibilities have been solved by Gurobi to optimality in a

limited amount of time taking on an average 284 sec-

onds and never more than 454 seconds. In all these in-

Two-phase Kernel Search: An Application to Facility Location Problems with Incompatibilities

109

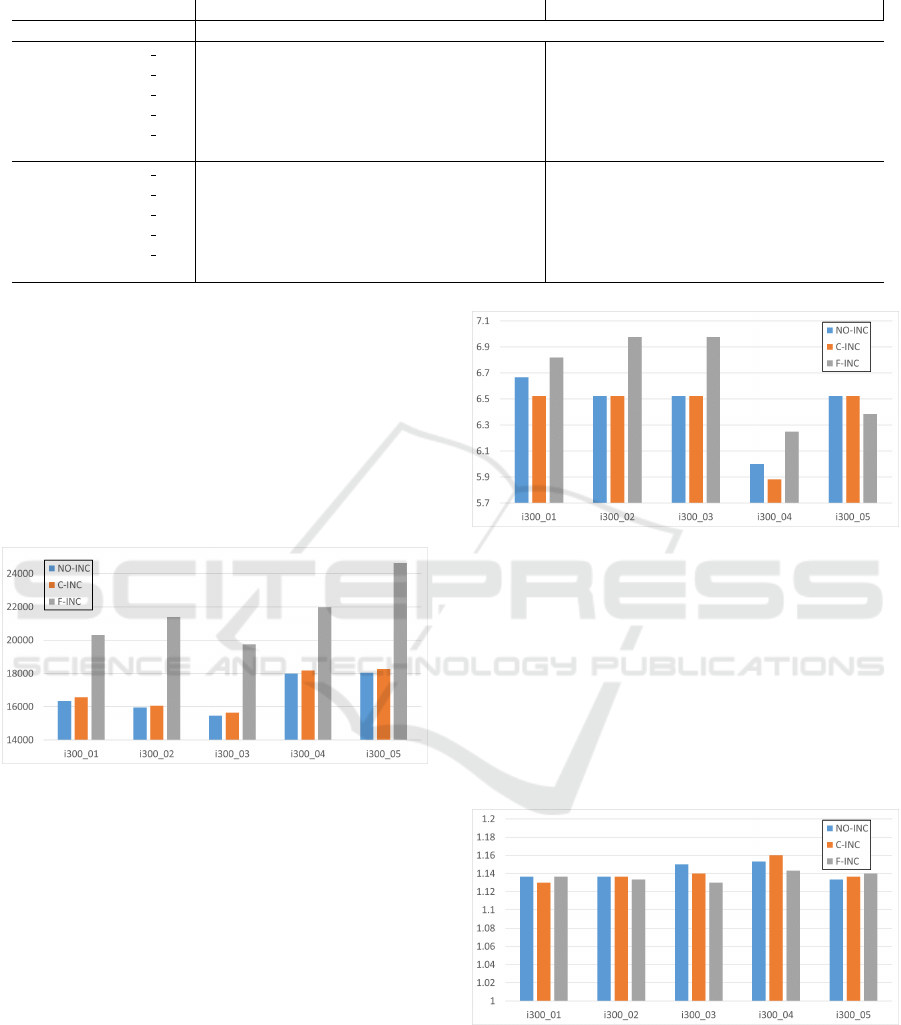
Table 1: Gurobi (1 h) vs. Two-Phase KS (15 min).

Gurobi Two-Phase KS

Variant Instance Obj # fac ttb gap(%) Obj # fac ttb err(%)

C-INC i300 01 16839.29 45 2590 0.52% 16794.99 45 763 -0.26%

i300 02 16362.08 46 1073 0.93 16356.64 46 592 -0.03

i300 03 15878.44 46 3600 0.61 15890.07 46 844 0.07

i300 04 18503.27 52 2240 0.73 18447.75 51 864 -0.30

i300 05 18521.48 46 2708 0.59 18533.73 47 895 0.07

Avg 17220.91 47 2442.2 0.68 17204.64 47 791.6 -0.09

F-INC i300 01 20531.57 41 1002 0.56% 20529.72 42 598 -0.01%

i300 02 22001.72 43 3035 2.88 21586.98 43 754 -1.89

i300 03 20147.43 44 1679 1.66 19935.44 43 781 -1.05

i300 04 22708.38 47 832 2.74 22409.77 48 793 -1.31

i300 05 25459.91 46 3513 4.91 25309.02 47 849 -0.59

Avg 22169.8 44.2 2012.2 2.55 21954.19 44.6 755 -0.97

stances, two-phase KS analyzes only a bunch of buck-

ets in the ﬁrst phase, always ﬁnding the optimal solu-

tion in a computational time reasonably lower than

the one required by the MIP solver.

For this reason, we do not report detailed results

on these computationally easy instances. Neverthe-

less, being all the optimal solutions available, we

can draw some managerial insights on the impact, in

terms of costs, of the presence of conﬂicts.

Figure 1: MSCFLP: Objective function values depending

on the incompatibility type.

Figure 1 shows the optimal objective function

value for each of the ﬁve instances when solving

MSCFLP in the case without incompatibilities (NO-

INC), for C-INC, and for F-INC.

Interesting enough the incompatibilities on the

customers have a limited impact on the solution by

only slightly increasing the total costs. On the con-

trary, incompatibilities among facilities, as expected,

have a signiﬁcant effect on total costs with an average

increase of 28.94%. Solutions without incompatibil-

ities open up, on average, 46.6 facilities out of 300,

whereas such a number reduces to 45 when consider-

ing F-INC.

Figure 2 points out that the average number of cus-

tomers per facility in the NO-INC case is ranging be-

tween 6 and 6.6 and that only slightly reduces (and

not for all instances) when incompatibilities on cus-

Figure 2: MSCFLP: Average number of active customers

per facility.

tomers are introduced. Incompatibility on facilities

seems to have a stronger impact even if the number of

customers per facility never increase over 7.

Figure 3 provides us the number of facilities that

in a multi-source problem serve each customer. It is

evident how such a number is always ranging between

1.12 and 1.16 with no clear pattern or dominance of

one case (NO-INC, C-INC or F-INC) over the others.

Figure 3: MSCFLP: Average number of opened facility per

customer.

6 CONCLUSIONS

Incompatibilities play an important role in many dif-

ferent combinatorial problems. Despite the fact that

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

110

the introduction of conﬂicts has a natural meaning

justiﬁed by several practical applications, the facility

location problems with incompatibilities have found

a limited attention in the literature.

We have studied the introduction of two types

of conﬂicts involving customers when served by the

same facility or among facilities themselves. Such

constraints have been added to both single- and multi-

source capacitated problems.

A two-phase Kernel Search has been implemented

to solve the problems. Its performance has been com-

pared to the exact solutions of the mathematical for-

mulations through the MIP solver Gurobi. Computa-

tional results on benchmark instances, duly modiﬁed

to include conﬂict graphs, show how two-phase KS is

extremely efﬁcient and effective getting, on average,

better solution than the ones found by Gurobi and in

a lower amount of time.

As future developments, we will consider the in-

troduction of a more general concept of incompatibil-

ity and we will analyze the impact in terms of costs

of a joint combination of all considered incompatibil-

ities.

REFERENCES

Ahuja, R. K., Orlin, J. B., Pallottino, S., Scaparra, M. P.,

and Scutell

a, M. G. (2004). A multi-exchange heuris-

tic for the single-source capacitated facility location

problem. Management Science, 50(6):749–760.

Angelelli, E., Mansini, R., and Speranza, M. G. (2010).

Kernel search: A general heuristic for the multi-

dimensional knapsack problem. Computers & Opera-

tions Research, 37(11):2017–2026.

Angelelli, E., Mansini, R., and Speranza, M. G. (2012).

Kernel search: A new heuristic framework for port-

folio selection. Computational Optimization and Ap-

plications, 51(1):345–361.

Avella, P. and Boccia, M. (2009). A cutting plane algorithm

for the capacitated facility location problem. Compu-

tational Optimization and Applications, 43(1):39–65.

Avella, P., Boccia, M., Mattia, S., and Rossi, F. (2021).

Weak ﬂow cover inequalities for the capacitated fa-

cility location problem. European Journal of Opera-

tional Research, 289(2):485–494.

Bettinelli, A., Cacchiani, V., and Malaguti, E. (2017). A

branch-and-bound algorithm for the knapsack prob-

lem with conﬂict graph. INFORMS Journal on Com-

puting, 29(3):457–473.

Chen, C.-H. and Ting, C.-J. (2008). Combining lagrangian

heuristic and ant colony system to solve the single

source capacitated facility location problem. Trans-

portation research part E: logistics and transportation

review, 44(6):1099–1122.

Colombi, M., Corber

an,

A., Mansini, R., Plana, I., and San-

chis, J. M. (2017). The directed proﬁtable rural post-

man problem with incompatibility constraints. Euro-

pean Journal of Operational Research, 261(2):549–

562.

Fern

andez, E. and Landete, M. (2015). Fixed-Charge Fa-

cility Location Problems, pages 47–77. Springer In-

ternational Publishing, Cham.

Fischetti, M., Ljubi

c, I., and Sinnl, M. (2016). Benders

decomposition without separability: A computational

study for capacitated facility location problems. Eu-

ropean Journal of Operational Research, 253(3):557–

569.

Gadegaard, S. L., Klose, A., and Nielsen, L. R. (2018).

An improved cut-and-solve algorithm for the single-

source capacitated facility location problem. EURO

Journal on Computational Optimization, 6(1):1–27.

Goossens, D. and Spieksma, F. C. (2009). The transporta-

tion problem with exclusionary side constraints. 4OR,

7(1):51–60.

Hamacher, H. W. and Nickel, S. (1998). Classiﬁcation of

location models. Location Science, 6(1-4):229–242.

Hanaﬁ, S., Mansini, R., and Zanotti, R. (2020). The multi-

visit team orienteering problem with precedence con-

straints. European journal of operational research,

282(2):515–529.

Ho, S. C. (2015). An iterated tabu search heuristic for

the single source capacitated facility location problem.

Applied Soft Computing, 27:169–178.

Klose, A. and Drexl, A. (2005). Facility location models

for distribution system design. European journal of

operational research, 162(1):4–29.

Lamanna, L., Mansini, R., and Zanotti, R. (2022). A two-

phase kernel search variant for the multidimensional

multiple-choice knapsack problem. European Journal

of Operational Research, 297(1):53–65.

Mansini, R. and Zanotti, R. (2020). A core-based exact

algorithm for the multidimensional multiple choice

knapsack problem. INFORMS Journal on Computing,

32(4):1061–1079.

Mar

ın, A. and Pelegr

ın, M. (2019). Adding incompatibil-

ities to the simple plant location problem: Formula-

tion, facets and computational experience. Computers

& Operations Research, 104:174–190.

Oliveira,

O., Matos, T., and Gamboa, D. (2020). A ramp

algorithm for large-scale single source capacitated fa-

cility location problems. In Matsatsinis, N. F., Mari-

nakis, Y., and Pardalos, P., editors, Learning and Intel-

ligent Optimization, pages 171–183, Cham. Springer

International Publishing.

S¸uvak, Z., Altınel,

I. K., and Aras, N. (2020). Exact solu-

tion algorithms for the maximum ﬂow problem with

additional conﬂict constraints. European Journal of

Operational Research, 287(2):410–437.

Two-phase Kernel Search: An Application to Facility Location Problems with Incompatibilities

111