ContourVerifier: A Novel System for the Robustness Evaluation of Deep
Contour Classifiers
Rania Khalsi
1
, Mallek Mziou Sallami
2
, Imen Smati
1
and Faouzi Ghorbel
1
1
CRISTAL Laboratory, GRIFT Research Group, Ecole Nationale des Sciences de l’Informatique (ENSI),
La Manouba University, 2010, La Manouba, Tunisia
2
CEA, Evry, France
Keywords:
Contours Classification, Abstract Interpretation, DNN Geometric Robustness, Uncertainty in AI.
Abstract:
DNN certification using abstract interpretation often deals with image-type data, and subsequently evaluates
the robustness of the deep classifiers against disturbances on the images such as geometric transformations,
occlusion and convolutional noises by modeling them as an abstract domain. In this paper, we propose Con-
tourVerifier, a new system for the evaluation of contour classifiers as we have formulated the abstract domains
generated by rigid displacements on contours. This formulation allowed us to estimate the robustness of
deep classifiers with different architectures and on different databases. This work will serve as a fundamental
building block for the certification of deep models developed for shape recognition.
1 INTRODUCTION
Deep neural networks have been widely used in vari-
ous applications fields. Recently, they have been em-
bedded in safety critical systems such as autonomous
driving (Bojarski et al., 2016), (Li et al., 2021), colli-
sion avoidance systems (Julian et al., 2016) and med-
ical image analysis (Shen et al., 2017). Despite their
widespread use, these methods are not yet trusted to
perform reliably and as expected for making critical
decisions. For example, it has been proven by (Good-
fellow et al., 2014) that neural networks are sensitive
to small perturbations and exhibit non-robust conduct
at times. For instance, two very similar inputs with
a dissimilarity in a single pixel or brightness could
result in different labels. This is due to their insta-
bility. So, it is often necessary to evaluate the ro-
bustness of Deep Neural Networks. To address this
need, many DNN verification systems have been pro-
posed in the last few years. They can be categorized
as either complete verifiers (Ehlers, 2017; Katz et al.,
2017; Tjeng et al., 2017; Wang et al., 2018b) or in-
complete verifiers (Dvijotham et al., 2018; Raghu-
nathan et al., 2018; Gehr et al., 2018) according to
whether the verification may or may not result in a
false positive. To choose between the two classes of
methods, a compromise between completeness and
scalability must be considered. In spite of this, the
community still lacks an analyzer that supports multi-
ple architectures with distinct types of activation and
different input formats. Indeed, most of the proposed
methods deal with image type data. However, sev-
eral DNN-based solutions have been proposed for the
shape classification (Droby and El-Sana, 2020), (Lu
et al., 2021)(Abeßer and M
¨
uller, 2019). Therefore,
it turns out to be useful to study the robustness of
deep contour classifiers. These latter can be disturbed
mainly by geometrical transformations unlike image
classifier whose brightness can be also perturbed. In
this paper, the focus is on the evaluation of robustness
of deep contour classifiers under euclidean transfor-
mations and for this, we use the theory of abstract in-
terpretation. Consequently, we have defined a new ab-
stract domain of contours type data in the case of ro-
tation and translation. Figure 1 presents the designed
system to verify the robustness propriety. The remain-
der of this paper is organised as follows: In the next
section, some related works are presented including
neural networks verification and the theory of abstract
interpretations. We describe ContourVerifier, our pro-
posed method in section 3 and define the Lower and
Upper bounds in the case of 2D contour translation
and rotation. In sections 4 and 5 the experimental set-
tings and results are presented and finally, a conclu-
sion at section 6.
Khalsi, R., Sallami, M., Smati, I. and Ghorbel, F.
ContourVerifier: A Novel System for the Robustness Evaluation of Deep Contour Classifiers.
DOI: 10.5220/0010994500003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 1003-1010
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
1003

Figure 1: ContourVerifier robustness analyzer for deep con-
tour classifiers.
2 BACKGROUND AND RELATED
WORKS
In the past few years, DNN verification topics have
been explored and researched extensively. Among
the well-known frameworks, we cite Reluplex (Katz
et al., 2017), PLANET (Bunel et al., 2018), ERAN
(Singh et al., 2018a), DeepPoly (Singh et al., 2019b),
DeepSymbol (Li et al., 2019), DeepG (Balunovic
et al., 2019) and PRODeep (Li et al., 2020). Using lin-
ear programming (Tjeng et al., 2017), linear approx-
imations (Weng et al., 2018) or abstract interpreta-
tion(Singh et al., 2019a), (Singh et al., 2018a), (Singh
et al., 2019c), formal approaches are the key techni-
cal insight behind the majority of those NN verifica-
tion’s system. The effectiveness of this class of meth-
ods has been proved through several research projects.
However, despite progress there remains serious chal-
lenges, not least in terms of supporting more NN ar-
chitectures, input format and increase the application
scope to real-world problems. In table 1, we list some
verifiers dealing with different data formats. While
there has been considerable interest in certifying the
robustness of image data type network classifiers, less
attention has been given to other models input types.
The most common used image datasets are MNIST
and CIFAR10. On the other hand, few verifiers deal
with audio datasets and among these methods, we cite
RnnVerif, Propagated-output Quantified Robustness
for RNNs (POPQORN) and Polyhedral Robustness
Verifier of RNNs (Prover). To the best of our knowl-
edge, there is no previous work done on evaluating
the robustness of deep 2D planar closed contour clas-
sifiers. As a result, we propose ContourVerifier, based
on the abstract interpretation.
2.1 Abstract Interpretations for Neural
Network Certification
The abstract interpretation (Cousot and Cousot, 1977)
is a general theory that allows the approximation of a
potentially infinite set of behaviors with a finite repre-
sentation. This theory has been widely used over the
last decades to build large-scale automatic code ana-
lyzers (Blanchet et al., 2003). Analyzers in fact are
verification tools whose common point is the predic-
tion of disturbed input model using an approximate
neural network behavior. The formulation of neural
network verification problem is as follow:
Let denote by R
¯
X,ε
the original inputs
¯
X perturbed by
ε. Verifying the robustness property for R
¯
X,ε
is check-
ing the property over the whole possible perturbation
of
¯
X.
Let C
L
be the set of outputs having the same label L.
¯
Y denotes the set of each prediction for each element
in R
¯
X,ε
.
C
L
= { ¯y ∈
¯
Y |argmax ¯y
i
= L} (1)
The (R
¯
X,ε
,C
L
) robustness property is verified only if
the outputs O
R
of R
¯
X,ε
are included in C
L
. However,
we have no knowledge about O
R
since we cannot con-
trol the behaviour of hidden layers. By considering a
new abstract domains α
R
, which is an abstraction of
¯
X, the (R
¯
X,ε
,C
L
) property is checked:
• If the outputs O
R
of R
¯
X,ε
are included in C
L
.
• If the outputs α
O
R
of α
R
(the abstraction of R
¯
X,ε
)
are included in C
L
.
2.2 Lower and Upper Bound for
Contrast and Geometrical Attacks
(Henry, 2014) defines the upper and lower bounds as
the longest execution time in the case of abstract inter-
pretation for computer science. In AI2, (Gehr et al.,
2018) defines the lower bound (LB) and upper bound
(UB) as the limits of the disturbance. For instance, if
the image brightness is perturbed, the (LB) represents
the minimum brightness value and (UB) is the maxi-
mum brightness value. The LB and the UB enable the
definition of abstract intervals. If we apply a 2D rota-
tion to the image, the contribution of the neighboring
pixels to the intensity of the perturbed pixel is pro-
portional to the distance from the initial pixel. This
approximation enables the estimation of the possible
LB and UB. Together, they give us the polyhedron
where each rotated pixel is going to end.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
1004

Table 1: Examples of state of the art verifiers dealing with different dataset formats.
Verifier Dataset Dataset type References
Verifier with constraints MNIST, CIFAR10
image (Bastani et al., 2016)
Planet MNIST image (Ehlers, 2017)
Reluplex
MNIST
Drebin
image
Multidimensional vector
(Katz et al., 2017)
MIPVerify
MNIST, CIFAR10
image (Tjeng et al., 2017)
Neurify
MNIST
Drebin
image
Multidimensional vector
(Wang et al., 2018a),(Henriksen and Lomuscio, 2020)
DeepZono
MNIST, CIFAR10
image (Singh et al., 2018a)
RefineZono
MNIST, CIFAR10
image (Singh et al., 2018b)
RefinePoly
MNIST, CIFAR10
image (Singh et al., 2019a)
DeepPoly
MNIST, CIFAR10
image
(Singh et al., 2019b),(Henriksen and Lomuscio, 2020)
VeriNet CIFAR10 image (Henriksen and Lomuscio, 2020)
POPQORN MNIST sequence dataset (Ko et al., 2019)
RnnVerif VCTK speech data (Jacoby et al., 2020)
DNN Robustness Guarantees on videos
UCF101 video dataset (Wu and Kwiatkowska, 2020)
Prover
FSDD
GSC v2
MNIST
0
audio/speech dataset
audio/speech dataset
Flatten each image into
one dimensional vector
(Ryou et al., 2021)
3 PROPOSED METHOD
The existing state of the art methods for the evaluation
of deep neural network classifiers are almost designed
for models with image type input. In this research,
we introduce ContourVerifier, a new ERAN-based ap-
proach for deep contour classifiers verification.
3.1 Lower and Upper Bound in the
Case of Translation
For a given contour C and a fixed batch size
Batch size, we define in algorithm 1 the UB and LB
respectively denoted by T
fU
and T
f L
to verify if ev-
ery contour, even perturbed by a given translation in
I = [a, b], is yet well classified or not. In fact, we do
not use the entire interval I as it is. However, we use a
partitioning technique combined with batching in or-
der to refine the UB and LB. By subdividing I into
several segments [δ1,δ2], we obtain precise intervals.
Hence, for each point of the contour, T
f L
corresponds
to the minimum value of all previous translated con-
tours and T
fU
is the maximum value of all previous
translated contours. The contour C could be trans-
lated along the x axis, y axis or both at the same time.
However, in the interests of simplification, algorithm
1 illustrates only translation along the x axis such as
the example presented in figure 2 (a) where I is set to
be [100,200].
3.2 Contours Lower and Upper Bound
in the Case of Rotation
For determining the upper and lower bounds, we con-
sider rotating the input noted by C with θ ∈ [α,β].
For this purpose, in algorithm 2, we start by convert-
ing the euclidean coordinates C
x
and C
y
of the contour
into polar coordinates (r,φ). where:
r =
p
x
2
+ y
2
(2)
And φ, in ]–π,π[, is obtained via the following for-
mula:
φ = 2 arctan
y
x +
p
x
2
+ y
2
(3)
Using the polar coordinates, we perform a rotation
with angles θ
1
and θ
2
respectively ∈ [α, β]. Next, we
reconvert the found rotated contours R C with θ1 and
R C with θ2 from Polar to Cartesian representation
and denote them C
φ
1
and C
φ
2
whose x and y coordi-
nates are obtained as follow:
x = r cosφ, y = r sinφ (4)
Let denote by T
LB
and T
UB
respectively the minimum
and the maximum of C
φ
1
and C
φ
2
. They are used for
initializing T
f L
and T
fU
for the first iteration. Next,
LB corresponds to the minimum between T
LB
and T
f L
and UB corresponds to the maximum value between
T
UB
and T
fU
.
4 EXPERIMENTAL SETTINGS
In this section, we present our experimental settings
including the used contour datasets and the imple-
mentation environment.
4.1 Datasets Description
We carry out our experiments based on two contours
datasets, the first is MPEG7 existing contour dataset
ContourVerifier: A Novel System for the Robustness Evaluation of Deep Contour Classifiers
1005

a b
Figure 2: UB and LB: a. Translation UB and LB in [100, 200] b. Rotation UB and LB with θ ∈ [
π
6
,
π
3
].
Algorithm 1: Lower & Upper Bound Translate Contour
with Batchsize.
procedure UB LB CONTOUR TRANSLATION
Input:
C ∈ 1 × dim
C
; p
c
; Batch size ∈ N;a, b
step =
(|b−a|)
Batch size
for k ∈ {0,Batch size} do
δ1 = a + k × step
δ2 = a + (k + 1) × step
T C with δ1
T C with δ2
T
LB
= min(T C with δ1, T C with δ2)
T
UB
= max(T C with δ1, T C with δ2)
if k = 0 then
T
f L
= T
LB
T
fU
= T
UB
else
T
f L
← min(T
LB
,T
f L
)
T
fU
← max(T
UB
,T
fU
)
end if
end for
Return T
f L
,T
fU
end procedure
and the second is a contour dataset generated from
MNIST numbers using a mathematical morphology
based algorithm.
1. MPEG-7 shape dataset consists of 70 types of ob-
ject contours, each having 20 different shapes, for
a total of 1400 shapes. The database is challeng-
ing due to the presence of examples that are visu-
ally dissimilar from other members of their class
and examples that are highly similar to members
of other classes.
2. MNIST shape dataset of handwritten digits (Le-
Cun, 1998; LeCun et al., 1998) is a sub-set of
a larger set available from MNIST. It contains
70000 samples divided into training set (60000
samples) and test set (10000 contours). 500 con-
tours are utilized for robustness test.
Algorithm 2: Lower & Upper Bound Rotate Contour with
Batchsize.
procedure ROTATION UB LB CONTOUR
Input: C ∈ 1 × dim
C
; α,β; Batch size ∈ N;
φ,r = cart2pol(C
x
,C
y
)
 convert Cartesian coordinates to Polar coordi-
nates
step =
|β−α|
Batch size
for k ∈ {0,. . . , Batch size}; do
θ
1
= α + k× step
θ
2
= α + (k +1)× step
C
φ1
= pol2cart(R C with θ
1
)
C
φ2
= pol2cart(R C with θ
2
)
T
LB
= min(C
φ1
,C
φ2
)
T
UB
= max(C
φ1
,C
φ2
)
if k = 0 then
T
f L
= T
LB
T
fU
= T
UB
else
T
f L
← min(T
LB
,T
f L
)
T
fU
← max(T
UB
,T
fU
)
end if
end for
Return T
f L
,T
fU
end procedure
Figure 3: MPEG7 Dataset: On the top some samples from
MPEG7 image dataset; On the bottom the corresponding
contour.
4.2 Datasets Processing
In this work, we assume that contours are represented
by their x and y Cartesian coordinates. We pro-
pose to re-parametrize them using the arc-length re-
parameterization given by formula 5. We suggest set-
ting the number of points to 120 points for the inves-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
1006

Table 2: Different deep neural network architectures for MPEG7 and MNIST contours classification.
Dataset Model Type #Units #Layers Accuracy
Contours Mpeg7 3 × 100 fully connected 51,471 3 61.42%
3 × 150 fully connected 92,171 3 65.23%
6 × 100 fully connected 81,771 6 66.19%
1 Conv Convolutional 41,402 4 70%
1Conv MaxPool Convolutional 51,502 5 70.5%
2 Conv1 MaxPool Convolutional 65,408 5 74.5%
3 Conv Convolutional 41,436 6 73.8%
Contours MNIST 3 × 100 fully connected 45,310 3 94.03%
3 × 150 fully connected 45,310 3 93.97%
6 × 100 fully connected 75,610 6 93.96%
1 Conv Convolutional 35,213 4 92.4%
1 Conv MaxPool Convolutional 45,341 5 93.7%
2 Conv1 MaxPool Convolutional 35,244 5 85.7%
3 Conv Convolutional 35,247 6 94.66%
Figure 4: MNIST Dataset: On the top some samples from
the MNIST image datest; On the bottom corresponding
MNIST contour dataset.
tigated datasets.
s(t) = 1/L
Z
q
x
t
(u)
2
+ y
t
(u)
2
du,t ∈ [0, 1] (5)
Where L represents the total length of the contour.
4.3 Implementation
We use Python for the implementation of the abstract
domain in both cases: translation and rotation. As
abstract interpretation analyzer, we use DeepPoly so-
lution. It is based on two main libraries: ERAN and
ELINA, coded in respectively Python and C program-
ming languages. The pretrained models presented
in table 2 are implemented, where fully-connected
layers and convolutional models are evaluated using
MNIST and MPEG7 datasets. We measure the ro-
bustness of these models and compare the obtained
results in section 5. This criterion is calculated as the
number of verified contours over the total number of
well classified instances by the neural network. The
robustness metric is set to:
Robustness =
Verified contours
Well classified contours
(6)
5 RESULTS
The introduced DeepPoly analyser adapted for mea-
suring the robustness of deep contour classifiers uses
the abstract interpretation through UB and LB intro-
duced in sections 3.1 and 3.2. It takes as input the dif-
ferent contours described in section 4.1 and processed
as mentioned in section 4.2 as well as the different
models detailed in table 2. Hence, we measure the ro-
bustness of these models in presence of two studied
attacks: rotation and translation. We consider rota-
tion intervals of 3° and translation intervals of 0.01
along the x axis. This choice of such little intervals is
justified by the fact that the contours in our study are
normalised during the training process. Using ERAN
for computing the robustness values in presence of
each attack with (batch size = 100), we obtain Figure
6 (resp Figure 7) that shows an example of robust-
ness variation function computed using equation 6 on
MPEG7 dataset (resp MNIST dataset) in case of rota-
tion and translation attacks. The results of the Mpeg7
data show that the 2Conv Maxpool model is more ro-
bust against rotation and translation attacks while the
f ully connected 6 × 100 model is the most vulnera-
ble. Often convolutional models are more robust than
f ully connected because such models contain a fea-
tures extraction block. This block gradually extracts
invariants which makes it possible to describe each
input so that it is subsequently classified through the
fully connected part.
Figure 7 shows the results obtained on MNIST
contours. The model with a single convolutional layer
is more robust against geometric translation and ro-
tation attacks. However, f ully connected 6 × 100,
f ullly connected 3 × 150 are the most vulnerable
against rotation. We notice that the convolutional
models are more robust for the two types of attacks
on the MNIST contours. In this case, the translation
attack is stronger than the rotation, indeed the robust-
ness decreases more quickly in the case of translation.
Models trained on MNIST contours are more resistant
against rotation. This may be due to the fact that the
ContourVerifier: A Novel System for the Robustness Evaluation of Deep Contour Classifiers
1007

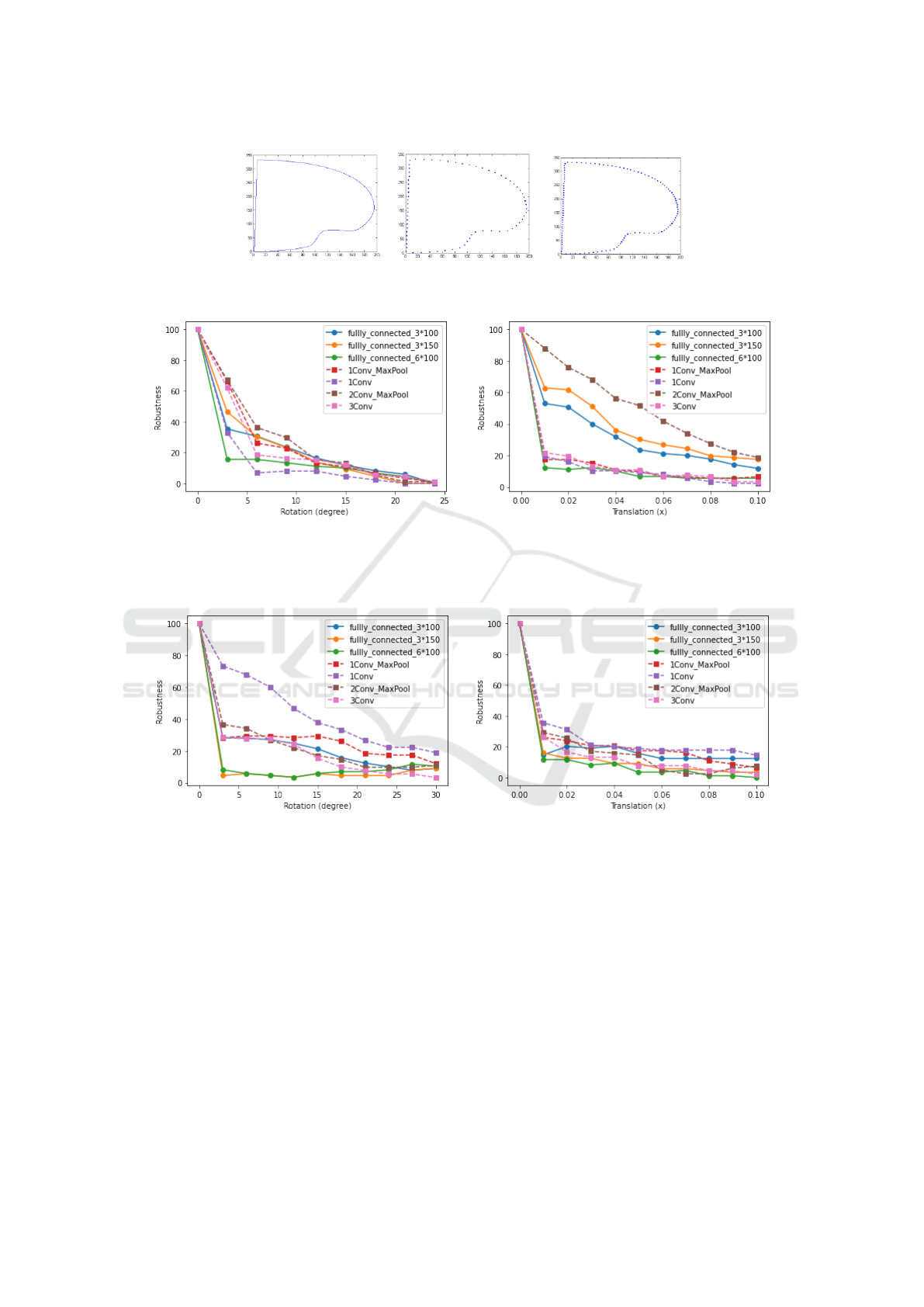
Figure 5: Contour arc-length re-parameterization. (a) Extracted contour from a shape that belongs to MPEG7 dataset. (b,c)
Contour arc-length re-parameterization with respectively 70 points and 120 points.
a b
Figure 6: a) Robustness variation according to the rotation computed on 100 contours from MPEG7 contour dataset with
different models. b) Robustness variation according to the translation computed on 100 contours from MPEG7 contour
dataset with different models.
a b
Figure 7: a) Robustness variation according to the rotation computed on 500 contours from MNIST contour dataset with
different models. b) Robustness variation aaccording to the translation computed on 500 contours from MNIST contour
dataset with different models.
shapes in the database already have different orien-
tations. There exists an infinity of possible models,
our objective is not to test them all or find the most
robust one in case of contour classification; We aim
through the models given by table 2 to test our verifi-
cation system. We conclude that the robustness varies
as a function of the attack and it is not necessarily
correlated with the model accuracy (Performance). In
figure 8, we present these two metrics for different
models tested on MPEG7 and MNIST datasets. The
last two bars on the right show respectively the accu-
racy (in blue) and the robustness (in orange) of a deep
neural network containing six layers each composed
of one hundred neurons. The model is trained and
tested on contours from MNIST dataset in presence
of a rotation attack in the interval [0°,3°]. Despite the
height of the accuracy which reached 93.96% , the
model robustness is equal to 8.14%. Even Though
this model performs well in terms of accuracy, it has
a low robustness. To sum up, the evaluation of con-
tour classifiers based on deep neural nets must take in
consideration both metrics: accuracy and robustness.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
1008

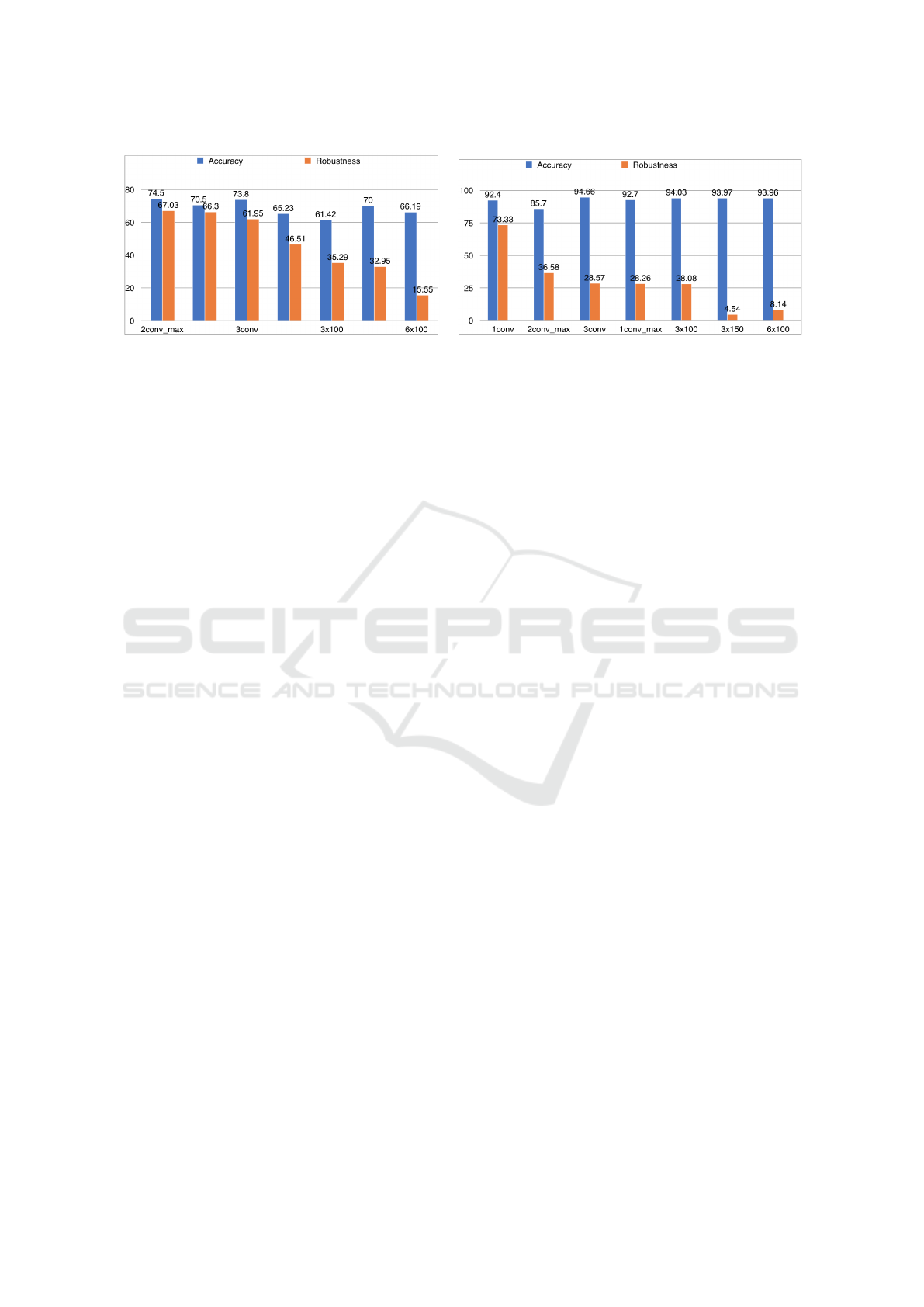
a b
Figure 8: a) Accuracy & Robustness variation (%) as a function of rotation attack of [0°,3°] tested on contours from MPEG7
dataset with different models. b) Accuracy & Robustness variation (%) as a function of rotation attack of [0°,3°] tested on
contours from MNIST contour dataset with different models.
6 CONCLUSIONS
This paper presents ContourVerifier: a novel system
for the robustness evaluation of deep contour classi-
fiers. Unlike the existing methods which deal with
only image, video, time series or audio data types,
our approach enables the verification of deep clas-
sifiers designed for shape recognition and consider-
ing contour information as a 2D closed planar shape.
We define the appropriate Upper and Lower bounds
of the shape perturbed with a translation or rotation.
Given this abstract domain, and a set of test contours,
ContourVerifier computes the robustness value of the
given pre-trained model using DeepPoly analyser. As
an initial step, we have considered rigid transforma-
tions of the contours. In further work, we aim to
extend ContourVerifier to support more perturbations
such as nonlinear and projective transformations.
REFERENCES
Abeßer, J. and M
¨
uller, M. (2019). Fundamental frequency
contour classification: A comparison between hand-
crafted and cnn-based features. In ICASSP 2019-
2019 IEEE International Conference on Acoustics,
Speech and Signal Processing (ICASSP), pages 486–
490. IEEE.
Balunovic, M., Baader, M., Singh, G., Gehr, T., and Vechev,
M. (2019). Certifying geometric robustness of neural
networks. In Advances in Neural Information Pro-
cessing Systems, pages 15313–15323.
Bastani, O., Ioannou, Y., Lampropoulos, L., Vytiniotis, D.,
Nori, A., and Criminisi, A. (2016). Measuring neural
net robustness with constraints. Advances in neural
information processing systems, 29:2613–2621.
Blanchet, B., Cousot, P., Cousot, R., Feret, J., Mauborgne,
L., Min
´
e, A., Monniaux, D., and Rival, X. (2003). A
static analyzer for large safety-critical software. In
Proceedings of the ACM SIGPLAN 2003 conference
on Programming language design and implementa-
tion, pages 196–207.
Bojarski, M., Del Testa, D., Dworakowski, D., Firner,
B., Flepp, B., Goyal, P., Jackel, L. D., Monfort,
M., Muller, U., Zhang, J., et al. (2016). End to
end learning for self-driving cars. arXiv preprint
arXiv:1604.07316.
Bunel, R. R., Turkaslan, I., Torr, P., Kohli, P., and
Mudigonda, P. K. (2018). A unified view of piece-
wise linear neural network verification. In Advances in
Neural Information Processing Systems, pages 4790–
4799.
Cousot, P. and Cousot, R. (1977). Abstract interpretation:
a unified lattice model for static analysis of programs
by construction or approximation of fixpoints. In Pro-
ceedings of the 4th ACM SIGACT-SIGPLAN sympo-
sium on Principles of programming languages, pages
238–252.
Droby, A. and El-Sana, J. (2020). Contourcnn: convolu-
tional neural network for contour data classification.
arXiv preprint arXiv:2009.09412.
Dvijotham, K., Stanforth, R., Gowal, S., Mann, T. A., and
Kohli, P. (2018). A dual approach to scalable verifica-
tion of deep networks. In UAI, volume 1, page 3.
Ehlers, R. (2017). Formal verification of piece-wise linear
feed-forward neural networks. In International Sym-
posium on Automated Technology for Verification and
Analysis, pages 269–286. Springer.
Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,
Chaudhuri, S., and Vechev, M. (2018). Ai2: Safety
and robustness certification of neural networks with
abstract interpretation. In 2018 IEEE Symposium on
Security and Privacy (SP), pages 3–18. IEEE.
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2014). Ex-
plaining and harnessing adversarial examples. arXiv
preprint arXiv:1412.6572.
Henriksen, P. and Lomuscio, A. (2020). Efficient neural
network verification via adaptive refinement and ad-
versarial search. In ECAI 2020, pages 2513–2520.
IOS Press.
ContourVerifier: A Novel System for the Robustness Evaluation of Deep Contour Classifiers
1009

Henry, J. (2014). Static Analysis by Abstract Interpretation
and Decision Procedures. PhD thesis, Universit
´
e de
Grenoble.
Jacoby, Y., Barrett, C., and Katz, G. (2020). Verifying recur-
rent neural networks using invariant inference. In In-
ternational Symposium on Automated Technology for
Verification and Analysis, pages 57–74. Springer.
Julian, K. D., Lopez, J., Brush, J. S., Owen, M. P., and
Kochenderfer, M. J. (2016). Policy compression
for aircraft collision avoidance systems. In 2016
IEEE/AIAA 35th Digital Avionics Systems Conference
(DASC), pages 1–10. IEEE.
Katz, G., Barrett, C., Dill, D. L., Julian, K., and Kochender-
fer, M. J. (2017). Reluplex: An efficient smt solver for
verifying deep neural networks. In International Con-
ference on Computer Aided Verification, pages 97–
117. Springer.
Ko, C.-Y., Lyu, Z., Weng, L., Daniel, L., Wong, N., and Lin,
D. (2019). Popqorn: Quantifying robustness of recur-
rent neural networks. In International Conference on
Machine Learning, pages 3468–3477. PMLR.
LeCun, Y. (1998). The mnist database of handwritten digits.
http://yann. lecun. com/exdb/mnist/.
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P., et al. (1998).
Gradient-based learning applied to document recogni-
tion. Proceedings of the IEEE, 86(11):2278–2324.
Li, G., Yang, Y., Qu, X., Cao, D., and Li, K. (2021). A
deep learning based image enhancement approach for
autonomous driving at night. Knowledge-Based Sys-
tems, 213:106617.
Li, J., Liu, J., Yang, P., Chen, L., Huang, X., and Zhang,
L. (2019). Analyzing deep neural networks with sym-
bolic propagation: towards higher precision and faster
verification. In International Static Analysis Sympo-
sium, pages 296–319. Springer.
Li, R., Li, J., Huang, C.-C., Yang, P., Huang, X., Zhang,
L., Xue, B., and Hermanns, H. (2020). Prodeep: a
platform for robustness verification of deep neural net-
works. In Proceedings of the 28th ACM Joint Meeting
on European Software Engineering Conference and
Symposium on the Foundations of Software Engineer-
ing, pages 1630–1634.
Lu, P., Liu, C., Mao, X., Zhao, Y., Wang, H., Zhang, H., and
Guo, L. (2021). Few-shot pulse wave contour classifi-
cation based on multi-scale feature extraction. Scien-
tific Reports, 11(1):1–11.
Raghunathan, A., Steinhardt, J., and Liang, P. (2018). Cer-
tified defenses against adversarial examples. arXiv
preprint arXiv:1801.09344.
Ryou, W., Chen, J., Balunovic, M., Singh, G., Dan, A., and
Vechev, M. (2021). Scalable polyhedral verification
of recurrent neural networks. In International Confer-
ence on Computer Aided Verification, pages 225–248.
Springer.
Shen, D., Wu, G., and Suk, H.-I. (2017). Deep learning in
medical image analysis. Annual review of biomedical
engineering, 19:221–248.
Singh, G., Ganvir, R., P
¨
uschel, M., and Vechev, M. (2019a).
Beyond the single neuron convex barrier for neural
network certification.
Singh, G., Gehr, T., Mirman, M., P
¨
uschel, M., and Vechev,
M. T. (2018a). Fast and effective robustness certifica-
tion. NeurIPS, 1(4):6.
Singh, G., Gehr, T., P
¨
uschel, M., and Vechev, M. (2018b).
Boosting robustness certification of neural networks.
In International Conference on Learning Representa-
tions.
Singh, G., Gehr, T., P
¨
uschel, M., and Vechev, M. (2019b).
An abstract domain for certifying neural networks.
Proceedings of the ACM on Programming Languages,
3(POPL):1–30.
Singh, G., Gehr, T., P
¨
uschel, M., and Vechev, M. T. (2019c).
Boosting robustness certification of neural networks.
In ICLR (Poster).
Tjeng, V., Xiao, K., and Tedrake, R. (2017). Evaluating
robustness of neural networks with mixed integer pro-
gramming. arXiv preprint arXiv:1711.07356.
Wang, S., Pei, K., Whitehouse, J., Yang, J., and Jana, S.
(2018a). Efficient formal safety analysis of neural net-
works. arXiv preprint arXiv:1809.08098.
Wang, S., Pei, K., Whitehouse, J., Yang, J., and Jana,
S. (2018b). Formal security analysis of neural net-
works using symbolic intervals. In 27th {USENIX}
Security Symposium ({USENIX} Security 18), pages
1599–1614.
Weng, L., Zhang, H., Chen, H., Song, Z., Hsieh, C.-J.,
Daniel, L., Boning, D., and Dhillon, I. (2018). To-
wards fast computation of certified robustness for relu
networks. In International Conference on Machine
Learning, pages 5276–5285. PMLR.
Wu, M. and Kwiatkowska, M. (2020). Robustness guaran-
tees for deep neural networks on videos. In Proceed-
ings of the IEEE/CVF Conference on Computer Vision
and Pattern Recognition, pages 311–320.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
1010