
Metaheuristics-based Exploration Strategies
for Multi-Objective Reinforcement Learning
Florian Felten
1 a
, Gr
´
egoire Danoy
1,2 b
, El-Ghazali Talbi
3 c
and Pascal Bouvry
1,2 d
1
SnT, University of Luxembourg, Esch-sur-Alzette, Luxembourg
2
FSTM/DCS, University of Luxembourg, Esch-sur-Alzette, Luxembourg
3
University of Lille, CNRS/CRIStAL, Inria Lille, France
Keywords:
Reinforcement Learning, Multi-objective, Metaheuristics, Pareto Sets.
Abstract:
The fields of Reinforcement Learning (RL) and Optimization aim at finding an optimal solution to a problem,
characterized by an objective function. The exploration-exploitation dilemma (EED) is a well known subject
in those fields. Indeed, a consequent amount of literature has already been proposed on the subject and shown
it is a non-negligible topic to consider to achieve good performances. Yet, many problems in real life involve
the optimization of multiple objectives. Multi-Policy Multi-Objective Reinforcement Learning (MPMORL)
offers a way to learn various optimised behaviours for the agent in such problems. This work introduces a
modular framework for the learning phase of such algorithms, allowing to ease the study of the EED in Inner-
Loop MPMORL algorithms. We present three new exploration strategies inspired from the metaheuristics
domain. To assess the performance of our methods on various environments, we use a classical benchmark
- the Deep Sea Treasure (DST) - as well as propose a harder version of it. Our experiments show all of the
proposed strategies outperform the current state-of-the-art ε-greedy based methods on the studied benchmarks.
1 INTRODUCTION
Reinforcement Learning (RL) has recently drawn a
lot of interest after the recent successes of this tech-
nique when applied to various types of problems.
Early applications initially targeted game problems
Silver et al. (2016), while more and more real life
problems, e.g. protein structure prediction Jumper
et al. (2021), have lately been addressed.
Nonetheless, most of the RL literature consid-
ers single-objective problems where real world prob-
lems often deal with multiple, generally contradicting
objectives. For instance, an autonomous car could
have to find a trade-off between battery usage and
the speed at which it reaches a destination. The class
of algorithms that aims at finding the best trade-offs
between these objectives using reinforcement learn-
ing is called Multi-Objective Reinforcement Learn-
ing (MORL). So far, little interest has been shown
in MORL compared to the amount of research being
a
https://orcid.org/0000-0002-2874-3645
b
https://orcid.org/0000-0001-9419-4210
c
https://orcid.org/0000-0003-4549-1010
d
https://orcid.org/0000-0001-9338-2834
held in RL.
The most frequent way of solving a multi-
objective problem with MORL is to reduce it to a
single-objective problem by merging the various ob-
jectives into a global one. The prominent merg-
ing function, called scalarization function, is a linear
weighted sum, but others exist e.g. Van Moffaert et al.
(2013). Despite its popularity, this approach has sev-
eral drawbacks. For example, finding the right scalar-
ization function is usually done via a trial and error
process, which is time consuming and can lead to sub-
optimal choices. Another example is that user prefer-
ences can be dynamically changing. In that case, the
algorithm would need to be entirely retrained for each
new user preference Hayes et al. (2021).
Multi-policy MORL algorithms address these is-
sues by learning multiple policies leading to good
trade-offs between objectives. These learning meth-
ods can be divided in two categories, outer-loop and
inner-loop Roijers et al. (2013); Hayes et al. (2021).
The outer-loop method, which is the most common,
consists in running multiple times single-objective RL
algorithms with varying parameters, as to aim for dif-
ferent trade-offs. The inner-loop method modifies the
learning algorithm itself to simultaneously learn mul-
662
Felten, F., Danoy, G., Talbi, E. and Bouvry, P.
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning.
DOI: 10.5220/0010989100003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 662-673
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tiple policies.
The exploration-exploitation dilemma (EED) con-
sists in finding a good trade-off between looking in
the neighborhood of known good solutions and ex-
ploring unknown regions. It can significantly influ-
ence the performance of RL algorithms. It has been
thoroughly studied in traditional RL settings Amin
et al. (2021) but rarely in multi-policy MORL. In fact,
to the best of our knowledge, no work has been ded-
icated to study the exploration question in inner-loop
algorithms yet Vamplew et al. (2017a).
This paper thus studies the EED for Multi-Policy
Inner-Loop MORL algorithms (MPILMORLs). It
presents three novel exploration strategies for MPIL-
MORLs inspired from the metaheuristic domain:
Pheromones-Based (PB), Count-Based (CB), Tabu-
Based (TB). These strategies are based on the idea
of repulsion from already visited state and actions.
In addition, a new episodic, deterministic bench-
mark environment, called Mirrored Deep Sea Trea-
sure (MDST) is introduced. This environment is a
harder version of the state-of-the-art Deep Sea Trea-
sure (DST) benchmark. Lastly, experiments are con-
ducted on the DST and MDST environments, show-
ing the three proposed strategies outperform state-of-
the-art techniques.
The remainder of this article is organized as fol-
lows: Section 2 describes related work, Section 3
presents a learning framework for multi-policy inner-
loop MORL algorithms as well as the three new ex-
ploration strategies, Section 4 contains our experi-
mental setup while results are presented and analysed
in Section 5. Finally Section 6 concludes our work
and provides some perspectives.
2 BACKGROUND
This section presents the related work and current
state-of-the-art upon which this paper builds. Sec-
tion 2.1 provides a short introduction to Reinforce-
ment Learning. Section 2.2 presents relevant work in
MORL. Finally, Section 2.3 introduces the EED in RL
and Optimization.
2.1 Reinforcement Learning
In reinforcement learning, an agent interacts with an
environment in order to maximize a reward signal.
The agent receives positive or negative feedback de-
pending on the actions it realized on the environment.
RL environments are usually modeled as Markov De-
cision Processes (MDP) Sutton and Barto (2018).
This paper restricts its study to deterministic
MDPs. A deterministic MDP is represented by a tu-
ple (S,A,r) where: S represents the set of possible
states the agent can observe in the environment, A is
the set of actions the agent can realize to interact with
the environment, r : S × A −→ R is the reward distri-
bution where r(s, a) represents the immediate reward
received after performing action a in state s.
The goal of single-objective RL algorithm is to
find a policy π(a|s) which maps each state to a proba-
bility of taking action a in state s. An optimal policy,
denoted π
∗
, is one which maximizes its state-value
function:
v
π
(s) = E
π
"
∞
∑
k=0
γ
k
r(s
t+k
,a
t+k
) | s
t
= s
#
where E
π
[·] represents the expected value of a
variable given that the agent follows policy π, start-
ing from state s at time step t. γ ∈ [0,1] is a discount
factor, adjusting the importance of long term rewards.
Similarly, the value of taking action a in state s
under policy π, called action-value function of policy
π, is defined as:
q
π
(s,a) = E
π
"
∞
∑
k=0
γ
k
r(s
t+k
,a
t+k
) | s
t
= s, a
t
= a
#
The main difference between RL and dynamic
programming (DP) is that the latter assumes a perfect
knowledge of the environment dynamics. Indeed, in
DP, the (S,A,r) tuple is known in advance and the al-
gorithm searches for the optimal policy whereas RL
does not know anything about the environment and
learns π
∗
by interacting with it. There exists a class of
RL algorithms which aim at learning a model of the
environment in order to be able to apply traditional
optimisation techniques, these are called model-based
RL Sutton and Barto (2018).
RL algorithms can learn on-policy, meaning the
agent follows the policy it is currently learning; or
off-policy, where the agent follows a behavioral pol-
icy which is different from the target policy being
learned.
2.2 Multi-Objective Reinforcement
Learning
The difference between traditional RL and MORL
is that the reward is a vector in the latter.
Thus, the rewards take a vector form r(s,a) =
(r
1
(s,a), .. ., r
m
(s,a)), with m being the number of
objectives. These environments can be expressed
using Multi-Objective Markov Decision Processes
(MOMDPs).
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning
663

In that setting, the state-value function has a vector
form and is defined as:
v
π
(s) = E
π
"
∞
∑
k=0
γ
k
r(s
t+k
,a
t+k
) | s
t
= s
#
The same reasoning applies to the action-value
function.
There exists two families of MORL algorithms
which aim at solving MOMDPs. The first one learns
one policy based on a scalarization of the problem and
is referred to as single-policy algorithms. The second
one, called multi-policy algorithms, is the one consid-
ered in this work and detailed hereinafter.
2.2.1 Multi-Policy Reinforcement Learning
Algorithms
This family of MORL algorithms aim at learning mul-
tiple policies leading to various optimal points in the
objective space. This class of algorithms is generally
considered in scenarios similar to the one illustrated
in Figure 1. These algorithms are generally trained
off-line and executed online as the user preferences do
not need to be specified a priori Roijers et al. (2013);
Hayes et al. (2021). Because of this train-test per-
spective, the most important factor for quality mea-
surements of these algorithms is the quality of the fi-
nal policies, rather than the rewards received during
learning Vamplew et al. (2011). In general, to ensure
optimality of the learned policies, the behavioral pol-
icy must guarantee to visit all the state-action pairs
in an infinite horizon, as to sample the entire search
space Van Moffaert and Now
´
e (2014).
There are two ways to learn multiple policies
called outer-loop and inner-loop. The first one re-
peats single-policy algorithms with different parame-
ters as to look for various policies e.g. Vamplew et al.
(2017a,b); Parisi et al. (2016); Oliveira et al. (2020).
MPILMORL. The second one, which is consid-
ered in this study, modifies the learning algorithm it-
self to simultaneously learn multiple policies. Thus,
these algorithms should be off-policy Barrett and
Narayanan (2008). They often rely on the concept
Pareto dominance to remove non optimal policies
from the learned set of policies. Formally, a policy
π Pareto dominates another policy π
0
if it is better in
one objective without being worse in any other objec-
tive:
π π
0
⇐⇒ ∀ j ∈ [1,m] : v
π
j
(s) ≥ v
π
0
j
(s) ∧
∃i ∈ [1, m] : v
π
i
(s) > v
π
0
i
(s)
∀s ∈ S
The set of all non-dominated solution points of a
problem is called a Pareto frontier, or Pareto front.
The first algorithm of this class is model-based and
was introduced in Barrett and Narayanan (2008). In
this algorithm, it is assumed the Pareto frontier has
a convex form and it proceeds by iterating over its
convex hull using linear scalarization. Wiering et al.
(2014) proposed to first learn a model of the environ-
ment and then apply the DP technique of Wiering and
de Jong (2007) to find the best policies.
The algorithms proposed in Van Moffaert and
Now
´
e (2014); Ruiz-Montiel et al. (2017) are capa-
ble of learning all the optimal deterministic non-
stationary policies in episodic environments. The dif-
ference with single policy algorithms is that in those
cases, since no scalarization is applied, the action-
values are sets of vectors. These sets, called
ˆ
Q sets,
contain the potential points on the Pareto frontier ac-
cessible through taking a particular action from a cur-
rent state. As an example of learning relation in that
setting, Van Moffaert and Now
´
e (2014) reuses the DP
equation of White (1982) to define
ˆ
Q(s,a) =
r(s,a) ⊕ γV
ND
(s
0
)
where r(s,a) is the expected immediate reward
vector observed after taking action a, in state s. ⊕
is a vector-sum between a vector and a set of vectors,
adding the former to each vectors in the set. V
ND
(s
0
)
is the set of non-dominated vectors of the unification
of the Q sets over all possible actions from the next
state s
0
reached by performing a when in s. It is de-
fined as:
V
ND
(s
0
) = ND(∪
a
0
∈A
ˆ
Q(s
0
,a
0
))
where the ND operator represents the pruning of
Pareto dominated points. Following the learned poli-
cies in deterministic environments can trivially be
done; both Van Moffaert and Now
´
e (2014); Ruiz-
Montiel et al. (2017) propose a tracking mechanism
as to retrieve the policies from the learned values.
However, in stochastic environments, following the
learned policies requires solving an NP-Hard problem
at every time step Roijers et al. (2021).
2.3 Exploration-exploitation Dilemma
The EED is a well known problem in RL as well as
in optimization. When looking for optima, there is
a trade-off between looking in the neighborhood of
good known solutions (exploitation) and trying to find
new solutions somewhere else in the objective space
(exploration). Too much exploitation would mean the
algorithm could get stuck in local optimum while too
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
664
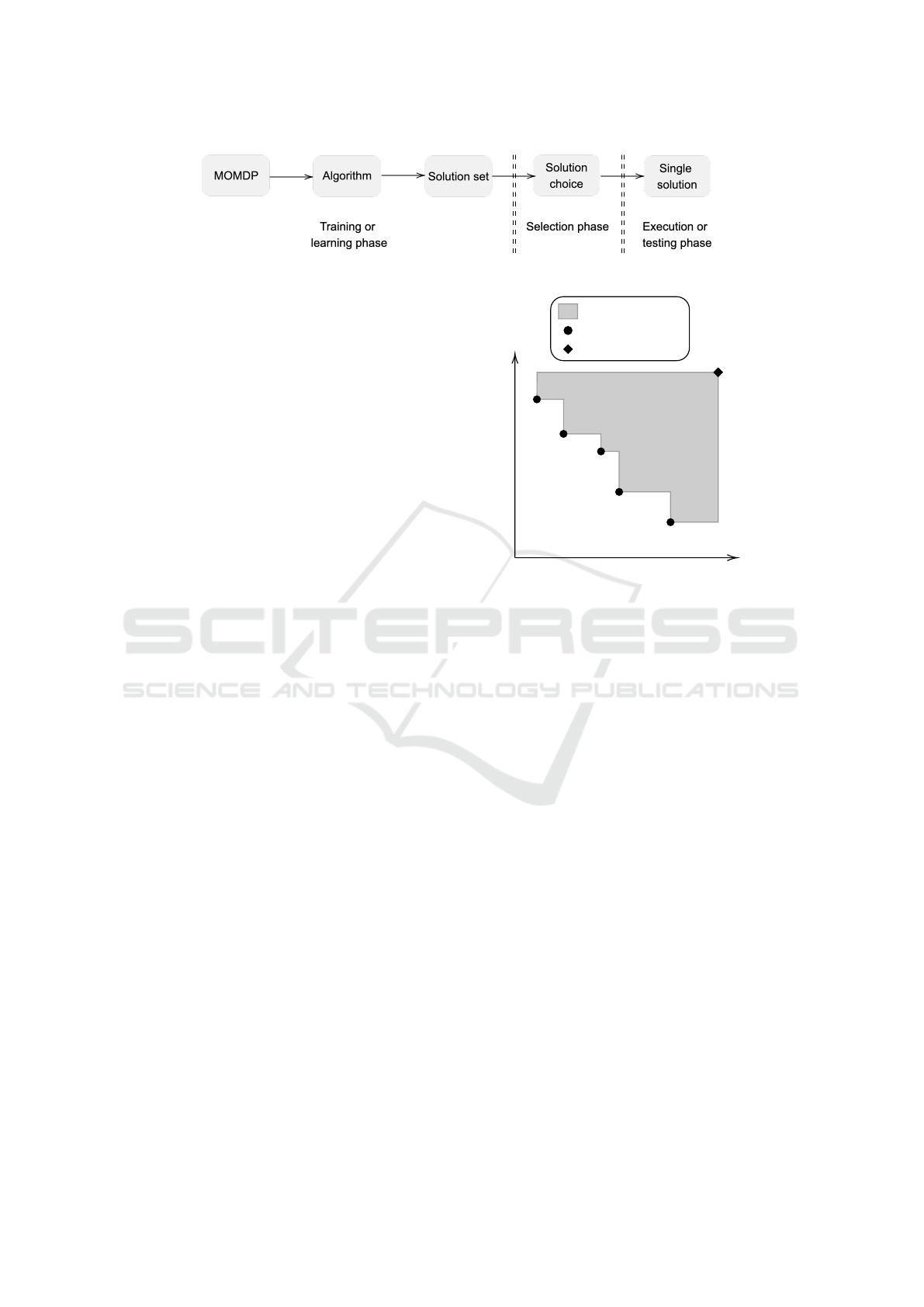
Figure 1: The train-test perspective in Multi-policy MORL. More scenarios can be found in Hayes et al. (2021).
much exploration would mean the algorithm poten-
tially does not converge to any optimum.
2.3.1 EED in RL
The EED is a well studied issue in RL Amin et al.
(2021). Different methods have been proposed to
make the agent exploit the already gained knowledge
while remaining curious about new areas. The most
common exploration strategies are ε-greedy, Boltz-
mann (softmax), Optimistic initialization, Upper con-
fidence bounds and Thompson sampling Vamplew
et al. (2017a). One key point here is to allow the agent
to sample the same state-action pairs multiple times as
the environment could be stochastic (rewards or tran-
sitions).
2.3.2 EED in Optimization
A considerable amount of literature on the EED sub-
ject has been published by the optimization commu-
nity. Indeed, some problems have a search space so
large it becomes practically infeasible to use an ex-
haustive search to find the best solution. In those
settings, metaheuristics allow to find satisfactory so-
lutions in reasonable time at the price of losing the
guarantee of global optimality Talbi (2009). These
are generally designed to find a good balance in the
EED in optimization algorithms.
Performance Indicators. In Multi-Objective Opti-
mization (MOO), solutions are constituted by sets of
points. In order to guide the choices of the algorithm,
it is convenient to have a scalar value evaluating the
quality of the current solutions. A good solution sets
should satisfy two properties: convergence, meaning
the points found in the solution set are close to the
Pareto front, and diversity meaning points in the solu-
tion set should be well spread in the objective space,
as to offer the user with a broad variety of choices. In
the MOO literature, multiple functions, called Perfor-
mance Indicators, have been proposed to reduce the
solution sets to a scalar value representing the diver-
sity and/or convergence criteria Talbi (2009).
For example, the hypervolume metric (HV) pro-
vides an indication on both the convergence and the
diversity of the current solution set Talbi (2009). It
f
2
f
1
Z
re f
Hypervolume
Solution point
Reference point
Figure 2: The unary hypervolume metric in a two objective
problem for a given solution set.
represents the volume of the area created from each
point in the solution set and a reference point in the
objective space. This reference point, Z
re f
is (care-
fully) chosen to be either a lower or an upper bound
in each objective. An example of hypervolume in a
two objective problem is given in Figure 2.
2.3.3 EED in Multi-policy MORL
Regarding the exploitation part, outer-loop MORL al-
gorithms generally rely on the scalarization function
applied to the vectors transforming the MOMDP to
an MDP to quantify the quality of the learned vectors.
In MPILMORL, the algorithms often rely on some
sort of scalarization of the sets based on performance
indicators coming from the MOO domain. For exam-
ple, Van Moffaert and Now
´
e (2014); Wang and Sebag
(2013) use the hypervolume indicator to evaluate the
quality of the sets.
So far, most of the research in multi-policy MORL
use ε-greedy as an exploration strategy. This is prob-
ably due to the fact that extending it to MORL is
straightforward Vamplew et al. (2017a). Nonethe-
less, Optimistic initialization and Softmax have re-
cently been studied in the context of outer-loop MP-
MORL in Vamplew et al. (2017a). The exploration
part of MPILMORL makes no exception. Van Mof-
faert and Now
´
e (2014) use a decaying ε-greedy as to
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning
665

converge to a greedy behavioral policy at the end of
the training phase. However, as mentioned earlier,
converging to a greedy policy at the training phase
for these algorithms is not so important because of
the train-test perspective. In that trend, others use
non-convergent behavioral policies in order to bene-
fit from much more exploration. For example, Ruiz-
Montiel et al. (2017) use a constant ε-greedy with
40% probability of choosing a random move for the
whole training.
Given the similarities of the problems, it seems
metaheuristics could be employed to control the EED
in MORL. This constitutes the core contribution of
this article, and is presented in the next section.
3 APPLYING OPTIMIZATION
METHODS TO MORL
This section studies the application of optimization
techniques in the learning phase of MPILMORL al-
gorithms i.e. in the first phase of Figure 1. The main
idea is to leverage and apply the existing knowledge
of the optimization community - in this case meta-
heuristics - to the MORL world. Three metaheuris-
tics are proposed to control the exploratory part of the
MORL agent.
The learning part of the agent presented in Sec-
tion 3.1. The exploitation mechanism is discussed in
Section 3.2. The core contribution is presented in Sec-
tion 3.3.
3.1 Learning Algorithm
Algorithm 1 is an abstraction of model-free MPIL-
MORL algorithms for episodic environments. It is
modular and allows to completely separate the learn-
ing from the exploration and exploitation parts in the
training phase.
The algorithm starts by initializing the Q sets (line
1). Then for n episodes, it trains on the environment
env. At each episode, the agent starts in an initial
state and realises actions until it reaches a terminal
state - env.end. Given the current observation obs
and a set of possible actions from that observation
env.Action(obs), the agent chooses the next action to
perform using a combination of heuristic Heuristic
and metaheuristic Meta (line 6–7). When the agent
performs an action in the environment, the reward
vector r and next observation are returned (line 8).
Using these information, the learning algorithm is ap-
plied to update the Q sets (line 9). The observation is
then updated to choose the move at next iteration (line
10). At the end of the episode, the metaheuristic can
also be updated in certain cases (line 11).
Algorithm 1: Learn: model-free MPILMORL learning
phase.
Input: Training episodes n, Environment
env, Heuristic function Heuristic,
Metaheuristic Meta, Metaheuristic
update U pdateMeta, QSets learning
mechanism U pdateQsets.
Output: The QSets Q.
1 begin
2 Q ←−
/
0
3 for e = 0 to n do
4 obs ←− env.Reset()
5 while not env.end do
6 A ←− env.Actions(obs)
7 a ←− Meta(obs, A,Q, Heuristic)
8 r,next obs ←− env.Step(a)
9 Q ←− U pdateQsets(r,obs,a,Q)
10 obs ←− next obs
11 Meta ←− U pdateMeta(Meta)
12 return Q
This algorithm brings flexibility. As a matter of
fact, it allows to replace one of its components with-
out the need to change the other ones. The learn-
ing part (UpdateQsets) can be implemented using the
work of Van Moffaert and Now
´
e (2014) or Ruiz-
Montiel et al. (2017). The Heuristic function em-
bodies the exploitation part of the algorithm and is
described in the next section. The metaheuristic part
- Meta and UpdateMeta - which controls the explo-
ration of the agent is then described in Section 3.3.
3.2 Exploitation
Exploitation is a crucial part of the algorithm. Since
each move quality is expressed as a set of vectors, the
exploitation heuristic (Heuristic) should be able to as-
sign a quality measure to those sets. As explained
above, the performance indicators from the MOO do-
main are a natural fit to assign a quality measure on
those sets. The study of the usage of performance in-
dicators in MPILMORL algorithms could be the sub-
ject of an article in itself. In this work, the hypervol-
ume metric is used to order those sets.
3.3 Exploration
Even though it has become a standard in RL, the ε-
greedy exploration strategy could be harmed by its
simplicity. It chooses the best action greedily with
1 − ε probability, and a random action in all other
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
666

cases. It seems more information could be leveraged
when exploring. Indeed, the algorithm could choose
a non-greedy move based on a score assigned to each
of them, as in the softmax exploration strategy. In ad-
dition, the algorithm could store moves which were
already sampled in order to focus on less explored ar-
eas.
Our proposition is based on the principle of repul-
sion: well exploited zones should be less attractive to
the behavioral policy, as to ensure more coverage of
the entire search space. We propose three exploration
strategies coming from the metaheuristics field: tabu-
based, count-based and repulsive pheromones-based.
These strategies and their associated algorithms can
be used as the metaheuristic part of Algorithm 1.
3.3.1 Tabu-based Metaheuristic (TB)
Tabu search is a well-known trajectory-based meta-
heuristic which has been widely used and tested on
various problems. The idea is to mark recently chosen
actions in a given state as tabu, meaning they should
not be considered the next time the agent encounters
the same state. The implementation of the Meta func-
tion for our problem is presented in Algorithm 2.
For every move choice, the agent first selects all
the current moves considered as non-tabu from the
list of possible moves (lines 1–5). It then either se-
lects a move randomly if no move is non-tabu (lines
8–9), or it computes a heuristic value from the Q set
of the considered move using the exploitation mech-
anism (line 11). The best move is chosen greedily as
the one having the largest heuristic value (line 12).
The tabu list is then updated to avoid taking the
same action the next time the agent encounters this
state (lines 14–16). This is the repulsive mechanism.
To ensure the state-action pairs can be sampled
multiple times, the tabu list is bounded by a parame-
ter τ. After a while, the state-action pairs are removed
from the tabu list, allowing to resample this combi-
nation. Choosing the size of the tabu list depends on
the size of the problem. No UpdateMeta function is
needed in this case.
3.3.2 Count-based Metaheuristic (CB)
This exploration strategy is commonly used in RL and
in optimization. The idea here is to reduce the score
associated to state-action pairs according to the num-
ber of times these pairs have been chosen. Its imple-
mentation is listed in Algorithm 3.
The metaheuristic starts by computing the heuris-
tic values of each possible move (line 2). Then, each
value is min-clipped with a value m > 0 to avoid
Algorithm 2: TB: Tabu-based Meta.
Input: Tabu list T , Max tabu size τ, Current
observation obs, Actions set A, QSets
Q, Heuristic function Heuristic.
Output: The next action to perform a.
1 begin
2 NT ←−
/
0
3 for a ∈ A do
4 if (obs,a) /∈ T then
5 NT = NT ∪ a
6
7 a ←− −1
8 if NT =
/
0 then
9 a ←− Random(|A|)
10 else
11 H ←− Heuristic(NT,Q,obs)
12 a ←− argmax
a∈NT
H(a)
13
14 T = T + (obs, a)
15 if |T | > τ then
16 T.pop()
17 return a
moves with a 0 valued heuristic. This value is then
divided by the number of times the state-action pair
has been selected, C
obs,a
. α and β are meta param-
eters allowing to control the exploration-exploitation
intensity depending on the problem at hand (lines 4–
6). Finally, the best action is chosen according to the
ratio computed earlier and the related count is updated
(lines 8–9).
Our repulsing mechanism in this case relies on the
count. Because C
obs,a,t
is unbounded, there always
exists a time step t where the value of the greedy ac-
tion according to the Heuristic function will be re-
duced as much as to choose another action. This is
why the actions are chosen deterministically, using
the argmax operator, while keeping the guarantee of
visiting all state-action pairs in an infinite horizon. No
UpdateMeta function is needed in this case either.
3.3.3 Repulsive Pheromones-based
Metaheuristic (PB)
Inspired from the Ant-Q algorithm introduced in
Gambardella and Dorigo (1995), the algorithm de-
fined in Algorithm 4 uses the concept of repulsive
pheromones as Meta function.
In this case, the agent leaves a pheromone on the
path it has taken. Similar to the CB approach, these
pheromones are used to reduce the score associated to
state-action pairs which have been chosen recently.
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning
667
Algorithm 3: CB: Count-based Meta.
Input: Observation-Action choice counts C,
Minimum hypervolume value m,
Heuristic weight α, Count weight β,
Current observation obs, Actions set
A, QSets Q, Heuristic function
Heuristic.
Output: The next action to perform a.
1 begin
2 H ←− Heuristic(A,Q,obs)
3
4 S ←−
/
0
5 for (a,η) ∈ H do
6 S
a
←−
([η]
m
)
α
(C
obs,a
)
β
7
8 action ←− argmax
a∈A
S
a
9 C
obs,action
←− C
obs,action
+ 1
10 return action
The difference with the CB approach is that
pheromones evaporate after each episode (see Algo-
rithm 5), as to increase the probability for an agent to
take an already explored path and resample it.
As in Algorithm 3, the agent starts by applying the
heuristic function to the Q(s, a) sets (line 2). Then,
this value is divided by the amount of pheromones
assigned to that state-action pair, noted P
obs,a
. The
min-clipping approach is used here as well to ensure
all heuristic values are greater than zero (lines 4–6).
In this case, the pheromones P are bounded be-
cause of the evaporation mechanism presented in Al-
gorithm 5. Therefore, there might exists a heuristic
score for an action a such that S
a
> S
a
0
∀a
0
∈ A ∀t in a
given state. Hence, this action might always be cho-
sen, leading to never exploring the other ones. This
is why the actions’ scores are first normalized before
the metaheuristic samples the action according to the
generated distribution (lines 8–9). The pheromones
are then updated (line 10).
Finally, the UpdateMeta is used for the evapora-
tion mechanism as shown in Algorithm 5. This al-
gorithm multiplies all pheromones by an evaporation
factor ρ.
4 EXPERIMENTAL SETUP
This section presents how the performance of the
proposed metaheuristics-based exploration strategies
for MORL have been assessed. These have been
empirically evaluated against two state-of-the-art ap-
proaches presented in Section 4.1. The metrics used
Algorithm 4: PB: Pheromones-based Meta.
Input: Pheromones P, Minimum
hypervolume value m, Heuristic
weight α, Pheromones weight β,
Current observation obs, Actions set
A, QSets Q, Heuristic function
Heuristic.
Output: The next action to perform a.
1 begin
2 H ←− Heuristic(A,Q,obs)
3
4 S ←−
/
0
5 for (a,η) ∈ H do
6 S
a
←−
([η]
m
)
α
(P
obs,a
)
β
7
8 S
a
←−
S
a
∑
a
0
∈A
S
0
a
9 action ←− Sample(A,S)
10 P
obs,action
←− P
obs,action
+ 1
11 return action
Algorithm 5: UpdatePheromones: UpdateMeta providing
the evaporation system for PB.
Input: Pheromones P, Evaporation factor ρ.
Output: The updated pheromones UP.
1 begin
2 UP ←−
/
0
3 for P
o,a
∈ P do
4 UP = UP ∪ ρP
o,a
5 return UP
for comparison are presented in Section 4.2. The
experiments have been realised on a well-known
benchmark environment and a novel one detailed
in Section 4.3. The learning part of Algorithm 1
was implemented using the algorithm of Van Mof-
faert and Now
´
e (2014), with γ = 1. The hyper-
volume was used as heuristic function. The code
and results from the experiments can be found on
https://github.com/ffelten/PMORL/tree/icaart.
4.1 State-of-the-Art Exploration
Strategies
The considered traditional exploration strategies are
constant ε-greedy (Cε) as presented in Ruiz-Montiel
et al. (2017) and decaying ε-greedy (Dε) as presented
in Van Moffaert and Now
´
e (2014). The first one keeps
a constant exploration probability of 40%, while the
second decreases with the episodes, as to become
greedier at the end of the training i.e. ε = 0.997
episode
.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
668

4.2 Comparison Metrics
Single-objective RL contributions are usually evalu-
ated by their online performance, i.e. average reward
of their solution over time. MPMORL algorithms,
however, produce a set of solutions, where each solu-
tion’s evaluation is a vector. This, combined with the
fact that solutions can be incomparable in the Pareto
sense, makes it harder to assess the performance of
such algorithms Van Moffaert and Now
´
e (2014).
The usual approach in this context is to use the hy-
pervolume of the learned policies, also called offline
hypervolume Vamplew et al. (2011). In this study, the
hypervolume of the solution set seen from the initial
state across training episodes will be compared be-
tween strategies. This metric will be averaged over
40 runs and presented along with a 95% confidence
interval in a graph, for each of the studied metaheuris-
tics.
The results are also reported in a table contain-
ing the mean hypervolume and standard deviation
of the hypervolume of the vectors seen from the
starting state of the environments every 500 training
episodes. Cells are colored using a linear gradient;
the greener, the better. Additionally, to study the sta-
tistical difference between the methods, both ANOVA
and Turkey’s tests are performed on the hypervolume
metrics of each newly introduced metaheuristic and
the two state-of-the-art methods, with α = 0.05. In the
results table, the values for which the hypervolume
of the proposed metaheuristic-based strategy is bet-
ter than the state-of-the-art ones with statistical con-
fidence (i.e., ANOVA and Turkey tests positive) are
reported in bold.
Table 1: Hyperparameter values of the various metaheuris-
tics used in the experiments.
Metaheuristic Hyperparameters
TB τ = 150
CB α = 1, β = 3, m = 1
PB α = 1, β = 2, ρ = 0.9, m = 1
Cε ε = 0.4
Dε ε = 0.997
episode
Table 1 summarizes the hyperparameters values
for each strategy used in our experiments.
4.3 Environments
This section presents the two environments which
have been used to assess the performance of the pro-
posed heuristics. They are grid-based, episodic and
deterministic, and all objectives are to be maximized.
In all environments, the agent can choose to move in
1
2
3
5 8 16
24 50
74
124
Figure 3: The deep see treasure environment. The top left
corner is the agent’s starting cell, walls are represented as
black cells, terminal states are grey cells indicating the value
of the treasure.
−20 −18
−16
−14 −12 −10 −8
−6
−4 −2 0
0
20
40
60
80
100
120
Time objective
Treasure objective
Figure 4: Pareto Front of the DST.
the four cardinal directions. Going into walls or out
of the map leaves the agent in the same position.
Deep Sea Treasure. The DST environment shown
in Figure 3 is the most common benchmark used in
MORL. It was proposed in Vamplew et al. (2011)
and reused in various subsequent work Oliveira et al.
(2020); Van Moffaert and Now
´
e (2014); Wang and
Sebag (2013). Its particularity is that the shape of the
front is not convex (Figure 4), making it impossible
for methods using linear scalarization to discover all
of its points Roijers et al. (2013).
In this problem, the agent controls a submarine
starting on the top left corner of the map, s
0
. It per-
ceives only its x,y coordinates on the map. This envi-
ronment has two objectives, the first one is the value
of the treasures, the second one is time. Whenever the
agent performs an action, it obtains -1 on the time ob-
jective. If the agent encounters a treasure, it obtains
the value of the treasure on its first objective and the
episode is ended. An episode cannot last more than
1000 time steps.
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning
669

1
2
3
5 8 16
24 50
74
124
Figure 5: The Mirrored Deep Sea Treasure environment.
This environment has the same rules and Pareto frontier as
the DST but it is harder to discover all the optimal solutions
as half of the map leads to a dead end.
Mirrored Deep Sea Treasure. At the time of writ-
ing, the choice in deterministic, episodic, multi-
objective benchmarks is very limited. In fact, the DST
is the probably the only one which has been used in
various papers. However, the DST features a rather
small search space, making the learning phase in this
environment too easy when compared to real prob-
lems. To study the performance of our exploration
strategies on a larger search space without changing
their hyperparameters, a harder version of the DST is
proposed: the MDST, which is presented in Figure 5.
It is similar to the DST, except that the map has been
mirrored without treasures and the agent starts in the
middle of the top row. This problem is thus harder
to explore as it contains more state-action pairs, and
the agent can spend a lot of time in the left part of the
map which does not contain any treasure. Moreover,
because the pathway between the two halves of the
map is narrow, the agent can choose to go to the trea-
sures on the top of the map easily whereas the trea-
sures on the bottom require much more exploratory
moves. The Pareto front is the same as the DST (Fig-
ure 4).
5 EXPERIMENTAL RESULTS
This section presents and analyses the experimental
results obtained on the two environments presented
above using the three proposed metaheuristics, along
with the results of the two state-of-the-art ε-greedy
based methods.
5.1 Deep Sea Treasure
Figure 6 presents the evolution of the hypervolume
of the points seen from the starting state (V
ND
(s
0
))
through the training phase. The reference point Z
re f
was set to (0,−25) for both training and evaluation.
In this environment, the three proposed exploration
mechanisms (PB, TB, CB) clearly show a better per-
formance than the state-of-the-art approaches.
In particular, the PB metaheuristic is able to re-
trieve all the points in the front after 1750 episodes in
average. The CB exploration strategy requires more
episodes to find all the points as it exploits multiple
times close states before choosing to explore new fur-
ther states. The TB exploration strategy is not able to
learn the full front in the given training window. This
can probably be enhanced with better parameteriza-
tion of the tabu list size but is outside the scope of this
study.
Regarding the state-of-the-art exploration strate-
gies, Dε shows a rapid convergence at the beginning
of the training phase - when it follows a mostly ran-
dom policy - but quickly stops finding new policies
due to a lack of exploration. This was expected since
it is starting to converge to a greedy policy. This con-
firms the convergence of the behavioral policy to a
greedy policy is not necessary and can be harming
in this setting. Cε is the worst strategy in the early
episodes but shows better performance than the other
state-of-the-art strategy in the end as exploration is
maintained. It can also be noted that the confidence
interval of this strategy grows with the number of
episodes. This is due to the randomness of the algo-
rithm, which the newly introduced strategies do not
seem to suffer from. This could cause an unreliable
performance of the agent in real applications as it
probably would not be trained multiple times for each
problem.
Table 2 presents the mean and standard deviation
of the hypervolume every 500 episodes for each of
the studied strategies. Here also, the three proposed
metaheuristics clearly outperform the state-of-the-art
methods. This is confirmed by the ANOVA and
Turkey tests; the mean hypervolume of the proposed
strategies are statistically different from the ones of
the ε-greedy based approaches in all cases except one,
CB after 500 episodes.
5.2 Mirrored DST
Figure 7 shows the result of the experiments on the
newly introduced MDST environment. The reference
point Z
re f
was set to (0,−55) for the training and to
(0,−25) for the evaluation. As this environment is
more complex to learn, more training episodes are
presented.
Similarly to the DST, on this new environment
the proposed strategies allow for faster learning than
the state-of-the-art ones. No hyperparameter was
changed compared to the runs on the DST environ-
ment. This shows the proposed metaheuristics are ro-
bust to environmental changes.
The PB strategy is the only one to find all the op-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
670
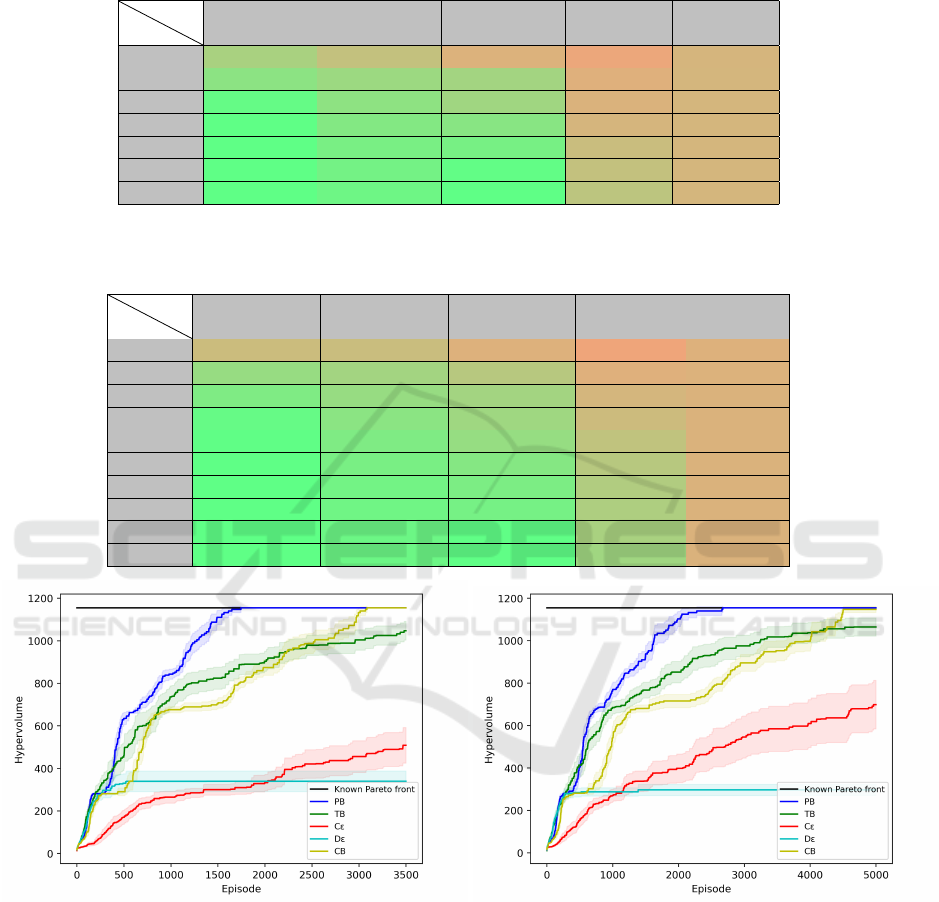
Table 2: Hypervolume mean and standard deviation from the vectors in the starting state for different strategies every 500
episodes on the DST. Bold figures signify the means are statistically different from the means of Cε and Dε according to
ANOVA and Turkey’s tests.
Eps.
Metas
PB TB CB Cε Dε
500 634.8 ± 92.8 460.9 ± 205.1 290.3 ± 58.4 170.4 ± 105.1 330.4 ± 10.7
1000 843.3 ± 76.1 736.3 ± 166.3 676.2 ± 46.8 264.8 ± 89.9 339.4 ± 144.1
1500 1110 ± 107.1 824.3 ± 167.3 703.8 ± 76.3 300.1 ± 83.2 339.6 ± 156.6
2000 1155 ± 0 903.9 ± 152 874.5 ± 117.5 333.1 ± 126.1 339.6 ± 157
2500 1155 ± 0 979.2 ± 153 987.6 ± 151.8 420.9 ± 215.5 339.6 ± 157
3000 1155 ± 0 1004.1 ± 154.8 1132.5 ± 79 455.7 ± 240.8 339.6 ± 157
3500 1155 ± 0 1047.6 ± 141.7 1155 ± 0 508.7 ± 269.2 339.6 ± 157
Table 3: Hypervolume mean and standard deviation from the vectors in the starting state for different strategies every 500
episodes on the MDST. Bold figures signify the means are statistically different from the means of Cε and Dε according to
ANOVA and Turkey’s tests.
Eps.
Metas
PB TB CB Cε Dε
500 405.1 ± 159.1 413.8 ± 169.9 281 ± 0 154.3 ± 102.9 284.1 ± 66.8
1000 765.3 ± 112.7 685.1 ± 96.8 542.1 ± 179.7 270.4 ± 94.2 287.3 ± 63.4
1500 937.5 ± 133.9 767.1 ± 119.6 680.8 ± 54.5 338.6 ± 154.8 296.7 ± 85.5
2000 1102.5 ± 114 852.2 ± 162.8 716.1 ± 100 398.4 ± 217.5 296.7 ± 85.5
2500 1140 ± 65.4 933.5 ± 172.4 771.3 ± 112.9 477.4 ± 262.5 296.7 ± 85.5
3000 1155 ± 0 975.4 ± 163.2 895.5 ± 126.8 545.9 ± 320 296.7 ± 85.5
3500 1155 ± 0 1017.9 ± 157.9 952.8 ± 151.6 584.8 ± 343.5 296.7 ± 85.5
4000 1155 ± 0 1037.7 ± 154.2 997.5 ± 149.8 609.4 ± 365.2 296.7 ± 85.5
4500 1155 ± 0 1056.3 ± 142.4 1140 ± 65.4 636 ± 372.6 296.7 ± 85.5
5000 1155 ± 0 1065 ± 137.5 1147.5 ± 46.8 698.8 ± 368.5 296.7 ± 85.5
Figure 6: Evolution of the hypervolume of the found poli-
cies during the training in the DST environment.
timal policies in the given training window. TB and
CB strategies are performing well when compared to
the two ε-greedy strategies but fail to find all optimal
strategies.
In this scenario again, Dε stops finding new poli-
cies as it becomes greedier and lacks exploration. Fi-
nally, Cε behaves the same as in the other environ-
ment, i.e. it keeps learning new points with episodes,
but with a high variance.
Figure 7: Evolution of the hypervolume of the found poli-
cies during the training in the Mirrored DST environment.
As for the DST, Table 3 presents numerical results
of the experiments. The same conclusion as for the
DST holds; metaheuristics inspired approaches are
statistically better than state-of-the-art approaches on
this environment.
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning
671

6 CONCLUSION
In this paper, a framework for multi-policy inner-loop
MORL training has been presented. It is modular; it
allows to change some of its part without the need to
change the others. From that framework, the possibil-
ity to apply state-of-the-art optimization methods to
MORL was identified.
Three new exploration strategies were presented
to solve the exploration problem in this setting: Re-
pulsive Pheromones-based, Count-based and Tabu-
based. These are inspired from existing work in meta-
heuristics. All three proposed strategies perform bet-
ter than current state-of-the-art, ε-greedy based meth-
ods on the studied environments. Also, it is shown
that behavioral policies which do not converge to be-
come greedy perform better than converging ones in
the learning phase.
Because of the lack of benchmark environments,
this paper also proposes a new benchmark called the
Mirrored Deep Sea Treasure. It is a harder version of
the well known Deep Sea Treasure.
As future work, we plan to introduce new
(stochastic) benchmarks, use MORL algorithms to
control actual robots, and to continue to study the
application of traditional optimization techniques to
MORL.
ACKNOWLEDGEMENTS
This work is funded by the Fonds National de la
Recherche Luxembourg (FNR), CORE program un-
der the ADARS Project, ref. C20/IS/14762457.
REFERENCES
Amin, S., Gomrokchi, M., Satija, H., van Hoof, H., and
Precup, D. (2021). A Survey of Exploration Methods
in Reinforcement Learning. arXiv:2109.00157 [cs].
arXiv: 2109.00157.
Barrett, L. and Narayanan, S. (2008). Learning all opti-
mal policies with multiple criteria. In Proceedings of
the 25th international conference on Machine learn-
ing - ICML ’08, pages 41–47, Helsinki, Finland. ACM
Press.
Gambardella, L. M. and Dorigo, M. (1995). Ant-Q: A Re-
inforcement Learning approach to the traveling sales-
man problem. In Prieditis, A. and Russell, S., editors,
Machine Learning Proceedings 1995, pages 252–260.
Morgan Kaufmann, San Francisco (CA).
Hayes, C., R
˘
adulescu, R., Bargiacchi, E., K
¨
allstr
¨
om, J.,
Macfarlane, M., Reymond, M., Verstraeten, T., Zint-
graf, L., Dazeley, R., Heintz, F., Howley, E., Irissap-
pane, A., Mannion, P., Nowe, A., Ramos, G., Restelli,
M., Vamplew, P., and Roijers, D. (2021). A Practi-
cal Guide to Multi-Objective Reinforcement Learning
and Planning.
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov,
M., Ronneberger, O., Tunyasuvunakool, K., Bates, R.,
ˇ
Z
´
ıdek, A., Potapenko, A., Bridgland, A., Meyer, C.,
Kohl, S. A. A., Ballard, A. J., Cowie, A., Romera-
Paredes, B., Nikolov, S., Jain, R., Adler, J., Back, T.,
Petersen, S., Reiman, D., Clancy, E., Zielinski, M.,
Steinegger, M., Pacholska, M., Berghammer, T., Bo-
denstein, S., Silver, D., Vinyals, O., Senior, A. W.,
Kavukcuoglu, K., Kohli, P., and Hassabis, D. (2021).
Highly accurate protein structure prediction with Al-
phaFold. Nature, 596(7873):583–589.
Oliveira, T., Medeiros, L., Neto, A. D., and Melo, J. (2020).
Q-Managed: A new algorithm for a multiobjective re-
inforcement learning. Expert Systems with Applica-
tions, 168:114228.
Parisi, S., Pirotta, M., and Restelli, M. (2016). Multi-
objective Reinforcement Learning through Continu-
ous Pareto Manifold Approximation. Journal of Ar-
tificial Intelligence Research, 57:187–227.
Roijers, D. M., R
¨
opke, W., Nowe, A., and Radulescu,
R. (2021). On Following Pareto-Optimal Policies in
Multi-Objective Planning and Reinforcement Learn-
ing.
Roijers, D. M., Vamplew, P., Whiteson, S., and Dazeley,
R. (2013). A survey of multi-objective sequential
decision-making. Journal of Artificial Intelligence Re-
search, 48(1):67–113.
Ruiz-Montiel, M., Mandow, L., and P
´
erez-de-la Cruz, J.-
L. (2017). A temporal difference method for multi-
objective reinforcement learning. Neurocomputing,
263:15–25.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,
van den Driessche, G., Schrittwieser, J., Antonoglou,
I., Panneershelvam, V., Lanctot, M., Dieleman, S.,
Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I.,
Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel,
T., and Hassabis, D. (2016). Mastering the game of
Go with deep neural networks and tree search. Na-
ture, 529(7587):484–489.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-
ing: An Introduction. Adaptive Computation and Ma-
chine Learning series. A Bradford Book, Cambridge,
MA, USA, 2 edition.
Talbi, E.-G. (2009). Metaheuristics: From Design to Imple-
mentation, volume 74.
Vamplew, P., Dazeley, R., Berry, A., Issabekov, R., and
Dekker, E. (2011). Empirical evaluation methods
for multiobjective reinforcement learning algorithms.
Machine Learning, 84(1):51–80.
Vamplew, P., Dazeley, R., and Foale, C. (2017a). Soft-
max exploration strategies for multiobjective rein-
forcement learning. Neurocomputing, 263:74–86.
Vamplew, P., Issabekov, R., Dazeley, R., Foale, C., Berry,
A., Moore, T., and Creighton, D. (2017b). Steering ap-
proaches to Pareto-optimal multiobjective reinforce-
ment learning. Neurocomputing, 263:26–38.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
672

Van Moffaert, K., Drugan, M. M., and Now
´
e, A. (2013).
Hypervolume-Based Multi-Objective Reinforcement
Learning. In Purshouse, R. C., Fleming, P. J., Fon-
seca, C. M., Greco, S., and Shaw, J., editors, Evolu-
tionary Multi-Criterion Optimization, Lecture Notes
in Computer Science, pages 352–366, Berlin, Heidel-
berg. Springer.
Van Moffaert, K. and Now
´
e, A. (2014). Multi-objective re-
inforcement learning using sets of pareto dominating
policies. The Journal of Machine Learning Research,
15(1):3483–3512. Publisher: JMLR. org.
Wang, W. and Sebag, M. (2013). Hypervolume indicator
and dominance reward based multi-objective Monte-
Carlo Tree Search. Machine Learning, 92(2):403–
429.
White, D. (1982). Multi-objective infinite-horizon dis-
counted Markov decision processes. Journal of Math-
ematical Analysis and Applications, 89(2):639–647.
Wiering, M. A. and de Jong, E. D. (2007). Comput-
ing Optimal Stationary Policies for Multi-Objective
Markov Decision Processes. In 2007 IEEE Interna-
tional Symposium on Approximate Dynamic Program-
ming and Reinforcement Learning, pages 158–165.
ISSN: 2325-1867.
Wiering, M. A., Withagen, M., and Drugan, M. M. (2014).
Model-based multi-objective reinforcement learning.
In 2014 IEEE Symposium on Adaptive Dynamic Pro-
gramming and Reinforcement Learning (ADPRL),
pages 1–6, Orlando, FL, USA. IEEE.
Metaheuristics-based Exploration Strategies for Multi-Objective Reinforcement Learning
673
