EuclidNets: Combining Hardware and Architecture Design for Efficient
Training and Inference
Mariana Oliveira Prazeres
1,2 a
, Xinlin Li
2
, Adam Oberman
1 b
and Vahid Partovi Nia
2 c
1
Department of Mathematics and Statistics, McGill University, Montreal, Canada
2
Huawei Noah’s Ark, Montreal, Canada
Keywords:
Neural Network Compression, Hardware-aware Architectures.
Abstract:
In order to deploy deep neural networks on edge devices, compressed (resource efficient) networks need to
be developed. While established compression methods, such as quantization, pruning, and architecture search
are designed for conventional hardware, further gains are possible if compressed architectures are coupled
with novel hardware designs. In this work, we propose EuclidNet, a compressed network designed to be
implemented on hardware which replaces multiplication, wx, with squared difference (x − w)
2
. EuclidNet
allows for a low precision hardware implementation which is about twice as efficient (in term of logic gate
counts) as the comparable conventional hardware, with acceptably small loss of accuracy. Moreover, the
network can be trained and quantized using standard methods, without requiring additional training time.
Codes and pre-trained models are available.
1 INTRODUCTION
While the majority of deep neural networks are de-
signed to be implemented on GPUs, they are increas-
ingly being deployed on edge devices, such as mo-
bile phones. These edge devices require compressed
(more efficient), hardware aware architectures, due
to memory and power constraints (Benmeziane et al.,
2021), which seeks to compress the architecture for a
given hardware design (e.g. GPU or lower precision
chips). However, special-purpose hardware is being
designed with neural network inference in mind. This
leads to a new problem formulation which we study
here: design an efficient hardware architecture which
allows networks to be trained on GPUs, then imple-
mented on the hardware.
The combined problem of hardware and network
design is complex, and the precise measurement of
efficiency is both device and problem specific, taking
into account latency, memory, energy consumption.
Here we deliberately oversimplify the problem in or-
der to make it tractable, by addressing a fundamental
element of hardware cost. As a coarse surrogate effi-
ciency, we use the number of logic gates required to
a
https://orcid.org/0000-0003-4422-7875
b
https://orcid.org/0000-0002-4214-7364
c
https://orcid.org/0000-0001-6673-4224
implement an arithmetic operation on chip . While
this is very coarse, and full costs will depend on other
aspects of hardware implementation, it nevertheless
represents a fundamental unit of cost in hardware de-
sign (Hennessy and Patterson, 2011).
In a standard architecture, weights are multiplied
by inputs, so the fundamental operation is multiplica-
tion S
conv
(x,w) = wx. In our work, we replace multi-
plication with the EuclidNet operator,
S
euclid
(x,w) = −
1
2
|x −w|
2
. (1)
which combines a difference with a squaring oper-
ator. We will refer to the family of networks that
use (1) as EuclidNets. EuclidNets are a compromise
between standard architecture, and AdderNets (Chen
et al., 2020), which remove multiplication entirely,
but at the cost of a significant loss of accuracy as well
as difficulty training. Replacing multiplication with
squaring is about half the cost (on chip), depending
on the number of bits used to represent the integer.
The feature representation of each of the architectures
is illustrated in Figure 1. EuclidNets can be imple-
mented on 8-bit precision without loss of accuracy,
see Table 1.
The squaring operator is cheaper (in terms of logic
gates) than multiplication and can be reduced to a
tiny look up table if run on integer values. (Baluja
Prazeres, M., Li, X., Oberman, A. and Nia, V.
EuclidNets: Combining Hardware and Architecture Design for Efficient Training and Inference.
DOI: 10.5220/0010988500003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 141-151
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
141

et al., 2018; Covell et al., 2019) prove replacing look
up table can replace actual float computing, but re-
sults in practice do not translate to inference speed-up
(Kersner, 2019). Works such as LookNN in (Razlighi
et al., 2017) take the first step in designing hardware
for look up table use. On a low precision chip, we can
compute S
euclid
for about half the cost as S
conv
, be-
cause hardware efficiencies for squaring two a fixed
precision integer more than offsets the additional cost
of a difference. At the same time, the network does
not lose expressivity, as explained below. To summa-
rize, we make the following contributions
• We design an architecture based on replacing the
multiplication S
conv
(x,w) = wx by the squared dif-
ference (1). Quantized networks using this opera-
tion require about half the cost (measured by gate
operators) on a custom chipset.
• These networks are just as expressive as convolu-
tional networks. In practice, they have compara-
ble accuracy (drop of less than 1 percent on Ima-
geNet on ResNet50 going from full precision con-
volutional to 8-bit Euclid).
• In contrast to other network compression tech-
niques, we can train and quantize these networks
on GPUs without additional cost or difficulty.
2 CONTEXT AND RELATED
WORK
Neural compression comes at the cost of a loss of
accuracy, and may also increase training time (to a
greater extent on quantized networks) (Frankle and
Carbin, 2018). Part of the drop in accuracy comes
simply from decreasing model size, which is re-
quired for IoT and edge devices (Wu et al., 2019).
Some of the most common neural compression meth-
ods include pruning (Reed, 1993), quantization (Guo,
2018), knowledge distillation (Hinton et al., 2015),
and efficient design (Iandola et al., 2016; Howard
et al., 2017; Zhang et al., 2018; Tan and Le, 2019).
Here we focus on a small, unorganized sub-field of
compression, that optimizes mathematical operations
in the network. This approach can be combined suc-
cessfully with common other compression methods
like quantization (Xu et al., 2020).
The most natural approach is low bit quantization
(Guo, 2018). The inference gains improves with low-
ering bit size, at the cost of accuracy drop and longer
training. In the extreme case of binary networks, op-
erations have negligible cost at inference but exhibits
a considerable accuracy drop (Hubara et al., 2016).
Knowledge distillation (Hinton et al., 2015) con-
sists of transferring information form a larger teacher
network to a smaller student network. The idea is eas-
ily extended by thinking of information transfer be-
tween different similarity measures, which (Xu et al.,
2020) explore in the context of AdderNets. Knowl-
edge distillation is an uncommon training procedure
and requires extra implementation effort. EuclidNet
keeps the accuracy without knowledge distillation.
We suggest a straightforward training using a smooth
transition between common convolution and Euclid
operation.
3 NETWORK ARCHITECTURE
AND SIMILARITY OPERATORS
Consider an intermediate layer of a neural network
with input x ∈ R
H×W×c
in
and output y ∈ R
H×W×c
out
where H,W are the dimensions of the input feature,
and c
in
,c
out
the number of input and output channels,
respectively. For a standard convolutional network,
represent the transformation from input to output via
weights w ∈ R
d×d×c
in
×c
out
as
y
mnl
=
m+d
∑
i=m
n+d
∑
j=n
c
in
∑
k=0
x
i jk
w
i jkl
(2)
Setting d = 1 recovers the fully-connected layer. We
can abstract the multiplication of the weights w
i jkl
by
x
i jkl
in the equation above by using a similarity mea-
sure S : R × R → R. The convolutional layer corre-
sponds to
S
conv
(x,w) = xw.
In our work, we replace S
conv
with S
euclid
, given by
(1). A number of works have also replaced the multi-
plication operator in a neural network. The most rel-
evant work is the AdderNet of (Chen et al., 2020),
which instead uses
S
adder
(x,w) = −|x − w|. (3)
replacing multiplication by the absolute value of the
difference. This operation can be implemented very
efficiently on a custom chipset: subtraction and ab-
solute value of a different of n-bit integers cost order
n gate operations, compared to order n
2
for multipli-
cation S
conv
(x,w) = xw. However, AdderNet comes
with a significant loss in accuracy, and is difficult to
train.
3.1 Other Measures of Similarity in
Neural Network Architectures
The idea of replacing multiplication operations to
save resources within the context of neural networks
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
142

Figure 1: Feature representation of traditional convolution with S(x,w) = xw (left), AdderNet S(x, w) = −|x − w| (middle),
EuclidNet S(x,w) = −
1
2
|x − w|
2
(right).
Table 1: Euclid-Net Accuracy with full precision and 8-bit quantization: Results on ResNet-20 with Euclidean similarity for
CIFAR10 and CIFAR100, and results on ResNet-18 for ImageNet. Euclid-Net achieves comparable or better accuracy with
8-bit precision, compared to the standard full precision convolutional network.
Network Quantization Chip Efficiency
Top-1 accuracy
CIFAR10 CIFAR100 ImageNet
S
conv
Full precision 7 92.97 68.14 69.56
8-bit 3 92.07 68.02 69.59
S
euclid
Full precision 7 93.32 68.84 69.69
8-bit 3 93.30 68.78 68.59
S
adder
Full precision 7 91.84 67.60 67.0
8-bit 3 91.78 67.60 68.8
BNN 1-bit 3 84.87 54.14 51.2
dates back to 1990s. Equally motivated by computa-
tional speed-up and hardware requirement minimiza-
tion, (Dogaru and Chua, 1999) define perceptrons that
use the synapse similarity,
S
synapse
(x,w) = sign(x) · sign(w) · min(|x|, |w|), (4)
which is cheaper than multiplication.
Although (4) has not been experimented with in
modern models and datasets, (Akbas¸ et al., 2015) in-
troduced a slight variation, the multiplication-free op-
erator,
S
mfo
(x,w) = sign(x) · sign(w) · (|x| + |w|)). (5)
Note that both (4) and (5) induce the l
1
-norm. (Mal-
lah, 2018) explains that the updated design choice
allows contributions from both operands x and w.
(Afrasiyabi et al., 2018) studies the similarity in im-
age classification on CIFAR10. Other applications of
(5) include (Badawi et al., 2017).
(You et al., 2020) further combines this similarity
with a bit-shift, and claims an improved accuracy with
negligible added cost. However, the plotted results for
AdderNet appear lower than those reported in (Chen
et al., 2020). Another follow-up work uses knowledge
distillation to further improve the accuracy of Adder-
Nets (Xu et al., 2020).
Instead of simply replacing the similarity on the
summation, there is also the possibility to replace
the full expression on (2). (Limonova et al., 2020a;
Limonova et al., 2020b) approximate the activation of
a given layer with an exponential term. Unfortunately,
it only leads to speed-up in certain cases and, in par-
ticular, it does not improve CPU inference time. Re-
ported accuracy on benchmark problems is also lower
than the typical baseline.
In a recent work, (Mondal et al., 2019) used three
layer morphological neural networks for image clas-
sification. Morphological neural networks were in-
troduced in 1990s by (Davidson and Ritter, 1990) and
use the notion of erosion and dilation to replace (2):
Erosion(x,w) = min
j
S(x
j
,w
j
) = min
j
(x
j
− w
j
),
Dilation(x,w) = max
j
S(x
j
,w
j
) = max
j
(x
j
+ w
j
).
The authors propose two methods of stacking layers
to expand networks, but admit the possibility of over-
fitting and difficult training issues, casting doubt on
scalability of the method.
EuclidNets: Combining Hardware and Architecture Design for Efficient Training and Inference
143

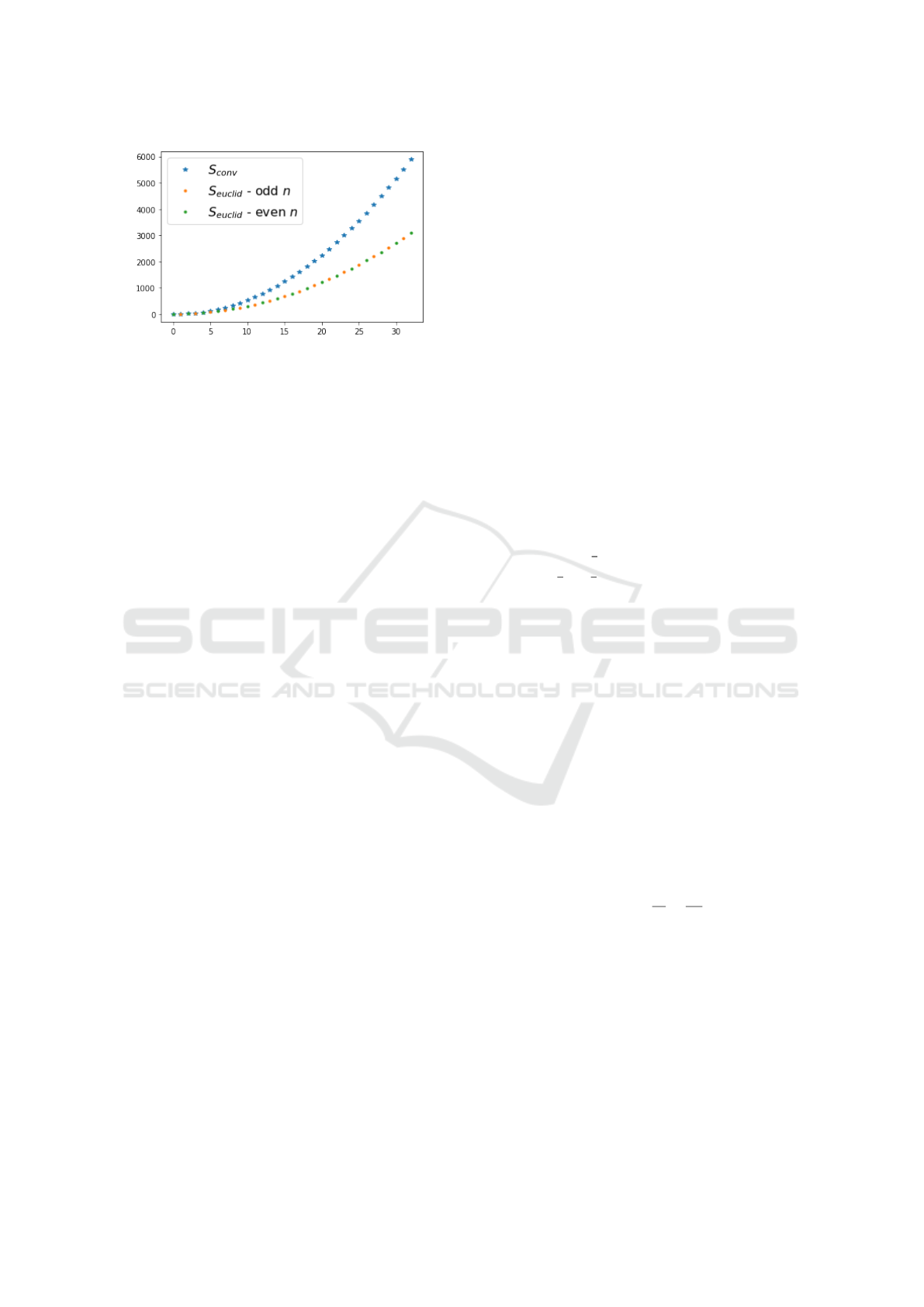
Figure 2: Comparison of the number of logic gates (y-axis)
as a function of the number of bits (x-axis) EuclidNet com-
pared with the standard ConvNet.
4 THEORETICAL RESULTS FOR
EuclidNets
4.1 Expressivity of the EuclidNet
Network
Networks using the EuclidNet operation as just as ex-
pressive as those using multiplication, thanks to the
polarization identity,
S
conv
(x,w) = S
euclid
(x,w) − S
euclid
(x,0) − S
euclid
(0,w)
which means that any multiplication operation can be
expressed using only Euclid operations.
4.2 Logic Gate Cost for EuclidNet
Compared to ConvNet
(multiplication)
The above similarity may not come across immedi-
ately as an improved choice on the cost of convo-
lutions. It requires personalized hardware to obtain
gains in inference speed like the other similarities.
For example, in a typical architecture, the cost of ad-
dition is very close to multiplication, and squaring
is usually not considered distinctly from multiplica-
tion (Limonova et al., 2020a, Table III). Hence, first
we discuss what these gains are theoretically. As for
training, unlike other competitors such as AdderNet
that embodies a considerable slow training, we im-
plement the Euclid similarity in a way that is only
slightly slower than S
conv
.
Here we provide a brief theoretical analysis of ba-
sic binary operations on custom hardware that is opti-
mized for model inference. Assuming equal cost be-
tween AND, XOR and OR gates, we first compute the
cost of gate-level integer operations, defined in Ap-
pendix 7.3. See Figure 2
The following formula gives the gate count of n-
bit operations:
S
conv
= 6n
2
− 8n + 3
S
euclid
= 3n
2
+ n/2 − 3
(with a minor modification to the second formula to
3n
2
+ n/2 − 3/2 when n is odd), refer to Table 6.
The hardware implementation of an n-bit adder
is implemented using one half-adder and n − 1 full-
adders. A half-adder circuit is made up of 1 XOR gate
and 1 AND gate, while the full-adder circuit requires
2 XOR gates, 2 AND gates and 1 OR gate. Therefore,
the cost of an n bit addition is 5n − 3.
There are n
2
AND gates for n-bit element wise
multiplications. A common architecture usually in-
clude (n − 1) n-bit adders besides the n
2
AND gates.
One n-bit adders is composed of one half-adder and
n − 1 full-adders. Hence the cost of multiplication is
6n
2
− 8n + 3.
In the case of squaring, there are less AND gates
representing element-wise multiplication. We con-
sider two different cases: i) if n is even the cost of
squaring is 3n
2
−
9
2
n ii) if n is odd, the cost of squar-
ing is 3n
2
−
9
2
n +
3
2
,
5 TRAINING EuclidNets
Training EuclidNets are much easier compared with
other competitors such as AdderNets. This makes
EuclidNet attractive for complex tasks such as im-
age segmentation, and object detection where train-
ing compressed networks are challenging and causes
large accuracy drop. However, EuclidNets are more
expensive than AdderNets on floating points, but their
quantization behavior unlike AdderNets resembles
traditional convolution to a great extent. In another
words EuclidNets are easy to quantize.
While training a network, it is more appropriate to
use the identity
S
euclid
(x,w) = −
x
2
2
−
w
2
2
+ xw, (6)
and use this equation while training EuclidNets on
GPUs which are optimized for inner product. There-
fore training EuclidNets doesn’t require additional
CUDA core (NVIDIA et al., 2020) implementation
unlike AdderNets. The official implementation of
AdderNet (Chen et al., 2020) reflects order of 20×
slower training than the traditional convolution on Py-
Torch. This is specially problematic for large net-
works and complex tasks that even traditional con-
volution training takes few days or even weeks. Eu-
clidNet training is 2× in the worst case and their im-
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
144

plementation is natural in deep learning frameworks
such as PyTorch and Tensorflow.
A common method in training neural networks is
fine-tuning, initializing with weights trained on differ-
ent data but with a similar nature. Here, we introduce
the idea of using a weight initialization from a model
trained on a related similarity.
Rather than training from scratch, we wish to fine-
tune EuclidNet starting from accurate CNN weights.
This is achieved by an “architecture homotopy” where
we change hyperparameters to convert a regular con-
volution to an Euclid operation
S(x,w; λ
k
) = xw − λ
k
x
2
+ w
2
2
(7)
with λ
k
= λ
0
+
1 − λ
0
n
· k
where n is the total number of epochs and 0 < λ
0
< 1
is the initial transition phase. Note that S(x,w, 0) =
S
conv
(x,w) and S(x,w,1) = S
euclid
(x,w) and equation
7 is the convex combination of the two similarities.
One may interpret λ
k
as a schedule for the homotopy
parameter, similar to how a schedule is defined for the
learning rate in training a deep network. We found
that a linear schedule above is effective empirically.
Transformations like (7) are commonly used in
scientific computing (Allgower and Georg, 2003).
The idea of using homotopy in training neural net-
works can be traced back to (Chow et al., 1991).
Recently, homotopy was used in deep learning in
the context of activation functions (Pathak and Paf-
fenroth, 2019; Cao et al., 2017; Mobahi, 2016;
Farhadi et al., 2020), loss functions (Gulcehre et al.,
2016), compression (Chen and Hao, 2019) and trans-
fer learning (Bengio et al., 2009). Here, we use ho-
motopy in the context of transforming network oper-
ations.
Fine-tuning method in (7) is inspired by continua-
tion methods in partial differential equations. Assume
S is a solution for a differential equation with the ini-
tial condition S(x, 0) = S
0
(x). In certain situations,
solving this differential equation for S(x,t) and then
evaluating at t = 1 might be simpler than solving di-
rectly for S
1
. One may think of this homotopy method
as an evolving neural network over time. At time zero
the neural network consists of regular convolutional
layers, but at time one transforms to Euclidean layers.
The homotopy method can be interpreted as a sort
of of knowledge distillation. Whereas knowledge dis-
tillation methods tries to match a student network to a
teacher network, the homotopy can be seen as a slow
transformation from the teacher network into a stu-
dent network. Figure 3 shows a scheme of the idea.
Curiously, problems that have been solved with ho-
motopic approaches have also been tackled by knowl-
edge distillation. For example, removing blocks or
layers from a network (Hinton et al., 2015; Chen and
Hao, 2019) along with transfer learning (Yim et al.,
2017; Bengio et al., 2009).
6 EXPERIMENTS
We consider try our proposed method on image classi-
fication task. Future work could be extended to other
domains of application such as natural language and
speech.
6.1 CIFAR10
First, we consider the CIFAR10 dataset, consisting of
32 × 32 RGB images with 10 possible classifications
(Krizhevsky et al., 2009). We normalize and augment
the dataset with random crop and random horizon-
tal flip. We consider two ResNet models (He et al.,
2015), ResNet-20 and ResNet-32.
We train EuclidNet using the optimizer from
(Chen et al., 2020), which we will refer to as Adder-
SGD, to evaluate EuclidNet under a similar setup. We
use initial learning rate 0.1 with cosine decay, mo-
mentum 0.9 and weight decay 5 × 10
−4
. We follow
(Chen et al., 2020) in setting the learning-rate scal-
ing parameter η. However, we use a batch-size of
128 for memory reasons. For traditional convolu-
tion network, we use the same hyper-parameters with
stochastic gradient descent optimizer.
In Table 3 we provide the details of classifica-
tion accuracy. We consider two different weight ini-
tialization for EuclidNets. First, we initialize ran-
domly and second, we initialize from weights pre-
trained on a convolutional network. The accuracy for
EuclidNets is approximately the same as for a stan-
dard ResNet. We see that for CIFAR10 training from
scratch achieves even a higher accuracy, while initial-
izing with convolution network and using linear Ho-
motopy training improves it even further.
During training, EuclidNets are unstable, despite
careful choice of the optimizer. In Figure 4 we com-
pare with training the corresponding convolutional
network. Fine-tuning directly from convolutional
weights is more stable than training from scratch as
expected. However, accuracy is lower but the conver-
gence is faster when we use homotopy training and
the accuracy is improved. Pre-trained convolution
weights are commonly available in the most of neu-
ral compression tasks, so initializing EuclidNets with
pre-trained convolution is more natural and prefer-
able.
EuclidNets: Combining Hardware and Architecture Design for Efficient Training and Inference
145

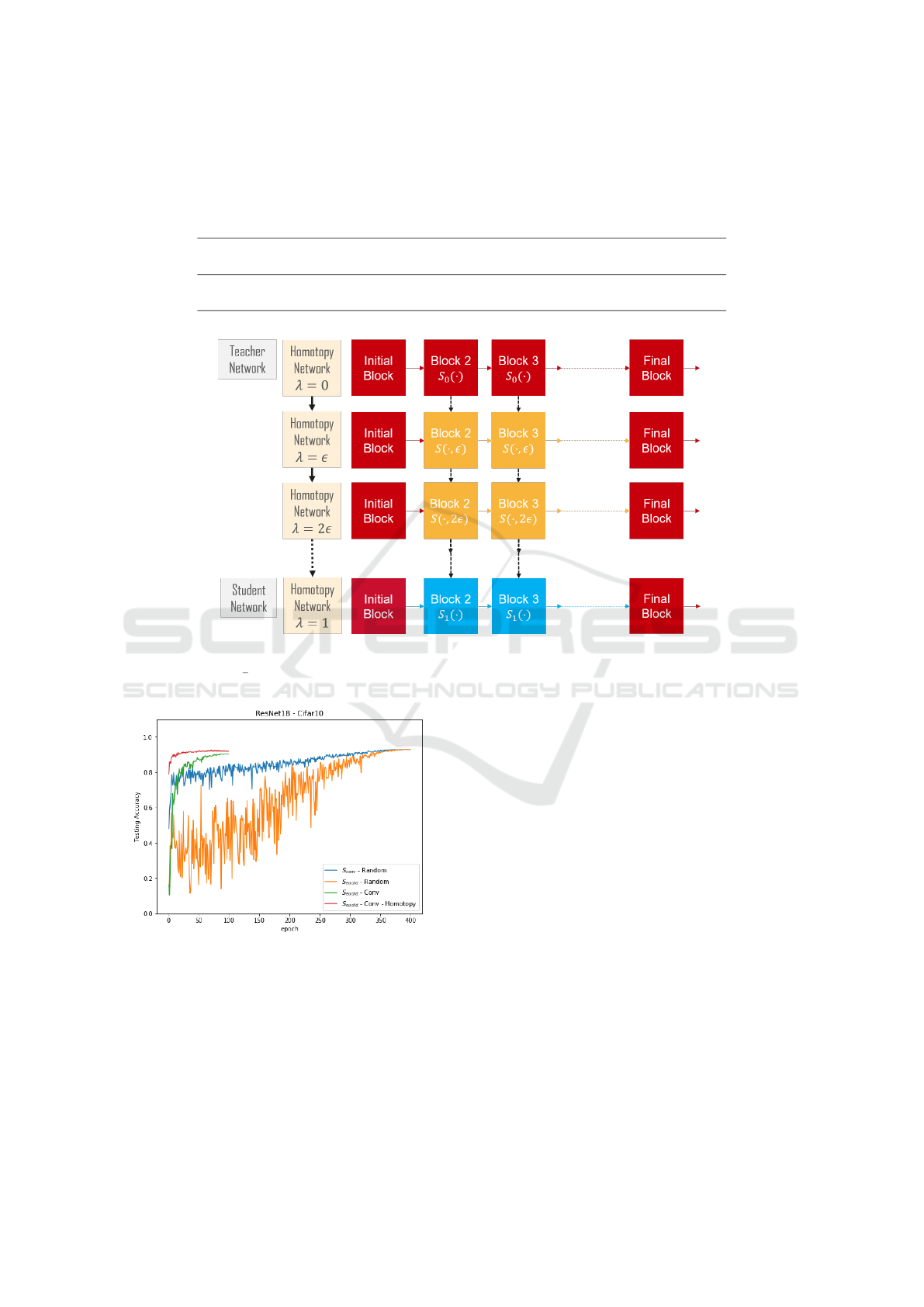
Table 2: Time (seconds) and maximum training batch-size that can fit in a single GPU Tesla V100-SXM2-32GB, during
ImageNet training. In parenthesis is the slowdown with respect to the S
conv
baseline. We do not show times for AdderNet,
which is much slower than both, because it is not implemented in CUDA.
Model Method
Maximum Batch-size Time per step
power of 2
integer Training Testing
ResNet-18
S
conv
1024 1439 0.149 0.066
S
euclid
512 869 (1.7×) 0.157 (1.1×) 0.133 (2×)
ResNet-50
S
conv
256 371 0.182 0.145
S
euclid
128 248 (1.5×) 0.274 (1.5×) 0.160 (1.1×)
Figure 3: Training schema of EuclidNet using Homotopy, i.e. transitioning from traditional convolution S(x, w) = xw towards
EuclidNet S(x,w) = −
1
2
|x − w|
2
through equation (7).
Figure 4: Evolution of testing accuracy during training of
ResNet-20 on CIFAR10, initialized with random weights,
or initialized from convolution pre-trained network. Ini-
tializing from a pre-trained convolution network speeds up
the convergence. EuclidNet is harder to train compared
with convolution network when both initialized from ran-
dom weights.
EuclidNets are not only faster to train compared
with other competitors, but also stand superior in
terms of accuracy. AdderNet performs slightly worse
but is much slower to train. The accuracy is signif-
icantly lower for the synapse and the multiplication-
free operator. In Table 4 we record top-1 accuracy ob-
tained in which AdderNet results are borrowed from
(Xu et al., 2020), that use knowledge distillation to
close the gap with the full precision but still falls short
compared with EuclidNet.
Training a quantized S
euclid
is very similar similar
to convolution. This allows a wider use of such net-
works for lower resource devices. Quantization of the
Euclid model to 8bits keeps accuracy drop within the
range of one percent (Wu et al., 2020) similar to tradi-
tional convolution so they are like convolution when
run on lower bits. Table 1 shows 8-bit quantization of
EuclidNet where the accuracy drop remains negligi-
ble. Similar to traditional convolution, EuclidNets on
CIFAR100 exhibit a larger accuracy drop compared
to CIFAR10, probably due to the complexity of the
classification problem.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
146

Table 3: Results on CIFAR10. The initial learning rate is adjusted for non-random initialization.
Model Similarity Initialization Homotopy Epochs
Top-1 accuracy
CIFAR10 CIFAR100
ResNet-20
S
conv
Random None 400 92.97 69.29
S
euclid
Random None 450 93.00 68.84
Conv
None 100 90.45 64.62
Linear 100 93.32 68.84
ResNet-32
S
conv
Random None 400 93.93 71.07
S
euclid
Random None 450 93.28 71.22
Conv
None 150 91.28 66.58
Linear 100 92.62 68.42
Table 4: Full precision results on ResNet-20 for CIFAR10 for different multiplication-free similarities.
Similarity S
conv
S
euclid
S
adder
S
mfo
S
synapse
Accuracy 92.97 93.00 91.84 82.05 73.08
6.2 ImageNet
Next, we consider EuclidNet classifier built on Ima-
geNet, a more challenging task ImageNet (Deng et al.,
2009). We train our baseline with standard augmen-
tations of random resized crop and horizontal flip and
normalization. We consider ResNet-18 and ResNet-
50 models. Hyper-parameters tuning follows Section
6.1.
Table 5 shows top-1 and top-5 classification accu-
racy. The accuracy from while EuclidNet is trained
from scratch is lower, showing the importance of ho-
motopy training. We believe that the accuracy drop
with no homotopy is the difficulty of tuning train-
ing hyper-parameters for a large dataset such as Im-
ageNet. Even though hyper-parameters that achieve
equivalent accuracy from random initialization exist,
they are too difficult to find. It is much easier to
use the existing hyperparameters of traditional convo-
lution, and transfer the geometry through homotopy
training.
7 CONCLUSION
Euclid networks are obtained from typical neural
models by replacing multiplication in convolutional
layers by the Euclidean similarity. They are designed
to be implemented on a custom designed low preci-
sion chipset, with the idea that subtraction and squar-
ing can be implemented using approximately half the
logic gates, compared to multiplication.
While other efficient architectures can be difficult
to train in low precision, EuclidNets are easily trained
in low precision. EuclidNets can be initialized with
weights trained on the correspondent ConvNet to save
training time, so on may regard them as a fine tuning
convolutional networks for a cheaper inference. The
homotopy method further improves training in such
scenarios and training using this method sometimes
surpass regular convolution accuracy. Future work
may focus on developing hardware that can realize
the expected inference time losses and try similar ex-
periments on down stream vision tasks like object de-
tection and segmentation.
7.1 Limitations
While gate counts provide a fundamental method for
assessing the cost of a chip, they are a crude estimate,
and the real costs (in terms of power usage, inference
time, and memory) of a chipset and architecture com-
bination are much more complex to estimate. True
final costs can require a hardware simulator or imple-
mentation. At the same time, the gate count provides
a first approximation to the cost, and the fact that we
can train and match accuracy in eight bit precision is
promising.
7.2 Societal Impact
Deep Neural Network inference is costly in terms of
power usage. If we can design and implement effi-
cient architectures, this will reduce the societal cost
of running these models on edge devices.
ACKNOWLEDGEMENTS
The authors would like to thank Vanessa Courville for
the helpful discussion on hardware design for Euclid-
Nets.
EuclidNets: Combining Hardware and Architecture Design for Efficient Training and Inference
147

Table 5: Full precision results on ImageNet. Best result for each model is in bold.
Model Similarity Initialization Homotopy Epochs Top-1 Accuracy Top-5 Accuracy
ResNet-18
S
conv
Random None 90 69.56 89.09
S
euclid
Random None 90 64.93 86.46
Conv
None 90 68.52 88.79
Linear
10 65.36 86.71
60 69.21 89.13
90 69.69 89.38
ResNet-50
S
conv
Random None 90 75.49 92.51
S
euclid
Random None 90 37.89 63.99
Conv
None 90 75.12 92.50
Linear
10 70.66 90.10
60 74.93 92.52
90 75.64 92.86
REFERENCES
Afrasiyabi, A., Badawi, D., Nasir, B., Yildi, O., Vural, F.
T. Y., and C¸ etin, A. E. (2018). Non-euclidean vec-
tor product for neural networks. In 2018 IEEE Inter-
national Conference on Acoustics, Speech and Signal
Processing (ICASSP), pages 6862–6866. IEEE.
Akbas¸, C. E., Bozkurt, A., C¸ etin, A. E., C¸ etin-Atalay, R.,
and
¨
Uner, A. (2015). Multiplication-free neural net-
works. In 2015 23nd Signal Processing and Com-
munications Applications Conference (SIU), pages
2416–2418.
Allgower, E. L. and Georg, K. (2003). Introduction to nu-
merical continuation methods. SIAM.
Badawi, D., Akhan, E., Mallah, M.,
¨
Uner, A., C¸ etin-Atalay,
R., and C¸ etin, A. E. (2017). Multiplication free neu-
ral network for cancer stem cell detection in h-and-
e stained liver images. In Compressive Sensing VI:
From Diverse Modalities to Big Data Analytics, vol-
ume 10211, page 102110C. International Society for
Optics and Photonics.
Baluja, S., Marwood, D., Covell, M., and Johnston, N.
(2018). No multiplication? no floating point? no prob-
lem! training networks for efficient inference. arXiv
preprint arXiv:1809.09244.
Bengio, Y., Louradour, J., Collobert, R., and Weston, J.
(2009). Curriculum learning. In Proceedings of
the 26th annual international conference on machine
learning, pages 41–48.
Benmeziane, H., Maghraoui, K. E., Ouarnoughi, H., Niar,
S., Wistuba, M., and Wang, N. (2021). A compre-
hensive survey on hardware-aware neural architecture
search. arXiv preprint arXiv:2101.09336.
Cao, Z., Long, M., Wang, J., and Yu, P. S. (2017). Hashnet:
Deep learning to hash by continuation. In Proceedings
of the IEEE international conference on computer vi-
sion, pages 5608–5617.
Chen, H., Wang, Y., Xu, C., Shi, B., Xu, C., Tian, Q., and
Xu, C. (2020). Addernet: Do we really need multi-
plications in deep learning? In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition, pages 1468–1477.
Chen, Q. and Hao, W. (2019). An efficient homotopy train-
ing algorithm for neural networks.
Chow, J., Udpa, L., and Udpa, S. (1991). Homotopy
continuation methods for neural networks. In 1991.,
IEEE International Sympoisum on Circuits and Sys-
tems, pages 2483–2486. IEEE.
Covell, M., Marwood, D., Baluja, S., and Johnston, N.
(2019). Table-based neural units: Fully quantizing
networks for multiply-free inference. arXiv preprint
arXiv:1906.04798.
Davidson, J. L. and Ritter, G. X. (1990). Theory of morpho-
logical neural networks. In Digital Optical Computing
II, volume 1215, pages 378–388. International Society
for Optics and Photonics.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-
Fei, L. (2009). ImageNet: A Large-Scale Hierarchical
Image Database. In CVPR09.
Dogaru, R. and Chua, L. O. (1999). The comparative
synapse: A multiplication free approach to neuro-
fuzzy classifiers. IEEE Transactions on Circuits and
Systems I: Fundamental Theory and Applications,
46(11):1366–1371.
Farhadi, F., Nia, V., and Lodi, A. (2020). Activation adap-
tation in neural networks. In Proceedings of the 9th
International Conference on Pattern Recognition Ap-
plications and Methods - Volume 1: ICPRAM,, pages
249–257. INSTICC, SciTePress.
Frankle, J. and Carbin, M. (2018). The lottery ticket hypoth-
esis: Finding sparse, trainable neural networks. arXiv
preprint arXiv:1803.03635.
Gulcehre, C., Moczulski, M., Visin, F., and Bengio,
Y. (2016). Mollifying networks. arXiv preprint
arXiv:1608.04980.
Guo, Y. (2018). A survey on methods and theo-
ries of quantized neural networks. arXiv preprint
arXiv:1808.04752.
He, K., Zhang, X., Ren, S., and Sun, J. (2015).
Deep residual learning for image recognition. corr
abs/1512.03385 (2015).
Hennessy, J. L. and Patterson, D. A. (2011). Computer ar-
chitecture: a quantitative approach. Elsevier.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
148

Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling
the knowledge in a neural network. arXiv preprint
arXiv:1503.02531.
Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D.,
Wang, W., Weyand, T., Andreetto, M., and Adam,
H. (2017). Mobilenets: Efficient convolutional neu-
ral networks for mobile vision applications. arXiv
preprint arXiv:1704.04861.
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and
Bengio, Y. (2016). Binarized neural networks. In Lee,
D., Sugiyama, M., Luxburg, U., Guyon, I., and Gar-
nett, R., editors, Advances in Neural Information Pro-
cessing Systems, volume 29. Curran Associates, Inc.
Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K.,
Dally, W. J., and Keutzer, K. (2016). Squeezenet:
Alexnet-level accuracy with 50x fewer parame-
ters and¡ 0.5 mb model size. arXiv preprint
arXiv:1602.07360.
Kersner, M. (2019). Convolutional network without multi-
plication operation.
Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple
layers of features from tiny images.
Limonova, E., Alfonso, D., Nikolaev, D., and Arlazarov,
V. V. (2020a). Resnet-like architecture with low hard-
ware requirements. arXiv preprint arXiv:2009.07190.
Limonova, E., Matveev, D., Nikolaev, D., and Arlazarov,
V. V. (2020b). Bipolar morphological neural net-
works: convolution without multiplication. In Twelfth
International Conference on Machine Vision (ICMV
2019), volume 11433, page 114333J. International
Society for Optics and Photonics.
Mallah, M. (2018). Multiplication free neural networks.
PhD thesis, Bilkent University.
Mobahi, H. (2016). Training recurrent neural networks by
diffusion. arXiv preprint arXiv:1601.04114.
Mondal, R., Santra, S., and Chanda, B. (2019). Dense mor-
phological network: An universal function approxi-
mator.
NVIDIA, Vingelmann, P., and Fitzek, F. H. (2020). Cuda,
release: 10.2.89.
Pathak, H. N. and Paffenroth, R. (2019). Parameter continu-
ation methods for the optimization of deep neural net-
works. In 2019 18th IEEE International Conference
On Machine Learning And Applications (ICMLA),
pages 1637–1643. IEEE.
Razlighi, M. S., Imani, M., Koushanfar, F., and Rosing, T.
(2017). Looknn: Neural network with no multiplica-
tion. In Design, Automation & Test in Europe Confer-
ence & Exhibition (DATE), 2017, pages 1775–1780.
IEEE.
Reed, R. (1993). Pruning algorithms-a survey. IEEE trans-
actions on Neural Networks, 4(5):740–747.
Tan, M. and Le, Q. V. (2019). Efficientnet: Rethink-
ing model scaling for convolutional neural networks.
arXiv preprint arXiv:1905.11946.
Wu, C.-J., Brooks, D., Chen, K., Chen, D., Choudhury, S.,
Dukhan, M., Hazelwood, K., Isaac, E., Jia, Y., Jia, B.,
et al. (2019). Machine learning at facebook: Under-
standing inference at the edge. In 2019 IEEE Inter-
national Symposium on High Performance Computer
Architecture (HPCA), pages 331–344. IEEE.
Wu, H., Judd, P., Zhang, X., Isaev, M., and Micikevicius, P.
(2020). Integer quantization for deep learning infer-
ence: Principles and empirical evaluation.
Xu, Y., Xu, C., Chen, X., Zhang, W., Xu, C., and Wang, Y.
(2020). Kernel based progressive distillation for adder
neural networks. arXiv preprint arXiv:2009.13044.
Yim, J., Joo, D., Bae, J., and Kim, J. (2017). A gift
from knowledge distillation: Fast optimization, net-
work minimization and transfer learning. In Proceed-
ings of the IEEE Conference on Computer Vision and
Pattern Recognition, pages 4133–4141.
You, H., Chen, X., Zhang, Y., Li, C., Li, S., Liu, Z., Wang,
Z., and Lin, Y. (2020). Shiftaddnet: A hardware-
inspired deep network. In Larochelle, H., Ranzato,
M., Hadsell, R., Balcan, M., and Lin, H., editors, Ad-
vances in Neural Information Processing Systems 33:
Annual Conference on Neural Information Processing
Systems 2020, NeurIPS 2020, December 6-12, 2020,
virtual.
Zhang, X., Zhou, X., Lin, M., and Sun, J. (2018). Shuf-
flenet: An extremely efficient convolutional neural
network for mobile devices. In Proceedings of the
IEEE conference on computer vision and pattern
recognition, pages 6848–6856.
APPENDIX
7.3 Hardware Details
We compute the number of logic gates required for
each integer operation.
7.4 Addition
A half-adder (HA) circuit is made up of 1 XOR gate
and 1 AND gate, while the full-adder (FA) circuit re-
quires 2 XOR gates, 2 AND gates and 1 OR gate.
Therefore, the cost of an n bit addition is
HA + (n − 1) × FA
= (1 XOR + 1 AND) + (n − 1) × (2 XOR + 2 AND + 1 OR)
= (2n − 1) AND + (2n − 1) XOR + (n − 1) OR
≈ 5n − 3
7.5 Multiplication
A common architecture usually include (n − 1) n-bit
Adders besides the n
2
AND gates, see Figure 5 top
panels. One n-bit adders is composed of one half-
adder (HA) and n − 1 full-adder (FA). We will con-
sider a n-bit adder as building block in our theoretical
analysis, although it could be optimized further.
EuclidNets: Combining Hardware and Architecture Design for Efficient Training and Inference
149

Figure 5: Binary multiplier (top panel) and binary squarer
(bottom panels) for number of bits n = 2 (left panels) and
n = 3 (right panels).
Hence the cost of multiplication is
n
2
AND + (n − 1) × (n − bit Adder)
= n
2
AND + (n − 1) × HA + (n − 1)
2
× FA
= n
2
AND + (n − 1) × (1 XOR+
1 AND) + (n − 1)
2
× (2 XOR + 2 AND + 1 OR)
= (3n
2
− 3n + 1) AND + (2n
2
− 3n + 1) XOR
+ (n
2
− 2n + 1) OR
≈ 6n
2
− 8n + 3
7.6 Squaring
In the case of squaring, we have less AND gates rep-
resenting element-wise multiplication, because some
values are repeated. We provide some examples in
Figures 6 and 7.
Figure 6: Binary Square for n = 4 bits.
In Figures 6 and 7, we see that some sums are ac-
tually a multiplication by a factor of 2. Multiplication
Figure 7: Binary Square for n = 5 bits.
by a factor of 2 can instead be though as a shift to-
wards the left in the addition.
1. If n is even, then only the middle column will shift
b
n
2
c =
n
2
values to the left. Also, the column on
the left will have the term A
2
n−1
. So, the sum with
maximum number of elements,
n
2
+ 1, will only
happen in one column, i = n − 1. Hence, we need
n
2
(n − 1)-bit adders. See Figure 8 for visual intu-
ition.
Figure 8: Intuition for square on n even.
Hence, the cost of squaring when n is even is:
n(n − 1)
2
AND +
n
2
× ((n − 1) − bit Adder)
=
n(n − 1)
2
AND +
n
2
× HA +
n
2
(n − 2) × FA
=
n(n − 1)
2
AND +
n
2
× (1 XOR + 1 AND)+
+
n
2
(n − 2) × (2 XOR + 2 AND + 1 OR)
=

3
2
n
2
− 2n

AND +

n
2
−
3
2
n

XOR +

1
2
n
2
− n

OR
≈ 3n
2
−
9
2
n
2. If n is odd, column i = n − 1, n, n + 1 will shift
b
n
2
c =
n−1
2
values to the left. Since columns
i = n − 2,n both have an A
2
i
term, the sum with
maximum number of elements,
n−1
2
+ 1, will hap-
pen at those columns. Hence, we need
n−1
2
n-bit
adders. See Figure 9 for visual intuition.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
150

Figure 9: Intuition for square on n odd.
Table 6: Similarity operator Gate Count.
Similarity Gate Count
S
conv
6n
2
− 8n + 3
S
euclid
n odd 3n
2
+
1
2
n −
3
2
n even 3n
2
+
1
2
n − 3
Hence, the cost of squaring when n is odd is:
n(n − 1)
2
AND +
n − 1
2
× (n − bit Adder)
=
n(n − 1)
2
AND +
n − 1
2
× HA +
n − 1
2
(n − 1) × FA
=
n(n − 1)
2
AND +
n − 1
2
× (1 XOR + 1 AND)+
+
n − 1
2
(n − 1) × (2 XOR + 2 AND + 1 OR)
=

3
2
n
2
− 2n +
1
2

AND +

n
2
−
3
2
n +
1
2

XOR+
+

1
2
n
2
− n +
1
2

OR
≈ 3n
2
−
9
2
n +
3
2
.
Moreover, in Figure 5 (bottom panels), we present
the corresponding hardware schemes for n = 2,3.
EuclidNets: Combining Hardware and Architecture Design for Efficient Training and Inference
151