
A-Index: Semantic-based Anomaly Index for Source Code
E. N. Akimova
1,2 a
, A. Yu. Bersenev
1,2
, A. S. Cheshkov
3
, A. A. Deikov
1,2
, K. S. Kobylkin
1,2
,
A. V. Konygin
1 b
, I. P. Mezentsev
1,2
and V. E. Misilov
1,2 c
1
N. N. Krasovskii Institute of Mathematics and Mechanics, Ekaterinburg, Russian Federation
2
Ural Federal University, Ekaterinburg, Russian Federation
3
Huawei Russian Research Institute, Moscow, Russian Federation
Keywords:
Anomaly Detection, Code Quality, Defect Prediction.
Abstract:
The software development community has been using handcrafted code quality metrics for a long time. De-
spite their widespread use, these metrics have a number of known shortcomings. The metrics do not take
into account project-specific coding conventions, the wisdom of the crowd, etc. To address these issues, we
propose a novel semantic-based approach to calculating an anomaly index for the source code. This index
called A-INDEX is the output of a model trained in unsupervised mode on a source code corpus. The larger
the index value, the more atypical the code fragment is. To test A-INDEX we use it to find anomalous code
fragments in Python repositories. We also apply the index for a variant of the source code defect prediction
problem. Using BugsInPy and PyTraceBugs datasets, we investigate how A-INDEX changes when the bug is
fixed. The experiments show that in 63% of cases, the index decreases when the bug is fixed. If one keeps
only those code fragments for which the index changes significantly, then in 71% of cases the index decreases
when the bug is fixed.
1 INTRODUCTION
Source code metrics are an important part of the soft-
ware measurement process. Despite their widespread
usage, work is still ongoing to develop new metrics
(Sharma and Spinellis, 2020). As a rule, metrics are
calculated, using source code, and can be used for
code representation. In addition, metrics can be ex-
plicit (traditional or handcrafted) or implicit (Nu
˜
nez-
Varela et al., 2017), (Afric et al., 2020, Appendix).
Explicit metrics can be interpreted, but at the same
time they have known drawbacks since they are in-
vented by a human and implemented as an algorithm.
Implicit metrics are usually poorly interpreted, but
capable of capturing complex non-obvious patterns.
In addition, implicit metrics are able to adapt to the
data on which they were trained. One of such prob-
lems where implicit metrics can be more efficient than
handcrafted is the problem of defect prediction (Aki-
mova et al., 2021a). Defect prediction is one of the
key challenges in software development. Any new ad-
a
https://orcid.org/0000-0002-4462-5817
b
https://orcid.org/0000-0002-0037-2352
c
https://orcid.org/0000-0002-5565-0583
vances in the problem are welcome as they can lead to
better code quality and software reliability. Usually,
the defect prediction problem is posed as a classifica-
tion problem with two classes: code with defects and
code without defects (Allamanis et al., 2018). Since
the class with defective code is small, there is a class
imbalance problem (Alsawalqah et al., 2017). One
way to tackle the issue is to consider a defective code
as a kind of anomalous one. The work (Ray et al.,
2016) demonstrates that it is not only convenient, but
also quite natural to consider a defective code anoma-
lous. The authors find that code with bugs tends to
be more entropic (i.e. unnatural), becoming less so as
bugs are fixed.
In this work, we propose a unsupervised semantic-
based approach to calculating A-INDEX — anomaly
index for source code. The higher the index is, the
more likely a code is atypical. We use the resulting
anomaly index to find anomalous Python code and
present some found code fragments. In addition, we
use this index for one of the variants of the source
code defect prediction problem. We show on bug-fix
datasets BugsInPy (Widyasari et al., 2020), PyTrace-
Bugs (Akimova et al., 2021b), that the anomaly in-
dex of the fragment often decreases when the bug is
Akimova, E., Bersenev, A., Cheshkov, A., Deikov, A., Kobylkin, K., Konygin, A., Mezentsev, I. and Misilov, V.
A-Index: Semantic-based Anomaly Index for Source Code.
DOI: 10.5220/0010984600003176
In Proceedings of the 17th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2022), pages 259-266
ISBN: 978-989-758-568-5; ISSN: 2184-4895
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
259

fixed. In this paper we investigate the following re-
search questions.
1. Can the anomaly index be used to detect suspi-
cious (unusual and possibly defective) code?
2. Can the anomaly index be useful within one sepa-
rate repository?
3. Is there a connection between the value of the
anomaly index and the presence of a bug in the
code?
4. Is the anomaly index related to known software
metrics?
Our contribution:
• we present an unsupervised semantic-based ap-
proach to calculating the implicit anomaly index
for the source code;
• we detect atypical code in Python code;
• we evaluate this index on the bug-fix datasets.
2 RELATED WORK
Anomaly detection is the identification of data that
significantly different from most other data. Typi-
cally, abnormal data indicate a specific type of prob-
lem, such as banking fraud, structural defect, health
problems.
With regard to software development, anomaly
detection is used, for example, to detect vulnerabil-
ities in programs (Feng et al., 2003). Anomaly de-
tection for logs is used to diagnose deviations in the
programs (Le and Zhang, 2021). One of the popular
applications of the anomaly detection problem is de-
fect prediction. Due to the imbalance of the classes,
such an application seems natural.
The closest to our work is (Ray et al., 2016),
where the authors investigate the hypothesis that un-
natural in some sense code is suspicious. For this,
a modified n-gram language model for Java source
code is constructed, which estimates the conditional
probability of the next token appearance. Thus, the
approach makes it possible to find an unnatural (hav-
ing a low probability) code from the point of view
of the language model. Since the language model
deals with syntax, code containing syntactic anoma-
lies would be unnatural. In our approach, anomaly
is estimated in the semantic contextual representation
space for Python code. Instead of taking syntactic-
level structure of code, the representation uses data
flow in the pre-training stage, which is a semantic-
level structure of code (Guo et al., 2021).
Here are some more examples of work related to
the anomaly detection in the source code. In (Neela
et al., 2017), the authors use explicit features and
the Gaussian distribution to model nondefective code,
and defective code is then predicted using the de-
viation from the model estimation. The possibility
of using explicit features and the k-nearest neighbors
algorithm for the anomaly detection in the source
code is demonstrated in (Moshtari et al., 2020). In
(Tong et al., 2018), the stacked denoising autoen-
coders (Vincent et al., 2010) are used to extract im-
plicit representations from the traditional software
metrics. A similar idea is implemented in (Sakurada
and Yairi, 2014) and (Afric et al., 2020) where the au-
toencoder on the explicit features is used for within-
project source code anomaly detection. In (Bryksin
et al., 2020), two approaches to code vector represen-
tation are implemented: a feature vector consisting of
51 explicit code metrics and an implicit n-gram ap-
proach. Additionally, several anomaly detection tech-
niques are tested: local outlier factor, isolation forest,
and autoencoder neural network. The authors focus
on two types of anomalies: syntax tree anomalies and
compiler-induced anomalies in the Kotlin code. The
found fragments of anomalous code are used by the
developers of the Kotlin compiler for more efficient
testing (Bryksin et al., 2020).
One more reason for using anomaly detection for
defect prediction is the possibility of applying unsu-
pervised learning (Allamanis et al., 2021). It is both
time-consuming and labor-intensive to create a big
labeled dataset, while modern machine learning ap-
proaches require a lot of data. And in many settings
labeled data is much harder to come by than unlabeled
data.
In the current work, we use GraphCodeBERT
(Guo et al., 2021), because in addition to using
the task of masked language modeling, it uses two
structure-aware pre-training tasks. One is to predict
code structure edges, and the other is to align rep-
resentations between source code and code structure.
Thus, such represention better takes into account the
internal structure of the code.
3 PROPOSED APPROACH
The concept of anomaly depends decisively on the
probabilistic space under consideration and on the
source code corpus used. The choice of the corpus
is determined by the problem to be solved. In this
work, we use a set of different repositories as a cor-
pus (see below for details). The general scheme of the
approach is shown in Fig. 1. All steps are described
in more detail below.
Before moving on to the details of our implemen-
ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering
260

Figure 1: A-INDEX overview: The source code of the pro-
grams is split into fragments. Each of the fragments is con-
verted to a fixed-dimensional vector using a Transformer-
based model. These vectors are the input to the variational
autoencoder. The reconstruction error is the resulting value
of the anomaly index.
tation, let’s list the main steps we need to take:
1. Choose code corpus and level of granularity.
2. Transform code fragments into vectors from R
n
,
where n is the fixed dimension of the representa-
tion space.
3. Train an anomaly model.
3.1 Code Corpus
We use an unlabeled source code corpus, which leads
us to unsupervised methods. Our current work uses
the Py150 corpus (Raychev et al., 2016), which con-
sists of the Python programs, collected from the
GitHub repositories by removing duplicate files, re-
moving project forks (copy of another existing repos-
itory), and keeping only programs that have no more
than 30,000 nodes in the abstract syntax tree. Fur-
thermore, only repositories with the permissive and
non-viral licenses such as MIT, BSD, and Apache are
used. The dataset is split into two parts 100,000 files
used for training and 50,000 files used for evaluation.
Also we use the Django repository
1
for within-project
anomaly detection. Django is one of the biggest a
Python-based free and open-source web framework.
The anomaly index is calculated for a fragment of
the source code. Therefore, each corpus file needs to
be converted into a set of fragments. In this work, in-
dividual functions act as code fragments. (Addition-
ally, we experimented with approaches where frag-
ments are defined by a sliding window of a fixed size,
but the results were worse.)
Before proceeding with the description of the code
representation, it is necessary to make a note about
the choice of the corpus. If the index is supposed
to be used within the framework of one project, then
this project or a part of it should be such a corpus.
The main requirement for the choice of the corpus
is its representativeness. The corpus should be large
1
https://github.com/django/django
enough to accommodate various coding conventions,
the wisdom of the crowd, etc.
3.2 Code Representation
The proposed approach uses GraphCodeBERT (Guo
et al., 2021) representation for code fragments. It is
a pre-trained model for a programming language that
considers the inherent structure of code. GraphCode-
BERT is semantic contextual multilingual represen-
tation based on the multi-layer bidirectional Trans-
former (Vaswani et al., 2017). The model follows
BERT (Devlin et al., 2019) and RoBERTa (Liu et al.,
2019). The resulting 768-dimensional vector repre-
sents a code fragment.
3.3 Anomaly Model
For anomaly detection the model uses variational
autoenconder (VAE), for details see (Kingma and
Welling, 2014), (Rezende et al., 2014). In the vari-
ational autoencoder, the loss function is composed of
two parts: the L
2
-loss (reconstruction loss) and Kull-
back — Leibler divergence (latent loss, (Kingma and
Welling, 2014, Appendix B)):
k
X − f (z)
k
+ D
KL
N (µ(X), Σ(X)) || N (0, I)
.
In this formula, we use the standard notation from
(Kingma and Welling, 2014). The first term
k
X − f (z)
k
tends to make the encoding-decoding
scheme as precise as possible. The second term
D
KL
N (µ(X), Σ(X)) || N (0, I)
tends to regularize
the organization of the latent space by making the dis-
tributions returned by the encoder close to a standard
normal distribution. Unlike other autoencoders that
represent each value of the encoding with a single
value, the variational autoencoder learns to represent
it as latent distributions and can approximate by virtue
of the Bayesian inference. This means that a varia-
tional autoencoder is more appropriate than a simple
autoencoder for the extrapolation tasks. The parame-
ters of our variational autoencoder were learned with
respect to the Gaussian distribution. The hidden size
of the autoencoder is a hyperparameter whose values
belong to the set {4, 8, 16, 32, 64, 128}.
To calculate A-INDEX, we use the reconstruction
error term. The larger this error, the worse the code
fragment matches the probabilistic model of the vari-
ational autoencoder. Let c be a code fragment, M
— trained anomaly model and R — code representa-
tion model (GraphCodeBERT in our case). Then the
anomaly index a
M
for code fragment c is defined as
follows:
a
M
(c) :=
k
R(c) − M(R(c))
k
.
A-Index: Semantic-based Anomaly Index for Source Code
261

A-INDEX can be viewed as some kind of code
quality metric. Unlike the standard metrics, the index
is implicit and depends significantly on the corpus by
which the underlying model is trained. The ability of
the index to adapt to a specific repository expands the
possibilities of its usage.
4 RESULTS
We carried out some experiments to study the prop-
erties of the index. Each experiment corresponds to a
research question (hereinafter RQ).
RQ1: Can A-Index be used to detect suspi-
cious code?
We train A-INDEX using Py150. The Py150
train/test split provides approximately 641, 000 code
fragments (individual fucntions) in training and ap-
proximately 314, 000 code fragments in testing. Ev-
ery fragment is represented by a 768-dimensional
vector. The training was not required to obtain such a
representation, since we were already using a model
with pre-trained weights. However, the proposed ap-
proach leaves room to fine-tune the code represen-
tation model for downstream tasks. The training of
VAE takes over 200 epochs using Adam with a learn-
ing rate of 0.001 and batch size of 128 as an optimiza-
tion algorithm.
To answer RQ1, we apply the index to detect atyp-
ical code fragments in the test part of the Py150 cor-
pus. Recall that the larger the reconstruction error, the
more likely the code fragment is atypical. Thus, the
analysis of code fragments with a high index value
gives an answer to the question whether it is possi-
ble to find suspicious (unusual and possibly defec-
tive) code using the proposed approach or not. With
thin analysis we found, that among the fragments that
got a large A-INDEX value, there are many one-line
functions that do not implement any logic, use bit-
wise operations, string variables, and non-standard
constructs.
Due to the natural limitations on the size and num-
ber of fragments, we present here only a few examples
of compact functions that have received a large index
value. One-line examples:
def Pop(): pass
def __UINT64_C(c): return c ## UL
def supportedExtensions():
return ['.bmp', '.jpg', '.jpeg', '.png']
def GetRValue(rgb): return rgb & 0xff
def setPlayerInvItemNum(index, invSlot, \
itemNum):
Player[index].char[TempPlayer[index].\
charNum].inv[invSlot].num = itemNum
def tzname(self, dt):
return self._name
Some examples of compact functions among the
most anomalous:
def setExposure(value):
global exposure
exposure = value
def isValid( self ) :
try :
self.__dictEntry()
return True
except :
return False
def __init__(self,X,K):
self.X=np.array(X)
self.K=K
self.labels=[]
self.centroids=[]
pass
Despite the fact that among the found functions
there are quite normal ones, many functions with a
large value of the anomaly index are not ideally im-
plemented. The Pop() function does not implement
the expected logic, the setExposure() function modi-
fies the global variable exposure and requires careful
handling.
Thus, using the index allows you to detect code
fragments that, in our opinion, are suspicious. Timely
detection of such code fragments, for example, during
the review stage, can improve the quality of the code
and the reliability of the program.
RQ2: Can A-Index be useful within one sepa-
rate repository?
In the previous experiment the model is trained
and applied to several repositories at once. To answer
RQ2, we train the model on the Python files of the
Django project repository. The trained model is ap-
plied to the test part of the same repository.
Since the listings of functions take up a lot of
space, in this case we will only limit ourselves to the
four functions that have received the highest value of
the anomaly index:
def duration_microseconds(delta):
return (24 * 60 * 60 * delta.days +\
delta.seconds) * 1000000 +\
delta.microseconds
ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering
262

def etag(etag_func):
return condition(etag_func=etag_func)
def b64_encode(s):
return base64.urlsafe_b64encode(s).\
strip(b'=')
def last_modified(last_modified_func):
return condition(last_modified_func=\
last_modified_func)
While these functions appear to be correct, some
of them nevertheless require special attention. Thus,
we conclude that the model can help find such code,
and, therefore, can be useful for application within a
separate repository.
We saw above that the model helps to find sus-
picious code, but is there a connection between the
value of the anomaly index and the presence of a
bug in the code? In (Ray et al., 2016), it was shown
that from the point of view of the syntactic language
model, the defective code is less natural than the bug-
free code. Below we raise this question again, but for
our model, which works in the space of semantic code
representation.
RQ3: Is there a connection between the value
of the A-Index and the presence of a bug in the
code?
To answer RQ3, we study how A-INDEX is related
to the presence of bugs or defects in code. To do this,
we use two available Python datasets. Each of the
datasets contains bug-fix pairs: a code fragment with
a bug and its fixed version. Our aim is to check how
A-INDEX changes when the bug is fixed.
The first dataset BugsInPy (Widyasari et al., 2020)
contains 493 real-life bugs. Since our implementation
of the index works at the function level, we dropped
the pairs, that have several functions changed. The
second dataset PyTraceBugs (Akimova et al., 2021b)
is much larger. It contains about 24 thousand bug-fix
pairs, automatically collected from the GitHub plat-
form.
The evaluation occurs as follows. We learn 6
anomaly detection models with different sizes of the
hidden layer of VAE: 4, 8, 16, 32, 64, and 128. Each
such model M gives its own version of the index a
M
.
We expected that the result would be better for the
medium size of the hidden layer (with a small size, in-
formation will be significantly lost, with a large size,
overfitting is possible). The experiments confirmed
our assumptions, and further we worked with the hid-
den layer size equal to 16.
For given model M and dataset D, we take bug-fix
pair (c
bug
, c
fix
) and calculate the anomaly index val-
ues: a
M
(c
bug
) and a
M
(c
fix
).
Let t be a threshold,
P := {(c
bug
, c
fix
)
a
M
(c
bug
) − a
M
(c
fix
) ≥ t},
U := {(c
bug
, c
fix
)
|a
M
(c
bug
) − a
M
(c
fix
)| < t},
N := {(c
bug
, c
fix
)
a
M
(c
bug
) − a
M
(c
fix
) ≤ −t},
p :=
|P|
|P| + |U| + |N|
· 100%,
u :=
|U|
|P| + |U| + |N|
· 100%,
n :=
|N|
|P| + |U| + |N|
· 100%,
and
p
0
:=
|P|
|P| + |N|
· 100%, n
0
:=
|N|
|P| + |N|
· 100%.
In other words, P is the set of those pairs from the
dataset D for which the anomaly index has decreased
by at least t when the bug was fixed. Similarly, N
is the set of those pairs for which the anomaly index
has increased by at least t when the bug was fixed.
And U is the set of those pairs for which the anomaly
index has changed less than t. For example, if t = 1,
then p
0
is the percentage of cases when the value of
the anomaly index on the bug is greater than on the
corresponding fix, if we discard all pairs for which
the difference in the value of the anomaly index does
not exceed 1. The results for each dataset are given
in Table 1 and Table 2. Thus, we see that when fixing
the bug, the value of the index usually decreases.
The following snippet shows the example of a
function with the large change in anomality between
the defective and correct code in the PyTraceBugs
dataset.
def audio_normalize(clip):
max_volume = clip.max_volume()
return volumex(clip, 1 / mindex)
def audio_normalize(clip):
max_volume = clip.max_volume()
if max_volume == 0:
# Nothing to normalize.
# Avoids a divide by zero error.
return clip.copy()
else:
return volumex(clip, 1 / max_volume)
The bug consists in the potential zero division.
Adding the code and comment which addresses this
issue significantly decreases the index of this frag-
ment (from 120 to 78).
RQ4: Is A-Index related to known software
metrics?
A-Index: Semantic-based Anomaly Index for Source Code
263
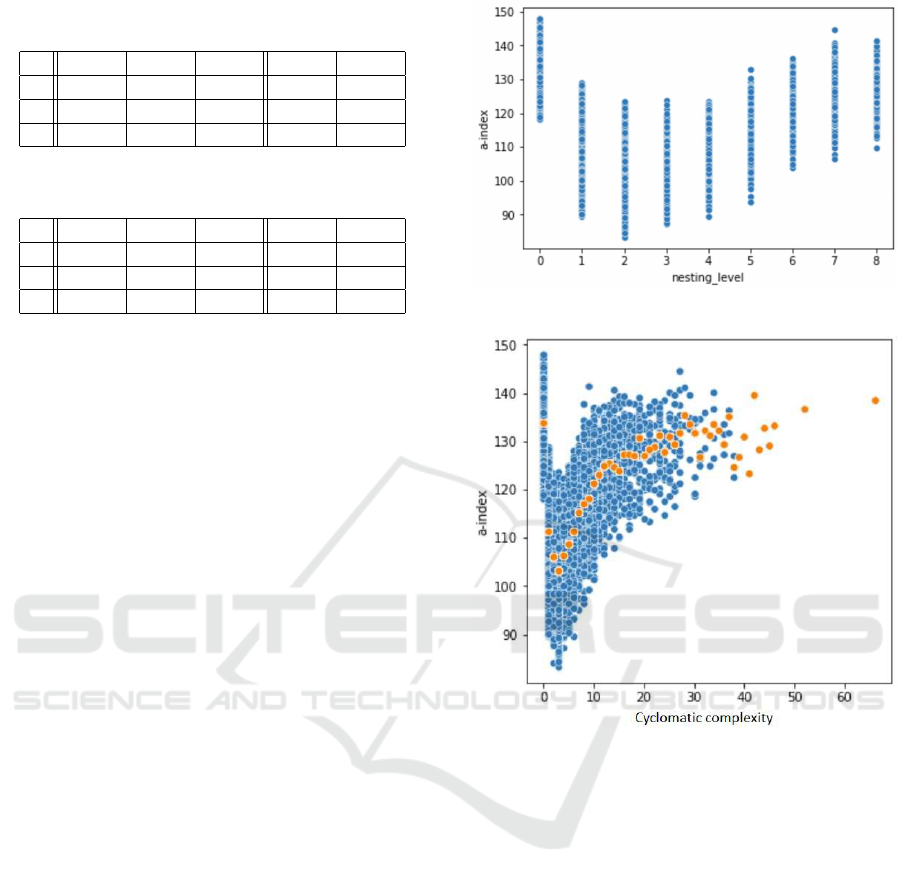
Table 1: Results of experiments with bug-fix pairs from the
BugsInPy dataset with a VAE hidden layer size of 16.
t p, % u, % n, % p
0
, % n
0
, %
0 63.16 0.00 36.84 63.16 36.84
1 42.86 37.59 19.55 68.67 31.33
2 36.09 49.62 14.29 71.64 28.36
Table 2: Results of experiments with bug-fix pairs from the
PyTraceBugs dataset with a VAE hidden layer size of 16.
t p, % u, % n, % p
0
, % n
0
, %
0 58.37 0.00 41.63 58.37 41.63
1 39.87 33.82 26.31 60.25 39.75
2 30.05 50.51 19.44 60.71 39.29
As A-INDEX represents a numeric estimate, com-
puted on source code, one might ask if it is related to
the known software metrics. Below, we answer this
RQ in the affirmative by establishing links between
A-INDEX and known source code metrics, computed
on source code at the granularity of functions and
methods. Specifically, we show that A-INDEX re-
flects certain aspects of complexity of source code
snippets.
In Python, as in many other programming lan-
guages, there is a class of statements, which are re-
sponsible for program flow management. This class
includes loops, conditional statements, handling of
exceptions and many other similar statements. A
source code snippet, incorporating many loops, con-
ditionals or other control flow patterns, is in fact
highly structured as it admits a variety of branches
along which program flow can go. Highly structured
source code is considered complex and generally re-
quires higher cost to maintain. As a consequence, it
is usually a good candidate for redesign.
It turns out that A-INDEX can reveal highly nested
source code. To explore this, we create a synthetic
dataset, which contains artificially generated snippets
with varying nesting level of program flow blocks,
specifically, nested loops, conditionals and try-except
blocks. The scatterplot is given on Fig. 2, demon-
strating the connection between nesting levels and A-
INDEX.
Here, nesting level of 0 corresponds to absence of
control flow blocks in source code. We see that A-
INDEX grows as nesting level increases for nesting
levels above 1.
High structural complexity of source code is mea-
sured by the well known source code metric called
cyclomatic complexity. Roughly, it is proportional to
the number of distinct branches in source code along
which program flow can go. It not only accounts
for common program flow blocks such as loops and
conditionals, but also for list comprehensions, which
Figure 2: Source code nesting level and A-INDEX.
Figure 3: Cyclomatic complexity and A-INDEX. Orange
points represent medians of A-INDEX over points at the
vicinity of a specific value of cyclomatic complexity.
might additionally include conditionals. The scatter-
plot on Fig. 3 emphazises the connection between A-
INDEX and cyclomatic complexity, computed on the
synthetic dataset.
Another source code pattern that A-INDEX re-
flects is related to complexity of expressions in source
code. Heavy expressions with many operands and op-
erations are also considered complex and error-prone.
Specifically, A-INDEX scores high values for snip-
pets with complex expressions. To explore this, we
again create a synthetic data set, which contains ar-
tificially generated snippets with varying numbers of
operands in every single expression, whose count of
source code lines is fixed. The graph on Fig. 4
shows A-INDEX rising when the number of expres-
sion operands increase.
Complexity of expressions in source code is mea-
sured by the well-known group of metrics, called Hal-
stead metrics. The maximal number of distinct ex-
ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering
264
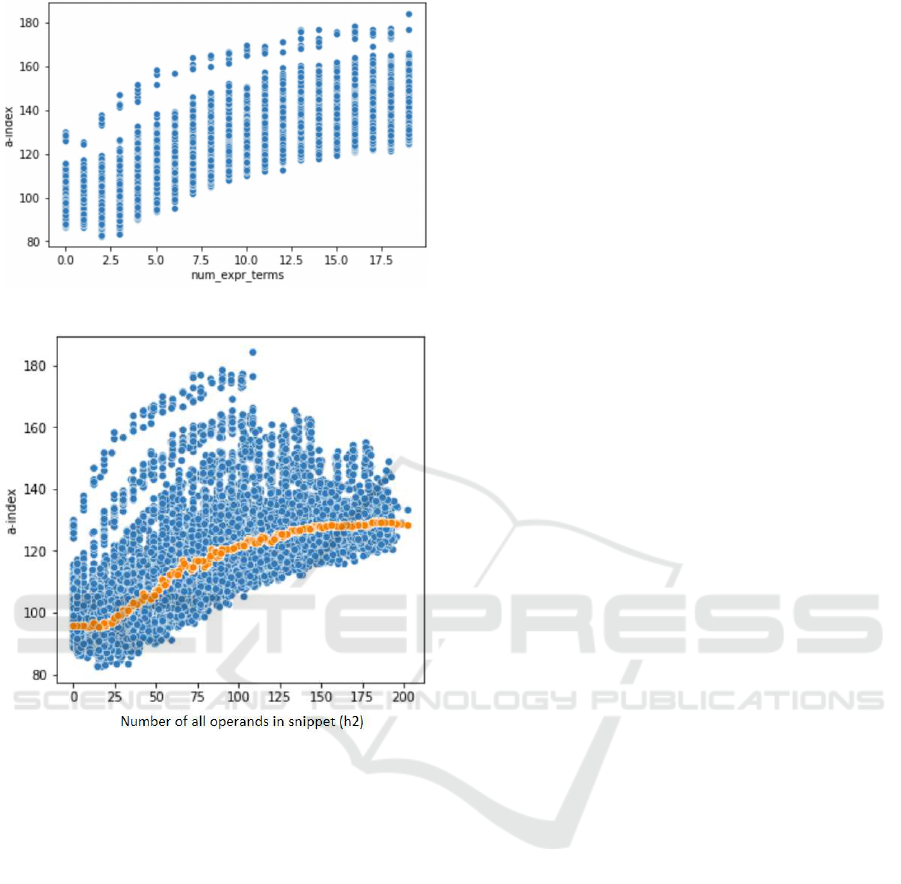
Figure 4: Number of expression operands and A-INDEX.
Figure 5: Total number of operands and A-INDEX. Or-
ange points represent medians of A-INDEX over points at
the vicinity of a specific value of total number of operands.
pression operands, arising in a single expression, is
most correlated with the metric from this group called
total number of operands and denoted by h
2
. This
metric not only accounts for expression operands but
also other types of operands. The scatterplot on Fig.
5 below demonstrates links between A-INDEX and h
2
on the synthetic dataset.
Finally, we observe that, in general, none of the
known source code metrics is significantly correlated
with A-INDEX on real source code when snippets
have counts of source code lines above some small
value. To explore on this conjecture, we conducted
experiments on Py150 dataset.
5 THREATS TO VALIDITY
5.1 Programming Language
Despite the fact that the proposed model is naturally
generalized to other programming languages, we car-
ried out experiments only for a single Python lan-
guage.
5.2 Code Representation
In the model, we use the representation of the code us-
ing GraphCodeBERT model. This way of represent-
ing code has worked well for many tasks in software
engineering (Guo et al., 2021). At the same time, if
some important information about the code was lost
at the stage of calculating embeddings, then later it
will not be available and, therefore, will not be taken
into account when detecting anomalies.
5.3 Code Granulation
In the current approach, code snippets correspond to
individual functions. Additionally, we experimented
with approaches where fragments are defined by a
sliding window of a fixed size, but the results were
worse. Despite the naturalness and prevalence of
these approaches, it seems interesting to conduct ex-
periments for other granulation levels.
6 CONCLUSION
We propose a novel semantic-based approach to cal-
culating the code anomaly index. The larger the index
value, the less typical the code fragment is. Unlike
standard code quality metrics, this index is implicit
and not handcrafted. Though it reflects some code
complexity patterns such as code nesting and com-
plexity of expressions, it does not reveal any close
connection with known source code metrics on real
codebases. In distinction to the metrics, it is able to
take into account local coding conventions, the wis-
dom of the crowd, etc. The index is defined as the
output of the anomaly model. The model is a combi-
nation of a Transformer and a variational autoencoder.
It is trained in an unsupervised mode for Python, but
the approach can be applied to other programming
languages. Moving forward, we would like to ex-
plore other representations for code fragments. To
evaluate the usefulness of the index, we used it to find
anomalies in the code. In addition, we investigated
the relationship between the values of the index and
A-Index: Semantic-based Anomaly Index for Source Code
265

the presence of bugs in the code. Despite the fact that
datasets with bugs were not used during training the
index (zero-shot learning), experiments have shown
that the value of the index usually decreases when the
bug is fixed. Thus, the evaluation shows the potential
of the index.
Computations were performed on the Uran super-
computer at the IMM UB RAS.
REFERENCES
Afric, P., Sikic, L., Kurdija, A. S., and Silic, M.
(2020). REPD: Source code defect prediction as
anomaly detection. Journal of Systems and Software,
168:110641.
Akimova, E. N., Bersenev, A. Y., Deikov, A. A., Kobylkin,
K. S., Konygin, A. V., Mezentsev, I. P., and Misilov,
V. E. (2021a). A survey on software defect prediction
using deep learning. Mathematics, 9(11).
Akimova, E. N., Bersenev, A. Y., Deikov, A. A., Kobylkin,
K. S., Konygin, A. V., Mezentsev, I. P., and Misilov,
V. l. E. (2021b). PyTraceBugs: A large python code
dataset for software defect prediction. In Proceedings
of the 28th Asia-Pacific Software Engineering Confer-
ence, pages 229–239.
Allamanis, M., Barr, E. T., Devanbu, P., and Sutton, C.
(2018). A survey of machine learning for big code
and naturalness. ACM Comput. Surv., 51(4).
Allamanis, M., Jackson-Flux, H., and Brockschmidt, M.
(2021). Self-supervised bug detection and repair.
CoRR, abs/2105.12787.
Alsawalqah, H., Faris, H., Aljarah, I., Alnemer, L., and
Alhindawi, N. (2017). Hybrid smote-ensemble ap-
proach for software defect prediction. In Silhavy,
R., Silhavy, P., Prokopova, Z., Senkerik, R., and
Kominkova Oplatkova, Z., editors, Software Engi-
neering Trends and Techniques in Intelligent Systems,
pages 355–366.
Bryksin, T., Petukhov, V., Alexin, I., Prikhodko, S., Shpil-
man, A., Kovalenko, V., and Povarov, N. (2020). Us-
ing large-scale anomaly detection on code to improve
kotlin compiler. MSR ’20, pages 455–465, New York.
Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K.
(2019). BERT: Pre-training of deep bidirectional
transformers for language understanding. In Proceed-
ings of the 2019 Conference of the North American
Chapter of the Association for Computational Lin-
guistics, pages 4171–4186, Minneapolis, Minnesota.
Feng, H., Kolesnikov, O., Fogla, P., Lee, W., and Gong,
W. (2003). Anomaly detection using call stack infor-
mation. In 2003 Symposium on Security and Privacy,
2003., pages 62–75.
Guo, D., Ren, S., Lu, S., Feng, Z., Tang, D., Liu, S.,
Zhou, L., Duan, N., Svyatkovskiy, A., Fu, S., Tu-
fano, M., Deng, S. K., Clement, C. B., Drain, D., Sun-
daresan, N., Yin, J., Jiang, D., and Zhou, M. (2021).
GraphCodeBERT: Pre-training code representations
with data flow. In ICLR 2021.
Kingma, D. P. and Welling, M. (2014). Auto-encoding
variational bayes. In 2nd International Conference
on Learning Representations, ICLR 2014, Banff, AB,
Canada, April 14–16, 2014, Conference Track Pro-
ceedings.
Le, V. and Zhang, H. (2021). Log-based anomaly detection
without log parsing. CoRR, abs/2108.01955.
Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen,
D., Levy, O., Lewis, M., Zettlemoyer, L., and Stoy-
anov, V. (2019). RoBERTa: A robustly optimized
bert pretraining approach. arXiv e-prints, page
arXiv:1907.11692.
Moshtari, S., Santos, J. C., Mirakhorli, M., and Okutan, A.
(2020). Looking for software defects? First find the
nonconformists. In SCAM 2020, pages 75–86.
Neela, K. N., Ali, S. A., Ami, A. S., and Gias, A. U. (2017).
Modeling software defects as anomalies: A case study
on promise repository. JSW, 12(10):759–772.
Nu
˜
nez-Varela, A. S., P
´
erez-Gonzalez, H. G., Mart
´
ınez-
Perez, F. E., and Soubervielle-Montalvo, C. (2017).
Source code metrics: A systematic mapping study.
Journal of Systems and Software, 128:164–197.
Ray, B., Hellendoorn, V., Godhane, S., Tu, Z., Bacchelli,
A., and Devanbu, P. (2016). On the ”naturalness” of
buggy code. ICSE ’16, pages 428–439.
Raychev, V., Bielik, P., and Vechev, M. (2016). Probabilistic
model for code with decision trees. SIGPLAN Not.,
51(10):731–747.
Rezende, D. J., Mohamed, S., and Wierstra, D. (2014).
Stochastic backpropagation and approximate infer-
ence in deep generative models. In ICML 2014, pages
1278–1286.
Sakurada, M. and Yairi, T. (2014). Anomaly detection
using autoencoders with nonlinear dimensionality re-
duction. In MLSDA’14.
Sharma, T. and Spinellis, D. D. (2020). Do we need im-
proved code quality metrics? ArXiv, abs/2012.12324.
Tong, H., Liu, B., and Wang, S. (2018). Software defect
prediction using stacked denoising autoencoders and
two-stage ensemble learning. Information and Soft-
ware Technology, 96:94–111.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,
L., Gomez, A. N., Kaiser, L., and Polosukhin, I.
(2017). Attention is all you need. NIPS’17, pages
6000–6010.
Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., and
Manzagol, P.-A. (2010). Stacked denoising autoen-
coders: Learning useful representations in a deep net-
work with a local denoising criterion. J. Mach. Learn.
Res., 11:3371–3408.
Widyasari, R., Sim, S. Q., Lok, C., Qi, H., Phan, J., Tay, Q.,
Tan, C., Wee, F., Tan, J. E., Yieh, Y., Goh, B., Thung,
F., Kang, H. J., Hoang, T., Lo, D., and Ouh, E. L.
(2020). BugsInPy: A database of existing bugs in
python programs to enable controlled testing and de-
bugging studies. ESEC/FSE 2020, pages 1556–1560.
ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering
266
