Improved Predictive Fundamental Period Formula for Reinforced

Concrete Structures through the Use of Machine Learning

Algorithms

Nathan Carstens

, George Markou

and Nikolaos Bakas

Department of Civil Engineering, University of Pretoria, South Africa

Department of RnD, RDC Informatics, Athens, Greece

Keywords: Machine Learning Algorithms, Fundamental Mode Formulae, Modal Analysis, Soil-structure Interaction,

Finite Element Method, Reinforced Concrete, Hybrid Modelling.

Abstract: With the development of technology and building materials, the world is moving towards creating a better and

safer environment. One of the main challenges for reinforced concrete structures is the capability to withstand

the seismic loads produced by earthquake excitations, through using the fundamental period of the structure.

However, it is well documented that the current design formulae fail to predict the natural frequency of the

considered structures due to their inability to incorporate the soil-structure interaction and other features of the

structures. This research work extends a dataset containing 475 modal analysis results developed through a

previous research work. The extended dataset was then used to develop three predictive fundamental period

formulae using a machine learning algorithm that utilizes a higher-order, nonlinear regression modelling

framework. The predictive formulae were validated with 60 out-of-sample modal analysis results. The numerical

findings concluded that the fundamental period formulae proposed in this study possess superior prediction

ability, compared to all other international proposed formulae, for the under-studied types of buildings.

1 INTRODUCTION

The soil-structure interaction (SSI) phenomenon is a

typical structural and geotechnical engineering issue,

still open regarding its practical applications. Further

investigation is required to develop simplified but

reliable methods to account for such a phenomenon

in routine structural analyses (Ceroni et al., 2012). In

calculating the appropriate seismic loads, the

fundamental period serves as one of the most critical

dynamic characteristics. In the event of a seismic

excitation, the interaction between the superstructure

(building) and substructure (soil) becomes critical as

it commences to alter the distribution of stresses and

strains within the superstructure, which alters the

expected results (Mourlas et al., 2019).

It is well known that computing the fundamental

mode of fixed-base structures through design code

formulae has its challenges (Mourlas et al., 2019).

Furthermore, some shortcomings exist in the stiffness

distribution of the structure due to a lack of adequate

consideration of the effects of shear walls, especially

in the Eurocode 8 design code (Gravett et al., 2019).

These considerations can cause a considerable

amount of over or under designing of reinforced

concrete (RC) structures, which can lead to

inadequate designs liable to seismic conditions. Thus,

it is crucial to establish a design tool that can

successfully predict the dynamic properties of a

variety of different RC structures.

It is usually not in favour of safety to analyse the

response of a fixed-base structure by neglecting the

SSI effect. In some cases, codes provide seismic

design provisions by reducing the base shear of the

fixed-base structures. In others, they suggest

performing advanced analysis to investigate the

overall effect (Mourlas et al., 2020). As a result, there

is a need for more accurate design expressions for RC

structures that can accurately predict their

fundamental period while accounting for SSI effects.

When it comes to the SSI effect, the reaction of a

building to a seismic event is evaluated in conjunction

with the compressibility of its surrounding soil. The

flexibility of the soil can impact its stress distribution

and displacement profiles, which can be distinguished

from standard fixed-base systems (Saadi, 2018,

Markou et al., 2018).

Carstens, N., Markou, G. and Bakas, N.

Improved Predictive Fundamental Period Formula for Reinforced Concrete Structures through the Use of Machine Learning Algorithms.

DOI: 10.5220/0010984500003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 647-652

ISBN: 978-989-758-547-0; ISSN: 2184-433X

647

A study conducted by Gravett et al. (2019)

determined that the current design code formula

assumes that all reinforced concrete structures have a

fixed base, resulting in errors of up to 85% for

international codes such as Eurocode 8. Upon further

investigation, it was concluded that a RC structure's

dynamic response could be significantly affected by

SSI and stiffness redistribution when susceptible to

seismic activity (Mourlas et al., 2019). See Table 1

below for a few design code formulae found in the

international literature.

Table 1: International design codes in practice.

Relevant Code Formulae

NEAK (New Greek

Antiseismic Code)

𝑇



=0.09

𝐻

√

𝐿



𝐻

𝐻+𝜌𝐿

Old Cyprus Code

𝑇



𝑁

Eurocode

𝑇



=𝐶



𝐻

.

In order to conduct this research report, the

application of finite element modelling, using

advanced modelling software, was utilised to

construct models representing various RC structures.

The finite element method (FEM) is frequently used

in computing engineering, and mathematical models,

the FEM allows for the numerical solution of

differential equations.

For this research project, the constructed FEM

models were analysed using modal analysis to get

results that would help the researcher identify and

understand the dynamic response of the various RC

structures. Eigen-value problems are common in

engineering. The parameter calculates the

fundamental periods of a structural system (Felippa,

2004). The solution method used for this research

project is called the subspace iteration algorithm

(Bathe et al., 1980). The solution is ideally suited for

large-scale structures.

By utilising HYMOD (Markou et al., 2015), one

can decrease the computational demands of the

numerical model, allowing us to perform any type of

analysis of various RC buildings at full-scale. With

Reconan FEA (2020) software, analyses are

performed to capture the complete nonlinear

structural response, either with or without the SSI

effect., while this was software used to perform the

modal analyses. It must be noted here that the modal

algorithm of Reconan FEA was validated through

numerous experimental data.

Based on the procedure described in Taljaard et

al., 2021 and Gravett et al., 2021, developing a dataset

through the use of 3D detailed modeling and then

using machine learning (ML) algorithms to develop

closed form solutions can be a very powerful tool in

developing new fundamental period formulae.

Therefore, the objective of this research work is to

extend the initial dataset developed by Gravett at al.,

2021, and use the extended dataset in developing a

more accurate fundamental period formula.

2 MACHINE LEARNING

This research work used the Julia ML framework.

Similar to Python, this is an open-source, high-level

language for dynamic programming. A mathematical

model in ML is designed to develop generalised

relationships between independent and dependent

variables due to their nonlinear characteristic. As

stated above, the focus of this research work is

developing software generated data that is used to

train ML algorithms to determine the fundamental

period of RC structures.

Table 2, shows the high-order nonlinear

regression algorithm that was used in this research

work to develop the improved formulae. This

algorithm was adopted from Gravet et al., 2021.

Table 2: Higher-Order Nonlinear Regression Algorithm

(Gravett et al., 2021).

Input: XX (matrix of Independent Variables), YY

(Vector of Dependent Variable), nlf (number

of nonlinear features to be kept in the model)

Out

ut: Prediction Formulae

1. Create all nonlinear features (anlf)

2. For i from 1 to nl

, do:

3. For

from 1 to anlf, do:

4. Add

feature to the model

5. Calculate Prediction Error, MAPE

6. END

7. Keep in the model the j

feature

which yields the minimum

rediction erro

8. END

Return: Prediction Formula

3 NUMERICAL CAMPAIGN

3.1 Database Development

In order to construct the extended database that would

consist of various RC structures, various geometrical

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

648

parameters of the initial model were modified. These

parameters include the height of the structures, base

conditions, stiffness distribution throughout the

structure, and the plan area of the structure. Figures 1

and 2 show different RC building models that were

created for the needs of the dataset development.

With all the models created and the parameters for

each model determined, the eigenfrequencies were

determined, and all the data were stored in an Excel

spreadsheet. Table 3 summarises the minimum and

maximum geometrical properties for the models that

were adjusted in this research work.

Figure 1: Different model geometries.

Figure 2: Different model base conditions.

Table 3: Minimum and maximum values of the newly

obtained HYMOD meshes.

Variables Minimum Maximum

Soil Depth (m) 1 60

Soil E (kPa) 65,000 700000

H (m) 3 30

L (m) 3.4 34.4

B (m) 3.4 34.4

(

)

0 85.29

3.2 Modal Analyses

For each of the numerical models, a modal analysis

was performed to determine the eigenfrequencies of

each model. For each model, only the two

translational modes were used to construct the

dataset. Translation oscillations along the global x-

and y-axis directions.

Figure 3 shows the effect of shear walls on the

computed fundamental period of the under-study RC

structures. It is evident that when shear walls are

added to the RC buildings they significantly lower the

fundamental period of the structure. Figure 4 shows

the relationship of the period of a structure and how

it is affected by the soil depth. It is easy to observe

that the SSI effect reaches a plateau as the depth

increases.

Figure 3: Shear wall effect on fundamental period.

Figure 4: Soil depth effect on the fundamental period.

3.3 Proposed Fundamental Period

Formulae

The ML algorithm is designed to determine the

number of features used within the design formulae.

For this research work, a design formula with 3, 5,

and 20 features were developed and parametrically

investigated. It must be noted here that the total

number of fundamental period results used in the

dataset to train and test was 790. Each fundamental

period formula is constructed through the use of the

following variables:

H the building's height (m)

ρ the percentage shear walls (%)

the soils' modulus of elasticity (kPa)

L the length of building parallel to the

oscillating direction (m)

B the width of the building perpendicular to the

oscillating direction (m)

D the soil depth (m)

0,1

0,3

0,5

0,7

0,9

1,1

5 152535

Period [s]

Structural Height [m]

No Shear Walls

Added Shear Walls

0,552

0,554

0,556

0,558

0,56

0,562

0 20406080

Period [s]

Soil Depth [m]

Improved Predictive Fundamental Period Formula for Reinforced Concrete Structures through the Use of Machine Learning Algorithms

649

3.3.1 3-Feature Formula

It should be noted that the three feature formulae do

not consider any SSI parameters. However, this

formula still yielded an absolute mean error of 3.43%.

The relationship can be seen in Eq. 1.

𝑇=



0.0310197 ∙ 𝐻



−



0.00011254 ∙ 𝜌 ∙ 𝐻





0.0000129093 ∙ 𝐻∙ 𝐵





+ 0.0110165

(1)

Figure 5: 3-Feature formula prediction vs numerically

predicted results.

Figure 6: 5-Feature formula prediction vs numerically

predicted results.

3.3.2 5-Feature Formula

Eq. 2 shows the 5-feature formula as it derived from

the training and testing of the extended dataset. The

absolute mean error for the 5-feature formula was

calculated as 2.70%, which is more accurate

compared to the 3-feature formula. This is attributed

to the inclusion of additional parameters that affect

the final predictions.

𝑇=



0.0296602 ∙ H



−



0.000154717 ∙ ρ ∙ H





0.0000210854 ∙ L ∙ B ∙ H





0.0000042983 ∙ 𝐻



∙



−



0.00000785228 ∙ ρ ∙ B ∙ H



+ 0.0229

(2)

3.3.3 20-Feature Formula

Finally, the most accurate formula is presented in Eq.

3. The absolute mean error of the 20-feature formula

was calculated as 1.49%. It is evident that the use of

SSI related parameters in this relationship, makes this

formula the most accurate when used on the training

and testing datasets. Fig. 7 shows the comparison

between the predictions derived from the proposed

formula and the numerical results.

𝑇=



0.0292939 ∙ H



−



0.000150825 ∙ ρ ∙ H





0.00000582242 ∙ H ∙ B







0.00000330369 ∙ ρ ∙

𝐻







0.000215881 ∙ H ∙ L



− 1.89375x10



∙

𝐸





∙D+



0.00000323855 ∙ L ∙ H ∙D



−



0.00000646154 ∙ ρ ∙ B ∙ H



−



0.0000000000925478 ∙ 𝐻∙ 𝐸



∙𝐷



−



0.0000000000406192 ∙ 𝜌∙ 𝐸



∙𝐷





0.000000194394 ∙ 𝐷∙ 𝜌







0.0037148 ∙ 𝐵





0.000000358861 ∙ 𝜌 ∙𝐻∙ 𝐷





0.0000000000662381 ∙ 𝐸



∙𝐷





−



0.000000278639 ∙ 𝐷





−



0.000000000113737 ∙

𝐿∙𝐸



∙𝐷



−



0.0000016727 ∙ 𝐵







0.0000309934 ∙ 𝐿∙ 𝐷



−



0.00178654 ∙ 𝐿





0.000000645744 ∙ 𝐿





+ 0.00239996

(3)

Figure 7: 20-Feature formula prediction vs numerically

predicted results.

4 VALIDATIONS OF RESULTS

To further test the ability of the proposed formulae to

predict the fundamental period of RC structures, a

dataset was developed for validation purposes. For

this reason, 60 out-of-sample building models were

constructed and used to further validate the ability of

the proposed formulae in predicting the fundamental

period of RC buildings with and without SSI effects.

From Figures 8 - 10 it is evident that comparing

the proposed formulae manage to predict the out-of-

sample data with high accuracy. The most significant

improvement was seen with the 3-feature proposed

0,2

0,4

0,6

0,8

1,2

00,511,5

Formula Predicted Values [s]

Numerically Predicted Values [s]

0,2

0,4

0,6

0,8

1,2

0 0,5 1 1,5

Formula Predicted Values [s]

Numerically Predicted Values [s]

0,2

0,4

0,6

0,8

1,2

0 0,5 1 1,5

Formula Predicted Values

[s]

Numerically Predicted Values [s]

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

650

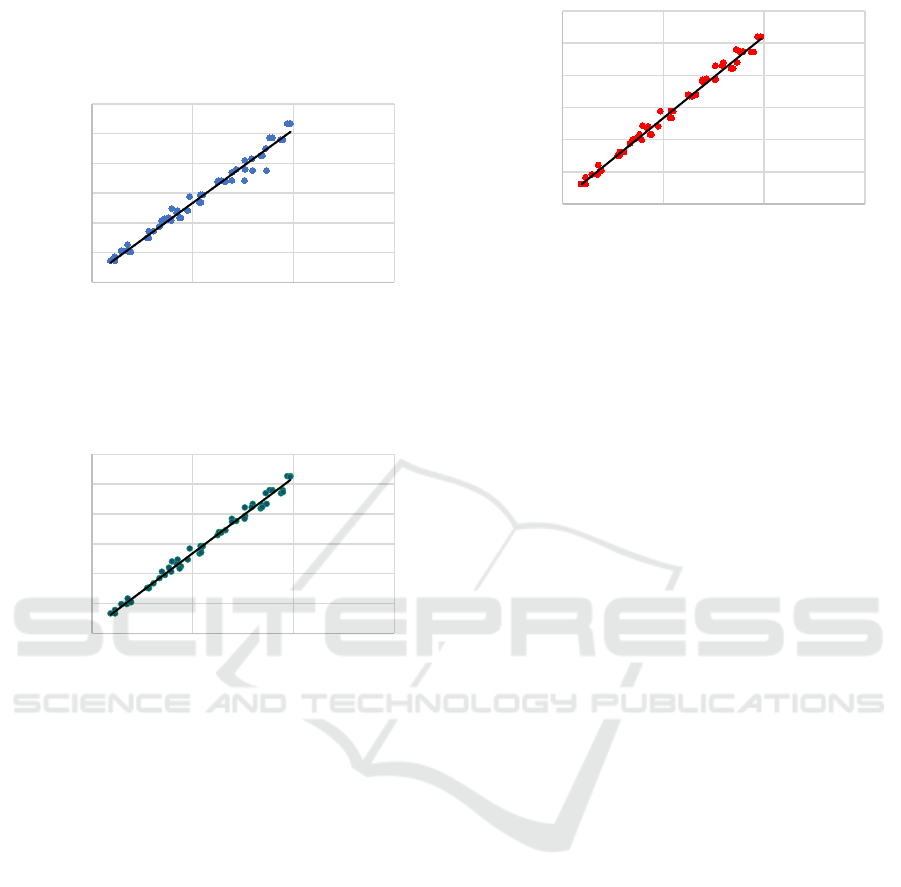
formula that improved with 4.19% from the results

obtained by Gravett et al., (2021). The 20-feature

formula also had a significant improvement of 0.22%.

Figure 8: Correlation of 3-feature formula on validation

dataset.

Figure 9: Correlation of 5-feature formula on validation

dataset.

5 CONCLUSIONS AND FUTURE

WORK

790 fundamental period results were used to train an

ML algorithm and develop accurate design formulae

to calculate the fundamental period of RC structures.

The three proposed formulae were then tested with

out-of-sample data comprising 60 new RC models

constructed in a manner that foresaw the use of new

parameters compared to the models used to train and

test the formulae. This served as the validation phase

in which the design formulae showcased a high

degree of correlation, effectively proving their

accuracy and extendibility.

According to the numerical investigation, the

most accurate proposed formula on train, test and

validation data was the 20-feature, which was found

to be improved compared to the one proposed by

Gravett et al., 2021.

Figure 10: Correlation of 20-feature formula on validation

dataset

Finally, this research work will foresee a further

dataset extension and also take into account the infill

walls of RC buildings. The asymmetry of buildings

should also be investigated in the near future and how

that affects the fundamental period of RC structures

when the SSI effect is accounted for.

REFERENCES

Bathe, K.J. and Ramaswamy, S., 1980. An accelerated

subspace iteration method. Computer Methods in

Applied Mechanics and Engineering, Vol 23, No 3, pp.

313-331.

Ceroni, F., Sica, S., Pecce, M. and Garofano, A., 2012.

Effect of Soil-Structure Interaction on the dynamic

behaviour of masonry and RC buildings. Proceedings

of the 15

World Conference on Earthquake

Engineering (WCEE)., p. 10.

Felippa, C., 2004. Introduction to finite element methods,

University of Colorado., p. 885.

Gravett, D.Z., Mourlas, C., Markou, G. and Papadrakakis,

M., 2019. Numerical performance of a new algorithm

for performing modal analysis of full-scale reinforced

concrete structures that are discretised with the

HYMOD approach, COMPDYN 2019, 7

International

Conference on Computational Methods in Structural

Dynamics and Earthquake Engineering, 24-26 June

2019, Crete, Greece..

Gravett, Z.D., Mourlas, C., Taljaard V.L., Bakas P.N.,

Markou, G. and Papadrakakis, M. (2021), New

Fundamental Period Formulae for Soil-Reinforced

Concrete Structures Interaction Using Machine

Learning Algorithms and ANNs, Soil Dynamics and

Earthquake Engineering, 144 (2021), 106656.

Markou, G., Sabouni, R., Suleiman, F. and El-Chouli, R.,

2015. Full-Scale Modeling of the Soil-Structure

Interaction Problem Through the Use of Hybrid Models

(HYMOD), International Journal of Current

Engineering and Technology, Vol 5, No2, p. 15.

Markou, G., AlHamaydeh, M. and Saadi, D., 2018. Effects

of the soil-structure-interaction phenomenon on RC

y = 0,9873x + 0,041

R² = 0,9789

0,2

0,4

0,6

0,8

1,2

00,511,5

Formula Predicted Period [s]

Numerically Predicted Period [s]

y = 1,0126x + 0,0316

R² = 0,9912

0,2

0,4

0,6

0,8

1,2

0 0,5 1 1,5

Formula Predicted Period [s]

Numerically Predicted Period [s]

y = 1,0159x + 0,0267

R² = 0,9888

0,2

0,4

0,6

0,8

1,2

00,511,5

Formula Predicted Period [s]

Numerically Predicted Period [s]

Improved Predictive Fundamental Period Formula for Reinforced Concrete Structures through the Use of Machine Learning Algorithms

651

structures with pile foundations. Proceedings of the 9th

GRACM International Congress on Computational

Mechanics.

Mourlas, C., Gravett, D.Z., Markou, G. and Papadrakakis,

M., 2019. Investigation of the soil-structure interaction

effect on the dynamic behaviour of multi-storey RC

buildings. VIII international conference on

computational methods for coupled problems in science

and engineering.

Mourlas, C., Khabele, N., Bark, H.A., Karamitros, D.,

Taddei, F., Markou, G. and Papadrakakis, M., 2020.

The Effect of Soil-Structure Interaction on the

Nonlinear Dynamic Response of Reinforced Concrete

Structures. International Journal of Structural Stability

and Dynamics, Vol 20, No 13), p. 39.

Reconan FEA v2.00, User’s Manual. 2020.

https://www.researchgate.net/publication/342361609_ReC

onAn_v200_Finite_Element_Analysis_Software_User

's_Manual

Saadi, D., 2018. Nonlinear FEA of Soil-Structure-

Interaction Effects on RC Shear-Wall Structures. PhD

thesis. American University of Sharjah.

Taljaard, V.-L., Gravett, D.Z., Mourlas, C., Bakas, N.,

Markou, G. and Papadrakakis, M., “Development of a

New Fundamental Period Formula by Considering

Soil-Structure Interaction with the Use of Machine

Learning Algorithms”, COMPDYN 2021, 27-30 June

2021, Streamed from Athens, Greece.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

652