Addressing the Challenges of Last-mile: The Drone Routing Problem

with Shared Fulﬁllment Centers

Maria Elena Bruni and Sara Khodaparasti

Department of Mechanical, Energy and Management Engineering, University of Calabria, Rende, Cosenza, Italy

Keywords:

Drone Routing Problem, Drone Energy Consumption, Uncertainty.

Abstract:

With the easing of restrictions worldwide, drones will become a preferred transportation mode for last-mile

deliveries in the coming years. Drones offer, in fact, an optimal solution for many challenges faced with

last-mile delivery as congestion and emissions and can streamline the last leg of the supply chain. Despite

the common conviction that drones will reshape the future of deliveries, numerous hurdles prevent practical

implementation of this futuristic vision, among which the limited drone range and payload. To overcome this

issue, big companies such as Amazon, are already ﬁling up patents for the development of fulﬁlment centers

where drones can be restocked before ﬂying out again for another delivery, effectively extending their range.

Only a few authors have addressed the joint problem of operating these facilities and providing services to

retail companies. This paper addresses this problem and proposes a mathematical formulation to show the

viability of the proposed approach.

1 INTRODUCTION

The last few years have seen a sharp increase of the

paradigms of on-demand economy and e-commerce.

To catch up with these trends, new last-mile delivery

systems, exploiting the use of drones, have been en-

visioned to reduce delivery times, avoid trafﬁc delays

and potentially cut costs in the long term.

Although drones are used in a number of appli-

cations within logistics and delivery, this ambitious

program has yet to be implemented on a large scale.

The vision of drone-based last-mile solutions, within

a fully automated delivery system, is challenged by

intrinsic characteristic as small payload, limited bat-

tery capacity and regulatory and safety issues of air

control administrations. Despite these unsolved ques-

tions, the idea of using drones for parcel delivery is

gaining ground. We should hence expect that, in a

near future, these types of delivery systems will be

more common for products and services and there

will be greater adoption of this technology. In prepa-

ration for this possible future, Amazon released a

number of patents for different types Fulﬁllment Cen-

ters (FCs) that would accommodate the landing and

takeoff of drones in dense urban settings. These sta-

tions, networked with a central control and a plurality

of drones, include a number of services from pack-

age handling to recharging/refueling operations. This

raises emerging problems relative to the location of

new, maybe big, FCs closer to customers and the man-

agement of delivery services provided. A possible

promising solution for enhancing the use of drones

in the last-mile, is the adoption of a shared use of FCs

among retail companies providing drone delivery ser-

vices. As a matter of facts, sharing FCs could sensibly

reduce the total number of drones in the sky and the

total operational costs of companies. This paradigm,

dealing with the complexity of the sharing economy,

raises signiﬁcant challenges to policy and decision-

makers, as well as operational issues to be addressed.

This paper takes a step in this direction, provid-

ing a guide to retail companies for drone routing and

FCs choice, to better control the whole process, offer-

ing practical insights on how to to manage this new

system. The problem is complicated, since it merges

complexity of a combined location-routing problem

with new operational challenges related to the use

of drones, among which energy consumption—which

nonlinearly depends on the payload, battery weight,

and travel time— and uncertainty in ﬂight duration.

The remainder of this paper is organized as follows.

Section 2 provides a detailed review of the relevant

literature. The problem under study is described in

Section 3. In Section 4, computational results are dis-

cussed. Finally, Section 5 presents conclusions and

directions for future research.

362

Bruni, M. and Khodaparasti, S.

Addressing the Challenges of Last-mile: The Drone Routing Problem with Shared Fulﬁllment Centers.

DOI: 10.5220/0010983100003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 362-367

ISBN: 978-989-758-548-7; ISSN: 2184-4372

2 LITERATURE REVIEW

To put the contribution of the present paper in the

right stream, we restrict our attention to routing prob-

lems where drones are used to directly deliver parcels

to customers.

A pure drone delivery problem was addressed in

(Dorling et al., 2016), where two multi-trip vehicle

routing formulations differing only in terms of the ob-

jective function (either total operating cost or total de-

livery time) were proposed. A simulated annealing

algorithm was designed to solve the model heuristi-

cally. A package delivery problem with autonomous

drones considering the battery capacity and its rela-

tion with payload and ﬂight range was considered in

(Choi and Schonfeld, 2017). The objective function

was expressed as the total cost including the cost as-

sociated to the estimated users’ waiting time. In an-

other study, the drone delivery problem was addressed

in a multi-trip context (Troudi et al., 2018), where

the minimization of total travel distance, drone ﬂeet

size, and number of batteries is considered. All the

previous contributions failed to take into account the

nonlinear nature of the energy constraints, hamper-

ing in this way the successful application of drone-

based delivery systems. An important exception is a

recent paper (Cheng et al., 2020), where the multi-trip

drone routing problem is formulated as a two-index

model, and the energy consumption depends nonlin-

early on the payload and linearly on travel distance.

Some valid cuts are presented and a branch-and-cut

algorithm is developed. (Kim et al., 2021) proposed

a drone routing model with multiple depots and mul-

tiple drones, with ﬂight range constraints. The objec-

tive function minimizes the sum of routing and drone

usage costs. Following the location routing context,

in (Kim et al., 2017) the use of drones for a pickup

and delivery problem arising in healthcare is inves-

tigated. The authors proposed a set covering model

to ﬁnd the optimal number of locations used as de-

pots, followed by a multi-depot drone routing model.

A Lagrangian Relaxation method was also proposed

to solve the model. Another applicative context of

drone location routing is patrol application (Liu et al.,

2019). The model ﬁnds the optimal location of sites to

launch the drones and the optimal drone routes mini-

mizing the total cost, including the base establishment

cost, drone usage cost, and the ﬂight cost. (Torabbeigi

et al., 2020) proposed two mathematical formulations

involving strategic and operational plans to optimize

the drone routes for parcel delivery. At the strate-

gic level, a set covering model is solved to determine

the minimum number of depots to open such that all

customers are covered; next, at the operational stage,

a drone routing model is solved in order to ﬁnd the

minimum number of required drones to dispatch from

the open depots and the corresponding optimal drone

paths. The authors include energy consumption con-

straints into the problem and model them as a linear

functions in terms of payload and travel time.

3 MATHEMATICAL

FORMULATION

We introduce in this section the Drone Routing Prob-

lem with Shared FCs (DRP-ShaFC) as a tailored

location-routing problem, where the operational chal-

lenges related to the use of drones, among which en-

ergy consumption and uncertainty in ﬂight duration,

are taken into account. Our model also includes,

rather originally, a latency objective, i.e. the sum of

arrival times at the customers, which is a compelling

measure for customer-oriented problems, where cus-

tomers’ demand should be met in a timely fashion.

We assume that a set D of distributed FCs are

available to be used to enhance last-mile delivery.

We can consider any type of FCs, truck-based ware-

houses, local re-stocking stations for drones or bee-

hives as well. To offer landing, takeoff, package han-

dling, recharging services, the FC operator requires a

tariff (in the foregoing denoted by T ).

A retail company owning k drones, should bring

items to a set C of customers on the ground. Each

drone makes multiple stops per trip: a single trip

consists of the drone starting at a given FC, where

it would be loaded with the customers’ orders up to

its payload capacity Q, and visiting one or more cus-

tomers. At the end of each ﬂight, the drone is sent

back to one of the FCs, not necessarily the same of

the departure.

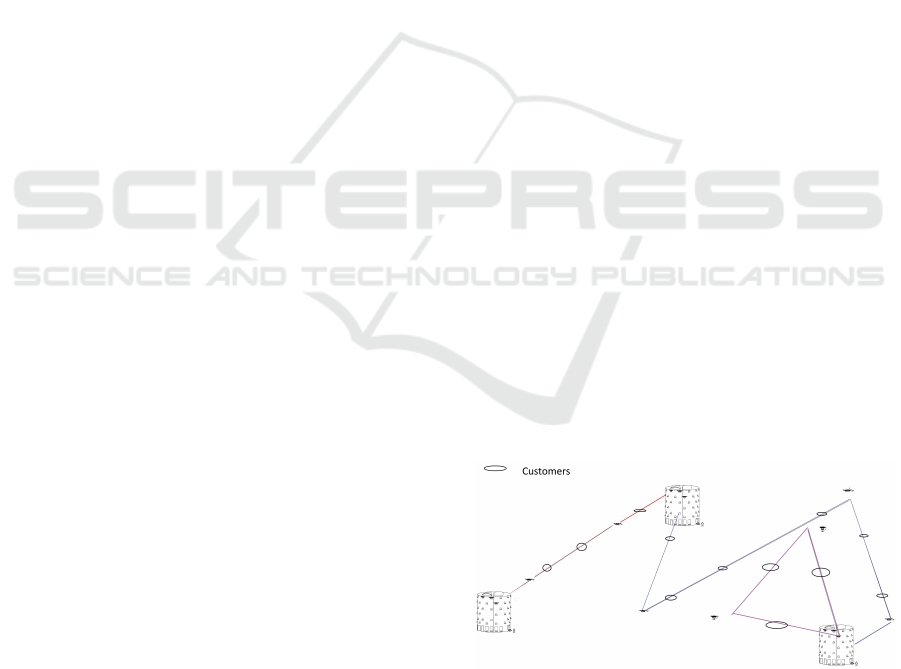
Figure 1: Scheme of the delivery system.

Figure 1 represents the delivery scheme. The

drone energy consumption between the FCs and the

delivery points determines the optimal delivery route

based on the battery capacity. Instead of assum-

ing that drone endurance is limited by a ﬁxed ﬂight

Addressing the Challenges of Last-mile: The Drone Routing Problem with Shared Fulﬁllment Centers

363

Figure 2: Multi-layer network.

time, we consider energy consumption as a (nonlin-

ear) function of payload, battery weight, and travel

time. In particular, let t

i j

be the travel time between

nodes i and j, W + M = Γ (W is the frame weight

(in kg) and M (kg) is the battery weight). The energy

consumed by the drone, carrying a payload d

is ex-

pressed as k(Γ + d

)

3/2

i j

where k =

ρξh

(here g is

the gravity constant (in N), ρ is the ﬂuid density of air

(in kg/m

), ξ is the area of spinning blade disc (in m

)

and h is the number of rotors) (Cheng et al., 2020).

The mathematical formulation is essentially de-

veloped based on an extension of the multi-layer net-

work, which has been proved to be superior to other

models, for a wide range of routing problems (for

more information, please see (Nucamendi-Guill

et al., 2016), (Bruni et al., 2020)).

The multi-layer network is displayed in Figure

2 where the customers and the FCs are depicted by

squares and circles. The auxiliary FCs 0 and m + 1

are added to specify, respectively, the start and the

end of each tour. The network contains N + 1 levels

(positions) where N = |C| − k + 1 is an upper bound

on the number of visited customers in a tour. Let

L = {0,··· , r, · ·· , N} be the set of levels. Levels

N to 2 represent the position of the visited customer

within the tour and include copies of customers, FCs

and the auxiliary FC 0. Instead level 1 corresponds

to the last visited customer within the drone trip and

includes only copies of customers and of the auxil-

iary FC m + 1. For the sake of completeness we also

consider level 0 to specify the FC that retrieves the

drone. A feasible solution in the multi-layer network

is made of k distinct drone trips where each trip starts

from a copy of one of the FCs, that is directly linked

to the auxiliary FC 0, and is followed a subset of cus-

tomers. The last visited customer is the one followed

by the auxiliary FC m +1 that is directly connected to

the Fcs that retrieves the drone. Based on the struc-

ture of the multi-layer network, we deﬁne two set of

position dependent binary variables: x

, i ∈ C which

indicate if customer i is visited in position r (meaning

that is the r

-last one), y

i j

, r ≥ 1 to show that cus-

tomer j is visited right after node i ∈ D ∪C in posi-

tion r and w

i j

, r ≥ 2 which tell if customer j is the

ﬁrst one to be visited by a drone launched from the

FC i ∈ D and there are r −1 customers to be visited in

the trip. We also extend the deﬁnition of variables y

and w to account for the end of each drone trip where

j(m+1)

, j ∈ C takes 1 if the customer j is the last

stop of the trip drone, and therefore is followed by

the dummy FC m+ 1; also, w

, j ∈ C, i ∈ D takes 1 if

after serving the last customer j, the drone is retrieved

at the FC i. Binary variables z

indicate if the FC i is

used or not. The total load carried by the drone upon

departure from customer i to reach customer j is de-

noted by u

i j

; if customer j is the ﬁrst customer after

the drone departure from the FC f , its load is denoted

by v

f j

. The accumulated energy consumption upon

arrival at node i ∈ C ∪ D is denoted by e

. Let deﬁne

V = D

∪C ∪ D, where D

= {0, m + 1} is the set of

auxiliary FCs introduced to specify the start and the

end of each drone trip. The total number of FCs used

is limited to N

and each FC i ∈ D can host at most

drones. Using the above notation, the model is

formulated as

min

∑

i∈D

∑

j∈C

∑

r∈L

r6=1

i j

∑

i∈C

∑

j∈C

j6=i

∑

r∈L

i j

∑

i∈D

(1)

∑

r∈L

= 1 i ∈ C (2)

∑

r∈L

∑

j∈C

0 j

= k (3)

∑

i∈C

∑

r∈L

∑

j∈C

0 j

(4)

∑

j∈C

j6=i

i j

= x

r+1

i ∈ C,r ∈ L \ {N} (5)

∑

i∈C∪{0}

i6= j

i j

= x

j ∈ C, r ∈ L \ {N} (6)

0 j

= x

j ∈ C (7)

∑

i∈D

i j

≥ y

0 j

, j ∈ C, r ∈ L \ {1} (8)

≥ w

i j

, i ∈ D, j ∈ C, r ∈ L, \{1} (9)

∑

i∈D

≤ N

(10)

∑

j∈C

∑

r∈L

i j

≤ N

i ∈ D (11)

∑

i∈D

j(m+1)

j ∈ C (12)

j(m+1)

≥

∑

i∈D

(13)

∑

j∈C

≤

∑

r∈L\{1}

∑

j∈C

i j

i ∈ D (14)

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

364

i j

≥ d

∑

r∈L\{1}

i j

, i ∈ D, j ∈ C (15)

i j

≤ Q

∑

r∈L\{1}

i j

, i ∈ D, j ∈ C (16)

i j

≥ d

∑

r∈L

i j

, i, j ∈ C, i 6= j (17)

i j

≤ (Q − d

)

∑

r∈L\{N}

i j

, i, j ∈ C, i 6= j (18)

∑

h∈D

∑

j∈C

j6=i

−

∑

j∈C

j6=i

i j

= d

, i ∈ C (19)

+ k(Γ + u

i j

)

3/2

i j

≤ e

+ M

i j

(1 −

∑

r∈

L\{N}

i j

) i, j ∈ C, i 6= j

(20)

+ k(Γ + v

i j

)

3/2

i j

≤ e

+ M

i j

(1 −

∑

r∈

L\{1}

i j

) i ∈ D, j ∈ C

(21)

+ k Γ

3/2

∑

i∈D

≤ B j ∈ C,i ∈ D (22)

= 0 i ∈ D (23)

∈ {0,1} i ∈ D (24)

∈ {0,1} i ∈ C, r ∈ L (25)

0 j

∈ {0,1} j ∈ C, r ∈ L (26)

j(m+1)

∈ {0,1} j ∈ C (27)

i j

∈ {0,1} i, j ∈ C, i 6= j, r ∈ L, r 6= N (28)

i j

∈ {0,1} i ∈ D, j ∈ C, r ∈ L \ {1} (29)

i j

∈ {0,1} i ∈ C, j ∈ D (30)

i j

≥ 0 i, j ∈ C, i 6= j (31)

≥ 0 i ∈ D (32)

where M

i j

and M

i j

are the ”big-M” parameters.

The objective function (1) minimizes the total

waiting times of the customers plus the cost associ-

ated to the use of the FCs. Constraints (2) ensure that

each customer is visited exactly once. Constraint (3)

ensures the use of exactly k drones. Constraint (4), (5)

and (6) guarantee the continuity of each tour. Con-

straints (7) force nodes to be connected to node 0 at

level N. Constraints (8) and (9) allow starting a drone

route only from used facilities. Constraint in (10) and

(11) represent the restriction on the maximum number

of facilities used and the number of drones that each

facility can handle. Constraints (12)-(13) deﬁne the

relation between the last customer visited and the des-

tination facility. Constraints (14) determine the return

of drones to facilities. Constraints (15)–(19) are used

to limit the drone payload (Nucamendi-Guill

en et al.,

2018). Constraints (20)–(23) represent the drone en-

ergy consumption. Finally, Constraints (24)–(32) es-

tablish the nature of the variables.

As known, weather conditions, wind direction and

aerial congestion can inﬂuence the travel time of the

drone and hence, the energy consumption. In this

paper, we consider drone travel time as an uncer-

tain parameter belonging to a box uncertainty U

∞

{ξ|||ξ||

∞

≤ Ψ}, where here Ψ is a parameter control-

ling the size of the uncertainty set.

Following the robust paradigm in (Ben-Tal et al.,

2015), the robust counterpart of the proposed model

can be derived as follows.

min

∑

r∈L

r6=1

r (

i j

+ Ψ

i j

∑

i∈C

∑

j∈C

j6=i

∑

r∈L

r (

i j

+ Ψ

i j

∑

i∈D

+ k(Γ +u

i j

)

3/2

(

i j

+ Ψ

i j

) ≤ e

+ M

i j

(1 −

∑

r∈L\{N}

i j

)

i, j ∈ C, i 6= j

+ k(Γ +v

i j

)

3/2

(

i j

+ Ψ

i j

) ≤ e

+ M

i j

(1 −

∑

r∈L\{1}

i j

)

i ∈ D, j ∈ C

+ k Γ

3/2

∑

i∈D

(

+ Ψ

≤ B j ∈ C,i ∈ D

(2)-(19),(23)-(32)

(33)

(34)

(35)

(36)

where the uncertain parameter t

i j

falls within the sym-

metric box [

i j

− Ψ

i j

+ Ψ

i j

4 COMPUTATIONAL

EXPERIMENTS

In this section, we conduct some experiments to show

the validity of the proposed formulation.

All the experiments were executed on an Intel

Core i7-10750H, with 2.60 GHz CPU and 16 GB

RAM working under Windows 10 with the algebraic

modeling language AIMMS 4.79.2.5. Since model

(1)–(32) is a nonlinear MIP model with box uncer-

tainty set, we solved it using the outer approximation

algorithm with a time limit of 500 seconds. The Outer

approximation algorithm is considered as the state-of-

the-art approach for solving MINLP models. The al-

gorithm follows a basic decomposition approach and

solves an alternating sequence of nonlinear subprob-

lems and relaxed MIP master problems that provide,

respectively, upper and lower bounds. If the origi-

nal MINLP model is convex, the algorithm guaran-

tees to ﬁnd the global optimal solution (Duran and

Grossmann, 1986). We used the A1 and A2 instances

presented in (Cheng et al., 2020). The demand distri-

bution varied between values from [0.1, 0.7] kg for the

ﬁrst 40% of customers and from [0.1, 1.5] kg for the

remaining customers. Two conﬁgurations (Centeres

and Marginal) were selected for the FCs locations,

either in the center of the customers area or in the

outskirts. In the problem analysis, values of 2,3,5,6

were chosen as the maximum number of drones per

Addressing the Challenges of Last-mile: The Drone Routing Problem with Shared Fulﬁllment Centers

365

Table 1: Results for Set A1 instances.

Centered Marginal

Instance |C| |D| k N

Obj CPU (s) Obj CPU (s)

A 10 1 10 5 2 2 7.016 7.09 6.635 2.85

A 10 2 6.796 2.02 6.557 2.68

A 10 3 6.838 4.11 NFS 500

A 10 4 6.568 2.77 N.A. N.A.

A 10 5 6.956 2.75 NFS 500

A 15 1 15 5 3 2 12.09 33.38 12.05 35.1

A 15 2 12.524 48.49 12.252 30.17

A 15 3 11.999 37.94 12.127 32.12

A 15 4 12.241 42.86 12.346 41.78

A 15 5 12.327 47.55 11.873 51.74

A 20 1 20 5 4 3 12.602 336.83 12.591 305.37

A 20 2 12.667 442.88 12.559 440.93

A 20 3 12.68 496.25 12.684 425.31

A 20 4 - 500 - 500

A 20 5 - 500 - 500

Avg 166.99 257.87

Table 2: Results for Set A2 instances.

Centered Marginal

Instance |C| |D| k N

Obj CPU (s) Obj CPU (s)

A2 10 1 10 5 2 2 6.901 2.51 6.759 2.16

A2 10 2 6.712 2.68 - 500

A2 10 3 6.787 2.05 - 500

A2 10 4 6.808 2.13 N.A. N.A.

A2 10 5 6.795 2.57 - 500

A2 15 1 15 5 3 2 12.11 37.94 12.165 30.95

A2 15 2 12.035 34.72 12.032 30.43

A2 15 3 11.934 22.27 11.795 26.58

A2 15 4 12.313 47.91 12.247 41.05

A2 15 5 12.108 20.58 12.342 20.6

A2 20 1 20 5 4 3 12.312 302.21 12.791 273.28

A2 20 2 12.625 452.68 12.163 434.08

A2 20 3 12.425 451.64 12.561 403.01

A2 20 4 - 500 - 500

A2 20 5 - 500 - 500

Avg 158.79 284.14

FC. The tariff for using a FC has been set according

to (Aurambout et al., 2019) as the potential average

cost across the whole industry, inclusive economies

of scales multiplied by the average number of cus-

tomers serviced. We remark that in the considered

experiments the FC tariff has been considered inde-

pendent from the speciﬁc location. In fact, given the

limited drone range, the more the FCs are close to the

customers, the higher will be the number of compa-

nies willing to use the service. Even though the FC

building cost is higher as we approach the city center,

it is also true that the massive use of the service by

commercial companies could lower the tariffs, given

that the FC economic return is higher. Hence, consid-

ering the same tariff for both conﬁgurations is, in our

opinion, reasonable.

Finally, we considered a homogeneous ﬂeet of 2,

3, 4, 7 or 8 Alta 8 drones with the following char-

acteristics: W = 6.2 (kg), M = 2.8 (kg), h = 8, ρ =

1.204(kq/m

),ξ = 0.1256(m

), B = 0.355 (kWh).

Tables 1 and 2 present the characteristic of the in-

stances considered, the objective function value (Obj)

and the solution time in seconds (CPU) for set A1 and

A2. As a general observation, we note that the com-

8 10 12 14

18 20

2.7

2.8

2.9

3.1

D1(4)

D2(2),D5(2)

D2,D3,D4,D5

Cost for using the FCs

Total latency

= 4

= 2

= 1

Figure 3: Trade-off between latency and cost.

putational time is quite limited, especially consider-

ing that this problem is a tactical operational problem.

For some instances, however, it was not possible to

ﬁnd a solution within 500 seconds (a dash is reported

in the Tables). The position of the FCs does not seem

to inﬂuence a lot the total latency since on average the

percentage difference is quite low and below 5%. We

notice, however that one instance (A1 10 4) becomes

infeasible when the FCs are marginally placed in the

customer’s area.

Figure 3 shows the impact of the number of drones

that each FCs can dispatch. As it is evident, to quickly

satisfy the delivery demand it is beneﬁcial for the de-

livery company to use more FCs. We observe that the

total latency could decrease from around 3 hours to

2.6 hours. However, the cost for using the FCs can

considerably increase.

5 CONCLUSIONS

In this paper, we addressed a new emerging prob-

lem in last-mile logistics, namely the joint manage-

ment of FCs and autonomous vehicles. The process is

modeled as a variant of the location routing problem,

called DRP-ShaFC. The main characteristics of this

new problem are the drones intrinsic properties, as

a limited battery capacity, payload, and the weather-

related uncertainties that lead to uncertain ﬂight dura-

tion. Moreover, business oriented objectives, as cus-

tomer satisfaction (through the latency) and the cost

of using distributed FCs are also taken into account.

The model introduced can be solved to optimality for

instances with limited size. For larger instances, efﬁ-

cient solution methods should be proposed and tested.

This aspect becomes crucial in view of possible ex-

tensions where the optimization of the FC tariffs is

embedded into the model. This might be done by a

combinatorial bi-level programming approach able to

model the hierarchical decision-making process.

An interesting avenue for future research is the in-

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

366

corporation of green criteria, to assess the environ-

mental impact of this paradigm compared to tradi-

tional non shared systems. In this respect, we hope

that this paper will foster new researches to soon open

the way of a large-scale implementation of this shared

delivery system, where different FCs jointly provide

services to drone delivery companies. This, in turn,

could better satisfy the booming customers demand

for on-time and fast delivery services.

REFERENCES

Aurambout, J.-P., Gkoumas, K., and Ciuffo, B. (2019). Last

mile delivery by drones: an estimation of viable mar-

ket potential and access to citizens across european

cities. European Transport Research Review, 11(1):1–

21.

Ben-Tal, A., Den Hertog, D., and Vial, J.-P. (2015). Deriv-

ing robust counterparts of nonlinear uncertain inequal-

ities. Mathematical programming, 149(1):265–299.

Bruni, M. E., Khodaparasti, S., and Demeulemeester,

E. (2020). The distributionally robust machine

scheduling problem with job selection and sequence-

dependent setup times. Computers & Operations Re-

search, 123:105017.

Cheng, C., Adulyasak, Y., and Rousseau, L.-M. (2020).

Drone routing with energy function: Formulation and

exact algorithm. Transportation Research Part B:

Methodological, 139:364–387.

Choi, Y. and Schonfeld, P. M. (2017). Optimization of

multi-package drone deliveries considering battery ca-

pacity. In Proceedings of the 96th Annual Meeting of

the Transportation Research Board, Washington, DC,

USA, pages 8–12.

Dorling, K., Heinrichs, J., Messier, G. G., and

Magierowski, S. (2016). Vehicle routing problems for

drone delivery. IEEE Transactions on Systems, Man,

and Cybernetics: Systems, 47(1):70–85.

Duran, M. A. and Grossmann, I. E. (1986). An outer-

approximation algorithm for a class of mixed-integer

nonlinear programs. Mathematical programming,

36(3):307–339.

Kim, S., Kwak, J. H., Oh, B., Lee, D.-H., and Lee, D.

(2021). An optimal routing algorithm for unmanned

aerial vehicles. Sensors, 21(4):1219.

Kim, S. J., Lim, G. J., Cho, J., and C

e, M. J. (2017).

Drone-aided healthcare services for patients with

chronic diseases in rural areas. Journal of Intelligent

& Robotic Systems, 88(1):163–180.

Liu, Y., Liu, Z., Shi, J., Wu, G., and Chen, C. (2019). Op-

timization of base location and patrol routes for un-

manned aerial vehicles in border intelligence, surveil-

lance, and reconnaissance. Journal of Advanced

Transportation, 2019.

Nucamendi-Guill

en, S., Angel-Bello, F., Mart

ınez-Salazar,

I., and Cordero-Franco, A. E. (2018). The cumula-

tive capacitated vehicle routing problem: New formu-

lations and iterated greedy algorithms. Expert Systems

with Applications, 113:315–327.

Nucamendi-Guill

en, S., Mart

ınez-Salazar, I., Angel-Bello,

F., and Moreno-Vega, J. M. (2016). A mixed integer

formulation and an efﬁcient metaheuristic procedure

for the k-travelling repairmen problem. Journal of the

Operational Research Society, 67(8):1121–1134.

Torabbeigi, M., Lim, G. J., and Kim, S. J. (2020). Drone de-

livery scheduling optimization considering payload-

induced battery consumption rates. Journal of Intelli-

gent & Robotic Systems, 97(3):471–487.

Troudi, A., Addouche, S.-A., Dellagi, S., and Mhamedi,

A. E. (2018). Sizing of the drone delivery ﬂeet con-

sidering energy autonomy. Sustainability, 10(9):3344.

Addressing the Challenges of Last-mile: The Drone Routing Problem with Shared Fulﬁllment Centers

367