Differential-linear Attacks on Permutation Ciphers Revisited:

Experiments on Ascon and DryGASCON

Aslı Bas¸ak Civek

and Cihangir Tezcan

Informatics Institute, Department of Cyber Security, CyDeS Laboratory, Middle East Technical University, Ankara, Turkey

Keywords:

Lightweight Cryptography, Cryptanalysis, Differential-linear Analysis, NIST.

Abstract:

Ascon and DryGASCON are very similar designs that were submitted to NIST’s lightweight cryptography

standardization process. While Ascon made it to the ﬁnals, DryGASCON was eliminated in the second

round. We analyze these algorithms against truncated, linear and differential-linear distinguishers to compare

their security. We correct 2, 3, 3.5-round truncated differentials and 5-round differential-linear distinguishers

that were given for DryGASCON-128. Moreover, we provide the longest practical differential-linear distin-

guisher of DryGASCON-128. Finally, we compare the security of Ascon-128 and DryGASCON-128 against

differential-linear cryptanalysis.

1 INTRODUCTION

With the developing technology, the production and

usage of resource-constrained devices such as RFID,

IoT, and medical implants have increased. Since

some of these devices cannot effectively use existing

cryptographic standards, algorithms that use less en-

ergy and power and are also resistant to side-channel

attacks were needed. Therefore, the National In-

stitute of Standards and Technology (NIST) initi-

ated a competition-like process to select one or more

lightweight standards (McKay et al., 2016). There

were 57 candidates at the beginning and 56 of them

were accepted to the ﬁrst round in April 2019. After

the ﬁrst round, 24 of them were eliminated in August

2019. And ﬁnally, 10 of them made it to the ﬁnals in

March 2021. The competition is expected to last two

more years, and some analyses are expected from the

cryptography community to help to choose the win-

ner.

We performed this study

in order to help the

NIST’s elimination process. We focused on two com-

petitors: Ascon and DryGASCON to compare their

security due to their similar designs. While Dry-

GASCON was eliminated in the second round, Ascon

made it to the ﬁnals. They have equivalent permu-

https://orcid.org/0000-0002-2115-3028

https://orcid.org/0000-0002-9041-1932

This article is based on one of the author’s M.Sc. thesis

(Civek, 2021)

tations, but DryGASCON-128’s round number is 11

instead of 12. It uses Ascon’s 5x5 S-box but repre-

sents it in little-endian. But more importantly, it uses

a different rotation function than Ascon alongside 2

different rotations. So our main focus was to see if the

changes in its permutation made DryGASCON better

than Ascon.

In this work, we focused on differential-linear

distinguishers, and indirectly truncated differential

cryptanalysis and linear cryptanalysis of Ascon (Do-

braunig et al., 2016) and DryGASCON (Riou, 2019).

There was a 4-round differential-linear distinguisher

for Ascon-128 that later turned into a 5-round key re-

covery attack (Tezcan, 2020). For DryGASCON-128,

there was a 5-round theoretical differential-linear dis-

tinguisher (Tezcan, 2020). Since there was no practi-

cal differential-linear distinguisher for DryGASCON,

we decided to provide one to compare it with As-

con’s. On our way to do that we realized that the

initial 3-round probability one truncated differential

distinguisher provided by its designer (Riou, 2019)

was erroneous. We also observed that this misinter-

pretation led to other faulty analyses, which were a

2-round probability one truncated differential distin-

guisher (Tezcan, 2020) that was used in a 5-round

differential-linear distinguisher and an improved 3.5

round probability one truncated differential distin-

guisher (Tezcan, 2020). We believe the reason for

these faulty analyses was the discrepancy between

the provided code and the paper of DryGASCON’s

submission ﬁle. The provided 3-round truncated dif-

202

Civek, A. and Tezcan, C.

Differential-linear Attacks on Permutation Ciphers Revisited: Experiments on Ascon and DryGASCON.

DOI: 10.5220/0010982600003120

In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 202-209

ISBN: 978-989-758-553-1; ISSN: 2184-4356

ferential distinguisher by its designer (Riou, 2019)

and the provided code of DryGASCON have a dif-

ferent approach on handling the rotations; they move

in the opposite direction. We corrected these analy-

ses and provide them in our study. Then we used the

corrected 5-round theoretical differential-linear dis-

tinguisher (Tezcan, 2020) of DryGASCON to pro-

vide its practical results. After that, we provide a new

5-round practical differential-linear distinguisher that

gives better results in terms of bias and data complex-

ity. The linear approximations used in this analysis

were found with lineartrails tool (Dobraunig et al.,

2015a) that has different search methods for ﬁnding

characteristics. In the type-I method, it is allowed to

have active bits anywhere on the permutation with-

out any limitation. In the type-II method, the active

bits are only allowed in the small portion of the ci-

pher which is responsible to produce the ciphertext

in sponge constructions. The analysis of Ascon de-

pends on the type-II search method because, in that

way, it is possible to turn this distinguisher into an at-

tack. However, the analysis of DryGASCON so far

depends on the type-I search method because even

though their designs are similar, DryGASCON uses

some additional functions which made the attack pro-

cess more complicated. So instead of using the type-II

method, the type-I method was used to understand its

general resistance against linear cryptanalysis. In our

analysis, we also used the type-I method to improve

the existing analysis. But for the sake of comparison,

we provide its type-II analysis as well. The analysis

results can be seen in Table 1.

According to these results, it is possible to say

that the changes to Ascon’s permutation did not make

DryGASCON stronger than Ascon. But since Ascon

has one more round than DryGASCON, we may say

that DryGASCON may be more susceptible to this

kind of analysis. But note that this conclusion does

not apply to the attack phase.

2 PRELIMINARIES

2.1 Ascon

Ascon (Dobraunig et al., 2016) is a cipher suite

that has authenticated encryption with associated data

(AEAD) and hashing capabilities. It is currently one

of the ﬁnalists in the NIST lightweight cryptogra-

phy competition. It was also the primary choice

in the CAESAR competition’s (Bernstein, 2013)

lightweight applications category.

Ascon is a substitution-permutation network

(SPN) based algorithm. Its mode of operation de-

pends on the MonkeyDuplex structure; hence its secu-

rity requires the uniqueness of a nonce. Its encryption

process contains initialization, processing of associ-

ated data, processing the plaintext, and ﬁnalization.

Ascon has two variants with different round num-

bers and data block sizes; Ascon-128 and Ascon-

128a. Ascon-128 has a 320-bit state that is formed

by 64 words. These are 64-bit IV, 128-bit secret key,

and 128-bit nonce. Its permutation process is ap-

plied a = 12 (during initialization and ﬁnalization)

and b = 6 times ( during encryption). In the substi-

tution layer, its 5x5 S-box updates its state 64 times

in parallel. Then in the diffusion layer, the function

) is applied to each word. The permutation layer

can be described as follows:

← Σ

),0 ≤ i ≤ 4

← Σ

) = x

⊕ (x

≫ 19) ⊕ (x

≫ 28)

← Σ

) = x

⊕ (x

≫ 61) ⊕ (x

≫ 39)

← Σ

) = x

⊕ (x

≫ 1) ⊕ (x

≫ 6)

← Σ

) = x

⊕ (x

≫ 10) ⊕ (x

≫ 17)

← Σ

) = x

⊕ (x

≫ 7) ⊕ (x

≫ 41)

Ascon is being analyzed since 2014 and the sum-

mary of these analyses was presented on Ascon’s of-

ﬁcial website

. In this work, we mainly focused on

the differential-linear analysis of Ascon-128. This

method was applied in (Dobraunig et al., 2015b),

(Bar-On et al., 2019), and (Tezcan, 2020) in terms of

key recovery attacks. We used the approach of (Tez-

can, 2020) when performing cryptanalysis of Dry-

GASCON, so we will explain their methodology.

2.2 DryGASCON

DryGASCON (Riou, 2019) is a cipher suite that

provides AEAD and hashing functionality. It was

a candidate in NIST’s Lightweight Cryptography

competition but eliminated after the second round.

DryGASCON uses a permutation that is a gen-

eralized version of Ascon, namely Gascon. It

uses a new construction named DrySponge as a

mode of operation. DrySponge is based on Duplex

Sponge construction, but the combination of the in-

put with the state and the extraction of output from

the state is different. DryGASCON has two in-

stances: DryGASCON-128 which was the primary

submission, and DryGASCON-256. Like Ascon-128,

DryGASCON-128 has a 320-bit state formed by 64-

bit words. But unlike Ascon, constant addition de-

pends on the current round instead of a total number

https://ascon.iaik.tugraz.at/publications.html

Differential-linear Attacks on Permutation Ciphers Revisited: Experiments on Ascon and DryGASCON

203

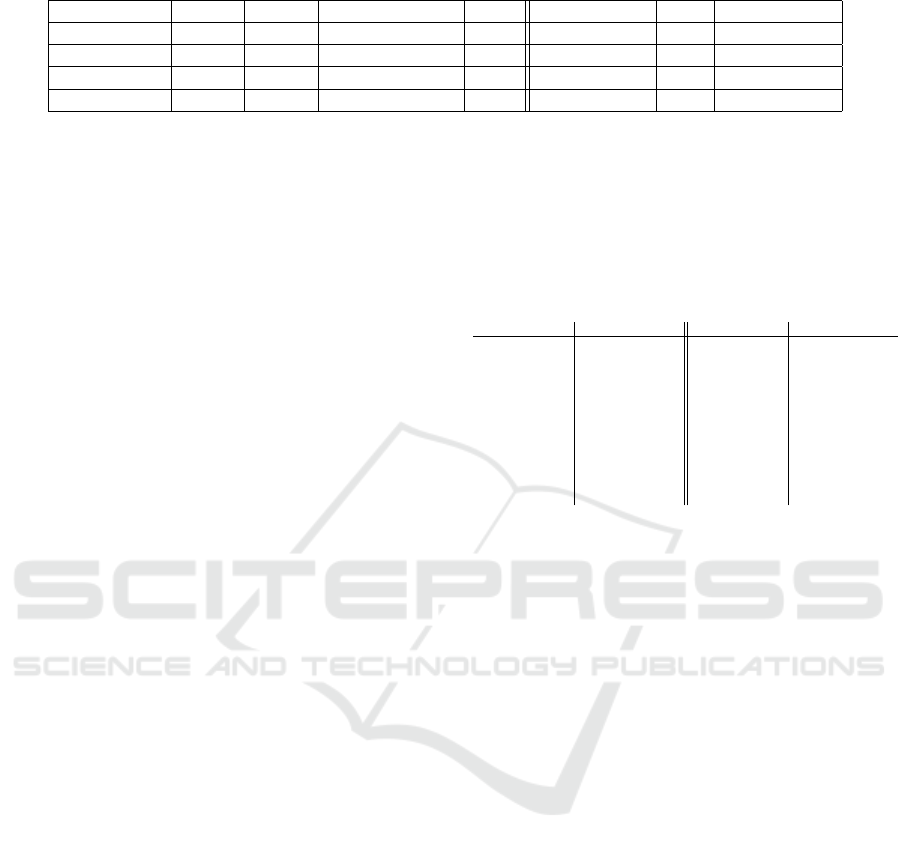
Table 1: Comparison of differential-linear analysis of Ascon128 and DryGASCON-128.

Algorithm Round Type Theoretical Bias Data Practical Bias Data Rerefence

Ascon 4/12 Type-II 2

−15

−1.68

(Tezcan, 2020)

DryGASCON 4/11 Type-II 2

−15

−1.67

Sec. 3.2

DryGASCON 5/11 Type-I 2

−29

61.28

- - (Tezcan, 2020)

DryGASCON 5/11 Type-I - - 2

−5.34

Sec. 3.2

of rounds. Its round number is 11 instead of 12. It

uses Ascon’s 5x5 S-box except represents it in little-

endian. In the substitution layer, this S-box updates

its state 64 times in parallel. Then in the diffusion

layer, the function Σ

) is applied to each word. The

permutation layer can be described as follows:

) = x

⊕ (x

≫ 19) ⊕ (x

≫ 28)

) = x

⊕ (x

≫ 61) ⊕ (x

≫ 38)

) = x

⊕ (x

≫ 1) ⊕ (x

≫ 6)

) = x

⊕ (x

≫ 10) ⊕ (x

≫ 17)

) = x

⊕ (x

≫ 7) ⊕ (x

≫ 40)

The linear layer of DryGASCON-128 is similar to

the linear layer of Ascon-128. But in DryGASCON

two rotations are different, namely Σ

and Σ

. They

were changed into 38 from 39 in Σ

and 40 from 41 in

. The rotation function is also different. According

to (Riou, 2019), every 64-bit word rotates once with

an odd shift to make sure that a difference in half of

an input word will be propagated to the other half of

the matching output word.

DryGASCON was ﬁrst analyzed in (Tezcan,

2020) in terms of differential-linear cryptanalysis.

This analysis focused on the constrained version

of DryGASCON. Namely, it did not take into ac-

count the Mix128 function, which is a unique prop-

erty of DryGASCON. They provided a theoretical 5-

round differential-linear distinguisher (Tezcan, 2020)

of DryGASCON and in this study, we aimed to im-

prove their results by providing a practical distin-

guisher. Recently, (Liang et al., 2021) presented

a practical forgery attack for DryGASCON without

reusing the nonce.

2.3 Undisturbed Bits

Undisturbed bits (Tezcan, 2014) can be used to cre-

ate longer and in some cases favorable differentials in

improbable, impossible, and truncated cryptanalysis.

For an S-box, they can be thought of as probability

one truncated differentials. An output bit is said to

be undisturbed if its difference stays invariant for a

certain input difference.

(Tezcan, 2016) showed that Ascon has 23 undis-

turbed bits in the forward direction and 2 undisturbed

bits in the backward direction. Since Ascon and Dry-

GASCON share the same S-box, the same analysis

also applies to it. Then (Tezcan, 2020) used it to

provide probability one truncated differential distin-

guisher of Ascon and DryGASCON. The undisturbed

bits of both algorithms can be seen in Table 2.

Table 2: Undisturbed bits of Ascon and DryGASCON.

Input Difference Output Difference Input Difference Output Difference

00001 ?1??? 10000 ?10??

00010 1???1 10001 10??1

00011 ???0? 10011 0???0

00100 ??110 10100 0?1??

00101 1???? 10101 ????1

00110 ????1 10110 1????

00111 0??1? 10111 ????0

01000 ??11? 11000 ??1??

01011 ???1? 11100 ??0??

01100 ??00? 11110 ?1???

01110 ?0??? 11111 ?0???

01111 ?1?0?

In this study, we are using undisturbed bits to build

a probability one truncated differential distinguisher

of DryGASCON-128.

2.4 Truncated Differential

Cryptanalysis

Differential cryptanalysis (Biham and Shamir, 1991)

aims to see how a ﬁxed input difference affects the

output difference. There are several methods of ap-

plying this technique, one of which is truncated differ-

ential cryptanalysis (Knudsen, 1994). In this method,

the differences do not have to be fully speciﬁed; sim-

ply ﬁxing a few bits in the input and output differen-

tials is enough. It can be constructed as probability

one for some rounds throughout the cipher by using

undisturbed bits.

In (Tezcan, 2016), a 3.5-round probability one

truncated differential distinguisher was provided for

Ascon. Since the permutation of Ascon and Dry-

GASCON are similar, (Riou, 2019) stated the same

approach is acceptable for DryGASCON. Then they

provided a 3-round probability one truncated differen-

tial distinguisher for DryGASCON and stated that it is

the longest one possible (Riou, 2019). Then (Tezcan,

2020) observed the two S-boxes have non-zero output

difference after 3.5-round, so they were active. So

(Tezcan, 2020) improved Riou’s result by providing

a 3.5-round probability one truncated differential dis-

tinguisher. After that, they used a 2-round version of

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

204

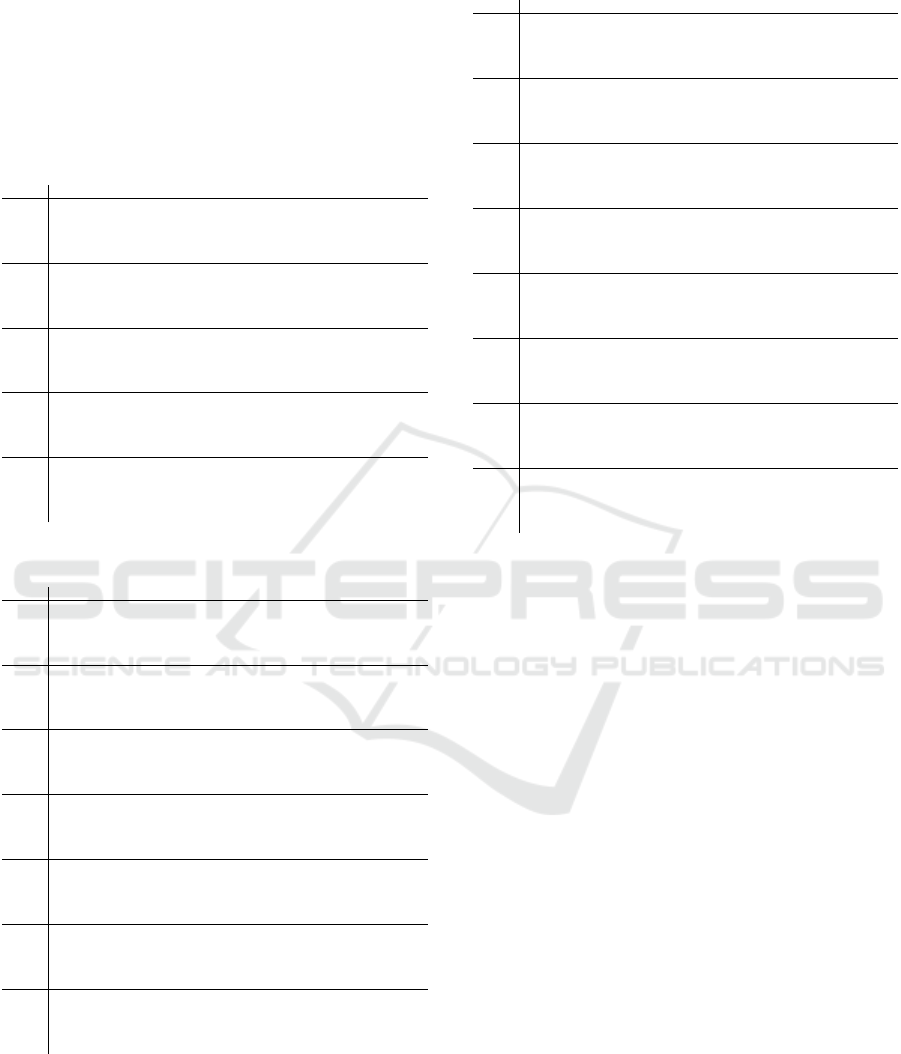
this distinguisher to build a 5-round differential-linear

distinguisher (Tezcan, 2020). We examined both of

their results and realized that these 2, 3, 3.5-round

distinguishers were reported wrong due to misinter-

pretation of the diffusion direction of the bits. The

correction of these 2, 3, 3.5 round distinguishers can

be seen in Table 3, 4, 5 respectively.

Table 3: Corrected results of 2-round distinguisher.

Round 2-Round Truncated Differential of GASCON

C5R11

0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000010000000000000000000000000000000000000

I 0000000000000000000000000010000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

00000000000000000000000000?0000000000000000000000000000000000000

S1 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

00000000000000000000000000?0000000000000000000000000000000000000

00000000?00000000000000000?00000000?0000000000000000000000000000

0000000000000?000000000000?00000000000000000000000000000?0000000

P1 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

00000000000000?00000000000?0000000000000000000000000000000000?00

00000000?0000??00000000000?00000000?00000000000000000000?0000?00

S2 0000000000000??00000000000?00000000000000000000000000000?0000?00

00000000?0000??00000000000?00000000?00000000000000000000?0000?00

00?0000??0000??0000000?000???000000?00?0000?00000?0000???0000?00

???00000?0000??00000000?00???000000?00?0000??000?00000?0?0000?00

P2 0000000000000??0??0000000??00??0?000000000000??000000000?0??0?00

0?0000?0?000???000??000000?0000?00??0000?0000000?0000??0?0000?00

0??0000??0000??00000000000?0?000000?0000000??000??00000??0000?00

Table 4: Corrected results of 3-round distinguisher.

Round 3- Round Truncated Differential of GASCON

C5R11

0000000100000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

I 0000000000000000000000000000000000000000000000000000000000000000

0000000100000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

0000000?00000000000000000000000000000000000000000000000000000000

S1 0000000?00000000000000000000000000000000000000000000000000000000

0000000?00000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

0000000?000000000000000000?0000000000?00000000000000000000000000

P1 0000000?00?0000000000000000000000000000?000000000000000000000000

0000000?0000?0000000000000000000000000000000000?0000000000000000

0000000000000000000000000000000000000000000000000000000000000000

0000000?00?0?0000000000000?0000000000?0?0000000?0000000000000000

S2 0000000?00?0?0000000000000?0000000000?0?0000000?0000000000000000

0000000?00?0?0000000000000?0000000000?0?0000000?0000000000000000

0000000?0000?0000000000000?0000000000?000000000?0000000000000000

0000000??0?0?00?0?000?00???00000000?0?0?0000000??00?0?0000000?00

0000?0??00?0???00000000000?00?0?00?00?0??0?0000?00000000?0?00000

P2 000000???0?0??0??000000000?00?0000000?0??0?0?00?00?0000000?00000

0000000?00?0?0????000000?0?0000?00?00?0?00?0?00?00?0?00000000000

?000000?0?00?0?0000?000000??0000000?0?0000?0000?000000000?000?00

?000?0?????0??????0?0?00????0?0?00??0?0??0?0?00??0????00???00?00

S3 ?000?0?????0??????0?0000?0??0?0?00??0?0??0?0?00?00?0?000???00?00

?000?0?????0??????0?0?00????0?0?00??0?0??0?0?00??0????00???00?00

?????0????????????????????????????????????????0????????????0???0

?????0????????????????0???????0?00???????0??????????????????0???

P3 ?0???0?????????????????0????0????0????????????????????0???????0?

???????????????????????0????????????0?0??0?0????????????????0???

??????????????????0??????????????0?????????????????????????????0

2.5 Linear Cryptanalysis

Linear Cryptanalysis (Matsui, 1993) tries to ﬁnd a

connection between plaintext bits, subkey bits, and

ciphertext bits to obtain a linear expression of the ci-

pher. This can be done by constructing a linear ap-

Table 5: Corrected results of 3.5-round distinguisher.

Round 3.5- Round Truncated Differential of GASCON

C5R11

1000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

I 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

?000000000000000000000000000000000000000000000000000000000000000

1000000000000000000000000000000000000000000000000000000000000000

S1 0000000000000000000000000000000000000000000000000000000000000000

?000000000000000000000000000000000000000000000000000000000000000

?0000000000000?00000000000000000000000000?0000000000000000000000

1000000000000000000100000000000000000000000000000000000000000010

P1 0000000000000000000000000000000000000000000000000000000000000000

?0000?0000000000000000000000000000000000?00000000000000000000000

?0000000000000000000?00000000000000?0000000000000000000000000000

?0000?00000000?0000??00000000000000?0000??00000000000000000000?0

S2 ?0000?00000000000001?00000000000000?0000?00000000000000000000010

?0000?00000000?00001?00000000000000?0000??0000000000000000000010

?0000?00000000?0000??00000000000000?0000??00000000000000000000?0

???00?00?0000??000???0000000?000000?0000??00?0?00?0000??0000???0

???00????00000?0000??000?0000?00000?0000??00?0000??000?0000??0?0

P2 ?00???00??0000000001?01?00000001?10?0??0?00?00000001?00000000010

?0000?0100?0?0?00????0001?000000000?0000??000??0000000?00001?010

?0?00?0??000???0000??0000?000000000?0000??0000000??000??0000???0

???????????0???00????0????00??0???0?0??0??0????00????0??000????0

S3 ???????????0???00????01???000?01?10?0??0??0????00??1?0??000????0

???????????0???00????01???00??01?10?0??0??0????00??1?0??000????0

???00????0?0???00????000??00??00000?0000??00???00??000??000????0

???????????????????????????????????????0????????????????0???????

??????????????????????????????0?????????????????????????????????

P3 ????????????????????????????????????????????????????????????????

????????????????0??????????????????????1????????????????1???????

???00????0?0???0???????0???????????????0???????????0????000?????

???????????????????????????????????????a????????????????b???????

S4 ???????????????????????????????????????a????????????????b???????

???????????????????????????????????????a????????????????b???????

proximation table (LAT) using the S-box of the al-

gorithm. Since it is computationally infeasible to

exhaustively search every linear characteristic, lin-

eartrails tool (Dobraunig et al., 2015a) does this by

using a heuristic approach. In this tool, there are dif-

ferent search types for ﬁnding suitable characteristics

according to usage areas. Type-I characteristics have

no restrictions; active bits are allowed to be on any

bits of the permutation. Therefore, it can be mostly

used to give an idea about the resistance of the cipher

against linear cryptanalysis instead of being used to

attack a sponge construction. Type-II characteristics

have a condition that states the active bits must be in

the outer part of the state, and other bits should not

contain any masks. It can be used for key recovery

attacks on sponge constructions.

In this study, we used linear cryptanalysis to an-

alyze and build differential-linear distinguishers for

Ascon-128 and DryGASCON-128. We used lin-

ear characteristics that were provided by (Dobraunig

et al., 2016) and (Riou, 2019). We also used lin-

eartrails tool (Dobraunig et al., 2015a) to ﬁnd linear

characteristics of DryGASCON.

Differential-linear Attacks on Permutation Ciphers Revisited: Experiments on Ascon and DryGASCON

205

3 DIFFERENTIAL-LINEAR

CRYPTANALYSIS

Differential-linear cryptanalysis (Langford and Hell-

man, 1994) is a method that combines differential

cryptanalysis (Biham and Shamir, 1991) and linear

cryptanalysis (Matsui, 1993). This way, short differ-

ential, and linear characteristics can be combined to

obtain long differential-linear distinguishers that may

be longer than the longest differential or linear char-

acteristics. In this technique, the cipher E is divided

into two parts: E

and E

. In here, E

represents a

truncated differential λ

→ λ

with probability p = 1.

And E

represents a linear approximation ∇

→ ∇

with probability 1/2 + q , where q is the bias. Then

their combination E = E

◦ E

is used to ﬁnd a distin-

guisher for the algorithm. Note that the masked input

bits of the linear approximation should match the zero

difference in the output bits of truncated differentials.

For distinguishing cipher E from a random permu-

tation, a suitable number of plaintext pairs with input

difference λ

is used. The permutation is applied to

each pair, and it is checked if the corresponding ci-

phertexts c1,c2 have the same parity of the mask ∇

This condition is checked with a suitable number of

data. As a result of this, the probability is being ap-

proximately 1/2 shows that the cipher behaves ran-

domly. If not, the cipher might be weak against this

technique. The size of this deviation gives an idea

about how weak the cipher is.

According to (Biham et al., 2002), this technique

is still possible if the masked bits of the ﬁrst round

of linear approximation match with the non-zero but

ﬁxed difference at the end of the truncated differen-

tial. If p is less than 1, it is still possible to build

the distinguisher (Biham et al., 2002). If that is the

case, the bias of this distinguisher can be calculated

as approximately 2pq

and the data complexity is

O(p

−2

−4

) chosen plaintexts approximately, where

O is the big O notation. These calculations come

from Matsui’s Piling-up lemma (Matsui, 1993). If the

probability is p = 1, these turned into θ(q

−4

) chosen-

plaintext for data complexity and 2q

for the bias.

3.1 Ascon

Differential-linear cryptanalysis was applied to 4,5

rounds of Ascon-128 as a key recovery attack (Tez-

can, 2020). To be able to do that, they gave dif-

ferences to the nonce, namely the words x

and x

And since the plaintext is XORed with x

to gen-

erate the ciphertext, they examined the differences

in the output only for x

. They provided a 4-round

differential-linear characteristic by using the 2-round

linear approximation that comes from (Dobraunig

et al., 2015a) and a 2-round probability one truncated

differential. In their previous work, they provided a

3.5-round probability one truncated differential dis-

tinguisher (Tezcan, 2016) by using the undisturbed

bits of Ascon. But they did not use this 3.5 round dis-

tinguisher when building the differential-linear dis-

tinguisher, because it has contained differences in

words x

, x

, and x

. So it was infeasible for per-

forming a key recovery attack with this one. Instead,

they used a 2-round distinguisher with the combina-

tion of a type-II linear approximation with bias 2

−8

They used the type-II characteristics because the last

round of the approximation should have masks only in

word x

, and the rest should have been free from any

masks. According to this study, the theoretical bias

was 2pq

= 2 · 1 · 2

−8

= 2

−15

. Then they practically

veriﬁed these results and found out that the practical

results of these biases were 2

−2.41

−1.68

−2.41

and

−1.68

while key bits are (0, 0), (0, 1), (1, 0), and (1,

1) in the activated S-box, respectively. This makes all

of the practical biases better than the theoretical bias

−15

. The reason for the gap between theoretical and

practical biases was explained with slow diffusion and

the existence of multiple linear characteristics (Tez-

can, 2020).

To perform this attack, they used 2

random

nonces and performed this experiment with 1000 ran-

dom keys for the 4-round permutation (Tezcan, 2020).

They repeated this experiment for 4 possible key pairs

using 2

samples but they could not distinguish the

second key bit because they observed the same biases

regardless of the second key bit. So they captured

the second key bit using another 2

samples by ro-

tating the initial difference. So capturing the whole

128-bit key required 64 · 2 · 2

= 2

sample (Tezcan,

2020). They extended this attack to 5-rounds using

a 3-round probability one truncated differential dis-

tinguisher and 2-round linear approximation with a

31.44

time complexity. To extend this to a 6-round

attack, they used 2

random nonces and repeated the

experiment with 128 random keys by rotating the in-

put difference to every possible position. This opera-

tion was performed with 2·2

·128·64·4 = 2

com-

plexity.

3.2 DryGASCON

Since Ascon and DryGASCON have similar designs,

(Riou, 2019) stated that the cryptanalysis of Ascon

can be applied on DryGASCON with some modiﬁca-

tions. They indicated the Mix128 function, a unique

property of DryGASCON does not really have any

effect on DryGASCON’s security. So the analysis

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

206

should have been performed on the constrained ver-

sion of DryGASCON; namely GASCON

C5R11

permu-

tation.

The designer of DryGASCON presented their

own cryptanalysis results on the algorithm proposal

(Riou, 2019). These included linear cryptanalysis and

the truncated differential cryptanalysis of DryGAS-

CON. They provided various linear approximations

that they constructed by using lineartrails tool (Do-

braunig et al., 2015a). They also provided a 3-round

probability one truncated differential distinguisher,

and stated there are no longer truncated differential

distinguishers than this one. This result was improved

in (Tezcan, 2020) by providing a 3.5-round truncated

differential distinguisher. Because the non-zero val-

ues in the third round actually were revealing some

characteristics for the next layer. In the same study,

a 5-round theoretical differential-linear distinguisher

was presented. This distinguisher contained a linear

approximation provided by (Riou, 2019) with 2

−15

bias, and a 2-round probability one truncated differ-

ential distinguisher. Unlike the analysis of Ascon-

128, the linear approximation of this distinguisher

was type-I, instead of type-II. Because even though

the permutation of Ascon and DryGASCON were

similar, the attack process was going to be compli-

cated due to the additional functions of DryGAS-

CON. So they used a type-I approximation and gave

the initial difference in x

and x

, instead of x

and

to grant a general opinion about its security against

differential-linear cryptanalysis. The theoretical bias

of this operation was presented in (Tezcan, 2020) as

2pq

= 2 · 1 · (2

−15

)

= 2

−29

and they said they need

61.28

samples to distinguish it from a random permu-

tation, according to Algorithm 1 of (Blondeau et al.,

2011).

In this study, we aimed to verify the 5-round the-

oretical differential-linear distinguisher provided by

(Tezcan, 2020) in practice. During this process, we

realized that the initial 3-round probability one trun-

cated differential distinguisher provided by its de-

signer (Riou, 2019) was erroneous. Moreover, the

other 2 and 3.5 round distinguishers (Tezcan, 2020)

were built according to this analysis (Riou, 2019), so

they were also erroneous. We believe the reason for

these faulty analyses was the discrepancy between the

provided code and the paper of DryGASCON’s sub-

mission ﬁle. Because we realized the bits move in

the opposite direction in the provided code than the

presented initial analysis. First, we corrected them all

and presented them in Section 2.4.

In our experiment phase, we used 2-round prob-

ability one truncated differential distinguisher pro-

vided by (Tezcan, 2020) that we corrected, and a 3-

round linear approximation with 2

−15

bias provided

by (Riou, 2019) to build a 5-round differential-linear

distinguisher. But the corrected 2-round truncated dif-

ferential distinguisher was no longer compatible with

this linear approximation. Namely, the masked input

bits of the linear approximation did not match with the

zero difference in the output bits of the truncated dif-

ferential distinguisher, so this was not a distinguisher

anymore. Since DryGASCON is rotation invariant,

we found the compatible one by rotating this differ-

ence 64 times and experimentally checking each of

them. This distinguisher can be seen in Table 6.

Table 6: 5-Round distinguisher of DryGASCON.

Round 2- Round Truncated Differential Distinguisher of GASCON

C5R11

0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000001000000000000000000000000000000000000000

I 0000000000000000000000001000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

000000000000000000000000?000000000000000000000000000000000000000

S1 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

000000000000000000000000?000000000000000000000000000000000000000

000000?00000000000000000?00000000?000000000000000000000000000000

00000000000?000000000000?00000000000000000000000000000?000000000

P1 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

000000000000?00000000000?0000000000000000000000000000000000?0000

000000?0000??00000000000?00000000?00000000000000000000?0000?0000

S2 00000000000??00000000000?00000000000000000000000000000?0000?0000

000000?0000??00000000000?00000000?00000000000000000000?0000?0000

?0000??0000??0000000?000???000000?00?0000?00000?0000???0000?0000

?00000?0000??00000000?00???000??0?00?0000??000?00000?0?0000?0000

P2 00000000000??0??0000000??00??00000000000000??000000000?0??0?00?0

0000?0?000???000??000000?0000?0???0000?0000000?0000??0?0000?0000

?0000??0000??00000000000?0?0000?0?0000000??000??00000??0000?0000

Round 3-Round Linear Approximation of GASCON

C5R11

0001000000000000000000000000100000000010000100000001000000100001

0000000000000000000000000000000000000000000000000000000000000000

P2 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000110000000

0001000000000000000000000000100000000010000100000001000110100000

0000000000000000000000000000000000000000000000000000000000000000

P3 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000100000000000000100000000000000000001

0000000000000000000000000000000000000000000000000000000000000000

P4 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000001

0000000000000000000000000000000000000000000000000000000000000000

1110001101111100010011110001101101101110100011010101001111100110

P5 1110000010000110001010011110100011100100101101110110011010101111

0000000000000000000000000000000000000000000000000000000000000000

A similar analysis of Ascon (Tezcan, 2020) in-

cluded the usage of random nonces and keys. Since

the initial state of DryGASCON did not have the key

and the nonce in the same location as Ascon, we ap-

plied the basic approach when performing this exper-

iment. We used 2

random plaintext pairs and per-

muted each pair with the input difference. Then we

checked if the corresponding ciphertexts c1, c2 have

the same parity of the ﬁrst round of the linear approx-

imation’s mask. We rotated the input difference 64

times and observed how much that they deviate from

1/2 to have the best possible bias. Our experiments

showed that 2

−7.96

bias is obtainable with 2

data for

Differential-linear Attacks on Permutation Ciphers Revisited: Experiments on Ascon and DryGASCON

207

distinguishing 5 rounds of DryGASCON from a ran-

dom permutation. This was signiﬁcantly better than

the theoretical bias 2

−29

and 2

61.28

data complexity.

In the continuation of the experiment, we searched

for better linear approximations by using the lin-

eartrails tool (Dobraunig et al., 2015a). We could not

ﬁnd a better theoretical bias than 2

−15

. But our exper-

iments show that it is possible to have a better bias in

practice. With performing the same experiment with

a new 3-round linear approximation that has a 2

−15

bias, we showed that 2

−5.35

total bias is obtainable,

and 2

samples are enough to distinguish 5-round of

DryGASCON from a random permutation. This 5-

round differential-linear distinguisher can be seen in

Table 7.

Table 7: 5-Round new distinguisher of DryGASCON.

Round 2- Round Truncated Differential Distinguisher of GASCON

C5R11

0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000100000000000000000000000

I 0000000000000000000000000000000000000000100000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000?00000000000000000000000

S1 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000?00000000000000000000000

0000000000000000000000000000000?00000000?00000000000000000?00000

0000000000?00000000000000000000000000000?000000000000?0000000000

P1 0000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

00000?0000000000000000000000000000000000?00000000000?00000000000

00000?0000?00000000000000000000?00000000?00000000000??0000?00000

S2 00000?0000?00000000000000000000000000000?00000000000??0000000000

00000?0000?00000000000000000000?00000000?00000000000??0000?00000

00000?0000???0000?00000?0000?00??00000???000?0000000??0000??0000

00000?0000?0?00000?000??0000?00????000???00?00000000??0000?00000

P2 00?00?0??0?000000000??00000000000000??00??0000000??0??0000000000

?0000?0000?0??0000?0000000?0000?0?0?0000?000000??000???000?0?000

00000?0000??00000??000??0000000???0000?0?00000000000??0000??0000

Round 3-Round Linear Approximation of GASCON

C5R11

0000000000000000000000000000000000000000000000000000000110000000

0001000000000000000000000000100000000010000100000001000000100000

P2 0001000000000000000000000000100000000010000100000001000000100001