Online Set Cover with Rated Subsets

Christine Markarian

Department of Engineering and Information Technology,

University of Dubai, Dubai, U.A.E.

Keywords:

Online Set Cover, Rating, Optimization, Online Algorithms, Competitive Analysis, Randomized Rounding.

Abstract:

In this paper, we introduce the Online Set Cover With Rated Subsets problem (OSC-RS), a generalization of

the well-known Online Set Cover problem, in which we are given a universe of elements and a collection of

subsets of the universe, each associated with a subset cost and a rating cost. In each step, the algorithm is given

a request containing elements from the universe. The algorithm serves a request by assigning it to a number

of purchased subsets that jointly cover the requested elements. The algorithm pays the subset costs associated

with the subsets purchased and for each request, it pays the sum of the rating costs associated with the subsets

assigned to the request. The aim is to serve all requests as soon as revealed, while minimizing the total subset

and rating costs paid. OSC-RS is motivated by intrinsic client-service-providing scenarios in which service

providers are rated and their ratings are included in the decision-making process, so as higher-rated service

providers are associated with lower rating costs. That is, the decisions about serving clients take into account

the quality of the services provided. We propose the ﬁrst online algorithm for OSC-RS and evaluate it using

the standard notion of competitive analysis. The latter compares the performance of the online algorithm to

that of an optimal ofﬂine algorithm that is assumed to know all the input sequence in advance.

1 INTRODUCTION

In our digital world today, nearly every service or

product offered is accompanied with a rating (Landy

and Farr, 1980). We rely on customer reviews to make

most of our day-to-day decisions, including which ho-

tel to stay in, which restaurant to go to, and which

course to register for. The customer review system

is applied in almost every industry, urging companies

to keep good reputation in order to succeed or even

survive (Trenz and Berger, 2013; Zhou et al., 2014).

Despite the vital role played by customer review sys-

tems in ensuring quality control for companies, most

real-world optimization problems studied thus far in

algorithmic theory do not include the rating factor in

their optimization model.

In this paper, aiming to better reﬂect today’s real-

world companies, that highly rely on customer review

systems, we introduce the concept of rating in the op-

timization objective. In particular, we address a vari-

ant of the well-known Set Cover (SC), a fundamen-

tal problem in operations research, computer science,

and combinatorics (Feige, 1998; Slavık, 1997). SC

has numerous applications in scheduling, budgeting,

networks among others (Vemuganti, 1998). Given a

universe of elements and a collection of subsets of the

universe, each associated with a positive cost, SC asks

to purchase subsets of minimum total costs that can

cover the elements of the universe.

In the online setting (Borodin and El-Yaniv,

2005), elements of the universe are revealed to the

online algorithm over time and the problem is known

as the Online Set Cover problem (OSC) (Alon et al.,

2009). OSC appears, among many other applica-

tions, in client-service-providing scenarios in which

elements represent clients and subsets represent ser-

vice providers. Covering elements is translated to

serving clients and subset costs are equivalent to ser-

vice providing costs, where each service provider can

serve a subset of the clients.

2 ONLINE SET COVER WITH

RATED SUBSETS (OSC-RS)

In this paper, we study the Online Set Cover With

Rated Subsets problem (OSC-RS), a generalization

of OSC, in which we are given a universe of n ele-

ments and a collection of m subsets of the universe,

each associated with a positive subset cost and a pos-

itive rating cost. In each step, the algorithm is given

a request containing at most k elements from the uni-

verse. Each element may belong to at most d subsets.

The algorithm serves a request by assigning it to a

number of purchased subsets that jointly cover the re-

Markarian, C.

Online Set Cover With Rated Subsets.

DOI: 10.5220/0010976900003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 455-461

ISBN: 978-989-758-569-2; ISSN: 2184-4992

455

quested elements. The algorithm pays the subset costs

associated with the subsets purchased and for each re-

quest, it pays the sum of the rating costs associated

with the subsets assigned to the request. The aim is to

serve all requests as soon as revealed, while minimiz-

ing the total subset and rating costs paid. Note that in

OSC (Alon et al., 2009), a single element arrives in

each time step. Hence, OSC-RS generalizes OSC by

setting the number of elements per request to 1 and all

rating costs to 0.

OSC-RS is motivated by intrinsic client-service-

providing scenarios in which service providers are

rated and their ratings are included in the decision-

making process, so as higher-rated service providers

are associated with lower rating costs. That is, the

higher the rating of a service provider, the lower is its

rating cost. Consider a company that assigns service

providers to serve its clients. Unlike in the Online Set

Cover problem, in OSC-RS, the decisions about serv-

ing clients take into account the quality of the ser-

vices provided. Hence, the company does not only

aim to minimize its classical costs, but considers low-

rated services to be additional costs that represent its

reputation-maintainance costs. In OSC-RS, this is re-

ﬂected in the rating costs associated with the subsets

in addition to the subset costs.

2.1 Our Contribution

We propose the ﬁrst online algorithm for OSC-RS and

evaluate it using the standard notion of competitive

analysis, which is deﬁned as follows. An online al-

gorithm has competitive ratio c (or is c-competitive)

if for all input sequences, the cost incurred by the on-

line algorithm is at most c times the cost of an optimal

ofﬂine algorithm that knows the entire input sequence

in advance and is optimal. The input to an online al-

gorithm is revealed in portions over time, and the al-

gorithm is expected to react to each portion while tar-

geting the given optimization goal against the whole

input sequence. Unlike ofﬂine algorithms that react

once to a given input sequence, the challenge of an

online algorithm is to react to each of the input por-

tions as soon as revealed, without knowing about the

remaining input sequence in advance.

2.2 Relationships with Other Problems

The special case of OSC-RS in which each request

is composed of one element, can be solved by trans-

forming a given instance of the problem into an in-

stance of the Non-metric Online Facility Location

problem (non-metric OFL) (Alon et al., 2006), de-

ﬁned as follows. Given a collection of potential facil-

ity locations. Each facility can be opened by paying

its so-called opening cost. Clients arrive at different

locations over time. Non-metric OFL asks to connect

each arriving client to an open facility. Connecting

a client to an open facility incurs the so-called con-

necting cost between the client and the facility, which

is the distance between the client location and the fa-

cility location. The transfomation works as follows.

Each subset is formed as a facility location and fa-

cility opening costs correspond to subset costs. Each

element is formed as a client and the connecting cost

between a client and a facility is set to the rating cost

of the subset corresponding to the facility. If an ele-

ment does not belong to a subset, the connecting cost

between the corresponding client and the correspond-

ing facility is set to inﬁnity. Every time a client is

connected to a facility, the corresponding subset’s rat-

ing cost is paid.

Our algorithm for OSC-RS which we describe in

the coming sections will handle requests composed of

any bounded number of elements.

As mentioned earlier, OCS-RC generalizes the

Online Set Cover problem (OSC) due to (Alon et al.,

2009), in which the number k of elements in each re-

quest is 1 and all rating costs are 0.

– There is Ω(

lognlogm

loglogn+loglogm

) lower bound on the

competitive ratio of any deterministic algorithm

for OSC, where n is the number of elements and

m is the number of subsets, due to (Alon et al.,

2009).

– There is Ω(log nlog m) lower bound on the com-

petitive ratio of any randomized polynomial-time

algorithm for OSC, under the assumption that

BPP 6= NP, due to (Korman, 2005).

2.3 Competitive Ratio

Our algorithm for OSC-RS has an O(logd log n) com-

petitive ratio, where:

– d is the maximum number of subsets any element

can belong to.

– n is the total number of elements.

2.4 Algorithmic Techniques

Our online algorithm is based on randomized round-

ing, a technique used to solve many online optimiza-

tion problems (Markarian, 2021; Markarian et al.,

2021; Hamann et al., 2018; Markarian, 2018; Alon

et al., 2006). Moreover, the algorithm is based on

a transformation of a given OSC-RS instance into a

graph-theoretic problem instance, as input portions

appear over time.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

456

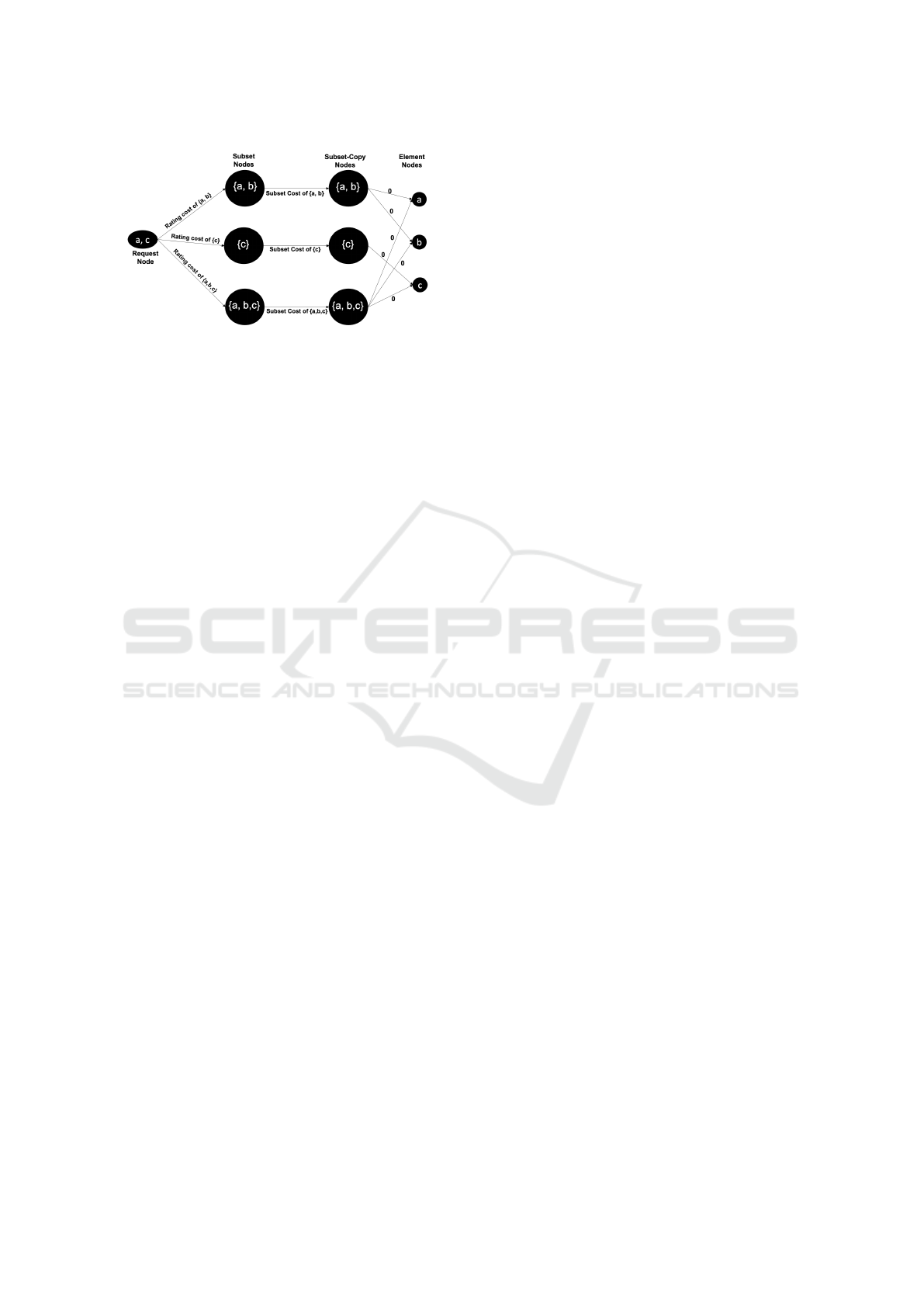
Figure 1: OSC-RS graph instance of three elements, three

subsets, and a request of two elements.

3 TRANSFORMATION OF

OSC-RS INSTANCE

Given an instance I of the Online Set Cover With

Rated Subsets problem (OSC-RS). We transform I

into a directed edge-weighted graph problem in-

stance, as follows. We refer the reader to Figure 1

for an illustration.

The Nodes of the Graph Are Formed as Follows:

– We associate each element in the universe with an

element node.

– We associate each subset with two nodes: a subset

node and a subset-copy node.

– We associate each request with a request node.

The Edges of the Graph Are Formed as Follows:

– We add a directed edge from each subset-copy

node to each element node if the corresponding

subset contains the corresponding element. These

edges have weight 0.

– We add a directed edge from each subset node

to its corresponding subset-copy node, of weight

equal to the corresponding subset cost.

– For each request, we add a directed edge from

the request node to each subset node which corre-

sponds to a subset containing at least one element

comprising the request. The weight of each out-

going edge to a subset node will be equal to the

rating cost of the corresponding subset.

Recall that the goal of the algorithm is to assign

each request to a number of subsets that jointly cover

the elements of the request. On a given time step, the

algorithm may purchase new subsets by paying their

subset costs. This goal is tansformed in our graph

problem as follows.

Initially, the subset nodes, the subset-copy nodes,

and the element nodes are formed, including the

weighted edges between them, as described above.

In each step, as soon as a new request arrives:

– The algorithm forms a request node associated

with the request and adds all the outgoing edges

from it, as described above.

– The algorithm ﬁnds a directed path from the re-

quest node to each of the element nodes corre-

sponding to the elements of the request. To do

this, the algorithm purchases edges of the graph

that form the desired paths.

– The algorithm pays the subset costs and the rat-

ing costs associated with the purchased edges, as

follows. Whenever the algorithm purchases an

edge that connects a subset node to its subset-

copy node, the corresponding subset cost is paid.

Whenever the algorithm purchases an edge con-

necting a request node to a subset node, the corre-

sponding rating cost of the subset is paid.

It is easy to see that a feasible solution for the

graph instance formed from a given instance I of

OSC-RS according to the transformation above, im-

plies a feasible solution for I, of the same cost.

4 ONLINE ALGORITHM

In this section, we present an online algorithm that

ﬁnds a feasible solution for the graph problem de-

scribed in the previous section. This implies a feasible

solution for any given instance of OSC-RS.

The algorithm is randomized and has two phases.

In the ﬁrst phase, the algorithm uses a randomized

approach to purchase edges from the graph, that may

form an infeasible solution. In the second phase, the

algorithm may buy further edges to guarantee a feasi-

ble solution.

This idea has been implemented in other algo-

rithms for similar online problems (Markarian, 2021;

Markarian et al., 2021; Hamann et al., 2018; Markar-

ian, 2018; Alon et al., 2006).

A fractional value v

is assigned to each edge e

in the graph, all set to 0 initially and non-decreasing

throughout the execution of the algorithm. The con-

cepts of maximum ﬂow and minimum cut will be

used. The maximum ﬂow from node i to node j is the

smallest total fractional values of edges which would

break the directed path from i to j if removed. These

edges are called minimum cut edges.

The algorithm chooses a random value q, indepen-

dently among 2

logn

random variables that are uni-

formly distributed in the interval [0, 1], where n is the

Online Set Cover With Rated Subsets

457

total number of elements. This value q will be used

by the algorithm in its ﬁrst phase when choosing the

edges.

Recall that the edges of the graph are directed and

weighted, as per the transformation described in the

previous section. We refer to the weight of an edge e

by w

The online algorithm reacts to each new element s

in a given request as follows:

If the algorithm’s current outputted solution does

not contain a directed path from the request node to

the element node associated with s, the algorithm per-

forms the following:

Phase 1. The algorithm calculates the maximum

ﬂow from the request node to the element node as-

sociated with s. As long as this value does not exceed

1, the algorithm constructs a minimum cut Q and in-

creases the fractional value of each edge in Q , based

on its weight and the cardinality of Q , using the equa-

tion below:

← v

(1 +

) +

|Q | · w

When the maximum ﬂow is at least 1, the algo-

rithm adds each edge whose fractional value exceeds

q (the random value described earlier) to the solution.

Phase 2. At this point, the algorithm might have

constructed an infeasible solution - that depends on

the randomization process. To ensure a feasible solu-

tion, the algorithm observes the edges in the solution

so far outputted. If the solution does not contain a di-

rected path from the request node to the element node

associated with s, the algorithm calculates a shortest

weighted directed path from the request node to the

element node and adds the edges of this path to the

solution.

The two phases of the algorithm are depicted in

Algorithm 1.

5 COMPETITIVE ANALYSIS

In this section, we prove an upper bound on the com-

petitive ratio of the algorithm presented in the previ-

ous section.

As mentioned in Section 3, the expected cost of

the solution for a given instance I of OSC-RS is less

or equal to the expected solution cost of the corre-

sponding graph instance. Hence, to analyze the com-

petitive ratio of the algorithm, we observe the total

expected cost of edges purchased by the algorithm in

comparison to that of an optimal ofﬂine solution.

Algorithm 1: Online Algorithm for OSC-RC.

Phase 1.

– While the maximum ﬂow from the request node to

the element node associated with s is less than 1:

Construct a minimum cut Q from the request

node to the element node associated with s and in-

crease the fractional value v

of each edge e ∈ Q ,

using the equation below:

← v

(1 +

) +

|Q | · w

– Add each edge e to the solution if its value v

ex-

ceeds q.

Phase 2.

If there is no directed path from the request node

to the element node associated with s in the current

solution, add to the solution the edges of a smallest

weighted path from the request node to the element

node associated with s.

Notice that the algorithm may purchase edges in

the ﬁrst and second phases. Let S

and S

denote the

the edges purchased by the algorithm in Phase 1 and

Phase 2, respectively. We will analyze the expected

cost of each collection separately. We denote by Opt

the cost of an optimal ofﬂine solution.

Phase 1 - Analysis. In the ﬁrst phase, the algorithm

purchases an edge whenever the fractional value as-

sociated with it becomes at least q (recall the num-

ber generated by a random process before the ar-

rival of any request). Let us observe an edge e and

i : 1 ≤ i ≤ 2

logn

. Let X

e,i

be the variable indicating

whether e has been purchased by the algorithm or not.

Recall that w

and v

denote the weight and fractional

value of an edge e, respectively. We can now express

the expected cost C

of the collection S

as follows:

∑

e∈S

logn

∑

i=1

· Exp [X

e,i

] (1)

= 2

logn

∑

e∈S

(2)

To make a comparison to the cost of the optimal

ofﬂine solution, we need to observe the minimum cuts

constructed, since the algorithm purchases edges of

minimum cuts constructed in the ﬁrst phase. The ﬁrst

observation which allows the comparison is that each

minimum cut generated by the algorithm contains at

least one edge that is in the optimal ofﬂine solution.

Observation 1. Each minimum cut constructed by

the algorithm contains at least one optimal edge.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

458

This observation is true because of the deﬁnition

of minimum cut and since any optimal algorithm is

supposed to output a directed feasible path for the

given element. The second observation which allows

the comparison is the number of times the algorithm

constructs a minimum cut.

Observation 2. The algorithm constructs O(Opt ·

log|Q|) minimum cuts, where |Q| is the size of the

biggest minimum cut constructed.

Proof. Observe the optimal edges. We show that each

such edge would show up in a bounded number of

minimum cuts, since its fractional value will eventu-

ally become 1 and so it won’t show up in any later

minimum cut, according to the algorithm’s design.

Let us ﬁx any optimal edge and look at the equa-

tion of the algorithm to check how many times we

need to perform a fractional increase until the frac-

tional value of this edge becomes 1. Notice that

O(w

log|Q|) fractional increases are needed to make

the value of the edge become at least 1. On the other

hand, as per the ﬁrst observation, each minimum cut

contains at least one optimal edge. Therefore, the

algorithm constructs O(Opt · log |Q|) minimum cuts,

where |Q| is the size of the biggest minimum cut con-

structed.

To achieve the desired upper bound, we will need

to give an upper bound on |Q|. Since each element

may belong to at most d subsets, then there are at

most d directed paths from the request node to each

element node. Therefore, |Q| ≤ d and so the num-

ber of minimum cuts constructed is upper bounded

by O(Opt · log |d|).

The next thing to look at is the total fractional in-

crease associated with each minimum cut. Since we

have an upper bound on the number of minimum cuts

constructed, we can conclude an upper bound on the

expected cost C

of the algorithm in Phase 1.

Lemma 1. Each minimum cut constructed is associ-

ated with a maximum of 2 fractional increase.

Proof. We observe any minimum cut Q. Each edge e

in Q causes a fractional increase of w



·w



based on the algorithm’s equation. Notice that before

an increase is made, the maximum ﬂow is less than 1.

Hence,

∑

e∈Q

< 1. Hence, we conclude the follow-

ing.

∑

e∈Q



· w



< 2

Therefore, we have that

∑

e∈S

≤ O(Opt ·

logd). Thus,

≤ O(Opt · log n · log d) (3)

Phase 2 - Analysis. We now bound the expected

cost C

of the collection S

of edges purchased by

the algorithm in Phase 2.

The ﬂow of a path will be the minimum value

among the edge values of a given path. We ﬁx an

element node u and an i: 1 ≤ i ≤ 2

logn

. We calcu-

late the probability that there is no feasible path pur-

chased by the algorithm in Phase 1 for u, for a single

i. In terms of ﬂow, the latter is the probability that q

is more than the ﬂow of each directed path to u. Let

Q be a minimum cut constructed at the end of Phase

1. Before executing Phase 2, we have that the sum of

ﬂow associated with all paths to u is at least 1 accord-

ing to the algorithm. Therefore, the probability that

there is no feasible path purchased by the algorithm

in Phase 1 for u, considering a single i, is:

∏

e∈Q

(1 − v

) ≤ e

−

∑

e∈Q

≤

Now we calculate the probability considering all

i: 1 ≤ i ≤ 2

logn

and conclude the following. The

probability that there is no feasible path purchased by

the algorithm in Phase 1 for u is at most

Hence, the algorithm purchases a smallest

weighted path from the request node to u with prob-

ability at most

. Obviously, this path is upper

bounded by Opt, since it is a smallest weighted path.

Since we have a total of n elements, each arriving

exactly once, we can conclude the following.

≤ n ·

Opt

Therefore, we following theorem holds.

Theorem 1. There is an O(log d log n)-competitive

randomized algorithm for the Online Set Cover With

Rated Subsets problem, where d is the maximum num-

ber of subsets any element can belong to, and n is the

number of elements.

6 CONCLUDING THOUGHTS

We have initiated in this paper the study of the im-

pact of rated resources on decision-making. We have

generalized the well known Online Set Cover problem

(OSC) by associating each subset with a price that de-

pends on the rating of the subset or resource it repre-

sents. In other words, upon purchasing a resource, the

Online Set Cover With Rated Subsets

459

decision-maker pays in addition to the actual cost of

the resource, the price for good quality service.

Our simple yet effective model is one way to rep-

resent resource ratings and relate them to the opti-

mization objective. There are different ways this can

be done, for example, rather than paying the sum of

the rating costs for each subset serving a request, one

could pay the average rating cost of these subsets in-

stead.

Also, each request could be associated with an

amount of money one is willing to pay to get a higher

rated service for the request. In many real-world busi-

ness scenarios, customers are often given options to

choose from when it comes to quality of services.

Hence, the decision maker would take into account

the quality of service requested when assigning re-

sources to clients. For instance, a rating cost would

not have to be paid if the request is not made for a

high-rated service.

Furthermore, the ratings in our model are assumed

to be ﬁxed throughout time, which is not the case in

actual rating systems. One may want to include dy-

namic pricing for these ratings. From an algorithmic

perspective, it could be that extensions of the existing

algorithm would solve the variants that arise from dy-

namic pricing - a similar study as the one in (Feldkord

et al., 2017) for leasing problems.

We have initiated this study by targeting OSC.

There are a lot of other well-studied online resource

allocation problems to explore. Many of these would

serve as real-world decision-making problems in the

context of rating, such as variants of the Online Fa-

cility Location problem (Alon et al., 2006; Meyer-

son, 2001; Markarian et al., 2021; Markarian and

Khallouf, 2021; Markarian and auf der Heide, 2019)

and variants of the Online Connected Dominating Set

problem (Hamann et al., 2018; Markarian and Kassar,

2020).

REFERENCES

Alon, N., Awerbuch, B., Azar, Y., Buchbinder, N., and

Naor, J. (2006). A general approach to online net-

work optimization problems. ACM Transactions on

Algorithms (TALG), 2(4):640–660.

Alon, N., Awerbuch, B., Azar, Y., Buchbinder, N., and

Naor, J. (2009). The online set cover problem. SIAM

Journal on Computing, 39(2):361–370.

Borodin, A. and El-Yaniv, R. (2005). Online computa-

tion and competitive analysis. Cambridge University

Press.

Feige, U. (1998). A threshold of ln n for approximating set

cover. Journal of the ACM (JACM), 45(4):634–652.

Feldkord, B., Markarian, C., and auf der Heide, F. M.

(2017). Price ﬂuctuation in online leasing. In Gao,

X., Du, H., and Han, M., editors, Combinatorial Op-

timization and Applications - 11th International Con-

ference, COCOA 2017, Shanghai, China, December

16-18, 2017, Proceedings, Part II, volume 10628 of

Lecture Notes in Computer Science, pages 17–31.

Springer.

Hamann, H., Markarian, C., auf der Heide, F. M., and

Wahby, M. (2018). Pick, pack, & survive: Charg-

ing robots in a modern warehouse based on online

connected dominating sets. In Ito, H., Leonardi,

S., Pagli, L., and Prencipe, G., editors, 9th Inter-

national Conference on Fun with Algorithms, FUN

2018, June 13-15, 2018, La Maddalena, Italy, volume

100 of LIPIcs, pages 22:1–22:13. Schloss Dagstuhl -

Leibniz-Zentrum f

ur Informatik.

Korman, S. (2005). On the use of randomization in the on-

line set cover problem. Master’s thesis, Weizmann In-

stitute of Science, Israel.

Landy, F. J. and Farr, J. L. (1980). Performance rating. Psy-

chological bulletin, 87(1):72.

Markarian, C. (2018). An optimal algorithm for online

prize-collecting node-weighted steiner forest. In Il-

iopoulos, C. S., Leong, H. W., and Sung, W., editors,

Combinatorial Algorithms - 29th International Work-

shop, IWOCA 2018, Singapore, July 16-19, 2018, Pro-

ceedings, volume 10979 of Lecture Notes in Computer

Science, pages 214–223. Springer.

Markarian, C. (2021). Online non-metric facility location

with service installation costs. In Filipe, J., Smi-

alek, M., Brodsky, A., and Hammoudi, S., editors,

Proceedings of the 23rd International Conference on

Enterprise Information Systems, ICEIS 2021, Online

Streaming, April 26-28, 2021, Volume 1, pages 737–

743. SCITEPRESS.

Markarian, C. and auf der Heide, F. M. (2019). Online

algorithms for leasing vertex cover and leasing non-

metric facility location. In Parlier, G. H., Liberatore,

F., and Demange, M., editors, Proceedings of the 8th

International Conference on Operations Research and

Enterprise Systems, ICORES 2019, Prague, Czech

Republic, February 19-21, 2019, pages 315–321.

SciTePress.

Markarian, C. and Kassar, A. (2020). Online deterministic

algorithms for connected dominating set & set cover

leasing problems. In Parlier, G. H., Liberatore, F., and

Demange, M., editors, Proceedings of the 9th Interna-

tional Conference on Operations Research and Enter-

prise Systems, ICORES 2020, Valletta, Malta, Febru-

ary 22-24, 2020, pages 121–128. SCITEPRESS.

Markarian, C., Kassar, A., and Yunis, M. M. (2021). An

algorithmic approach to online multi-facility location

problems. In Parlier, G. H., Liberatore, F., and De-

mange, M., editors, Proceedings of the 10th Interna-

tional Conference on Operations Research and En-

terprise Systems, ICORES 2021, Online Streaming,

February 4-6, 2021, pages 29–35. SCITEPRESS.

Markarian, C. and Khallouf, P. (2021). Online metric fa-

cility service leasing with duration-speciﬁc dormant

fees. In Panetto, H., Macchi, M., and Madani, K., edi-

tors, Proceedings of the 2nd International Conference

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

460

on Innovative Intelligent Industrial Production and

Logistics, IN4PL 2021, October 25-27, 2021, pages

25–31. SCITEPRESS.

Meyerson, A. (2001). Online facility location. In Proceed-

ings 42nd IEEE Symposium on Foundations of Com-

puter Science, pages 426–431.

Slavık, P. (1997). A tight analysis of the greedy algorithm

for set cover. Journal of Algorithms, 25(2):237–254.

Trenz, M. and Berger, B. (2013). Analyzing online cus-

tomer reviews-an interdisciplinary literature review

and research agenda.

Vemuganti, R. R. (1998). Applications of Set Covering, Set

Packing and Set Partitioning Models: A Survey, pages

573–746. Springer US, Boston, MA.

Zhou, L., Ye, S., Pearce, P. L., and Wu, M.-Y. (2014).

Refreshing hotel satisfaction studies by reconﬁguring

customer review data. International journal of hospi-

tality management, 38:1–10.

Online Set Cover With Rated Subsets

461