
iRNN: Integer-only Recurrent Neural Network
Eyy
¨
ub Sari, Vanessa Courville and Vahid Partovi Nia
∗
Huawei Noah’s Ark Lab, Canada
Keywords:
Recurrent Neural Network, LSTM, Model Compression, Quantization, NLP, ASR.
Abstract:
Recurrent neural networks (RNN) are used in many real-world text and speech applications. They include
complex modules such as recurrence, exponential-based activation, gate interaction, unfoldable normalization,
bi-directional dependence, and attention. The interaction between these elements prevents running them
on integer-only operations without a significant performance drop. Deploying RNNs that include layer
normalization and attention on integer-only arithmetic is still an open problem. We present a quantization-aware
training method for obtaining a highly accurate integer-only recurrent neural network (iRNN). Our approach
supports layer normalization, attention, and an adaptive piecewise linear approximation of activations (PWL),
to serve a wide range of RNNs on various applications. The proposed method is proven to work on RNN-
based language models and challenging automatic speech recognition, enabling AI applications on the edge.
Our iRNN maintains similar performance as its full-precision counterpart, their deployment on smartphones
improves the runtime performance by 2×, and reduces the model size by 4×.
1 INTRODUCTION
RNN (Rumelhart et al., 1986) architectures such as
LSTM Hochreiter and Schmidhuber (1997) or GRU
Cho et al. (2014) are the backbones of many down-
stream applications. RNNs now are part of large-scale
systems such as neural machine translation Chen et al.
(2018); Wang et al. (2019a) and on-device systems
such as Automatic Speech Recognition (ASR) He et al.
(2019). RNNs are still highly used architectures in
academia and industry, and their efficient inference
requires more elaborated studies.
In many edge devices, the number of computing
cores is limited to a handful of computing units, in
which parallel-friendly transformer-based models lose
their advantage. There have been several studies in
quantizing transformers to adapt them for edge devices
but RNNs are largely ignored. Deploying RNN-based
chatbot, conversational agent, and ASR on edge de-
vices with limited memory and energy requires further
computational improvements. The 8-bit integer neural
networks quantization (Jacob et al., 2017) for convolu-
tional architectures (CNNs) is shown to be an almost
free lunch to tackle the memory, energy, and latency
costs, with a negligible accuracy drop (Krishnamoor-
thi, 2018).
Intuitively, quantizing RNNs is more challenging
∗
Corresponding author
because the errors introduced by quantization will
propagate in two directions, i) to the next layers, like
feedforward networks ii) across timesteps. Further-
more, RNN cells are computationally more complex;
they include several element-wise additions and mul-
tiplications. They also have different activation func-
tions that rely on the exponential function, such as
sigmoid and hyperbolic tangent (tanh).
Accurate fully-integer RNNs calls for a new cell
that is built using integer friendly operations. Our main
motivation is to enable integer-only inference of RNNs
on specialized edge AI computing hardware with no
floating-point units, so we constrained the new LSTM
cell to include only integer operations.
First we build a fully integer LSTM cell in which
its inference require integer-only computation units,
see Figure 1. Our method can be applied to any RNN
architecture, but here we focus on LSTM networks
which are the most commonly used RNNs.
Our contributions can be summarized as
•
providing a quantization-aware piecewise linear
approximation algorithm to replace exponential-
based activation functions (e.g. sigmoid and tanh)
with integer-friendly activation,
•
introducing an integer-friendly normalization layer
based on mean absolute deviation,
• proposing integer-only attention,
110
Sari, E., Courville, V. and Partovi Nia, V.
iRNN: Integer-only Recurrent Neural Network.
DOI: 10.5220/0010975700003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 110-121
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
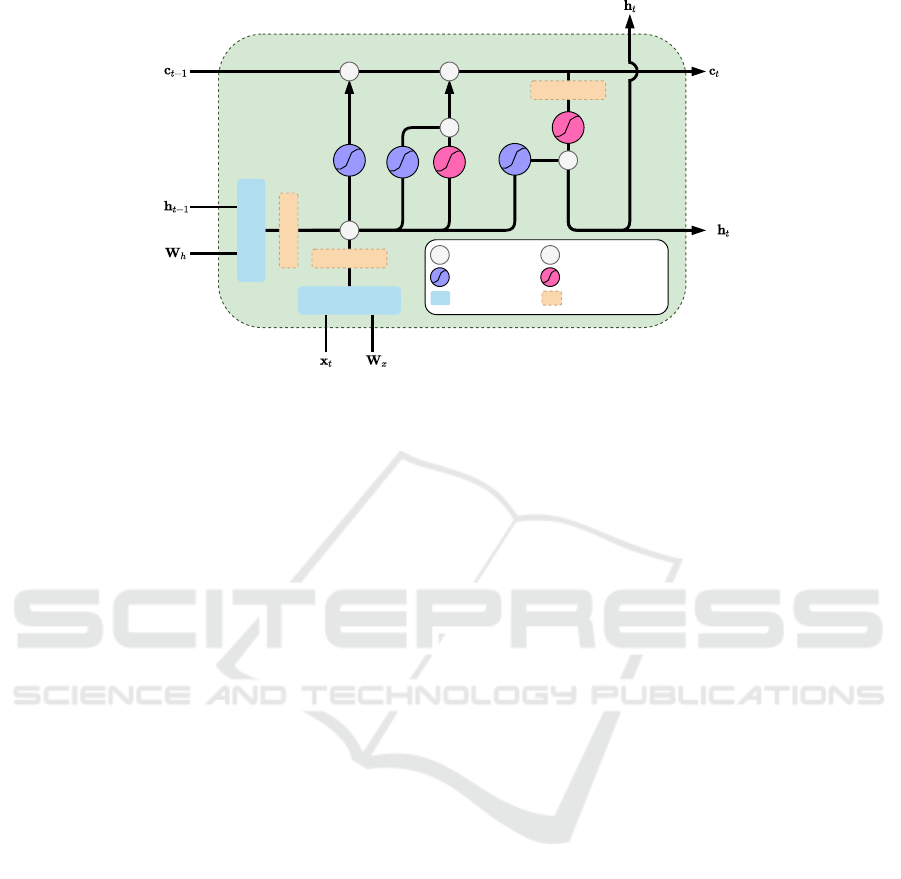
QMatmul
QMadNorm
QMadNorm
QMatmul
QMadNorm
X
+
X
+
X
+
Quantized addition
Quantized sigmoid
PWL
Quantized multiplication
X
Quantized tanh PWL
Quantized matmul
Quantized MadNorm
(optional)
Figure 1: Example of an integer-only LSTM cell (iLSTM). Layer normalization change to quantized integer friendly MadNorm
(QMadNorm), full-precision matrix multiplications change to integer matrix multiplication (QMatmul), sigmoid and tanh
activations are replaced with their corresponding piecewise linear (PWL) approximations.
•
wrapping up these new modules into an LSTM cell
towards an integer-only LSTM cell.
We also implement our method on an anonymous
smartphone, effectively showing
2×
speedup and
4×
memory compression. It is the proof that our method
enables more RNN-based applications (e.g. ASR) on
edge devices.
2 RELATED WORK
With ever-expanding deep models, designing efficient
neural networks enable wider adoption of deep learn-
ing in industry. Researchers recently started working
on developing various quantization methods (Jacob
et al., 2017; Hubara et al., 2018; Darabi et al., 2018;
Esser et al., 2020). Ott et al. (2016) explores low-bit
quantization of weights for RNNs. They show binariz-
ing weights lead to a massive accuracy drop, but ternar-
izing them keeps the model performance. Hubara et al.
(2018) demonstrate quantizing RNNs to extremely low
bits is challenging; they quantize weights and matrix
product to 4-bit, but other operations such as element-
wise pairwise and activations are computed in full-
precision. Hou et al. (2019) quantize LSTM weights
to 1-bit and 2-bit and show empirically that low-bit
quantized LSTMs suffer from exploding gradients.
Gradient explosion can be alleviated using normal-
ization layers and leads to successful training of low
bit weights Ardakani et al. (2018). Sari and Partovi Nia
(2020) studied the effect of normalization in low bit
networks theoretically, and proved that low-bit train-
ing without normalization operation is mathematically
impossible; their work demonstrates the fundamental
importance of involving normalization layers in quan-
tized networks. He et al. (2016) introduce Bit-RNN
and improve 1-bit and 2-bit RNNs quantization by con-
straining values within fixed range carefully; they keep
activation computation and element-wise pairwise op-
erations in full-precision. Kapur et al. (2017) build
upon Bit-RNN and propose a low-bit RNN with mini-
mal performance drop, but they increase the number of
neurons to compensate for performance drop; they run
activation and pair-wise operations on full-precision
as well.
Wu et al. (2016) is a pioneering work in LSTM
quantization, which demonstrated speed-up inference
of large-scale LSTM models with limited performance
drop by partially quantizing RNN cells. Their pro-
posed method is tailored towards specific hardware.
They use 8-bit integer for matrix multiplications and
16-bit integer for tanh, sigmoid, and element-wise
operations but do no quantize attention Bluche et al.
(2020) propose an effective 8-bit integer-only LSTM
cell for Keyword Spotting application on microcon-
trollers. They enforce weights and activations to be
symmetric on fixed ranges
[−4,4]
and
[−1,1]
. This
prior assumption about the network’s behaviour re-
strict generalizing their approach for wide range of
RNN models. They propose a look-up table of 256
slots to represent the quantized tanh and sigmoid acti-
vations. However, the look-up table memory require-
ment explodes for bigger bitwidth. Their solution
does not serve complex tasks such as automatic speech
recognition due to large look up table memory con-
sumption. While demonstrating strong results on Key-
word Spotting task, their assumptions on quantization
iRNN: Integer-only Recurrent Neural Network
111

range and bitwidth make their method task-specific.
3 BACKGROUND
We use the common linear algebra notation and use
plain symbols to denote scalar values, e.g.
x ∈ R
, bold
lower-case letters to denote vectors, e.g.
x ∈ R
n
, and
bold upper-case letters to denote matrices, e.g.
X ∈
R
m×n
. The element-wise multiplication is represented
by .
3.1 LSTM
We define an LSTM cell as
i
t
f
t
j
t
o
t
= W
x
x
t
+ W
h
h
t−1
, (1)
c
t
= σ(f
t
) c
t−1
+ σ(i
t
) tanh(j
t
), (2)
h
t
= σ(o
t
) tanh(c
t
), (3)
where
σ(·)
is the sigmoid function;
n
is the input
hidden units dimension, and
m
is the state hidden
units dimension;
x
t
∈ R
n
is the input for the current
timestep
t ∈ {1, ...,T }
;
h
t−1
∈ R
m
is the hidden state
from the previous timestep and
h
0
is initialized with
zeros;
W
x
∈ R
4m×n
is the input to state weight ma-
trix;
W
h
∈ R
4m×m
is the state to state weight matrix;
{i
t
,f
t
,o
t
} ∈ R
m
are the pre-activations to the
{
input,
forget, output
}
gates;
j
t
∈ R
m
is the pre-activation to
the cell candidate;
{c
t
,h
t
} ∈ R
m
are the cell state and
the hidden state for the current timestep, respectively.
We omit the biases for the sake of notation simplicity.
For a bidirectional LSTM (BiLSTM) the output hidden
state at timestep
t
is the concatenation of the forward
hidden state
−→
h
t
and the backward hidden state
←−
h
t
,
[
−→
h
t
;
←−
h
t
].
3.2 LayerNorm
Layer normalization Ba et al. (2016) standardizes in-
puts across the hidden units dimension with zero lo-
cation and unit scale. Given hidden units
x ∈ R
H
,
LayerNorm is defined as
µ =
1
H
H
∑
i=1
x
i
, ˆx
i
= x
i
− µ (4)
σ
2
std
=
1
H
H
∑
i=1
ˆx
2
i
, σ
std
=
q
σ
2
std
(5)
LN(x)
i
= y
i
=
ˆx
i
σ
std
(6)
where
µ
(4) is the hidden unit mean,
ˆx
i
(4) is the
centered hidden unit
x
i
,
σ
2
std
(5) is the hidden unit
variance, and
y
i
(6) is the normalized hidden unit. In
practice, one can scale
y
i
by a learnable parameter
γ
or shift by a learnable parameter
β
. The LayerNormL-
STM cell is defined as in Ba et al. (2016).
3.3 Attention
Attention is often used in encoder-decoder RNN ar-
chitectures (Bahdanau et al., 2015; Chorowski et al.,
2015; Wu et al., 2016). We employ Bahdanau atten-
tion, also called additive attention (Bahdanau et al.,
2015). The attention mechanism allows the decoder
network to attend to the variable-length output states
from the encoder based on their relevance to the cur-
rent decoder timestep. At each of its timesteps, the
decoder extracts information from the encoder’s states
and summarizes it as a context vector,
s
t
=
T
enc
∑
i=1
α
ti
h
enc
i
(7)
α
ti
=
exp(e
ti
)
∑
T
enc
j=1
exp(e
t j
)
(8)
e
ti
= v
>
tanh(W
q
h
t−1
+ W
k
h
enc
i
) (9)
where
s
t
is the context at decoder timestep
t
which is
a weighted sum of the encoder hidden states outputs
h
enc
i
∈ R
m
enc
along encoder timesteps
i ∈ {1,...,T
enc
}
;
0 < α
ti
< 1
are the attention weights attributed to each
encoder hidden states based on the alignments
e
ti
∈ R
;
m
dec
and
m
enc
are respectively the decoder and en-
coder hidden state dimension;
{W
q
∈ R
m
att
×m
dec
,W
k
∈
R
m
att
×m
enc
}
are the weights matrices of output dimen-
sion
m
att
respectively applied to the query
h
t−1
and the
keys
h
enc
i
;
v ∈ R
m
att
is a learned weight vector. The
context vector is incorporated into the LSTM cell by
modifying (1) to
i
f
j
o
= W
x
x
t
+ W
h
h
t−1
+ W
s
s
t
(10)
where W
s
∈ R
4m
dec
×m
enc
.
3.4 Quantization
Quantization is a process whereby an input set is
mapped to a lower resolution discrete set, called the
quantization set
Q
. The mapping is either performed
from floating-points to integers (e.g. float32 to int8)
or from a dense integer to another integer set with
lower cardinality, e.g. int32 to int8. We follow the
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
112
Quantization-Aware Training (QAT) scheme described
in Jacob et al. (2017).
Given
x ∈ [x
min
,x
max
]
, we define the quantization
process as
q
x
= q(x) =
j
x
S
x
m
+ Z
x
(11)
r
x
= r(x) = S
x
(q
x
− Z
x
) (12)
S
x
=
x
max
− x
min
2
b
− 1
, Z
x
=
j
−x
min
S
x
m
(13)
where the input is clipped between
x
min
and
x
max
be-
forehand;
b.e
is the round-to-nearest function;
S
x
is the
scaling factor (also known as the step-size);
b
is the
bitwidth, e.g.
b = 8
for 8-bit quantization,
b = 16
for 16-bit quantization;
Z
x
is the zero-point corre-
sponding to the quantized value of 0 (note that zero
should always be included in
[x
min
,x
max
]
);
q(x)
quan-
tize
x
to an integer number and
r(x)
gives the floating-
point value
q(x)
represents, i.e.
r(x) ≈ x
. We refer
to
{x
min
,x
max
,b, S
x
,Z
x
}
as
quantization parameters
of
x
. Note that for inference,
S
x
is expressed as a
fixed-point integer number rather than a floating-point
number, allowing for integer-only arithmetic computa-
tions (Jacob et al., 2017).
4 METHODOLOGY
In this section, we describe our task-agnostic
quantization-aware training method to enable integer-
only RNN (iRNN).
4.1 Integer-only Activation
First, we need to compute activation functions without
relying on floating-point operations to take the early
step towards an integer-only RNN. At inference, the
non-linear activation is applied to the quantized input
q
x
, performs operations using integer-only arithmetic
and outputs the quantized result
q
y
. Clearly, given the
activation function
f
,
q
y
= q( f (q
x
))
; as the input and
the activation output are both quantized, we obtain
a discrete mapping from
q
x
to
q
y
. There are several
ways to formalize this operation. The first solution is
a Look-Up Table (LUT), where
q
x
is the index and
q
y
= LUT[q
x
]
. Thus, the number of slots in the LUT is
2
b
(e.g. 256 bytes for
b = 8
bits input
q
x
). This method
does not scale to large indexing bitwidths, e.g. 65536
slots need to be stored in memory for 16-bit activation
quantization. LUT is not cache-friendly for large num-
bers of slots. The second solution is approximating the
full-precision activation function using a fixed-point
integer Taylor approximation, but the amount of com-
putations grows as the approximation order grows. We
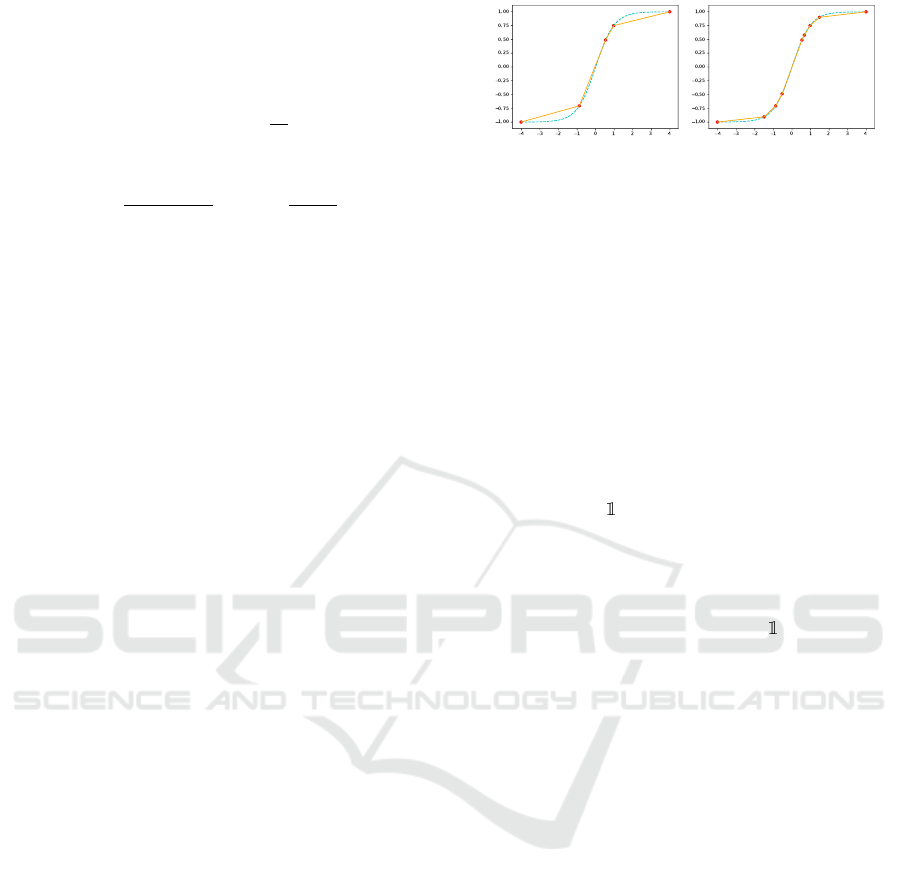
Figure 2: Tanh approximations using quantization-aware
PWLs with 4 knots (left panel), 16 pieces (right panel) using
(14). The dashed cyan curves are the true tanh functions,
while the solid orange curves are its approximation from
Algorithm 1. Red dots are the knots. The more we add
pieces, the better the approximation is. Our algorithm is able
to prioritize sections of the function with more curvatures.
propose to use a
Quantization-Aware PWL
that se-
lects PWL knots during the training process to produce
the linear pieces. Therefore the precision of approxi-
mation adapts to the required range of data flow auto-
matically and provides highly accurate data-dependent
activation approximation with fewer pieces.
A PWL is defined as follows,
g(x) =
N
∑
i=1
[k
i
,k
i+1
)
a
i
(x − k
i
) + b
i
, (14)
where
N
is the number of linear pieces defined by
N + 1
knots (also known as cutpoints or breakpoints);
{a
i
,k
i
,b
i
= f (k
i
)}
are the slope, the knot, and the in-
tercept of the
i
th
piece respectively;
A
(x) = 1
is the
indicator function on
A
. The more the linear pieces,
the better the activation approximation is (see Figure
2). A PWL is suitable for simple fixed-point integer
operations. It only relies on basic arithmetic operations
and is easy to parallelize because the computation of
each piece is independent. Therefore, the challenge
is to select the knot locations that provide the best
PWL approximation to the original function
f
. Note
in this regime, we only approximate the activation
function on the subset corresponding quantized inputs
and not the whole full-precision range. In our proposed
method if
x = k
i
then
g(x) = g(k
i
) = b
i
, i.e. recovers
the exact output
f (k
i
)
. Hence, if the PWL has
2
b
knots
(i.e.
2
b
− 1
pieces), it is equivalent to a look-up table
representing the quantized activation function. Thus,
we constraint the knots to be a subset of the quan-
tized inputs of the function we are approximating (i.e.
{k
i
}
N+1
i=1
⊆ Q ).
We propose a recursive greedy algorithm to locate
the knots during the quantization-aware PWL. The
algorithm starts with
2
b
− 1
pieces and recursively re-
moves one knot at a time until it reaches the specified
number of pieces. The absolute differences between
adjacents slopes are computed, and the shared knot
from the pair of slopes that minimizes the absolute
difference is removed; see Appendix Figure 3. The
algorithm is simple to implement and applied only
iRNN: Integer-only Recurrent Neural Network
113

once at a given training step; see Appendix Algorithm
1. This algorithm is linear in time and space com-
plexity with respect to the number of starting pieces
and is generic, allowing it to cover various nonlinear
functions. Note that the PWL is specific to a given
set of quantization parameters, i.e. the quantization
parameters are kept frozen after its creation.
At inference, the quantization-aware PWL is com-
puted as follows
q
y
=
j
N
∑
i=1
[q
k
i
,q
k
i+1
)
S
x
a
i
S
y
(q
x
− q
k
i
) +
b
i
S
y
m
+ Z
y
,
where the constants are expressed as fixed-point inte-
gers.
4.2 Integer-only Normalization
Normalization greatly helps the convergence of quan-
tized networks (Hou et al., 2019; Sari and Partovi Nia,
2020). There is a plurality of measures of location
and scale to define normalization operation. The com-
monly used measure of dispersion is the standard devi-
ation to define normalization, which is imprecise and
costly to compute on integer-only hardware. However,
the mean absolute deviation (MAD) is integer-friendly
and defined as
d =
1
H
H
∑
i=1
|x
i
− µ| =
1
H
H
∑
i=1
| ˆx
i
|. (15)
While the mean minimizes the standard deviation, the
median minimizes MAD. We suggest measuring de-
viation with respect to mean for two reasons: i) the
median is computationally more expensive ii) the abso-
lute deviation from the mean is closer to the standard
deviation. For Gaussian data, the MAD is
≈ 0.8σ
std
so
that it might be exchanged with standard deviation. We
propose to LayerNorm in LSTM with MAD instead of
standard deviation and refer to it as MadNorm., where
(6) is replaced by
y
i
=
ˆx
i
d
. (16)
MadNorm involves simpler operations, as there is no
need to square and no need to take the square root
while taking absolute value instead of these two op-
erations is much cheaper. The values
{µ, ˆx
i
,d,y
i
}
are
8-bit quantized and computed as follows
q
µ
=
j
S
x
S
µ
N
N
∑
i=1
q
x
i
− NZ
x
m
+ Z
µ
, (17)
q
ˆx
i
=
j
S
x
S
ˆx
(q
x
i
− Z
x
) −
S
µ
S
ˆx
(q
µ
− Z
µ
)
m
+ Z
ˆx
, (18)
q
d
=
j
S
ˆx
S
d
N
N
∑
i=1
|q
ˆx
i
− Z
ˆx
|
m
+ Z
d
, (19)
q
y
i
=
j
S
ˆx
S
y
S
d
(q
ˆx
i
− Z
ˆx
)
max(q
d
,1)
m
+ Z
y
, (20)
where all floating-point constants can be expressed
as fixed-point integer numbers, allowing for integer-
only arithmetic computations. Note that (17-20) are
only examples of ways to perform integer-only arith-
metic for MadNorm, and may change depending on
the software implementation and the target hardware.
We propose to quantize
{v,W
q
,W
k
}
to 8-bit. The vec-
tors
h
t−1
and
h
enc
i
are quantized thank to the previous
timestep and/or layer. The matrix multiplications in
(9) are performed in 8-bit and their results are quan-
tized to 8-bit, each with their own quantization param-
eters. Since those matrix multiplications do not share
the same quantization parameters, the sum (9) require
proper rescaling and the result is quantized to 16-bit.
We found 8-bit quantization adds too much noise, thus
preventing the encoder-decoder model to work cor-
rectly. The tanh function in (9) is computed using
quantization-aware PWL and its outputs are quantized
to 8-bit. The alignments
e
ti
are quantized to 16-bit (9).
The exponential function in
α
ti
is computed using a
quantization-aware PWL, with its outputs quantized to
8-bit. We found that quantizing the softmax denomina-
tor (8) to 8-bit introduces too much noise and destroys
attention. 8-bit attention does not offer enough flex-
ibility and prevents fine grained decoder attention to
the encoder. We left the denominator in 32-bit integer
value and defer quantization to 8-bit in the division.
The context vector
s
t
is quantized to 8-bit. Note that in
practice we shift the inputs to softmax for numerical
stability reasons (i.e. e
ti
− max
j
e
t j
).
Theorem 1
(Scale convergence)
.
Suppose
X
i
pairwise
independent samples from the same probability
space
(Ω,F ,Pr)
with
µ = IE(X
i
)
and are absolutely
integrable, then
D
n
=
1
n
∑
n
i=1
|X
i
−µ|
converges almost
surely to
˜
σ = IE(|X − µ|).
Proof:
Absolutely integrable condition assures the
existence of
µ = IE(X
i
) < IE(|X
i
|) < ∞
and hence the
existence of
IE|X
i
− µ| < IE|X
i
| + µ < ∞
. The proof is
straightforward by applying the standard strong law of
large numbers to Y
i
= |X
i
− µ|.
One may prove the central limit theorem by re-
placing absolute integrability with square integrability,
and exchanging pairwise independence with mutual
independence. Convergence to the population scale
˜
σ
in Theorem 1 paves the way to show that our Mad-
Norm enjoys a concentration inequality similar to Lay-
erNorm.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
114

Theorem 2
(Concentration inequality)
.
Suppose the
random variable
X
with mean
µ
is absolutely inte-
grable with respect to the probability measure
P
. Then
for a positive k,
Pr
|
X −µ
˜
σ
| < k
≥ 1 −
1
k
Proof:
Take
Y = |
X−µ
˜
σ
|
. The random variable
X
is
absolutely integrable, and so is Y .
IE(Y ) =
Z
∞
0
Y dP =
Z
k
0
Y dP +
Z
∞
k
Y dP
≥ 0 + k
Z
∞
k
Y dP = k Pr(Y > k),
it follows immediately that Pr
|
X−µ
˜
σ
| > k
≤
1
k
.
Theorem 2 assures that independent of distribution of
data, this MadNorm brings the mass of the distribution
around the origin. This is somehow expected from any
normalization method. It is not surprising to see that
LayerNorm also has a similar property, and therefore
in this sense LayerNorm and MadNorm assures the
tail probability far from the origin is negligible.
There is a slight difference between the concen-
tration inequality of LayerNorm and MadNorm. The
LayerNorm provides a tighter bound, i.e. the bound
in Theorem 2 changes from
1 −
1
k
to
1 −
1
k
2
but it also
requires more assumptions like the square integrability
of X.
4.3 Integer-only Attention
Attention plays a crucial role in modern encoder-
decoder architectures. The decoder relies on attention
to extract information from the encoder and provide
predictions. Attention is the bridge between the en-
coder and the decoder. Careless quantization of at-
tention breaks apart the decoder due to quantization
noise.
4.4 Integer-only LSTM Network
A vanilla LSTM cell comprises matrix multiplications,
element-wise additions, element-wise multiplications,
tanh, and sigmoid activations (1 - 3). We quantize the
weights matrices
W
x
and
W
h
to 8-bit. The inputs
x
t
and hidden states
h
t−1
are already 8-bit quantized from
the previous layer and from the previous timestep. The
cell states
c
t
are theoretically unbounded (2); therefore
the amount of quantization noise potentially destroys
the information carried by
c
t
, if it spans a large range.
When performing QAT on some pre-trained models, it
is advised to quantize
c
t
to 16-bit. Therefore,
c
t
is 8-bit
quantized unless stated otherwise but can be quantized
Table 1: Word-level perplexities on PTB with a LayerNorm
LSTM and quantized models with a different number of
PWL pieces. LayerNorm is replaced with MadNorm for the
quantized models (iRNN). Best results are averaged across
3 runs ± standard deviation.
LayerNorm LSTM val test
Full-precision 98.58 ± 0.35 94.84 ± 0.21
PWL4 101.40 ± 0.70 98.11 ± 0.75
PWL8 98.14 ± 0.11 95.03 ± 0.16
PWL16 98.09 ± 0.06 94.92 ± 0.05
PWL32 97.97 ± 0.01 94.81 ± 0.02
to 16-bit if necessary. Matrix multiplications in (1)
are performed with 8-bit arithmetic, and their outputs
are quantized to 8-bit based on their respective quanti-
zation parameters. The sum between the two matrix
multiplications outputs in (1) requires proper rescal-
ing, because they do not share the same quantization
parameters. The results of the sum are quantized to
8-bit; however, 16-bit quantization might be necessary
for complex tasks. The sigmoid and tanh activations
in (2) and (3) are replaced with their own quantization-
aware PWL, and their output is always quantized to
8-bit. The element-wise multiplications operations are
distributive, and sharing quantization parameters is not
required. In (2), the element-wise multiplications are
quantized to 8-bit, but can be quantized to 16-bit if
c
t
is quantized to 16-bit as well; the element-wise addi-
tions are quantized based on
c
t
’s bitwidth (i.e. 8-bit or
16-bit).
The element-wise multiplications between sigmoid
and tanh in (3) is always quantized to 8-bit, because
h
t
are always quantized to 8-bit. Following this recipe,
we obtain an integer-only arithmetic LSTM cell, see
Figure. 1. For LSTM cells with LayerNorm quantized
MadNorm layers are used instead of LayerNorm. Ap-
pendix A.1 provides details about quantization of other
types of layers in an LSTM model.
5 EXPERIMENTS
We evaluate our proposed method, iRNN, on language
modeling and automatic speech recognition. We also
implemented our approach on a smartphone to bench-
mark inference speedup, see 5.4.
5.1 Language Modeling on PTB
As a proof of concept, we perform several experiments
on full-precision and fully 8-bit quantized models on
the Penn TreeBank (PTB) dataset (Marcus et al., 1993).
We report perplexity per word as a performance metric.
For the quantized models, the LayerNorm is re-
placed with MadNorm. We do not train full-precision
iRNN: Integer-only Recurrent Neural Network
115

Table 2: Word-level perplexities on WikiText2 with Mo-
grifier LSTM and quantized models with different number
of PWL pieces. Best results are averaged across 3 runs
±
standard deviations.
Mogrifier LSTM val test
Full-precision 60.27 ± 0.34 58.02 ± 0.34
PWL8 60.91 ± 0.04 58.54± 0.07
PWL16 60.65 ± 0.09 58.21 ± 0.08
PWL32 60.37 ± 0.03 57.93 ± 0.07
models with MadNorm to make our method compa-
rable with common full-precision architectures. We
can draw two conclusions from the results presented
in Table 1, i) replacing LayerNorm by MadNorm does
not destroy model performance, ii) using eight lin-
ear pieces is enough to retain the performance of the
model, but adding more linear pieces improves the per-
formance. We could obtain even superior results in the
quantized model compared to the full-precision model
because of the regularization introduced by quantiza-
tion errors.
5.2 Language Modeling on WikiText2
We evaluated our proposed method on the WikiText2
dataset (Merity et al., 2016) with a state-of-the-art
RNN, Mogrifier LSTM (Melis et al., 2020). The
original code
1
was written in TensorFlow, we reim-
plemented our own version in PyTorch by staying as
close as possible to the TensorFlow version. We follow
the experimental setup from the authors
2
as we found
it critical to get similar results. We use a two layer
Mogrifier LSTM. The setup and hyper-parameters for
the experiments can be found in Appendix A.2.2 to
save some space. We present our results averaged
over 3 runs in Table 2. We use the best full-precision
model, which scores
59.95
perplexity to initialize the
quantized models. Our method is able to produce 8-
bit quantized integer-only Mogrifier LSTM with simi-
lar performance to the full-precision model with only
about 0.3 perplexity increase for the quantized model
with a PWL of 32 pieces and a maximum of about
0.9
perplexity increase with a number of pieces as
low as 8. Interestingly, a pattern emerged by dou-
bling the number of pieces, as we get a decrease in
perplexity by about
0.3
. We also perform a thorough
ablation study of our method in Appendix Table 5. Sur-
prisingly, we found that stochastic weight averaging
for quantized models exhibits the same behavior as
for full-precision models and improved performance
1
https://github.com/deepmind/lamb
2
https://github.com/deepmind/lamb/blob/
254a0b0e330c44e00cf535f98e9538d6e735750b/lamb/
experiment/mogrifier/config/c51c838b33a5+ tune
wikitext-2 35m lstm mos2 fm d2 arms/trial 747/config
Table 3: WER% on LibriSpeech with ESPRESSO LSTM
(Encoder-Decoder LSTM with Attention) with LM shallow
fusion. *(160 pieces were used for the exponential function).
ESPRESSO LSTM set clean other
Full-precision dev 2.99 8.77
iRNN PWL96* dev 3.73 10.02
Full-precision test 3.37 9.49
iRNN PWL96* test 4.11 10.71
thanks to regularization. While experiments on the
PTB dataset were a demonstration of the potential of
our method, these experiments on WikiText2 show
that our proposed method is able to stay on par with
state-of-the-art RNN models.
5.3 ASR on LibriSpeech
ASR is a critical edge AI application, but also challeng-
ing due to the nature of the task. Voice is diverse in
nature as human voice may vary in pitch, accent, pro-
nunciation style, voice volume, etc. While we showed
our method is working for competitive language mod-
eling task, one can argue ASR is a more practical and
at the same time more difficult task for edge and IoT
applications. Thefore, we experiment on an ASR task
based on the setup of Wang et al. (2019b) and their
ESPRESSO framework
3
. We used an LSTM-based At-
tention Encoder-Decoder (ESPRESSO LSTM) trained
on the strong ASR LibriSpeech dataset (Panayotov
et al., 2015). Experiments setup and hyper-parameters
are provided in Appendix A.2.3 We initialize the
quantized model from the pre-trained full-precision
ESPRESSO LSTM. In our early experiments, we
found that quantizing the model to 8-bit would not
give comparable results. After investigation, we no-
ticed it was mainly due to two reasons, i) the cell states
c
t
had large ranges (e.g.
[−17,15]
), ii) the attention
mechanism was not letting the decoder attend the en-
coder outputs accurately. Therefore, we quantize the
pre-activation gates (1), the element-wise multiplica-
tions in (2) and cell states
c
t
to 16-bit. The attention
is quantized following our described integer-only at-
tention method. Everything else is quantized to 8-bit
following our described method. The quantized model
has a similar performance to the full-precision model,
with a maximum of
1.25
WER% drop (Table 3). We
believe allowing the model to train longer would re-
duce the gap.
5.4 Inference Measurements
We implemented an 8-bit quantized integer-only
LSTM with PWL model based on a custom PyTorch
3
https://github.com/freewym/espresso
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
116

Table 4: Inference measurements on an anonymous smart-
phone based on a custom fork from PyTorch 1.7.1. The
model is a one LSTM cell with a state size of 400.
LSTM ms iter/s speedup
Full-precision 130 7.6 1.00×
iRNN PWL32 84 11.8 1.54×
iRNN PWL8 61 14.9 1.95×
iRNN without QAct 127 7.8 1.02×
(Paszke et al., 2019) fork from 1.7.1. We implemented
an integer-only PWL kernel using NEON intrinsics.
We benchmark the models on an anonymous smart-
phone using the
speed benchmark torch
tool
4
. We
warm up each model for 5 runs and then measure the
inference time a hundred times and report an average.
The sequence length used is 128, and the batch size
is one. We benchmark our iRNN LSTM model us-
ing PWLs with 32 pieces, and 8 pieces which achieve
up to
2×
speedup. We also evaluate our iRNN with
full-precision computations (iRNN w/o QAct) for the
activation where no speedup was observed for this
state size. We believe it is due to round-trip conver-
sions between floating-points and integers (Table 4).
There is a lot of room for improvements to achieve
even greater speedup, such as writing a
C++
integer-
only LSTM cell, fusing operations, and better PWL
kernel implementation.
6 CONCLUSION
We propose a task-agnostic and flexible methodol-
ogy to enable integer-only RNNs. To the best of
our knowledge, we are the first to offer an approach
to quantize all existing operations in modern RNNs,
supporting normalization and attention. We evalu-
ated our approach on high-performance LSTM-based
models on language modeling and ASR, which have
distinct architectures and variable computation re-
quirements. We show that RNN can be fully quan-
tized while achieving similar performance as their full-
precision counterpart. We benchmark our method on
an anonymous smartphone, where we obtain
2×
infer-
ence speedup and
4×
memory reduction. This allows
to deploy a wide range of RNN-based applications on
edge and on specialized AI hardware and microcon-
trollers that lack floating point operation.
4
https://github.com/pytorch/pytorch/blob/1.7/binaries/
speed benchmark torch.cc
REFERENCES
Ardakani, A., Ji, Z., Smithson, S. C., Meyer, B. H., and
Gross, W. J. (2018). Learning recurrent binary/ternary
weights. arXiv preprint arXiv:1809.11086.
Ba, J., Kiros, J. R., and Hinton, G. E. (2016). Layer normal-
ization. ArXiv, abs/1607.06450.
Bahdanau, D., Cho, K., and Bengio, Y. (2015). Neural ma-
chine translation by jointly learning to align and translate.
In Bengio, Y. and LeCun, Y., editors, 3rd International
Conference on Learning Representations, ICLR 2015, San
Diego, CA, USA, May 7-9, 2015, Conference Track Pro-
ceedings.
Bluche, T., Primet, M., and Gisselbrecht, T. (2020). Small-
footprint open-vocabulary keyword spotting with quan-
tized lstm networks. arXiv preprint arXiv:2002.10851.
Chen, M. X., Firat, O., Bapna, A., Johnson, M., Macherey,
W., Foster, G., Jones, L., Schuster, M., Shazeer, N., Par-
mar, N., Vaswani, A., Uszkoreit, J., Kaiser, L., Chen, Z.,
Wu, Y., and Hughes, M. (2018). The best of both worlds:
Combining recent advances in neural machine translation.
In Proceedings of the 56th Annual Meeting of the Asso-
ciation for Computational Linguistics (Volume 1: Long
Papers), pages 76–86, Melbourne, Australia. Association
for Computational Linguistics.
Cho, K., Van Merri
¨
enboer, B., Bahdanau, D., and Ben-
gio, Y. (2014). On the properties of neural machine
translation: Encoder-decoder approaches. arXiv preprint
arXiv:1409.1259.
Chorowski, J., Bahdanau, D., Serdyuk, D., Cho, K., and
Bengio, Y. (2015). Attention-based models for speech
recognition. arXiv preprint arXiv:1506.07503.
Darabi, S., Belbahri, M., Courbariaux, M., and Nia, V. P.
(2018). BNN+: improved binary network training. CoRR,
abs/1812.11800.
Esser, S. K., McKinstry, J. L., Bablani, D., Appuswamy, R.,
and Modha, D. S. (2020). Learned step size quantization.
In ICLR. OpenReview.net.
Gal, Y. and Ghahramani, Z. (2016). A theoretically grounded
application of dropout in recurrent neural networks. In
Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., and
Garnett, R., editors, Advances in Neural Information Pro-
cessing Systems, volume 29. Curran Associates, Inc.
He, Q., Wen, H., Zhou, S., Wu, Y., Yao, C., Zhou, X., and
Zou, Y. (2016). Effective quantization methods for recur-
rent neural networks. arXiv preprint arXiv:1611.10176.
He, Y., Sainath, T. N., Prabhavalkar, R., McGraw, I., Alvarez,
R., Zhao, D., Rybach, D., Kannan, A., Wu, Y., Pang, R.,
et al. (2019). Streaming end-to-end speech recognition for
mobile devices. In ICASSP 2019-2019 IEEE International
Conference on Acoustics, Speech and Signal Processing
(ICASSP), pages 6381–6385. IEEE.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Comput., 9(8):1735–1780.
Hou, L., Zhu, J., Kwok, J. T.-Y., Gao, F., Qin, T., and Liu,
T.-y. (2019). Normalization helps training of quantized
lstm.
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and
iRNN: Integer-only Recurrent Neural Network
117

Bengio, Y. (2018). Quantized neural networks: Training
neural networks with low precision weights and activa-
tions. Journal of Machine Learning Research, 18(187):1–
30.
Izmailov, P., Podoprikhin, D., Garipov, T., Vetrov, D.,
and Wilson, A. G. (2018). Averaging weights leads to
wider optima and better generalization. arXiv preprint
arXiv:1803.05407.
Jacob, B., Kligys, S., Chen, B., Zhu, M., Tang, M., Howard,
A. G., Adam, H., and Kalenichenko, D. (2017). Quantiza-
tion and training of neural networks for efficient integer-
arithmetic-only inference. 2018 IEEE/CVF Conference
on Computer Vision and Pattern Recognition, pages 2704–
2713.
Kapur, S., Mishra, A., and Marr, D. (2017). Low precision
rnns: Quantizing rnns without losing accuracy. arXiv
preprint arXiv:1710.07706.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization. CoRR, abs/1412.6980.
Krause, B., Kahembwe, E., Murray, I., and Renals, S. (2018).
Dynamic evaluation of neural sequence models. In Dy,
J. and Krause, A., editors, Proceedings of the 35th Inter-
national Conference on Machine Learning, volume 80
of Proceedings of Machine Learning Research, pages
2766–2775. PMLR.
Krishnamoorthi, R. (2018). Quantizing deep convolutional
networks for efficient inference: A whitepaper. arXiv
preprint arXiv:1806.08342.
Marcus, M. P., Santorini, B., and Marcinkiewicz, M. A.
(1993). Building a large annotated corpus of English: The
Penn Treebank. Computational Linguistics, 19(2):313–
330.
Melis, G., Ko
ˇ
cisk
´
y, T., and Blunsom, P. (2020). Mogrifier
lstm. In International Conference on Learning Represen-
tations.
Merity, S., Xiong, C., Bradbury, J., and Socher, R. (2016).
Pointer sentinel mixture models. CoRR, abs/1609.07843.
Mikolov, T., Sutskever, I., Deoras, A., Le, H.-S., Kombrink,
S., and Cernocky, J. (2012). Subword language modeling
with neural networks. preprint (http://www. fit. vutbr.
cz/imikolov/rnnlm/char. pdf), 8:67.
Ott, J., Lin, Z., Zhang, Y., Liu, S.-C., and Bengio, Y. (2016).
Recurrent neural networks with limited numerical preci-
sion. arXiv preprint arXiv:1608.06902.
Panayotov, V., Chen, G., Povey, D., and Khudanpur, S.
(2015). Librispeech: an asr corpus based on public do-
main audio books. In Acoustics, Speech and Signal Pro-
cessing (ICASSP), 2015 IEEE International Conference
on, pages 5206–5210. IEEE.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga,
L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison,
M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai,
J., and Chintala, S. (2019). Pytorch: An imperative style,
high-performance deep learning library. In Wallach, H.,
Larochelle, H., Beygelzimer, A., d
'
Alch
´
e-Buc, F., Fox, E.,
and Garnett, R., editors, Advances in Neural Information
Processing Systems, volume 32. Curran Associates, Inc.
Rumelhart, D., Hinton, G. E., and Williams, R. J. (1986).
Learning internal representations by error propagation.
Sari, E. and Partovi Nia, V. (2020). Batch normalization in
quantized networks. In Proceedings of the Edge Intelli-
gence Workshop, pages 6–9.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wo-
jna, Z. (2016). Rethinking the inception architecture for
computer vision. In Proceedings of the IEEE conference
on computer vision and pattern recognition, pages 2818–
2826.
Wang, C., Wu, S., and Liu, S. (2019a). Accelerating trans-
former decoding via a hybrid of self-attention and recur-
rent neural network. arXiv preprint arXiv:1909.02279.
Wang, Y., Chen, T., Xu, H., Ding, S., Lv, H., Shao, Y., Peng,
N., Xie, L., Watanabe, S., and Khudanpur, S. (2019b).
Espresso: A fast end-to-end neural speech recognition
toolkit. In 2019 IEEE Automatic Speech Recognition and
Understanding Workshop (ASRU), pages 136–143.
Werbos, P. J. (1990). Backpropagation through time: what
it does and how to do it. Proceedings of the IEEE,
78(10):1550–1560.
Wu, Y., Schuster, M., Chen, Z., Le, Q. V., Norouzi, M.,
Macherey, W., Krikun, M., Cao, Y., Gao, Q., Macherey,
K., et al. (2016). Google’s neural machine translation
system: Bridging the gap between human and machine
translation. arXiv preprint arXiv:1609.08144.
Yang, Z., Dai, Z., Salakhutdinov, R., and Cohen, W. W.
(2018). Breaking the softmax bottleneck: A high-rank
rnn language model.
A APPENDIX
A.1 Specific Details on LSTM-based
Models
For BiLSTM cells, nothing stated in section Integer-
only LSTM network is changed except that we enforce
the forward LSTM hidden state
−→
h
t
and the backward
LSTM hidden state
←−
h
t
to share the same quantiza-
tion parameters so that they can be concatenated as a
vector. If the model has embedding layers, they are
quantized to 8-bit as we found they were not sensitive
to quantization. If the model has residual connections
(e.g. between LSTM cells), they are quantized to 8-bit
integers. In encoder-decoder models the attention lay-
ers would be quantized following section Integer-only
attention. The model’s last fully-connected layer’s
weights are 8-bit quantized to allow for 8-bit matrix
multiplication. However, we do not quantize the out-
puts and let them remain 32-bit integers as often this is
where it is considered that the model has done its job
and that some postprocessing is performed (e.g. beam
search).
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
118

Table 5: Ablation study on quantized Mogrifier LSTM training on WikiText2. iRNN w/o PWL is the quantized model using
LUT instead of PWL to compute the activation function. Best results are averaged across 3 runs, and standard deviations are
reported.
iRNN Mogrifier LSTM val test
w/o PWL 60.40 ± 0.05 57.90 ± 0.01
w/o Quantized Activations 60.40 ± 0.03 57.95 ± 0.003
w/o Quantized Element-wise ops 60.08 ± 0.10 57.61 ± 0.23
w/o Quantized Matmul 60.10 ± 0.05 57.64 ± 0.10
w/o Quantized Weights (Full-precision) 60.27 ± 0.34 58.02 ± 0.34
A.2 Experimental Details
We provide a detailed explanation of our experimental
setups.
A.2.1 LayerNorm LSTM on PTB
We provide detailed information about how the lan-
guage modeling on PTB experiments are performed.
The vocabulary size is 10k, and we follow dataset pre-
processing as done in Mikolov et al. (2012). We report
the best perplexity per word on the validation set and
test set for a language model of embedding size 200
with one LayerNormLSTM cell of state size 200. The
lower the perplexity, the better the model performs. In
these experiments, we are focusing on the relative in-
crease of perplexity between the full-precision models
and their 8-bit quantized counterpart. We did not aim
to reproduce state-of-the-art performance on PTB and
went with a naive set of hyper-parameters. The full-
precision network is trained on for 100 epochs with
batch size 20 and BPTT (Werbos, 1990) window size
of 35. We used the SGD optimizer with weight decay
of
10
−5
and learning rate 20, which is divided by 4
when the loss plateaus for more than 2 epochs with-
out a relative decrease of
10
−4
in perplexity. We use
gradient clipping of 0.25. We initialize the quantized
models from the best full-precision checkpoint and
train from another 100 epochs. For the first 5 epochs
we do not enable quantization to gather range statistics
to compute the quantization parameters.
A.2.2 Mogrifier LSTM on WikiText2
We describe the experimental setup for Mogrifier
LSTM on WikiText2. Note that we follow the setup of
Melis et al. (2020) where they do not use dynamic eval-
uation (Krause et al., 2018) nor Monte Carlo dropout
(Gal and Ghahramani, 2016). The vocabulary size is
33279. We use a 2 layer Mogrifier LSTM with em-
bedding dimension 272, state dimension 1366, and
capped input gates. We use 6 modulation rounds per
Mogrifier layer with low-rank dimension 48. We use
2 Mixture-of-Softmax layers (Yang et al., 2018). The
input and output embedding are tied. We use a batch
size of 64 and a BPTT window size of 70. We train the
full-precision Mogrifier LSTM for 340 epochs, after
which we enable Stochastic Weight Averaging (SWA)
(Izmailov et al., 2018) for 70 epochs. For the optimizer
we used Adam (Kingma and Ba, 2014) with a learning
rate of
≈ 3 × 10
−3
,
β
1
= 0
,
β
2
= 0.999
and weight
decay
≈ 1.8 × 10
−4
. We clip gradients’ norm to 10.
We use the same hyper-parameters for the quantized
models from which we initialize with a pre-trained
full-precision and continue to train for 200 epochs.
During the first 2 epochs, we do not perform QAT,
but we gather min and max statistics in the network
to have a correct starting estimate of the quantization
parameters. After that, we enable 8-bit QAT on every
component of the Mogrifier LSTM: weights, matrix
multiplications, element-wise operations, activations.
Then we replace activation functions in the model with
quantization-aware PWLs and continue training for
100 epochs.
Table 6: Word-level perplexities on PTB for a full-precision
LSTM with LayerNorm and a full-precision model with
MadNorm. Best results are averaged across 3 runs, and
standard deviations are reported.
Full-precision model val test
LayerNorm LSTM 98.58 ± 0.35 94.84 ± 0.21
MadNorm LSTM 97.20 ± 0.47 93.63 ± 0.74
We perform thorough ablation on our method to
study the effect of each component. Quantizing the
weights or the weights and matrix multiplications cov-
ers about
0.1
of the perplexity increase. There is a
clear performance drop after adding quantization of
element-wise operations with an increase in perplex-
ity of about
0.3
. This is both due to the presence of
element-wise operations in the cell and hidden states
computations affecting the flow of information across
timesteps and to the residual connections across layers.
On top of that, adding quantization of the activation
does not impact the performance of the network.
A.2.3 ESPRESSO LSTM on LibriSpeech
The encoder is composed of 4 CNN-BatchNorm-
ReLU blocks followed by 4 BiLSTM layers with 1024
iRNN: Integer-only Recurrent Neural Network
119

Figure 3: Example of an iteration from our proposed quantization-aware PWL Algorithm 1. The algorithm proceeds to reduce
the number of pieces by merging two similar adjacents pieces. In this figure, the slopes
S
12
and
S
23
are the most similar pieces;
therefore, the knot k
2
is removed.
Algorithm 1: The algorithm recursively reduced the number of pieces until the wanted number of pieces is achieved.
The algorithm needs to be provided the function to approximate
f
, the input scaling factor
S
x
and zero-point
Z
x
, the
quantization bitwidth
b
and the number of linear pieces wanted. One iteration of select knots can be viewed in Figure
3.
def select knots(knots, intercepts, pwl nb):
dknots ← knots[1:] − knots[:−1]
dintercepts ← intercepts[1:] − intercepts[:−1]
slopes ← dintercepts/dknots
if len (slopes) == pwl nb:
return knots, slopes, intercepts
else:
diff adj slopes ←
slopes[:−1]− slopes[1:]
knot index to remove ← argmin diff adj slopes
remaining knots ← knots.remove(knot index to remove)
remaining intercepts ← intercepts.remove(knot index to remove)
return select knots(remaining knots, remaining intercepts, pwl nb)
def create quantization aware pwl(f, input scale, input zero point, b, pwl nb):
quantized knots ← [0,...,2
b
− 1] // Generate every q
x
knots ← input scale (quantized knots − input zero point) // Generate every r
x
intercepts ← f (knots)
{knots, slopes, intercepts} ← select knots(knots, intercepts, pwl nb)
return knots, slopes, intercepts
units. The decoder consists of 3 LSTM layers of units
1024 with Bahdanau attention on the encoder’s hidden
states and residual connections between each layer.
The dataset preprocessing is exactly the same as in
Wang et al. (2019b). We train the model for 30 epochs
on one V100 GPU, which takes approximately 6 days
to complete. We use a batch size of 24 while limiting
the maximum number of tokens in a mini-batch to
26000. Adam is used with a starting learning rate of
0.001
, which is divided by 2 when the validation set
metric plateaus without a relative decrease of
10
−4
in performance. Cross-entropy with uniform label
smoothing
α = 0.1
(Szegedy et al., 2016) is used as
a loss function. At evaluation time, the model predic-
tions are weighted using a pre-trained full-precision
4-layer LSTM language model (shallow fusion). Note
that we consider this language model an external com-
ponent to the ESPRESSO LSTM; we do not quantize
it due to the lack of resources. However, we already
show in our language modeling experiments that quan-
tized language models retain their performance. We
refer the reader to Wang et al. (2019b) and training
script
5
for a complete description of the experimental
setup. We initialize the quantized model from the pre-
trained full-precision ESPRESSO LSTM. We train the
5
https://github.com/freewym/espresso/blob/master/
examples/asr librispeech/run.sh
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
120

quantized model for only 4 epochs due to the lack of
resources. The quantized model is trained on 6 V100
GPUs where each epoch takes 2 days, so a total of
48 GPU days. The batch size is set to 8 mini-batch
per GPU with maximum 8600 tokens. We made these
changes because otherwise, the GPU would run out of
VRAM due to the added fake quantization operations.
For the first half of the first epoch, we gather statistics
for quantization parameters then we enable QAT. The
activation functions are swapped with quantization-
aware PWL in the last epoch. The number of pieces
for the quantization-aware PWLs is 96, except for the
exponential function in the attention, which is 160 as
we found out it was necessary to have more pieces
because of its curvature. The number of pieces used
is higher than in the language modeling experiments
we did. However, the difference is that the inputs to
the activation functions are 16-bit rather than 8-bit al-
though the outputs are still quantized to 8-bit. It means
we need more pieces to capture the inputs resolution
better. Note that it would not be feasible to use a 16-bit
Look-Up Table to compute the activation functions due
to the size and cache misses, whereas using 96 pieces
allows for a 170x reduction in memory consumption
compared to LUT.
iRNN: Integer-only Recurrent Neural Network
121
