
Attributed-based Label Propagation Method for Balanced
Modularity and Homogeneity Community Detection
Jenan Moosa
1a
, Wasan Awad
1b
and Tatiana Kalganova
2c
1
College of Information Technology, Ahlia University, Manama, Bahrain
2
College of Engineering, Design and Physical Sciences, Brunel University, London, U.K.
Keywords: Community Detection, Label Propagation, Homogeneity, Covid-19, Modularity.
Abstract: Community Detection is an expanding field of interest in many scopes, e.g., social science, bibliometrics,
marketing and recommendations, biology etc. Various community detection tools and methods have been
proposed in the last years. This research is to develop an improved Label Propagation algorithm (Attribute-
Based Label Propagation ABLP) that considers the nodes’ attributes to achieve a fair Homogeneity value,
while maintaining high Modularity measure. It also formulates an adaptive Homogeneity measure, with
penalty and weight modulation, that can be utilized in consonance with the user’s requirements. Based on the
literature review, a research gap of employing Homogeneity in Community Detection was identified, and
accordingly, Homogeneity as a constraint in Modularity based methods is investigated. In addition, a novel
dataset constructed on COVID-19 contact tracing in the Kingdom of Bahrain is proposed, to help identify
communities of infected persons and study their attributes’ values. The implementation of proposed algorithm
performed high Modularity and Homogeneity measures compared with other algorithms.
1 INTRODUCTION
Extensive research was done to detect communities
within networks, detected communities are densely
connected nodes that are strongly connected to each
other in or the subnetwork (community) than to the
rest of the network(WU et al., 2020). In social
networks, a community can be defined as a group of
nodes or persons that are similar to each other and
dissimilar from the rest of the group (Raghavan et al.,
2007). This indicates that the group of nodes in one
community will most likely share the same
characteristics or interests. Whereas in attributed
networks, the nodes in a community will most likely
share the same attributes’ values.
To assess the output of generated communities,
different number of measures are being used,
including Modularity measure which indicates the
quality of the generated partitions or communities.
However, the integration of different types of
constrains or external information on community
composition was rarely investigated (Viles &
a
https://orcid.org/0000-0002-9081-7748
b
https://orcid.org/0000-0001-7152-3480
c
https://orcid.org/0000-0003-4859-7152
O’Malley, 2017), and Homogeneity as constraint still
remains uncharted. In consequence, the detected
communities might contain irrelevant nodes in one
cluster even-though the communities scored a good
fitness score in other measures such as Modularity.
To overcome this, a Homogeneity measure can be
integrated with Modularity, to consolidate the
evaluation process. So, a method that maximizes both
Modularity and Homogeneity is proposed, with
Modularity and Homogeneity as objective functions.
On the other hand, as constrained community
detection shows robust performance on noisy data
since it uses background knowledge(Nakata &
Murata, 2015) and the restriction of the type
considered here has, to our knowledge, remained
unstudied, Modularity with Homogeneity as a
constraint is also tested to adjust the detection of
homogenous communities.
The scientific contributions of this paper are:
1. Develop an Attribute-Based Label
Propagation algorithm that considers the
nodes’ attributes to achieve a fair
Moosa, J., Awad, W. and Kalganova, T.
Attributed-based Label Propagation Method for Balanced Modularity and Homogeneity Community Detection.
DOI: 10.5220/0010928200003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 905-912
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
905

Homogeneity value, while maintaining a high
Modularity measure.
2. Formulate an adaptive Homogeneity measure,
with penalty and weight modulation, that can
be utilized based on the user’s requirements.
3. A research gap of employing Homogeneity in
Community Detection was identified, and
accordingly, Homogeneity as a constraint in
Modularity based methods is investigated.
4. Design a novel dataset based on COVID-19
contact tracing in the Kingdom of Bahrain, to
help identify communities of infected persons
and study their attributes’ values.
2 RELATED WORK
Effective community detection is an important tool
for analyzing networks; it provides thorough
knowledge of the network, in addition to the structure
and functional characteristics of the network (WU et
al., 2020). Community detection problem is getting
more attention, as different algorithms and techniques
have been proposed, which includes traditional
algorithms (Fortunato, 2010)(Shen et al., 2009),
evolutionary algorithms (Karimi et al., 2020)(N.
Chen et al., 2020), heuristic (Clauset et al., 2004;
Sobolevsky et al., 2014) hierarchical clustering (Lu et
al., 2015) , spectral clustering (Luxburg, 2007), label
propagation (Raghavan et al., 2007), neural networks
(Bruna, 2017), etc.
2.1 Evaluation Measures
The detected communities are evaluated using a
number of evaluation measures such as Modularity
(M. E. J. Newman & Girvan, 2004), which measures
the fraction of the edges in the network that connect
vertices of the same type (i.e., within-community
edges) minus the expected value of the same quantity
in a network with the same community divisions but
random connections between the vertices. Modularity
has been used to compare the quality of the partitions
obtained by different methods, but also as an
objective function to optimize (M. Newman, 2003).
Homogeneity was also used as an objective
function (Wu & Pan, 2016), a measure was proposed
based on Shannon information entropy theory in
which the entropy of a set, measures the average
Shannon information content of the set.
Unfortunately, the modularity values produced in this
research were significantly lower than others.
Moayedikiaa (Moayedikia, 2018) used the
proposed Homogeneity in (Wu & Pan, 2016) as an
objective function by developing an attributed
community detection algorithm wrapped by
Harmony Search that relies on nodes’ importance to
form communities. Yet this algorithm performed a
long execution time, and it also suffered from
entrapment in local optima. Another research
proposed a method for community detection based on
a higher-order feature termed Attribute Homogenous
Motif (P. Li et al., 2018), which integrates both node
attributes and higher-order structure of the network.
However, the modularity was neglected in this
research.
The evaluation measures used can assess one
criterion only, so different measures are used to
evaluate different aspects of the result. As one method
might generate results that perform well in one
evaluation measure while fail to achieve a fair result
in another one. Thus, an evaluation technique that
takes this issue into account needs to be studied.
2.2 Community Detection with
Constraints
Constrained community detection approaches are
used to take advantage of the existing side
information of the network (Ganj et al., 2018). This
aids in generating more efficient and actionable
results, and help develop data mining techniques that
can handle complex and domain-specified constraints
(Ganji et al., 2017). Table 1 presents several
constrained community detection methods, along
with the evaluation measure used to evaluate the
results.
Table 1: Community detection with constraints.
Paper Method Constraints Objective function
(Ganj, Bailey
and Stuckey,
2018)
Lagrangian
Constrained
Must-Link,
Cannot-Link
Normalized Mutual
Information,
Noise Sensitivit
y
(Ganji, Bailey
and Stuckey,
2017)
Programming
modelling technology
Global,
Community and
Instance level
Normalized Mutual
Information,
Modularity, Run-Time
(Chin and
Ratnavelu,
2017)
Label propagation
algorithm with
constraints
Propagating
labels,
Communities’
Exemption
Normalized Mutual
Information,
Modularity
(Chin and
Ratnavelu,
2016)
Constrained Label
Propagation Number of links
of a node to the
nodes in a
community
Normalized Mutual
Information,
Normalized Variation
Information,
Modularity,
Modularity density
Most of the current community detection methods
consider the structural information of networks, but
disregard the fruitful information of the nodes, and this
results in the failure of detecting semantically
meaningful communities (P. Li et al., 2018). However,
Homogeneity was never studied as a constraint, and
was always treated as an objective function.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
906

The two objective functions (Modularity and
Homogeneity) are conflicting, which means that
improving one of them leads to degradation of
another (Moayedikia, 2018). Modularity has proven
its effectiveness in evaluating community detection
problem, many algorithms are based on modularity
maximization (Tsung et al., 2020). Hence comes the
idea of testing the Homogeneity as a constraint, in
addition to testing it as an objective function. As
constrained algorithms are effective in dealing with
combined optimization problems, due to its wide
representation scope and generally applicable solving
methods(Y. C. Chen et al., 2010).
3 PROPOSED METHODS
In this section, new Attribute-Based Label
Propagation (ABLP) algorithms based on attributes’
regulation are proposed.
3.1 ABLP Algorithm
The proposed method is an Attribute-Based Label
Propagation Algorithm is a Modularity maximization
based on Label Propagation algorithm with regards to
homogeneity. As Label Propagation is considered as
one the effective algorithms amongst the existing
algorithms used for community detection because of
its time efficiency (Chin & Ratnavelu, 2017).
Algorithm 1: ABLP.
The concept of the algorithm is based on
examining the neighbors of the node in the network.
Each node (x) will be labeled with a number that
indicates its community. First each node will have a
unique label, and then the labels will propagate
throughout the process. The label of x will be changed
based on its neighbors’ labels. Node x will also check
the attribute of its neighbor, nodes with similar
attributes will most likely have the same label. This
step will be iterated, and each node will update its
label at every step, the node will get the label that the
maximum number of neighbors carry. Finally, x will
join the community that contains most of his
homogeneous neighbors. In this way, ABLP
algorithm tries to maximize Modularity and
Homogeneity at the same time.
3.2 Constrained ABLP Algorithm
The same concept of the proposed ABLP is followed,
with regards of homogeneity as a constraint, which
penalizes the Modularity measure by minimizing it
based on the achievement of the homogeneity value.
So ideally, if the homogeneity degree is high, the
modularity measure should remain at its best.
However, if the homogeneity degree is low, the
Modularity value should be punished and reduced.
Algorithm 2: Constrained ABLP.
The Constrained Attribute-Based Label
Propagation algorithm is a highest-modularity,
homogeneity constraint-satisfying solution for the
community detection problem in attributed networks.
The algorithm considers the run that generates the
maximum constrained Modularity and proposed
measure of Penalized Homogeneity degrees.
4 PROPOSED EVALUATION
MEASURE
In this section, Homogeneity Degree that considers
the networks’ structure, in addition to a Penalized
Homogeneity measure are proposed. These measures
will later be used to evaluate a number of social
networks in the community detection problem.
Attributed-based Label Propagation Method for Balanced Modularity and Homogeneity Community Detection
907

4.1 Evaluation Measures
Homogeneity in community detection was first
proposed by (Wu & Pan, 2016), it was defined based
on Shannon information entropy theory, the entropy
of a set measures the average Shannon information
content of it. This homogeneity measure considers the
proportion of the number of nodes with a certain
attribute in a community to the total number of nodes
in a community. The measure does not consider the
network structure, as real-world datasets might have
some aspects that need to be considered.
As homogeneity was used as an objective
function to measure the homogeneity of the detected
communities in the network as one unit, here is the
proposal of a new of homogeneity measure that
evaluates the homogeneity degree in each
community, based on specified attribute values.
The formula will calculate the number of nodes
with the specified attribute divided by the total
number of nodes in the cluster. It reflects the standard
deviation; however, standard deviation finds how
concentrated the data is around the mean, in our case,
the mean will be ignored, µ=0;
The closer the value is to 1, the more
homogeneous the cluster is. This can be calculated in
𝐻𝑐
which is the Homogeneity of community k.
Hd =
(1)
Where Hd
is the average Homogeneity degree in
the Communities: att is the number of attributes in the
network, n
att
is the number of nodes with each
attribute in a community, and N is the total number of
nodes in the community. The square value is
calculated as it adds more weighting to the
differences which makes the value more significant.
4.2 Penalized Homogeneity Degree
It should be noted that the Homogeneity degree (Hd)
measure proposed in section 4.1
does not consider the
number of communities and number of nodes in each
community compared to the total number of nodes in
the network. To add more flexibility and user-
preference to the proposed measure, a penalty will be
given, to ensure that nodes among all detected
communities are homogeneous, and that distribution
is fair.
To add more restrictions to the homogeneity
degree, we consider (P), a penalty that takes the
number of nodes for each attribute in the community
compared to the total number of nodes with this
attribute in the network.
P=1−
𝑛
()
N
()
(2)
Where n
att
is the number of nodes with each
attribute in a community, and N
att
is the number of
nodes with this attribute in the network, for the
attribute that owns the maximum number of nodes in
each community.
PHd= Hd - P
(3)
Where PHd measures the Penalized Homogeneity
Degree. This allows the user to apply an impartial
penalty for algorithms that detect a large number of
communities that contain a small number of nodes
with a certain attribute. It is also possible to set a
weight for the penalty, and consider more attribute,
based on the user’s requirement of how important
each attribute is.
MAWPHd= Hd - P∗𝑤 Hd − (P
∗𝑤
)
(4)
Multi-Attribute Weighted Penalized
Homogeneity degree can be calculated using the
MAWPHd measure. Where z is the number of
attributes to be considered, and w is the weight of
penalty to be applied.
On the other hand, to calculate Modularity
constrained by Homogeneity, the Penalized
Homogeneity Degree will be subtracted from 1 to
minimize the penalty of constraint. Because the
higher the Homogeneity value, the less punishment is
applied on the Modularity.
Q(C: H) =
|Q-1- Penalized Homogeneity Degree | (5)
Where Q(C: PHd) calculates the Modularity with
Penalized Homogeneity as Constraint, Q represents
Modularity, H is the Homogeneity (can be Hd
or PHd,
based on the experiment, dataset or research
requirements).
The proposed measures of (PHd) and
(MAWPHd) allow a more flexible mensuration of
Homogeneity on different types of attributed
networks, based on the user-defined requirements.
5 RESULTS AND DISCUSSION
In this section, the algorithm will be implemented on
two datasets in addition to a proposed dataset of
COVID-19 contact tracing. The results will be
compared to several existing algorithms. And then
will be compared in term of Modularity, and the
proposed measures of Homogeneity.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
908

5.1 Datasets
The datasets used for the experiments are attributed
social networks from the literature, in addition to a
proposed real-world dataset based on the contact
tracing of COVID-19 infected persons in the
Kingdom of Bahrain.
1 Political Books (PolBooks) a social network
consists of nodes representing books about US
politics. Edges represent frequent co-purchasing of
books by the same buyers. Books were labelled by
Newman (M. E. J. Newman, 2006) with an attribute
describing their political alignments. It consists of
105 nodes, and 441 edges (Figure 1).
Figure 1: US Political books network (Triangles: neutral,
dots: conservative, and squares: liberal) (Q. Wu et al., 2013).
2 American College Football network, represents
the games between Division IA colleges during
regular season fall in 2000 (Girvan & Newman,
2002). It consists of 115 teams and 613 games,
divided into 12 conferences (Figure 2).
Figure 2: American College football network (each team is
represented by a different color) (Binesh & Rezghi, 2018).
3 Proposed Dataset: COVID-19 Contact
Tracing: The COVID-19 pandemic has been termed
as the most consequential global crisis since the
World Wars. Because of the rapid prevalence of this
virus, health organizations all over the world tend to
track and store all data related to this pandemic. This
includes the contact tracing, number of cases, number
of deaths, etc. The availability of rich textual data
from various online sources can be used to understand
the growth, nature and spread of COVID-19(Usman
et al., 2020). According to World Health
Organization (World Health Organization, 2021),
contact tracing is the process of identifying,
assessing, and managing people who have been
exposed to a disease to prevent onward transmission.
When systematically applied, contact tracing will
break the chains of transmission of an infectious
disease and is thus an essential public health tool for
controlling infectious disease outbreaks. When contact
tracing data is compiled it can be represented by a
network, and hence structured into a graph, which can
be analysed using graph mining techniques.
As any network can be outlined in a graph, and
the graph is composed of a set of nodes which can be
individuals or entities, and edges that represent the
connections and interactions between the nodes(Bedi
& Sharma, 2016).
A dataset was proposed in (Moosa et al., 2021), it
is based on the spread of virus between countries. An
open-source contact tracing data was used to follow
the spread of virus from January to March 2020,
between the countries worldwide, which started in
China and expanded to other countries. Each country
is represented by a node, and an edge is used when a
country has a contact infected person from another
country. Unfortunately, this dataset cannot be used in
this research as it is not attributed network.
The data used to form this dataset was available
on Bahrain’s Ministry of Health website, and was
publicly available, it contained the contact tracing of
citizens who were infected by the COVID-19 virus,
the details include the case number, age, nationality,
gender, travel history (if any), and the other case
number contacted which caused the infection. Since
the data was publicly available on the website and it
does not contain any personal information which
makes it impossible to recognize any of the cases, it
did not require any ethical approval. The cases cover
the period 01/April/2020 to 10/May/2020.
Figure 3: Proposed Dataset: COVID-19 contact tracing in
the Kingdom of Bahrain.
The dataset consists of 750 cases represented by
nodes and 589 relationships between the cases
(contacted persons) represented by edges. Other cases
were ignored as the source of getting the virus was
unknown as they were tested as part of a campaign to
obtain random samples from the community or tested
positive after developing symptoms without clear
idea of the contacted persons.
Attributed-based Label Propagation Method for Balanced Modularity and Homogeneity Community Detection
909
5.2 Experiments of Work
The proposed ABLP algorithm, along with several
existing algorithms will be implemented. The
algorithms used for comparison are:
- Asynchronous Label Propagation (LPA)
(Raghavan et al., 2007)
- Graph Embedding with Self Clustering
(GEMSEC) (Rozemberczki et al., 2019)
- An Edge Enhancement Approach for Motif-
aware (EdMot) (P.-Z. Li et al., 2019)
- Deep Autoencoder-like Nonnegative Matrix
Factorization (DANMF) (Ye et al., 2018)
5.3 Results
The main purpose of proposing the algorithm is to
maximize homogeneity, while maintaining a high
Modularity value. So, the Homogeneity degree will
be calculated and compared as an objective function.
And then the results will be tested again with
consideration of Homogeneity as a constraint.
5.3.1 Homogeneity as an Objective Function
It is observed that considering the nodes’ attributes
values will result in more homogeneous
communities. Nodes with similar attributes are
beyond any doubt share the same value, however,
they may not necessarily be neighbours or share
direct ties. So, paying more attention to the node’s
values helps detect denser communities in terms of
interests or preferences.
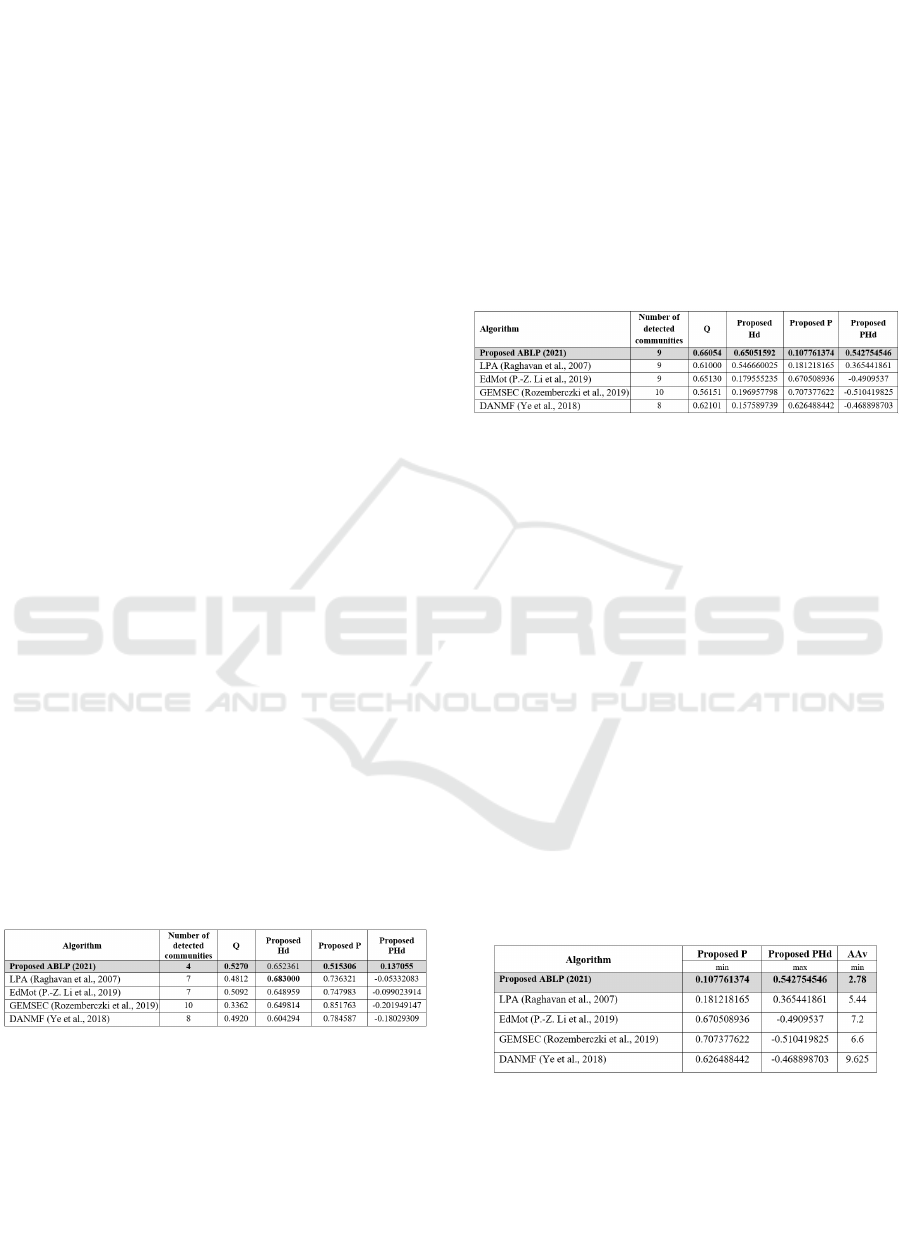
The results are shown in Tables 1,2,3 and 4. Where
Hd states the proposed Homogeneity measure in
detected communities (equation 1), P is the proposed
penalty measure (equation 2) and PHd is the proposed
Penalized Homogeneity degree values (equation 3).
Table 1: Results on Books Dataset.
As seen in Table1, the highest modularity value
was achieved in Books dataset by the proposed
Attribute-Based Label Propagation algorithm with a
value of 0.527, followed by EdMot algorithm with a
value of 0.5092.
As for the Homogeneity degree (before applying
the penalty), LPA achieved a high rate, however its
penalty was high because it detected two small
communities with node sizes 4 and 3, and all nodes in
both communities had the same attribute value. This
resulted in a high penalty and therefore a very low
penalized homogeneity degree. GEMSEC also had an
elevated penalty value for the same reason. This gives
rise to ABLP algorithm achieving the highest
assessment value among all other algorithms.
The Modularity measure values of American
College Football dataset were likely close by the expe-
rimented algorithm. However, Homogeneity measure
was significantly low as the communities detected
included nodes from diversified conference values.
Table 2: Results on Football Dataset.
For a higher homogeneity value, the community
should contain nodes with the least number of
attribute values possible. To better understand what
happened, the average number of attribute values in a
community can be calculated, and obviously, the
closer the value to 1, the better.
In American College football dataset, the number
of attribute values is 12, which can be considered high
to some extent compared to Books dataset which
consisted of 3 attribute values. It was observed that
when a community consists of nodes with more than
3 different attribute values, the homogeneity value is
relatively low. To prove this, a measure of Average
Attribute value (AAv) in a community is proposed
and calculated, as seen in Table 3. It can be clearly
perceived that higher Average Attribute value result
in higher penalty and thus a lower PHd value. This
draws a conclusion, that having multiple attribute
values in one community results in a non-
homogeneous environment.
Table 3: The average number of attribute value.
As for the proposed dataset, since it is a real-
world contact tracing network, and the number of
edges is less than the number of nodes, so the penalty
will not be considered as the nodes did not have
enough connections with one another.
The highest modularity value was again achieved
by the ABLP followed by EdMot. As well as the
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
910
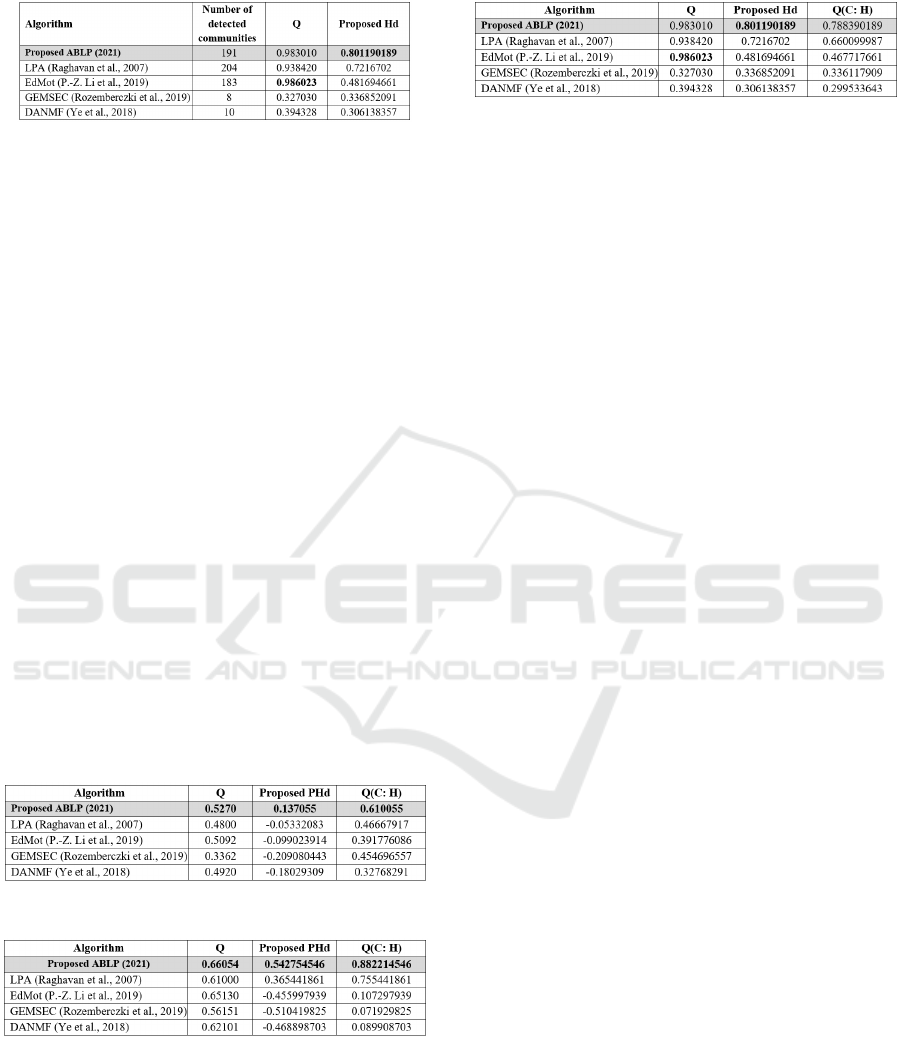
Table 4: Results on Proposed dataset.
homogeneity value which was the highest in the
proposed measure and the Label Propagation
Algorithm. It is also noticeable that while Edmot
achieved a high modularity value, it scored a
comparatively low homogeneity measure. As for
GEMSEC and DANMF, both algorithms detected a
low number of communities with high number of
nodes in one community, then divided the rest of the
nodes on the remaining communities. This manifestly
resulted in a low modularity value as well as a low
homogeneity measure.
5.3.2 Homogeneity as Constraint
Here the homogeneity is treated as a constraint, which
minimizes the Modularity value based on the
achievement of the homogeneity value. When the
Homogeneity value is high, modularity measure
should remain at its best. On the contrary, when the
value of Homogeneity is low, the Modularity value
should be punished and reduced. This is tested with
the same experiments, as seen in Table 5 and 6.
Where Q(C: H) is the value of Modularity constrained
with Homogeneity (equation 5). For Books and
Football datasets, PHd Homogeneity value is
considered since a penalty was applied.
Table 5: Homogeneity as constraint in Books dataset.
Table 6: Homogeneity as constraint in Football dataset.
And as the proposed COVID-19 dataset did not
need the penalty measure, the value of constrained
Homogeneity will be Hd.
Testing the homogeneity as a constraint helps in
evaluating the results in terms of Modularity and
Homogeneity at the same time. Here is it assumed
that both measures have the same importance or
Table 7: Homogeneity as constraint in proposed dataset.
weight in the results. However, a weight can be
assigned to the measures based on how important
each measure is. This will facilitate in the evaluation
process based on the defined user requirements,
which are aligned with the dataset itself. So, if the
user is interested more in the Homogeneity than
Modularity, a ratio of 70/30 can be applied, where
Homogeneity is responsible for 70% of the measure
and the Modularity is for the other 30%. This can be
calculated as |1- (0.3 * Q – 0.7 *H). In other words,
this way can be personalized according to the nature
of the dataset and the expected detected communities.
6 CONCLUSION
Community detection in attributed networks can be
evaluated in many aspects. The mostly used
evaluation measures such as Modularity, cannot
address the evaluation of Homogeneity. Hence,
Attribute-Based Label Propagation ABLP algorithm,
that considers the attribute values of nodes while
maintaining a high Modularity, and Homogeneity and
values is proposed. And to support evaluating the
proposed algorithm, an adaptable homogeneity
measure is also proposed. This measure assesses the
homogeneity in an attributed network and can be
penalized based on the type of the dataset.
Experiments on existing social networks were
conducted as well as on the newly proposed COVID-
19 dataset which is based on the contact tracing of the
virus infected persons in the Kingdom of Bahrain.
The algorithm appears to have good results in terms
of the discussed evaluation measures. As future work,
we tend to study the attribute consideration on the
familiar community detection algorithms.
REFERENCES
Bedi, P., & Sharma, C. (2016). Community detection in
social networks. Wiley Interdisciplinary Reviews: Data
Mining and Knowledge Discovery, 6(3), 115–135.
https://doi.org/10.1002/widm.1178
Binesh, N., & Rezghi, M. (2018). Fuzzy clustering in
community detection based on nonnegative matrix
factorization with two novel evaluation criteria. Applied
Soft Computing Journal, 69, 689–703. https://doi.org/
Attributed-based Label Propagation Method for Balanced Modularity and Homogeneity Community Detection
911

10.1016/j.asoc.2016.12.019
Bruna, J. (2017). Community Detection with Graph Neural
Networks. Stat, 1050, 27.
Chen, N., Hu, B., & Rui, Y. (2020). Dynamic Network
Community Detection with Coherent Neighborhood
Propinquity. IEEE Access, 8(November), 27915–27926.
https://doi.org/10.1109/ACCESS.2020.2970483
Chen, Y. C., Guan, Z., Peng, Y., Shao, X., & Hasseb, M.
(2010). Technology and system of constraint
programming for industry production scheduling — Part
I_ A brief survey and potential directions. Frontiers of
Mechanical Engineering in China, 5(1), 455–464.
Chin, J. H., & Ratnavelu, K. (2017). A semi-synchronous
label propagation algorithm with constraints for
community detection in complex networks. Nature
Publishing Group, 7(1), 1–12. https://doi.org/10.1038/
srep45836
Clauset, A., Newman, M. E. J., & Moore, C. (2004). Finding
community structure in very large networks. Physical
Review E, 70(6), 066111.
Fortunato, S. (2010). Community detection in graphs.
Physics Reports, 486(3–5), 75–174.
Ganj, M., Bailey, J., & Stuckey, P. J. (2018). Lagrangian
Constrained Community Detection. The Thirty-Second
AAAI Conference on Artificial Intelligence (AAAI-18),
2983–2990.
Ganji, M., Bailey, J., & Stuckey, P. J. (2017). A Declarative
Approach to Constrained Community Detection.
International Conference on Principles and Practice of
Constraint Programming, 477–494.
Girvan, M., & Newman, M. E. J. (2002). Community
structure in social and biological networks. Proceedings
of the National Academy of Sciences, 99(12), 7821–7826.
Karimi, F., Lotfi, S., & Izadkhah, H. (2020). Multiplex
community detection in complex networks using an
evolutionary approach. Expert Systems with
Applications, 146, 113184. https://doi.org/10.1016/j.es
wa.2020.113184
Li, P.-Z., Huang, L., Wang, C.-D., & Lai, J.-H. (2019).
EdMot : An Edge Enhancement Approach for Motif-
aware Community Detection. The 25th ACM SIGKDD
International Conference on Knowledge Discovery &
Data Mining, 479–487. https://doi.org/10.1145/
3292500.3330882
Li, P., Huang, L., Wang, C., Huang, D., & Lai, J. (2018).
Community Detection Using Attribute Homogenous
Motif. IEEE Access, 6, 47707–47716. https://doi.org/
10.1109/ACCESS.2018.2867549
Lu, H., Halappanavar, M., & Kalyanaraman, A. (2015).
Parallel heuristics for scalable community detection.
Parallel Computing, 47, 19–37. https://doi.org/10.1016/
j.parco.2015.03.003
Luxburg, U. Von. (2007). A Tutorial on Spectral Clustering.
Statistics and Computing, 17(4), 395–416.
Moayedikia, A. (2018). Multi-objective community
detection algorithm with node importance analysis in
attributed networks. Applied Soft Computing Journal, 67,
434–451. https://doi.org/10.1016/j.asoc.2018.03.014
Moosa, J., Awad, W., & Kalganova, T. (2021). Intelligent
Community Detection : Comparative Study
(COVID19 Dataset). EAMMIS 2021: Artificial
Intelligence Systems and the Internet of Things in the
Digital Era, 239, 189–196.
Nakata, K., & Murata, T. (2015). Fast Optimization of
Hamiltonian for Constrained Community Detection.
Complex Networks VI, 79–89.
Newman, M. (2003). Fast algorithm for detecting community
structure in networks. Physical Review E, 69(6), 066133.
Newman, M. E. J. (2006). Modularity and community
structure in networks. The National Academy of Sciences,
103(23), 8577–8582.
Newman, M. E. J., & Girvan, M. (2004). Finding and
evaluating community structure in networks. Physical
Review E - Statistical, Nonlinear, and Soft Matter
Physics, 69(2 2), 1–16. https://doi.org/10.1103/Phys
RevE.69.026113
Raghavan, U. N., Albert, R., & Kumara, S. (2007). Near
linear time algorithm to detect community structures in
large-scale networks. Physical Review E - Statistical,
Nonlinear, and Soft Matter Physics, 76(3), 1–11.
https://doi.org/10.1103/PhysRevE.76.036106
Rozemberczki, B., Davies, R., Sarkar, R., & Sutton, C.
(2019). GemSec: Graph embedding with self clustering.
Proceedings of the 2019 IEEE/ACM International
Conference on Advances in Social Networks Analysis
and Mining, ASONAM 2019, 65–72. https://doi.org/
10.1145/3341161.3342890
Shen, H., Cheng, X., Guo, F., Gao, L., & Yong, X. (2009).
Detecting the overlapping and hierarchical community
structure in complex networks. New Journal of Physics,
11(3), 033015. https://doi.org/10.1088/1367-2630/11/3/
033015
Sobolevsky, S., Campari, R., Belyi, A., & Ratti, C. (2014). A
General Optimization Technique for High Quality
Community Detection in Complex Networks. Physical
Review E, 90(1), 012811.
Tsung, C. K., Ho, H. J., Chen, C. Y., Chang, T. W., & Lee,
S. L. (2020). Detecting overlapping communities in
modularity optimization by reweighting vertices.
Entropy, 22(8), 819. https://doi.org/10.3390/E22080819
Usman, M., Iqbal, W., Mary, Q., & Qadir, J. (2020).
Leveraging Data Science To Combat COVID-19 : A
Comprehensive Review. IEEE Transactions on Artificial
Intelligence, 1(1), 85–103. https://doi.org/10.13140/
RG.2.2.12685.28644/4
Viles, W., & O’Malley, J. (2017). Constrained Community
Detection in Social Networks. arXiv prep.
World Health Organization. (2021). Contact tracing in the
context of COVID-19: Interim guidance. Paediatrics and
Family Medicine, WHO/2019-nCoV/Contact_Tracing/
2020.1, 1–11. https://doi.org/10.15557/PiMR.2020.0005
WU, L., ZHANG, Q., CHEN, C.-H., GUO, K., & WANG,
D. (2020). Deep Learning Techniques for Community
Detection in Social Networks. IEEE Access, 8, 96016–
96026. https://doi.org/10.1109/ACCESS.2020.2996001
Wu, P., & Pan, L. (2016). Multi-objective community
detection method by integrating users ’ behavior
attributes. Neurocomputing, 210, 13–25. https://doi.org/
10.1016/j.neucom.2015.11.128
Ye, F., Chen, C., & Zheng, Z. (2018). Deep autoencoder-like
nonnegative matrix factorization for community
detection. International Conference on Information and
Knowledge Management, Proceedings, 1393–1402.
https://doi.org/10.1145/3269206.3271697
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
912
