Study on Applying Decentralized Evolutionary Algorithm to Asymmetric
Multi-objective DCOPs with Fairness and Worst Case
Toshihiro Matsui
a
Nagoya Institute of Technology, Gokiso-cho Showa-ku Nagoya Aichi 466-8555, Japan
Keywords:
Multi-objective, Fairness, Asymmetry, Distributed Constraint Optimization, Evolutionary Algorithm, Sam-
pling, Multiagent System.
Abstract:
The Distributed Constraint Optimization Problem (DCOP) is a fundamental research area on cooperative prob-
lem solving in multiagent systems. An extended class of DCOPs represents a situation where each agent
locally evaluates its partial problem with its individual constraints and objective functions on the variables
shared by neighboring agents. This is a multi-objective problem on the preference of individual agents, and
a set of aggregation and comparison operators is employed for a metric of social welfare among the agents.
We concentrate on the case of social welfare criteria based on leximin/leximax that captures fairness among
agents. Since the constraints in the practical settings of asymmetric multi-objective DCOPs are too dense for
exact solution methods, scalable but inexact solution methods are necessary. We focus on employing a version
of an evolutionary algorithm called AED which was designed for the original class of DCOPs. We apply the
AED algorithm to asymmetric multi-objective DCOPs to handle asymmetry. We also replace the criteria in
the sampling process by one of the social welfare criteria and experimentally investigate the sampling criteria
in the search process.
1 INTRODUCTION
The Distributed Constraint Optimization Problem
(DCOP) is a fundamental research area on coopera-
tive problem solving in multiagent systems (Fioretto
et al., 2018). With this approach, the status, the
relationships and the decision making of agents are
represented as a combinational optimization problem
whose variables, constrains, and objective functions
are partially shared by agents. A problem is solved
by a decentralized optimization method that is per-
formed by agents who exchange their information.
An extended class of DCOPs represents a situation
where each agent locally evaluates its partial problem
with its individual constraints and objective functions
on the variables shared by neighboring agents (Mat-
sui et al., 2018a). The local evaluation is aggre-
gated, and the assignment to the variables is glob-
ally optimized. This is a multi-objective problem on
the preference of individual agents. A set of aggre-
gation and comparison operators is employed for a
metric of social welfare among the agents. We con-
centrate on a case of social welfare criteria based on
a
https://orcid.org/0000-0001-8557-8167
leximin/leximax that captures fairness among agents.
Such a class of optimization problems is important for
modeling practical situations where inequality among
agents should be reduced. Due to the complexity
of DCOPs, inexact solution methods have been em-
ployed to solve large-scale and densely constrained
problems that cannot be handled by exact solution
methods. Since the constraints in the practical set-
tings of asymmetric multi-objective DCOPs are too
dense for exact solution methods, scalable but inexact
solution methods are necessary. In particular, oppor-
tunities are available to investigate evolutionary algo-
rithms that are applied to multimodal problems, in-
cluding multi-objective settings. Therefore, we em-
ploy a version of an evolutionary algorithm called
AED, which was designed for the original class of
DCOPs (Mahmud et al., 2020). We apply the AED
algorithm to asymmetric multi-objective DCOPs to
handle asymmetry. In addition, we replace the criteria
in the sampling process by one of the social welfare
criteria. We experimentally investigate the modified
AED algorithms and show the effect and influence of
our proposed approach.
Matsui, T.
Study on Applying Decentralized Evolutionar y Algorithm to Asymmetric Multi-objective DCOPs with Fairness and Worst Case.
DOI: 10.5220/0010919500003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 417-424
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
417

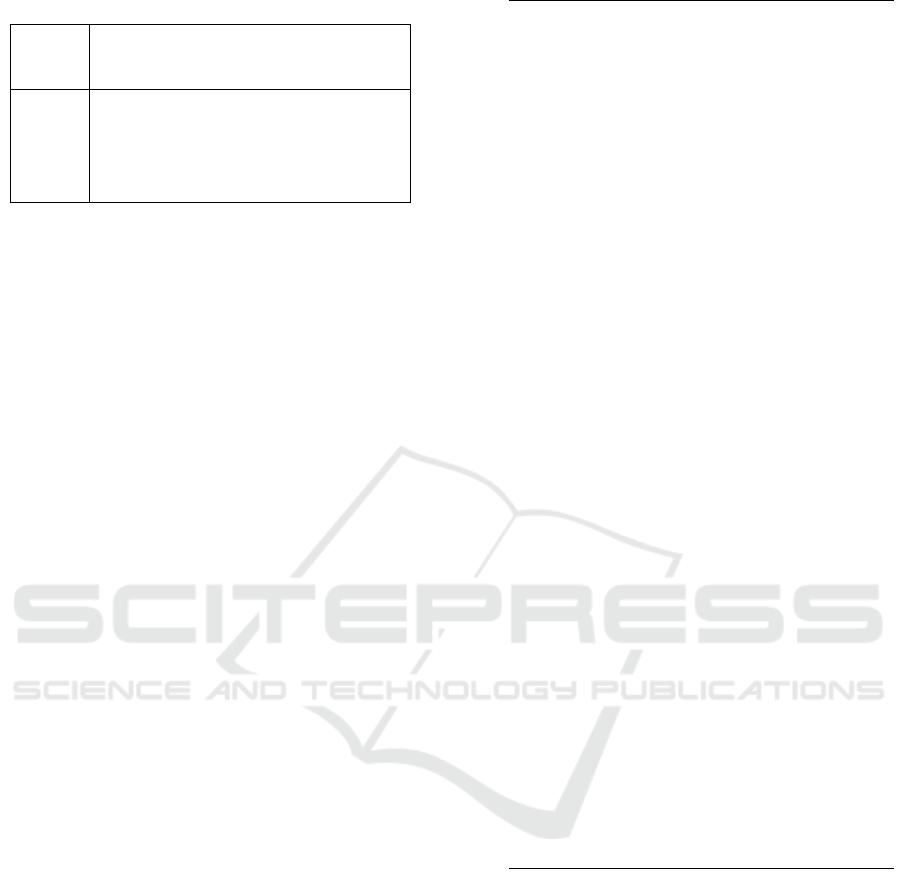
Table 1: Notations and parameters for AED.
P
∗
∗
set of individuals
I. f itness fitness of individual I
I.x
i
assignment to variable x
i
in individual I
N
i
set of neighborhood agents of agent a
i
IN size of initial P
a
i
ER coefficient for the size of several P
∗
∗
α, R
max
parameters for sampling of individuals
β, O
max
parameters for sampling of assignments to vari-
ables
MI number of iterations between two migration
steps
2 PRELIMINARIES
2.1 DCOP
A Distributed Constraint Optimization Problem
(DCOP) is defined by hA, X, D, Fi where A is a set
of agents, X is a set of variables, D is a set of the
domains of the variables, and F is a set of objective
functions related to a constraint. Variable x
i
∈ X rep-
resents the state of agent i ∈ A. Domain D
i
∈ D is
a discrete finite set of values for x
i
. Objective func-
tion f
i, j
(x
i
, x
j
) ∈ F defines a cost extracted for each
pair of assignments to x
i
and x
j
. The objective value
of assignment {(x
i
, d
i
), (x
j
, d
j
)} is defined by binary
function f
i, j
: D
i
× D
j
→ N
0
. For assignment A of
the variables, global objective function F(A) is de-
fined as F(A ) =
∑
f
i, j
∈F
f
i, j
(A
↓x
i
, A
↓x
j
), where A
↓x
i
is
the projection of assignment A on x
i
.
The value of x
i
is controlled by agent i, which lo-
cally knows the objective functions that are related to
x
i
in the initial state. The goal is to find global opti-
mal assignment A
∗
that minimizes the global objec-
tive value in a decentralized manner. For simplicity,
we focus on the fundamental case where the scope
of the functions is limited to two variables, and each
agent controls a single variable.
The solution methods for DCOPs are categorized
into exact and inexact solution methods (Fioretto
et al., 2018). The exact methods include a few classes
of algorithms based on tree search and dynamic pro-
gramming (Modi et al., 2005; Petcu and Faltings,
2005). However, the complexity of such exact meth-
ods is generally exponential for several size param-
eters of problems. Therefore, applying exact meth-
ods to large-scale and densely constrained problems is
difficult. Inexact solution methods consist of a num-
ber of approaches, including stochastic hill-climbing
local search (Zhang et al., 2005) and sampling meth-
ods (Nguyen et al., 2019; Mahmud et al., 2020). We
focus on the AED algorithm (Mahmud et al., 2020),
which is a decentralized evolutionary algorithm for
DCOPs. Their study shows that AED outperformed
the other sampling-based local search methods.
1 Construct a BFS tree on a constraint graph.
2 Share an initial set of individuals P
a
i
by a protocol on
the BFS tree.
3 Itr ← 1.
4 until Itr is less than a cutoff cycle do begin
5 P
selected
← a set of |N
i
| × ER individuals sampled
from P
a
i
allowing to select the same elements
.
6 P
new
← {P
n
1
new
, ..., P
n
|N
i
|
new
} consisting of sets of the
same size generated from P
selected
by
partitioning its elements.
7 for n
j
in N
i
do begin
8 Update individuals in P
n
j
new
by sampling each
assignment to a
i
’s variable.
9 Send P
n
j
new
to n
j
.
10 end
11 for P
n
i,k
new
received from n
k
in N
j
do begin
12 Update individuals in P
n
i,k
new
by selecting each best
assignment to a
i
’s variable.
13 Return P
n
i,k
new
to n
k
.
14 end
15 for P
n
j
new
returned from n
j
in N
j
do begin
16 P
a
i
← P
a
i
∪ P
n
j
new
.
17 end
18 B ← argmin
I∈P
a
i
I. f itness.
19 Update and commit the globally best solution
using B by a protocol on the BFS tree
executing in background.
20 P
a
i
← a set of |N
i
| × ER individuals sampled from
P
a
i
disallowing to select the same elements.
21 if Itr mod MI = 0 then begin
22 for n
j
in N
i
do begin
23 Send a set of ER individuals, which is
sampled from P
a
i
disallowing to select
the same elements, to n
j
.
24 end
25 for P
n
k
migrated
received from n
k
in N
j
do begin
26 P
a
i
← P
a
i
∪ P
n
k
migrated
.
27 end
28 end
29 Itr ← Itr + 1.
30 end
Figure 1: Summarized pseudo code of AED (agent a
i
).
2.2 AED
The Anytime Evolutionary DCOP Algorithm (AED)
(Mahmud et al., 2020) is a solution method based on
an evolutionary algorithm for DCOPs. It is performed
using a spanning tree on a constraint graph to aggre-
gate solutions and determine the best assignment to
the variables of agents. It is also an anytime algo-
rithm that synchronizes the best solutions of agents in
each iteration of a solution process. A breadth-first-
search (BFS) tree, which is built in a preprocessing,
is employed to reduce the delay in communication.
We show the pseudo-code and related notations of the
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
418

AED based on a previous work (Mahmud et al., 2020)
in Figure 1 and Table 1. The processing is performed
in a synchronized manner. The algorithm basically
maintains sets of candidate solutions (individuals) and
fitness values attached to the solutions. A fitness value
I. f itness is defined as the total cost value for a (par-
tial) solution.
After the construction of a BFS tree, a set of initial
solutions is generated and shared by all the agents by
an initialization protocol on the BFS tree. In the ini-
tialization step, each agent randomly generates a set
of IN initial candidate solutions, which only contains
the assignment to its own variable, and exchanges the
partial solutions with all the neighborhood agents to
aggregate them. Then the aggregated partial solutions
are evaluated, and their partial fitness values are at-
tached to the information of the partial solutions. The
sets of partial solutions with fitness values are aggre-
gated in a bottom-up manner based on a BFS tree. As
a result, the agent of the root node obtains an initial
set of global solutions with fitness values. Note that
each fitness value is doubled, since two agents that
are related to each constraint redundantly evaluate the
same cost value. Therefore, the root agent corrects
the fitness value by dividing by two. The initial set of
solutions with fitness values is propagated to all the
agents in a top-down manner. Initial global solutions
P
a
i
are independently updated by each agent a
i
in the
following phase of a decentralized synchronized pro-
cess.
The main optimization part is repeated until a ter-
mination condition is satisfied. In each iteration, the
following processing is performed. First, each agent
generates sets of solutions P
j
new
for each neighbor-
hood agent a
j
by sampling from its local set of so-
lutions P
a
i
. The sampling of solution I
j
is performed
with the probability P(I
j
) defined as
P(I
j
) =
R
α
j
∑
I
k
∈P
a
i
R
α
k
(1)
R
j
= R
max
×
|I
worst
. f itness − I
j
. f itness| + 1
|I
worst
. f itness − I
best
. f itness| + 1
, (2)
where I
worst
and I
best
are the best and worst solutions
in a set of solutions.
Then the agent updates the assignment to its own
variable in each P
j
new
by sampling from the variable’s
domain. The sampling of assignment d
i
is performed
with the probability P(d
j
) defined as
P(d
j
) =
W
β
d
i
∑
d
k
∈D
i
W
β
d
k
(3)
W
d
i
= O
max
×
|O
worst
. f itness − O
d
i
. f itness| + 1
|O
worst
. f itness − O
best
. f itness| + 1
(4)
O
d
i
=
∑
n
k
∈\n
j
f
i,k
(I.x
i
, I.x
k
) − min
d
j
∈D
j
f
i, j
(I.x
i
, d
j
), (5)
where O
worst
and O
best
are the best and worst evalua-
tion for all values in a variable’s domain.
The update is locally performed. Note that the at-
tached fitness values can be locally updated by adding
the difference cost value of each constraint. The dif-
ference cost value δ
∗
is calculated as
δ
∗
=
∑
n
k
∈N
∗
f
∗,k
(I.x
new
∗
, i.x
k
) − f
∗,k
(I.x
old
∗
, i.x
k
). (6)
The updated P
j
new
is passed to neighborhood agent
a
j
. After all updates are received, each agent updates
the assignment to its own variable in each P
i,k
new
re-
ceived from neighborhood agent a
k
. Here, the peer
agent selects the best assignment to its own variable
for each solutions so that it helps the update by the
sender agent. The best assignment I.x
j
is shown as
I.x
j
= argmin
d
j
∈D
j
∑
n
k
∈N
j
f
j,k
(d
j
, I.x
k
). (7)
Here each fitness value is also updated by Equa-
tion (6). The updated solutions are returned to a
k
.
Then each agent merges each P
j
new
updated by both
related agents to its own set of solutions P
a
i
. Here the
current locally best solution is updated if it is found in
P
a
i
. The best solution is propagated with a distributed
snapshot algorithm performed in the background, and
the assignments to the decision variables of the agents
are updated to the best available solution at the same
iteration. Then local set of solutions P
a
i
is updated by
sampling from itself to maintain the size of P
a
i
.
In each MI iteration, a migration process is inter-
mittently performed by exchanging and merging parts
of the local solutions between each pair of neighbor-
ing agents. See a previous work (Mahmud et al.,
2020) for details.
2.3 AMODCOP
An Asymmetric Multiple Objective DCOP on the
preferences of agents (AMODCOP) (Matsui et al.,
2018a) is defined by hA, X, D, Fi, where A, X and D
are similarly defined as DCOP. Agent i ∈ A has its
local problem defined for X
i
⊆ X. For neighborhood
agents i and j, X
i
∩X
j
6=
/
0. F is a set of objective func-
tions f
i
(X
i
). Function f
i
(X
i
) : D
i
1
× · ·· × D
i
k
→ N
0
represents the objective value for agent i based on
the variables in X
i
= {x
i
1
, ·· · , x
i
k
}. For simplicity, we
concentrate on the case where each agent has a single
variable and relates to its neighborhood agents with
binary functions, which are asymmetrically defined
for two related agents. Variable x
i
of agent i is re-
lated to other variables by objective functions. When
Study on Applying Decentralized Evolutionary Algorithm to Asymmetric Multi-objective DCOPs with Fairness and Worst Case
419

x
i
is related to x
j
, agent i evaluates objective func-
tion f
i, j
(x
i
, x
j
). On the other hand, j evaluates an-
other function f
j,i
(x
j
, x
i
). Each agent i has function
f
i
(X
i
) that represents the local problem of i that ag-
gregates f
i, j
(x
i
, x
j
). We define the local evaluation of
agent i as summation f
i
(X
i
) =
∑
j∈Nbr
i
f
i, j
(x
i
, x
j
) for
neighborhood agents j ∈ Nbr
i
related to i by objec-
tive functions.
Global objective function F(A ) is defined as
[ f
1
(A
1
), ·· · , f
|A|
(A
|A|
)] for assignment A to all the
variables. Here A
i
denotes the projection of assign-
ment A on X
i
. The goal is to find assignment A
∗
that
minimizes the global objective based on a set of ag-
gregation and evaluation structures.
2.4 Criterion of Social Welfare
Since multiple objective problems among individual
agents cannot be simultaneously optimized in gen-
eral cases, several criteria such as Pareto optimality
are considered. However, there are generally a huge
number of candidates of optimal solutions based on
such criteria. Therefore, several social welfare and
scalarization functions are employed. With aggre-
gation and comparison operators ⊕ and ≺, the min-
imization of the objectives is represented as A
∗
=
argmin
≺
A
⊕
i∈A
f
i
(A).
Several types of social welfare (Sen, 1997) and
scalarization methods (Marler and Arora, 2004) are
employed to handle objectives. In addition to the
summation and comparison of scalar objective val-
ues, we consider several criteria based on the worst
case objective values (Matsui et al., 2018a). Although
some operators and criteria are designed for the maxi-
mization problems of utilities, we employ similar cri-
teria for minimization problems.
Summation
∑
a
i
∈A
f
i
(X
i
) only addresses the total
cost values. Min-max criterion minmax
a
i
∈A
f
i
(X
i
)
improves the worst case cost value. This criterion
is called the Tchebycheff function. To improve the
global cost values, ties on min-max are broken by
comparing the summation values; the criterion is
Pareto optimal (Marler and Arora, 2004).
Leximin for maximization problems is an exten-
sion of max-min, which is the maximization version
of min-max. For this criterion, utility values are repre-
sented as a sorted objective vector v
v
v = {v
1
, ·· · , v
|A|
}
whose values are sorted in ascending order, and the
comparison of two vectors is based on the dictionary
order of the values in the vectors. Maximization with
leximin is Pareto optimal and relatively improves the
fairness among the objectives. To employ this cri-
terion in the optimization process, partial sorted ob-
jective vectors for subsets of agents are employed,
and addition operator is generalized so that the val-
ues of two vectors are merged and resorted. See lit-
erature (Matsui et al., 2018a) for details. We employ
‘leximax’, which is an inverted leximin for minimiza-
tion problems, where cost values are sorted in de-
scending order. Our major goal is the optimization on
leximax, while we also investigate the effect of em-
ploying other criteria in the search process.
2.5 Issue on Solution Methods
Several exact solution methods based on tree search
and dynamic programming for AMODCOPs with
preferences for individual agents have been pro-
posed (Matsui et al., 2018a). However, such meth-
ods cannot be applied to large-scale and complex
problems with dense constraints/functions, due to the
combinatorial explosion of sub-problems. Although
several approximations have been proposed for such
solution methods (Matsui et al., 2018b), the accuracy
of the solutions decreases when a number of con-
straints are eliminated from densely constrained prob-
lems. While several local search methods were ad-
dressed in earlier studies for such problems (Matsui
et al., 2018b), further investigation is necessary. In a
related work (Matsui, 2021), a simple stochastic lo-
cal search method have been applied to AMODCOPs
in which variants of a min-max criterion improve the
worst case cost value among agents. However, each
agent locally updates a single partial solution only
considering a limited view of neighborhood agents in
the search process, while a few pieces of summarized
global information are shared.
On the other hand, evolutionary algorithms are
often employed for multimodal problems, includ-
ing multi-objective ones, in the area of centralized
solvers. Therefore, we focus on AED, as a solution
method for AMODCOPs with optimization criteria
considering fairness. To apply the AED to this class
of problems, several extensions of the data structure,
optimization criteria and operators are required. Our
main interest is the influence of such optimization cri-
teria to the search process.
3 APPLYING AED TO AMODCOP
WITH LEXIMAX
3.1 Handling Asymmetric Constraints
and Replacing Fitness
Since the original AED algorithm is designed for
symmetric DCOPs, several modifications are neces-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
420

sary to handle asymmetric constraints. Since our in-
terest in this study is the optimization on leximax cri-
terion that considers the fairness among agents, we re-
place each fitness value I. f itness by sorted cost vector
I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s. The aggregation and comparison operators
for sorted cost vectors are also employed.
In the initialization phase that aggregates the
global solutions, a BFS tree on a constraint graph is
employed. For the original DCOPs, in the aggrega-
tion of cost values based on a BFS tree, each binary
constraint is redundantly evaluated by two agents re-
lated to the constraint. This doubles the aggregated
cost value, and the agent of the root node in the BFS
tree corrects the aggregated cost value by dividing it
by two. In our case, the constraints are asymmetri-
cally defined. Therefore, each agent independently
evaluates its related constraints.
In a part of the main phase, each agent stochas-
tically update the assignment to its own variable for
all candidate solutions and locally updates the related
cost values. In the original AED, the local update of
the cost values can be easily performed by adding/-
subtracting new/old cost values of related constraints
because of the symmetric constraints and aggregation
with the summation operator. However, for asymmet-
ric multi-objective problems, such an operation is im-
possible because the change of assignment to its own
variable also changes the evaluation of the neighbor-
hood agents. For this issue, we have to delegate the
evaluation of the constraints to the agent on the op-
posite side. Moreover, a view of individual agents’
cost values is necessary for each solution. We apply
these extensions to the original algorithm and denote
the additional view of agent a
i
’s cost value attached
to a solution I by I. f itness
i
. The views of the cost
values are generated in the initialization phase of Pa
i
and maintained in the main phase when candidate so-
lutions are updated and reevaluated.
With the extensions above, each agent locally
evaluates the update of the cost values. When agent a
i
evaluates its new assignment d
new
i
in a solution I, its
new local cost value is computed as
F
i
(A
new
i
) =
∑
n j
∈
N
i
f
i, j
(d
new
i
, I.x
j
). (8)
The local cost value of neighborhood agent a
j
∈ N
i
is
evaluated as
F
j
(A
new
j
) =I. f itness
j
+
f
j,i
(I.x
j
, d
new
i
) − f
j,i
(I.x
j
, I.x
i
).
(9)
The local cost value of a
k
in other agents is still
I. f itness
k
.
When agent a
i
updates its own assignment in
solution I, affected local cost values I. f itness
i
and
I. f itness
j
∈ N
i
are updated. In addition, I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s is
also updated by each new F
k
(A
new
k
) with the follow-
ing steps.
1. I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s ← I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s  I. f itness
k
2. I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s ← I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s ⊕ F
k
(A
new
k
)
Here  removes an element from a sorted objective
vector and ⊕ inserts an element to the objective vec-
tor.
Although such views require additional resources,
this is an inherent issue with this class of problems.
The publication of cost values is another issue. How-
ever, to evaluate fairness or inequality among agents,
some published information is necessary. In our ex-
perimental extension, each solution I redundantly has
I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s and a set of I. f itness
i
to avoid recalculation
of sorted cost vectors, but I. f
f
f i
i
it
t
tn
n
ne
e
es
s
ss
s
s is a compressed
representation as shown in Section 3.3. While oppor-
tunities can be found to reduce the revealed informa-
tion using several additional techniques, we concen-
trate on a search process with criteria and operators
for the extended class of problems.
3.2 Sampling with Leximax Criterion
As mentioned above, our major interest is the appli-
cation of sampling methods to find quasi-optimal so-
lutions for asymmetric multi-objective problems with
the criterion of fairness. We aim to improve the solu-
tion minimizing cost vectors with leximax. Therefore,
the fitness value of each solution is modified to cost
vectors, where its cost values are sorted in descending
order. The best solution in the anytime update pro-
cess is selected according to the order based on lex-
imax. Note that other criteria, including summation
and maximum value, can still be evaluated, because
all the individual cost values are held in the cost vec-
tor.
Alghough the best solution is chosen with the lex-
imax criterion, different criteria can be employed for
the sampling operation in the search process. Since a
sampling-based search has a property of local search,
such criteria might be relatively efficient. In addition
to the sampling operation, some techniques are nec-
essary to compute the probability distribution for the
criteria. We investigate the following criteria in the
sampling.
3.2.1 Summation, Maximum Value and
Augmented Tchebycheff Function
With the summation operator, the total cost value for
all agents
∑
a
i
∈A
F
i
is employed, as in the original
AED. As shown above, for asymmetric constraints,
each agent evaluates the change of the cost values in
opposite agents related to the agent. For this case, as a
Study on Applying Decentralized Evolutionary Algorithm to Asymmetric Multi-objective DCOPs with Fairness and Worst Case
421

baseline, we also evaluate a version that employs the
summation to select the best solution.
Minimizing the maximum cost value for all agents
max
a
i
∈A
F
i
will also improve the evaluation on lexi-
max. However, the multimodality of the cost space
with an evaluation based on the maximum value
can be relatively high. Therefore, as employed in
multi-objective optimization, we also employ the aug-
mented Tchebycheff function max
a
i
∈A
F
i
+ w
∑
a
i
∈A
F
i
in which the ties of the maximum cost value are bro-
ken by the summation value. To be employed in the
numeric operation, the summation value is multiplied
by a sufficiently small coefficient value w and added
to the maximum value.
3.2.2 Scalarized Leximax and Trimmed
Leximax
Our major concern is whether sampling based on
leximax has some effect in the class of evolution-
ary algorithms for DCOPs. To apply leximax crite-
ria to sampling operation base on the numeric opera-
tion, scalarization of sorted objective vectors is neces-
sary. Here we employ a simple method based on the
dictionary order on sorted objective vectors (Matsui
et al., 2018b). With the given minimum and maxi-
mum cost values c
⊥
and c
>
, the scalar value s(c) =
s(c)
(|A|−1)
for sorted cost vector c
c
c is recursively de-
fined as s(c)
(k)
= s(c)
(k−1)
·(|c
>
−c
⊥
|+1)+(c
k
−c
⊥
)
and s(c)
(0)
= 0, where v
k
is the k
th
cost value in sorted
vector c. Note that k = 1 corresponds to the first cost
value in a sorted cost vector. While this operation is
computationally expensive, it can be performed using
multi-precision variables.
Since the operation of leximin needs relatively
high computational cost, we mitigate this issue by
trimming the sorted cost vectors. Here, we only con-
sider from the first to the n-th maximum values in a
vector and convert them to a scalar value. In addition,
ties of trimmed evaluation values can be broken us-
ing a small summation value that resembles the aug-
mented Tchebycheff function.
3.3 Implementation and Complexity
Although the total cost values based on the summa-
tion criterion can be computed from the sorted
cost vectors, we independently maintained the total
cost value from the fitness values. As a maximum
value, we employed the first element of each sorted
cost vector. We used a run-length representation of
the sorted cost vectors (Matsui et al., 2018a) imple-
mented using a map data structure, so that the addi-
tion/subtraction of each cost value is relatively easily
performed with the indices of the cost values in the
map. We employed the MPIR library for the compu-
tation with multi-precision variables to scalarize the
sorted cost vectors for leximax. In this case, some
part of the scalarized values might be lost in the com-
putation of the probability for the sampling due to the
underflow by casting them to the floating point type
variables.
An extension with objective vectors requires a rel-
atively large overhead to the original processing. Al-
though the operation cost and memory usage for mul-
tiple objectives basically increase linearly with the
number of objectives (i.e., the number of agents) in
the worst case, there are opportunities to reduce them
with additional techniques.
4 EVALUATION
We experimentally evaluated our proposed approach.
We employed problems with 50 variables and c asym-
metric binary constraints. The variables take values
from the common domain of size |D
i
| for each prob-
lem setting. We evaluated with cases from the follow-
ing types of cost functions.
• random: Random integer values in [1, 100] based
on uniform distribution.
• gamma92: Rounded random integer values in
[1, 100] based on gamma distribution with α = 9
and β = 2.
We compared the following criteria for sampling.
• sum: Summation of the local cost values for all
agents.
• sum-sum: ‘sum’ with the selection of the best so-
lution based on summation. This combination is
considered as a baseline.
• max: Maximum local cost value.
• maxsum: Augmented Tchebycheff function in
which the ties of ‘max’ are broken with the ad-
ditional summation value.
• lxm: Leximax criterion.
• tlxm3, tlxmh: Trimmed ‘lxm’ that only considers
the higher part of the cost values in the sorted cost
vectors. ‘tlxm3’ limits the number of cost values
to three. ‘tlxmh’ employs the half of the cost val-
ues in a sorted cost vector.
• tlxm3sum: A modified ‘tlxm3’ in which the ties of
‘max’ are broken with the additional summation
value.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
422

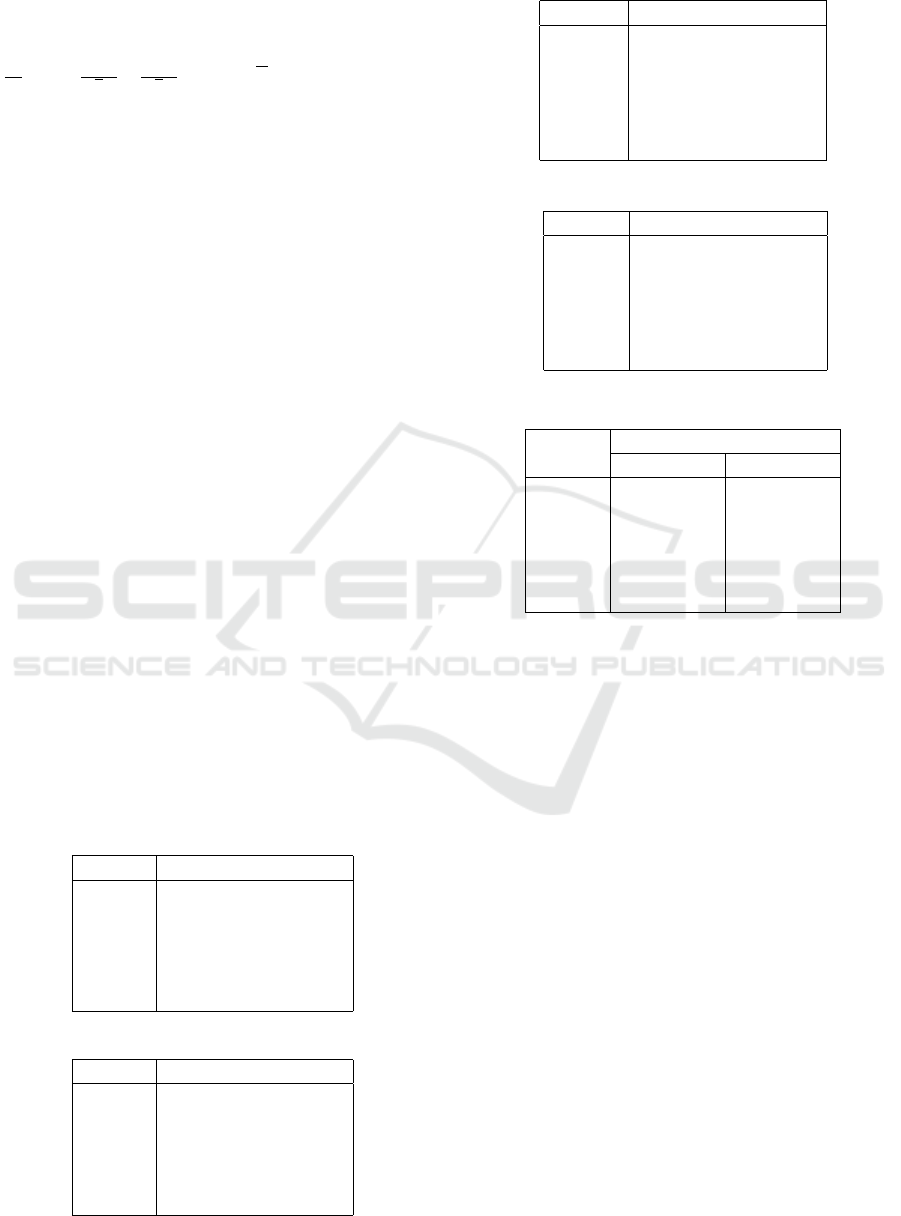
Except for sum-sum, the best solution is selected un-
der the leximax criterion. In addition to several cri-
teria, we also evaluate the results with the Theil in-
dex T , which is a measurement of unfairness: T =
1
|A|
∑
|A|
i=1

f
i
(X
i
)
f
ln
f
i
(X
i
)
f

, where f denotes the average
value for all f
i
(X
i
). T takes zero if all f
i
(X
i
) are iden-
tical. With preliminary experiments, we set the fol-
lowing parameters for the AED algorithm: IN = 5,
ER = 5, α = 1, R
max
= 5 β = 5, O
max
= 5 and MI = 5.
Although we set a small number of populations due to
relatively expensive computation, such a setting was
still effective in the original study of AED (Mahmud
et al., 2020). The cut-off iteration was 1000. The re-
sults were averaged over ten trials with different ini-
tial solutions on ten problem instances for each set-
ting.
Tables 2-5 show the final quality of the solutions
at the cut-off iterations. We evaluated the summation,
the maximum value and the Theil index for all the
local cost values of the agents. In the case of ran-
dom, d = 3 and c = 250 in Table 2, the maximum
cost value was most minimized by maxsum, while
the other maximax/leximax based criteria were sim-
ilarly effective. Although ’sum‘, which selects the
best solution under the leximax criterion, relatively
reduced the maximum cost and the Theil index values
in comparison to the sum-sum, its perturbation on the
sampling process was insufficient. The leximax based
criteria reduced the Theil index well. However, lxm,
which exactly evaluated the criterion, did not produce
the best result. There are two possible reasons for the
result. The first is the influence of the locally optimal
solutions in the search process. The another is that
minimization on leximax does not completely corre-
spond to optimization on the Theil index. However,
tlxm3, which is an approximated version of leximax,
Table 2: Solution quality (random, d = 3, c = 250).
Alg. Sum. Max. Theil
sum 20766.4 634.4 0.0507
sum-sum 20039.0 724.9 0.0601
max 22424 573 0.0312
maxsum 22221.6 572.4 0.0331
lxm 22485.1 576.3 0.0317
tlxm3 22505.6 574.3 0.0307
tlxm3sum 22416.7 575.1 0.0320
tlxmh 22486.6 576.8 0.0317
Table 3: Solution quality (random, d = 5, c = 150).
Alg. Sum. Max. Theil
sum 10744.3 384.1 0.0989
sum-sum 10111.2 465.2 0.1236
max 12342.5 325.5 0.0476
maxsum 11913.5 321.7 0.0540
lxm 12107.9 318.6 0.0437
tlxm3 12283.1 322.2 0.0436
tlxm3sum 12216.1 321.5 0.0446
tlxmh 12142.2 319.2 0.0438
Table 4: Solution quality (gamma92, d = 3, c = 250).
Alg. Sum. Max. Theil
sum 8069.7 242.70 0.0406
sum-sum 7760.6 269.59 0.0462
max 8410.8 220.70 0.0321
maxsum 8259 220.45 0.0335
lxm 8374.2 220.90 0.0313
tlxm3 8379.9 220.30 0.0312
tlxm3sum 8382.8 220.34 0.0310
tlxmh 8373.9 220.90 0.0312
Table 5: Solution quality (gamma92, d = 5, c = 150).
Alg. Sum. Max. Theil
sum 4403.4 150.57 0.0704
sum-sum 4251.1 170.94 0.0786
max 4832.3 134.30 0.0487
maxsum 4633.3 133.19 0.0552
lxm 4757.3 132.84 0.0472
tlxm3 4792.9 133.08 0.0481
tlxm3sum 4781.7 133.11 0.0484
tlxmh 4762.5 132.83 0.0466
Table 6: Execution time (gamma92).
Alg. Exec. time [s]
d = 3, c = 250 d = 5, c = 150
sum 268.6 163.5
sum-sum 268.0 158.7
max 414.7 228.6
maxsum 433.3 236.0
lxm 505.4 280.2
tlxm3 460.1 234.6
tlxm3sum 469.0 243.7
tlxmh 483.9 256.4
found the fairest solution in the results. In the case of
random, d = 5 and c = 150 in Table 3, lxm found the
best solution for the minimum cost value, although
tlxm3 found the fairest solution, similar to the previ-
ous result.
In the results of Table 4 for a case of gamma 92,
the maximum cost values by min-max/leximax based
criteria are relatively similar due to the problem set-
ting related to the density of the constraints and the
gamma distribution of the cost values. On the other
hand, the difference between the Theil index value
of maxsum and that of leximax based criteria is rel-
atively large. In another case of gamma 92 shown in
Table 5, the result of tlxmh is best for the maximum
value and the Theil index.
In these results, the maximum cost value by ‘max‘
exceeds that of maxsum. This reveals the effect of tie-
breaking with an additional comparison of the sum-
mation values. However, regarding the Theil index,
the result was inverted, since the summation crite-
rion tends to increase inequality. The results reveal
the difficulty of exactly controlling the optimization
performance on the maximum value and the leximax
criterion. Considering the computational cost and ac-
curacy, the trimmed version of the leximax criterion
looks reasonable.
Study on Applying Decentralized Evolutionary Algorithm to Asymmetric Multi-objective DCOPs with Fairness and Worst Case
423

4000
4500
5000
5500
0 100 200 300
Total cost
Exec. time [s]
sum sum-sum
lxm tlxmh
120
140
160
180
200
0 100 200 300
Maximum cost
Exec. time [s]
sum sum-sum
lxm tlxmh
0.04
0.06
0.08
0.1
0 100 200 300
Theil index
Exec. time [s]
sum sum-sum
lxm tlxmh
Figure 2: Anytime curve (gamma92, d = 5, c = 150).
Table 6 compares the execution time of the so-
lution methods for 1000 iterations. The experiment
was performed on a computer with g++ (GCC) 8.5.0,
MPIR 3.0.0, Linux version 4.18, Intel (R) Core (TM)
i9-9900 CPU @ 3.10GHz and 64GB memory. As
the first study, the total computation time was evalu-
ated excluding communication delay. Note that there
are opportunities to improve our experimental imple-
mentation. A major common issue is the processing
to handle the sorted objective vectors and the lexi-
max criterion. For each criterion, the parts of the
process of sampling new solution sets were differ-
ently affected by the implementation techniques. Fig-
ure 2 shows several selected anytime curves of solu-
tion quality for gamma92, d = 5 and c = 150. While
the leximax-based criteria took a long execution time,
their results improved in relatively earlier steps of the
search process.
5 CONCLUSIONS
We applied an evolutionary algorithm called AED
to asymmetric multi-objective DCOPs in which opti-
mization is performed on a leximax criterion that im-
proves the worst case and fairness among agents. To
handle asymmetry constraints, we extended the struc-
ture in the algorithm. In addition, we replaced the cri-
teria in the sampling process by one of social welfare
criteria and experimentally investigated the sampling
criteria. Our result shows the effect of sampling based
on leximax-based criteria.
Our future work will include more exact evalu-
ations using improved implementation of the algo-
rithm, a comparison with different classes of algo-
rithms, detailed analysis on the search space of the
problems with leximax criterion, and applications to
practical domains.
ACKNOWLEDGEMENTS
This work was supported in part by JSPS KAKENHI
Grant Number JP19K12117.
REFERENCES
Fioretto, F., Pontelli, E., and Yeoh, W. (2018). Distributed
constraint optimization problems and applications: A
survey. Journal of Artificial Intelligence Research,
61:623–698.
Mahmud, S., Choudhury, M., Khan, M. M., Tran-Thanh,
L., and Jennings, N. R. (2020). AED: An Anytime
Evolutionary DCOP Algorithm. In Proceedings of the
19th International Conference on Autonomous Agents
and MultiAgent Systems, pages 825–833.
Marler, R. T. and Arora, J. S. (2004). Survey of
multi-objective optimization methods for engineer-
ing. Structural and Multidisciplinary Optimization,
26:369–395.
Matsui, T. (2021). Investigation on Stochastic Local Search
for Decentralized Asymmetric Multi-Objective Con-
straint Optimization Considering Worst Case. In
Proceedings of the 13th International Conference on
Agents and Artificial Intelligence, volume 1, pages
462–469.
Matsui, T., Matsuo, H., Silaghi, M., Hirayama, K., and
Yokoo, M. (2018a). Leximin asymmetric multiple
objective distributed constraint optimization problem.
Computational Intelligence, 34(1):49–84.
Matsui, T., Silaghi, M., Okimoto, T., Hirayama, K., Yokoo,
M., and Matsuo, H. (2018b). Leximin multiple objec-
tive dcops on factor graphs for preferences of agents.
Fundamenta Informaticae, 158(1-3):63–91.
Modi, P. J., Shen, W., Tambe, M., and Yokoo, M. (2005).
Adopt: Asynchronous distributed constraint optimiza-
tion with quality guarantees. Artificial Intelligence,
161(1-2):149–180.
Nguyen, D. T., Yeoh, W., Lau, H. C., and Zivan, R.
(2019). Distributed gibbs: A linear-space sampling-
based dcop algorithm. Journal of Artificial Intelli-
gence Research, 64(1):705–748.
Petcu, A. and Faltings, B. (2005). A scalable method for
multiagent constraint optimization. In Proceedings of
the 19th International Joint Conference on Artificial
Intelligence, pages 266–271.
Sen, A. K. (1997). Choice, Welfare and Measurement. Har-
vard University Press.
Zhang, W., Wang, G., Xing, Z., and Wittenburg, L. (2005).
Distributed stochastic search and distributed breakout:
properties, comparison and applications to constraint
optimization problems in sensor networks. Artificial
Intelligence, 161(1-2):55–87.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
424