
Grid Representation in Neural Networks for Automated Planning
Michaela Urbanovsk
´
a and Anton
´
ın Komenda
Department of Computer Science (DCS), Faculty of Electrical Engineering (FEE),
Czech Technical University in Prague (CTU), Karlovo namesti 293/13, Prague, 120 00, Czech Republic
Keywords:
Classical Planning, Domain-independent Planning, Neural Networks, Problem Representation.
Abstract:
Automated planning and machine learning create a powerful combination of tools which allows us to apply
general problem solving techniques to problems that are not modeled using classical planning techniques. In
real-world scenarios and complex domains, creating a standardized representation is often a bottleneck as it
has to be modeled by a human. That often limits the usage of planning algorithms to real-world problems.
The standardized representation is also not a suitable for neural network processing and often requires further
transformation. In this work, we focus on presenting three different grid representations that are well suited
to model a variety of classical planning problems which can be then processed by neural networks without
further modifications. We also analyze classical planning benchmarks in order to find domains that correspond
to our proposed representations. Furthermore, we also show that domains that are not explicitly defined on a
grid can be represented on a grid with minor modifications that are domain specific. We discuss advantages
and drawbacks of our proposed representations, provide examples for many planning benchmarks and also
discuss the importance of data and its structure when training neural networks for planning.
1 INTRODUCTION
Machine learning and usage of neural networks in the
classical planning field is an interesting research di-
rection of the recent years. Combination of powerful
automated planning techniques and machine learning
techniques such as neural networks promise great re-
sults towards general artificial intelligence. The plan-
ning algorithms provide strong problem solving tools
and the neural networks provide generalization to un-
seen inputs based on learned knowledge. The task of
combining the two comes with many challenges and
one of them is determining structure of the data.
Formulating a planning problem for off-the-shelf
planners has to be done by using a appropriate model-
ing language. The most prevalent one is PDDL (Aero-
nautiques et al., 1998) which uses a representation
based on first-order logic. It is understandable for hu-
mans who use it to describe the problem by hand. It
is, however, hard to interpret such language for statis-
tical machine learning techniques that want to learn
and generalize from problem definitions.
There are many opportunities in classical planning
where machine learning can be applied. In (Asai and
Fukunaga, 2017) and (Asai and Fukunaga, 2018), the
authors focus on creating a latent representation of
an image that represents the problem and generate its
PDDL representation.
There are also works that focus on improving
the classical planning search algorithms by using a
learned policy which tells the search next action to
use. On of them in (Toyer et al., 2020), where au-
thors use the PDDL representation directly to create
a neural network architecture capable of processing
any problem from a given problem domain. Authors
in (Groshev et al., 2018) use different problem repre-
sentation but also aim to learn a policy that improves
performance of a search. They learn from grid rep-
resentation of the problem that is further processed
by computer vision techniques such as convolutional
neural networks (LeCun et al., 1989) and attention
(Vaswani et al., 2017).
Another direction is learning a heuristic function
which can be used to guide any search algorithms to-
wards a solution. Heuristic function takes a state on
the input and returns a number which represents dis-
tance from said state to a goal state. On approach that
learns a heuristic is presented in (Shen et al., 2020)
where authors created a graph neural network which
is able to process any given problem regardless of its
size or domain. Less general approach is presented
in (Urbanovsk
´
a and Komenda, 2021) where authors
use different types of neural network architectures to
train neural network that returns heuristic values. This
Urbanovská, M. and Komenda, A.
Grid Representation in Neural Networks for Automated Planning.
DOI: 10.5220/0010918500003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 871-880
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
871

work uses grid representation of the problems such as
(Groshev et al., 2018).
In this work, we propose three novel representa-
tions of planning problems on a 2D and 3D grid which
can be utilized to train neural networks. We analyze
widely used planning benchmarks for domains that
are on a grid by default and use them as examples
for the grid representation. We also look at other do-
mains which are not on a grid by default but can be
transformed into a grid representation which supports
domain-independence of the proposed problem repre-
sentation. We also discuss the representations’ impact
on training neural networks and creating training data.
2 CLASSICAL PLANNING
BACKGROUND
Classical planning (Russell and Norvig, 2020) is a
form of general problem solving that starts in a fully
defined initial state and looks for a goal state. Each
state is formed by facts representing the truths about
the modelled world. Transitions between states are
performed by applying applicable actions. The notion
of applicability builds on the inner structure of the
states composed of the facts. States together with the
transitions create a graph which represents the state-
space of a problem. By using state-space search al-
gorithms we can find a path in such graph from the
initial state to a goal state. The path then represents
the sequence of applicable actions transforming the
initial state into one of the goal states.
State-space search algorithms can perform a blind
search and simply look through the states as they
get all explored, however in many cases the state-
space size is exponential and blind search is not good
enough to solve the problem at all or within a given
time limit. That is why most algorithms use a heuris-
tic function to guide the search and perform more in-
formed decisions when expanding the states.
2.1 Domain-independence
This works focuses mainly on the area of domain-
independent automated planning. Domain-
independent planning techniques can be applied
to any correctly formulated problem (for example
in PDDL) and they only use information about the
problem and its domain that are provided in the
standardized format.
Domain-independence is a very hard property to
achieve for neural networks as stated in (Geffner,
2018). Neural networks typically require fixed in-
put size and they tend to have lots of parameters that
have to be tuned. That presents a challenge in scal-
ing because every problem instance can have different
size but it also proposes a problem because changes
in parametrization might not have obvious results on
small data but can appear as a problem later when we
want the network to scale.
This challenge was tackled with HGNN in (Shen
et al., 2020) where authors use graph neural networks
which can scale on arbitrary large problems in arbi-
trary domains. The trade-off in this case is the size
and computational time of the architecture.
Similarly in (Groshev et al., 2018) the authors can
tackle any size of the Sokoban puzzle thanks to using
convolutional neural networks (LeCun et al., 1989)
but they are mostly focused on the Sokoban domain.
2.2 Problem Representation
We mentioned the PDDL language which is a widely
used language based on first-order logic that provides
the domain-independent planners with information
about the problem we aim to solve. It has to provide
two files; one contains the domain definition which
describes the world and its possible situations and ac-
tions and the second one contains specific definition
of the problem instance we want to solve.
Usage of a universal language such as PDDL al-
lows any planner to solve any problem but the bottle-
neck is often formulation of the problem since it has
to be created by a human. For humans, real-world
problems can be very hard and costly to formulate.
And once the problem is formulated there is no way
to check its completeness.
The same view can be taken from the other side.
In (Franc
`
es et al., 2019) the authors mentioned that
creating a grid representation of a problem can be
very costly and using the already formulated PDDL
is a better option. However, that holds only for prob-
lems that are already correctly formulated or prob-
lems where their formulation is tractable. There are
problem domains which are, for example, on a grid
by default and in that case the PDDL formulation does
not bring as much simplification.
In real-world scenarios such as forklift fleet, dis-
tribution warehouse or assembly line it is very costly
to have a human create PDDL representation of the
problem. Even though these complex problem would
benefit from using classical planning techniques. In-
stead of creating the PDDL definitions we could take
camera footage from the said warehouse and use im-
age processing techniques to create a grid represen-
tation that approximates the real-world noisy input.
Such approach would be less costly to create neces-
sary inputs than formulating the problems by hand.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
872

For real-world problems, the grid representation
can be seen as a latent space which allow us to use
classical planning techniques on the approximated
problem together with neural networks. There are
different types of input which can be processed by
a neural network for example vector representation.
However, size of the problem would scale with size of
the vector. Neural networks typically need fixed sized
input so using fully connected neural networks with
vector representation does not scale with the problem
size.
Another representation is graph representation
that is also used in (Shen et al., 2020). Graphs are
an intuitive way of modelling state-space of the prob-
lem. However, the state-space can be exponential and
using graph neural networks to process exponentially
large graphs is possible but very costly.
3 GRID REPRESENTATION
The set of problems from the International Plan-
ning Competition (IPC) contains classical planning
domains and problems which are typically used as
benchmarks to compare different planning algorithms
and heuristics (McDermott, 2000).
Since there are many architectures that use im-
age, grid or other 2D representation of the planning
problems, we looked at widely used IPC domains and
checked whether this property can be used as a benefit
for learning on planning problems.
The domains were provided via API of plan-
ning.domains
1
and we looked at the All-IPC STRIPS
set of problems which contains aggregation of the
planning domains over the years. From these domains
we aimed to collect
• set of domains which are on a grid by default
• set of domains which can be transformed into a
grid representation in an intuitive way
3.1 Grid Domains
Domains which are represented by a grid always con-
tain its definition in the problem definition file. We
found six domains which theoretically could be pro-
cessed by a suitable neural network architecture.
Problem definition that defines a grid structure
contains all its coordinates and also defines connec-
tions between them. Typically there are variables
x
i
where i ∈ {1,...,N} and y
j
where j ∈ {1,...,M}
which define the grid coordinates. Therefore we can
1
http://api.planning.domains/
simply construct a grid of dimensions N × M
which will correspond to the problem instance.
Next step is filling the grid with defined objects
from the problem instance. Typically there is a rela-
tion at(ob ject,x,y) which defines position of an ob-
ject on the grid. By collecting these propositions from
the problem we can create the initial state.
We found six IPC domains that can be constructed
this way. We used problem descriptions from edi-
tor.planning.domains
2
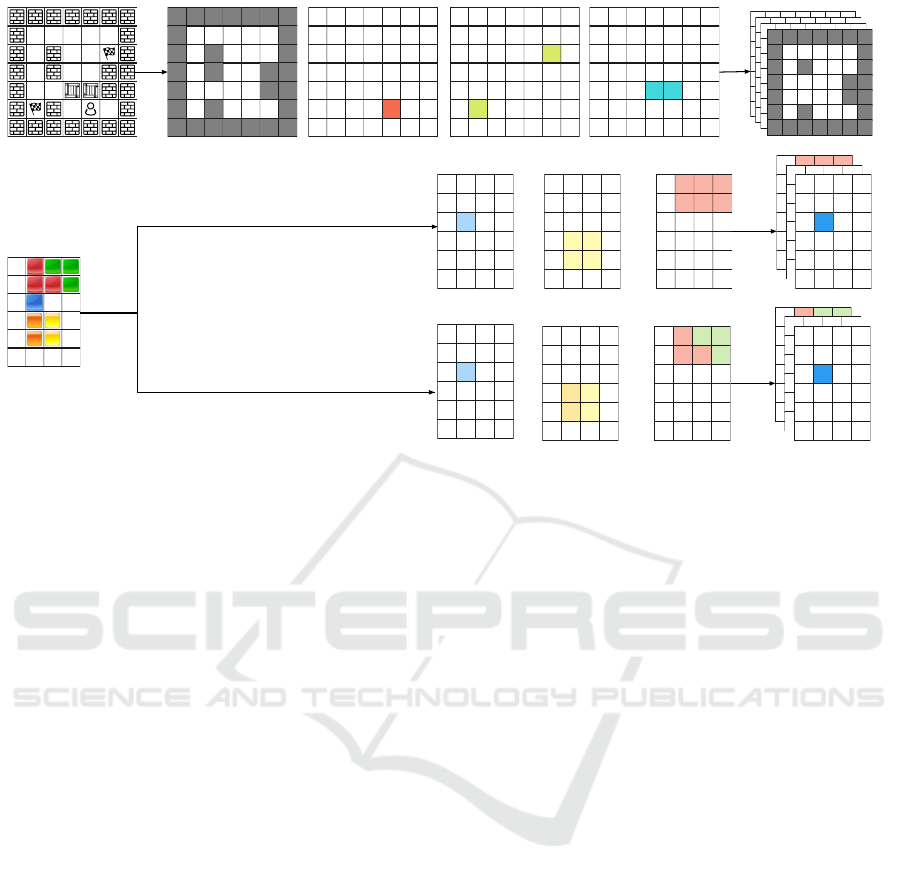
. In Figure 1 we can see the
grid representation for each of the above mentioned
domains. All the examples are instances from the IPC
domains data set.
• floortile. A set of robots use different colors to
paint floor tiles. They can move in four directions
and each one of them can use any color. Each
robot can paint only tile that is in front (up) and
behind (down) them. Once a tile has been painted
the robot cannot stand on it.
• pegsol. This domains simulates the Peg Solitaire
single-player board game. Game board at the start
of the game contains places where pegs can go
and one empty place. Valid move is jumping one
peg over another into an empty space. The goal
of the game is to end up with one peg at a defined
position.
• sokoban. In this puzzle game, the player has to
push boxes around a warehouse trying to get them
into storage locations. The player moves in four
directions and a box can be pushed only if there
is a clear space behind it. The goals is to store all
boxes.
• tetris. This domains is a simplified version of the
game Tetris. There are three types of pieces (1 ×
1,2 × 1, L) which are randomly distributed on a
grid. The goal is to free the upper half of the grid.
• tidybot. This domains models a house cleaning
task, in which one or more robots have to pick
up objects and put them to goal locations. The
world is structured as a 2D grid with navigable
locations and surfaces on which objects may lie.
Every robot has a gripper which can hold only one
object but the robots may also use a cart which can
carry more objects at the same time.
• visitall. An agent in the middle of a square grid
must visit all grid tiles. It can move in four direc-
tions.
Another related type of domains can be intuitively
represented by a grid with minor modifications to the
problem’s representation. For example logistics prob-
lem, where we have cities with different locations,
2
http://editor.planning.domains/
Grid Representation in Neural Networks for Automated Planning
873

trucks and airplanes and we aim to distribute pack-
ages using these vehicles to different locations. Such
scenario could be potentially projected on a grid us-
ing number of block between locations as an enumer-
ated distance function. Another domain which is a
good example is blocks world where we have a table
with different number of blocks and a robotic arm that
has to stack and unstack the blocks to achieve a given
configuration. Such modifications gave us six more
domains that could be represented by a grid.
• blocks. There are blocks placed on a table.
Robotic hand can move one block at a time and
has to stack them in desired configuration.
• depot. This domain combines the logistics and
blocks. domain. Trucks transport crates which
have to be stacked onto pallets in their destination.
• elevators. There is a building with N + 1 floors,
numbered from 0 to N. The building can be sep-
arated in blocks of size M + 1, where M divides
N. Adjacent blocks have a common floor. The
building has K fast (accelerating) elevators that
stop only in floors that are multiple of M/2 (so
M has to be an even number). Each fast elevator
has a capacity of X persons. Furthermore, within
each block, there are L slow elevators, that stop at
every floor of the block. Each slow elevator has a
capacity of Y .
• logistics There are several cities containing sev-
eral locations some of which are airports. There
are trucks which can drive within a city and air-
planes which can fly between airports. The goal
is to get packages from various locations to new
locations.
• parking. This domain involves parking cars on
a street with N curb locations and where cars can
be double-parked but not triple-parked. Goal is
to find a plan to move from one configuration of
parked cars to another.
• storage. Hoists move and store crates of good
from containers to depots with spatial maps.
The internal structure and actions of these do-
mains suggest that representing them on a grid is pos-
sible. In Figure 2 we show such representation for
each of these domains.
In the following sections, we will be focusing
mainly on domains that are represented by a grid by
the PDDL domain definition for simplicity.
4 PROPOSED PROBLEM
REPRESENTATIONS
In this section we would like to present three different
problem representations which can be used to process
grid-based domains with neural networks. One of the
approaches aim to stay in the 2D representation and
the others lift dimensionality of the problem repre-
sentation.
4.1 2D Projection
The representation described in Section 3 can be used
as a neural network input by itself. As we described it
can be constructed by directly parsing the PDDL and
encoding all facts (objects) into the constructed grid.
One advantage of this approach is small size of the
input because it is defined only in 2D. Problem with
this representation is number of present objects.
There are two encodings we can create for this
representation
• value per object type encoding, which assigns one
value to each object type
• value per object instance encoding, which assigns
one value to one object regardless of its type.
We see a clear example in Figure 3 where we have
examples for Sokoban and Tetris domain. Sokoban
uses the value per object type encoding that assigns
one value to one object type. In this example, this
type of encoding does not omit any information as
each object can be present only at one grid tile at a
time. In the Sokoban domain in general, the value per
object type encoding works as long as the initial state
does not contain two objects as the same tile. This
situation can happen when a box starts on a goal tile.
This type of encoding does not work for the Tetris
domain as we see in Figure 3. The value per object
type encoding looses information about the location
of individual blocks. The red and green blocks be-
come indistinguishable as well as the yellow and or-
ange blocks.
A way to overcome such problem is using a value
per object instance encoding which assigns a different
value to each Tetris block regardless of its type. This
encoding does allow us to tell the blocks apart. The
problem is in the semantics of such encoding. When
we use one value for one object type the encoding is
consistent and the network can learn a meaning be-
hind the values. In case of using a different value for
each block instance the values loose their semantics in
the problem domain. One value can represent differ-
ent block types across the training data which means
that it does not have a connection to a specific block
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
874

white
black
floortile
initial state
goal state
pegsol
initial state
goal state
sokoban
initial state
goal state
tetris
initial state
goal state
tidybot
initial state
goal state
visitall
initial state
goal state
Figure 1: Visualisation of all grid domains in All-IPC STRIPS.
blocks
A
B
C
D
initial state
A
B
C
D
goal state
depot
initial state
goal state
elevators
0 122
5
11
1
4
6
13
8
10
7
9
3
...
initial state
6
12
2
5
11
1
4
0
13
8
10
7
9
3
goal state
logistics
initial state
goal state
parking
2 5
23 9
20 25
6 21
26 3
27 14
17 24
0 18
1 8
10 16
22 4
19 13
7 12
11 15
initial state
2
5
23
9
20
25
6 21
26
3
27
14
17
24
0
18
1
8
10
16
22
4 19
13
7
12
11
15
goal state
storage
initial state
goal state
Figure 2: Visualisation of all domains adapted to grids in All-IPC STRIPS.
Grid Representation in Neural Networks for Automated Planning
875

1 1 1 1 1
1 0 0 0 0
1 0 1 0 0
1 0 1 0 0
1 0 0 4 4
1 1
0 1
3 1
1 1
1 1
1 3 1 0 2
1 1 1 1 1
0 1
1 1
0 3 3 3
0 3 3 3
0 1 0 0
0 2 2 0
0 2 2 0
0 0 0 0
0 4 5 5
0 4 4 5
0 1 0 0
0 2 3 0
0 2 3 0
0 0 0 0
value per object type
value per object instance
value per object type
Sokoban
Tetris
Figure 3: Example of 2D representation encoding for a
Sokoban and Tetris instance.
type. It also goes the other way, we might represent a
1 × 1 block type by a certain value which then gains
semantics that does not have to be correct as we can
use the same value to represent a different block type
in different instance
3
.
This can also be a problem during training if we
only use domains with up to K Tetris blocks. If we
then deploy instances with K + 1 blocks or more the
trained networks may not know how to treat the added
block encoding.
4.2 3D Object Type Projection
To create a universal grid encoding mechanism we
have to overcome the problems of encoding the ob-
jects. One way of doing so is creating a multi-
dimensional representation of the grid. Transforming
the grid to 3D allows us to create one grid for each
object type which creates a representation suitable for
convolutional neural networks. We create an input of
size N × M ×C where N and M represent size of the
original 2D grid and C represents a number of object
types on the grid. Therefore, for one domain we are
able to create inputs with fixed C dimension and pro-
cess them with convolutional kernels.
This representation does not eliminate the encod-
ing problem completely but it converts it to creating
an encoding in terms of one object type. Such trans-
formation can be beneficial if there is an even distri-
bution of the object types. However, in case of a prob-
lem with multiple instances of one object type is does
not simplify the problem.
3
Note that the values in Figure 3 are only illustrative.
The values could be replaced with any other encoding such
as values from interval h0, ..., 1i.
In Figure 4 we see that representing the Sokoban
domain in 3D representation is possible but as we al-
ready stated, the 2D representation is enough infor-
mative for this particular domain. Therefore we can
just use one-hot encoding in every object type grid
and create a 3D representation with objects in each
layer encoded by 1.
The Tetris example shows that the problem that
occured in creating the 2D representation persists
even when creating a separate grid for each object
type. The one-hot encoding is not informative enough
to carry all information about the blocks. To add the
information back into the 3D representation we can
create a separate encoding for each object type grid.
By using the value per object encoding per object type
we create an encoding for every object instance in
each object grid. But since each grid only contains
one object type we do not loose semantics of the val-
ues because they are defined by the object type grid
position in the input and not the value itself.
Similarly to the previous case, where we train on
maximum K instances per object type and then en-
counter K + 1 instances the network does not have
any knowledge about the meaning of K + 1 encoding.
The difference in this case is that the semantics of the
K + 1 object are clear from the grid it is presented on.
Therefore we do not expect the network to learn the
full context of the object just distinguish objects of
one type.
4.3 3D Object Instance Projection
Besides creating a grid for each object type in the
problem we can also try to look at it the other way
and create a grid for every object instance in the prob-
lem.
The construction of such representation is analo-
gous to the 3D but instead of creating a grid for every
object type we create a grid for every single object
present in the problem definition. That way we create
a complete one-hot encoding that separates definition
of every object.
In Figure 5 we can see how the encoding looks
in practice if we encode one object into one separate
grid. This encoding it purely one-hot and creates an
input that is suitable for neural networks. One draw-
back of this representation is the number of grid we
have to create because it changes with the number of
objects in the problem. If we want to reuse the archi-
tecture on different problems from the same domain
or different problems altogether, this problem has to
be tackled.
The traditional convolutional kernel would not be
usable in this case because of arbitrary number of ob-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
876
1
1
1
1
Sokoban
1 1
1 1 1 1 1
1
1 1
1 1
1
1 1
1
1
1 1
1 1
1 1
1 1 1 1 1
1
1 1
1
1
1
walls
agent
goals
boxes
Tetris
1
1 1
1 1
1 1 1
1 1 1
1
1 2
1 2
1 2 2
1 1 2
1x1
1x1
2x1
2x1
L
L
one- hot encoding per object type
value per object encoding per object type
1
1 1 1 1 1
1
1 1
1 1
1
1 1
1
1
1 1
1 1
1 1
1 1 1 1 1
1
1 1
neural network input
1
1
1
1
neural network input
neural network input
Figure 4: Example of 3D object type projection encoding for a Sokoban and Tetris instance.
jects that results in different size of dimension C for
different problems. One solution that seems reason-
able is using multi-dimensional convolutional kernel
that would be invariant towards such issue.
We also look at the problem of semantics once
again but in terms of third dimension of the created
input data. The network cannot tell which grid be-
longs to which object type and therefore we should
supply additional information to the network in order
to train it. Another way would be creating a fixed en-
coding of object types which is the same in terms of
one problem domain. We could then use the encod-
ing’s value for the corresponding layers instead of the
1 in one-hot representation. Example of such encod-
ing is displayed in Figure 6. We still keep the ”one
grid per layer” rule with the addition of using object
type encoding as additional information.
4.4 Domain-independence of the
Proposed Representations
We showed that constructing grid representation from
PDDL can be done by only parsing the PDDL grid
definition and positioning defined objects in the grid.
That is a category of problem domains which is per-
fectly suitable for our proposed representations.
As we showed in Figure 2 we are also able to
create a grid representation for domains that do not
contains an explicit grid definition. Even thought the
transformation of such domains had to be done by
hand using a human intuition.
That does not imply that all existing planning do-
mains can be represented on a grid. But it shows
us that many of them can be if we create the cor-
rect parser for their PDDL. Automatizing the PDDL
to grid representation parsing by creating a parser per
domains would be beneficial for training neural net-
works as every grid can be transformed into one of
our proposed representations.
5 NEURAL NETWORKS FOR
PLANNING
We proposed three novel representations which can
be used in neural network training for various types
of architectures. In this work, we do not refer to a
specific neural network architecture but rather address
the neural network training as a whole.
Neural networks typically train on large amounts
of unstructured noisy data which does not corre-
spond with learning in planning. Planning problems
are well-defined, deterministic and contain no noise.
Therefore, learning on planning problems is not a typ-
ical task defined in the neural network domain. Main
property of neural networks, which is important to
planning, is generalizing over unseen problems.
5.1 Data Generation
In order to generalize, a neural network typically has
to see a sufficient number of training problems. In
case of planning, the IPC domains we discuss in this
Grid Representation in Neural Networks for Automated Planning
877

1
1
Sokoban
1
1 1 1 1 1
1
1 1
1 1
1
1 1
1
1
1 1
1 1
1 1
1 1 1 1 1
1
1 1
1 1
walls
agent
goal
box
Tetris
1
1
1
1 1
1
1x1 2x1
L
1
1 1 1 1 1
1
1 1
1 1
1
1 1
1
1
1 1
1 1
1 1
1 1 1 1 1
1
1 1
neural network input
1
1
neural network input
1
goal
1
box
1
1
2x1
1
1 1
L
1
1
1
Figure 5: Example of 3D object instance projection encoding for a Sokoban and Tetris instance.
Tetris
1
2
2
3 3
3
1x1
2x1
L
1
1
neural network input
2
2
2x1
3
3 3
L
1
1
1
Figure 6: Example of 3D encoding alternative for Tetris
which includes information about the object type.
works usually have units or tens of problems in them.
Therefore, we cannot use these domains directly to
train any network. Training on such a small data set
can lead to problems like overfitting or memorization
rather then learning.
There are planning problem domains with exist-
ing generators such as the ones provided in learning
track of IPC 2008. But generators do not exist for
all mentioned IPC domains. The only solution is of-
ten creating one’s own data generator for the problem
domain.
5.1.1 Properties of Generated Data
If we want the neural network to learn properties of a
problem domain we have to supply problem instances
that are going to show all of them. Training on in-
stances that are too simple can cause worse generaliz-
ing abilities. On the other hand, training on ”difficult”
instances can cause the network to overlook the basic
concepts of the domain. That lead us to definition of
a ”hard problem instance”.
We are well capable to construct problems that are
hard for most humans but in terms of machine learn-
ing this metric can be completely different. There are
ways of measuring hardness of a level of Sokoban for
example in (Bento et al., 2019) but they do not pro-
vide a general metric that can measure hardness of the
level with respect to a machine learning algorithm.
For techniques such as bootstrapping (Arfaee
et al., 2010), creating problems of increasing hardness
is crucial. Bootstrapping starts training with a set of
problems that should be ”solvable” for the neural net-
work. Then it shows the network different problems
that should be harder and if there is a problem the net-
work cannot solve it gets added to the training set.
This learning technique is very beneficial because
the network starts with the ”simple” instances and
learns basic concepts and structures present in the
problem. And further on it generalizes to more dif-
ficult instances while still using the base level knowl-
edge and being able to solve the simple problems.
5.2 Training
Typically, when training a neural network we need
inputs (problem instances) but also labels which are
the desired outputs we want to see from the network.
If we want to train a network that outputs heuristic
value, its output will be a single number.
Usually, when we train a network to return a value
we want to minimize the difference between the ex-
pected output y and returned value x.
loss(x,y) = |x − y|
However, in this case lowering the difference be-
tween the values does not tell us anything about the
quality of the learned heuristic. We do not care as
much for the exact value as we care for the process
behind its computation. One heuristic value also does
not bring as much information as a set of values for
different states in the state-space of one problem in-
stance.
Heuristic values put the states into perspective and
we can compare which states would be expanded
when during the search. That leads us to the ideal
situation which would be using the search algorithm
itself in the loss function.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
878

If we had the optimal (or existing) solution to the
problem in training data we could just plug the neural
network into the search as a heuristic and evaluate dif-
ference between the expected solution and the newly
found one. That would be the best metric to tell how
well does the neural network work as a heuristic func-
tion.
6 CONCLUSION
We proposed three novel planning problem represen-
tations suitable for training neural networks that can
be created from PDDL problem definition. We an-
alyzed IPC planning domains to filter out domains
which are explicitly defined on a grid which makes
them great candidates for our grid-based representa-
tions. We also picked domains which are not defined
on a grid and showed that it is still possible to use
a grid representation even when no grid is defined in
their PDDL.
We showed examples of all proposed representa-
tions and described their advantages and drawbacks.
The biggest advantage of problems represented by
grids is the grid structure which can be easily used
for neural network training. If we used such repre-
sentation on outputs from the available PDDL data
generators it would mean more reliable training data
for architectures that require the grid-based input.
We also discussed the domain-independence of
the representations as well as possible automatising
in terms of creating PDDL parsers that would be able
to create grid representations solely from the PDDL
files.
Finally, we shortly discussed training neural net-
works for planning. We pointed out problems like
obtaining high quality data, properties that the data
should have, hardness of the problems and choosing
correct loss function for training.
Main drawback of these representations is the lack
of action information. In order to correctly compute
heuristic or solve a planning problem, it is necessary
to understand the transition system of the problem and
how it is created. In this case, we only aim to repre-
sent the problem in a convenient manner and assume
that further information is provided as another input
to the architecture.
In the future, we would like to focus on N-
dimensional representation that would be able to add
definition of actions into the grid representation as
well. Next focus is on the PDDL to grid parsers which
could be beneficial set of tools for trying out different
machine learning techniques such as the mentioned
bootstrapping.
ACKNOWLEDGEMENTS
The work of Michaela Urbanovsk
´
a was
supported by the OP VVV funded project
CZ.02.1.01/0.0/0.0/16019/0000765 “Research
Center for Informatics” and the work of Anton
´
ın
Komenda was supported by the Czech Science
Foundation (grant no. 21-33041J).
REFERENCES
Aeronautiques, C., Howe, A., Knoblock, C., McDermott,
I. D., Ram, A., Veloso, M., Weld, D., SRI, D. W., Bar-
rett, A., Christianson, D., et al. (1998). Pddl— the
planning domain definition language. Technical re-
port, Technical Report.
Arfaee, S. J., Zilles, S., and Holte, R. C. (2010). Boot-
strap learning of heuristic functions. In Felner, A. and
Sturtevant, N. R., editors, Proceedings of the Third
Annual Symposium on Combinatorial Search, SOCS
2010, Stone Mountain, Atlanta, Georgia, USA, July
8-10, 2010. AAAI Press.
Asai, M. and Fukunaga, A. (2017). Classical planning in
deep latent space: From unlabeled images to PDDL
(and back). In Besold, T. R., d’Avila Garcez, A. S.,
and Noble, I., editors, Proceedings of the Twelfth In-
ternational Workshop on Neural-Symbolic Learning
and Reasoning, NeSy 2017, London, UK, July 17-18,
2017, volume 2003 of CEUR Workshop Proceedings.
CEUR-WS.org.
Asai, M. and Fukunaga, A. (2018). Classical planning in
deep latent space: Bridging the subsymbolic-symbolic
boundary. In Thirty-Second AAAI Conference on Ar-
tificial Intelligence.
Bento, D. S., Pereira, A. G., and Lelis, L. H. S. (2019).
Procedural generation of initial states of sokoban. In
Kraus, S., editor, Proceedings of the Twenty-Eighth
International Joint Conference on Artificial Intelli-
gence, IJCAI 2019, Macao, China, August 10-16,
2019, pages 4651–4657. ijcai.org.
Franc
`
es, G., Corr
ˆ
ea, A. B., Geissmann, C., and Pommeren-
ing, F. (2019). Generalized potential heuristics for
classical planning. In Proceedings of the Twenty-
Eighth International Joint Conference on Artificial In-
telligence, IJCAI-19, pages 5554–5561. International
Joint Conferences on Artificial Intelligence Organiza-
tion.
Geffner, H. (2018). Model-free, model-based, and general
intelligence. CoRR, abs/1806.02308.
Groshev, E., Tamar, A., Goldstein, M., Srivastava, S., and
Abbeel, P. (2018). Learning generalized reactive poli-
cies using deep neural networks. In 2018 AAAI Spring
Symposium Series.
LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard,
R. E., Hubbard, W., and Jackel, L. D. (1989). Back-
propagation applied to handwritten zip code recogni-
tion. Neural computation, 1(4):541–551.
Grid Representation in Neural Networks for Automated Planning
879

McDermott, D. V. (2000). The 1998 AI planning systems
competition. AI Mag., 21(2):35–55.
Russell, S. J. and Norvig, P. (2020). Artificial Intelligence:
A Modern Approach (4th Edition). Pearson.
Shen, W., Trevizan, F. W., and Thi
´
ebaux, S. (2020). Learn-
ing domain-independent planning heuristics with hy-
pergraph networks. In Beck, J. C., Buffet, O., Hoff-
mann, J., Karpas, E., and Sohrabi, S., editors, Pro-
ceedings of the Thirtieth International Conference on
Automated Planning and Scheduling, Nancy, France,
October 26-30, 2020, pages 574–584. AAAI Press.
Toyer, S., Thi
´
ebaux, S., Trevizan, F. W., and Xie, L. (2020).
Asnets: Deep learning for generalised planning. J.
Artif. Intell. Res., 68:1–68.
Urbanovsk
´
a, M. and Komenda, A. (2021). Neural net-
works for model-free and scale-free automated plan-
ning. Knowledge and Information Systems, pages 1–
36.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,
L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.
(2017). Attention is all you need. In Advances in
neural information processing systems, pages 5998–
6008.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
880
