Grouping of Maintenance Actions with Deep Reinforcement Learning

and Graph Convolutional Networks

David Kerkkamp

1 a

, Zaharah A. Bukhsh

2 b

, Yingqian Zhang

2 c

and Nils Jansen

1 d

Radboud University, Nijmegen, The Netherlands

Eindhoven University of Technology, Eindhoven, The Netherlands

Keywords:

Maintenance Planning, Deep Reinforcement Learning, Graph Neural Networks, Sewer Asset Management.

Abstract:

Reinforcement learning (RL) has shown promising performance in several applications such as robotics and

games. However, the use of RL in emerging real-world domains such as smart industry and asset management

remains scarce. This paper addresses the problem of optimal maintenance planning using historical data. We

propose a novel Deep RL (DRL) framework based on Graph Convolutional Networks (GCN) to leverage the

inherent graph structure of typical assets. As demonstrator, we employ an underground sewer pipe network.

In particular, instead of dispersed maintenance actions of individual pipes across the network, the GCN en-

sures the grouping of maintenance actions of geographically close pipes. We perform experiments using the

distinct physical characteristics, deterioration proﬁles, and historical data of sewer inspections within an urban

environment. The results show that combining Deep Q-Networks (DQN) with GCN leads to structurally more

reliable networks and a higher degree of maintenance grouping, compared to DQN with fully-connected layers

and standard preventive and corrective maintenance strategy that are often adopted in practice. Our approach

shows potential for developing efﬁcient and practical maintenance plans in terms of cost and reliability.

1 INTRODUCTION

The goal of reinforcement learning (RL) is to learn

an optimal policy for sequential decision problems

by maximizing a cumulative reward signal (Kaelbling

et al., 1996). Deep Reinforcement Learning (DRL)

has elevated RL to handle previously intractable prob-

lems. DRL is a data-driven method for ﬁnding op-

timal strategies that do not rely on human expertise

or manual feature engineering (Sun et al., 2021; Lu-

ong et al., 2019). Application domains of DRL are,

for instance, communications and networking (e.g.

throughput maximization, caching, network security

(Luong et al., 2019)), or games (e.g. TD-Gammon by

Tesauro (1995) and playing Atari with DQN (Mnih

et al., 2013)). Other practical domains in which DRL

has been applied include robotics, natural language

processing, and computer vision (Chen et al., 2017;

Li, 2017). However, the use of RL in emerging real-

world domains such as smart industry and asset man-

agement remains scarce.

This paper addresses the problem of optimal

maintenance planning using historical data. We pro-

https://orcid.org/0000-0003-3676-0960

https://orcid.org/0000-0003-3037-8998

https://orcid.org/0000-0002-5073-0787

https://orcid.org/0000-0003-1318-8973

pose a novel DRL framework based on Graph Con-

volutional Networks (GCN) to leverage the inherent

graph structure of typical assets. As a demonstra-

tor, we employ an underground sewer pipe network.

Sewer pipe networks are an essential part of urban in-

frastructure. Failure of pipe assets can cause service

disruptions, threats to public health, and damage to

surrounding buildings and infrastructure (Tscheikner-

Gratl et al., 2019). Because the sewer infrastructure is

underground, inspections and rehabilitation activities

are expensive and labor-intensive, while the budget is

often constrained (Fontecha et al., 2021; Hansen et al.,

2019; Yin et al., 2020). Therefore, a maintenance

strategy balancing reliability and costs is needed to

achieve an adequate level of service.

Existing research focuses mainly on developing

methods to model the deterioration of pipe assets. The

works of Weeraddana et al. (2020), Yin et al. (2020),

Hansen et al. (2019) and Fontecha et al. (2021) are

primarily aimed at deterioration modeling for predict-

ing failure risks, without using relational and geo-

graphical information of the pipe network. Although

a deterioration model is required for creating main-

tenance plans, it does not provide a solution to the

optimal planning task.

We propose to investigate the capabilities of DRL

for ﬁnding the best rehabilitation moment for groups

574

Kerkkamp, D., Bukhsh, Z., Zhang, Y. and Jansen, N.

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks.

DOI: 10.5220/0010907500003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 574-585

ISBN: 978-989-758-547-0; ISSN: 2184-433X

of pipe assets. The critical planning constraints are

minimum total cost and adequate reliability of the

network. We attempt to reduce the cost by con-

sidering the physical state of the neighboring pipes

when choosing rehabilitation actions. The grouping

of maintenance actions can save the additional setup,

labor, and unavailability cost of the network (Rokstad

and Ugarelli, 2015; Pargar et al., 2017). Graph neu-

ral networks in general and GCNs speciﬁcally are an

excellent tool for capturing such a network topology,

where a DRL framework can be used in combination

to ﬁnd optimal actions given the constraints. To sum-

marise, the objective of the study is to demonstrate

the potential of the DRL framework for solving main-

tenance planning problems having network topology.

Recently DRL has been combined with Graph

Neural Networks (GNN) for addressing problems

in several domains, including network optimization

(Yan et al., 2020; Sun et al., 2021; Almasan et al.,

2020), symbolic relational problems (Janisch et al.,

2021) and dynamic scheduling in ﬂexible manufac-

turing systems (Hu et al., 2020). However, to the best

of our knowledge, DRL and GNNs are not investi-

gated to solve the maintenance planning problem of

infrastructure assets.

The key contributions of this study are:

• A deep reinforcement learning framework using

GCNs to learn optimal maintenance plans for in-

frastructure assets. The approach is generic and

can be applied to any infrastructure asset planning

problem with a network topology.

• An evaluation of the framework on a case study

with real-world data of a sewer network.

• A comparison with multiple baseline strategies to

show the potential of our approach.

The remainder of this article is structured as follows.

Section 2 describes the related work that combines

DRL with GNN. Section 3 explains the problem de-

scription along with a formal problem statement. The

background of the proposed methodology is given in

Section 4. The methodology and empirical setup of

experiments are discussed in Section 5, followed by

evaluations and results in Sections 6. Finally we pro-

vide concluding remarks and future work in Section 7.

2 RELATED WORK

Many recent studies of underground pipe rehabilita-

tion mainly focus on deterioration modeling. Yin

et al. (2020) found that most of the studies concen-

trate on the prediction of future pipe conditions at the

individual level, but few take the spatial information

of pipe assets into account. According to Rokstad and

Ugarelli (2015), there are some examples of grouping

based on location in literature, but they plan for a lim-

ited time horizon and only consider a subset of pipes

for rehabilitation. Furthermore, existing studies are

often site-speciﬁc, which makes it only representative

for the used case study (Tscheikner-Gratl et al., 2019).

Fontecha et al. (2021) propose a framework for pre-

dicting failure risks using multiple machine learning

techniques. They recognize that pipe failures are spa-

tially correlated. Instead of predicting for individual

pipes, failure risks are predicted for cells in a grid that

are placed over the sewer network. Li et al. (2011)

aims at ﬁnding a grouping for a set of pipes to be re-

placed, using the genetic algorithm to minimize to-

tal cost. However, they ﬁx the set of pipes within a

given horizon beforehand and do not take into account

changes in physical condition over the years.

Recently, learning-based approaches have been

studied for solving combinatorial optimization prob-

lems on graph-structured data, like the Traveling

Salesman Problem (TSP). Dai et al. (2018) present

a framework for learning greedy heuristics for graph

optimization problems, including TSP, using a com-

bination of deep graph embedding and Deep Q-

Network (DQN) (Mnih et al., 2013). Joshi et al.

(2019) propose a supervised deep learning approach

for solving TSP using GNN. The authors wish to in-

corporate RL into their framework in the future to be

able to handle arbitrary problem sizes. Prates et al.

(2019) also investigate the use of GNN to solve TSP,

using a supervised training method involving stochas-

tic gradient descent. da Costa et al. (2020) apply

DRL trained with a policy gradient for learning im-

provement heuristics for TSP. The neural network ar-

chitecture includes elements from GNN and recurrent

neural networks.

Computer network optimization is also a domain

where learning-based methods have been applied and

where the usage of GNN has been proposed to model

computer networks. Almasan et al. (2020) apply

DQN with a network architecture based on message

passing neural network to optimize the routing of traf-

ﬁc demands on computer networks. Sun et al. (2021)

learn optimal placement schemes for virtual network

functions that serve as middleware for network traf-

ﬁc, using REINFORCE policy gradient method (Sut-

ton et al., 1999) and graph network (Battaglia et al.,

2018). Yan et al. (2020) create virtual network

embedding to optimize resource utilization, using

A3C policy gradient algorithm (Mnih et al., 2016)

and graph convolutional networks (Kipf and Welling,

2017).

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks

575

Another domain is planning. Janisch et al. (2021)

propose a relational DRL framework to solve sym-

bolic planning problems based on a custom GNN im-

plementation and learning with a policy gradient al-

gorithm. Garg et al. (2019) provide a neural transfer

framework that trains on small planning problems and

transfers to larger ones, using an RL algorithm that in-

corporates graph attention network (Veli

ckovi

c et al.,

2018).

3 PROBLEM DESCRIPTION

In this section, we describe the general problem set-

ting as a maintenance optimization problem. On a

high level, a number of assets may deteriorate over

time. Each asset has a certain status related to the

deterioration that depends on the age and other prop-

erties of the asset. Based on its status, each asset

may need one out of multiple possible maintenance

actions. There is a cost associated with the mainte-

nance actions, and furthermore, there is a (high) cost

imposed in case an asset is near failure because of a

lack of maintenance.

In our particular setting, we assume that the as-

sets form a network, for instance, they are connected

if they are in proximity to each other. We are thus in-

terested in the simultaneous rehabilitation for groups

of geographically close assets instead of interventions

on individual assets at different moments. Such a

grouping is motivated by the fact that the grouping of

interventions can save the additional setup, labor, and

unavailability costs as shown in Rokstad and Ugarelli

(2015); Pargar et al. (2017). The overall objective is

to plan maintenance for the set of assets in a way that

the assets do not deteriorate to near failure while the

overall cost is minimized.

3.1 Formal Problem Statement

We formalize the underlying optimization prob-

lem. The assets are Assets = {asset

,... ,asset

and each asset 1 ≤ i ≤ n has a status status

∈

{healthy,near fail} and an age age

∈ N. For simplic-

ity, we assume the status is either near fail or healthy.

Together, a state of this maintenance system is

given by the features hage

,status

,. .. ,age

,status

As we consider a network of assets, we asso-

ciate a distance between assets, given as a function

dist : Assets × Assets → N that deﬁnes a natural num-

ber as the distance between two assets, for instance

dist(asset

,asset

) = 5 as a distance of 5 meters be-

tween asset

and asset

for 1 ≤ i, j ≤ n.

We assume that we can capture deterioration by

discrete probability distributions over time. There-

fore, depending on the age and the current status of an

asset, there is a probability that its status will change,

here, that the asset will approach to near failure. For-

mally, we have a function

: N × {status

} → Distr(status

)

where Distr(status

) describes a (discrete) probabil-

ity distribution over the status of an asset asset

. For

example, an asset of age 60 years that has not failed

yet may have a high probability of 80% of failing:

(60,healthy)(near fail) = 0.8. Note that these prob-

abilities are individual for each asset and may depend

on multiple factors beyond the age, such as materials

or environmental conditions.

The action space Act

for asset

consists of the

maintenance actions with

Act

= {do nothing

,maintain

,replace

We denote a maintenance action for asset

by a

∈

Act

. Different actions have different effects on the as-

set’s failure probability, e.g. maintain reduces the fail-

ure probability due to repairs applied and replace sets

the failure probability to a very low value because the

asset is replaced. Naturally, more maintenance ac-

tions may be deﬁned. The joined action space for

the maintenance system is then Act =

Act

. How-

ever, as mentioned before, it may be beneﬁcial to

group maintenance actions, that is, performing ac-

tions for multiple assets at once. The grouped ac-

tion space is then Act

= P (Act), the powerset of the

joined maintenance actions. Intuitively, a grouped ac-

tion is a subset of all potential maintenance actions

for the assets. Finally, we deﬁne the maintenance

cost. Each action a

for asset asset

has an associ-

ated cost c(a

), denoted, for instance, by c(replace

)

for replacing asset

. Moreover, there is a distinct

(high) cost c(near fail

) for an asset failing. To cap-

ture the effect of performing group maintenance ac-

tions for assets that are close to each other, we de-

ﬁne a group discount based on the distance between

assets. Essentially, for assets that are near to each

other, group actions may be performed and based

on the number of assets that are part of that action,

cost is reduced. The grouping cost reduction function

D: Act

→ R maps a subset of actions to a real num-

ber, yielding the group cost function c

: Act → N

with c

,. .. ,a

) =

∑

i=1

c(a

) − D(a

,. .. ,a

) and

m ≤ n.

The objective is now to minimize the overall

maintenance cost of the system. This problem can

be captured by a Markov decision process Puterman

(1994) deﬁned on the state space of the maintenance

system. Depending on the size of the system, this

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

576

problem may then be solved by techniques such as

value iteration or linear programming. In our setting,

however, we take a data driven approach to handle

real-world problems that (1) would require an explicit

creation of states and probabilities and (2) may be ar-

bitrarily large. Therefore, in the following, we de-

tail our deep reinforcement learning approach and the

concrete case study.

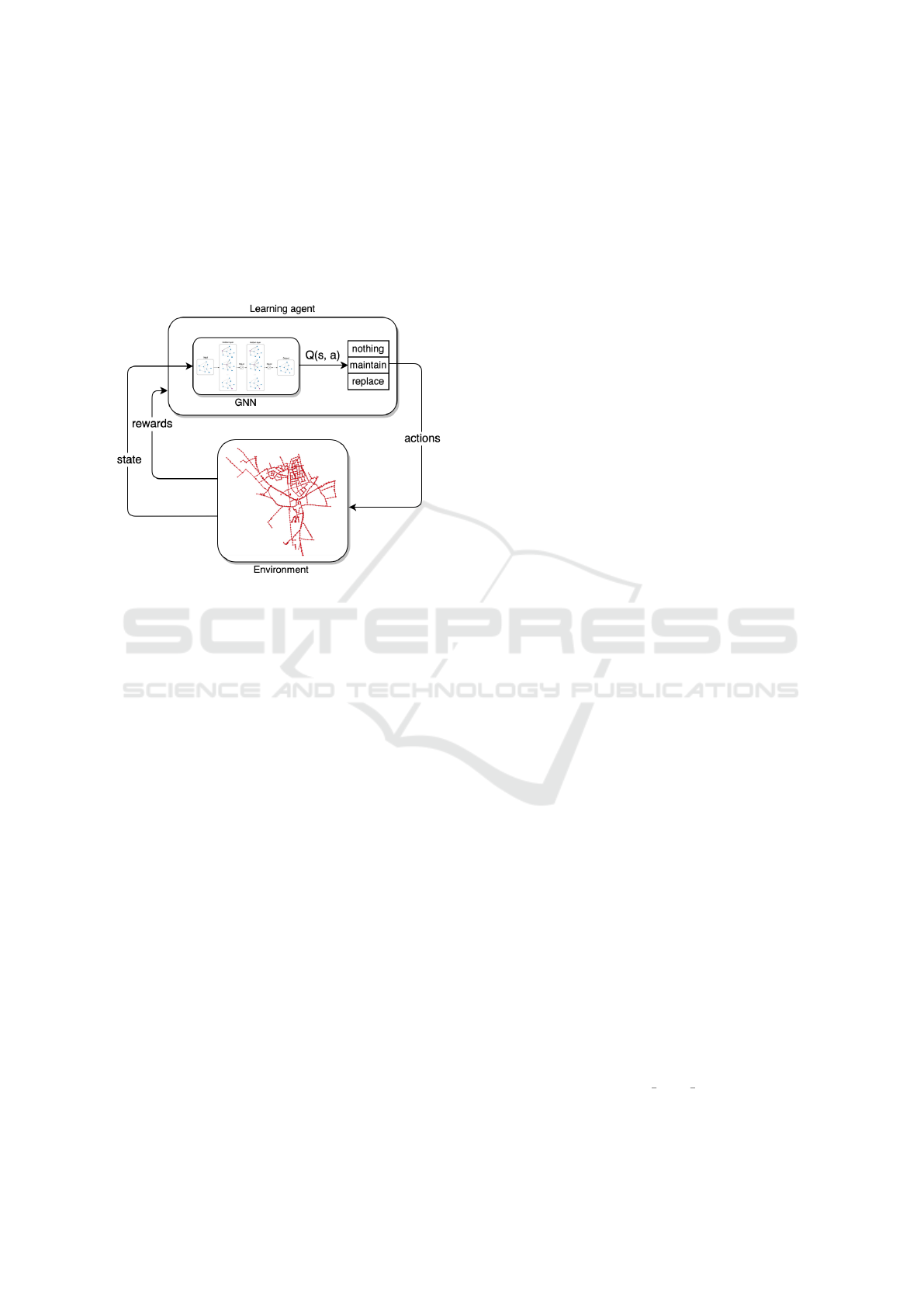
Figure 1: Interaction between DRL learning agent and en-

vironment, and the position of the GCN within the agent.

4 BACKGROUND

4.1 Deep Q Networks

Reinforcement learning algorithms aim at learning a

long-term strategy to maximize a cumulative reward.

An optimal strategy is learned by iteratively explor-

ing the state and action spaces, directed by the reward

function (Kaelbling et al., 1996). Q-learning (Watkins

and Dayan, 1992) is an RL algorithm that learns a pol-

icy π mapping states to actions. Every possible state-

action pair is stored in a table, and during training,

each entry is updated iteratively according to rewards

received. Rewards received in the future are geomet-

rically discounted using a discount factor γ ∈ [0, 1].

These values are called Q-values, and they represent

the expected cumulative discounted reward for exe-

cuting action a at state s and then following policy

π. Q-values are updated using the Bellman equation

deﬁned below (Kaelbling et al., 1996):

Q(s,a) = R(s, a) + γmax

Q(s

) (1)

where Q(s,a) is the Q-value function and R(s,a) the

reward function.

As problems become more complex with high-

dimensional state and action spaces, basic Q-learning

is not practical to use. Deep Q-Network (DQN) is

an algorithm proposed by (Mnih et al., 2013) based

on Q-learning that uses deep neural networks (DNN)

to estimate the Q-value function Q(s,a;θ) ≈ Q(s,a)

with parameters θ. This allows for leveraging the

generalization ability of DNN to estimate Q-values

for previously unseen state-action pairs. The DQN is

both a model-free and an off-policy algorithm (Mnih

et al., 2013). Due to the model-free feature, the con-

trol task is solved using samples obtained from the

simulated environment, without constructing an ex-

plicit model of the environment. With off-policy ap-

proach, the DQN follows a behaviour distribution and

ensures that the state space is adequately explored

while learning the greedy strategy a = max

Q(s,a; θ).

Practically, this means that an ε-greedy strategy is ap-

plied. The agent selects an action according to the

greedy strategy with probability 1 − ε, and selects a

random action with probability ε to provide a trade-

off between exploring new state-action pairs and ex-

ploiting the learned knowledge.

4.1.1 Double DQN

Double Deep Q-network (DDQN) is an improvement

on DQN proposed by van Hasselt et al. (2015). They

show that DQN sometimes suffers from overestima-

tions of Q-values. The computation of the target in the

optimization step of DQN includes a maximization

operator over estimated action values. Here, the same

value is used for selection and evaluation, making it

more likely to select overestimated values. DDQN

thus decouples action selection from evaluation. To

achieve this, DDQN evaluates the greedy policy with

an online Q-network, but it uses the target network for

estimating its value.

4.2 Graph Convolutional Networks

Graph Convolutional Network (GCN) is a neural net-

work model that directly encodes graph structure

(Kipf and Welling, 2017). The goal is to learn a func-

tion of features on a graph. It takes as input an m × n

feature matrix X consisting of feature vectors x

length n for each node i with 1 ≤ i ≤ m. It also takes

an adjacency matrix A describing the graph structure.

It produces a node-level output matrix with dimen-

sions m× o, where o is the number of output features.

The propagation function of GCN for layer l is:

f (H

(l)

,A) = σ



−

(l)



(2)

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks

577

where

A = I + A is the adjacency matrix with added

self-loops,

D is the diagonal node degree matrix of

and σ is a non-linear activation function.

5 METHODOLOGY AND

EMPIRICAL SETUP

5.1 Case Study: A Sewer Pipe Network

As a driver case for our work, we consider a real case

study of a network of sewer pipes. We choose a subset

of 942 pipes (assets) for evaluation of the DRL frame-

work. The available features for each pipe include

geographical location, material, length, and age. The

geographical location of the pipes is used to construct

the distance function described in Section 3. An ex-

ample in the context of our case study is given in the

following subsection. The resulting network serves

as input to the GCN. For deterioration modeling, we

utilize pipe failure rates extracted from a dataset of

26,285 manual pipe inspections. The inspections are

performed according to a standardized classiﬁcation

scheme and provide damage observations of the in-

spected pipes. Every observed damage is assigned to

a class from 1 (minor damage) to 5 (worst damage).

The maintenance optimization problem can be

tackled in two ways. The ﬁrst involves the model-

ing of deterioration of the assets under consideration

to estimate the failure behavior. The second consists

of ﬁnding the best moment for rehabilitation of assets,

given a deterioration model. In this work, we focus on

the latter. We employ a DRL framework with GNN

to plan rehabilitation activities, using a simple dete-

rioration model based on the exponential distribution

and failure rates obtained from historical data. Us-

ing a GNN to estimate failure rates and probabilities

is an exciting direction to explore in the future. This,

however, requires more extensive historical condition

monitoring data than is currently available.

We advocate investigating the capabilities of deep

reinforcement learning (DRL) in this setting. The

DRL agent follows the Double DQN algorithm (van

Hasselt et al., 2015; Mnih et al., 2013) and uses a

GNN to model the Q-value function. For this, we em-

ploy Graph Convolutional Networks (GCN) by Kipf

and Welling (2017). The DRL agent receives, at each

timestep, a representation of the sewer network’s state

from a simulated environment and uses the GCN to

select the next action to take based on this state (i.e.,

which pipes to maintain/replace). It then applies the

action to the environment and receives the next state

and a reward to evaluate the action taken. The inter-

action between the DRL agent and the environment is

depicted in Figure 1.

The transition dynamics are deterministic and

use the exponential distribution, which is commonly

used for modeling the lifespan of deteriorating assets

(Scheidegger et al., 2011; Birolini, 2013). There is

no uncertainty in our deterioration model because the

lifespan of underground sewer pipes is typically very

long, and they often are in use for an extended period

having a lifespan of 50 to 100 years (Petit-Boix et al.,

2016; Scheidegger et al., 2011). This is because sewer

pipes deteriorate slowly, resulting in a steady perfor-

mance for years. Therefore, it is highly unlikely that

failures occur in relatively newer pipes.

It is also important to note that we choose to use

a cost model with symbolic costs. This is because a

comprehensive cost model includes direct repair ex-

penses and indirect costs related to equipment and

labor costs. Additionally, performing maintenance

on pipe network results in additional social costs

due to service unavailability, trafﬁc disruptions, dam-

aged properties in case of leakage, and health hazards

(Scheidegger et al., 2011). The monetization of such

indirect and social costs is complicated because they

are qualitative and not easily quantiﬁed. To monetize

all costs into a realistic cost model, dedicated valu-

ation methods are needed, often based on historical

maintenance data (Tscheikner-Gratl et al., 2019).

In the following, we explain how a graph is con-

structed from data and describe how the environment

simulates the sewer network by providing details of

states, actions, rewards, and transition dynamics.

5.2 Graph Representation

In order to apply a GCN to our speciﬁc case study

data, a graph representation is required. Let G =

(V,E) be a graph representing the sewer network

with nodes V and edges E. Let A be an adjacency

matrix with dimensions |V | × |V | where each entry

i j

∈ {0,1} denotes the absence or existence of an

edge between nodes i and j with 1 ≤ i, j ≤ |V |. Ev-

ery node v ∈ V corresponds to a sewer pipe, and ev-

ery edge e ∈ E represents a connection between two

pipes. The sewer network can be captured in a graph

in two ways. The ﬁrst way resembles the real-world

pipe layout, such that there exists an edge between

two nodes only if the corresponding sewer pipes are

physically connected. The second way is based on a

distance measure. In this case, there exists an edge

between two nodes if their corresponding pipes are

within a given distance. We model the sewer network

based on the latter. For this, we deﬁne a distance mea-

sure by considering the distance between the coordi-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

578

nates of the start and end points of the pipes in the

physical world. Let dist(c

) denote the distance in

meters between coordinates c

and c

and let c

and c

denote the coordinates corresponding to the start and

end points, respectively, of pipe i. Then the entries

of the adjacency matrix A are deﬁned as follows, for

given distance r.

i j











i 6= j ∧ (dist(c

) < r ∨

dist(c

) < r ∨

dist(c

) < r ∨

dist(c

) < r)

0 otherwise

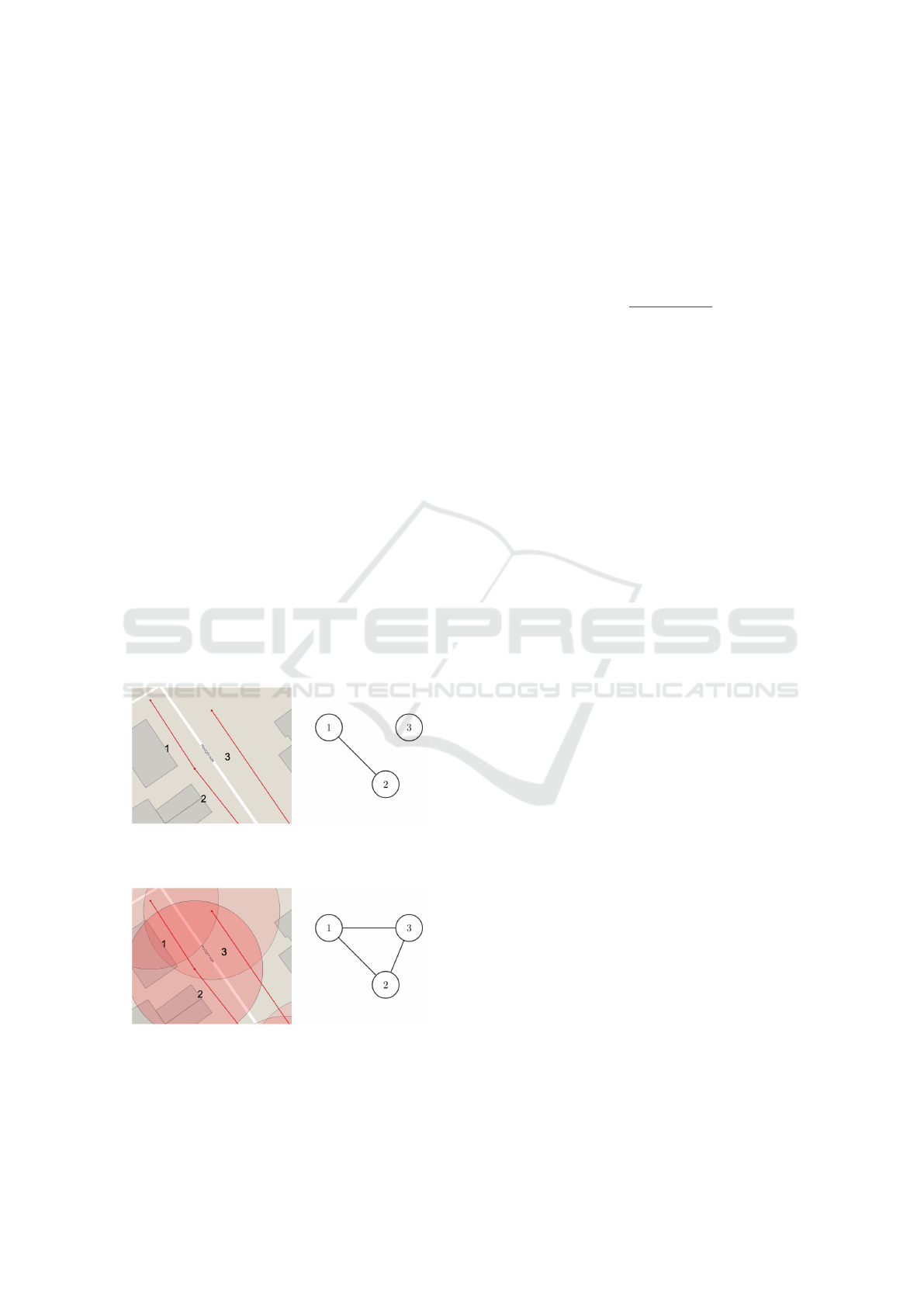
The sewer network graph representation of three spa-

tially close pipes are illustrated in Figure 2 based on

both, physical network and distance-based method.

5.3 Modeling of the Environment

5.3.1 Pipe Deterioration

To model the pipe deterioration mechanism, we use

a pipe-speciﬁc failure rate f r depending on the mate-

rial. We use damage observations from the inspection

records of the complete dataset to obtain these fail-

ure rates. We treat observations with damage class

4 or higher as a failure. We then count the num-

ber of failures per inspected pipe, divide them by the

(a) Graph based on physical pipe connections, where

nodes are only connected if their corresponding pipes

are connected in the real world.

(b) Graph with edges between nodes that have the start

or end points of their corresponding pipes within 20

meters distance of each other.

Figure 2: Two ways of representing the sewer pipes as

graph.

pipe length and average the result per material type

to obtain a failure rate per meter for each material

type. Let n f

denote the number of observed failures

of pipe i, I = {1, ...,N} a set of material types, and

B = {B

,..., B

} a set of pipes, where B

is a set of

pipes of material type j ∈ I. The failure rate m f r

material j is then obtained in the following way:

m f r

∑

i∈B

(n f

)

(3)

where l

is the length of pipe i. Finally, for each of

the 942 pipes under consideration, the pipe-speciﬁc

failure rate f r

is obtained by multiplying the failure

rate corresponding to the pipe material with the pipe’s

length.

The probability of failure p f is estimated using

the failure rates extracted from historical data and the

exponential distribution reliability function (Birolini,

2013) as follows:

p f

= 1 − rl

= 1 − e

− f r

aux

(4)

where p f

is the failure probability of pipe i at

timestep t, rl

the reliability level, f r

the failure rate

and aux

an auxiliary variable for the pipe age. An

auxiliary variable represents the physical condition of

the pipe, which can either improve or deteriorate de-

pending on the chosen actions. In summary, pipe de-

terioration depends on age, material, and length. The

deterioration model described above simpliﬁes real-

ity to simulate the sewer network for the DRL agent.

More sophisticated ways of modeling deterioration

and extraction of failure rates from available data are

still an open problem.

5.3.2 States

Every node in the graph representing the pipe network

has a vector of features m

= hl

,mat

,age

f r

,aux

, p f

,rl

i, with 1 ≤ i ≤ m (m being total num-

ber of nodes) and where l

is the length, w

and h

are

the diameter width and height of the pipe, mat

is the

material, age

is the age, f r

is the failure rate, aux

is an auxiliary variable for the age that represents the

change in physical state of the pipe, p f

is the proba-

bility of failure and rl

is the reliability. On each step

aux

, rl

and p f

are updated depending on the action

applied. The age

is incremented to reﬂect the actual

age and does not depend on applied actions to avoid

modiﬁcations to the original age values of the pipes.

All feature vectors form a feature matrix with dimen-

sions m ×n representing the environment state, where

n is the number of features. In addition, there is an ad-

jacency matrix A = m × m representing a set of edges

connecting the nodes.

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks

579

5.3.3 Actions

At each time step t the DRL agent selects the best ac-

tion for each pipe given the current state, resulting in

a vector a = ha

,..., a

i. The set of actions con-

sists of three types, such that at each timestep t for

each pipe i, an agent can choose a

∈ {0,1, 2}. Action

0 means do nothing, action 1 is maintain, and action

2 is replace.

5.3.4 Reward Function

The reward function R(s

) provides the immediate

reward for taking actions a

from state s

. Since the

total cost should be minimized, we inverse the reward

function. As described, in each timestep t an action

is applied to every pipe i. This results in a reward

vector r

= hr

+ b

,..., r

+ b

i where each r

and b

are obtained in the following way:











0 if a

= do

nothing and p f

< 0.9

−1 if a

= do nothing and p f

≥ 0.9

−0.5 if a

= maintain and p f

> 0.5

−1 if a

= maintain and p f

≤ 0.5

−0.8 if a

= replace and p f

> 0.5

−1 if a

= replace and p f

≤ 0.5

(

0.1 if a

6= 0 ∧ ∃ j, j 6= i ∧ A

i j

= 1 ∧ a

6= 0

0 otherwise

A penalty of −1 is introduced to discourage the

agent from selecting maintenance or replacement ac-

tions for pipes that are in good shape. The same

penalty helps to ensure a sufﬁcient reliability level if

a pipe has a high probability of failure, but the agent

chooses to do nothing. Practically, these penalty val-

ues relate to the impact on trafﬁc, surroundings, and

network unavailability in case of pipe failures.

In addition, grouped rehabilitation is rewarded. If

for a certain pipe i the maintain or replace action is

selected, while one of these actions is also selected

for any neighbor j of pipe i (i.e. there is an edge con-

necting i and j), then both pipes i and j receive a small

bonus (or cost reduction) of 0.1, denoted above by b

These bonus values are concerned with cost reduction

due to one-time setup and transportation costs if pipes

in closed proximity are maintained together.

5.3.5 Transitions

When actions are applied to the network, the environ-

ment moves ahead one timestep and produces a new

state representation and a reward. The state represen-

tation consists of a new matrix of pipe features. The

adjacency matrix remains the same since the layout

of the sewer network is ﬁxed. Because the environ-

ment is modeled as MDP, the next state is only de-

pendent on the previous state and action. For the next

timestep, the age feature age

t+1

is increased by one

year, and the auxiliary feature aux

t+1

describing the

physical state of pipe i is computed as follows:

aux

t+1











aux

+ 1 if a

= do nothing

aux

− 10 if a

= maintain and

aux

> 10

aux

if a

= maintain and

aux

≤ 10

1 if a

= replace

So if do nothing is applied to a pipe, the auxiliary

feature increases by 1 year, if maintain is applied, it

decreases by 10 years and if replace is applied, it is

reset to 1. Based on this auxiliary age feature, the

new failure probability and reliability are computed

for every pipe using the exponential distribution given

in equation 4.

6 EVALUATION AND RESULTS

6.1 Implementation

We implement the DRL framework with DDQN in

Python. The environment is a custom OpenAI Gym

environment. For the neural network architecture

with GCN, we use PyTorch Geometric (Fey and

Lenssen, 2019).

The network takes a 942 × 11 node feature matrix

as input for 942 pipes with 9 features. The material

is represented using one-hot encoding. The dataset

has 3 material types, resulting in 3 material columns

(hence the input shape). Besides the node features,

the network takes the adjacency matrix describing the

edge connections. The network architecture consists

of two GCNConv layers with an output size of 32, each

followed by a ReLU activation function. The ﬁnal

layer is a fully connected Linear with output size 3

(# actions). For network optimization, AdamW is used

with MSELoss.

We compare DRL with GCN (referred to as

DRL+GCN) to several baselines to show the potential

of applying GCN in a DRL framework. First, we ap-

ply the same DRL framework, but the GCN architec-

ture is replaced for a simple, fully connected Linear

layer with the same input and output size (referred to

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

580

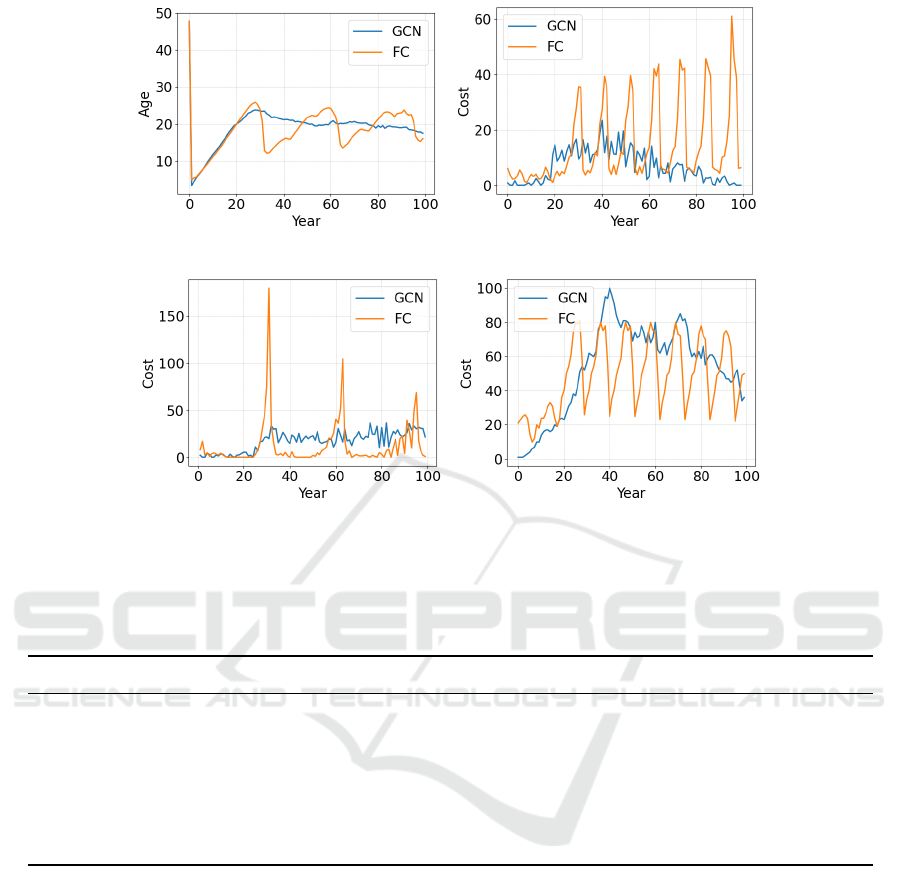
(a) Mean pipe age per year. (b) Maintenance costs per year.

1st.

(d) ‘Do nothing’ penalties per year.

Figure 3: Breakdown of the total costs per year of each action type for DRL+GCN and DRL+FC. The top left diagram shows

the mean pipe age, which is inﬂuenced by intervention actions.

Table 1: Comparison of DRL+GCN with DRL having fully connected layers, two preventive and one corrective baselines.

DRL+GCN DRL+FC Replace Greedy Maintain-10

Mean # pipes per group 2.74 2.02 - - -

% groups with >1 pipe 56% 30% - - -

Mean reliability 0.46 0.42 0.32 0.56 0.15

Interventions per year 45.26 55.94 20.77 378.45 94.2

Interventions per pipe 4.80 5.94 2.44 40.18 10

Total cost based on reward function 8362 8077 21,769 15,526 50,908

as DRL+FC). We also compare with non-RL strate-

gies traditionally applied in industry (Ahmad and Ka-

maruddin, 2012), including time-based preventive,

greedy preventive, and corrective approaches. The

time-based approach suggests maintain action for all

pipes based on a time interval of 10 years. The

greedy preventive approach chooses maintain action

as cheapest intervention as soon as the p f

> 0.5. In

the corrective approach, interventions are taken after

failure, represented as p f

> 0.95. The rationale be-

hind choosing a threshold of 0.95, instead of 0.9 as in

the reward function, is, because in the corrective ap-

proach, pipes are only replaced after they have already

failed. We use the same simulated environment, in-

cluding reward functions, penalties, and bonus costs,

for all three baselines for fair comparison. This re-

sults in two preventive strategies, i.e, Maintain-10 and

Greedy, and one corrective strategy, i.e, Replace.

6.2 Training

A graph is constructed from the pipes in the dataset,

which consists of two coordinate points. A node rep-

resents a pipe, and an edge exists between two pipes

if any of their points are within a range of 20 meters

of each other. We train the network using a Google

Colab notebook with GPU for 6000 episodes of 100

timesteps with a replay memory size of 500. The net-

work weights are updated by selecting random sam-

ples from replay memory with a batch size of 32 and

computing the expected accumulated discounted re-

ward with discount factor γ = 0.9. The DRL agent

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks

581

follows an ε-greedy strategy with ε annealed linearly

from 1 to 0.01, and the learning rate of the optimizer

is set to 1 × 10

−4

6.3 Results

After training, we generate maintenance plans for

a planning horizon of 100 years for all 942 pipes.

For the ﬁrst year, the DRL+GCN maintenance plan

proposes to replace most of the pipes because ini-

tially, the average pipe age is 48 years, causing low-

reliability levels. This is because the probability of

failure of pipes is based on failure rates and the cur-

rent age of the pipe. When most pipes are replaced,

the reliability becomes very high, as can be seen by a

peak in Figure 5a. Then, as the reliability decreases

over the years, the number of rehabilitation actions

starts to increase, resulting in higher yearly costs, as

shown in Figure 6a. Also, note that the DRL+GCN

agent suggests frequent interventions in a planning

horizon resulting in a steady reliability level and to-

tal intervention costs, as can be noted in Figure 3.

One of the key goals to employ GCN with DRL

is to achieve intervention grouping to optimize main-

tenance plans. A group is deﬁned as a set of pipes

such that edges connect the corresponding nodes in

the graph. The higher the number of pipes per group,

the more rehabilitation activities are concentrated in

a smaller amount of different geographical locations,

resulting in less setup and transportation costs as

shown in (Rokstad and Ugarelli, 2015; Pargar et al.,

2017). The GCN creates a plan in which 56% of

the groups have more than one pipe, resulting in an

average of 2.74 pipes per group across 100 years

(see Table 1). An example of grouping produced by

Figure 4: Example of a grouping of interventions on pipes

that are close to each other, produced by the DRL+GCN

approach for year 50 of the maintenance plan.

the DRL+GCN approach is shown in Figure 4. We

present a comparison with baselines in the following

section.

6.4 Baseline Comparison

We compare the proposed DRL+GCN approach with

four other baselines. Table 1 provides the compari-

son of all the considered approaches. The costs dis-

played are the values produced by the reward func-

tion. This includes the costs of the actions themselves,

bonus values for grouped rehabilitation, and penal-

ties for both unnecessary interventions and poor re-

liability while no intervention is suggested. The strat-

egy with the lowest cost while maintaining an ade-

quate reliability level is preferred. The greedy ap-

proach shows the highest average reliability, but it is

also signiﬁcantly more expensive than the two DRL-

based strategies. Maintain-10 does not perform well

in terms of both cost and reliability. The corrective ap-

proach (Replace) gives relatively low reliability while

also incurring high costs. Although the replace strat-

egy shows the least number of interventions, the over-

all reliability of the network is also low because pipes

deteriorate until they fail, incurring higher costs.

(a) DRL approach.

(b) Preventive approach.

Figure 5: Mean reliability per year for each strategy.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

582

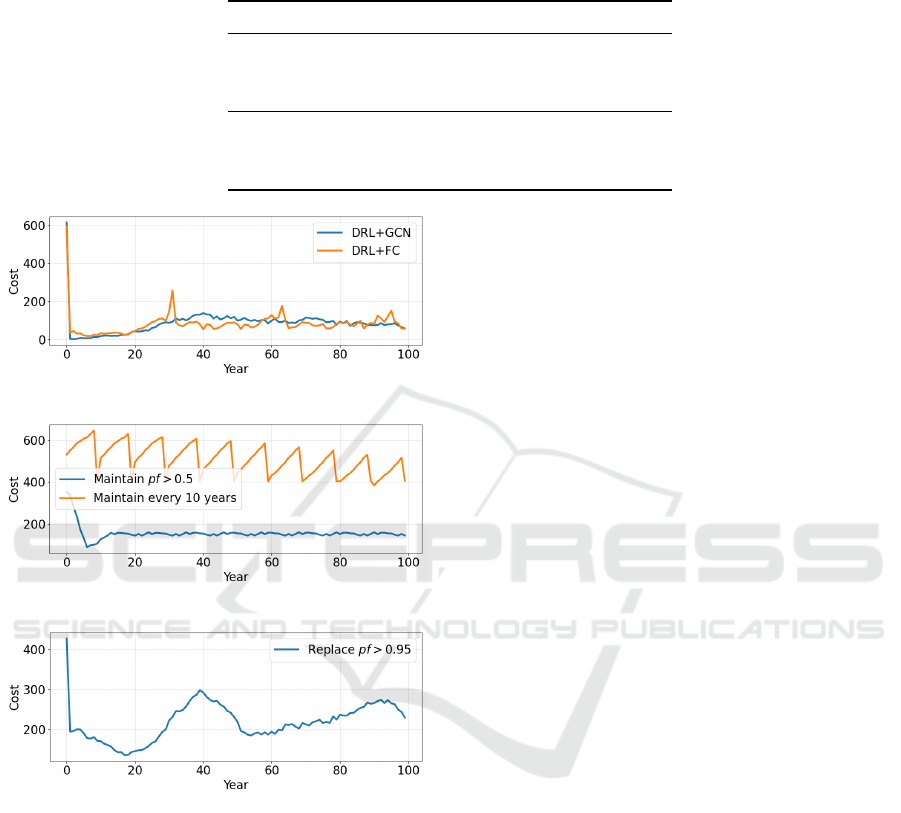
Table 2: Breakdown of total costs of each action for the DRL approaches with GCN and fully-connected (FC) layer over

100 years, as computed with the reward function. The highest costs are caused by doing nothing, incurring penalties for low

reliability levels. Without the penalties, the GCN approach performs signiﬁcantly better than the FC method.

GCN FC

Cost of maintenance actions 683.6 1451.2

Cost of replacement actions 2332.4 1752.3

Cost of do nothing actions/penalties 5346.0 4873.0

Total cost based on reward function 8362.0 8076.5

Total without action ‘nothing’ penalties 3016.0 3203.5

Total without any penalties or bonus 3196.0 3491.8

(a) DRL approach.

(b) Preventive approach.

Figure 6: Total cost per year for each strategy, as computed

by the reward function.

We provide a detailed comparison of DRL+GCN

and DRL+FC approaches. The GCN favors replace-

ment actions, while FC prefers maintenance. Figure

3 shows the costs per year of each action according

to the reward function. The FC chooses actions ac-

cording to a recurring pattern where the pipes age and

deteriorate to the point that the reliability becomes too

low, triggering many interventions simultaneously. In

contrast, the GCN approach spreads the interventions

more realistically over the years, resulting in a more

stable reliability level and fewer yearly cost ﬂuctua-

tions compared to the FC plan. This is also aligned

with real budgeting of infrastructure agencies where

a limited budget is available for rehabilitation activi-

ties each year (Rokstad and Ugarelli, 2015; Li et al.,

2011). Stable annual costs are therefore desirable.

A maintenance plan with ﬂuctuating costs that cause

the budget to be only partially utilized in some years,

while causing a deﬁcit in other years, would be inefﬁ-

cient and unsuitable in practice. Furthermore, the FC

approach is likely to pose an additional risk of pipe

failure since the pipes deteriorate for a extended pe-

riod before any action is suggested. In the current

conﬁguration, the GCN approach is more expensive

mainly because of the ‘do nothing’-actions, which in-

cur penalties for pipes with low reliability. Figure 3d

shows that for GCN, these yearly penalties get to a

peak and then gradually decrease. For the FC plan,

however, the same pattern keeps repeating without

improvement. When only the costs for maintenance

and replacement without penalties are taken into ac-

count, the GCN is less expensive, as shown in table

Figure 5 and 6 provide an overview of averaged

reliability and cost per year for the complete plan-

ning horizon. It is noted that the greedy approach

shows overall high reliability, but it is substantially

more expensive compared to other approaches. Our

DRL+GCN approach is second in terms of aver-

aged reliability and costs. Besides, we also com-

pare metrics related to the grouping of intervention

actions for the DRL approaches. Taking all metrics

from Table 1 into account, we see that although the

DRL+GCN strategy is slightly more expensive than

the simpler variant DRL+FC, it provides better relia-

bility, a higher degree of grouping, and fewer number

of interventions.

7 CONCLUSIONS AND FUTURE

WORK

This work presents a deep reinforcement learning

framework that combines DDQN and GCN for the re-

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks

583

habilitation planning of sewer pipes. The DRL agent

learns an improved policy in terms of lower cost and

higher reliability and uses GCN to leverage the rela-

tional information encoded in the graph structure of

the sewer network. Our framework is successfully

evaluated on a real dataset to show its potential for

applications in infrastructure maintenance planning.

The proposed approach is network and environment

agnostic, is not intended to solve the speciﬁc case

study described in this paper but to serve as a feasi-

bility study for applying the combination of deep rein-

forcement learning with graph neural networks for as-

set management problems. Different neural network

architectures can be plugged in, and the environment

can be easily modiﬁed with speciﬁc problem settings.

An asset deterioration model that more accurately

resembles reality remains an open problem for the fu-

ture. This includes a more sophisticated way of ex-

tracting/predicting fail rates and the use of additional

data sources to include geographic and demographic

data of the surrounding area, such as trafﬁc load, tree

density, and soil information of assets network. An-

other future problem is a reward function that better

accounts for different costs (e.g., replacement cost,

failure cost, unavailability costs) and asset-speciﬁc

aspects (e.g., material, length, impact on surrounding

infrastructure).

ACKNOWLEDGEMENTS

This research has been partially funded by NWO un-

der the grant PrimaVera NWA.1160.18.238.

REFERENCES

Ahmad, R. and Kamaruddin, S. (2012). An overview of

time-based and condition-based maintenance in in-

dustrial application. Computers & Industrial Engi-

neering, 63(1):135–149.

Almasan, P., Su

arez-Varela, J., Badia-Sampera, A., Rusek,

K., Barlet-Ros, P., and Cabellos-Aparicio, A. (2020).

Deep Reinforcement Learning meets Graph Neural

Networks: exploring a routing optimization use case.

arXiv:1910.07421 [cs]. arXiv: 1910.07421.

Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-

Gonzalez, A., Zambaldi, V., Malinowski, M., Tac-

chetti, A., Raposo, D., Santoro, A., Faulkner, R., Gul-

cehre, C., Song, F., Ballard, A., Gilmer, J., Dahl, G.,

Vaswani, A., Allen, K., Nash, C., Langston, V., Dyer,

C., Heess, N., Wierstra, D., Kohli, P., Botvinick, M.,

Vinyals, O., Li, Y., and Pascanu, R. (2018). Relational

inductive biases, deep learning, and graph networks.

Birolini, A. (2013). Reliability engineering: theory and

practice. Springer Science & Business Media.

Chen, Y. F., Everett, M., Liu, M., and How, J. P. (2017). So-

cially aware motion planning with deep reinforcement

learning. In 2017 IEEE/RSJ International Confer-

ence on Intelligent Robots and Systems (IROS), pages

1343–1350.

da Costa, P. R., Rhuggenaath, J., Zhang, Y., and Akcay,

A. (2020). Learning 2-opt heuristics for the traveling

salesman problem via deep reinforcement learning. In

Asian Conference on Machine Learning, pages 465–

480. PMLR.

Dai, H., Khalil, E. B., Zhang, Y., Dilkina, B., and Song,

L. (2018). Learning combinatorial optimization algo-

rithms over graphs.

Fey, M. and Lenssen, J. E. (2019). Fast graph represen-

tation learning with PyTorch Geometric. In ICLR

Workshop on Representation Learning on Graphs and

Manifolds.

Fontecha, J. E., Agarwal, P., Torres, M. N., Mukherjee,

S., Walteros, J. L., and Rodr

Aguez, J. P. (2021). A

two-stage data-driven spatiotemporal analysis to pre-

dict failure risk of urban sewer systems leveraging ma-

chine learning algorithms. Risk Analysis.

Garg, S., Bajpai, A., and Mausam (2019). Size Independent

Neural Transfer for RDDL Planning. Proceedings of

the International Conference on Automated Planning

and Scheduling, 29:631–636.

Hansen, B. D., Jensen, D. G., Rasmussen, S. H., Tamouk,

J., Uggerby, M., and Moeslund, T. B. (2019). General

Sewer Deterioration Model Using Random Forest. In

2019 IEEE Symposium Series on Computational In-

telligence (SSCI), pages 834–841.

Hu, L., Liu, Z., Hu, W., Wang, Y., Tan, J., and Wu,

F. (2020). Petri-net-based dynamic scheduling of

ﬂexible manufacturing system via deep reinforcement

learning with graph convolutional network. Journal of

Manufacturing Systems, 55:1–14.

Janisch, J., Pevn

y, T., and Lis

y, V. (2021). Symbolic Rela-

tional Deep Reinforcement Learning based on Graph

Neural Networks. arXiv:2009.12462 [cs]. arXiv:

2009.12462.

Joshi, C. K., Laurent, T., and Bresson, X. (2019). An ef-

ﬁcient graph convolutional network technique for the

travelling salesman problem.

Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).

Reinforcement Learning: A Survey. Journal of Artiﬁ-

cial Intelligence Research, 4:237–285.

Kipf, T. N. and Welling, M. (2017). Semi-supervised clas-

siﬁcation with graph convolutional networks.

Li, F., Sun, Y., Ma, L., and Mathew, J. (2011). A grouping

model for distributed pipeline assets maintenance de-

cision. In 2011 International Conference on Quality,

Reliability, Risk, Maintenance, and Safety Engineer-

ing, pages 601–606.

Li, Y. (2017). Deep reinforcement learning: An overview.

arXiv preprint arXiv:1701.07274.

Luong, N. C., Hoang, D. T., Gong, S., Niyato, D., Wang,

P., Liang, Y.-C., and Kim, D. I. (2019). Applica-

tions of Deep Reinforcement Learning in Communi-

cations and Networking: A Survey. IEEE Communi-

cations Surveys Tutorials, 21(4):3133–3174. Confer-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

584

ence Name: IEEE Communications Surveys Tutori-

als.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap,

T. P., Harley, T., Silver, D., and Kavukcuoglu, K.

(2016). Asynchronous methods for deep reinforce-

ment learning.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing.

Pargar, F., Kauppila, O., and Kujala, J. (2017). Inte-

grated scheduling of preventive maintenance and re-

newal projects for multi-unit systems with grouping

and balancing. Computers & Industrial Engineering,

110:43–58.

Petit-Boix, A., Roig

e, N., de la Fuente, A., Pujadas, P.,

Gabarrell, X., Rieradevall, J., and Josa, A. (2016). In-

tegrated structural analysis and life cycle assessment

of equivalent trench-pipe systems for sewerage. Wa-

ter Resources Management, 30(3):1117–1130.

Prates, M., Avelar, P. H. C., Lemos, H., Lamb, L. C., and

Vardi, M. Y. (2019). Learning to Solve NP-Complete

Problems: A Graph Neural Network for Decision

TSP. Proceedings of the AAAI Conference on Arti-

ﬁcial Intelligence, 33(01):4731–4738. Number: 01.

Puterman, M. L. (1994). Markov Decision Processes: Dis-

crete Stochastic Dynamic Programming. Wiley Series

in Probability and Statistics. Wiley.

Rokstad, M. M. and Ugarelli, R. M. (2015). Minimising the

total cost of renewal and risk of water infrastructure

assets by grouping renewal interventions. Reliability

Engineering & System Safety, 142:148–160.

Scheidegger, A., Hug, T., Rieckermann, J., and Maurer,

M. (2011). Network condition simulator for bench-

marking sewer deterioration models. Water Research,

45(16):4983–4994.

Sun, P., Lan, J., Li, J., Guo, Z., and Hu, Y. (2021). Combin-

ing Deep Reinforcement Learning With Graph Neu-

ral Networks for Optimal VNF Placement. IEEE

Communications Letters, 25(1):176–180. Conference

Name: IEEE Communications Letters.

Sutton, R. S., McAllester, D., Singh, S., and Mansour, Y.

(1999). Policy gradient methods for reinforcement

learning with function approximation. NIPS’99, page

1057–1063, Cambridge, MA, USA. MIT Press.

Tesauro, G. (1995). Temporal difference learning and td-

gammon. Commun. ACM, 38(3):58–68.

Tscheikner-Gratl, F., Caradot, N., Cherqui, F., Leit

ao, J. P.,

Ahmadi, M., Langeveld, J. G., Gat, Y. L., Scholten,

L., Roghani, B., Rodr

ıguez, J. P., Lepot, M., Stege-

man, B., Heinrichsen, A., Kropp, I., Kerres, K.,

do C

eu Almeida, M., Bach, P. M., de Vitry, M. M.,

Marques, A. S., Sim

oes, N. E., Rouault, P., Her-

nandez, N., Torres, A., Werey, C., Rulleau, B., and

Clemens, F. (2019). Sewer asset management – state

of the art and research needs. Urban Water Journal,

16(9):662–675.

van Hasselt, H., Guez, A., and Silver, D. (2015). Deep re-

inforcement learning with double q-learning.

Veli

ckovi

c, P., Cucurull, G., Casanova, A., Romero, A., Li

P., and Bengio, Y. (2018). Graph attention networks.

Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-

chine Learning, 8(3):279–292.

Weeraddana, D., Liang, B., Li, Z., Wang, Y., Chen, F.,

Bonazzi, L., Phillips, D., and Saxena, N. (2020). Uti-

lizing machine learning to prevent water main breaks

by understanding pipeline failure drivers.

Yan, Z., Ge, J., Wu, Y., Li, L., and Li, T. (2020). Automatic

Virtual Network Embedding: A Deep Reinforcement

Learning Approach With Graph Convolutional Net-

works. IEEE Journal on Selected Areas in Communi-

cations, 38(6):1040–1057. Conference Name: IEEE

Journal on Selected Areas in Communications.

Yin, X., Chen, Y., Bouferguene, A., and Al-Hussein, M.

(2020). Data-driven bi-level sewer pipe deterioration

model: Design and analysis. Automation in Construc-

tion, 116:103181.

Grouping of Maintenance Actions with Deep Reinforcement Learning and Graph Convolutional Networks

585