A Multi-stage Integer Linear Programming Problem for Personnel and

Patient Scheduling for a Therapy Centre

Georgia Fargetta

and Laura Scrimali

University of Catania, Department of Mathematics and Computer Science, Via Andrea Doria, 6, 95125, Catania, Italy

Keywords:

Personnel Scheduling, Assignment Problem, Mathematical Programming, Integer Programming.

Abstract:

In this paper, we propose a multi-stage integer linear programming problem to solve the scheduling of speech-

language pathologists involved in conventional treatments as well as in augmentative and alternative commu-

nication therapies. In order to reduce the complexity of this problem, we suggest a hierarchical approach that

breaks the problem into three sub-problems: patient selection for augmentative and alternative communica-

tion therapies, therapists’ shift assignment, and routing optimization of home-based rehabilitation services.

The resulting models were tested on data collected in a physiotherapy centre in Acireale (Catania, Italy),

using AMPL optimization package and Genetic Algorithm implemented in Matlab. From the results of the

case study, the model ensures to maximize the number of patients eligible for augmentative and alternative

communication therapies, to assign sustainable therapist schedule, and to optimize the home therapy routing.

1 INTRODUCTION

The nurse scheduling problem is one of the main is-

sues in healthcare system. It aims to assign a num-

ber of nurses to a number of shifts in order to sat-

isfy hospital demand (Van den Bergh et al., 2013).

Scheduling in healthcare is often planned manually

and it is time-consuming. Therefore, the automatic

assignment of shifts can lead to improvements in ef-

ﬁciency, personnel and patient satisfaction, and staff

workload.

This research aims at presenting the multi-stage inte-

ger linear programming problem for determining the

proper scheduling of speech-language pathologists.

The model is tested on a case study conducted in

a speech therapy centre in Acireale (Catania, Italy),

where qualiﬁed therapists are involved in conven-

tional treatments as well as in Augmentative Alterna-

tive Communication (for simplicity, AAC) therapies.

In addition, all the therapists, apart from the therapy

sessions at the centre, have to provide rehabilitation

services in patients’ homes. In this paper, we deal

with the following problems encountered by the per-

sonnel and patients of the speech therapy centre:

1. selection of patients for AAC therapy according

to their priority levels;

https://orcid.org/0000-0002-6444-1564

https://orcid.org/0000-0002-7652-4172

2. assignment of therapists’ shifts (for conventional

and AAC therapies) to optimize their workload;

3. planning of the routes/reducing time for the deliv-

ery of home-based therapy.

Therefore, we propose a hierarchical approach that

breaks the problem into three sub-problems: the se-

lection of the maximum number of patients for AAC

therapies, the achievement of an equitable distribu-

tion of therapists’ workload, and decrease in the trans-

fer time of therapists, who have to change location

during the working day, respectively (Ogulata et al.,

2008). The ﬁrst sub-problem is to determine the max-

imum number of patients beneﬁting from AAC ther-

apies, with respect to predetermined staff capacity.

Because of the extremely high demand of this ser-

vice, selection of patients must be done before the

scheduling. In this step, the selection of patients for

AAC treatment among the total number of patients is

made according to their priority decided by doctors.

In the second sub-problem, we minimize the penalty

of each soft constraint and, in particular, we ﬁnd the

optimal assignment of therapists’ shifts on weekdays

from Monday to Saturday. Thus, the important goal

of this study is to provide a balanced schedule for ev-

ery speech therapist. The AAC therapy is scheduled

throughout a week, in order to replicate what really

happens in the centre we analyzed. Finally, in the

third sub-problem, we determine the minimum cost

354

Fargetta, G. and Scrimali, L.

A Multi-stage Integer Linear Programming Problem for Personnel and Patient Scheduling for a Therapy Centre.

DOI: 10.5220/0010902500003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 354-361

ISBN: 978-989-758-548-7; ISSN: 2184-4372

on the journeys made by therapists so as to minimize

their travel time. The remainder of this paper is orga-

nized as follows. Section 2 is devoted to the related

literature. Section 3 presents the proposed method-

ology which encompasses parameters, model formu-

lation, and solution method. Section 4 describes the

case study and the numerical experiment results. Fi-

nally, Section 5 draws the conclusions and illustrates

further research issues.

2 RELATED WORK

The problem addressed in this paper relates to a model

described in (Ogulata et al., 2008), where a hierarchi-

cal mathematical programming problem is proposed

to generate weekly staff scheduling. The model is de-

composed into three hierarchical stages: the selection

of patients, the assignment of patients to the staff, and

the scheduling of patients throughout a day.

In the past years, several approaches were proposed,

such as tabu search (Burke et al., 2006), genetic al-

gorithms (Aickelin and Dowsland, 2004), learning

methodologies (Aickelin et al., 2007; Euchi et al.,

2020), scatter search (Burke et al., 2010), and mathe-

matical programming (Ogulata and Erol, 2003; Wolfe

and Young, 1965; Warner, 1976). The approach used

is to penalize the violation of the constraints in the

objective function. In real applications, it is often dif-

ﬁcult to ﬁnd feasible solutions. In (Legrain et al.,

2015), the authors study the scheduling process for

two types of nursing teams, regular teams from care

units and the ﬂoat team that covers for shortages in the

hospital. The corresponding multi-objective model

and heuristics are presented. In (El Adoly et al.,

2018), the authors study a nurse scheduling prob-

lem to minimize the overall hospital cost, and max-

imize nurses’ preferences, while taking into consider-

ation the governmental rules and hospital standards.

The mathematical model presented is based on multi-

commodity network ﬂow model. In (Berrada et al.,

1996; Bl

ochliger, 2004), a multi-objective approach

is introduced that differentiates between hard and soft

constraints. In (Valouxis and Housos, 2000), a non-

optimal solution is generated by solving the mathe-

matical model, and a post-optimization phase using

tabu search is performed. In (Wong et al., 2014), the

authors solve the nurse scheduling problem in a Hong

Kong emergency department with a two-phase heuris-

tic implemented in Excel. In (Shao et al., 2014), the

authors present an algorithm for supporting weekly

planning of therapists. In particular, it allows one to

match patient demand with therapist skills while min-

imizing treatment, travel, administrative and mileage

reimbursement costs. Solutions are found with a par-

allel Greedy Randomized Adaptive Search Procedure

(GRASP) that exploits a novel decomposition scheme

and employs a number of beneﬁt measures that ex-

plicitly address the trade-off between feasibility and

solution quality.

This paper is builds on the work of (Ogulata et al.,

2008), but with the following extensions: 1) in our

model all the patients receive basic treatments at the

centre and some of them are eligible for the AAC ther-

apy program; 2) only some therapists in the centre are

qualiﬁed to deliver AAC therapies; 3) AAC qualiﬁed

therapists may also deliver conventional treatments;

4) some patients (AAC and not) receive home-based

rehabilitation services.

3 PROPOSED METHODOLOGY

This section presents the assumption of the model and

the formulation. The assumptions of the model are

deﬁned as below:

• the number of patients eligible to start the AAC

program is known and ﬁxed;

• the number of therapists in the speech centre is

known and constant;

• the velocity of the vehicles used for delivering

home-based therapy is constant, and the trafﬁc

conditions are not taken into consideration.

The overall problem was broken down into three hier-

archical sub-problems, since it was rather difﬁcult to

solve the entire problem within an acceptable time for

even small size problem instances (Ogulata and Erol,

2003). The ﬁrst sub-problem, called “AAC patient se-

lection” aims to get the list of patients whose AAC

therapy will be scheduled for the following weeks.

These patients receive special therapies only from

qualiﬁed AAC therapists, while continuing with con-

ventional treatments delivered by the other therapists.

The second stage called ”Shift assignment” aims to

get the weekly shifts for both AAC and basic thera-

pists. Lastly, the third stage called ”Travelling thera-

pist problem” aims to get the best route of therapists

for delivering home-based sessions during a working

day. Mathematical programming models correspond-

ing to each stage are explained in detail in the follow-

ing subsections.

A Multi-stage Integer Linear Programming Problem for Personnel and Patient Scheduling for a Therapy Centre

355

3.1 Problem I: Augmentative

Alternative Communication Patient

Selection

The purpose of this stage is to select patients that will

be scheduled for the following weeks from the candi-

date list, considering therapists’ capacity and priority

of patients. The ﬁrst step of the process is then to de-

termine the maximum number of patients beneﬁting

from the AAC therapy, with respect to the predeter-

mined staff capacity. Moreover, patients may have

different priority levels. This difference must be in-

cluded in an efﬁcient scheduling plan. Priority of pa-

tients are categorized into three levels as high, normal,

and low according to specialized doctors. In addition,

AAC therapy sessions are longer than conventional

ones; hence, it is important to balance the distribution

of patients among therapists.

Indices and Parameters

• P: number of patients;

• p: patients index;

• w

: priority level of patients;

• t

: basic treatment time of pth patient;

• t

AAC

: AAC treatment time of pth patient;

• H: total weekly hours;

• T

AAC

: total weekly hours of AAC sessions.

Decision Variables. Decision variables at this stage

are deﬁned as followed;

(

1 if pth patient is selected,

0 otherwise.

Objective Function Problem I. In the objective

function (1), total number of selected patients is max-

imized considering priority factor of patients.

max

∑

p=1

(1)

Subject to:

∑

p=1

AAC

) ≤ H; (2)

≤ 1.5, ∀p ∈ P; (3)

∑

p=1

AAC

≤ T

AAC

; (4)

Constraint (2) ensures that the total sum of the therapy

times for all patients must not exceed the total time

available in a working week. Inequality (3) expresses

that each patient does an hour and a half weekly each

basic treatment. Finally, inequality (4) establishes

that the sum over all the time for all AAC patients is

less or equal than the total hours devote to AAC ses-

sions per week. We remark that when patients com-

plete the AAC program, it is necessary to update the

list of eligible ones, and a new optimal selection is

performed.

3.2 Problem II: Shift Assignment

In this section, we present the second sub-problem in

which we focus on the planning of the shifts. The as-

signment of shifts is based on the schedules and the

availability of the therapy centre to which we are re-

ferring. In particular, we differentiate the shifts in

the following way: the morning shift, the afternoon

shift and the shift for AAC therapy, during the work-

ing week from Monday to Saturday, excluding Sat-

urday afternoon. The shift assignment is going to be

the same and is repeated for each week. Some pa-

tients change as the weeks change but the number of

patients in the ﬁrst sub-problem can be catered for ev-

ery week. The aim of this sub-problem is to minimize

the sum of all the deviations of the soft constraints,

multiplied each by an appropriate weight.

Indices

• C = {1, . . . , c} set of therapists working for the

AAC program.

• T = {c + 1, . . . , t} set of shift workers.

• I = C ∪ T = {1, . . . i, . . . , t} set of the total number

of therapists in the centre.

• L = {1, 2, 3} set of shifts, with the typical element

of the set denoted by l, where

– l = 1 = M : morning shift;

– l = 2 = A : afternoon shift;

– l = 3 = AAC : AAC shift.

• J = {1, . . . , j, . . . , 6} set of working days.

The days will be identiﬁed as follows:

– j = 1: Monday;

– j = 2: Tuesday;

– j = 3: Wednesday;

– j = 4: Thursday;

– j = 5: Friday;

– j = 6: Saturday.

• S: set of soft constraints;

• W

: weight parameter ∀s ∈ S assigned to each vi-

olation of soft constraints.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

356

Decision Variables

i jl











1 if the therapist i is assigned to the shift l

on the day j,

0 otherwise.

Hard Constraints

∑

i∈C

i j3

= 2, j = 2, 4; (5)

∑

i∈I

i22

≥ 3; (6)

∑

i∈I

i51

≥ 1; (7)

∑

l∈L

i jl

= 1, ∀i ∈ C, j ∈ J; (8)

i j1

+ X

i j2

= 1, ∀i ∈ T, j ∈ J; (9)

i62

= 0, ∀i ∈ I; (10)

i j2

= 0, ∀i ∈ C, j = 2, 4; (11)

i j3

= 0, ∀i ∈ T, ∀ j ∈ J (12)

i j3

= 0, ∀i ∈ C, j = 1, 3, 5; (13)

∑

j∈J

i j3

≥ T

AAC

, ∀i ∈ C; (14)

Constraint (5),(6) and (7) ensure that two therapists

are required for AAC shifts, three therapists are re-

quired for Tuesday afternoons and one for Friday

mornings, respectively. Constraints (8) and (9) state

that each therapist only has to do one shift a day. Con-

straint (10) speciﬁes that the centre is closed on Sat-

urday afternoon. Constraints (11) and (13) state that

each AAC therapist has not to do afternoon shift on

Tuesday and Thursday, and has not to do AAC shift

on Monday, Wednesday and Friday. Constraint (12)

ensures that shift workers have not to do AAC shift.

Finally, inequality (14) establishes that the therapists

have to do at least T

AAC

hours per week. We empha-

size that we set the constraints according to the spe-

ciﬁc centre under consideration. They can be modi-

ﬁed as needed and adapted to other situations.

Soft Constraint. Now, we present the soft con-

straints and introduce the variables that take into ac-

count the deviations of the constraints from their pre-

determined goals. These variables will then be min-

imized in the objective function in order to obtain

the best possible solution, trying to reduce the devi-

ations from these constraints. We denoted by d

≥ 0,

si j

≥ 0 and d

si j

≥ 0, d

−

≤ 0 the positive and the neg-

ative deviations, respectively, associated to the soft

constraint s ∈ S, i ∈ I and j ∈ J.

The soft constraints are the following:

∑

j∈J

i j2

+ X

i j2

) + 6

∑

j∈J

i j3

+ d

≥ 36, ∀i ∈ C;

(15)

∑

j∈J

i j3

− d

−

≤ 18, ∀i ∈ C; (16)

∑

j∈J

i j2

+ X

i j1

) + d

≥ 36, ∀i ∈ T ; (17)

i j3

+ X

i( j+1)1

− (d

4i j

+ d

−

4i j

) = 1, ∀i ∈ C, j ∈ J

(18)

i j2

+ X

i( j+1)2

− (d

5i j

+ d

−

5i j

) = 1, ∀i ∈ T, j ∈ J

(19)

i j1

+ X

i( j+1)1

− (d

6i j

+ d

−

6i j

) = 1, ∀i ∈ T, j ∈ J

(20)

Constraint (15) and (16) establish that it is preferable

that the therapists do at least thirty six hours a week.

Constraint (18) states that is preferable that the ther-

apists do no more than eighteen hours per week of

AAC sessions. Finally, equalities (17), (19) and (20)

ensure that is preferable that they do not have two con-

secutive mornings or afternoons.

Objective Function Problem II. The overall ob-

jective function to be minimized is given by the sum

of all the deviations of the soft constraints described

above, each multiplied by an appropriate weight, cho-

sen on the basis of the importance of the violated con-

straint.

min



∑

i∈C

∑

i∈C

−d

−

∑

i∈T

∑

i∈C

∑

j∈J

4i j

− d

−

4i j

) +W

∑

i∈T

∑

j∈J

5i j

− d

−

5i j

)

∑

i∈T

∑

j∈J

6i j

− d

−

6i j

)



; (21)

The minimization of the objective function, subject to

the constraints already described, guarantees a solu-

tion that satisﬁes all the hard constraints and violates

the soft constraints as little as possible.

3.3 Problem III: Travelling Therapist

Problem

In this section, we optimize the routing from one loca-

tion to another one during the working day. The prob-

lem can be deﬁned as an asymmetric multiple Trav-

eling Salesman Problem with Time Windows (mT-

SPTW) (Bektas, 2006), and additional constraints,

such as an upper bounded variable of the number of

therapists, and the maximum traveling time or dis-

tance of each therapist. We also include time window

A Multi-stage Integer Linear Programming Problem for Personnel and Patient Scheduling for a Therapy Centre

357

at each location. Usually, the mTSP is speciﬁed as an

integer programming formulation.

Sets and Parameters

• G = (V, E);

• V = {v

, . . . v

, . . . , v

} set of vertices;

• E = {(v

, v

)} set of edges, which satisfy the sym-

metric property;

• I = {1, . . . i, . . . , t} set of the total number of ther-

apists in the centre, where i is the general one;

• TW indicates the time window. It is important to

remark the role of this parameter as each therapist

takes at least 2 hours for home-based therapies

(considering transfer time and therapy session),

before leaving for a new destination. Morevoer,

the daily working hours are limited.

• ˆc

, where ˆc

= c

+ c

is the total cost con-

sidered;

• c

ordinary cost (distance or duration) associated

with E. The costs could be symmetric if c

= c

∀(v

, v

) ∈ E and asymmetric otherwise;

• c

cost of the time window TW , where every

therapist has to do the therapy in each location,

which takes about 2 hours;

•

I upper bound of the therapist i, namely, the ac-

tual number of therapist used, i.e. the number of

available therapists;

• c

cost of the involvement of a therapist i ∈ I, i.e a

ﬁxed cost aiming to minimize their number;

• D maximum length of any tour in the solution.

Decision Variables

hki

(

1 if therapist i chooses the edge(v

, v

0 otherwise.

Objective Function Stage III

min

∑

h=0

∑

k=0

ˆc

∑

i=1

hki

+t · c

(22)

Subject to

∑

h=0

∑

i=1

hki

= 1, ∀k = 1, . . . , n, (23)

∑

k=0

∑

i=1

hki

= 1, ∀h = 1, . . . , n, (24)

∑

h=1

∑

i=1

1ki

= t, ∀k = 1, . . . , n, (25)

∑

k=1

∑

i=1

h1i

= t, ∀h = 1, . . . , n, (26)

∑

h=1

∑

k=1

· y

hki

≤ D, ∀i ∈ I (27)

+ sub tour elimination constraints (28)

The objective function (22) represents the mini-

mization of the cost of the journey, where ˆc

is ex-

pressed as a weight on each edge, based on the dis-

tance or the cost of the journey, and c

is the cost of

involvement of the therapist i. Constraints (23) and

(24) state that in each node v

only one edge enters

and exits ∀h, k = 1, . . . n. Constraints (25) and (26)

are the usual assignment constraints for the starting

and the ending point, using the binary variable. Con-

straints (27) ensures that the tour length of each ther-

apist is under the speciﬁed bound D.

4 CASE STUDY

In order to apply our models, a data set of the speech

therapy centre of Acireale, Sicily (Italy) is used. In

this centre, there are two therapists assigned to work

on the AAC project and six conventional therapists,

who are working 6 days a week for 6 hours a day. To

solve the mathematical models, AMPL and CPLEX

solver for the ﬁrst and the second problem and GA

Matlab code for the third problem were used.

4.1 Problem I

In this stage, priority of patients, which was cate-

gorized into three levels as high, medium, and low,

according to specialized doctors’ view, is reﬂected in

the model. Determination of these weights (w

) for

each priority level depends on the decision maker’s

preferences. The difference between the weights

for different levels of priorities should be selected

large enough to maintain a certain hierarchy between

priorities. Our selection of weights is just a case

for an illustration of the model. We ﬁxed w

= 0.8,

= 0.5 and w

= 0.2 for high, medium and low

level, respectively. We considered the number of

patients equal to 50, (P = 50), who ask to participate

in the AAC program in addition to basic therapy. This

particular therapy can only be carried out by some

therapists because the staff must be qualiﬁed for this

additional therapy. In fact, Table 1 shows that only

21 patients were selected among those who asked to

participate in the special AAC program, as a conse-

quence the following Table 1 represents the patients

that are selected for the AAC treatment, considering

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

358

only the two therapists who are involved in the

AAC shift. Unselected patients are not ignored, but

will continue to be followed through basic therapy,

because they do not have severe language difﬁculties

and do not urgently need additional therapy.

Table 1: Selected Patients Number.

Weight Patient i Selected

= 0.2

1 0

15 0

= 0.5

16 1

26 1

27 0

40 0

= 0.8

41 1

50 1

In this case study, the treatment time was classi-

ﬁed into two categories; t

and t

AAC

were assigned to

symbolize basic treatment (45 min) and AAC treat-

ment (≥ 60 min), respectively. Finally, we ﬁxed 24

weekly hours dedicated to basic therapy by each AAC

therapist and 12 hours carried out simultaneously by

both AAC therapists. Therefore the total hours avail-

able to AAC therapists is H = 60.

4.2 Problem II

In this stage, we considered two therapists i = 1, 2

who perform both basic shifts and AAC treatments

and six shift workers, i = 3, . . . 8. In the centre un-

der study, the weekly work is structured from Mon-

day to Friday, morning (M) and afternoon (A), and

on Saturday only in the morning. In particular, the

AAC treatment is carried out only on Tuesday, Thurs-

day and Saturday mornings, indicated with the index

l = 3. We remind that the centre is closed on Saturday

afternoons. In the objective function (21), we ﬁxed

= 0.84, W

= 0.3, W

= 0.58, W

= 0.88, W

0.67, W

= 0.68, which represent the weight associ-

ated with the soft constraint. The greater the weight,

the greater the importance of the soft constraint. We

ﬁxed t

= 0.75 and t

AAC

= 2 to deﬁne the following

constraint:

0.75x

≤ 1.5, ∀p ∈ P; (29)

∑

p=1

≤ 12. (30)

In Table 2, we provide the shifts for the eight ther-

apists that we have considered.

Table 2: Therapists’ shifts.

Morning Afternoon AAC

Mon 4, 7, 8 1, 2, 3, 5, 6

Tue 3, 5, 6 4, 7, 8 1, 2

Wed 7, 8 1, 2, 3, 4, 5, 6

Thu 3, 4, 5, 6 7, 8 1, 2

Fri 7, 8 1, 2, 3, 4, 5, 6

Sat 3, 4, 5, 6, 7, 8 closed 1, 2

4.3 Problem III

In this subsection we investigate the problem of mov-

ing from one location to another one considering ﬁxed

time windows. In fact, during the working day, ther-

apists have to move from one therapy centre to an-

other one, from one centre to another location to de-

liver home-based rehabilitation services, or from one

house to another one. We considered

I = 8 ther-

apists, who have the starting point at the centre of

Acireale and we supposed that patients’ houses are in

the other locations considered, to simulate that some

therapies are carried out directly at home. The cor-

responding multiple traveling salesmen problem was

implemented using the genetic algorithm with multi-

chromosome representation as in (Kir

aly and Abonyi,

2015). The algorithm considers that each therapist

starts at the ﬁrst location, and ends at the ﬁrst loca-

tion, but travels to a unique set of cities in between.

We assume that the ﬁrst location is the central location

placed in Acireale, Italy, then each therapist has her

own patients in different places. As a consequence,

except for the starting point, each location is visited

by exactly one therapist. The algorithm uses a special,

so-called multi-chromosome genetic representation to

code solutions into individuals. Special genetic oper-

ators (even complex ones) are used. The number of

therapists that every day have to travel from one lo-

cation to another is minimized during the algorithm.

The algorithm also considers additional constraints,

such as the minimum number of locations that the

therapists visit and the maximum distance travelled

by each therapist. We ﬁxed D = 80 kilometers as the

maximum tour length for each therapist, since a work-

ing day lasts only six hours. We considered the objec-

tive function (22), where the weights, considered as

distances and costs, associated with the edges, are de-

ﬁned as

A Multi-stage Integer Linear Programming Problem for Personnel and Patient Scheduling for a Therapy Centre

359

− x

)

+ (y

− y

)

, ∀v

, v

∈ V. (31)

We solved this problem using a genetic algorithm

(GA), implemented in Matlab (Kir

aly and Abonyi,

2015), tested on MacBook Air (2021), processor Ap-

ple M1 8 Core, 3.2 GHz, RAM 8 GB.

For instance, we obtained the total distance traveled

by all the therapists equal to 379 kilometers, obtained

by 474 number of iterations and 19 time in millisec-

onds until the solution was given. The following plots

explain better the solution reached.

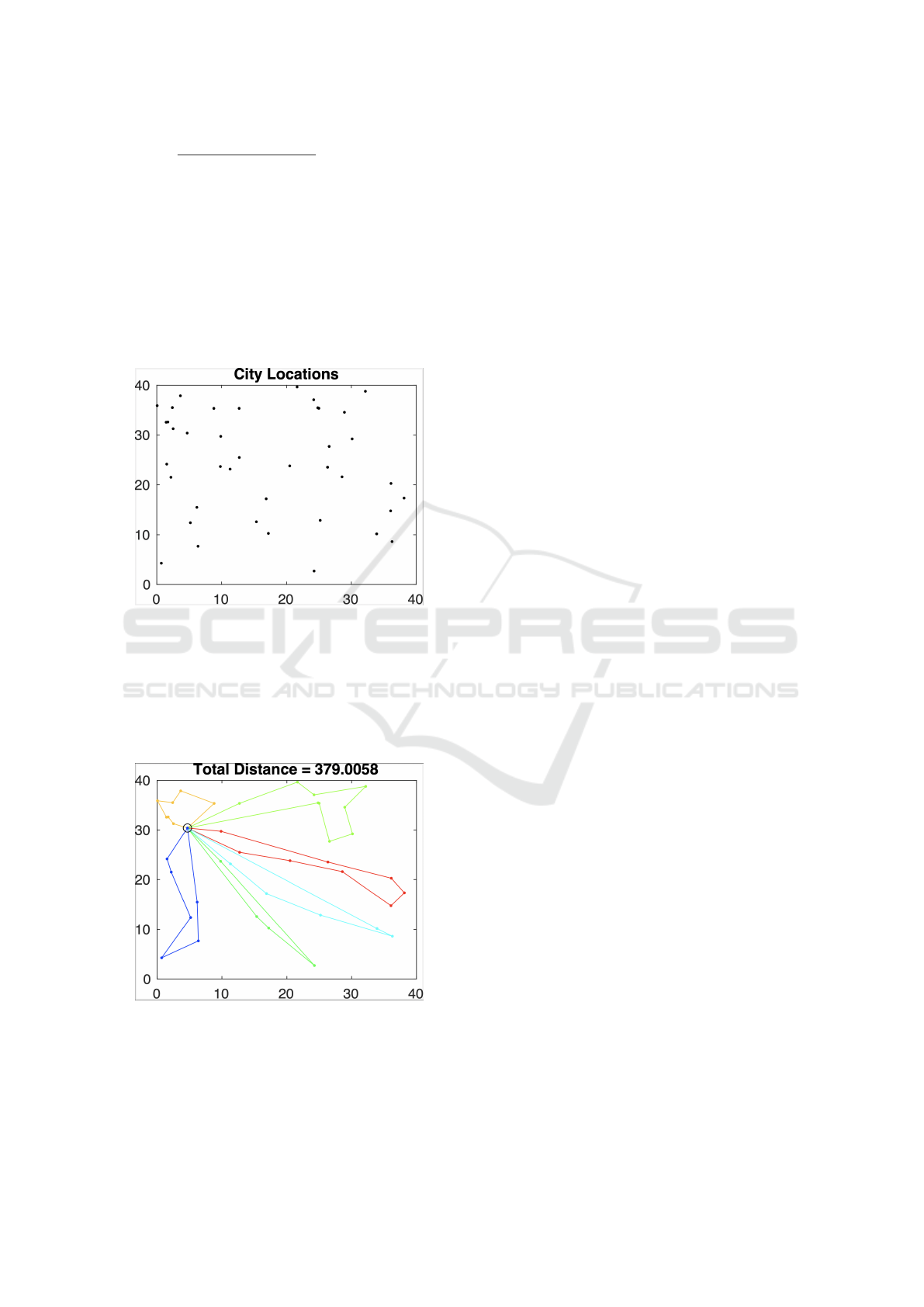
Figure 1: City Locations.

Figure 1 represents the different 40 locations cho-

sen in the example. It is necessary that therapists

move from one location to another, because some

therapies, especially on younger people, are carried

out in places where they spend a lot of their life, for

example at home or in parks or even at school.

Figure 2: Total Distance.

Figure 2 shows the routes solution of each thera-

pist. As a conclusion, we underline that the minimum

number of therapists needed to reach all the 40 lo-

cations in one day is six. As a consequence of the

six hours a day of each therapist, the time spent for

travel inﬂuence the number of patients that could be

treated. The Figure 2 underlines that some therapists

are forced to face even long distances on a daily basis

to satisfy the request of their patients.

5 CONCLUSIONS

This paper presented a multi-stage integer linear pro-

gramming problem to solve the scheduling of speech-

language pathologists involved in conventional treat-

ments as well as Augmentative Alternative Commu-

nication therapies. In order to reduce the complexity

of this problem, we developed a mathematical model

based on a hierarchical approach. Thus, the prob-

lem was broken down into three sub-problems. Our

aims were: the selection of the maximum number of

patients, who can use the Augmentative Alternative

Communication therapy program in addition to basic

therapy; the achievement of an equitable distribution

of therapists’ workload to optimize work shifts and

distribute them optimally during the week; the de-

crease of the time-wasting of therapists during trans-

fers, who have to move for home-based therapies and

have to change location during the working day. The

model was tested on a therapy centre and the solution

time was acceptable for the hierarchical implementa-

tion, with AMPL optimization package and Genetic

Algorithm implementation in Matlab to ﬁnd the so-

lution in a faster way and to avoid the limitations of

AMPL software. The model presented has some lim-

itations that encourage us to further investigate the

problem and improve our achievements. In fact, we

did not take into consideration the preferences of ther-

apists about their shifts, and the staggered entry times

due to COVID-19 pandemic. As a future research,

we can also explore the model with a higher number

of therapists and patients.

ACKNOWLEDGEMENTS

The research was partially supported by the research

project “Programma ricerca di ateneo UNICT 2020-

22 linea 2-OMNIA” University of Catania. This sup-

port is gratefully acknowledged.

REFERENCES

Aickelin, U., Burke, E., and Li, J. (2007). An estimation of

distribution algorithm with intelligent local search for

rule-based nurse rostering. Journal of the Operational

Research Society, 58:1574–1585.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

360

Aickelin, U. and Dowsland, K. (2004). An indirect genetic

algorithm for a nurse scheduling problem. Computers

& Operations Research, 31:761–778.

Bektas, T. (2006). The multiple traveling salesman prob-

lem: an overview of formulations and solution proce-

dures. omega, 34(3):209–219.

Berrada, I., Ferland, J., and Michelon, P. (1996). A multi-

objective approach to nurse scheduling with both hard

and soft constraints. Socio-Economic Planning Sci-

ences, 30:183–193.

ochliger, I. (2004). Modeling staff scheduling problems.

a tutorial. European Journal of Operational Research,

158:533–542.

Burke, E., Curtois, T., Qu, R., and Van den Berghe, G.

(2010). A scatter search method- ology for the nurse

rostering problem. Journal of the Operational Re-

search Society, 61:1667–1679.

Burke, E., De Causmaecker, P., Petrovic, S., and Van den

Berghe, G. (2006). Meta-heuristics for handling time

interval coverage constraints in nurse scheduling. Ap-

plied Artiﬁcial Intelligence, 20:743–766.

El Adoly, A., Gheith, M., and Fors, N. (2018). A new for-

mulation and solution for the nurse scheduling prob-

lem: A case study in egypt. Alexandria Engineering

Journal, 57:2289–2298.

Euchi, J., Zidi, S., and Laouamer, L. (2020). A hybrid

approach to solve the vehicle routing problem with

time windows and synchronized visits in-home health

care. Arabian Journal for Science and Engineering,

45:10637—-10652.

Kir

aly, A. and Abonyi, J. (2015). Redesign of the supply of

mobile mechanics based on a novel genetic optimiza-

tion algorithm using google maps api. Engineering

Applications of Artiﬁcial Intelligence, 38:122–130.

Legrain, A., Bouarab, H., and Lahrichi, N. (2015). The

nurse scheduling problem in real-life. Journal of Med-

ical Systems, 39(160).

Ogulata, S., Koyuncu, M., and Esra, K. (2008). Personnel

and patient scheduling in the high demanded hospital

services: a case study in the physiotherapy service.

Journal of medical systems, 32(3):221–228.

Ogulata, S. N. and Erol, R. (2003). A hierarchical multi-

ple criteria mathematical programming approach for

scheduling general surgery operations in large hospi-

tals. Journal of Medical Systems, 27(3):259–270.

Shao, Y., Bard, J., Qi, X., and Jarrah, A. (2014). The trav-

eling therapist scheduling problem. IE Transactions,

47(7):683—-706.

Valouxis, C. and Housos, E. (2000). Hybrid optimization

techniques for the workshift and rest assignment of

nursing personnel. Artiﬁcial intelligence in Medicine,

20:155–175.

Van den Bergh, J., Jeroen, B., Bruecker Philippe, D., Erik,

D., and Boeck Liesje, D. (2013). Personnel schedul-

ing: A literature review. European Journal of Opera-

tional Research, 226:367–385.

Warner, D. (1976). Scheduling nursing personnel according

to nursing preference: a mathematical programming

approach. Oper. Res., 44:842–856.

Wolfe, H. and Young, J. (1965). Stafﬁng the nursing unit,

part i: Controlled variable stafﬁng. Nursing Research,

14(3):236–243.

Wong, T., Xu, M., and Chin, K. (2014). A two-stage heuris-

tic approach for nurse scheduling problem: A case

study in an emergency department. Computers & Op-

erations Research, 51:99–110.

A Multi-stage Integer Linear Programming Problem for Personnel and Patient Scheduling for a Therapy Centre

361