Predicting Trains Delays using a Two-level Machine Learning

Approach

Hassiba Laifa

, Raoudha Khcherif and Henda Ben Ghezala

RIADI Laboratory, ENSI, University of Manouba, Manouba, Tunisia

Keywords: Train Delay, Prediction, Machine Learning, Classification, Regression, LightGBM.

Abstract: Train delay is a critical problem in railway systems. A previous prediction of delays is a critical issue

advantageous for passengers to re-plan their journeys more reliably. It is also essential for railway operators

to control the feasibility of timetable realization for more efficient train schedules. This paper aims to present

a novel two-level Light Gradient Boosting Machine (LightGBM) approach that combines classification and

regression in a hybrid model. It was proposed to predict passenger train delays on the Tunisian railway.

The first level indicates the class of delay, where the delays are divided into intervals of 5 minutes ([0,5],

[6,10], …, [>60]), 13 classes in total were obtained. The second level then predicts the actual delay in minutes,

considering the expected delay class at the first level. This model was trained and tested based on the historical

data of train operation collected by the Tunisian National Railways Company (SNCFT) and infrastructure

characteristics. Our methodology consists of the following phases: data collection, data cleaning, complete

data analysis, feature engineering, modeling and evaluation. The obtained results indicate that the two-level

approach based on the LightGBM model outperforms the one-level method. It also outperformed the

benchmark models.

1 INTRODUCTION

Rail transport in Tunisia is regarded as a significant

mode of transportation for both goods and people.

The Tunisian rail network comprises 23 lines, 2165

km, 267 stations and stops. It also has 4 road-rail links

to promote bimodal passenger transport by

combining rail and road transport. This network

ensures daily 316 train runs including 246 passenger

trains

Punctuality is considered the primary measure of

the performance of a railway system and is an

essential factor for efficiency in the railway sector.

On the Tunisian railway, trains that had a delay more

significant than 15 minutes were considered delayed.

On the other hand, they were considered within the

given time frame if they had a delay of fewer than 15

minutes. Thus, the punctuality rate of trains

formulated by the Tunisian Ministry of transport =

(Number of trains-Number of trains> 15) / Number of

trains. For example, the punctuality of Tunisian

https://orcid.org/0000-0002-9290-2794

https://orcid.org/0000-0002-6874-1388

http://www.sncft.com.tn/

passenger trains in 2019 was only about 23%, which

is deemed deficient.

For the records registered by the SNCFT, these

delays have different causes, such as disruptions in

the operation flow, infrastructure problems

(construction work, repair work, accidents), and

weather conditions.

A late train is likely to propagate its delay with

other trains. Thus, managing these delays

(rescheduling) allows traffic managers to change the

direction of trains to use the rail network

appropriately. In this context, delay prediction is one

of the most significant challenges to improving traffic

management and dispatch. This prediction will

minimize delays and prevent problems in the railway

plan. It will also be of great help for passengers to

plan their itinerary according to their work, also for

traffic managers to reschedule the other trains.

Thus, this work aims to predict passenger train delays

in Tunisia. Therefore, this work presents a hybrid

classification–regression approach. A new method

Laifa, H., Khcherif, R. and Ben Ghezala, H.

Predicting Trains Delays using a Two-level Machine Learning Approach.

DOI: 10.5220/0010898300003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 737-744

ISBN: 978-989-758-547-0; ISSN: 2184-433X

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

737

called ‘‘two-level lightGBM’’ is proposed. At the

first level, a lightGBM classifier is applied to predict

the interval of delay ([0,5], [6,10] …). This level is

used to construct a new feature. The newly created

features should help improve the overall model

performance. A lightGBM regressor is used at the

second level to predict a delay in minutes considering

the predicted delay class at the first level. This model

was trained and tested using the historical data of train

operation collected by the SNCFT and infrastructure

characteristics information.

To validate this approach, it has been compared

with several benchmark approaches, including

random forest, support vector machine, artificial

neural network and xgboost. Furthermore, the two-

level approach was also applied to the benchmark

models to obtain a fair, balanced comparison. The

validation results indicate that the proposed two-level

lightGBM method outperforms these benchmark

approaches in prediction accuracy for both one-level

and two-level modeling. In addition, a 7%

improvement in the accuracy of the lightGBM model

after two-level modeling was observed. Additionally,

an amelioration in all benchmark models' accuracy

was observed after the two-level application.

This paper is organized as follows: We introduce

the predictive analytics process in the second section.

Section 3 presents previous research on machine

learning for passenger train delay prediction. Section

4 describes our methodology and the different phase

of its application. Then, in section 5, we evaluate the

proposed methodology and compare obtained results.

Finally, we finish this manuscript with concluding

remarks and our future perspectives in section 6.

2 PREDICTIVE ANALYTICS

Predictive analytics includes statistical models,

machine learning algorithms and data mining

techniques that analyze historical and real-time data

to predict future events. Predictive analytics play an

essential role in theory building, testing, and

assessing relevance. It includes two components: (1)

Predictive models, designed for predicting new/future

observations or scenarios. (2) Methods for evaluating

the predictive power (predictive accuracy) of a model

(Shmueli and Koppius, 2011). Predictive models

include (but are not limited to):

- Supervised learning: The input for training is

presented with a pair of examples containing

features (X1, X2, ..., Xn) and their desired target

(Y). The machine deals with labeled data,

meaning the target is predefined. The goal is to

learn a rule that maps inputs to outputs. It

involves two general methods, differs in the type

of target.

• Classification: the target has a

categorical data type (two or more

classes); for example, predict if the train

will be delayed or not.

• Regression: the targets are continuous,

for example, predict how many minutes

the train will be delayed.

- Unsupervised learning: the model work on its

own to discover and identify clusters or groups

of similar records (i.e., clustering methods such

as K-means, K-medoids, Fuzzy c-means). The

machine deals with unlabeled data, meaning the

target is not predefined.

This work aims to build a hybrid classification-

regression approach for trains delay prediction in the

Tunisian railway system.

3 RELATED WORKS

The railway transportation systems show significant

interest in machine learning and artificial intelligence

technologies to collect, process, and analyze large

amounts of data to extract useful information. To this

end, several works have tried to establish a

relationship between the delays of the trains and the

various characteristics of the railway system and

develop different methods to construct prediction

models. Our work focused on recent research that has

developed machine-learning models to address

passenger train delay prediction.

The artificial Neural Network (ANN) model has

been intensively used in the literature to address trains

delays prediction. The authors in (Yaghini et al.,

2013) used it to predict the delay of passenger trains

in Iranian Railways. Besides, (Bosscha, 2016) aims to

expect secondary delays in a railway network using a

recurrent neural network. ANN was the most accurate

method when applied and evaluated using the

decision tree model with and without adaboost, as

demonstrated in (Nilsson and Henning, 2018).

Predictive algorithms based on artificial neural

networks (Back-Propagation Neural Network

(BPNN), Wavelet Neural Network (WNN) and

genetic algorithms (BPNN optimized by Genetic

Algorithm (GA-BPNN) and WNN optimized by

Genetic Algorithm (GA-WNN)) were applied in (Liu

et al., 2017) for train arrival time prediction, the

results showed that the GA-BPNN is the more

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

738

efficient model. Support Vector Regression (SVR)

model is used for the first time in (Marković et al.,

2015) to analyze train arrival delays on the Serbian

railways where the SVR model outperformed the

ANN algorithm. The Linear Regression (LR) model

was used in (Li, Daamen and Goverde, 2016) to

predict the peak hour dwell times, while the k-nearest

neighbor (K-nn) model was employed to estimate the

off-peak-hour dwell times using data from Dutch

railway stations. Moreover, Random Forest (RF)

method was widely used in literature to predict trains

delays and has shown promising results. Three

different algorithms (Extreme Learning Machines

(ELM), Kernel Regularized Least Squares (KRLS)

and Random Forests (RF)) were applied in (Oneto et

al, 2016) to address train delay prediction problem

relying on data provided by the Italian railway system

and weather information. The performance

comparison indicates that RF consistently performed

the other algorithms. Besides, the random forest

outperformed the other evaluated methods in (Jiang

et al., 2019 ; Arshad and Ahmed, 2019 ; Li, Wen, Hu.,

Xu, Huang, and Jiang, 2020). Instead, the study

carried out in (Mou et al.,2019) proposed a Short-

Term Long Memory (LSTM) model to predict the

train arrival delay. Comparing its performance with

RF and ANN shows that the proposed model

outperformed the RF and ANN. Work in (Shi et

al.,2019) presents the first application of the Gradient

Boosting Regression Tress (GBRT) model to predict

train delay. The provided results demonstrate that the

proposed model based on GBRT had a higher

prediction precision and outperformed the SVR and

the RF models. Statistical analysis was applied in

(Kecman et al., 2015) to predict the lengths of running

and dwelling times using three global predictive

models, namely Robust Linear Regression (LTS),

Regression Trees (RT) and Random Forests (RF), and

local models applied in a particular train line, station

or block section, based on the LTS with some

refinements. These models were tested using delay

history data from Rotterdam and The Hague in the

Netherlands. The results indicate that the local

models gave better accuracy and computation time

results. A deep learning (DL) approach, namely CLF-

Net, which combines 3-Dimensional Convolutional

Neural Networks (3D CNN), Long Short-Term

Memory (LSTM) recurrent neural network, and

Fully-Connected Neural Network (FCNN)

architectures, was developed in (Huang et al.,2020) to

predict train delay of two high-speed rail (HSR) lines

in China.

Furthermore, some researches combine two or

more models, such as in (Lulli et al., 2018) where a

hybrid approach that combines the Decision Tree

(DT) and Random Forest regression (RF) was

proposed to predict the running time, the dwell, the

train delay, and the penalty costs. The authors in (Nair

et al., 2019) also addressed the problem of forecasting

train delays up to 24 h in advance by applying a data-

driven method that combines a set of simulation and

statistical approaches as an ensemble method. The

proposed method was tested using extensive data

from the train network of Germany, and the obtained

results demonstrate that the process based on

ensemble outperformed the component models.

Furthermore, a coupled classification–regression

model was proposed in (Nabian et al., 2019) where a

bi-level random forest was formed of: i) a random

forest classifier in the first level to predict whether a

train delay will increase, decrease, or remain

unchanged; and ii) a random forest regressor to

estimate delay in minutes given the predicted delay

class at primary level. Further, a two-stage prediction

model is built-in (Gao et al., 2020). The first stage

predicts the total buffer time of delayed trains in

sections and stations, and the second stage predicts

the recovery time of primary delay based on the first

stage results.

Our previous work (Laifa et al., 2021) presents

the first application of the LightGBM algorithm to

predict trains delays using real Tunisian railway

network data records. Our method based on

LightGBM regressor had outperformed the tested

models, namely ANN, XGBoost, RF and SVR.

We can conclude that different machine learning

methods have been widely used in train delay

predictions. However, the outperformed model

differs from one study to another, depending on the

used data case considering the unique features of

different railway networks.

4 PROPOSED APPROACH

To predict delays in the Tunisian railway system, we

proposed an approach that consists of four main steps

including:

• Data collection,

• Data preparation including data cleaning,

visualization and feature engineering.

• Modeling,

• Evaluation.

The proposed approach is presented in Figure 1.

Predicting Trains Delays using a Two-level Machine Learning Approach

739

Figure 1: Proposed approach.

4.1 Data Collection

The used database is collected from the National

Tunisian Railway Company (SNCFT). It consists of

12350 travel samples, from 1.1.2019 to 31/12/2019,

including 55 passenger trains and 4 main destinations

(Tunis-Nabeul, Tunis-Sousse, Tunis-Tozeur, Tunis-

Sfax). The dataset has the following features:

Table 1: Data features summary.

Features Definition

Trains

information

Train Unique code of each

train

Code_cir Running frequency

(daily, only Saturday

and Sunday, etc.

Infrastructure

information’s

Line The railroad took by the

train

Direction Railroad is a single-

track or a double-track.

Destination Departure station to

target station

Distance The traveling distance

Nbr_station Number of stations and

stops between the

departure and the target

Calendar

information’s

Date Date of travel

Weekday Day of travel (for

Monday to Sunday)

Holiday A boolean variable

indicates if the journey

is a holiday or not.

Month Month of travel (from

January to December)

Season Season of travel

(Winter, Spring,

Summer or Autumn)

Delays

information

Motifs The reason behind the

delay.

Departure

delay

It shows how much time

(in minutes) a train

takes to begin its new

journey after the

scheduled departure

time.

Departure

time

The time when the train

departed.

Arrival

time

The time at which the

train arrives at a given

station.

Arrival

delay

Reveals how much time

(in minutes) a train

takes to arrive after the

scheduled arrival time

(Our target variable).

4.2 Data Preparation

The collected data suffer from some problems that

why a cleaning step is inevitable to improve data

quality before model training. Therefore, we have

applied a cleaning operation set to solve the data

shortcomings in this phase. It deals with null values,

handling outliers and transforming incorrect format.

For null values, we dropped records with a null

value in Arrival_delay. The remaining was filled

either with the median in numerical feature (as to

outliers’ existence as observed in Figure 2) or with an

"Unknown" value if the feature was categorical.

Figure 2: Departure delay histogram.

Then we transformed the data type of departure

delay from an object into numeric. Finally, all

cleaning operations were executed using the Python

libraries.

Data cleanin

Data

aration

Data visualization

Features engineering

Data

Trains operations

records from

SNCFT

Modeling

Classification

New feature construction

Regression

Benchmarks

Evaluation

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

740

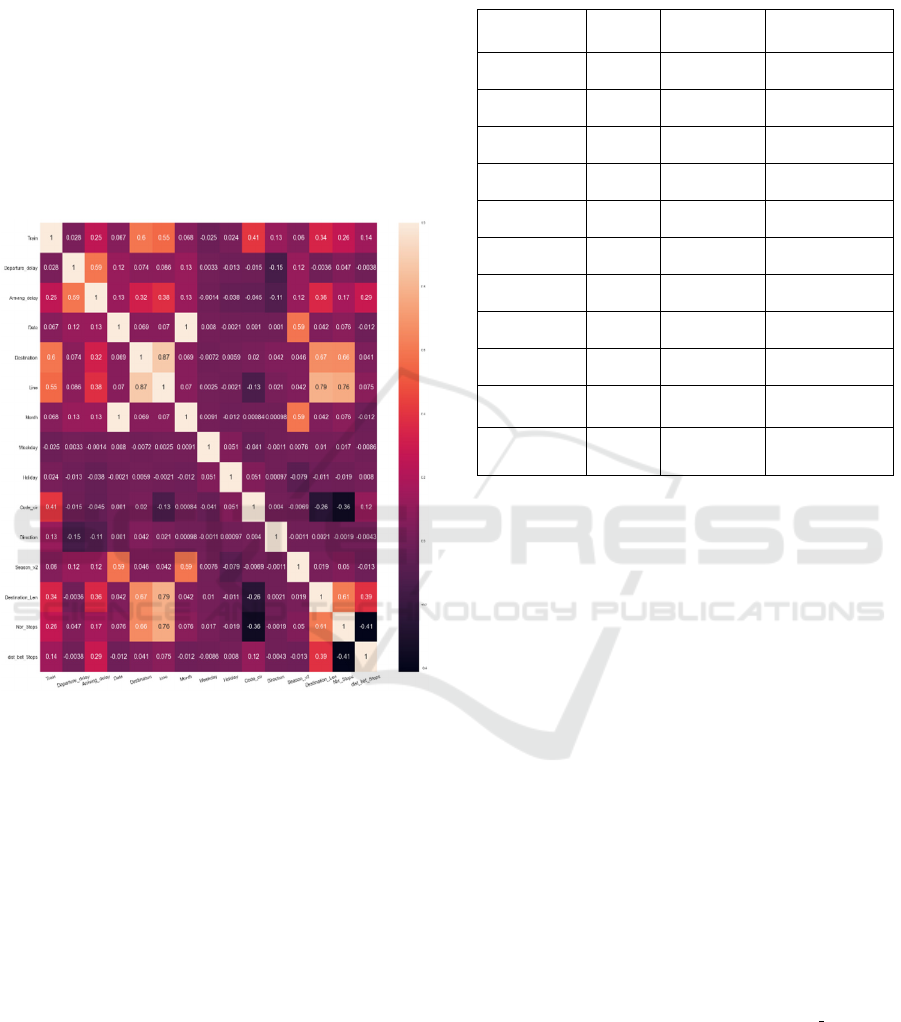
Where the cleaning step finished, we visualized

our data to understand better and find the features that

affect train delay. The data were evaluated in various

ways, including univariate, bivariate, and

multivariate analysis. For example, to discover the

relationship between all dataset features, we

implemented the correlation matrix following in

figure 3. The light color presents a strong correlation

between the variables corresponding to the x-axis and

the y-axis. The lighter the color of the square, the

more the correlation is positive. Conversely, the dark

color has a weak correlation, the darker the color of

the square, the more negative the correlation.

Figure 3: Correlation matrix.

Visualizations processes were applied using the

Python Library 'matplotlib'. Then, the features likely

to affect train delays were selected as the model

features (inputs(X)).

The model can only analyze digital data, for this,

a feature engineering phase is necessary to convert

the categorical columns into numerical values.

Therefore, we applied cyclic encoding to transform

cyclic variables (such as weekdays, months and

season), one-hot-encoding, presented by the

"get_dummies()" function, to convert categorical

variables that have fewer than five values and target-

encoding for the remaining categorical variables

(trains and motifs).

Table 2 summarize our feature engineering phase

where:

Cyclic-enc =

cyclic encoding,

One-h-enc =

one-

hot-encoding,

Target-enc =

target-encoding,

Type-tf =

type transformation, Cat =

categorical,

Flt = float, Obj =

object, Int = integer.

Table 2: Features engineering summary.

Features Initiate

type

Encoding

type

Pre-processing

type

Trains Cat Target-enc Flt

Motifs Cat Target-enc Flt

Destination Cat One-h-enc Int

Direction Cat One-h-enc Int

Line Cat One-h-enc Int

Weekday Cat Cyclic-enc Int

Month Cat Cyclic-enc Int

Season Cat Cyclic-enc Int

Holiday Cat One-h-enc Int

Departure

delay

Obj Type-tf Flt

Arrival

delay

Obj Type-tf Flt

4.3 Modeling

LightGBM algorithm (Ke et al., 2017) is a gradient

boosting framework that uses a histogram-based

decision tree learning algorithm. It is based on two

novel techniques: Gradient-based One-Side Sampling

(GOSS) and Exclusive Feature Bundling (EFB). With

GOSS, a significant proportion of data instances with

small gradients is excluded to reduce the number of

data instances. Only the rest is used to estimate the

information gain. However, the EFB, which consists

of bundling exclusive features, is employed to

effectively reduce the number of features.

It is considered an efficient model that can handle

large-scale data and achieve better accuracy with

faster training speed and minimum memory usage. It

also supports parallel and distributed learning.

From these advantages, LightGBM is widely used

in many research areas and has shown promising

results in different machine learning tasks.

Additionally, this algorithm was appropriately

applied in our study because most of the features in

our datasets had a categorical data type, and the

number of features was augmented after the features-

engineering step.

We proposed in this paper an approach that mix

lightGBM classifier and lightGBM regressor to

predict train delays. The following figure details the

Predicting Trains Delays using a Two-level Machine Learning Approach

741

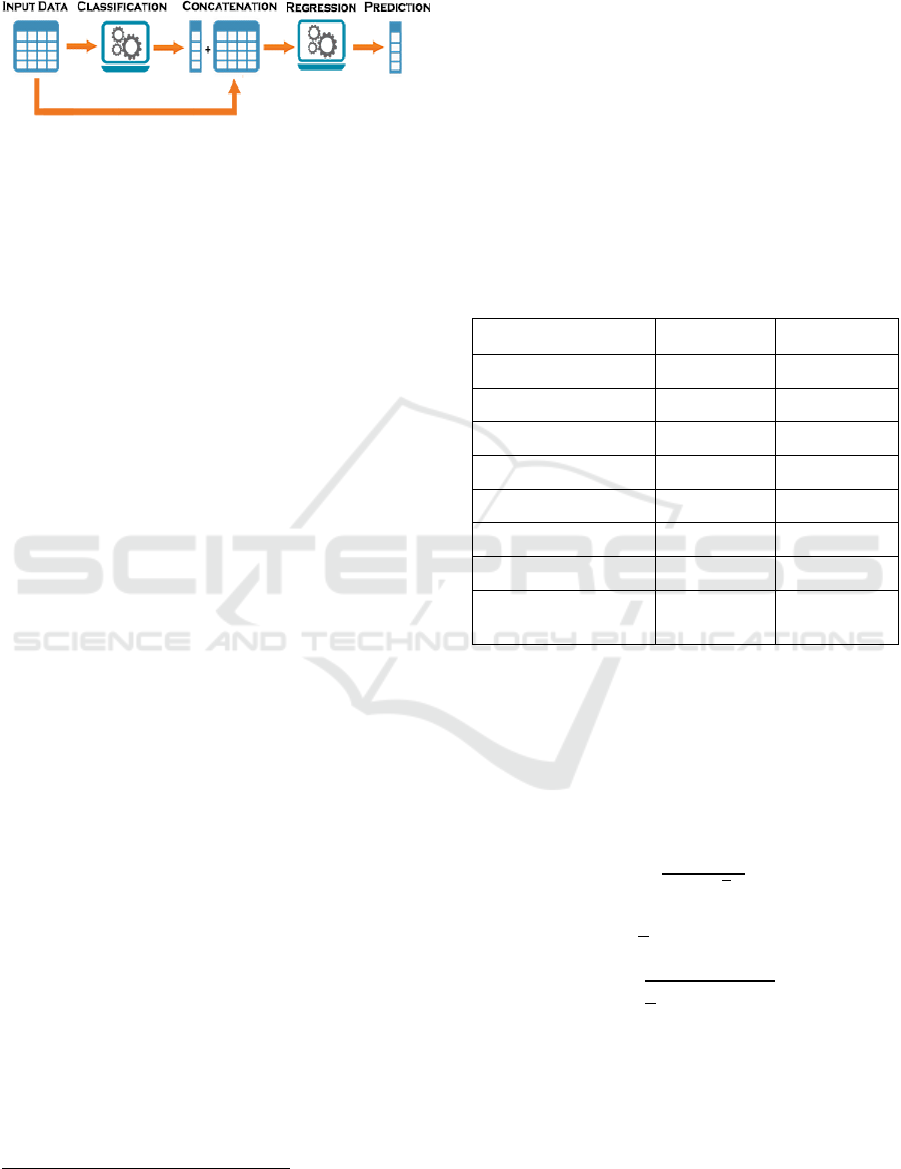
modeling phase, where the hybrid approach is

applied.

Figure 4: Two-level modeling.

• Classification:

This phase presents a novel contribution where we

proposed and implemented a classification model as

a first level of learning that classifies the delays in

intervals of 5 minutes.

After the cleaning and features engineering

phases, the obtained data are passed to classification

modeling, where we deployed a classification model

based on a lightGBM classifier algorithm that

classified the delays in intervals of 5 minutes ([0,5],

[6,10],…, [>60]), a total of 13 classes were obtained.

We chose short intervals so that the model is more

precise and that the information is not lost, i.e., a

delay between 0 and 5 and more accurate than a delay

between 0 and 10 or between 0 and 15.

Then, the predicted classes of all rows are added

to the initial data as a new feature.

• Regression:

In the second level of learning, we implemented a

regression learning based on a lightGBM regressor to

predict the delay in minutes. The new data include the

newly created features that should be useful in

improving the overall model performance at this level

of learning.

4.4 Evaluation

4.4.1 Benchmarks Models

To evaluate our proposed approach, we used the

following benchmarks models:

• Support Vector Regression (SVR) (Smola

and Schölkopf, 2004).

• Random forest (RFR) (Breiman, 2001).

• Extreme Gradient Boosting (XGboost)

(Chen and Guestrin, 2016).

• Artificial Neural Network (ANN) (Hopfield,

1988).

https://github.com/Microsoft/LightGBM

The processed data were separated into 80 % for

training and 20% for testing to apply the models. We

used the official python implementation of the

Lightgbm model

. All the experiments were

conducted on an I7 3.2 GHz 8-core CPU and 16 GB

of memory.

The default hyperparameters were applied in

LightGBM, XGBoost, Random Forest and SVM

models.

We applied testing values for the ANN

hyperparameters to choose the optimal one for each

hyperparameter. Table 3 summarizes all

combinations of hyperparameters values with the

optimal one.

Table 3: ANN hyperparameters summary.

Hyperparameter Tested values Optimal value

Epoch 50, 100, 150 150

Hidden layers 1, 2, 3 1

Input layer neurons 16,32,64, 128 64

Hidden layer neurons 16,32,64, 128 32

Batch Size 32, 50, 100 50

Drop-out 0, 0.1, 0.2 0.1

Activation Function / Relu

Optimization

Algorithm

/ Adam

4.4.2 Evaluation Metrics

Three evaluation factors were employed in this study

to evaluate the performance of the applied models,

namely R-squared (R²) (1), Mean absolute error

(MSE) (2) and Root Mean Squared Error (RMSE) (3).

These statistical parameters are defined as follows:





=1−

∑

(







)







∑

(



)







(1)

 =





∑|





−





(2)

 =







∑(





−

)







(3)

where n denotes the Number of target values y = (







, . . ., 



) and ŷ is the predicted value of y.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

742

5 RESULTS

Table 4 present the performance of the proposed

hybrid approach of the lightGBM algorithm (2L-

LGBM) in terms of R², MAE and RMSE in both

training and test data. As followed in the table, the

accuracy of the proposed approach reached 87% in

test data and as is observed, the training model hasn't

been overfitted in the learning process.

Table 4: Two-level LightGBM performance.

R² MAE RMSE

Training

87.83 6.10 11.91

Test

87.17 6.84 13.37

Our previous work (Laifa et al., 2021) presented a

one-level learning approach where we applied the

regression level directly. However, the actual work

differs from that with two levels of learning and the

input data of regression level has an additional

feature, namely “Interval” created by the first level.

Table 5 presents the results of our previous work

where the lightGBM regressor (LGBM) is compared

with Support Vector Machine regressor (SVM),

Random Forest regressor (RF), Extreme Gradient

Boosting regressor (XGB), Artificial Neural Network

regressor (ANN) algorithms using test data.

Table 5: One-level approaches performance.

Models R-squared Running time (s)

LGBM 80.31 0.67

ANN 78.92 45.41

RF 77.11 17.98

XGB 76.44 4.03

SVM 76.03 10.89

It is clear that the lightGBM outperforms the other

tested model in terms of R-squared and is the faster

one with minimum running time.

Table 6 compares the performance results when

applying the two-level modeling to all the tested

models in test data. Two-level LGBM (2L-LGBM),

two-level NN (2L-NN), two-level RF (2L-RF), two-

level XGB (2L-XGB), two-level (2L-SVM).

Observing Tables 5 and 6, we see that the

lightGBM model outperforms the benchmark models

in both one-level and two-level learning approaches.

We can also see by comparing Tables 5 and 6 that the

two-level approach of all models is accurate better

Table 6: Two-level results for all models.

Models R²

MAE RMSE

2L-LGBM 87.52 6.84 13.37

2L-ANN 81.26 9.30 16.15

2L-RF 83.77 7.81 15.03

2L-XGB 84.58 7.47 14.65

2L-SVM 80.55 9.35 16.46

than the one-level approach. Specially, around 7%

improvement in LightGBM model performance, 8 %

for XGBoost, 4% for SVM, 6% for Random forest

and 3% for ANN after two-level modeling.

6 CONCLUSION

We proposed in this paper a hybrid approach with two

levels of learning, namely a two-level system.

Primary level introduced in classification task that

constructs new feature to improve prediction

accuracy. In this level, the class of delay, categorized

in intervals of 5 minutes, is predicted. The new

feature was added to the initial dataset. The secondary

level presented in regression learning indicates delays

in minutes. The proposed approach was trained and

tested using historical data of train operation collected

by the SNCFT of Tunisia. It consists of four main

steps: data collection, data preparation; includes data

cleaning, visualization and feature engineering; two-

level modeling and evaluation. The statistical results

indicate that the approach based on two levels of

learning performs better than that one-level learning.

We also found that the model based on the lightGBM

algorithm outperforms all tested models in both two-

level and one-level learning. The prediction accuracy

of the proposed approach reached 87 %, which

improves the prediction accuracy effectively.

Our upcoming work will focus on

hyperparameters optimization and features selection

techniques for better performance; furthermore, we

will integrate external data sources that can impact

train delays, such as weather information, to improve

prediction accuracy.

REFERENCES

Arshad, M., & Ahmed, M. (2019). Train delay estimation

in Indian railways by including weather factors through

machine learning techniques. Recent Advances in

Computer Science and Communications, 12, 1-00.

Predicting Trains Delays using a Two-level Machine Learning Approach

743

Bosscha, E. (2016). Big data in railway operations: Using

artificial neural networks to predict train delay

propagation (Master's thesis, University of Twente).

Breiman, L. (2001). Random forests. Machine learning,

45(1), 5-32.

Chen, T., & Guestrin, C. (2016). Xgboost: A scalable tree

boosting system. Proceedings of the 22nd ACM sigkdd

international conference on knowledge discovery and

data mining (pp. 785-794).

Gao, B., Ou, D., Dong, D., & Wu, Y. (2020). A Data-Driven

Two-Stage Prediction Model for Train Primary-Delay

Recovery Time. International Journal of Software

Engineering and Knowledge Engineering, 30(07), 921-

940.

Hopfield, J. J. (1988). Artificial neural networks. IEEE

Circuits and Devices Magazine, 4(5), 3-10.

Huang, P., Wen, C., Fu, L., Peng, Q., & Tang, Y. (2020). A

deep learning approach for multi-attribute data: A study

of train delay prediction in railway systems.

Information Sciences, 516, 234-253.

Jiang, C., Huang, P., Lessan, J., Fu, L., & Wen, C. (2019).

Forecasting primary delay recovery of high-speed

railway using multiple linear regression, supporting

vector machine, artificial neural network, and random

forest regression. Canadian Journal of Civil

Engineering, 46(5), 353-363.

Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W.,

... & Liu, T. Y. (2017). Lightgbm: A highly efficient

gradient boosting decision tree. Advances in neural

information processing systems, 30, 3146-3154.

Kecman, P., & Goverde, R. M. (2015). Predictive

modelling of running and dwell times in railway traffic.

Public Transport, 7(3), 295-319.

Laifa, H., & Ghezalaa, H. H. B. (2021). Train delay

prediction in Tunisian railway through LightGBM

model. Procedia Computer Science, 192, 981-990.

Li, D., Daamen, W., & Goverde, R. M. (2016). Estimation

of train dwell time at shortstops based on track

occupation event data: A study at a Dutch railway

station. Journal of Advanced Transportation, 50(5),

877-896.

Li, Z., Wen, C., Hu, R., Xu, C., Huang, P., & Jiang, X.

(2020). Near-term train delay prediction in the Dutch

railways network. International Journal of Rail

Transportation, 1-20.

Liu, Y., Tang, T., & Xun, J. (2017). Prediction algorithms

for train arrival time in urban rail transit. In 2017 IEEE

20th International Conference on Intelligent

Transportation Systems (ITSC) (pp. 1-6). IEEE.

Lulli, A., Oneto, L., Canepa, R., Petralli, S., & Anguita, D.

(2018). Large-scale railway networks train movements:

a dynamic, interpretable, and robust hybrid data

analytics system. In 2018 IEEE 5th International

Conference on Data Science and Advanced Analytics

(DSAA) (pp. 371-380). IEEE.

Marković, N., Milinković, S., Tikhonov, K. S., &

Schonfeld, P. (2015). Analyzing passenger train arrival

delays with support vector regression. Transportation

Research Part C: Emerging Technologies, 56, 251-262.

Mou, W., Cheng, Z., & Wen, C. (2019). Predictive Model

of Train Delays in a Railway System. In

RailNorrköping 2019. 8th International Conference on

Railway Operations Modelling and Analysis

(ICROMA), Norrköping, Sweden, June 17th–20th,

2019 (No. 069, pp. 913-929). Linköping University

Electronic Press.

Nabian, M. A., Alemazkoor, N., & Meidani, H. (2019).

Predicting near-term train schedule performance and

delay using bi-level random forests. Transportation

Research Record, 2673(5), 564-573.

Nair, R., Hoang, T. L., Laumanns, M., Chen, B., Cogill, R.,

Szabó, J., & Walter, T. (2019). An ensemble prediction

model for train delays. Transportation Research Part C:

Emerging Technologies, 104, 196-209.

Nilsson, R., & Henning, K. (2018). Predictions of train

delays using machine learning.

Oneto, L., Fumeo, E., Clerico, G., Canepa, R., Papa, F.,

Dambra, C., ... & Anguita, D. (2016). Advanced

analytics for train delay prediction systems by including

exogenous weather data. In 2016 IEEE International

Conference on Data Science and Advanced Analytics

(DSAA) (pp. 458-467). IEEE.

Shi, R., Wang, J., Xu, X., Wang, M., & Li, J. (2019). Arrival

Train Delays Prediction Based on Gradient Boosting

Regression Trees. In International Conference on

Electrical and Information Technologies for Rail

Transportation (pp. 307-315). Springer, Singapore.

Shmueli, G., Koppius, O. R. (2011). Predictive analytics in

information systems research. MIS Quarterly, 553-572.

Smola, A. J., & Schölkopf, B. (2004). A tutorial on support

vector regression. Statistics and Computing, 14(3), 199-

222.

Yaghini, M., Khoshraftar, M. M., & Seyedabadi, M. (2013).

Railway passenger train delay prediction via neural

network model. Journal of advanced transportation,

47(3), 355-368.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

744