
Identifying Soft Cores in Propositional Formulæ
Gilles Audemard
a
, Jean-Marie Lagniez
b
, Marie Miceli
c
and Olivier Roussel
d
CRIL, Univ. Artois & CNRS, Lens, France
Keywords:
SAT, Explanation, #SAT, Max#SAT.
Abstract:
In view of the emergence of explainable AI, many new concepts intend to explain why systems exhibit cer-
tain behaviors while other behaviors are excluded. When dealing with constraints, explanations can take the
form of subsets having few solutions, while being sufficiently small for ensuring that they are intelligible
enough. To make it formal, we present a new notion, called soft core, characterizing both small and highly
constrained parts of GCNF instances, whether satisfiable or not. Soft cores can be used in unsatisfiable in-
stances as an alternative to MUSes (Minimal Unsatisfiable Subformulæ) or in satisfiable ones as an alternative
to MESes (Minimal Equivalent Subformulæ). We also provide an encoding to translate soft cores instances
into MAX#SAT instances. Finally, we propose a new method to solve MAX#SAT instances and we use it to
extract soft cores.
1 INTRODUCTION
Nowadays, SAT is well known and used for solv-
ing many different problems such as planning, ver-
ification, cryptography or mathematical conjectures
(Biere et al., 1999), (Heule et al., 2016). Solvers
become increasingly efficient and new applications
emerge frequently. When a problem is modeled as
a SAT instance, it is often observed that its set of so-
lutions may differ from the one that was expected. It
may be due to errors in modeling, or result from the
fact that the problem is too constrained. In both cases,
it is worth providing the user with some form of ex-
planation clearing up why the expected solutions are
impossible.
In the particular case when the set of constraints is
unsatisfiable, a MUS (Minimally Unsatisfiable Sub-
set) can be extracted and reported to the user as an
explanation of the discrepancy between the solutions
obtained and those being expected. A MUS is a subset
of constraints which is unsatisfiable but whose each
proper subset of it is satisfiable (Bruni and Sassano,
2001). It can be seen as a minimal (for inclusion) part
of the formula which is unsatisfiable. As instances
may contain an exponential number of MUSes com-
pared to their number of elements, one element from
a
https://orcid.org/0000-0003-2604-9657
b
https://orcid.org/0000-0002-6557-4115
c
https://orcid.org/0000-0002-2591-6491
d
https://orcid.org/0000-0002-9394-3897
each MUS has to be modified or removed to make
the instance satisfiable. In some practical applications
like hardware and software verification (Liffiton and
Sakallah, 2008), finding all MUSes is valuable to get
the best diagnostic in order to repair errors. How-
ever, when it comes to explaining to human users,
returning an exponential number of MUSes does not
make sense. As in extreme cases its size edges toward
the size of the formula, returning a single MUS may
also overwhelm the user. Accordingly, the search for
a smallest MUS (SMUS) has been the central topic
of several papers (Ignatiev et al., 2015), (Mneimneh
et al., 2005). Obviously, generating a smallest MUS
of a CNF formula is more computationally difficult
than extracting any MUS, as these problems are in
FP
NP
and FP
Σ
p
2
respectively (Ignatiev et al., 2015).
However, a SMUS may still be not succinct enough
or may pinpoint a part of the formula that would be
irrelevant when taking into account the entire prob-
lem.
When the set of constraints at hand is satisfi-
able, the notion of MUS trivializes and the notion of
Minimal Equivalent Subformula (MES) (Belov et al.,
2014) can be more suited. Given a set of constraints
C , a MES is a minimal (for inclusion) subset of con-
straints C
0
⊆ C which is equivalent to C . Even if com-
puting a MES might gather interesting information,
it does not help in detecting which part of the for-
mula is hard to solve. Moreover, like MUSes, a MES
and even a smallest MES (SMES) may not be small
486
Audemard, G., Lagniez, J., Miceli, M. and Roussel, O.
Identifying Soft Cores in Propositional Formulæ.
DOI: 10.5220/0010892700003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 486-495
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

enough to be handled by users.
To deal with these issues, we introduce in the fol-
lowing a generalization of the notion of MUS to both
satisfiable and unsatisfiable formulæ. A soft core is a
subset of constraints which is both small and highly
constrained, meaning it has a limited number of mod-
els. Identifying a soft core is clearly a bi-criteria op-
timization problem, where both the size of the soft
core and its number of models matter. Depending on
the context, it may be more important to reduce the
size of the soft core, even if we obtain more models.
Alternatively, in other cases, reducing the number of
models will be the main objective, even if this gives
larger soft cores.
Soft cores can be proven useful in different appli-
cation scenarios. They pinpoint the most constrained
parts of the formula, and determinate which con-
straints prevent expected solutions from being pos-
sible. For example, they can be used in scheduling
problems to find which part needs to be relaxed, or in
the analysis of mathematical conjectures (Heule et al.,
2016). Indeed, for such case, once the parameters of a
conjecture (e.g. a number of colors) are instantiated,
the problem can often be encoded by constraints. Ex-
cept for small values of the parameters, the resulting
formula is hard to be solved. Besides, if the formula
is unsatisfiable, a MUS is expected to be quite large,
since conjectures generally use a minimum number
of hypotheses. Thus, soft cores may provide informa-
tion and can become the start of mathematical proof
if the models admitted have specific characteristics or
are not numerous.
Soft cores can also be used in debugging tools, as
in (Dodaro et al., 2018), whose purpose is to help the
user to model problems. Generally, problems are not
modeled directly into SAT, but first in higher level
modeling languages and then transformed into SAT
instances. When encoded as CNF formulæ, problems
loose a lot of structural information, and a simple nat-
ural constraint (for example, ”we want at least par-
ticipate in three sessions among the five available”,
as s
1
+ s
2
+ s
3
+ s
4
+ s
5
> 3) might become a large
set of clauses, whose decision variables are not dis-
tinguishable from auxiliary ones, and which, if not
gathered into groups, can be lost among other clauses.
Then, using a Group CNF (GCNF) formula instead of
a CNF formula can be preferred to keep structural in-
formation, and to treat together clauses issued from a
former higher-level constraint.
We propose using soft cores to determine, when
modeling a problem into SAT, which parts of the
formula would be hard to explore, in order to either
change modeling or use the information when solving
the generated instance.
The paper is organized as follows. First, we
formally define soft cores, and show that the de-
cision problem related to soft cores is an NP
PP
-
hard problem by printing out a reduction from E-
MAJSAT (Pipatsrisawat and Darwiche, 2009). Af-
terwards, we demonstrate how to turn instances of
the soft cores problem into instances of MAX#SAT,
an NP
PP
-complete problem (Fremont et al., 2017).
Finally, from a practical side, we present an exact
MAX#SAT solver. We show how to leverage it for
computing soft cores and we compare it to the approx-
imate MAX#SAT solver Maxcount, (Fremont et al.,
2017), the only available tool for solving MAX#SAT
instances up to now.
2 PRELIMINARIES
Boolean Logic. We consider standard Boolean
logic. Let L
P
be a language of formulæ over an
alphabet P of Boolean variables also called atoms,
denoted by a, b, c, . . . The symbols ∧, ∨, ¬, ⇒ and
⇔ represent the standard conjunctive, disjunctive,
negation, material implication and equivalence
connectives, respectively. Propositional formulæ are
built in the usual way from variables, connectives
and parentheses. They are denoted by greek letters
as α, β, Γ, ∆, . . . We denote by Var(Γ) the set of
variables appearing in a formula Γ. For convenience
we sometimes write Γ(X) to represent that Γ is
assumed to be defined on variables X. A literal is a
variable or its negation. A term is a conjunction of
literals (`
1
∧ . .. ∧ `
s
) while a clause is a disjunction
of literals (`
1
∨ . .. ∨ `
s
). A unit clause is formed of
one literal.
Interpretation and Model. An interpretation
(or an assignment) ω to P is a mapping from P
to {true, false}. ω is complete when all variables
are assigned, otherwise it is partial. A variable
not assigned is said to be free. The set of all
interpretations is denoted by Ω. An interpretation
ω is a model of a formula Γ ∈ L
P
if and only if
it makes it true in the usual truth functional way.
On the contrary, an interpretation is a counter-
model if it does not satisfy the formula. The set
of models admitted by Γ is denoted Mod(Γ), with
Mod(Γ) = {ω ∈ Ω | ω is a model of Γ}. |= and ≡
denote respectively logical entailment and logical
equivalence. Let Γ and ∆ be two distinct propositional
formulæ, Γ |= ∆ if and only if Mod(Γ) ⊆ Mod(∆)
and Γ ≡ ∆ if and only if Mod(Γ) = Mod(∆).
Identifying Soft Cores in Propositional Formulæ
487

CNF and DNF. A propositional formula is in
Conjunctive Normal Form (CNF) (resp. in Disjunc-
tive Normal Form (DNF)) when it is written as a
conjunction of clauses (resp. a disjunction of terms).
Alternatively, CNF (resp. DNF) can be represented
by their set of clauses (resp. set of terms). The size
of the CNF Ψ (resp. DNF), denoted by |Ψ|, is its
number of clauses (resp. terms). The conditioning of
a CNF formula Ψ by a consistent term γ is the CNF
formula Ψ|
γ
, obtained from Ψ by first removing each
clause containing a literal ` ∈ γ and then removing all
occurrences of ¬` from the remaining clauses. When
a CNF formula contains a unit clause {`}, Ψ and Ψ|
`
are equisatisfiable. The unit propagation of clause
{`} is the conditioning of Ψ on `. A CNF formula
with no unit clause is said to be closed under propa-
gation. The Boolean Constraint Propagation (BCP),
is an algorithm that, given a CNF formula, returns an
equivalent CNF closed under unit propagation.
Related Problems. Many problems revolve around
solutions (or lack thereof) of a given CNF formula
Ψ. The decision problem determining whether
a model of Ψ exists is the Boolean Satisfiability
Problem (SAT) (Biere et al., 2009). A more general
problem is the counting problem #SAT (Thurley,
2006), (Lagniez and Marquis, 2017) which returns
the number of models of Ψ over its own set of
variables, denoted by k Ψ k. When Var(Ψ) is a
proper subset from the initial alphabet P, i.e. there
are free variables that are omitted in Ψ, we denote
its model count over P by k Ψ k
P
. When Ψ ∈ L
P
and X ⊆ P, ∃X.Ψ is a quantified Boolean formula
denoting (up to logical equivalence) the most general
consequence of Ψ which is independent from the
variables of X (Lang et al., 2003). Observe that
Var(∃X.Ψ) ⊆ Var(Ψ) \ X . The problem #∃SAT
(Aziz et al., 2015) is to determine the number of
models of a quantified CNF formula ∃X.Ψ.
Transforming a Propositional Formula into a CNF
Form. Tseitin encoding scheme is a linear-time
query-equivalent encoding scheme to translate any
propositional formula Γ into a CNF formula Ψ
(Tseitin, 1983). To do this, auxiliary variables are
added in order to represent subformulæ. Since
each additional variable is defined from the input
variables, both formulæ have the same number of
models (Lagniez et al., 2020). More precisely, the
models of the resulting CNF encoding are extensions
of the models of the input formula, but no model
is created nor removed. It is also possible to use
a more compact encoding that does not consider
equivalence but only implication. This encoding,
called Plaisted&Greenbaum encoding (Plaisted and
Greenbaum, 1986), does not preserve the number of
models but is equivalent modulo forgetting on the
auxiliary variables.
Group CNF. Given a CNF formula, clauses can
be semantically linked and thus gathered into groups
G = {G
1
,G
2
,. . . , G
m
} (Liffiton and Sakallah, 2008).
Concretely, each group is associated with an identi-
fier which is assigned to the clauses that compose
it. In some problems, it is also relevant to gather
integrity constraints into a dedicated group denoted
by D. A group CNF (GCNF) formula Φ = D ∪ G
with G = {G
1
,G
2
,. . . , G
m
} can be interpreted as D ∧
G
1
∧ . .. ∧ G
m
. Thus, all notions introduced so far
on CNF naturally extend on GCNF by considering
D∧G
1
∧. . .∧G
m
. Considering GCNF instead of CNF
becomes really crucial when the solution of the mod-
eled problem must satisfy some integrity constraints
and when we have to select some groups, which taken
together with D respect some interesting properties
(Nadel, 2010), (Liffiton and Sakallah, 2008), (Belov
et al., 2014).
3 PROBLEM STATEMENT AND
COMPUTATIONAL
COMPLEXITY
In this section, we first introduce the new notion of
soft core, whose objective is to determine a small
set of groups that constrains the most a GCNF for-
mula. Then, we will show that computing a soft core
whose size is predetermined is an NP
PP
-hard problem
by proposing a reduction from E-MAJSAT (Pipatsri-
sawat and Darwiche, 2009), which is the prototypical
NP
PP
-complete problem (Littman et al., 1998).
3.1 Definition of a soft core
Informally, a soft core is a subset of a propositional
formula, that is small both in size and in the number
of models admitted. More formally, it is defined as an
element of the Pareto frontier of the problem whose
purpose is to find a subset of the formula with two
objective functions to be minimized: (a) its size and
(b) its number of models. This is detailed in Defini-
tion 1.
Definition 1. Given a GCNF formula Φ = D ∪G, G
0
is a soft core of Φ if and only if:
1. G
0
⊆ G ;
2. ∀G
00
⊆ G, with G
0
6= G
00
and |G
00
| ≤ |G
0
|,
k D ∪ G
00
k
Var(Φ)
≥k D ∪ G
0
k
Var(Φ)
.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
488

To simplify, we restrict the bi-criteria problem to a
single criterion optimization problem by fixing the
size of the subset. This size k is chosen by the user.
Then, a k-soft core is a subset of the formula of size k
with a minimum number of models. We note that, in
general, a k-soft core is not a soft core because k may
not appear on the Pareto frontier of the bi-criteria op-
timization problem.
Definition 2. Given a GCNF formula Φ = D ∪ G
and an integer k with k ≤ |G |, G
0
is a k-soft core if
and only if:
1. G
0
⊂ G and |G
0
| = k ;
2. ∀G
00
⊆ G and G
00
6= G
0
, with |G
00
| = k,
k D ∪ G
00
k
Var(Φ)
>k D ∪ G
0
k
Var(Φ)
.
We also define the decision problem associated to the
optimization problem.
Definition 3. Given a GCNF formula Φ = D ∪ G,
k ∈ N and m ∈ N, a subset G
0
of G is said to be a
hk, mi-soft core if |G
0
| ≤ k and k D ∪ G
0
k
Var(Φ)
≤ m.
As already mentioned in the introduction, it is easy
to demonstrate that soft cores generalize both SMES
and SMUS notions. Indeed, given a CNF formula
Ψ, the problem of minimizing k for hk,0i-soft core
can be seen as a generalization of SMUS when
treating unsatisfiable formulæ and minimizing k for
hk, k Ψ ki-soft core can be seen as a generalization of
SMES when treating satisfiable formulæ.
In the following section, we analyze the computa-
tional complexity of the decision version of the k-soft
core problem.
3.2 Reduction from E-MAJSAT to
hk, mi-soft core
We prove that hk, mi-soft core is NP
PP
-hard by consid-
ering a reduction in polynomial time from the NP
PP
-
complete problem E-MAJSAT (Littman et al., 1998).
This problem is defined as follows. Let Ψ be a propo-
sitional formula in CNF defined over X ∪Y , where X
and Y are two disjoint sets of propositional variables.
Does there exist an assignment ω over X such that
the majority of assignments over Y satisfies Ψ|w? In
other words, E-MAJSAT determines if an assignment
ω over X such as k Ψ(ω,Y ) k
Var(Ψ)
>
1
2
× 2
|Y|
exists.
Proposition 1. Finding a hk,mi-soft core is NP
PP
-
hard.
Proof. Let us consider a CNF formula Ψ defined
over the set of propositional variables X ∪ Y , with
X = {x
1
,x
2
,. . . , x
n
}. Without loss of generality
we suppose that Ψ is not a tautology. Now, let us
associate with Ψ the GCNF formula Φ = D ∪G, with:
G. G simulates the choices of variables x
i
∈
X thanks to 2 × n propositional variables C =
{c
x
1
,c
¬x
1
,. . . , c
x
n
,c
¬x
n
}. Each pair {c
x
i
,c
¬x
i
}, that we
note c
`
, represents the choice of a literal ` in the cho-
sen assignment of X. If x
i
is true, then c
x
i
and there-
fore c
`
are also true. Otherwise, if x
i
is false, then c
¬x
i
is true and c
`
is false.
G = {G
`
s.t. Var(`) ∈ X and G
`
= {c
`
}} (1)
We denote by G
0
the set of groups whose unitary
clause c
`
(either c
x
i
or c
¬x
i
) are fixed to true. In order
to select a well constructed interpretation ω of X,
such as it does not contain both c
x
i
and c
¬x
i
, we want
to fix k = n, ensuring that exactly n choices are made.
To do this, we have to add constraints to D.
D. Nothing ensures that x
i
and its complementary ¬x
i
will not be chosen together. To detect this situation,
we add a first constraint to D:
s ⇔
_
x∈X
(c
x
⇔ c
¬x
) (2)
Equation 2 introduces a new propositional variable s
which is logically defined by C. Then, s indicates if
ω is consistent (meaning well constructed): if at least
one pair x
i
and ¬x
i
is set to true, then s is true, other-
wise s is false. We use this new variable to make im-
possible the selection of an inconsistent ω by adding
to D the following constraint:
s ∨ ((c
x
⇒ x) ∧ (c
¬x
⇒ ¬x) ∧ ¬Ψ) (3)
Then, given the selected interpretation ω, Equation 3
either states the number of models of ¬Ψ conditioned
by ω if ω is well constructed or if not, states 2
|Var(Ψ)|
models. In the E-MAJSAT problem, we search for
an assignment of X such that we get at least
1
2
× 2
|Y|
models, whereas when computing a hk, mi-soft core,
we search for k groups such that we have at most m
models. Thus, we use the fact that minimizing the
number of models of Ψ is maximizing the number of
counter models of Ψ and we consider the negation of
Ψ. We obtain the following GCNF:
Φ = G ∧
s ⇔
_
x∈X
(c
x
⇔ c
¬x
)
!
∧ (s ∨ ((c
x
⇒ x) ∧ (c
¬x
⇒ ¬x) ∧ ¬Ψ))
(4)
For the sake of simplicity, we chose to not translate
Equations 2 and 3 into CNF formulæ. However, and
Identifying Soft Cores in Propositional Formulæ
489

as pointed out in Section 2, this translation into a
CNF formula with the same number of models can
be done in polynomial time using Tseitin encoding.
Now, let us demonstrate that by fixing m = (2
n
−1)×
2
|Var(Ψ)|
+
1
2
× 2
|Y|
− 1, we intend to prove that there
is an assignment w over X such that the majority of
assignments over Y satisfies Φ|w, if and only if there
exists a G
0
⊆ G s.t. |G
0
| ≤ k and k D ∪ G
0
k
Var(Φ)
≤ m.
First, let us remark that after selecting n groups, n
variables of C are units and the remaining n variables
of C are free. From now on, two cases have to be
considered: (a) the selected groups are inconsistent
in a sense that there exists a literal ` of X such that
G
`
and G
¬`
have been selected and (b) the selected
groups are consistent in a sense that there does not
exist such a literal `. The remaining case, which
consists in the situation where there exists a literal `
of X such that neither G
`
or G
¬`
has been selected, is
a consequence of case (a). Indeed, since |G| = 2 ×|X|
and only one group is associated with each literal of
X, if there exists a literal ` of X such that neither G
`
or G
¬`
have been selected, then there exists `
0
of X
such that G
`
0
and G
¬`
0
has been selected (Dirichlet’s
drawer principle).
a. Then, let us show that whatever the selected groups
G
0
which fall in case (a), we have k D ∪ G
0
k
Var(Φ)
=
2
n
× 2
|Var(Ψ)|
. If there exists a literal ` of X such that
G
`
and G
¬`
have been selected, then s is necessary
true by Equation 2. By both replacing s by > in Equa-
tion 3 and simplifying Equation 2 we get D = >. Con-
sequently, the number of models of D ∪ G
0
is given by
the number of free variables in D ∪ G
0
over Var(Φ),
which are the variables of Ψ as well as half of the vari-
ables of C, thus n + |Var(Ψ)| free variables. Then,
whatever the n selected groups, we always have in
case (a):
m
1
= k D ∪ G
0
k
Var(Φ)
= 2
n
× 2
|Var(Ψ)|
= (2
n
− 1) × 2
|Var(Ψ)|
+ 2
|Var(Ψ)|
(5)
Since we supposed that Ψ 6≡ >, then
k Ψ k
Var(Ψ)
< 2
|Var(Ψ)|
and we have m < m
1
.
Consequently, we can not find out a subset G
0
⊆ G
that is a hk, mi-soft core of Φ for k = n and
m = (2
n
− 1) × 2
|Var(Ψ)|
+
1
2
× 2
|Y|
− 1 if we are in
case (a).
b. Let us consider the second case (b). By Dirich-
let’s drawer principle, G
0
will only consider one group
for each literal, G
0
= {G
`
1
,G
`
2
,. . . , G
`
n
}, such that
Var(`
i
) = x
i
and x
i
∈ X. Then, D ∪ G
0
is equal
to D ∪ {c
`
1
,c
`
2
,. . . , c
`
n
}, which is equivalent to Γ =
D ∧ c
`
1
∧ c
`
2
∧ . . . ∧ c
`
n
. We can show that the only
situation where s is not true by Equation 2 is when
c
¬`
1
, c
¬`
2
,. . . , c
¬`
n
are all set to false. Indeed, for all
remaining 2
n
− 1 cases, there exists `
i
such that c
`
i
and c
¬`
i
are true, which makes s = >. For each w
c
assignment of c
¬`
1
, c
¬`
2
, . . ., c
¬`
n
, in these 2
n
− 1
cases we have Γ|
w
c
= >. Thus, all variables from
Ψ are free and the number of models is 2
|Var(Ψ)|
.
When we consider the interpretation w
0
c
that makes
all c
¬`
1
,c
¬`
2
,. . . , c
¬`
n
set to false, s would also be set
to false by Equation 2. Thus, we get:
Γ|
w
0
c
≡ D ∧ c
`
1
∧ c
`
2
∧ . . . ∧ c
`
n
∧ ¬c
¬`
1
∧ ¬c
¬`
2
∧ . .. ∧ ¬c
¬`
n
≡ ¬s ∧ `
1
∧ `
2
∧ . . . ∧ `
n
∧ ¬Ψ
∧ c
`
1
∧ c
`
2
∧ . .. ∧ c
`
n
∧ ¬c
¬`
1
∧ ¬c
¬`
2
∧ . .. ∧ ¬c
¬`
n
(6)
Since all the variables except those of Y are units,
then k Γ|
w
0
c
k
Var(()Φ)
=k (¬Ψ)|
`
1
,`
2
,...,`
n
k
Var(Ψ)
. Con-
sequently, in case (b) we have:
m
2
= k D ∪ G
0
k
Var(Φ)
= (2
n
− 1) × 2
|Var(Ψ)|
+ k (¬Ψ)|
`
1
,`
2
,...,`
n
k
Var(Ψ)
(7)
Finally, G
0
is a hk, mi-soft core of Φ if and only if G
0
falls in the case (b) and m
2
≤ (2
n
−1)×2
|Var(Ψ)|
+
1
2
×
2
|Y|
− 1 which implies that k (¬Ψ)|
`
1
,`
2
,...,`
n
k
Var(Ψ)
≤
1
2
× 2
|Y|
− 1. Since all variables of X are assigned, the
last assertion is true only when (¬Ψ)|
`
1
,`
2
,...,`
n
has a
minority of models over Y , which is the case when
Ψ|
`
1
,`
2
,...,`
n
has a majority of models over Y . We have
proven that there is an assignment w over X such that
the majority of assignments over Y satisfies Ψ|
w
if and
only if there exists a hk,mi-soft core of Φ.
Proposition 1 shows that it is theoretically possible to
leverage an E-MAJSAT solver in order to compute a
k-soft core. However, in practice, the transformation
of an instance of k-soft core into an instance of E-
MAJSAT is not straightforward and more importantly
(to the best of our knowledge) no E-MAJSAT solver
is available. In the next section, we propose a more
convenient transformation from an instance of the
soft core problem to an instance of MAX#SAT, an-
other NP
PP
-complete problem. MAX#SAT is to de-
termine an assignment of some variables that max-
imizes the number of models of a given CNF for-
mula. The possibility of using an available tool to ap-
proximate MAX#SAT (https://github.com/dfremont/
maxcount) is also an argument for using such transla-
tion.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
490

4 EXTRACTING A k-soft core
A naive way to extract a k-soft core from a GCNF
formula would be to enumerate all possible combina-
tions of k groups, extract the selection from the for-
mula and call a model counter to compute its num-
ber of models over the whole alphabet. Obviously, in
practice this is feasible only on very small instances.
Then, we propose an alternative procedure, which
also guarantees completion, that encodes the problem
as an instance of the problem MAX#SAT.
4.1 Translation to MAX#SAT
MAX#SAT is a recent optimization problem, de-
fined as an extension of the #SAT problem and
useful in different applications, such as planning
and probabilistic inference (Fremont et al., 2017).
Let Ψ be a CNF formula defined on three distinct
sets of variables, X, Y , and Z, respectively called
maximization, counting and existentially quanti-
fied variables. The MAX#SAT problem is to find
the truth assignment ω
X
over the variables X that
maximizes k ∃Z.Ψ(ω
X
,Y, Z) k
Y
. In other words,
ω
X
is the assignment that maximizes the number of
assignments to Y such that Ψ(ω
X
,Y, Z) is satisfiable.
Thus, MAX#SAT can succinctly be summarized
as max
X
#Y ∃Z.Ψ(X,Y, Z). Its decision version is
NP
PP
-complete (Fremont et al., 2017).
To the best of our knowledge, the only imple-
mentation of MAX#SAT is Maxcount (Fremont
et al., 2017), an approximate solver that takes upon
entry a CNF formula and a (X,Y, Z)-partition of its
variables, Z being possibly empty. Maxcount returns
the best truth assignment found over X , alongside its
approximate projected model count. As it is, it can
not be used to extract a k-soft core. Then, we propose
an encoding to transform linearly any k-soft core
instance into a MAX#SAT one.
Addition of Selectors. Let Φ =
D ∪ {G
1
,G
2
,. . . , G
m
} be a GCNF formula.
First, to be able to extract groups from Φ, a new
variable x
i
called a selector is added to every clause
from the same group G
i
∈ Φ. For each i ∈ {1 . . . m},
we obtain the augmented group G
∗
i
=
V
|G
i
|
j=1
(α
j
∨¬x
i
).
Thus, selectors have the same behavior than iden-
tifiers in GCNF: we can interpret groups as sets
of clauses gathered together via selectors and the
augmented formula as a CNF. Let Y be Var(Φ)
and X = {x
1
,. . . , x
m
} the set of selector variables.
Then, we note Ψ the CNF formula obtained, with
Ψ(X,Y ) = D ∧
V
m
i=1
G
∗
i
. When a selector x
i
is fixed
to false, the set of clauses associated is satisfied
and thus, said to be deactivated. Otherwise, the
selector is removed and the set of clauses is activated.
Conditioning Ψ(X,Y ) on any truth assignment ω
X
over X removes all groups whose selectors have been
set to false and extracts the remaining.
Negation of the Formula. Let Θ be (
V
ω
X
(x
i
)=1
G
i
),
i.e., the subset of groups selected by the assignment to
X. Then, Ψ(X,Y )|
ω
X
= D∧Θ. To make Θ a soft core,
we want to find ω
X
that minimizes k D ∧ Θ k
Y
. As
minimizing the number of models of a propositional
formula corresponds to maximizing its number of
counter-models, we can use MAX#SAT to compute
a soft core from a CNF formula, provided it has been
negated first. By De Morgan’s law, negating Ψ results
in the DNF formula Ψ
∗
(X,Y ) = ¬D ∨
W
m
i=1
¬G
∗
i
.
Thus, solving max
X
#Y (¬Ψ
∗
(X,Y )) extracts a soft
core. However, Maxcount asks for a CNF input.
Transformation into a CNF. As pointed out in
Section 2, a DNF formula can be linearly transformed
into a CNF formula by adding auxiliary variables.
To keep the correct number of models, all the
auxiliary variables that are not logically defined by
Var(Ψ(X,Y )) are put into Z, which we recall is the set
of variables to be existentially quantified. To be more
precise, this applies when the Plaisted&Greenbaum
scheme is used. As Tseitin scheme ensures that the
number of models is kept, auxiliary variables can
either be in Y or Z. Whatever the encoding selected,
let us call
ˆ
Ψ(X,Y, Z) the CNF formula that encodes
Ψ
∗
(X,Y ).
Activation of k Selectors. Solving
max
X
#Y ∃Z.
ˆ
Ψ(X,Y, Z) results into an assign-
ment ω
X
over X that selects the set of groups
minimizing k Ψ(ω
X
,Y ) k
Y
, which without further
constraint, would correspond to all groups of Φ.
To guarantee that exactly k groups are selected, we
add over the selectors X the cardinality constraint
∑
m
i=1
x
i
= k, translated into a CNF formula Γ (As
´
ın
et al., 2011) defined over X and Z
0
, with X ∩ Z
0
=
/
0,
Z
0
being the set of auxiliary variables mandatory
to generate the selected encoding. The resulting
formula is Ψ
k
(X,Y, Z
00
) =
ˆ
Ψ(X,Y, Z) ∧ Γ(X, Z
0
),
with Z
00
= Z ∪ Z
0
. Whenever ω
X
falsifies Γ(X, Z
0
),
k ∃Z
00
.Ψ
k
(ω
X
,Y, Z
00
) k
Y
would be equal to zero.
Therefore, ω
X
can not be the solution to max-
imizing the number of models and solving
max
X
#Y ∃Z
00
.Ψ
k
(X,Y, Z
00
) has to return a k-soft
core.
To sum up, given a GCNF formula Φ = D ∧
V
m
i=1
G
i
, we compute a k-soft core by considering the
Identifying Soft Cores in Propositional Formulæ
491

following MAX#SAT formulation, τ being the trans-
formation chosen to get a CNF from a DNF and χ the
CNF encoding of the cardinality constraint :
max
X
#Y ∃Z
00
.(τ(¬(
m
^
i=1
|G
i
|
^
j=1
(α
j
∨¬x
i
))) ∧ χ(
m
∑
i=1
x
i
= k))
As already mentioned, there exists only one soft-
ware able to handle the MAX#SAT problem, and it
returns only an approximation. In the next section,
we propose a new and exact approach to tackle the
MAX#SAT problem.
4.2 Algorithm for Computing
MAX#SAT
Algorithm 1 provides the pseudo-code of Function
max#SAT that solves exactly MAX#SAT and which
takes upon entry a CNF Ψ and a (X,Y, Z)-partition
of its variables, respectively the counting, optimiza-
tion and existentially quantified variables. It returns a
term t, corresponding to an assignment of some vari-
ables of X, and the projected number of models of
∃Z.Ψ(t,Y, Z) over Y .
By construction, t is such that all complete
interpretations w of X extending t respect k
∃Z.Ψ(t,Y, Z) k
Y
=k ∃Z.Ψ(w,Y, Z) k
Y
. Based on the
model counter d4 (Lagniez and Marquis, 2017),
max#SAT is a top-down tree-search algorithm which
is, in our case, decomposed into two parts: (a) as
long as the current formula contains variables from
X, we branch on such variables. We keep the assign-
ment that maximizes the number of projected models,
k ∃Z.Ψ(t,Y, Z) k
Y
, which is computed in the second
part (b) of the tree as soon as there is no more vari-
ables from X to select and by considering in priority
variables from Y .
We also take advantage of the dynamic decom-
position and cache implementation of d4. Let Ψ be
the current formula. Ψ can be partitioned into dis-
joint subformulæ {Ψ
1
,. . . , Ψ
d
}, when for each i, j
∈ {1, . . ., d} with i 6= j, Ψ
i
and Ψ
j
do not share any
variable (i.e. Var(Ψ
i
) ∩ Var(Ψ
j
) =
/
0). Then, each
subformula Ψ
i
is treated separately and their solu-
tions aggregated afterwards. Furthermore, we use a
cache to avoid computing once more an already en-
countered subformula. Each time a new value of ht, k
∃Z.Ψ(t,Y, Z) k
Y
i is computed, it is stored in a map.
If a previously computed formula is found again, then
the cache would return the combination saved.
First, at line 1, one tests whether the formula Ψ
is satisfiable. If not, whatever the interpretation con-
sidered on X is, the number of models corresponding
would be equal to zero and max#SAT returns h
/
0,0i.
BCP simplifies Ψ at line 2 and returns an equiva-
lent formula Ψ
0
alongside the unit literals which were
propagated. If Ψ
0
has already been cached, max#SAT
returns cache[Ψ
0
] (line 3). Afterwards, we construct
ret (line 4), the temporary result that will be returned
at line 21 and which initially contains an empty term
with a neutral number of models.
connectedComponent partitions Ψ
0
into a set of
disjoint connected components at line 8. If there are
more than one component, then at line 8, the cur-
rent solution is equal to the aggregation of the solu-
tions of all its sub-components. As they do not share
any variables, Ψ
0
≡ Ψ
1
∧ .. . ∧ Ψ
n
. Then, ∃Z.Ψ
0
≡
∃Z.(Ψ
1
∧.. .∧Ψ
n
) ≡ ∃Z.(Ψ
1
)∧.. .∧∃Z.(Ψ
n
). There-
fore, the number of projected models k ∃Z.Ψ
0
k
Y
is
equal to k ∃Z.Ψ
1
k
Y
×. . . × k ∃Z.Ψ
n
k
Y
, and the as-
signments over X are concatenated.
If Ψ
0
can not be partitioned into more than one
component ( j = 1), a variable from X (or if X is
empty, Y ) is selected (lines 11-13). If Y is also empty,
then the only remaining variables are existentially
quantified and the current branch can be stopped, as
we already know that the current assignment has an
extension on Z that satisfies Ψ
0
. Otherwise, regard-
less of whether the decision variable is from X, we
compute via two recursive calls to max#SAT the solu-
tions for either conditioning Ψ
0
by v or ¬v (lines 15
and 16). If v is a maximization variable (line 17), then
the current number of models is equal to the one given
by the conditioning that resulted the higher number of
models. If v is a counting variable (line 18), then the
current number of models is equal to the sum of the
two solutions, as in normal model counters. In line 19,
we replace ret by the computed result we just stored
in cache[Ψ
0
].
Finally, at line 20, we update the current result
stored in ret by extending its term with the unit lit-
erals of X that have been computed by BCP, and by
multiplying its number of models with the free vari-
ables of Ψ
0
belonging to Y .
5 EXPERIMENTAL RESULTS
We experimentally evaluated our MAX#SAT encod-
ing of k-soft core instances on both the state-of-art ap-
proximate solver Maxcount and our complete solver
based on the algorithm max#SAT, to compare their
performance. To the best of our knowledge, as there
is no similar notion of soft cores in the literature, we
can not rely on existing benchmarks to experiment
on. Thus, as performance was not the primary con-
cern in this paper, we only considered small satisfi-
able instances crafted by a random 3-CNF formulæ
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
492

Input: Ψ: a CNF formula,
(X,Y, Z): a partition of Var(Ψ).
Output: ret = ht, ci s.t. any interpretation of X that extends t is a solution for MAX#SAT, and c the
number of models obtained.
if Ψ is unsat then return h
/
0,0i ;
(Ψ
0
, units) ← BCP(Ψ)
if cache[Ψ
0
] 6=
/
0 then return cache[Ψ
0
] ;
ret ← h
/
0,1i;
{Ψ
1
,. . . , Ψ
j
} ← connectedComponent(Ψ
0
)
if j > 1 then
for Ψ
i
∈ {Ψ
1
,. . . , Ψ
j
} do
ret ← ret × max#SAT(Ψ
i
, X, Y, Z)
end
else if j = 1 then
v ← undef
if Var(Ψ
0
) ∩ X 6=
/
0 then
v ← selectVar(Var(Ψ
0
) ∩ X)
else if var(Ψ
0
) ∩ Y 6=
/
0 then
v ← selectVar(Var(Ψ
0
) ∩Y )
end
if v 6= undef then
ht
1
,v
1
i ← max#SAT({Ψ
0
∧ v}, X, Y , Z)
ht
2
,v
2
i ← max#SAT({Ψ
0
∧ ¬v}, X, Y , Z)
if v ∈ X then
cache[Ψ
0
] ← (v
1
> v
2
) ? ht
1
,v
1
i : ht
2
,v
2
i
else
cache[Ψ
0
] ← h
/
0,v
1
+ v
2
i
end
ret ← cache[Ψ
0
]
end
end
return ret × h {` ∈ units | Var(`) ∈ X}, 2
|(Var(Ψ)\(var(Ψ
0
)∪Var(units)))∩Y|
i
Algorithm 1: Function max#SAT.
generator, with ten different variables and a clause-
to-variables ratio of 4.2. Afterwards, we translated all
problems into MAX#SAT instances using the encod-
ing presented in the previous section, with one clause
per group. We considered three variants, depending
on the transformation selected to get back a CNF. If
the Plaisted&Greenbaum scheme was used, then all
auxiliary variables were existentially quantified. Oth-
erwise, with the Tseitin scheme, auxiliary variables
were added on one side to the counting set, and on
the other to the existentially quantified one, which we
denote respectively by Tseitin(Y ) and Tseitin(Z).
For each instance, we measured the time in (sec-
onds) required by max#SAT and Maxcount to termi-
nate, as well as the number of models found. While
max#SAT is exact, Maxcount is an approximate model
counter. Thus, the estimated number of models is im-
portant to evaluate correctly the soft cores selected
by Maxcount. Furthermore, Maxcount takes upon
entry the number of copies n of the formula to use
in the self-decomposition. We have tested each in-
stance with a n set to 0, 3 and 5. When n is equal
to zero, the assignment to X is given at random with
no constraints, and during our experiments, it always
returned a solution that violated the cardinality con-
straint. However, setting n to a much higher integer
(n = 5) did not result into a better estimated count,
and increased significantly the runtime. To be fair, we
only report Maxcount with n = 3, the best parameter
from all tested.
All the experiments have been conducted on a
cluster of Intel XEON X5550 (2,66 Ghz) bi-core pro-
cessors with 32 GiB RAM. Each solver was run with
a time-out of three hours and a memory limit of 32
GiB of per input instance.
Table 1 reports the results for each considered
Identifying Soft Cores in Propositional Formulæ
493
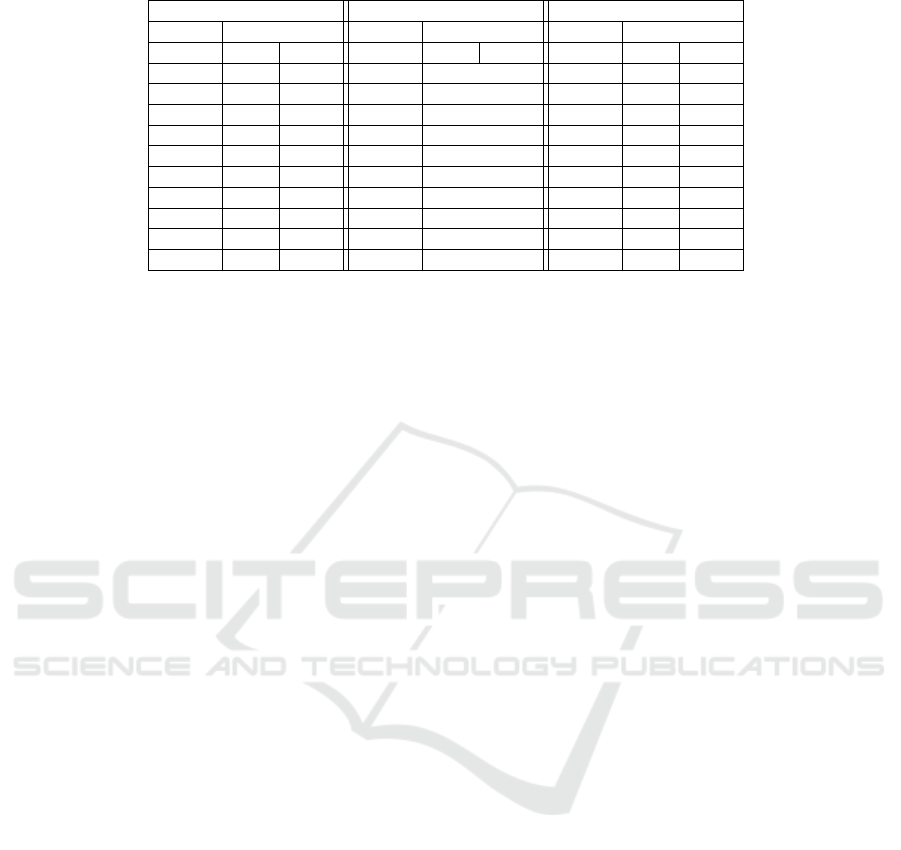
Table 1: Computing soft cores from random 3-CNF formulæ.
P&G Tseitin (Y) Tseitin (Z)
max#SAT Maxcount max#SAT Maxcount max#SAT Maxcount
time(s) #mod time(s) time(s) #mod time(s) time(s) #mod time(s)
102 560 92 135 timeout 107 536 77
91 560 84 147 timeout 101 560 86
91 576 99 136 timeout 111 560 85
99 547 81 151 timeout 95 544 80
85 560 89 130 timeout 105 564 89
105 536 99 148 timeout 100 544 84
95 576 99 137 timeout 125 576 105
107 576 102 153 timeout 102 576 92
94 560 92 137 timeout 115 560 85
107 576 102 142 timeout 97 532 90
variant. As each instance contains 42 clauses and
thus, 42 selectors, we set k equal to 5 in order to re-
strict the number of possible combinations,
42
5
being
already equal to 859, 668. Yet, the naive method pro-
posed in the introduction of Section 4 did not termi-
nate within the specified time. As the structure stays
the same, i.e., instances are all composed of 42 ternary
clauses, all formulæ after translation were up to 462
variables, with respectively 1625 and 1667 clauses for
the Plaisted&Greenbaum or Tseitin transformations.
As max#SAT is complete, it returns the assignment
on X that maximizes the number of models of the
negated formula. We did not report the number of
models computed, as it is always the same, which is
here equal to 640 models.
The experiment shows that Maxcount only termi-
nates when auxiliary variables are put into Z, and is
slightly faster if the encoding variables are equivalent
to the subformulæ they represent, as in the Tseitin
scheme. The results given with max#SAT are a mir-
ror image of Maxcount: besides giving a solution
when counting the auxiliary variables, selecting the
Plaisted&Greenbaum scheme is faster than using the
Tseitin transformation. In most cases, Maxcount is
faster than max#SAT but it also always returns an esti-
mated count that is lower than the optimum solution.
Obviously, this experiment is only an outline of what
could be solved by Maxcount and max#SAT, the pri-
mary objective being to show that on small instances,
max#SAT is rather competitive with Maxcount. How-
ever, on larger instances, Maxcount may scale up bet-
ter than MAX#SAT, as it is an approximate solver.
6 CONCLUSION AND
PERSPECTIVES
In order to explain results from CNF formulæ, we
introduced a new notion called soft core, which is
a sufficiently small and highly constrained part of a
formula. Soft cores can be used to identify which
constraints should be relaxed in order to obtain other
solutions, to select the most relevant constraints in
the formula or to help when modeling. Identifying
soft cores is a bi-criteria optimization problem where
both the size and the number of models of the sub-
formula have to be minimized. In this article, we fo-
cused on the restricted problem k-soft core where the
size of the soft core is given by the user, thus becom-
ing a single objective function problem. We showed
the NP
PP
-hardness of the decision version of the k-
soft core problem by considering a reduction from E-
MAJSAT, and proposed an encoding to transform k-
soft core instances into MAX#SAT ones, as well as
a first exact MAX#SAT solver. At last, an experi-
mental evaluation on randomly small generated CNF
formulæ has been realized.
As expected, even the restricted version k-soft
core is a difficult problem. At the present time, as
long as the cardinality constraint is considered glob-
ally, only small instances can be envisioned. Indeed,
the major part of the tree search corresponds to as-
signments that falsify the cardinality constraint. Thus,
pruning them would improve the performance. Fur-
thermore, the cardinality constraint, in addition to in-
crease the size of the formula, may prevent it to be
partitioned into disjoint components, which would
also fasten the runtime. Thus, to be more effective
when searching for k-soft cores, a first improvement
is to handle directly the cardinality constraint. A sec-
ond perspective is to stop considering the problem as
a MAX#SAT instance, but to use a dedicated solver
whose purpose would be to minimize directly the
number of models, and use the input formula with-
out transforming it. Finally, we could also compute
approximately soft cores by considering local search:
we first pick k groups from the formula, and we
switch elements one by one until no switch decreases
the number of models admitted.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
494

REFERENCES
As
´
ın, R., Nieuwenhuis, R., Oliveras, A., and Rodr
´
ıguez-
Carbonell, E. (2011). Cardinality networks: a theoret-
ical and empirical study. Constraints, 16(2):195–221.
Aziz, R. A., Chu, G., Muise, C. J., and Stuckey, P. J. (2015).
#∃SAT: Projected model counting. In Proceedings of
SAT’05, volume 9340 of Lecture Notes in Computer
Science, pages 121–137.
Belov, A., Janota, M., Lynce, I., and Marques-Silva, J.
(2014). Algorithms for computing minimal equivalent
subformulas. Artif. Intell., 216:309–326.
Biere, A., Cimatti, A., Clarke, E. M., and Zhu, Y. (1999).
Symbolic model checking without bdds. In Proceed-
ings of TACAS’99, volume 1579 of Lecture Notes in
Computer Science, pages 193–207.
Biere, A., Heule, M., van Maaren, H., and Walsh, T., edi-
tors (2009). Handbook of Satisfiability, volume 185 of
Frontiers in Artificial Intelligence and Applications.
IOS Press.
Bruni, R. and Sassano, A. (2001). Restoring satisfiability
or maintaining unsatisfiability by finding small unsat-
isfiable subformulae. Electron. Notes Discret. Math.,
9:162–173.
Dodaro, C., Gasteiger, P., Reale, K., Ricca, F., and
Schekotihin, K. (2018). Debugging non-ground ASP
programs: Technique and graphical tools. CoRR.
Fremont, D. J., Rabe, M. N., and Seshia, S. A. (2017). Max-
imum model counting. In Proceedings of AAAI’17,
pages 3885–3892.
Heule, M. J. H., Kullmann, O., and Marek, V. W. (2016).
Solving and verifying the boolean pythagorean triples
problem via cube-and-conquer. In Proceedings of
SAT’16, volume 9710 of Lecture Notes in Computer
Science, pages 228–245.
Ignatiev, A., Previti, A., Liffiton, M. H., and Marques-Silva,
J. (2015). Smallest MUS extraction with minimal hit-
ting set dualization. In Proceedings of CP’15, volume
9255 of Lecture Notes in Computer Science, pages
173–182.
Lagniez, J., Lonca, E., and Marquis, P. (2020). Definability
for model counting. Artif. Intell., page 103229.
Lagniez, J. and Marquis, P. (2017). An improved Decision-
DNNF compiler. In Proceedings of IJCAI’17, pages
667–673.
Lang, J., Lin, F., and Marquis, P. (2003). Causal theories
of action: A computational core. In Proceedings of
IJCAI’03, pages 1073–1078.
Liffiton, M. H. and Sakallah, K. A. (2008). Algorithms
for computing minimal unsatisfiable subsets of con-
straints. J. Autom. Reason., 40(1):1–33.
Littman, M. L., Goldsmith, J., and Mundhenk, M. (1998).
The computational complexity of probabilistic plan-
ning. J. Artif. Intell. Res., 9:1–36.
Mneimneh, M. N., Lynce, I., Andraus, Z. S., Silva, J. P. M.,
and Sakallah, K. A. (2005). A branch-and-bound al-
gorithm for extracting smallest minimal unsatisfiable
formulas. In Proceedings of SAT’05, volume 3569 of
Lecture Notes in Computer Science, pages 467–474.
Nadel, A. (2010). Boosting minimal unsatisfiable core ex-
traction. In Proceedings of FMCAD’10, pages 221–
229.
Pipatsrisawat, K. and Darwiche, A. (2009). A new d-dnnf-
based bound computation algorithm for functional E-
MAJSAT. In Proceedings of IJCAI’09, pages 590–
595.
Plaisted, D. A. and Greenbaum, S. (1986). A structure-
preserving clause form translation. J. Symb. Comput.,
2(3):293–304.
Thurley, M. (2006). Sharpsat - counting models with ad-
vanced component caching and implicit BCP. In Pro-
ceedings of SAT’06, volume 4121 of Lecture Notes in
Computer Science, pages 424–429.
Tseitin, G. S. (1983). On the complexity of derivation in
propositional calculus. In Automation of Reasoning,
pages 466–483.
Identifying Soft Cores in Propositional Formulæ
495
