
A Framework for Generating Playstyles of Game AI with Clustering of
Play Logs
Yu Iwasaki
1
and Koji Hasebe
2
1
Master’s Program in Computer Science, Degree Programs in Systems and Information Engineering,
Graduate School of Science and Technology, University of Tsukuba, Tsukuba, Japan
2
Faculty of Engineering, Information and Systems, University of Tsukuba, Tsukuba, Japan
Keywords:
Game AI, Playstyle, Clustering.
Abstract:
Many attempts have been made to implement agents for playing games with particular playstyles. Most
of these were aimed at generating agents with predetermined playstyles. To this end, they set the reward
function to increase the reward as the agent acquires their intended playstyles. However, it is not easy to
generate unexpected playstyles through this approach. In this study, we propose a framework to generate
multiple playstyles without predefining them. The proposed framework first arranges a set of reward functions
regarding the target game and repeats to select a function and make an agent learn with it. Each learned agent
is made to play the game, and those whose scores are higher than a predetermined threshold are selected.
Finally, each cluster obtained from clustering the play logs (i.e., metrics on the behavior in the game) of the
selected agents is considered a playstyle. As a result, it is possible to generate playstyles that play the game
well using this procedure. We also applied the proposed framework to a roguelike game, MiniDungeons, and
observed that multiple playstyles were generated.
1 INTRODUCTION
With the rapid development of game AI technologies,
agents (computer programs that play games) that sur-
pass human professionals, such as AlphaZero (Silver
et al., 2017), have appeared for perfect information
games. More recently, there have been various studies
to go beyond just playing the game well, such as the
agents to play imperfect information games (Brown
and Sandholm, 2019) and research to imitate human
play by agents (Ortega et al., 2013).
Several attempts have also been made to im-
plement agents for playing games with particular
playstyles (Tychsen and Canossa, 2008; Holmgård
et al., 2014; Holmgård et al., 2016; Holmgård et al.,
2019; Ishii et al., 2018; Tampuu et al., 2017; Fan
et al., 2019). Here, the playstyle means a set of char-
acteristic behavior of a player (Tychsen and Canossa,
2008). For example, in the poker, some styles use
bluffs and prefer stable wins. Most previous studies
aimed at generating agents with specific and prede-
termined playstyles. To this end, they commonly in-
troduced a reward function (a function for an agent
to learn playing games) in advance to emerge the in-
tended playstyle. However, it is not easy to generate
unexpected playstyles using this approach.
In this study, we propose a framework to gener-
ate multiple playstyles (including unexpected ones)
for playing games well without predefining the aimed
styles and the corresponding reward functions. The
proposed framework first arranges a set of reward
functions regarding the target game and repeats to
select a function and make an agent learn with it.
As a result, various agents learned with different re-
ward functions are generated. These learned agents
are made to play the game and selected those whose
scores (evaluated by the predetermined utility func-
tion for the game) are higher than a predetermined
threshold. Finally, the play logs (the metrics record-
ing the behavior in a game) of the selected agents
are clustered, and the resulting clusters are regarded
as the playstyles. Through the above procedure, it is
possible to generate multiple characteristic styles for
playing the game well.
To evaluate the performance of the proposed
framework, we conducted an experiment to generate
playstyles for the roguelike game called MiniDun-
geons (Holmgård et al., 2014). In the experiments,
we use a genetic algorithm called NeuroEvolution
of Augmenting Topologies (NEAT) (Stanley and Mi-
Iwasaki, Y. and Hasebe, K.
A Framework for Generating Playstyles of Game AI with Clustering of Play Logs.
DOI: 10.5220/0010869500003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 605-612
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
605

ikkulainen, 2002) for agent learning. We created 96
functions from the set of reward functions using a grid
search method. The utility function was defined to
give a high score when the agent safely reached the
exit in three evaluation stages. Under the above set-
tings, the experimental results show that 41 agents
trained on 41 reward functions, respectively, could
obtain scores above the threshold. As a result, we ob-
tained four playstyles.
There are various possible applications of the pro-
posed framework. When conducting test play in game
development using agents, it is useful to improve the
game and remove bugs by testing in various styles and
agents with a predetermined one. Additionally, the
proposed framework is useful for analyzing the char-
acteristics of games.
The remainder of the paper is organized as fol-
lows. Section 2 presents related work. Section 3
presents the formal description of our target problem.
Section 4 describes the proposed framework. Section
5 presents the experimental results of the proposed
framework. Finally, Section 6 presents the conclusion
and future studies.
2 RELATED WORK
Tychsen et al. (Tychsen and Canossa, 2008) is one
of the earliest studies on playstyle in games. They
defined the notion of playstyle as a set of character-
istic behavior of a player and analyzed the behavior
of players in the game called Hitman: Blood Money
by measuring various metrics of play logs, such as the
player’s position in the game field. Additionally, they
reported that these metrics could range from high to
low abstraction. They claimed that these are useful
for analysis with proper preprocessing.
Holmgård et al. (Holmgård et al., 2014; Holmgård
et al., 2016) presented a model of the evolution of
player’s decision-making and created five agents with
different playstyles through learning. They generated
agents specified by linear networks and used an evo-
lutionary strategy to optimize agents. Here, they de-
fined reward functions to emerge the predetermined
playstyles in advance. For example, the reward func-
tion for the playstyle called Monster Killer was de-
fined as the more monsters the agent kills, the bigger
the reward.
Ishii et al. (Ishii et al., 2018) generated agents with
two playstyles, called close-range and long-range at-
tacks, on the fighting game platform FightingICE.
Their idea was to use Monte Carlo tree search and
measure the distance to the opponent and the number
of actions suitable for the aimed playstyle when eval-
uating the agent’s reward.
Tampuu et al. (Tampuu et al., 2017) generated the
playstyles of cooperation and hostility on the hockey
game called Pong of Atari 2600. These playstyles
were implemented by defining two distinct reward
functions based on deep Q-network (Mnih et al.,
2013). The cooperation and hostility playstyles were
generated by taking negative and positive rewards, re-
spectively.
Fan et al. (Fan et al., 2019) developed an agent
to entertain novice players of the game, Go using
heuristics that selects different moves for different
strategies. The heuristics were originally developed
by (Ikeda and Viennot, 2013) based on the Monte
Carlo tree search and applied it to the agent playing
Go called Leela, which was based on AlphaGo Zero.
Here, the strategies taken by the heuristics were de-
veloped by defining different rewards for the results
of game play.
In the above studies, agents with specific styles
were developed in common by predefining aimed
playstyles and reward functions adjusted to the styles.
As applications of these studies, there are attempts to
automatically validate level design (Holmgård et al.,
2014) and attract human players (Fan et al., 2019).
However, it is not easy to generate playstyles that
are unexpected in advance using the approach in
the previous studies. On the other hand, the pro-
posed method has the advantage of generating multi-
ple playstyles to identify the potential playstyles with-
out defining the playstyles in advance.
There have been many attempts at modeling cog-
nitive, affective, and behavioral responses of players,
predicting human experience and characteristics from
gameplay inputs(Yannakakis et al., 2013). Drachen
et al. (Drachen et al., 2009) collected play logs from
over 1,000 players of the game called Tomb Raider:
Underworld, and classified them into multiple player
types. In (Drachen et al., 2009), six distinct features
were picked out from the collected play logs and clas-
sified them with clustering and self-organizing maps.
As a result, they clarified that there were four dis-
tinct types of players. This approach must collect a
lot of data from human players for analyzing. In ad-
dition, game designers cannot have collected and an-
alyzed data when they want to change the game me-
chanics through trial and error during game develop-
ment, i.e. before release. Therefore, this study trains
agents with many reward weights, generating agents
with more behavioral patterns, instead of collecting
human players’ data.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
606

3 PROBLEM DESCRIPTION
In this section, we give a formal definition of
playstyles and the problem description of playstyle
generation addressed in this paper.
First, we define games as the complete infor-
mation extensive-form games in game theory (cf.
(Osborne and Rubinstein, 1994; Leyton-Brown and
Shoham, 2008)). An extensive-form game is a model
where one or more players make consecutive deci-
sions according to their policy and each player ob-
tains a reward according to the result. However, for
the sake of simplicity, we only consider games with a
single player where there is no probabilistic choice of
action.
Definition 1 (Game). A game is a tree defined as a
tuple (A, H, Z, χ, σ, u), where
• A is the set of actions;
• H is the set of non-terminal nodes of game tree;
• Z is the set of terminal nodes of game tree, disjoint
from H;
• χ : H → 2
A
is the action function, which assigns
to each choice node a set of possible actions;
• σ : H ×A → H ∪Z is the successor function, which
maps a non-terminal node and an action to a new
node;
• u : Z → R is the utility function (where R denotes
the set of real numbers).
An agent conducts consecutive decision-making
on a game, and as a result, acquires some utility on
a terminal node. The utility function u is a function
determining the utility according to the result of game
play. A game is designed so that maximization of the
utility leads to the achievement of the game objective.
For example, in Super Mario Bros., the utility is the
score displayed in the upper right corner of a screen,
and the more objectives a player achieves in the game,
such as “getting to the goal faster” or “getting more
coins,” the higher the utility it gains.
Next, we introduce the reward function. This
function is used by agents to learn the game in our
framework described in the next section. Here, the
reason for providing the reward function separately
from the utility function is that it is difficult to train
the agents directly by the utility function.
Definition 2 (Reward Function). A reward func-
tion f
w
: D
1
× ··· × D
n
→ R for game play is de-
fined as f
w
(d
1
, . . . , d
n
) =
∑
n
i=1
w
i
× d
i
, where w de-
notes the vector of weights to parameters and w =
(w
1
, . . . , w
n
) ∈ W (= W
1
× ··· × W
n
). Also, let D
i
⊂
R, W
i
⊂ R.
Here, each parameter d
i
of a reward function is a
numerical value representing a certain feature of the
agent’s behavior in the game. For example, in the case
of Super Mario Bros., the number of coins acquired
and the number of jumps may be parameter values.
The reward for play is defined as the sum of each pa-
rameter d
i
multiplied by a predefined weight w
i
.
Next, we introduce the model that constitutes an
agent. A model has parameters to infer the correct
labels and optimizes them by learning datasets. That
is, it takes non-terminal nodes as inputs and outputs
the next action to be taken that maximizes the reward
function. Originally, the model outputs values of all
possible actions, but for the sake of simplicity, we as-
sume that it takes an action with the largest value and
omit the detailed descriptions.
Definition 3 (Model). The model that constitutes an
agent is defined as the function m : H → A.
For example, an instance of the Deep Q-Network
or NEAT correspondents to a model m. The set of
models is denoted by M.
Next, we define the learned model. This repre-
sents the model learned by a reward function.
Definition 4 (Learned Model). A model m trained by
a reward function is denoted as the learned model m
∗
:
H → A. The set of learned models is denoted as M
∗
.
Here, if g : H ×A → D is a function that returns a vec-
tor of measurements where an agent takes an action
on a non-terminal node, then an action a on a non-
terminal node h satisfies a = arg max
a
0
∈χ(h)
f
w
(g(h, a
0
)).
For a given reward function f
w
and a learned
model m
∗
, we use z[ f
w
, m
∗
] to denote the terminal
node reached by an agent repeating to take actions so
as to maximize its reward determined by f
w
and m
∗
at each node. Here, note that the utility is defined as
a part of the game, while the reward is a criterion for
the agent to select the optimal action in the learning.
Next, we define the feasible solution, which is a
pair ( f
w
, m
∗
) that leads to a utility exceeding a prede-
fined threshold.
Definition 5 (Feasible Solution). Let θ be a real num-
ber and called a threshold. For a given reward func-
tion f
w
and a learned model m
∗
, if u(z[ f
w
, m
∗
]) ≥ θ,
then the tuple of ( f
w
, m
∗
) is called a feasible solution.
The set of feasible solutions (for a threshold θ) is de-
noted by E.
Thus, a feasible solution can be regarded as an
agent which plays the game well.
Next, we define the play log. Intuitively, this is a
real vector representation of a record of game play by
an agent.
A Framework for Generating Playstyles of Game AI with Clustering of Play Logs
607
Definition 6 (Play Log). A real vector recording of
the occurrence of various events in game play by an
agent based on a feasible solution ( f
w
, m
∗
) is called
a play log. We define the function pl : F
w
× M
∗
→ Y
that returns the play log for a given feasible solution,
where Y = Y
1
× ··· ×Y
n
for each Y
i
⊂ R.
Next, we define the playstyle. Intuitively, the
playstyle is a set of characteristic behaviors of an
agent.
Definition 7 (Playstyle). For a given set E (= ∪
k
i=1
E
i
)
of feasible solutions, a playstyle on granularity k is a
set E
i
(for i = 1, . . . , k) if satisfies the following con-
ditions.
• Condition 1:
E
i
∩ E
j
=
/
0 (∀i, j ≤ k with i 6= j).
• Condition 2:
k
1
|E
i
|
∑
( f
w
,m
∗
)∈E
i
pl( f
w
, m
∗
)
−
1
|E
j
|
∑
( f
w
,m
∗
)∈E
j
pl( f
w
, m
∗
)k ≥ δ
b
(∀i, j ≤ k).
• Condition 3:
∀( f
w
a
, m
∗
a
) ∈ E
i
, ∀( f
w
b
, m
∗
b
) ∈ E
i
(kpl( f
w
a
, m
∗
a
) − pl( f
w
b
, m
∗
b
)k ≤ δ
i
) (∀i ≤ k).
Here, δ
b
∈ R is the threshold on the distances between
playstyles and δ
i
∈ R is the threshold on the distances
between individuals in the playstyle.
Intuitively, Condition 1 means that each subset E
i
of the feasible solutions is a partition of set E. Condi-
tion 2 means that the average distance of play logs of
any two subsets E
i
and E
j
must be more than or equal
to δ
b
. Condition 3 means that the distance between
any two play logs generated by feasible solutions in
E
i
must be less than or equal to δ
i
.
Finally, we describe the problem of playstyle gen-
eration addressed in this study.
Definition 8 (Playstyle Generation Problem).
Playstyle generation problem is a problem to find a
class {E
1
. . . , E
k
} of playstyles for a given game G
and a granurality k.
4 FRAMEWORK FOR
PLAYSTYLE GENERATION
4.1 Procedure to Generate Playstyles
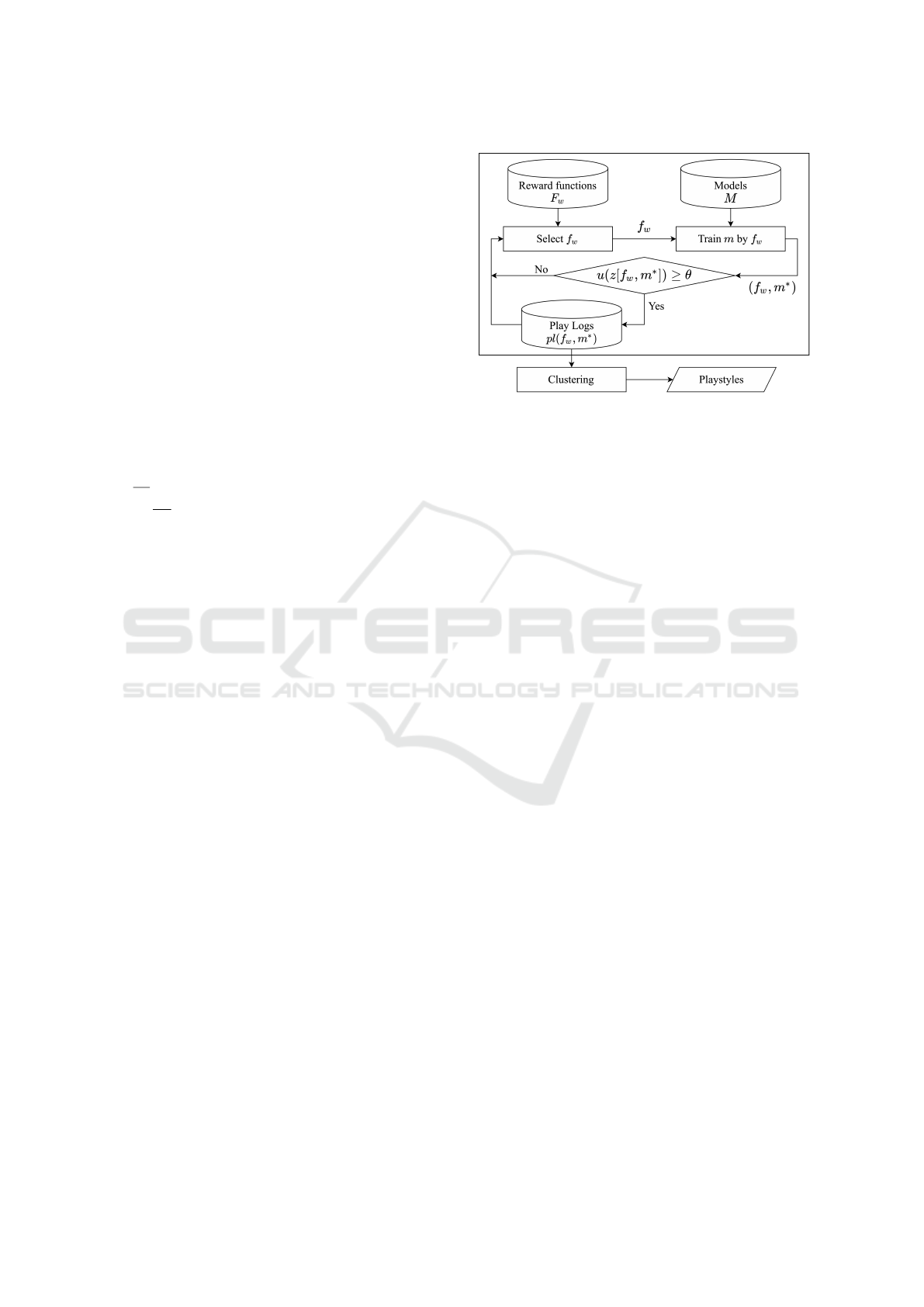
The procedure to generate playstyles using this frame-
work is as follows. (See also Figure 1 for the graphi-
cal presentation.)
For a given game G, the framework first provides
a set F
w
of various types of reward functions for the
Figure 1: Procedure of the playsytle generation by the
framework.
agent to learn to play this game. It also determines the
types of behavior of interest for the agent playing the
game generated through this framework, and which
features are recorded as play logs. That is, the func-
tion pl is defined. Furthermore, some parameters and
variables, such as the threshold θ and k for clustering,
are determined.
Next, the proposed framework makes agents learn
with reward functions in F
w
and selects only those sat-
isfying u(z[ f
w
, m
∗
]) ≥ θ. Specifically, a reward func-
tion f
w
∈ F
w
is selected and generate a model m by
learning with this function. Then, the learned agent
is made to play the game. Play log whose utility ex-
ceeds the threshold θ is saved; otherwise, the agent
is discarded. By repeating the above procedure, a set
of logs that play the game well is obtained. Here, to
efficiently obtain a model that plays the game well, it
is necessary to select a reward function from F
w
that
is likely to generate such a model.
Finally, the collected play logs are classified into
k clusters using some clustering technique; each is re-
garded as a playstyle playing game well.
4.2 Selection of Reward Functions
When selecting a function from a set of reward func-
tions, it is necessary to efficiently and evenly select
ones that are likely to generate agents that play well.
As such a method, grid search is a brute force search
for combination of input values. Since an advantage
of the grid search is simple and easy to implement,
our experiments adopt this method. Other methods
include particle swarm optimization and Bayesian op-
timization. These methods are convenient for effi-
ciently finding a plurality of semi-optimal solutions.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
608

4.3 Generating Learning Models and
Play Logs
Since the play logs identify the playstyle, the elements
of the play log recorded as a vector are the numerical
values of the events considered necessary for identify-
ing the playstyle in the game. However, each reward
function describes how the agent ought to behave in
the game.
In our framework, the model used for agent train-
ing is independent of any specific method if it out-
puts the action that maximizes the value of a given
reward function for the input state. Examples of such
learning models include genetic algorithms (Srinivas
and Patnaik, 1994) and deep reinforcement learning
(Mnih et al., 2013).
5 EXPERIMENTS
5.1 Setting Game and Model
In this study, we conducted experiments with a rogue-
like game to evaluate the effectiveness of the proposed
framework. We used MiniDungeons (Holmgård et al.,
2014; Holmgård et al., 2016), a model developed by
Holmgård with Java, in this experiment. Here, we
reimplemented this game with Python to run in the
OpenAI Gym environment. We set multiple stages
and parameters and domains of reward functions.
The agent in this game aims to move from the
starting point to the goal without dying. This agent
can repeatedly move one square up, down, left, and
right. Each stage is a two-dimentional grid includ-
ing some special types of cells indicating the starting
point, blocks, treasures, monsters, potions, and exit.
When the agent arrives at each treasure, monster po-
tion, and exit, it receives a predetermined reward. Fur-
thermore, a negative reward is obtained as a penalty
for the passage of time for each movement.
In this experiment, we use NeuroEvolution of
Augmenting Topologies (NEATs) as the learning
model of agents. A reward function is initially set for
each NEAT. Then, the individual, which is identical
to its model, receives a state from the environment.
Then, the agent evaluates the reward of the state or
action by its reward function. Finally, it outputs an
action selected by the network to the environment.
These operations are repeated until the agent reaches
the goal, the physical strength less than or equal to 0,
or the specified number of turns has passed. After the
play, the total rewards obtained during this play are set
to the fitness of the agent, and the agent’s play log is
Table 1: Parameters of reward functions and weights.
Parameter Weight
Movement (-2, -1, 0)
Reaching the exit (-100, 100)
Acquisition of a tresure (-40, 40)
Acquisition of a potion (-30, 30)
Defeating a monster (-50, 50)
Death (-100, 100)
recorded. Agents optimized for the reward functions
are generated so that individuals with high fitness sur-
vive by natural selection.
The input layer of the individual is set as eight
neurons and receives information from the environ-
ment about the shortest distance to each object and
the remaining health. Here, there are two possible
distances: the distance when approaching the object
safely avoiding monsters, and the distance without
avoiding them. The action corresponding to the out-
put neuron with the maximum value is selected at
each decision point, and the agent moves one square
toward the selected object.
5.2 Setting Framework
The utility function of MiniDungeons was set as “it
returns 1 if the agent reaches the exit without dy-
ing within the time limit at all stages, and 0 other-
wise.” The threshold of the feasible solution was set
as “reaching the exit without dying within the time
limit at all stages (i.e., the value 1).”
Here, the reward functions have six parameters.
Table 1 presents the types of values fed into parame-
ters and weights. We set the reward functions so that
the absolute value of the exit and death were equal,
and the absolute values were in the order of mon-
ster, treasure, and potion. The values of reward func-
tions were searched by grid search and direct prod-
uct of weights on Table 1. Thus, the number of re-
ward functions searched was 3 × 2
5
= 96. For exam-
ple, if the weights of the reward functions parameters
are (−2, 100, 40, −30, −50, −100), and the measured
values for each event are (20, 1, 2, 0, 3, 0), then the re-
ward is 10, the value of the inner product. The play
log expressed in vector form is used for clustering
when generating playstyles. This play log contains
the number of visits to each cell.
Figure 2 shows examples of the training and eval-
uation stages used in the experiments. Three training
stages were used for training individuals of NEAT.
The individual’s utility with the highest fitness was
examined to exceed the threshold in three evaluation
stages. It was judged that the agent played the game
A Framework for Generating Playstyles of Game AI with Clustering of Play Logs
609

!"# !$#
Figure 2: Examples of training stage (a) and evaluation
stage (b).
Table 2: Parameter settings.
Paramerter Value
Initial Health 30
Health required to defeat a monster 10
Health recovered by a potion 10
Maximum number of movements 200
Number of individuals of population 75
Number of populations 50
well if it reached the exit without dying in all evalua-
tion stages. Separating used stages makes it possible
to select reward functions that more generally satisfy
the rule of the game. These stages were randomly
generated according to a predetermined appearance
ratio of objects.
Table 2 presents the parameters of MiniDungeons
and NEAT. Each population of NEAT consists of 50
individuals and 75 populations were trained. Thus,
360, 000 individuals were trained and 96 candidates
were generated, and only those with utilities exceeded
the threshold were used to create playstyles.
5.3 Results for the Framework
Under the above settings, the experimental results
show that 48 out of 96 individuals optimized on 96
reward functions satisfied the condition of the evalu-
ation stages. The 48 feasible solutions were classi-
fied into 11 clusters with x-means (Pelleg and Moore,
2000). Here, the play logs of three evaluation stages
were used as the criterion for classification. The x-
means automatically estimates the number of clusters;
however, the number of estimated clusters varies de-
pending on random numbers. Thus, x-means were
repeated 1000 times, and 11, the number of clusters
that appeared most frequently, was adopted.
7 out of 11 clusters were excluded because their
sizes were less than 4, being difficult to analyze
playstyles. Table 3 shows the detail of four clusters
whose sizes are greater than or equal to 5. Each clus-
ter 5, 7, 9, and 10 have a size greater than or equal to
Table 3: Generated clusters.
ID Size Name
5 11 Runner
7 11 Consumer
9 10 Treasure Collector
10 5 Coward
Figure 3: Comparison of behavioral characteristics between
cluster (by measuring play logs).
5 and accounts for 75% of the total.
Cluster 5 (named Runner) was negatively re-
warded by treasures on all reward functions and was
negatively rewarded by either monster, treasure, or
both. Thus, it gave priority to the exit and avoids other
objects as much as possible. Cluster 7 (Consumer)
was positively rewarded with curiosity by treasures,
potions, and monsters on all reward functions. Clus-
ter 9 (Treasure Collector) was positively rewarded by
treasures on all reward functions. Cluster 10 (Cow-
ard) was positively rewarded by potions and treasures;
however, it was negatively rewarded by monsters.
We analyzed the events measured by agents on
three evaluation stages for each cluster to investigate
the characteristics of these clusters. Figure 3 shows
the radar chart of the event logs. The events measured
were the number of monsters killed and the number
of potions and treasures obtained. Figure 3 shows the
plot of the average of the measured logs for all reward
functions in each cluster.
The shape of the cluster 5 (Runner) is smaller than
the other clusters. The reason is that agents disliked
other objects and immediately headed for the exit. It
is considered that agents acquired some potions and
treasures along the way to reach the exit in the short-
est path. Cluster 7 (Consumer) has the largest shape
and is close to an equilateral triangle. Agents of this
cluster killed monsters instead of other clusters and
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
610

Table 4: Variance of logs per cluster for play logs.
Group ID Move Monster Potion Treasure
PlayLog
5 91.7 0.6 45.8 0.3
7 775.3 0 0 0
9 411.4 0.81 30.0 1.6
10 299.3 0.6 0 0.2
RewardWeights
4 8425.4 0 202.6 250
5 20087.2 248.5 467.8 241.3
6 6303.8 0.41 229.8 183.4
9 7557.6 1.3 134.0 260.8
10 3442.1 0 27.2 50.1
acquired potions and treasures at the same rate. In
cluster 9 (Treasure Collector), the percentage of the
number of treasures acquired is large. Only the num-
ber of monsters killed is small in cluster 10 (Coward).
This tendency is also seen in Treasure Collector; how-
ever, there is the difference that agents take more po-
tions to heal and put their safety first.
The generated playstyles have different priori-
ties for objects; thus, behaving differently on stages.
Therefore, the reward functions are considered to
change the personality and preferences of agents.
Thus, it is considered that the framework could gener-
ate playstyles without predefining playstyles and re-
ward functions by searching these reward functions
and clustering on only the feasible solutions.
5.4 Comparison with Clustering for
Reward Functions
As an auxiliary evaluation, we also confirmed
whether a similar playstyle could be obtained by clus-
tering the vectors of weights for the parameters of the
reward functions, instead of clustering play logs.
In the experiment, 48 reward functions whose util-
ities exceed the threshold were classified by the x-
means based on the weights for the parameters. They
were classified into 11 clusters, five of which have
sizes greater than or equal 6. This result indicates that
the individuals in the same cluster behaved similarly
due to the similarity of the reward functions. How-
ever, compared to clustering play logs, the individu-
als in the same cluster often behaved differently. As
an illustration of this result, Figure 4 shows the mea-
surement of logs when clustering on reward functions.
Clusters 4, 6, and 9, on average, avoided monsters,
and Clusters 5 and 10, on average, were interested in
all objects. The reason is that individuals with differ-
ent behavior were mixed in the same cluster, averag-
ing behavior. Table 4 summarizes the variance of logs
per cluster for play logs and reward functions. In the
Figure 4: Comparison of behavioral characteristics between
cluster (by measuring reward functions).
cluster generated by values of reward functions, each
individual behaves differently, increasing variances.
These results suggest that when generating playstyles,
it is better to convert reward functions into play logs
by playing games and then classify play logs with
clustering. The reason is that playstyles are identi-
fied based on information of events in games that can
be observed by humans and machines.
6 CONCLUSIONS AND FUTURE
WORK
In this study, we proposed a framework for generating
multiple playstyles for playing games well without
predefining the aimed styles and the corresponding
reward functions. The basic idea was to classify the
play logs of agents who learned the game using dif-
ferent reward functions and who could play the game
well. The proposed framework makes agents train
by reward functions and select those whose scores
exceed the threshold. Then, play logs of the se-
A Framework for Generating Playstyles of Game AI with Clustering of Play Logs
611

lected agents are classified with clustering, generat-
ing playstyles. We applied our proposed framework
to the roguelike game and demonstrated that multiple
playstyles were generated.
In future studies, we will verify the effectiveness
of the proposed framework by adopting it on more
complex games, such as Super Mario Bros., consist-
ing of many possible actions and states. We are also
interested in using a genetic algorithm called Qual-
ity Diversity (Pugh et al., 2016) in our framework to
make more effective and expressive the playstyle gen-
eration, especially MAP-Elites (Mouret and Clune,
2015).
REFERENCES
Brown, N. and Sandholm, T. (2019). Superhuman ai for
multiplayer poker. Science, 365(6456):885–890.
Drachen, A., Canossa, A., and Yannakakis, G. N. (2009).
Player modeling using self-organization in tomb
raider: Underworld. In 2009 IEEE symposium on
computational intelligence and games, pages 1–8.
IEEE.
Fan, T., Shi, Y., Li, W., and Ikeda, K. (2019). Posi-
tion control and production of various strategies for
deep learning go programs. International Conference
on Technologies and Applications of Artificial Intelli-
gence, pages 1–6.
Holmgård, C., Green, M. C., Liapis, A., and Togelius, J.
(2019). Automated playtesting with procedural per-
sonas through mcts with evolved heuristics. Transac-
tions on Games, 11:352–362.
Holmgård, C., Liapis, A., Togelius, J., and Yannakakis,
G. N. (2014). Evolving personas for player decision
modeling. In Conference on Computational Intelli-
gence and Games, pages 1–8.
Holmgård, C., Liapis, A., Togelius, J., and Yannakakis,
G. N. (2016). Evolving models of player decision
making: Personas versus clones. Entertainment Com-
puting, 16:95–104.
Ikeda, K. and Viennot, S. (2013). Production of various
strategies and position control for monte-carlo go —
entertaining human players. Conference on Computa-
tional Inteligence in Games, pages 1–8.
Ishii, R., Ito, S., Ishihara, M., Harada, T., and Thawonmas,
R. (2018). Monte-carlo tree search implementation of
fighting game ais having personas. In Conference on
Computational Intelligence and Games, pages 1–8.
Leyton-Brown, K. and Shoham, Y. (2008). Essentials of
Game Theory: A Concise Multidisciplinary Introduc-
tion. Morgan and Claypool Publishers.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing atari with deep reinforcement learn-
ing. arXiv:1312.5602.
Mouret, J.-B. and Clune, J. (2015). Illuminating search
spaces by mapping elites. arXiv:1504.04909.
Ortega, J., Shaker, N., Togelius, J., and Yannakakis, G. N.
(2013). Imitating human playing styles in super mario
bros. Entertainment Computing, 4:93–104.
Osborne, M. J. and Rubinstein, A. (1994). A course in game
theory. MIT press.
Pelleg, D. and Moore, A. W. (2000). X-means: Extend-
ing k-means with efficient estimation of the number
of clusters. In Proceedings of the International Con-
ference on Machine Learning, pages 727–734.
Pugh, J. K., Soros, L. B., and Stanley, K. O. (2016). Qual-
ity diversity: A new frontier for evolutionary compu-
tation. Frontiers in Robotics and AI, 3.
Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,
M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,
Graepel, T., et al. (2017). Mastering chess and shogi
by self-play with a general reinforcement learning al-
gorithm. arXiv:1712.01815.
Srinivas, M. and Patnaik, L. M. (1994). Genetic algorithms:
A survey. Computer, 27(6):17–26.
Stanley, K. O. and Miikkulainen, R. (2002). Evolving neu-
ral networks through augmenting topologies. Evolu-
tionary Computation, 10:99–127.
Tampuu, A., Matiisen, T., Kodelja, D., Kuzovkin, I., Korjus,
K., Aru, J., Aru, J., and Vicente, R. (2017). Multiagent
cooperation and competition with deep reinforcement
learning. PLoS ONE, 12:1–15.
Tychsen, A. and Canossa, A. (2008). Defining personas in
games using metrics. In Conference on future play,
pages 73–80.
Yannakakis, G. N., Spronck, P., Loiacono, D., and André,
E. (2013). Player modeling. In Artificial and Compu-
tational Intelligence in Games. Dagstuhl Publishing.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
612
