
Community Detection based on Node Relationship Classification
Shunjie Yuan, Hefeng Zeng and Chao Wang
School of Cyber Engineering, Xidian University, Xi’an 710126, China
Keywords:
Complex Network, Community Detection, Machine Learning.
Abstract:
Community detection is a salient task in network analysis to understand the intrinsic structure of networks. In
this paper, we propose a novel community detection algorithm based on node relationship classification. The
node relationship between two neighboring nodes is defined as whether they affiliate to the same community. A
trained binary classifier is deployed to classify the node relationship, which considers both the local influence
from the two nodes themselves and the global influence from the whole network. According to the classified
node relationship, community structure can be detected naturally. The experimental results on both real-
world and synthetic networks demonstrate that our algorithm has a better performance compared to other
representative algorithms.
1 INTRODUCTION
In recent years, complex networks have been ap-
plied in several fields, such as social networks (Zheng
et al., 2019; Li et al., 2012), genetic biology (Hu
et al., 2018), disease prevention and control (Goltsev
et al., 2012) as well as transportation (Dong et al.,
2016). Community detection is a fundamental task in
complex networks because many further works such
as information propagation and influence maximiza-
tion depend on community structure. Community
structure is a series of sets of nodes, where nodes
within the same community are tightly connected and
links between the different communities are relatively
sparse. The purpose of community detection is to de-
tect these node sets.
Because of the importance of community de-
tection, many community detection algorithms have
been proposed. And these algorithms have already
been deployed in many real-world applications such
as link prediction (Wang et al., 2016), recommender
systems (Moradi et al., 2015), detection of terror-
ist groups in online social networks (Benigni et al.,
2017). However, the existing community detection
algorithms cannot fully satisfy the need of the current
applications with respect to accuracy because of the
variety of network structures. On the other hand, sev-
eral algorithms detect community structure only from
a single perspective, which may limit the performance
of these methods. For example, GN (Girvan and New-
man, 2002) algorithm detects communities from a
global view by removing edges with large between-
ness. On the contrary, LPA (Raghavan et al., 2007) al-
gorithm detects communities from a local view, where
the community of a node is determined by its neigh-
boring nodes.
Given two neighboring nodes in a network, the
node relationship of whether belonging to the same
community for these two nodes is specific. If the
node relationship between all nodes and their cor-
responding neighbors can be obtained, the commu-
nity structure can be detected naturally. In this paper,
we propose an algorithm called CDNC (Community
Detection Based on Node Relationship Classification)
to detect community structure. A trained classifier is
built to classify the node relationship from both the
global and local perspectives. Then we detect com-
munity structure based on the classified node relation-
ship. The main contributions of this paper are sum-
marized as follows. First, we propose a new perspec-
tive for community detection—transforming commu-
nity detection to node relationship classification. Sec-
ond, we design the method CDNC based on node re-
lationship classification. Third, our method does not
require parameter settings and does not rely on prior
knowledge, such as the number of communities. Ex-
perimental results on several real-world and synthetic
networks demonstrate that our algorithm has a bet-
ter performance compared with other competing al-
gorithms in most cases.
The structure of this paper is as follows. In Sec-
tion 2, we introduce the related work on community
596
Yuan, S., Zeng, H. and Wang, C.
Community Detection based on Node Relationship Classification.
DOI: 10.5220/0010850600003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 596-601
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

detection. In Section 3, we present the CDNC algo-
rithm in detail including the basic principle and the
steps. In Section 4, we present two evaluation metrics
and analyze the performances of CDNC and other al-
gorithms on both real-world and synthetic networks.
At last, we conclude this paper in Section 5.
2 RELATED WORK
Many methods have been proposed for community
detection from different perspectives during the past
decades, such as the divisive hierarchical clustering
methods (Girvan and Newman, 2002), label prop-
agation (Raghavan et al., 2007; Zong-Wen et al.,
2014), methods based on random walk (Pons and
Latapy, 2005; Rosvall and Bergstrom, 2008), meth-
ods based on modularity optimization (Blondel et al.,
2008; Newman, 2004), and methods based on intelli-
gent computing algorithms (Moradi and Parsa, 2019;
Cai et al., 2020; Ding et al., 2018; Hu et al., 2020; Li
et al., 2020).
Girvan Newman (GN) algorithm (Girvan and
Newman, 2002) is a typical divisive hierarchical clus-
tering method, proposed by Newman and Girvan. The
main idea of this algorithm is that the bigger between-
ness an edge has, the more likely this edge is between
different communities. By calculating the between-
ness of each edge and removing the edges with big
betweenness iteratively, the community structure will
appear gradually.
The label propagation algorithm (Raghavan et al.,
2007) was proposed by Raghavan et al. in 2007,
which starts by marking each node with a unique la-
bel and then iterates through all nodes until each node
has the same label as most of its neighbors have. The
striking advantage of this algorithm is its high speed
and simplicity. But the random update orders of the
algorithm cause the instability of the detected com-
munity structure. Liang et al.(Zong-Wen et al., 2014)
introduced consensus weight to the basic label propa-
gation algorithm and proposes a method named the
label propagation algorithm with consensus weight
(LPAcw) which enhances both the stability and the
accuracy of community detection greatly.
The idea of the random walk was proposed by
Pearson (Pearson, 1905). Since then, the random
walk has been used in many different fields including
community detection where the main principle is that
the random walker tends to become trapped within
communities because of the high connectivity within
communities. Based on the random walk, many al-
gorithms have been put forward, such as WalkTrap
(Pons and Latapy, 2005) and Infomap (Rosvall and
Bergstrom, 2008). The complexity of WalkTrap is
O(mn
2
), which means WalkTrap is not suitable for
large-scale networks. Infomap is also based on in-
formation theory, which regards community detection
as a coding problem——the optimal partition corre-
sponding to the minimum description length princi-
ple.
The concept of modularity was put forward by
Newman (Newman and Girvan, 2004) ,which is
used as a metric to measure partitions. The ba-
sic idea of modularity optimization algorithms is to
optimize modularity because greater modularity al-
ways corresponds to a better community partition.
However, modularity optimization has been proved
to be an NP-complete problem (Fortunato, 2010).
The modularity optimization algorithms such as Lou-
vain (Multilevel),(Blondel et al., 2008) Fastgreedy
(FG)(Newman, 2004) are devised to approximate the
optimal modularity.
So far researchers have designed many algorithms
based on intelligent computing algorithms such as ge-
netic evolution (Moradi and Parsa, 2019), convolu-
tional neural network (Cai et al., 2020), Hopfield neu-
ral network (Ding et al., 2018), and graph embedding
(Hu et al., 2020). Moradi et al. use genetic evolution
to optimize modularity (Moradi and Parsa, 2019). Cai
et al. elaborately represent edges as images firstly,
then perform edge classification with a convolutional
neural network, finally detect communities based on
edge classification (Cai et al., 2020). Ding et al. pro-
pose a method that detects community structure by
maximizing modularity with a Hopfield neural net-
work (Ding et al., 2018). Hu et al. utilize the graph
representation learning algorithm to represent nodes,
then apply the spectral clustering algorithm to detect-
ing communities with the node embeddings (Hu et al.,
2020).
Figure 1: The overview of the algorithm CDNC proposed
in this paper.
3 THE CDNC ALGORITHM
Given a network G, there are only two types of node
relationship between two neighboring nodes, affiliat-
ing to the same community or not. If we can pre-
cisely predict this node relationship for all neighbor-
ing node pairs and then connect the nodes that belong
to the same community, the community structure can
Community Detection based on Node Relationship Classification
597

be detected naturally. The overview of the proposed
algorithm CDNC is illustrated in Figure 1.
Selection of features. We believe that whether af-
filiating to the same community for two neighboring
nodes depends on the global influence from the whole
network and the local influence from the two nodes
themselves. The betweenness (Wang et al., 2008)
is selected to measure the global influence, because
the bigger betweenness the edge has, the more un-
likely these two nodes over the edge are in the same
communities. The Jaccard coefficient (Hamers et al.,
1989) of these two nodes and the cosine of vectors
as well as the relative Euclidean distance of vectors
of these two nodes are used to assess the local influ-
ence since a bigger Jaccard coefficient and two similar
vectors indicate that these two nodes are more likely
to be in the same community. In this algorithm, we
use node2vec (Grover and Leskovec, 2016) to vec-
torize nodes. Node2vec is an algorithmic framework
for representational learning on graphs. The experi-
ments demonstrate that these features are useful and
indispensable when considering the complex network
structure.
Binary classification. We train a fully connected
neural network with four inputs and one output as a
binary classifier and select the binary cross-entropy
as the loss function, which is widely used in binary
classification. Adam is selected as the gradient de-
scent method, and the ReLU and Sigmoid functions
are used as the activation functions in hidden layers
and output layer respectively. The prediction accu-
racy of the trained binary classifier on the test dataset
is higher than 97%, but it still exists misprediction.
Therefore, we introduce modularity as a supplemen-
tary criterion to judge whether two nodes belong to
the same community, which is based on the idea that
the true prediction of node relationship always corre-
sponds to larger modularity.
Community detection. First, we extract the data
from the target network which consists of quadruples
including the relative betweenness, the Jaccard coef-
ficient, the relative Euclidean distance of vectors as
well as the cosine of vectors. Second, we feed the
dataset to the classifier and obtain the prediction of the
node relationship. Then we connect the nodes that af-
filiate to the same community according to the predic-
tion. The detailed algorithm procedure is illustrated in
Algorithm 1. The time complexity of this algorithm is
O(nkc) where k and c are the average degree and the
average community size of the network respectively.
Algorithm 1.
Input:
The target network: G = (V,E)
The Node Relationship classifier: model
Output:
Community information C
1: Extract the data from the target network G for
node relationship classification.
2: Use the model to classify the node relationship
and get the classified result R.
3: for node in V do
4: for neighbor in node’s neighbors do
5: if node and neighbor belong to the same
community according to R then
6: Compute the modularity M1 if they
are not in the same community
7: Compute the modularity M2 if they
are in the same community
8: if M2 >M1 then
9: Node and neighbor belong to the
same community
10: end if
11: end if
12: end for
13: end for
14: return C
4 NUMERICAL EXPERIMENTS
In this section, we evaluate the performance of CDNC
on both the real-world networks and synthetic net-
works and compare it with other representative com-
munity detection algorithms including GN, LPA,
WalkTrap, Infomap, Multilevel, and FG.
4.1 Training Data
Several networks generated by LFR Benchmark (Lan-
cichinetti et al., 2008) are used to extract the training
dataset to train the binary classifier. The parameter of
LFR Benchmark generating networks is illustrated in
Table 1. The total number of nodes varies from 100
to 1000; the average degree varies from 10 to 50; the
maximum degree varies from 40 to 80; the mixing pa-
rameter µ varies from 0.1 to 0.9.
Table 1: The main parameters of LFR Benchmark to gener-
ate training networks.
Parameter N t1 t2 K Maxk µ
100-1000 2 1 10-50 40-80 0.1-0.9
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
598

4.2 Evaluation Metrics
To quantify the performance of community detection
algorithms, Normalized Mutual Information (NMI)
(Danon et al., 2005) and Adjusted Rand Index (ARI)
(Rand, 1971) are selected to evaluate the perfor-
mance. NMI is a metric to measure the similarity be-
tween different sets, which measures how close the
predicted communities are to the ground truth, and is
defined as:
NMI(X ,Y ) =
−2
∑
C
x
i=1
∑
c
y
j=1
N
i j
log
N
i j
N
N
i
N
j
∑
c
x
i=1
N
i
log
N
i
N
+
∑
c
y
j=1
N
j
log
N
j
N
(1)
where x is the real partition, y is partition found by
the algorithm, c
x
is the number of communities in x
and c
y
is the number in y, N is the number of nodes
in the network, N
i j
is the number of nodes shared by
community i in x and community j in y, N
i
denotes
the sum over row i of matrix N
i j
, and N
j
denotes the
sum over column j. ARI is also a metrics to com-
pare two partitions, evaluating the outcome of an al-
gorithm, which is defined as:
ARI =
∑
i j
n
i j
2
− [
∑
i
a
i
2
∑
j
b
j
2
]/
n
2
1
2
[
∑
i
a
i
2
+
∑
j
b
j
2
] − [
∑
i
a
i
2
∑
j
b
j
2
]/
n
2
(2)
where n
i j
, a
i
and b
j
are values from the contingency
table.
4.3 Simulation on Real-world Networks
In this section, we evaluate our proposed algorithm
CDNC on several real-world networks to demonstrate
its superiority compared to several representative
community detection algorithms. These real-world
networks including Zachary’s karate club (Zachary,
1977), Dolphin (Lusseau et al., 2003), Polbooks,
and American college football (Girvan and Newman,
2002) are widely used to assess the performance of
community detection algorithms. The statistics of
these networks are listed in Table 2. Karate is a
friendship network among 34 members in a karate
club, which is divided into two groups. Dolphins
is a social network of frequent associations among
62 dolphins where nodes represent dolphins, edges
represent the association. Polbooks is a network
of books about US politics where nodes represent
books, edges between books represent frequent co-
purchasing of books. Football is an undirected net-
work from the American football games, where nodes
represent teams, and an edge represents a match be-
tween two teams.
Table 2: Statistics of several real-world networks with
ground-truth partition.
Network Nodes Edges Communities Average degree
Karate 34 78 2 4.5
Dolphins 62 159 2 5.1
Polbooks 105 441 3 8.4
Football 115 613 12 10.6
Table 3: Results of CDNC and other methods in terms of
NMI and ARI on the four real-world networks with ground-
truth partition.
Karate Dolphins Polbooks Football
NMI ARI NMI ARI NMI ARI NMI ARI
CDNC 1.00 1.00 0.77 0.83 0.56 0.69 0.89 0.78
Infomap 0.69 0.70 0.56 0.36 0.49 0.53 0.91 0.89
Multilevel 0.58 0.46 0.51 0.32 0.51 0.55 0.89 0.80
FG 0.69 0.68 0.57 0.45 0.53 0.63 0.69 0.47
GN 0.57 0.46 0.55 0.39 0.55 0.68 0.87 0.77
LPA 0.83 0.88 0.59 0.44 0.50 0.53 0.90 0.82
WalkTrap 0.50 0.33 0.53 0.41 0.54 0.65 0.88 0.81
The experimental result is illustrated in Table 3.
Compared with other algorithms, CDNC achieves the
highest NMI and ARI values in Karate, Dolphins, and
Polbooks, which indicates CDNC can provide a more
robust community structure with better partition qual-
ity. In Football, Infomap performs the best. In a word,
CDNC works better on these real-world networks.
4.4 Simulation on Synthetic Networks
We generate several synthetic networks to evaluate
CDNC and other competing algorithms with LFR
Benchmark, which has some parameters to control
the attributes of the generated networks. The mixing
parameter µ is one of these parameters, which con-
trol the complexity of networks by inter-community
edges. The inter-community edges, also called noise
edges, are added more and more to a synthetic net-
work while increasing the mixing parameter µ. Here
we mainly explore the influence of the complexity and
size of networks on the performance of these commu-
nity detection methods.
First, we verify the influence of the size of net-
works on the performance of these algorithms by in-
creasing the number of nodes from 1k to 10k and fix-
ing other parameters. The results of the algorithms
are shown in Figure 2, where Figure 2 shows the re-
sults of NMI, and Figure 3 shows the results of ARI.
We find that the performance of our algorithm, LPA,
and WalkTrap is much better than other algorithms
no matter on NMI or ARI, and almost without fluctu-
ation.
Then, we demonstrate the influence of the com-
plexity of networks on the performance of these algo-
rithms. We fix other parameters to N = 1000, K = 20,
Community Detection based on Node Relationship Classification
599
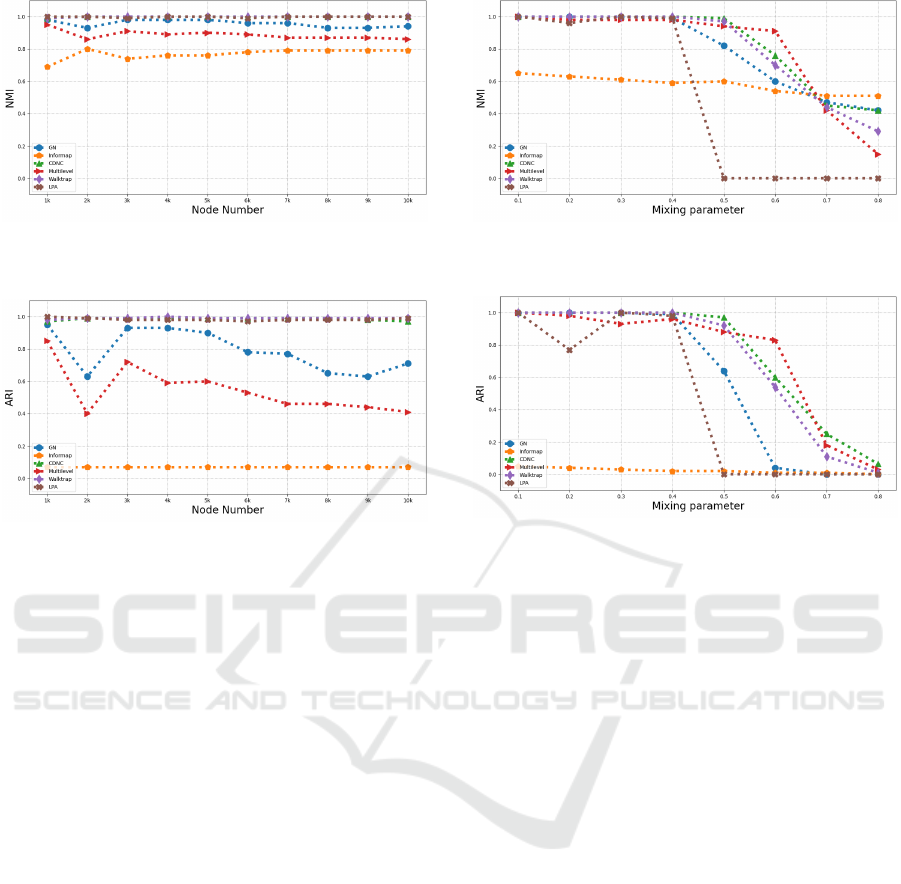
Figure 2: Results of different algorithms in terms of NMI
on synthetic networks with varying numbers of nodes.
Figure 3: Results of different algorithms in terms of ARI on
synthetic networks with varying numbers of nodes.
MaxK = 100 and vary the mixing parameter µ from
0.1 to 0.8 to generate a series of networks with dif-
ferent quantities of noise edges. The results of the
algorithms are shown in Figure 4 and Figure 5, where
Figure 4 shows the results of NMI and Figure 5 shows
the results of ARI. With the increasing of µ, the ef-
fectiveness of all algorithms is attenuated. When µ
is between 0.1 and 0.5, our algorithm always has the
best performance. When µ = 0.6, the result of CDNC
is worse than Multilevel but better than other algo-
rithms both in Figure 4 and 5. When µ is bigger than
0.7, Infomap performs the best, CDNC and GN algo-
rithms perform slightly worse than it but better than
others in Figure 4. In Figure 5, we can see that our
algorithm performs better than other algorithms, only
when µ=0.6, Multilevel algorithm has a higher ARI
value.
5 CONCLUSIONS
In this paper, we transform community detection to
node relationship classification and propose an algo-
rithm called CDNC to detect community structure
based on node relationship classification. A binary
classifier is trained to classify node relationship which
considers both the global influence and the local in-
fluence. The experiments demonstrate that our algo-
Figure 4: Results of different algorithms in terms of NMI
on synthetic networks with varying mixing parameter.
Figure 5: Results of different algorithms in terms of ARI on
synthetic networks with varying mixing parameter.
rithm has higher accuracy compared to other repre-
sentative algorithms on both the synthetic and real-
world networks. In the future, we hope to implement
CDNC in parallel and use it for overlapping commu-
nity detection.
ACKNOWLEDGEMENTS
This work was supported in part by the National Key
Research and Development Program of China under
Grant 2016YFB0801100
REFERENCES
Benigni, M. C., Joseph, K., and Carley, K. M. (2017). On-
line extremism and the communities that sustain it:
Detecting the isis supporting community on twitter.
PloS one, 12(12):e0181405.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-
vre, E. (2008). Fast unfolding of communities in large
networks. Journal of statistical mechanics: theory
and experiment, 2008(10):P10008.
Cai, B., Wang, Y., Zeng, L., Hu, Y., and Li, H. (2020).
Edge classification based on convolutional neural net-
works for community detection in complex network.
Physica A: Statistical Mechanics and its Applications,
556:124826.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
600

Danon, L., Diaz-Guilera, A., Duch, J., and Arenas, A.
(2005). Comparing community structure identifica-
tion. Journal of statistical mechanics: Theory and ex-
periment, 2005(09):P09008.
Ding, J., Sun, Y.-z., Tan, P., and Ning, Y. (2018). Detecting
communities in networks using competitive hopfield
neural network. In 2018 International Joint Confer-
ence on Neural Networks (IJCNN), pages 1–7. IEEE.
Dong, L., Li, R., Zhang, J., and Di, Z. (2016). Population-
weighted efficiency in transportation networks. Scien-
tific reports, 6(1):1–10.
Fortunato, S. (2010). Community detection in graphs.
Physics reports, 486(3-5):75–174.
Girvan, M. and Newman, M. E. (2002). Community struc-
ture in social and biological networks. Proceedings of
the national academy of sciences, 99(12):7821–7826.
Goltsev, A. V., Dorogovtsev, S. N., Oliveira, J. G., and
Mendes, J. F. (2012). Localization and spreading of
diseases in complex networks. Physical review letters,
109(12):128702.
Grover, A. and Leskovec, J. (2016). node2vec: Scal-
able feature learning for networks. In Proceedings
of the 22nd ACM SIGKDD international conference
on Knowledge discovery and data mining, pages 855–
864.
Hamers, L. et al. (1989). Similarity measures in scientomet-
ric research: The jaccard index versus salton’s cosine
formula. Information Processing and Management,
25(3):315–18.
Hu, F., Liu, J., Li, L., and Liang, J. (2020). Community
detection in complex networks using node2vec with
spectral clustering. Physica A: Statistical Mechanics
and its Applications, 545:123633.
Hu, K., Hu, J.-B., Tang, L., Xiang, J., Ma, J.-L., Gao,
Y.-Y., Li, H.-J., and Zhang, Y. (2018). Predicting
disease-related genes by path structure and commu-
nity structure in protein–protein networks. Journal
of Statistical Mechanics: Theory and Experiment,
2018(10):100001.
Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008).
Benchmark graphs for testing community detection
algorithms. Physical review E, 78(4):046110.
Li, H.-J., Wang, L., Zhang, Y., and Perc, M. (2020). Opti-
mization of identifiability for efficient community de-
tection. New Journal of Physics, 22(6):063035.
Li, H.-J., Zhang, J., Liu, Z.-P., Chen, L., and Zhang, X.-S.
(2012). Identifying overlapping communities in social
networks using multi-scale local information expan-
sion. The European Physical Journal B, 85(6):1–9.
Lusseau, D., Schneider, K., Boisseau, O. J., Haase, P.,
Slooten, E., and Dawson, S. M. (2003). The bot-
tlenose dolphin community of doubtful sound features
a large proportion of long-lasting associations. Behav-
ioral Ecology and Sociobiology, 54(4):396–405.
Moradi, M. and Parsa, S. (2019). An evolutionary method
for community detection using a novel local search
strategy. Physica A: Statistical Mechanics and its Ap-
plications, 523:457–475.
Moradi, P., Ahmadian, S., and Akhlaghian, F. (2015). An
effective trust-based recommendation method using a
novel graph clustering algorithm. Physica A: Statisti-
cal mechanics and its applications, 436:462–481.
Newman, M. E. (2004). Fast algorithm for detecting com-
munity structure in networks. Physical review E,
69(6):066133.
Newman, M. E. and Girvan, M. (2004). Finding and eval-
uating community structure in networks. Physical re-
view E, 69(2):026113.
Pearson, K. (1905). The problem of the random walk. Na-
ture, 72(1867):342–342.
Pons, P. and Latapy, M. (2005). Computing communities
in large networks using random walks. In Interna-
tional symposium on computer and information sci-
ences, pages 284–293. Springer.
Raghavan, U. N., Albert, R., and Kumara, S. (2007).
Near linear time algorithm to detect community struc-
tures in large-scale networks. Physical review E,
76(3):036106.
Rand, W. M. (1971). Objective criteria for the evaluation of
clustering methods. Journal of the American Statisti-
cal association, 66(336):846–850.
Rosvall, M. and Bergstrom, C. T. (2008). Maps of random
walks on complex networks reveal community struc-
ture. Proceedings of the national academy of sciences,
105(4):1118–1123.
Wang, H., Hernandez, J. M., and Van Mieghem, P. (2008).
Betweenness centrality in a weighted network. Phys-
ical Review E, 77(4):046105.
Wang, Z., Wu, Y., Li, Q., Jin, F., and Xiong, W. (2016). Link
prediction based on hyperbolic mapping with commu-
nity structure for complex networks. Physica A: Sta-
tistical Mechanics and its Applications, 450:609–623.
Zachary, W. W. (1977). An information flow model for con-
flict and fission in small groups. Journal of anthropo-
logical research, 33(4):452–473.
Zheng, J., Wang, S., Li, D., and Zhang, B. (2019). Per-
sonalized recommendation based on hierarchical in-
terest overlapping community. Information Sciences,
479:55–75.
Zong-Wen, L., Jian-Ping, L., Fan, Y., and Petropulu, A.
(2014). Detecting community structure using label
propagation with consensus weight in complex net-
work. Chinese Physics B, 23(9):098902.
Community Detection based on Node Relationship Classification
601
