Statistical Model Checking for Probabilistic Temporal Epistemic Logics

Yenda Ramesh

and M. V. Panduranga Rao

Dept. of Computer Science and Engineering, Indian Institute of Technology Hyderabad, Sangareddy, Telangana, India

Keywords:

Probabilistic Epistemic Temporal Logics, Statistical Model Checking, Multi Agent Systems.

Abstract:

Interpreted Systems and epistemic temporal logics have been employed extensively to study the notion of

knowledge in Multi-Agent Systems. New model checking algorithms, as well as adaptations of existing algo-

rithms to this setting have been reported. For the most part, these algorithms have focused on exhaustive state

space exploration based approaches. While these approaches yield accurate results to model checking queries,

they are often expensive for realistic scenarios. So much so that, many of the applications studied in academic

literature deal with small state spaces. In order to scale to real life multi-agent systems with large state spaces,

an alternative to exhaustive exploration based techniques is needed. Statistical Model Checking was proposed

to alleviate this problem when model checking stochastic systems against temporal logic queries. In this paper,

we extend this technique to epistemic temporal logics. The ﬁrst version of the approach, which we call the

vanilla approach, would be to simply generate Monte Carlo samples of the runs of the system and evaluate the

query on them. The advantage that SMC is expected to bring is greatly diminished due to the knowledge op-

erator in such systems of logic. For large systems, this would entail an exhaustive exploration of epistemically

accessible global states. Our major contribution is to introduce a sampling based approach for the knowledge

operator as well. We show that this results in signiﬁcant performance gains at the expense of a marginal loss

in accuracy (1-2% in experimental results) for most epistemic operators. Speciﬁcally, we show evidence of a

dramatic improvement in time complexity for large Multi-Agent Systems. We substantiate the effectiveness

of the approach through case studies that involve a large number of agents.

1 INTRODUCTION

Multi-Agent Systems (MASs) have been used exten-

sively in the recent past to model Artiﬁcial Intelli-

gence, emergent behavior and cooperative and adver-

sarial systems. Several complex systems and deci-

sion support systems have been modeled and studied

as MAS. Such systems have been subjected to study

and analysis through techniques like formal methods

in Computer Science. Of particular interest is analysis

through model checking.

Traditionally, model checking has been used ex-

tensively to study reactive systems (Baier and Katoen,

2008). Model Checking involves algorithmically de-

ciding whether or not a system satisﬁes a desired

property. Naturally, both the system and the desired

property have to be described formally to be fed to the

algorithm. The system is usually described through

some variant of a Kripke Structure and the property,

as a formula in an appropriate temporal logic (Ben-

https://orcid.org/0000-0001-8232-8269

https://orcid.org/0000-0003-3761-8501

Ari et al., 1981; Pnueli, 1977; Vardi, 1996). For ex-

ample, modeling formalisms like Labeled Transition

Systems have successfully captured evolution dynam-

ics of reactive systems. However, they fall short of be-

ing able to model features of MAS that are pertinent

to artiﬁcial intelligence and decision making.

Fagin et al. (Fagin et al., 2003) proposed the use of

epistemic modal logic to capture the notion of knowl-

edge possessed by an agent. The knowledge opera-

tor that they deﬁned for computationally grounded se-

mantics (“Agent i knows that φ”) can also be extended

to other epistemic modalities like group knowledge,

distributed knowledge and common knowledge. The

introduction of the Interpreted Systems formalism al-

lowed MAS to be modeled by Kripke-like structures

enhanced by the epistemic or the knowledge compo-

nent, giving a computationally grounded semantics to

these modalities. Thus, it became possible to model

both dynamics and knowledge possessed by agents

naturally. Coupled with various systems of Epistemic

Temporal Logic (ETL), this provided a potent tool

for analysis of MAS. In this work, we use a proba-

bilistic extension of Interpreted Systems. We mention

Ramesh, Y. and Rao, M.

Statistical Model Checking for Probabilistic Temporal Epistemic Logics.

DOI: 10.5220/0010847900003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 53-63

ISBN: 978-989-758-547-0; ISSN: 2184-433X

that other versions of modal logic with, for example,

deontic and doxastic modalities have also been pro-

posed, which we will not consider in this work (Kauf-

mann et al., 2008).

For stochastic reactive systems, an alternative ap-

proach to exact model checking algorithms (that in-

volve exhaustive state space exploration) was pro-

posed (Nimal, 2010; Agha and Palmskog, 2018;

Younes et al., 2010; Legay et al., 2010). This ap-

proach, called Statistical Model Checking (SMC) is

essentially based on a Monte-Carlo sampling of the

runs of the system. Intuitively, the fraction of runs

that evaluate the formula to TRUE decides the out-

come of the model checking query. This variant has

found particular traction in situations where a trade-

off between accuracy and time/space complexity is

acceptable (Younes et al., 2004). This approach has

been extended to different variants of Stochastic Multi

Agent Systems (SMASs) as well (Herd et al., 2015b;

Herd et al., 2015a).

In this work, we propose an SMC algorithm

to check Probabilistic Epistemic Temporal logic K-

PCTL(B) against a stochastic version of Interpreted

Systems. A straightforward adaptation of the SMC

approach to this problem would be to simulate several

runs of the system and evaluate the epistemic tempo-

ral logic formulas on them. Indeed, this does give a

ﬁrst cut SMC algorithm. However, a bottleneck re-

mains for efﬁcient evaluation of the knowledge oper-

ator at a time step.

In the worst case, a (Stochastic) Multi Agent Sys-

tem with n agents having k local states each, has a

state space of size k

. This results in a running time

that is exponential in the number of agents. For sys-

tems that have a large number of agents, such time

complexity is expensive–most of the case studies re-

ported in literature involve small sized models. As ex-

ample of a system whose analysis can be expensive,

consider the spread of a pandemic among n agents.

Suppose φ is a propositional formula that evaluates

to TRUE iff at least 60% agents are infected. A perti-

nent query that would involve both temporal and epis-

temic operators is “What is the probability that agent i

knows that φ before τ time steps?”. Another example,

which has been constructed by Wan et al (Wan et al.,

2013), is that of online supermarkets. This system

has two agents, a customer agent and a server agent.

A useful query in this context is “what is the probabil-

ity that when a customer places an order online, she

knows that at least 90% of the items will be shipped

successfully?”.

Given this, we propose a sampling approach to

evaluate the knowledge operator as well. This needs

some innovation in the way the sampling is done, in

accordance with the knowledge operator. We analyze

the impact of this sampling approach on the accuracy,

and the resulting speed-up. We show empirical ev-

idence for a substantial improvement over the brute

force SMC for queries of nesting level of one. We

remark that we do not report evaluation of our sam-

pling approach against numerical approaches, as it is

well known that they do not scale well for systems

with a large state space. While the advantage of the

sampling algorithm over the brute force SMC is to be

expected, what is surprising is the degree of accuracy

that is achieved for a running time that is several or-

ders of magnitude lesser.

The paper is structured as follows. We begin, in

the next section, with a brief introduction to some pre-

liminary ideas, terminology and notation that will be

used in the rest of the paper. In section 3, we discuss

the SMC algorithms for various epistemic operators,

both brute force (which we call the “Vanilla” SMC al-

gorithm) and the Epistemic Sampling (ES) algorithm.

In section 4, we report case studies that substantiate

the effectiveness of the ES algorithm. To put our work

in context with some of the existing state of the art, we

discuss related work in section 5. We conclude the

paper in section 6, with a brief discussion of future

directions.

2 PRELIMINARIES

In this section, we discuss some basic deﬁnitions and

concepts that will be useful subsequently.

A Multi Agent System consists of several agents,

each of which can be in one of several local states. It

is also customary to designate a special environment

agent that is distinct from all other agents. Formally,

let A = {1.. .,n} denote a set of n agents. Corre-

sponding to each agent i ∈ A is a set L

of local states,

and a set of actions Act

. We denote the state of agent i

at time t by l

(t) ∈ L

. Similarly, l

(t) for the environ-

ment. Evolution of the system is essentially change

of states of these agents. The state space of the entire

system can therefore be described set of global states

G ⊆ L

× L

× ... × L

. One can then talk of a global

state g(t) ∈ G at time t that is a tuple aggregated from

the local states: g(t) = (l

(t).. .l

(t)l

(t)).

Associated with each agent i is a protocol A

, and

with the environment, a protocol A

that changes its

local state at each time step, in accordance with the

corresponding the action:

(t)

: α ∈ Act

−−−−−−→ l

(t + 1)

for l

(t),l

(t + 1) ∈ L

. Similarly, for the environment

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

agent:

(t)

: α ∈ Act

−−−−−−−→ l

(t + 1)

Consequently, the global state evolves from g(t) =

(t) ... l

(t)l

(t)) to g(t + 1) = (l

(t + 1). ..l

(t +

1)l

(t +1)). We can also deﬁne the initial global state:

= (l

,. ..l

), where l

are the local initial states.

We denote the local state of an agent i within a global

state g(t) by g(t)

We can also deﬁne a labeling function L : G →

, where AP is a set of atomic propositions that hold

true on a global state. An Interpreted System then, is

the tuple h(L

)

i∈A

,AP,Li, where i runs over all

agents and g

is a starting global state.

The evolution protocol is speciﬁc to the applica-

tion. Since we are interested in stochastic multi-agent

systems in this paper, we now discuss evolution for

such systems.

2.1 Stochastic Multi Agent Systems

A simple example of stochastic evolution is the case

when the agents are modeled as a Discrete Time

Markov Chain (DTMC). The evolution protocol A

for

an agent i is then simply a stochastic matrix P

with el-

ements p

(t)

−−→ l

(t + 1),

where p

is the probability of transition from the

state l

to l

and

∑

= 1. In the simplest set-

ting, action symbols may be omitted. The Stochastic

Multi Agent System is then merely an aggregation of

DTMCs–one DTMC for each agent. For incorporat-

ing synchronization and interaction, they can be aug-

mented with action symbols (Delgado and Benevides,

2009). For the purposes of demonstrating the sam-

pling approach over epistemic operators, the former

formulation sufﬁces. Indeed, this is what we employ

in this paper.

2.2 Epistemic Accessibility

For each agent i, we deﬁne the epistemic accessibil-

ity relation ∼

between the global states in G at time

snapshot t as follows: g(t) ∼

(t) if and only if

g(t)

= g

(t)

. In other words, two global states belong

to the same equivalence class with respect to ∼

if and

only if the local state of agent i is the same in both

the global states. Epistemically, these global states

are indistinguishable for agent i. Alternatively, these

global states are said to be epistemically accessible to

each other. Informally speaking, if a fact “holds” in

all such global states, the agent is said to know the

fact. We will formalize this notion later in subsection

2.4, while deﬁning the semantics of epistemic formu-

las.

We are now in a position to deﬁne global

model for an SMAS, which is a tuple hG,g

,{P

,∼

}

i∈A

,AP,Li where

• G, the set of global states, g

an initial global state,

the stochastic transition matrices for each agent

i and ∼

, the epistemic accessibility relations are

as deﬁned earlier.

• AP is a set of atomic propositions

• L : G → 2

is a labeling function that assigns

atomic propositions to the states in G.

Such a structure can be subjected to analysis

against desired properties through model checking. In

this paper, we will use K-PCTL(B) as the temporal

epistemic logic for formulating queries. As a running

example, we model simple epidemic dynamics in this

formalism. At any given point in time, every individ-

ual (agent) in the population is in one of the follow-

ing health states (Kermack and McKendrick, 1927):

Susceptible (S), Infected (I) or Recovered (R). The

transition from S to I to R is modeled as a simple

three-state DTMC. We use one atomic proposition a

on the set of global states that evaluates to TRUE for

all and only those global states with at least 60% of

the agents in the I state. Then an example query of

interest is: “what is the probability that agent i knows

that at least 60% of the population is infected?”

2.3 Measurability

An important criterion for statistical model check-

ing, and indeed probabilistic model checking, is that

the set of runs or trajectories should form a measur-

able set (Agha and Palmskog, 2018). It turns out

that this is indeed the case for a large variety of

practical stochastic systems–ranging from DTMCs to

stochastic discrete event systems. In particular, in our

setting, the deﬁnitions of the measurable space–the

sample space, the sigma algebra and the probability

measure–that is valid for Probabilistic Computation

Tree Logic (PCTL) model checking for DTMCs re-

main unchanged (Baier and Katoen, 2008). As we

will see in the next section, the only change will be

in the statistical model checking algorithm’s ability

to estimate the probability accurately. Speciﬁcally,

the algorithm for assigning truth values to the (state)

knowledge operators will be a (one-sided error) ran-

domized algorithm, prone to false positives.

2.4 K-PCTL(B)

Probabilistic extensions to Epistemic Temporal Log-

ics have been explored extensively in the past. For

Statistical Model Checking for Probabilistic Temporal Epistemic Logics

example, Delgado and Benevides (Delgado and Bene-

vides, 2009) introduced the Probabilistic Epistemic

Temporal Logic (PETL), which was revisited by Fu et

al (Fu et al., 2018) as K-PCTL. K-PCTL is PCTL aug-

mented with epistemic modalities. Since PCTL(B),

(PCTL with bounded Until) is a fragment of K-

PCTL(B), we will review PCTL syntax and semantics

when discussing K-PCTL(B). For statistical model

checking, the most conducive approach is to replace

the Until fragment of K-PCTL with the bounded Un-

til fragment. This is because, as will be seen shortly,

traditional SMC algorithms work by sampling ﬁnite-

length runs of the system. We call this version the

Bounded Probabilistic Computation Tree Logic of

Knowledge (K-PCTL(B)).

Syntactically, K-PCTL(B) has the following

grammar

φ := TRUE | a | φ ∧ φ | ¬φ | K

φ | E

φ | D

φ | C

| Pr

ψ = Xφ | φU

≤τ

where a ∈ AP is an atomic proposition.

We need the following terminology before dis-

cussing the semantics of the above grammar. A path

fragment σ = g

....g

is a sequence of global states

in the execution of the system M over T discrete time

units and where each state g

corresponding to state of

the system at t

time instant i.e. σ[t] = g

. The fact

that a state g (or a path σ) satisﬁes a K-PCTL(B) state

formula φ (or a path formula ψ) is denoted by g |= φ

(or σ |= ψ). Building upon the ∼

relation, we can de-

ﬁne relations that involve multiple agents. These re-

lations are ∼

i∈G

∼

, ∼

i∈G

∼

and ∼

, the

transitive closure of ∼

, where G is a group of agents.

These relations in turn are useful in deﬁning epis-

temic operators that involve a group of agents. Impor-

tant examples are the group, distributed and common

knowledge operators.

Semantics of the K-PCTL(B) is as follows. We

ﬁrst list semantics for the state formulas, which are

common in probabilistic temporal logic, along with

the epistemic fragment.

We note that there exists another popular variant of the

probabilistic operator: Pr

θ

, where ∈ {<,≤,≥, >} is a

comparison operator and θ ∈ [0,1].

State formulas:

g |= TRUE

g |= a iff a is true in the state s

g |= Φ

∧ Φ

iff g |= Φ

and g |= Φ

g |= ¬Φ iff g 2 Φ

Epistemic formulas:

g |= K

φ iff ∀g

∈ G,

g ∼

=⇒ g

|= φ

g |= E

φ iff g ∼

=⇒ g

|= φ

g |= D

φ iff g ∼

=⇒ g

|= φ

g |= C

φ iff g ∼

=⇒ g

|= φ

The K

φ operator says that “agent i knows that φ

(is TRUE)” if and only if φ is TRUE in all epistemi-

cally accessible global states–namely the global states

that are epistemically indistinguishable for agent i.

The group knowledge operator E

evaluates to

TRUE if and only if every agent in the group G knows

that φ.

The distributed knowledge operator D

evaluates

to TRUE if and only if the agents in the group G to-

gether know that φ. In other words, while individual

agents may not know that φ is TRUE, it can be in-

ferred from the knowledge possessed by the individ-

ual agents.

Finally, the common knowledge operator C

evaluates to TRUE if all the agents in the group G

know that φ, they all know that they know φ, ad in-

ﬁnitum. We use a syntactic characterization on the

model for designing the algorithm.

Now, we discuss the semantics of the path formu-

las, noting that σ[t] denotes the t

state in the path:

Path formulas:

σ |= X φ iff σ[1] |= φ

σ |= φ

≤τ

iff ∃j ≤ τ | σ[ j] |= φ

and ∀t < j | σ[t] |= φ

Finally, P

ψ estimates the probability measure of the

paths σ that start in g, and satisfy ψ.

We remark that PCTL(B) is K-PCTL(B) without

the epistemic fragment, namely, K

and C

PCTL is PCTL(B) augmented with the unbounded

until operator U with the semantics:

σ |= φ

Uφ

iff ∃j | σ[ j] |= φ

,and ∀t < j | σ[t] |= φ

2.5 Statistical Model Checking

Statistical Model Checking (SMC) works by Monte

Carlo sampling. Runs of the system are generated

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

through simulation and the temporal logic formula is

evaluated. SMC comes in two ﬂavors. The ﬁrst one,

generally referred to as qualitative SMC, involves

techniques like hypothesis testing to decide whether

a formula is TRUE or not. The second one, called

the estimation technique, tries to estimate the prob-

ability of a formula being true. In any case, the ap-

proach works by generating several runs (say, N) of

the system and evaluating the query on each run. In

the estimation problem, a Bernoulli random variable

is set to 1 iff the formula evaluates to TRUE the r

run. An estimate of the probability that the formula

is true is

∑

. Clearly, as the number of runs grows,

the accuracy of the estimate improves. Tail inequali-

ties like the Chernoff-Hoeffding bounds can be used

to estimate the minimum number of runs needed for a

desired accuracy and conﬁdence.

3 SMC ALGORITHMS FOR

EPISTEMIC OPERATORS

K-PCTL(B)

In this section, we discuss our main algorithms. Start-

ing with the basic knowledge operator in combination

with temporal operators, we move on to group, dis-

tributed and common knowledge operators.

3.1 SMC for K

φ (with Temporal

Operators)

We ﬁrst discuss the model checking subroutine for

the epistemic operator K

φ. We have to decide if

a global state g satisﬁes K

φ. An exhaustive algo-

rithm would work by looking at all the global states

that are epistemically accessible from g via the re-

lation ∼

((Delgado and Benevides, 2009)). The

global state g |= K

φ, if and only if φ is TRUE at

all such states. Once the truth value of K

φ is as-

certained, it is straightforward to evaluate larger for-

mula like Pr

≤τ

] through standard algo-

rithms (Baier and Katoen, 2008).

The computational bottleneck in this approach lies

in the following scenario. If there are n agents each

having k

local states, the number of epistemically ac-

cessible states can potentially be Π

. For example, if

all agents have the same number k of local states, the

global state space is of size k

. Exploring the entire

state space in the worst case is computationally very

expensive.

However, this gives a ﬁrst-cut SMC algorithm.

The algorithm proceeds by generating sample runs of

the system, as in the case of the SMC algorithm for

probabilistic temporal logics. For evaluation of the

epistemic operators, the algorithm resorts to exhaus-

tively visiting all epistemically accessible valid states.

We will call this the “Vanilla” SMC algorithm.

Can we extend the sampling procedure for evalu-

ating the truth value of epistemic operators as well?

The approach that we propose is to sample a “small”

number M of epistemically accessible states and

check if φ is TRUE or not, for only these states. We

call this the “Epistemic Sampling” (ES) Statistical

Model Checking approach. The approach for K

φ is

outlined in Algorithm 1. Let the global state of the

system at time t be g(t). The procedure K

for eval-

uating the knowledge operator takes in as input the

current global state g(t), the agent i for whom the

knowledge operator is to be evaluated, a user decided

sample size M, along with the SMAS. In the cur-

rent global state, suppose agent i has the local state

. Then in line 3, the algorithm calls a sampling rou-

tine to construct a sample S of the global states that

are epistemically accessible to g. The sampling rou-

tine is detailed in Algorithm 2. The procedure returns

TRUE if and only if all states in S satisfy φ. The sam-

pling routine works as follows. A global state is gen-

erated uniformly at random. One way of doing this

is as follows. For each agent, generate its local state

(uniformly) at random. Other ﬂavors could do this

without replacement. Line 6 is crucial, and depends

on the application at hand. A global state generated in

this way may be “illegal” due to two reasons: (a) the

state is semantically not possible in the system and

(b) it is epistemically inaccessible from g. Otherwise,

such a state would be called legal. This decision is

made by the isLegal function in line 6. A total of M

legal states generated this way are populated into the

set S and is returned. If isLegal is efﬁciently com-

putable (say in O(n

), for some constant c), then the

routine takes O(Mn

) steps. This is a signiﬁcant sav-

ing in comparison to the k

steps needed to explore

the state space exhaustively.

Algorithm 1.

1: procedure K

(g, i, Φ, M, SMAS)

2: Let the current (local) state of agent i be l

3: S ← A M-sized set of epistemically accessible

global states

4: if φ is TRUE in all states in S then

5: Return “yes”

6: else

7: Return “No”

However, this sampling has consequences on ac-

curacy. The following lemma is easy to see.

Lemma 1. If φ is TRUE on all epistemically accessi-

ble states, then Algorithm 1 returns TRUE. In other

words, the probability of false negatives is zero.

Statistical Model Checking for Probabilistic Temporal Epistemic Logics

Algorithm 2.

1: procedure SMC(M, SMAS)

2: Count ← 0, S ← Φ

3: while Count ≤ M do

4: Sample a global state uniformly at random

5: //For all agents j 6= i, generate a local state

6: if isLegal(g) then

7: S ← S

8: Count ← Count + 1

9: if no new global states to sample then

10: break

11: Return S

On the other hand, the formula φ may not be

TRUE on all the epistemically accessible global

states. Then, the algorithm could report a false posi-

tive if the sampling routine does not generate at least

one global state where φ is not TRUE. This leads to

the following lemma.

Lemma 2. If φ is FALSE on a fraction f > 0 of all

epistemically accessible global states, then the Algo-

rithm 1 will output FALSE with probability at least

1 − (1 − f )

Proof. Suppose g 6|= K

φ. Let the fraction of epis-

temically accessible global states that do not satisfy

φ be at least f . Then, in M samples, the probabil-

ity that a satisfying global state is always picked is at

most (1 − f )

. This is the probability of false pos-

itive at any given time step. Therefore, the proba-

bility that the false positive does not occur is at least

1 − (1 − f )

Therefore, the larger the fraction of global states

where φ is FALSE, the higher the chance that such

a state will be picked, and therefore, the lower the

chance of a false positive.

Hence, for example,

Corollary 1. For the formula Pr

(T U

≤τ

φ),

the probability that a false positive does not occur is

at least (1 − (1 − f )

)

We can also bound the false positive probabil-

ity for the bounded until fragment when both the

operands are epistemic operators.

Corollary 2. Let K

φ and K

φ be FALSE at every

step. Let the probability of false positive evalua-

tion by the ES algorithm at any point in time be,

for K

φ be p

and that for K

φ be p

. Then, for

the formula Pr

≤τ

], Pr[False positive] ≤

(1 − p

)

(1 − p

)

Proof. Suppose a run is (falsely) declared TRUE for

the formula, at time t. This will happen if K

is (falsely) evaluated to TRUE for t − 1 steps, af-

ter which K

is (falsely) evaluated to TRUE. For

the corresponding false positive probabilities, the

probability of false positive is (1 − p

)

M(t−1)

(1 −

)

. This is bounded from above by (1 − p

)

(1 −

)

We remark that Pr

≤τ

] can evaluate

to FALSE in other ways as well. For example, the

φ can be TRUE at all steps before τ, but K

φ never

evaluates to TRUE for all t ≤ τ. Analogous analysis

can be performed for these cases individually, which

we omit in the interest of space.

As a consequence of the above discussion, it is

easy to see that a given run of the system has the

following properties. A run that evaluates to TRUE

in the Vanilla SMC algorithm will also be evaluated

to TRUE by the ES algorithm. However, some runs

in the Vanilla SMC that evaluate to FALSE might

be evaluated to TRUE by the ES algorithm. Hence,

some of the Bernoulli random variables would take

the value 1, when in fact they should be 0.

Recall that the probability of false positives can be

controlled by the number M of epistemically acces-

sible states sampled. The presence of false positives

shifts the average of the distribution. It is easy to show

that if the false positive rate is small, so is the error in

probability estimation.

Theorem 3. Let the probability of false positive eval-

uation of the formula in the ES algorithm be p

f p

≈

δN

for δ > 0. Then, the probability that the estimate given

by the ES algorithm deviates from the actual mean p

is the same as that for the Vanilla algorithm.

Proof. Consider the vanilla algorithm that has N runs.

Let the outcomes of the N runs be deﬁned by inde-

pendent Bernoulli random variable X

, 1 ≤ N, and

∑

i=1

= X. Let p be the actual probability of the

formula being satisﬁed. Then, a simple application of

the Chernoff bound shows that

Pr(X ≥ (1 + δ)N p) ≤



(1 + δ)

(1+δ)



N p

for any δ > 0.

Consider now the Epistemic Sampling algorithm.

As we say previously, in this algorithm, some runs

may yield false positives. Let the number of runs now

be N

. Let the sum of the N

Bernoulli random vari-

ables be X

. The mean shifts to p + p

f p

where p

f p

the term due to false positives. We now bound from

above the probability that this random variable X

larger than the (1 + δ)N p. Then, an easy derivation

from ﬁrst principles follows. Recall the folklore Cher-

noff bound:

Pr(X

≥ c) ≤

E[e

]

(1)

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Using c = (1 + δ)N p and r = ln(1 + δ) for δ > 0,

we get

Pr(X

≥ (1 + δ)N p) ≤

pδ

(1 + δ)

(1+δ)N p

f p

(2)

If the same number of runs N is used, the bound

becomes:

Pr(X

≥ (1 + δ)N p) ≤



(1 + δ)

(1+δ)



N p

f p

(3)

Thus, for a sufﬁciently small false positive rate, the

bound does not loosen much.

3.2 Group, Distributed and Common

Knowledge

The sampling algorithms for the group and the dis-

tributed knowledge operators are straightforward. We

ﬁrst discuss them. The group operator E

is evaluated

as follows. It is easy to see that g |= E

(φ) evaluates

to TRUE if and only if g |= K

φ for all agents i ∈ G.

This suggests an easy extension to the Epistemic Sam-

pling algorithm: For all the agents in the group G,

evaluate K

φ through sampling. Return TRUE if and

only if it is TRUE for all such evaluations.

For the distributed knowledge operator, the fol-

lowing sampling based algorithm, listed in Algo-

rithm 3 is easy to conceive. In a sample of epistemi-

cally accessible states for the agents in G, check if the

formulas imply K

φ. Return TRUE if and only if it is

TRUE for all such evaluations.

Algorithm 3: Algorithm for evaluating Distributed knowl-

edge Operator.

1: procedure DISTRIBUTED KNOWL-

EDGE(gState,G,φ)

2: M ← number of agents in group G

3: for i ← 1 to M do

4: S

← a sample of epistemically related

states of gState w.r.t. agent i

5: S ← S

∩ S

∩ ... ∩ S

6: Check whether the formulas satisﬁed in S im-

ply φ

7: if all the states in S satisﬁes φ then

8: return T RUE

9: else

10: return FALSE

Semantically, the common knowledge operator

is the reﬂexive and transitive closure of the group

knowledge operator. This leads to a simple algorithm.

The common knowledge operator can be evaluated

through a recursive (depth-ﬁrst) search of the epis-

temically accessible global states in G. This is done

by generating a target number of samples of epistem-

ically accessible states. For each state, if the state

does not satisfy φ, the algorithm returns FALSE. Oth-

erwise, the sampling continues recursively from that

state. The algorithm is detailed in Algorithm 4.

In the next section, we provide empirical evidence

that this approach yields comparable accuracy in sig-

niﬁcantly lesser running time.

Algorithm 4: Evaluating Common Knowledge Operator By

Finding Transitive Closure.

1: procedure COMMON KNOWL-

EDGE(gState,A

,φ, List, currIndex)

2: List.add(gState)  Initially List is empty

3: i ← 0

4: while i < sampleSize do

5: newState ← Generate random epistemi-

cally accessible state from agent A

6: if List does not contain newState then

7: List.add(newState)

8: i ← i + 1

9: while currIndex < listSize do  Initally

currIndex is zero

10: currState ← List.get(currIndex)

11: currIndex ← currIndex + 1

12: if φ is not satisﬁed in currState then

13: return FALSE

14: else

15: nextState ← List.get(currIndex)

16: CommonKnowledge(nextState,A

,φ,

17: List,currIndex)

18: return T RUE

4 CASE STUDIES

We discuss two case studies. All experiments for

the two studies were conducted on the system with

Ubuntu 18.04.2 LTS (64-bit) operating system, In-

tel(R)Xeon(R) CPU E5-2690 v4 @ 2.60GHz Proces-

sor, 62 GiB RAM, and a 2TB hard disk. One way

of estimating the number of runs needed, that is com-

monly used for SMC, is to appeal to the Chernoff Ho-

effding bound. For the estimated probability p

to be

within ε of p with a high probability 1 − δ, one needs

at least ln

2/δ

2ε

samples. Therefore, we evaluate the

queries over 2335 runs which corresponds to ε = 0.03

and δ = 0.03.

4.1 Epidemic Spreading

Consider a disease which is spreading across a pop-

ulation of n agents. An agent progresses from being

susceptible to being infected. To focus the exposi-

tion on the model checking aspect, we use a simple

Statistical Model Checking for Probabilistic Temporal Epistemic Logics

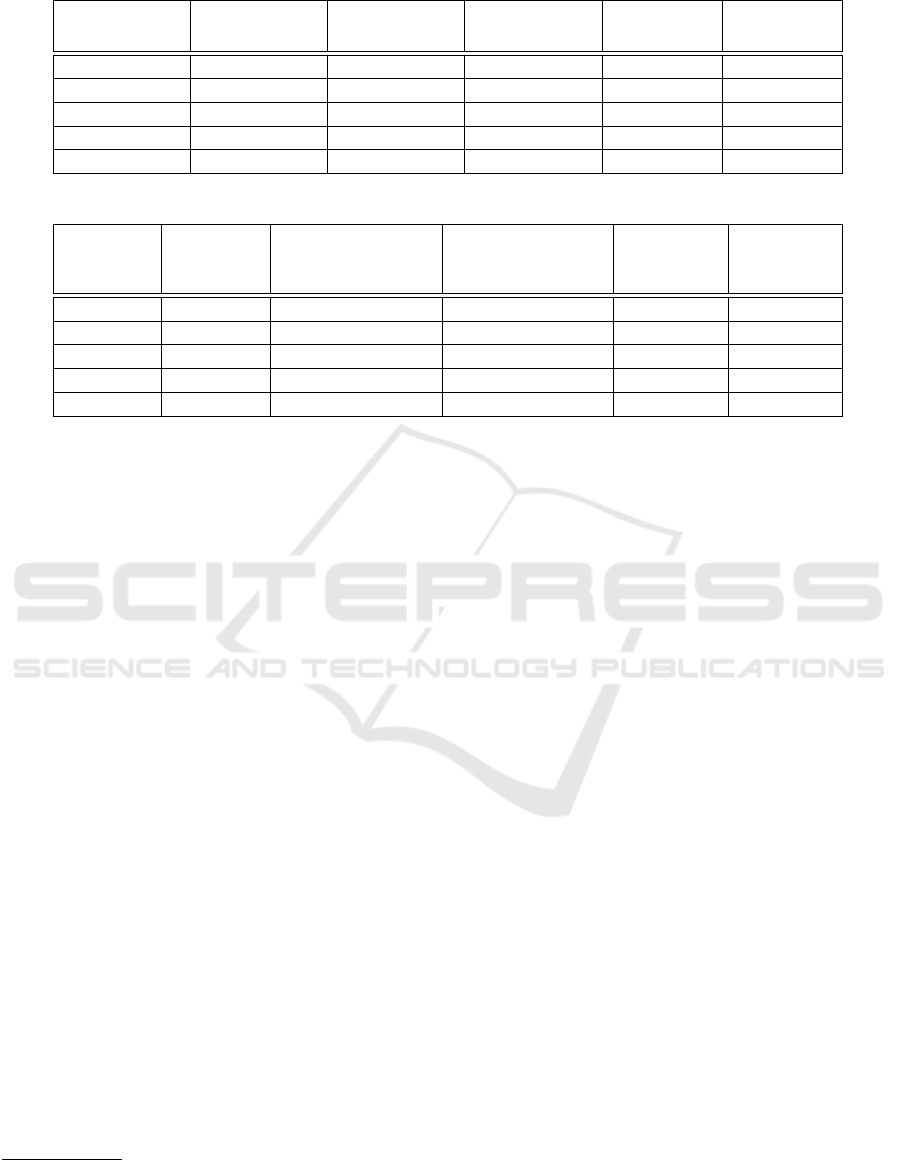
Table 1: Results of Query 1. Number of runs: 2335. The query evaluation time is measured in seconds.

n Sample Size

(M = n log n)

Prob Est (ES) Prob Est

(Vanilla)

Time (ES) Time

(Vanilla)

10 23 0.788 0.760 0.043 0.4

15 40 0.784 0.781 0.079 5.12

20 60 0.751 0.765 0.111 119

25 80 0.773 0.776 0.151 2734

30 102 0.792 0.778 0.190 56942

Table 2: Results of Query 2. Number of runs: 2335. The query evaluation time is measured in seconds.

n Sample

Size (M =

nlog n)

Prob Est (ES) Prob Est (Vanilla) Time (ES) Time

(Vanilla)

10 23 0.60 0.60 0.506 3.338

15 40 0.58 0.52 0.818 128

20 60 0.56 0.48 1.281 4693

25 80 0.52 0.42 1.905 169448

30 102 0.50 0.40 3.519 ≥ 500 hrs

epidemic “spread” dynamic–a susceptible agent gets

infected with probability 0.1 at each time step and an

infected agent recovers at each time step with proba-

bility 0.1. Initially, all the agents are susceptible.

The ﬁrst query asks “what is the probability that

agent i knows that 60% people are infected within 10

time steps”:

(TRUE U

τ≤10

(Atleast

60 % Agents Are Infected))

For all the queries, the number of global states

sampled, M in the algorithm listing, is n log n, where

n is the number of agents. We remark that nlog n is

a modest sample size, which may be increased for

greater accuracy. We evaluate this query for different

values of n in {10,15,20,25, 30}. We compare per-

formance of the Vanilla SMC with the proposed Epis-

temic Sampling approach. The results are detailed in

Table 1. The sample size, that is, the number of epis-

temically accessible global states is nlog n (column

2). It can be seen from columns 3 and 4 that the esti-

mates are close. What is striking is the difference be-

tween the times taken (columns 5 and 6). The Vanilla

SMC that visits every epistemically accessible global

state takes signiﬁcantly higher time.

The second, somewhat artiﬁcial query, asks “what

is the probability that agent i knows that num-

ber of recovered people are at most 60% Un-

til agent j knows that number of infected peo-

ple are at least 80%, within 15 time steps”:

(φ

) U

≤15

(φ

)), where φ

stands for

In general, the spread of an epidemic is modeled elab-

orately using, for example, differential equations (Kermack

and McKendrick, 1927).

“atmost 60% agents are recovered” and φ

stands for

“at least 80% agents are infected.

We evaluate this query for n in {10, 15,20, 25,30}.

Table 2 shows the results for the query. Notice that the

mismatch increases for a more complex query. This

is to be expected, since we keep the number of runs

same, in spite of higher chances of false positives.

Nevertheless, the difference between times taken con-

tinues to be signiﬁcant.

4.2 Group, Distributed and Common

Knowledge

We now discuss results for the epidemic case study

in the context of the group, distributed and com-

mon knowledge operators. We report results of

the cases when the numbers of agents are n in

{10,15, 20,25,30}. Further, we randomly select four

agents to form the group G.

4.2.1 Group Knowledge (E

)

In the epidemic setting, we use the group knowl-

edge operator to ask the query “what is the prob-

ability that every agent in group G, knows that

60% people are infected with in 10 time steps”:

(T RUE U

≤10

(φ

)), where φ evaluates to

TRUE iff at least 60% agents are infected.

Table 3 shows the results. We observe that the

probability estimates are close; however the ES ap-

proach yields a signiﬁcant gain in terms of running

time over the Vanilla SMC.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Table 3: Results for Pr

(T RUE U

≤10

(φ

)). Number of runs: 2335. The query evaluation time is measured in

seconds.

n Sample

Size (M =

nlog n)

Prob Est (ES) Prob Est (Vanilla) Time (ES) Time

(Vanilla)

10 23 0.769 0.752 0.048 3.78

15 40 0.764 0.745 0.072 83

20 60 0.767 0.751 0.108 1461

25 80 0.765 0.745 0.141 11211

30 102 0.774 0.755 0.619 256850

Table 4: Results for Pr

(T RUE U

≤10

(φ

)). Number of runs: 2335. The query evaluation time is measured in

seconds.

n Sample Size

(M = n log n)

Prob Est (ES) Prob Est

(Vanilla)

Time (ES) Time

(Vanilla)

10 23 0.739 0.734 0.049 0.178

15 40 0.756 0.748 0.075 3.814

20 60 0.773 0.768 0.098 105

25 80 0.795 0.782 0.145 2526

30 102 0.802 0.791 0.206 58588

Table 5: Results for Pr

(T RUE U

≤10

(φ

)). Number of runs: 2335. The query evaluation time is measured in

seconds.

n Sample Size

(M = n log n)

Prob Est (ES) Prob Est

(Vanilla)

Time (ES) Time

(Vanilla)

10 23 0.768 0.760 0.306 4.886

15 40 0.789 0.773 0.588 180

20 60 0.799 0.772 1.084 3256

25 80 0.795 0.780 1.728 31234

30 102 0.801 0.785 2.860 >150 hrs

4.2.2 Distributed Knowledge (D

)

As an example of the distributed knowledge opera-

tor, we ask “what is the probability that combined

knowledge among agents in group G, implies that

60% people are infected with in 10 time steps”:

(T RUE U

≤10

(φ

)), where φ is TRUE iff

at least 60% agents are infected. Table 4 shows the

results of the query.

4.2.3 Common Knowledge (C

)

Finally, as an example of the common knowledge

operator, we discuss the query “what is the proba-

bility that it is common knowledge among the G,

is 60% people are infected, within 10 time steps”:

(T RUE U

≤10

(φ

)), where φ

evaluates

to TRUE iff at least 60 % agents are infected. Ta-

ble 5 shows the results. When needing to perform

the closure, it can be seen that the ES algorithm fares

much better than the Vanilla algorithm in terms of

running time. There is, as expected, some loss in ac-

curacy. Unsurprisingly, the running time for the com-

mon knowledge is greater than that of group and dis-

tributed knowledge queries. The number of states to

be explored is the least for the distributed knowledge

operator, since it involves intersection. On the other

hand, sampling closure takes the most time. Inter-

mediate is the group knowledge operator, since it in-

volves taking union of epistemically accessible states

for various agents in the group G.

4.3 Online Shopping

The second case study that we report was used by

Wan et al (Wan et al., 2013) while discussing their

adaptation of the PCTL algorithm for the epistemic

operators. The setting is as follows. There is an on-

line shopping system, with three agents: a customer,

a server and the environment. When the customer re-

quests a delivery, the system will deliver the goods

successfully 95% of the time, and fail 5% of the time.

Statistical Model Checking for Probabilistic Temporal Epistemic Logics

Table 6: Results for the Online Shopping problem. Number of runs: 2335. The query evaluation time is measured in seconds.

Number of

Agents

Sample

Size

(

X(Success)))

(Pr

≥0.9

(

X(Success))

Time (in

seconds)

3 1 0.943 true 0.328

3 2 0.917 true 0.378

Figure 1: DTMC model of online shopping.

Figure 1 illustrates a DTMC model of this system.

The customer’s local state is S

, and the server’s state

is S

. The environment agent’s states are {S

}, re-

sulting in global states {S

}. We ask the fol-

lowing query: “when a customer places an order, she

knows that at least 90% of the items will be shipped

successfully”: K

(Pr

≥0.9

(X(Success f ul))). Table 6

shows the result of this query. These results are con-

sistent with those reported by Wan et al (Wan et al.,

2013).

5 RELATED WORK

Several variants of Interpreted Systems and ETLs

have been been proposed, along with the necessary

model checking algorithms. Much of early model

checking efforts for MAS was in the context of non-

deterministic systems (Lomuscio et al., 2003; Lo-

muscio and Raimondi, 2006; Kong and Lomuscio,

2017). Indeed, excellent tools like MCMAS (Model

Checker for Multi-Agent Systems) have been devel-

oped that implement these model checking algorithms

for MAS (Lomuscio et al., 2017).

However, as in the case of reactive systems, it

is desirable to do a quantitative analysis in the case

of Stochastic MAS (SMAS). A rich theory of proba-

bilistic model checking exists for analyzing stochas-

tic reactive systems. Discrete (and continuous) Time

Markov Chains (DTMCs) are popular examples of

modeling formalisms for such systems. Temporal

logics enhanced with the probability operator like

PCTL are good examples of query languages (Hans-

son and Jonsson, 1994). To ﬁll the gap for stochastic

MAS, stochastic versions of Interpreted Systems and

also epistemic temporal logics were introduced (Wan

et al., 2013; Delgado and Benevides, 2009; Huang

and Luo, 2013; Fu et al., 2018). Often, the Interpreted

System is modeled by some variant or a composition

of Markov chains (Wan et al., 2013). While compo-

sition do introduce an element of non-determinism,

as in the case of Markov Decision Processes, it was

still amenable to quantitative model checking (Del-

gado and Benevides, 2009). The model checking al-

gorithm, for say K-PCTL (PCTL augmented with the

knowledge operator), has a time complexity that is

polynomial in the size of the model and the epistemic

temporal logic formula (Wan et al., 2013; Fu et al.,

2018).

6 CONCLUSIONS AND FUTURE

DIRECTIONS

In this work, we discussed a statistical model check-

ing approach for answering queries in the probabilis-

tic epistemic temporal logic K-PCTL(B). We focused

on the estimation problem, whereas qualitative ques-

tions that make use of statistical methods like hypoth-

esis testing have also been discussed extensively in

the context of probabilistic temporal logics. Adapt-

ing these techniques to answer K-PCTK(B) queries

would be a natural next step.

Further, we propose to construct a user friendly

tool for nested queries involving epistemic and tem-

poral operators, on the lines of MCMAS (Lomuscio

et al., 2017) and Uppaal-SMC (David et al., 2015).

Empirical evaluation of the tool against large systems

and complex queries that involve several knowledge

and temporal operators would yield interesting in-

sights to model checking stochastic MASs. Extension

of this technique to other modalities that have practi-

cal applications would also be an interesting future

direction.

The approach discussed in this paper is particu-

larly conducive for large systems with many agents,

but a small loss in accuracy in answering the queries is

tolerable. Many MASs display this characteristic. A

practical direction is to explore such applications. We

used a simple epidemic propagation model to demon-

strate the ES algorithm, but extending it to realistic

spread models is an example of such a practical direc-

tion. Other applications could arise from the domain

of robotics (motion planning), IoT etc.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

REFERENCES

Agha, G. and Palmskog, K. (2018). A survey of statistical

model checking. ACM Transactions on Modeling and

Computer Simulation (TOMACS), 28(1):6.

Baier, C. and Katoen, J.-P. (2008). Principles of Model

Checking (Representation and Mind Series). The MIT

Press.

Ben-Ari, M., Manna, Z., and Pnueli, A. (1981). The tempo-

ral logic of branching time. In Proceedings of the 8th

ACM SIGPLAN-SIGACT Symposium on Principles of

Programming Languages, POPL ’81, page 164–176,

New York, NY, USA. Association for Computing Ma-

chinery.

David, A., Larsen, K. G., Legay, A., Miku

cionis, M., and

Poulsen, D. B. (2015). Uppaal SMC tutorial. In-

ternational Journal on Software Tools for Technology

Transfer, 17(4):397–415.

Delgado, C. and Benevides, M. (2009). Veriﬁcation of

epistemic properties in probabilistic multi-agent sys-

tems. In Multiagent System Technologies, pages 16–

28, Berlin, Heidelberg. Springer Berlin Heidelberg.

Fagin, R., Halpern, J. Y., Moses, Y., and Vardi, M. Y.

(2003). Reasoning About Knowledge. MIT Press,

Cambridge, MA, USA.

Fu, C., Turrini, A., Huang, X., Song, L., Feng, Y., and

Zhang, L. (2018). Model checking probabilistic epis-

temic logic for probabilistic multiagent systems. In

Lang, J., editor, Proceedings of the Twenty-Seventh In-

ternational Joint Conference on Artiﬁcial Intelligence,

IJCAI 2018, July 13-19, 2018, Stockholm, Sweden,

pages 4757–4763. ijcai.org.

Hansson, H. and Jonsson, B. (1994). A logic for reasoning

about time and reliability. Formal Aspects of Comput-

ing, 6(5):512–535.

Herd, B., Miles, S., McBurney, P., and Luck, M.

(2015a). Mc

mabs: A Monte Carlo model checker for

multiagent-based simulations. In Multi-Agent-Based

Simulation XVI - International Workshop, MABS

2015, Istanbul, Turkey, May 5, 2015, Revised Selected

Papers, pages 37–54.

Herd, B., Miles, S., McBurney, P., and Luck, M. (2015b).

Quantitative analysis of multiagent systems through

statistical model checking. In Engineering Multi-

Agent Systems - Third International Workshop, EMAS

2015, Istanbul, Turkey, May 5, 2015, Revised, Se-

lected, and Invited Papers, pages 109–130.

Huang, X. and Luo, C. (2013). A logic of probabilis-

tic knowledge and strategy. In International confer-

ence on Autonomous Agents and Multi-Agent Systems,

AAMAS ’13, Saint Paul, MN, USA, May 6-10, 2013,

pages 845–852.

Kaufmann, S., Condoravdi, C., and Harizanov, V. (2008).

Formal approaches to modality, pages 71–106. De

Gruyter Mouton Publishers.

Kermack, W. O. and McKendrick, A. G. (1927). A contri-

bution to the mathematical theory of epidemics. Pro-

ceedings of the Royal Society of London. Series A,

Containing Papers of a Mathematical and Physical

Character, 115(772):700–721.

Kong, J. and Lomuscio, A. (2017). Symbolic model check-

ing multi-agent systems against CTL*K speciﬁca-

tions. In Proceedings of the 16th Conference on Au-

tonomous Agents and MultiAgent Systems, AAMAS

2017, S

ao Paulo, Brazil, May 8-12, 2017, pages 114–

122. ACM.

Legay, A., Delahaye, B., and Bensalem, S. (2010). Sta-

tistical model checking: An overview. In Barringer,

H., Falcone, Y., Finkbeiner, B., Havelund, K., Lee, I.,

Pace, G., Ros¸u, G., Sokolsky, O., and Tillmann, N.,

editors, Runtime Veriﬁcation, pages 122–135, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Lomuscio, A., Qu, H., and Raimondi, F. (2017). MC-

MAS: an open-source model checker for the veriﬁca-

tion of multi-agent systems. Int. J. Softw. Tools Tech-

nol. Transf., 19(1):9–30.

Lomuscio, A. and Raimondi, F. (2006). The complexity of

model checking concurrent programs against CTLK

speciﬁcations. In 5th International Joint Conference

on Autonomous Agents and Multiagent Systems (AA-

MAS 2006), Hakodate, Japan, May 8-12, 2006, pages

548–550. ACM.

Lomuscio, A., Raimondi, F., and Sergot, M. J. (2003).

Towards model checking interpreted systems. In

The Second International Joint Conference on Au-

tonomous Agents & Multiagent Systems, AAMAS

2003, July 14-18, 2003, Melbourne, Victoria, Aus-

tralia, Proceedings, pages 1054–1055. ACM.

Nimal, V. (2010). Statistical approaches for probabilistic

model checking. PhD thesis, University of Oxford.

Pnueli, A. (1977). The temporal logic of programs. In 18th

Annual Symposium on Foundations of Computer Sci-

ence (SFCS 1977), pages 46–57.

Vardi, M. Y. (1996). An automata-theoretic approach to

linear temporal logic, pages 238–266. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Wan, W., Bentahar, J., and Ben Hamza, A. (2013). Model

checking epistemic–probabilistic logic using proba-

bilistic interpreted systems. Knowledge-Based Sys-

tems, 50:279–295.

Younes, H. L., Clarke, E. M., and Zuliani, P. (2010). Statis-

tical veriﬁcation of probabilistic properties with un-

bounded until. In Brazilian Symposium on Formal

Methods, pages 144–160. Springer.

Younes, H. L. S., Kwiatkowska, M. Z., Norman, G., and

Parker, D. (2004). Numerical vs. statistical probabilis-

tic model checking: An empirical study. In Tools and

Algorithms for the Construction and Analysis of Sys-

tems, 10th Intl. Conf., TACAS 2004, Barcelona, Spain,

March 29 - April 2, 2004, Proc., pages 46–60.

Statistical Model Checking for Probabilistic Temporal Epistemic Logics