
Multi-agent Policy Gradient Algorithms for Cyber-physical Systems with
Lossy Communication
Adrian Redder
1 a
, Arunselvan Ramaswamy
1 b
and Holger Karl
2 c
1
Department of Computer Science, Paderborn University, Germany
2
Hasso-Plattner-Institute, Potsdam University, Germany
Keywords:
Policy Gradient Algorithms, Multi-agent Learning, Communication Networks, Distributed Optimisation,
Age of Information, Continuous Control.
Abstract:
Distributed online learning over delaying communication networks is a fundamental problem in multi-agent
learning, since the convergence behaviour of interacting agents is distorted by their delayed communication.
It is a priori unclear, how much communication delay can be allowed, such that the joint policies of multiple
agents can still converge to a solution of a multi-agent learning problem. In this work, we present the decen-
tralization of the well known deep deterministic policy gradient algorithm using a communication network.
We illustrate the convergence of the algorithm and the effect of lossy communication on the rate of conver-
gence for a two-agent flow control problem, where the agents exchange their local information over a delaying
wireless network. Finally, we discuss theoretical implications for this algorithm using recent advances in the
theory of age of information and deep reinforcement learning.
1 INTRODUCTION
Centralized learning algorithms can usually be ex-
tended in a natural way to decentralized settings by
replacing global information with information that
has been communicated over a network. However,
the communication network typically induces infor-
mation delay, such that a centralized algorithm effec-
tively uses data that has a certain age of information
(AoI). In (Redder et al., 2021) practically verifiable
sufficient conditions were presented, such that the AoI
associated with data communicated over graph based
networks behaves so that convergence of a distributed
stochastic gradient descend scheme can be guaran-
teed.
In this paper, we go one step further and consider a
multi-agent learning setting, where distributed agents
seek to find local policies to solve a global learn-
ing problem. Specifically, we consider a multi-agent
learning algorithm, where agents update their local
policies conditioned on the policies of other agents
with a certain AoI, i.e. policies that the other agents
have used in the past.
a
https://orcid.org/0000-0001-7391-4688
b
https://orcid.org/0000-0002-8343-6322
c
https://orcid.org/0000-0001-7547-8111
Reinforcement learning (RL) problems pose addi-
tional challenges compared to stochastic optimisation
problems. In RL one typically optimizes a policy in
an online manner, where the interaction of the pol-
icy with an environment generates the observations
from the environment. In stochastic optimisation on
the other hand, one usually obtains observations of
an environment that are independent from the optimi-
sation variables of the problem. However, it was re-
cently shown that the convergence of many RL algo-
rithms can be analysed analogously to stochastic, iter-
ative gradient descend algorithms (Ramaswamy et al.,
2020). A natural question that therefore arises is,
whether one can decentralize, with the help of com-
munication, traditionally central RL algorithms to a
multi-agent setting without losing asymptotic conver-
gence guarantees.
In this paper, we therefore consider the decen-
tralization of the deep deterministic policy gradient
(DDPG) algorithm (Lillicrap et al., 2016) for the
multi-agent learning setting. We achieve this, by al-
lowing that the agents can frequently exchange their
current local policy and their local state-action pairs
over a communication network. At each local agent,
training is then performed by conditioning a policy
gradient step on the most recent available policy of
the other agents. For the communication network, we
282
Redder, A., Ramaswamy, A. and Karl, H.
Multi-agent Policy Gradient Algorithms for Cyber-physical Systems with Lossy Communication.
DOI: 10.5220/0010845400003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 282-289
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

present a simple illustrative model and present asso-
ciated conditions. We then show theoretically for this
model, that the effect of lossy communication on the
multi-agent learning algorithm will vanish asymptot-
ically. Therefore, asymptotic guarantees for the algo-
rithm with and without communication will be iden-
tical. Moreover, we also show that infinitely many
global state-action pairs, will reach each agent.
We apply our algorithm to a simple but illustrative
two-agent water filter flow control problem, where
two agents have to control the in- and outflow to wa-
ter filter. The agents have no information about the
dynamics of the flow problem and have no prior in-
formation of the strategy of the other agents. But, the
agents are allowed to communicate over a network,
which therefore enables the use of our algorithm. Our
simulations show how the communication network
influences the rate of convergence of our multi-agent
algorithm.
2 BACKGROUND ON RL IN
CONTINUOUS ACTION SPACES
In this section we recall preliminaries on RL in con-
tinuous action spaces. In RL an agent interacts with
an environment E that is modeled as a Markov deci-
sion process (MDP) with state space S , action space
A, Markov transition kernel P, scalar reward func-
tion r(s,a). It does so by taking actions via a policy
µ : S → A. The most common objective in RL is to
maximize the discounted infinite horizon return R
n
=
∑
∞
t=n
r(s
t
,a
t
) with discount factor α ∈ [0,1). The as-
sociated action-value function is defined as Q(s, a) =
E
µ,E
[R
1
| s
1
= s,a
1
= 1]. The optimal action-value
function is characterized by the solution of the Bell-
man equation
Q
∗
(s,a) = E
E
r(s, a) + α max
a
0
∈A
Q
∗
(s
0
,a
0
)
s,a
(1)
Q-learning with function approximation seeks to ap-
proximate Q
∗
by a parametrized function Q(s,a; θ)
with parameters θ. For an observed tuple (s,a,r,s
0
),
this can be done by performing a gradient descent step
to minimize the squared Bellman loss
Q(s,a, ; θ) −(r(s, a) + α max
a
0
∈A
Q(s
0
,a
0
;θ))
2
.
(2)
When the action space A is discrete, π(s) =
argmax
a∈A
Q(s,a; θ), ∀s ∈ S defines a greedy policy
with respect to Q(s,a,; θ). When A is continuous this
is not possible, but instead we can use Q(s, a; θ) to im-
prove a parametrized policy µ(s;φ) by taking gradient
steps in the direction of policy improvement with re-
spect to the Q-function:
∇
φ
µ(s;φ)∇
a
Q(s,a; θ)|
a=µ(s;φ)
(3)
In (Silver et al., 2014) it was shown that the expec-
tation of (3) w.r.t the discounted state distribution in-
duced by a behaviour policy
1
is indeed the gradient of
the expected return of the policy µ. In practice, how-
ever, we usually do not sample from this discounted
state distribution (Nota and Thomas, 2020), but still
use (3) with samples from the history of interaction.
When the parametrized functions in (2) and (3) are
deep neural networks the corresponding algorithm is
then known as the deep deterministic policy gradient
algorithm (DDPG) (Lillicrap et al., 2016).
3 DECENTRALIZED POLICY
GRADIENT ALGORITHM
This section describes the adaptation of the DDPG al-
gorithm to the decentralized multi-agent setting.
3.1 Two-agent DDPG with Delayed
Communication
To simplify the presentation, we consider only two
agents 1 and 2. Consider an MDP as defined in the
previous section and assume that agent 1 and 2 have
local action spaces A
1
and A
2
, respectively, such that
A = A
1
×A
2
is the global action space. Further, both
agents can observe local state trajectories s
n
1
∈ S
1
and
s
n
2
∈S
2
, such that S = S
1
×S
2
is the global state space.
Finally, we consider a global reward signal r
n
at every
time step n ≥ 0 that is observable by both agents.
The objective is that the agents learn local policies
µ
1
(s
1
;φ
1
) and µ
2
(s
2
;φ
2
) parametrized by φ
1
and φ
2
to
maximize the accumulated discounted reward. The
global policy is therefore given by µ = (µ
1
,µ
2
). We
propose to use the DDPG algorithm locally at every
agent to train the policies µ
1
and µ
2
. However, to exe-
cute the DDPG algorithm locally, each agent requires
access to the parameters φ
n
1
and φ
n
2
at every time step
n ≥ 0. These parameter vectors are inherent local in-
formation of the agents and therefore are not a priori
available at the corresponding other agent.
Let us therefore suppose that the agents use a com-
munication network to exchange φ
n
1
and φ
n
2
. Since
communication networks typically induce informa-
tion delays, only φ
n−τ
1
(n)
2
and φ
n−τ
2
(n)
1
are available
at agent 1 and 2, respectively. Here, τ
1
(n) denotes the
1
The behaviour policy is typically µ distorted by a noise
process to encourage exploration.
Multi-agent Policy Gradient Algorithms for Cyber-physical Systems with Lossy Communication
283

AoI of φ
n−τ
1
(n)
2
at agent 1 at every time step n ≥ 0.
We refer to τ
1
(n) and τ
2
(n) as the AoI random vari-
ables variables. The communication network will be
discussed in the next section.
Let
ˆ
φ
n
2
:
= φ
n−τ
1
(n)
2
denote the latest available
parameter vector of agent 2 at agent 1. Sup-
pose, that agent 1 has access to a local approxima-
tion Q
1
(s,a; θ
n
1
) of the optimal Q-function Q
∗
(s,a)
parametrized by θ
n
1
at time n. Further, suppose the
agent can sample a realization of the global state
s = (s
1
,s
2
). Then, at time n ≥ 0, agent 1 can calcu-
late a local policy gradient with respect to Q
1
that is
conditioned on the latest available policy of agent 2:
∇
φ
1
µ
1
(s
1
;φ
n
1
)∇
a
1
Q
1
(s,a; θ
n
1
)
s=s,a
1
=µ
1
(s
1
;φ
n
1
),a
2
=µ(s
2
;
ˆ
φ
n
2
)
.
(4)
Equation (4) is therefore the φ
1
component (3),
where φ
n
2
is replaced by φ
n−τ
1
(n)
2
. In Algorithm 1,
we use this policy gradient to train the local policy
at agent 1. The algorithm of agent 2 is defined anal-
ogously. We let both agents train its own local Q-
function using Deep Q-Learning. The agents might
also cooperate to find better approximations of the Q-
function (Mnih et al., 2016). Observe that Algorithm
1 requires complete global tuples (s, a, r, s
0
) to execute
the training steps. We therefore assume that the agents
exchange their local states and actions over the com-
munication network in addition to their local policy
parametrizations. Ones a complete tuple is available,
each agent stores it in a local replay memory. Then
the local Q-function and local policy is updated using
sampled batches from the replay memory.
We would like to point out that the difference com-
pared to the central DDPG algorithm (Lillicrap et al.,
2016) is that the Bellman loss gradient in line 12 and
the policy gradient in line 13 of the algorithm take
into account the most recent available parametrisation
of the policy of agent 2. This implies that depending
to this parametrization, i.e. the expected behaviour
of agent 2, agent 1 will update its Q-function and its
policy differently. For completeness, one should add
target networks to the algorithm, since they are an im-
portant ingredient to stabilize RL with neural network
function approximators (Lillicrap et al., 2016).
3.2 Wireless Network Environment
Recall that Algorithm 1 requires that the agents do
exchange their policy parameters φ
n
i
as well as their
local information (s
n
i
,a
n
i
), respectively. In this section
we describe a simple network environment used by
the two agents to exchange this information.
We represent the channel between the agents by
Algorithm 1: Algorithm at agent 1.
1 Randomly initialize critic and actor weights ;
2 Initialize replay memory R ;
3 for the entire duration do
4 Observe the current state s
n
1
;
5 Execute action a
n
1
= µ
1
(s
n
1
;φ
n
1
) ;
6 Allocate s
n
1
,a
n
1
and θ
n
1
for transmission to
agent 2 ;
7 Exchange data with agent 2 ;
8 Store new tuples (s,a,r,s
0
) in R ;
9 Sample a random batch of transitions
(s
l
,a
l
,r
l
,s
l+1
) from R ;
10 Compute targets y
l
= r
l
+
αQ
1
(s
l+1
,µ
1
(s
l+1
1
;φ
n
1
),µ
2
(s
l+1
2
;
ˆ
φ
n
1
);θ
n
1
) ;
11 Update critic to minimize
(Q
1
(s
l
,s
l
;θ
n
1
) −y
l
)
2
averaged over the
sampled batch ;
12 Update µ
1
using (4) averaged over the
sampled batch ;
13 end
a signal-to-interference-plus-noise-ratio (SINR) mod-
els
SINR
n
1
=
p
2
I
n
1
, SINR
n
2
=
p
1
I
n
2
. (5)
At agent 1, SINR
n
1
is the instantaneous SINR of a re-
ceived signal transmitted with power p
2
during time
slot n by agent 2; I
n
1
is the experienced interference-
noise power during time slot n with some unknown,
but stationary distribution. For a time slot n, we as-
sume that SINR
n
1
and SINR
n
2
are constant. Given
SINR
n
1
in (5), we assume an SINR-threshold β such
that whenever the event A
n
1
:
= {SINR
1,n
≥ β} occurs
a transmission from node 2 to 1 can be successfully
received; hence, errors are due to interference. The
event A
n
2
is defined analogously. The threshold β de-
pends on the modulation, coding and path character-
istics associated with each agent. The effective bit
rate R for the event A
n
1
is constraint by then Shannon
bounded R < B log
2
(1 + β) for a given bandwidth B.
Observe that typically the dimension of φ
n
is sig-
nificantly larger that the dimension of (s
n
i
,a
n
i
), since
the number of parameters of a function approxima-
tor (e.g. neural networks) would have to be increased
to allow better approximation as the dimension of
(s
n
i
,a
n
i
) increases. Lets assume that dim(φ) = d
1
and
that dim((s
i
,a
i
)) = d
2
, with d
1
>> d
2
.
Now, observe that we are only interested in the
most recent φ
n
i
, while for training of the actor-critic
algorithm we can use all samples (s
n
i
,a
n
i
). Therefore,
since d
1
>> d
2
, we may instead of transmitting a sin-
gle update for φ
i
transmit a large number of samples
(s
n
i
,a
n
i
). However, its unclear how we should weight
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
284

the two data transmissions. For example, if d
1
≈ kd
2
for some k ≥ 0 we could transmit k samples after ev-
ery transmission of some φ
n
i
and therefore give equal
bandwidth usage to both. However, we may fix any
ratio independent of d
1
and d
2
.
We now consider the following communication
protocol: Every agent keeps a backlog of samples that
have not been transmitted to the other agent. Then,
each agent transmits up to k ≥ 0 samples after every
complete transmission of its policy. Note that mul-
tiple events A
n
i
might need to occur to exchange all
components of some φ
n
i
, since d
2
is potentially large.
However, notice that the required number of events
is fixed and determined by d
1
and d
2
, the used cod-
ing scheme and the effective bit rate R. The follow-
ing lemma shows that under suitable conditions the
AoI variables τ
1
(n) and τ
2
(n) grow asymptotically
slower than
√
n. Moreover, it shows that infinitely
many global tuples reach each agent.
Lemma 1 . Suppose that p
1
> E [I
n
2
]β, p
2
> E [I
n
1
]β
and that the events A
n
i
are i.i.d., then we have that
P
τ
i
(n) >
√
n infinitely often
= 0 (6)
for both i ∈ {1,2}. Moreover, there is sequence
{n
k
i
}
k≥0
, such that all samples (s
n
k
i
i
,a
n
k
i
i
) have been re-
ceived at agent i.
Proof. It follows from p
1
> E [I
n
2
]β, p
2
> E [I
n
1
]β and
(Redder et al., 2021, Lemma 3) that P ((A
n
i
)
c
) > ε, for
some ε > 0. Here, (A
n
i
)
c
denotes the complement of
A
n
i
. Recall, that a fixed finite number of events A
n
i
guarantees successful exchange of some φ
n
i
. Let l ≥
0 be the required number of events. Using that the
events A
n
i
are i.i.d., tt can then be shown that
P (τ
i
(n) > m) ≤Cε
m
/l
, (7)
with some constant c independent of n and m. It fol-
lows that all τ
i
(n) are stochastically dominated by a
random variable with finite second moment, which
implies (6) using the Borel-Cantelli Lemma. In then
follows from (6) that there exists a sample path depen-
dent constant N, such that τ
i
(n) ≤
√
n for n ≥ N.
Remark 1 . For Lemma 1 we considered that the
interference-noise processes are stationary. How-
ever, one may also assume that the processes are
non-stationary, but instead that one is able to track
the processes mean asymptotically up some error
c ≥ 0. Then, assume p
1
> (E [I
n
2
] + c)β and p
2
>
(E [I
n
1
] + c)β in Lemma 1. Furthermore, it is sufficient
that these conditions hold merely periodically or with
some positive probability. Then the agents may use an
arbitrary medium access and power scheduling pro-
tocol at all other time instances. Finally, the i.i.d. as-
sumption in Lemma 1 can be weakened to merely ex-
ponential dependency decay as discussed in (Redder
et al., 2021), or even more generally to dependency
decay with certain summability properties.
3.3 Theoretical Implication of Lemma 1
A detailed theoretical analysis of Algorithm 1 is out
of the scope for this work. However, we would like to
explain the use Lemma 1.
Consider Algorithm 1, where policies and Q-
functions are approximated by feed forward neural
networks. It was recently shown in (Ramaswamy and
Hullermeier, 2021) that for a large class of activa-
tion functions, including the Gaussian error linear unit
(GELU), the gradient of the neural network with re-
spect to its parameters is locally Lipschitz continuous
in the parameter coordinate. Hence, ∇
φ
1
µ
1
(s;φ
1
) is
locally Lipschitz in the φ
1
coordinate.
Suppose that φ
n
1
is updated with a decreasing step
size sequence γ(n) with
∑
n≥0
γ(n) = ∞,
∑
n≥0
γ(n)
2
<
∞. Further, suppose that Algorithm 1 is stable, i.e.
sup
n≥0
kφ
n
1
k< ∞ a.s. and sup
n≥0
ks
n
k< ∞ a.s. Stability
of the algorithm iterates can be enforced by projecting
the iterates to sufficiently large compact set after each
update. The stability of the state trajectory can be re-
laxed to non-compact sets like R
d
see (Ramaswamy
and Hullermeier, 2021).
Under these assumptions, we can restrict our at-
tention to a compact set, where ∇
φ
1
µ
1
(s;φ
1
) is Lips-
chitz continuous in φ
1
. One can then show that the er-
ror in Algorithm 1, when considering θ
n−τ
1
(n)
2
instead
of θ
n
2
, satisfies
e
n
1
∈ o(γ(n)τ
1
(n)). (8)
It now follows from the assumption that γ is decreas-
ing with
∑
n≥0
γ(n)
2
< ∞ that γ(n) ∈ o(
1
/
√
n). Using
Lemma 1 we have that τ
1
(n) ≤
p
(n) for n ≥ N and a
sample bath dependent N ≥0. It therefore follows that
e
n
1
vanishes asymptotically. Hence, Algorithm 1 with
and without lossy communication behaves asymptot-
ically identical.
4 MULTI-AGENT
REINFORCEMENT LEARNING
FOR FLOW CONTROL
In this section we introduce a two-agent flow control
problem to illustrate the use of Algorithm 1. Flow
control is an important problem in chemical indus-
tries, data centre cooling and water treatment plants.
In our two-agent example each agent has to control
one valve of a flow control problem. Specifically, we
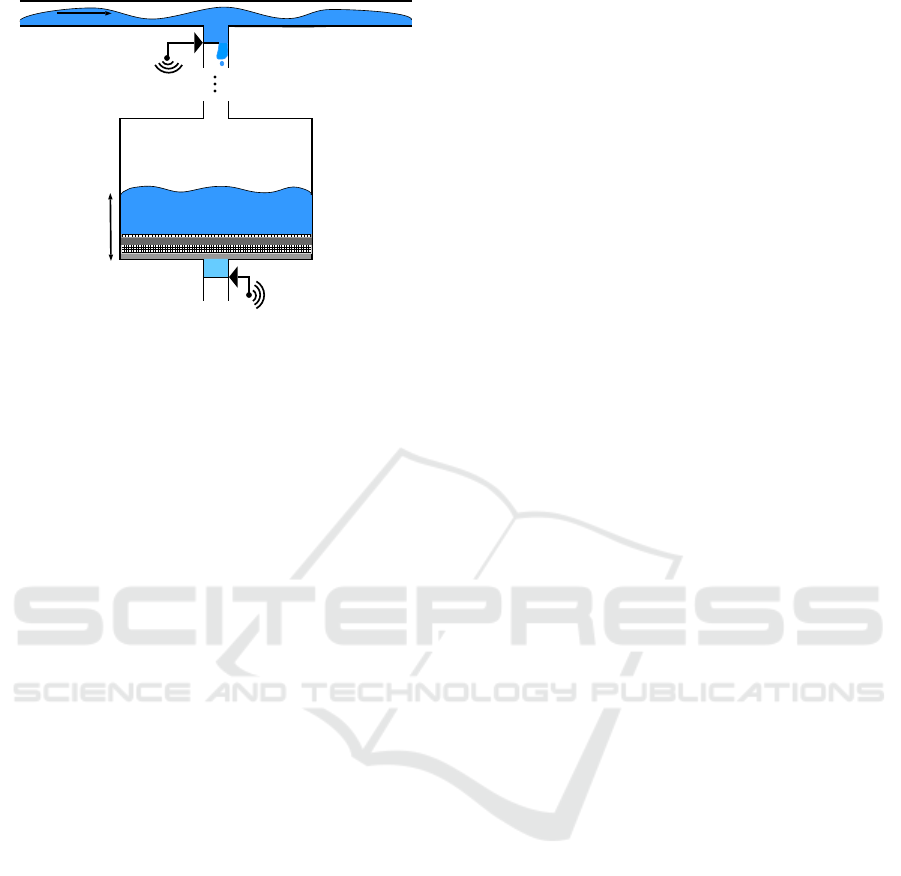
consider the water filter in Figure 1.
Multi-agent Policy Gradient Algorithms for Cyber-physical Systems with Lossy Communication
285
a
2
s
1
a
1
s
2
Agent 1
Agent 2
Figure 1: Illustration of the two agent water filter flow con-
trol problem.
4.1 Water Filter Flow Control Problem
In Figure 1 agent 1 has to control the inflow to the
water filter from a main water line using valve a
1
.
Agent 2 has to control the outflow of the water fil-
ter using valve a
2
. We consider that time is slotted
into small intervals of constant length ∆. The discrete
time steps are indexed by n ∈ N. We refer to a time
slot n as the time interval from time step n −1 to n.
For both agents, we consider that the valves can be
positioned continuously from close to open. There-
fore, at every time step n the agents have to pick ac-
tions a
n
1
,a
n
2
∈ [0,1] for the associated time slot n. For
every time slot n, we denote the sampled flow in the
main line by s
n
1
∈ S
1
⊂ R
≥0
and the sampled water
level in the water filter by s
n
2
∈ S
2
⊂ R
≥0
. The prob-
lem is complicated, since the agents have no informa-
tion about the dynamics of the main water line and
the water filter. Additionally, the agents have no in-
formation about the policy of the other agent, i.e. the
agents initially have no information about the strat-
egy of the other agent to control its valve. However,
we assume that the agents can use a wireless network
to exchange information, which therefore enables the
use of Algorithm 1.
Given s
n
1
and a
n
1
for some time step n, we assume
a continuous function f (s
n
1
,a
n
1
) that determines the in-
flow to the filter during time slot n. Equivalently, we
can assume that agent 1 can measure the inflow to
the filter. Other than that we make no additional as-
sumptions. The agents have no information about the
dynamics of the filter or of the flow in the main water
line. We consider that the agents have to learn how to
control the valves solely based on their local actions,
observations and the information communicated with
the other agent.
4.2 Partial Observability Issues
Algorithm 1 formulates a decentralized multi-agent
solution based on locally observed states. The train-
ing procedure, however, can use delayed global infor-
mation that has been communicated over a network.
The solution therefore falls under the paradigm of de-
centralized training with central data, but decentral-
ized execution. Depending on how the local state
spaces are defined, agents may or may not be able to
find good solutions for a problem, since the local poli-
cies should only use local states, such that inference
is decentralized.
Now consider the flow control problem of the pre-
vious subsection. If agent 1 can only observe the state
s
1
and never state s
2
, then it can only learn to take
very conservative actions, since it has no information
about the current amount of water in the water filter.
We expect better solutions, if both agents can observe
the whole state space s = (s
1
,s
2
). A system theoretic
solution to this would now be to utilize a suitable local
estimator and replace s
n
2
by an estimate ˆs
n
2
at agent 1to
execute a local policy that is functions of the global
state space. Alternative, one could directly replace s
n
2
by its delayed counterpart and utilize a recurrent ar-
chitecture for the policies µ
1
and µ
2
, see for example
(Hausknecht and Stone, 2015).
Since our objective with this example is to illus-
trate the effect of lossy communication on the learn-
ing algorithm and not the effect on the quality infer-
ence, we assume here for simplicity that both agents
can observe s
1
and s
2
. Below, we therefore formu-
late the MDP for the two-agent flow control problem,
where both agents observe s = (s
1
,s
2
). Moreover, the
agents therefore only need to communicate their local
actions a
n
1
and a
n
2
, as well as their policy parametriza-
tions φ
n
1
and φ
n
2
.
4.3 An MDP for Two-agent Flow
Control
We consider the following high-level objective for the
two-agent flow control problem:
(i) Maximize the through flow of the filter.
(ii) Avoid under- and overflows, i.e. 0 < s
n
2
< 1 for
all n ≥ 0.
(iii) Try to keep a reserve of s
n
2
≈ 1/2 as good as
possible for all n ≥ 0.
The state space for both agents is defined as S
1,2
:
=
S
1
×S
2
. The action spaces are defined as A
1
:
= [0,1]
and A
2
:
= [0,1], respectively. To achieve the for-
mulated objective, we consider a continuous reward
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
286
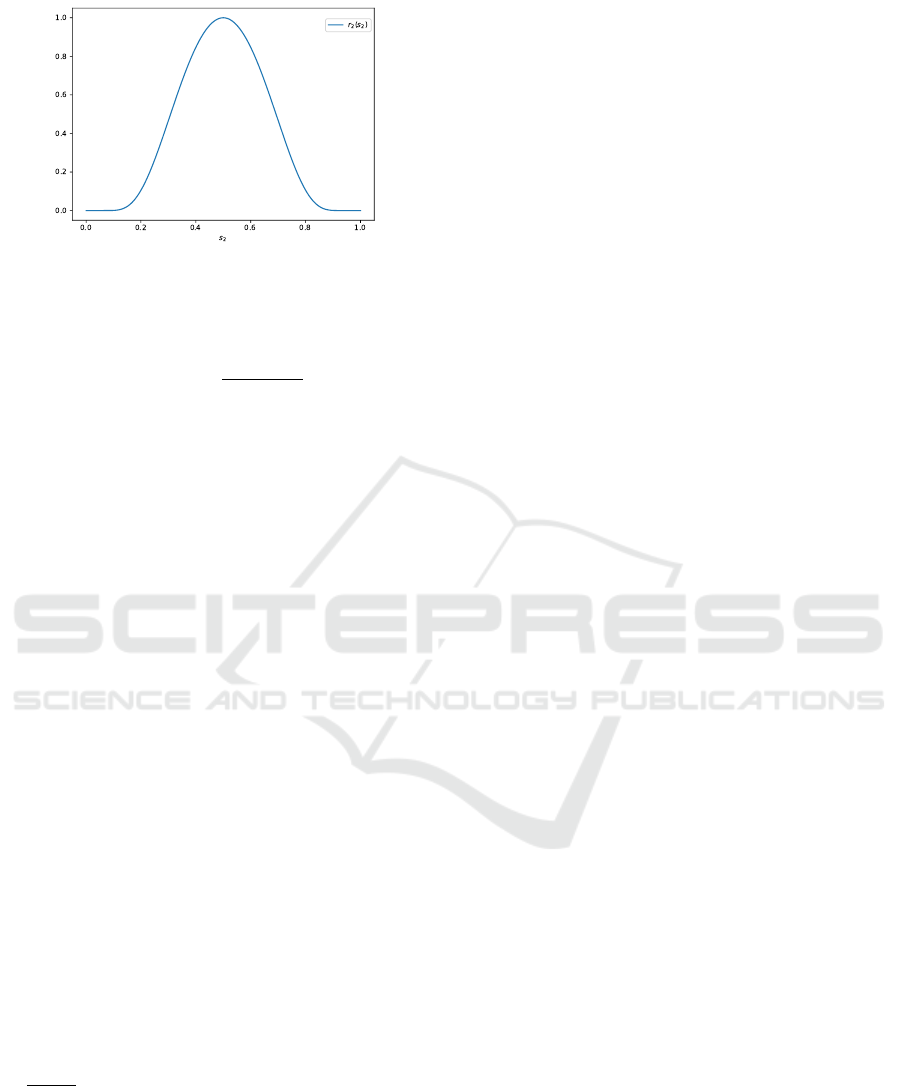
Figure 2: Plot of the second component, r
2
(s
2
), of the re-
ward function.
function r(s
1
,s
2
,a
1
) = f (s
1
,a
1
)c + r
2
(s
2
), with
r
2
(s
2
) = exp
(2s
2
−1)
2
(s
2
−1)s
2
, (9)
and some constant c > 0 that may be used to weight
the importance of (i) over (ii) and (iii). Recall that f
is the function that determines the inflow to the wa-
ter filter. The inflow can also be measured by agent 1
and communicated to agent 2 alongside a
1
, since the
reward is also only required for training and not for in-
ference. Figure 2 shows the second component of the
reward function. We choose this function to satisfy
point (ii) and (iii) of our objective. Clearly, various
other shapes for the reward function are possible.
5 NURMERICAL SIMULATION
In this section, we present the numerical evaluation of
Algorithm 1 for the water flow control MDP of Sec-
tion 4.3. Our goal is to illustrate the convergence of
our algorithm while the two agents communicate over
a lossy communication network. Most importantly,
we illustrate for this example how the lossy commu-
nication influences the rate of convergence of Algo-
rithm 1.
5.1 System and Algorithm Model
For our simulation we consider the following differ-
ential equation
A
ds
2
(t)
dt
−K
1
s
1
(t)a
1
(t)+K
2
(ρgs
2
(t))a
2
(t) = 0 (10)
to model the water filter. Here A is the area of the
water filter, ρ is the density of water, g the accel-
eration of mass, and K
1
and K
2
are constants. The
factor ρgs
2
(t) is the so called differential pressure at
time t (Rossiter, 2021). The second term is a bilin-
ear model for the inflow of the system. The third
term is a bilinear model for the outflow of the fil-
ter. The constant K
2
includes the resistance of the
filter and the resistance of the outflow pipe. This is
only an approximate model for “small” changes of
the flow. However, it serves the purpose for our eval-
uation. For our simulation, we solve equation (10)
numerically for time slots n of length ∆ = 1s, where
we assume that s
1
and s
2
are approximately constant
over each time slot. The agents then observe the sam-
ple of s
n
= (s
n
1
,s
n
2
) from the beginning of each time
slot. For the constants in eq. (10), we use K
1
= 0.1,
which corresponds to a maximum inflow of 10% of
the main flow, and K
2
= 10
−5
, which models the high
resistance of the water filter. Finally, we use c = 0.1 to
give high weight to balancing the water filter around
s
2
=
1
/2.
For Algorithm 1, we use the following set of pa-
rameters: Both agents approximate the Q-function by
a two-layer neural network with 256 and 128 Gaus-
sian error linear units (GELU’s) as activation’s. The
final single neuron output layer is linear layer. Both
policies µ
1
and µ
2
are also represented by two-layer
neural networks, where each layer has 64 GELU’s and
a tanh output layer. We use α = 0.95 and a training
batch size of 128. We also use target networks and
an Ornstein-Uhlenbeck noise process for exploration
(Lillicrap et al., 2016).
5.2 Network Model
To emulate a delaying communication network, we
merely consider two Bernoulli processes. We assume
that P (A
n
i
) = λ at every time step n for both agent 1
and 2. We then choose λ ∈ {1,
1
/2,
1
/4,
1
/8,
1
/16,
1
/32}.
Practically, this corresponds a suitable choice of the
power schedule p
1
and p
2
for given i.i.d. interference-
noise processes I
n
1
and I
n
2
. However, to make the com-
munication model more realistic, we assume a nar-
rowband wireless channel with B = 10Mhz and a typ-
ical choice β = 7. Then, we can obtain an effective
bitrate of 19
Mbit
/s. Now, suppose we code every real
number using 64 bits. Then, observe that each pol-
icy contains 4544 real-valued parameters and since
we merely require the exchange of the actions a
i
we
only need to exchange one real number to obtain a
sample (s
i
,a
i
). Therefore, we require at least 16 time
slots of successful communication to transmit a single
policy update, while in each time slot we can transmit
more than 300 samples. For our experiments, we give
roughly equal bandwidth usage to the parameter- and
sample transmissions. Specifically, each agent trans-
mits a single update to its parameter vector followed
by the transmission of up to 300 ·16 samples or until
its backlog is empty.
Multi-agent Policy Gradient Algorithms for Cyber-physical Systems with Lossy Communication
287
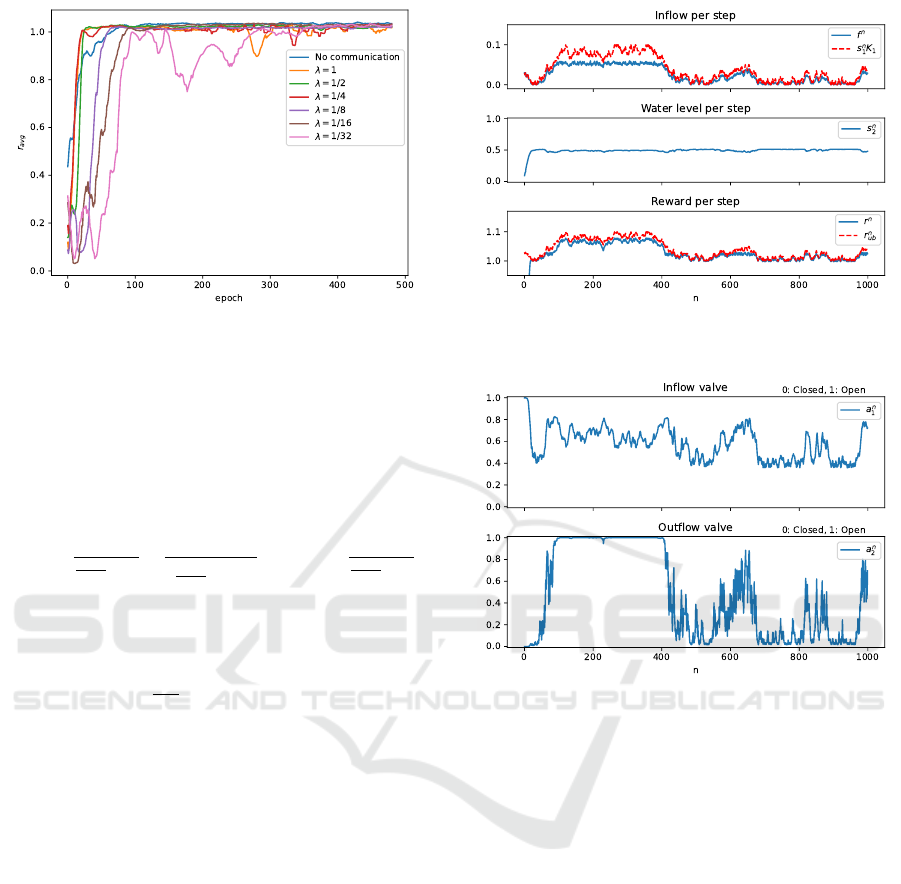
Figure 3: Average reward after each training epoch.
5.3 Training
We train the agents over 500 epochs with length T =
100. The Q- and policy networks are updated with the
ADAM optimizer (Kingma and Ba, 2015) using Ten-
sorflow 2. We use the following learning rate sched-
ules
γ(n) =
e
−8
n
1000
+ 1
+
e
−7
−e
−8
n
1000
+ 1
2
, δ(n) =
e
−8
n
1000
+ 1
(11)
These learning rates satisfy the standard assumptions
from the stochastic approximation (SA) literature, i.e.
they are not summable, but square summable. More-
over, they satisfy
γ(n)
δ(n)
→ 1. Although non-standard
in the SA literature, this assumption enables the use
of tools developed in (Ramaswamy and Hullermeier,
2021) to show the convergence of Algorithm 1 (Red-
der et al., 2022).
Figure 3 shows the average reward at the end
of each training epoch evaluated without exploration
noise on a new trajectory of length T = 1000 for ev-
ery λ. Observe that for all λ the algorithm converges
to a policy of similar average reward compared to Al-
gorithm 1 without communication and global infor-
mation access. Moreover and as expected, as λ de-
creases the rate of convergence also decreases. How-
ever, for λ ∈ {1,
1
/2,
1
/4} the effect of lossy communi-
cation seams to be minor.
After training, we evaluated the final policies on
a new trajectory. For illustration we show the results
for λ = 1/16. In Figure 4 we show the inflow to the
water filter, the water level in the filter and the re-
ward per step. In the water level plot, we see that
the agents learned to quickly balance the water level
around the desired height s
n
2
=
1
/2. The inflow is upper
bounded by the maximal possible inflow for a
n
1
= 1.
The reward per step is upper bounded by 1 plus the
aforementioned upper bound. However, the maximal
Figure 4: Main flow, inflow and water level during one tra-
jectory after training.
Figure 5: Actions associated with the simulated trajectory
after training.
possible inflow and therefore the maximal possible re-
ward per step may not be obtainable, since opening
the inflow valve fully may lead to an increase of the
desired height even when the outflow valve is fully
opened. We can observe this between time step n = 50
to n = 400. For this, consider the associated actions
during the trajectory in Figure 5. We see that when
the inflow is to large in [50,400], agent 1 has to re-
duce the inflow to the system, while agent 2 has to
fully open the outflow. In this time interval the inflow
part of the reward becomes significant and therefore
the agents learned to maximize the inflow.
We can also observe that for the second halve of
the trajectory the algorithm could potentially improve
with longer training. Here, the agents mainly balance
the water level at the desired height, since the inflow
is relatively small and since we chose c = 0.1. How-
ever, opening the inflow valve more can still lead to a
slightly larger reward per step. In summary, we have
seen that agents are able to learn non-trivial policies
for an unknown environment in the presence of highly
uncertain communication.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
288

6 CONCLUSIONS
We showed how the DDPG algorithm can be imple-
mented in a distributed, multi-agent scenario using a
communication network. We gave a theoretical dis-
cussion of the impact of the communication errors on
the learning algorithm and validated the convergence
of our algorithm for a two-agent example. For future
work, we are interested in a fully end-to-end learning
based solution, where agents use communicated, de-
layed state information as their local states. This can
be done using recurrent architectures for the policies
µ
1
and µ
2
. The architecture would use the most recent
available state and its corresponding age. The objec-
tive is that the recurrent architecture internally pre-
dicts the true current state, and then selects an action
conditioned on the prediction error and the policy that
one would associate with global state observations.
ACKNOWLEDGEMENTS
Adrian Redder was supported by the German Re-
search Foundation (DFG) - 315248657 and SFB 901.
We would also like to thank Eva Graßkemper for cre-
ating Figure 4.
REFERENCES
Hausknecht, M. and Stone, P. (2015). Deep recurrent q-
learning for partially observable mdps. In 2015 aaai
fall symposium series.
Kingma, D. P. and Ba, J. (2015). Adam: A method for
stochastic optimization. In ICLR.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2016). Con-
tinuous control with deep reinforcement learning. In
ICLR (Poster).
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,
Harley, T., Silver, D., and Kavukcuoglu, K. (2016).
Asynchronous methods for deep reinforcement learn-
ing. In International conference on machine learning,
pages 1928–1937. PMLR.
Nota, C. and Thomas, P. S. (2020). Is the policy gradi-
ent a gradient? In Proceedings of the 19th Interna-
tional Conference on Autonomous Agents and Multi-
Agent Systems, pages 939–947.
Ramaswamy, A., Bhatnagar, S., and Quevedo, D. E. (2020).
Asynchronous stochastic approximations with asymp-
totically biased errors and deep multi-agent learning.
IEEE Transactions on Automatic Control.
Ramaswamy, A. and Hullermeier, E. (2021). Deep q-
learning: Theoretical insights from an asymptotic
analysis. IEEE Transactions on Artificial Intelligence.
Redder, A., Ramaswamy, A., and Karl, H. (2021). Prac-
tical sufficient conditions for convergence of dis-
tributed optimisation algorithms over communica-
tion networks with interference. arXiv preprint
2105.04230.
Redder, A., Ramaswamy, A., and Karl, H. (2022). Asymp-
totic convergence of deep multi-agent actor-critic al-
gorithms. Under review for AAAI 2022.
Rossiter, A. (2021). Modelling, dynamics and con-
trol. https://controleducation.group.shef.ac.uk/
chaptermodelling.html. Accessed: 25.05.2021.
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and
Riedmiller, M. (2014). Deterministic policy gradient
algorithms. In International conference on machine
learning, pages 387–395. PMLR.
Multi-agent Policy Gradient Algorithms for Cyber-physical Systems with Lossy Communication
289
