Towards Circular and Asymmetric Cooperation in a Multi-player

Graph-based Iterated Prisoner’s Dilemma

Tangui Le Gl

eau

1,2

, Xavier Marjou

, Tayeb Lemlouma

and Benoit Radier

Orange Labs, Lannion, France

IRISA, Lannion, France

Keywords:

Game Theory, Non-cooperative Games, Iterated Prisoner’s Dilemma, Tit-for-Tat.

Abstract:

In collaborations involving multiple actors, it is well known that tensions between individual interest and global

welfare can emerge: actors are personally incentivized to have selﬁsh behavior whereas mutual cooperation

may provide a better outcome for all. Known as social dilemmas, these cooperation paradigms have aroused

renewed interest in solving social issues, particularly in environmental and energy issues. Hybrids methods

with Reinforcement Learning (RL) policies and Tit-for-Tat (TFT) strategies have proven successful to identify

fruitful collaboration in complex social dilemmas. However, there are also many situations, where cooperation

cannot always be given back directly, and has instead to be carried out through one or more intermediary actor(s).

This speciﬁcity ruins win-win approaches like TFT. To address this speciﬁcity, we introduce a Graph-based

Iterated Prisoner’s Dilemma: a N-player game in which the possible cooperation between players is modeled

by a weighted directed graph. In addition to this new paradigm, we propose a graph-based TFT algorithm that

we evaluate on multiple scenarios and compare to other algorithms. Our experiments show that leveraging a

graph-based structure in the original TFT algorithm allows it to spread favor better collaboration synergies in

most situations.

1 INTRODUCTION

Humanity and industry face numerous issues of co-

operation where various self-interested actors inter-

vene. Sometimes, while there is no direct personal

incentive to cooperate, mutual cooperation can pro-

vide better outcomes for all actors. Such situations

involving multiple non-cooperative intelligent agents

exist or will exist in various areas where resources

are scarce like energy among electricity, road trafﬁc

among independent autonomous vehicles, and decen-

tralized multi-agent systems (such as machine learning

on private devices). Faced with the proliferation of

these intelligent multi-agent situations and faced with

social and environmental issues such as a possible up-

coming shortage of energy and natural resources, it

is increasingly vital to focus more on the studies of

learning agents in non-cooperative games (Hager et al.,

2019).

This category of games where players have no

incentive to cooperate despite optimal mutual coop-

eration is known as social dilemmas. For decades,

matrix games have been very popular: with atomic

actions (cooperation/defection), three kinds of canon-

ical games have emerged. They all have in common

point at least one incentive to choose defection. It can

either be fear (the fear of being exploited by a defector

while cooperating) like in trust problems known as

the Stag Hunt, or greed (the temptation to exploit a

cooperator) in the Chicken Game. At last, when both

fear and greed incentivize players to defect, they face

the famous Prisoner’s Dilemma (PD). Social dilemmas

have been well studied for many years. The notion of

general-sum non-cooperative games is quite ancient

(Nash, 1951) as well as the formulation of the PD

(Flood, 1958). Therefore, numerous real life situations

have been modeled by such dilemmas: from climate

change and environmental security (Soroos, 1994) to

institutions negotiation with N-person version of the

PD as well as tax policies (Zheng et al., 2020).

If the formulation of this problem is rather simple,

the issue of efﬁcient behaviors facing such dilemmas

has raised a huge interest for decades. In a seminal

work, (Axelrod and Hamilton, 1981) tackles the ques-

tion of the Iterated Prisoner’s Dilemma (IPD) and pro-

poses to oppose various agents in a tournament where

they should maximize their rewards playing succes-

sively a PD. According to Axelrod, the key of success

Gléau, T., Marjou, X., Lemlouma, T. and Radier, B.

Towards Circular and Asymmetric Cooperation in a Multi-player Graph-based Iterated Prisoner’s Dilemma.

DOI: 10.5220/0010837900003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 293-303

ISBN: 978-989-758-547-0; ISSN: 2184-433X

293

rests on four properties: a ”good” agent should be nice,

provokable, forgiving and clear to understand. The

winner of IPD tournament was the algorithm Tit-for-

Tat (TFT) introduced by Anatol Rapoport (Rapoport

et al., 1965): this simple algorithm (essentially re-

producing the behavior of its partner) fulﬁlls the four

properties, manages to encourage cooperation and to

be robust to defection. Subsequently, variants of TFT

(Verhoeff, 1998) or alternatives (Nowak and Sigmund,

1993) have also fueled interest in social dilemmas. Re-

inforcement Learning (RL) methods have also been

used to study the IPD (Izquierdo et al., 2008).

Later, the emergence of Deep Reinforcement

Learning (Mnih et al., 2015) brought a new interest

since the training of complex policies has made pos-

sible the study of cooperation in more realistic social

dilemmas (Leibo et al., 2017; Jaques et al., 2019).

However, (Lerer and Peysakhovich, 2017) has shown

empirically that a Tit-for-Tat strategy remains neces-

sary to help RL policies not to fall in Nash equilibrium

(mutual defection), which suggests that studying TFT

keeps a huge interest, in particular to complement RL

policies in more general non-cooperative games.

Tit-for-Tat has been well studied and performs well.

However in some realistic situations, direct coopera-

tion may be less optimal or even impossible. Indeed,

sometimes cooperation has to go through one or more

indirect cooperator(s). Whereas it exists an optimal

multi-agent collaboration, the cooperation is now not

necessary bilateral and then the basic TFT strategies

are inefﬁcient.

To address and study this asymmetry and possibly

enable circular cooperation, we introduce the Graph-

based Iterated Prisoner’s Dilemma (GIPD), a novel

kind of

-player Prisoner’s Dilemma with a graph-

structure to better generalize the complexity of possi-

ble cooperation between players. The key element of

our formalism is a weighted directed graph which sets

the maximal authorized cooperation for each pair of

players. To tackle this new paradigm, we extend the

classic TFT to create a novel algorithm: the Graph-

based Tit-for-Tat (GTFT). To address the asymmetry

and weighted cooperation, our extension adopts a ﬂow

network approach to detect and maintain cycles of

cooperation within the players.

We simulate our GTFT on dilemmas involving

various patterns of circularity, and compare it to some

classic TFT. We also conduct some experiments on

the choice of the TFT functions involved in GTFT.

We study the relevance of the graph-based structure

and the choice of parameters with ﬁve designed social

metrics.

In section 2, we deﬁne social dilemmas in par-

ticular the continuous PD. Before proposing our ap-

proach of GTFT in section 5, we discuss about other

formalisms in section 3 for the

-player IPD and intro-

duce our model of GIPD in section 4. At last, methods,

results and discussions are presented in sections 6 and

2 DEFINITIONS OF SOCIAL

DILEMMAS

Social dilemmas are multi-player games where at least

one of its Nash equilibria is not optimal. The literature

describes them as situations where multiple players

can choose between cooperation and defection in a

game where mutual cooperation is optimal whereas

they all are incentivized to defect. In this section,

we recall the formalism of those social dilemmas in

particular the so-called Prisoner’s Dilemma (PD) and

its continuous version.

2.1 Classic Social Dilemma

Matrix games with two players provide a basic frame-

work to introduce social dilemmas (Axelrod and

Hamilton, 1981): Two players A and B choose be-

tween cooperation and defection, and they receive one

of the four possible payoffs given by Table 1: they

are denoted in the literature by R (Reward for mutual

cooperation), S (Sucker for being exploited by a de-

fector), P (Punishment for mutual defection) and T

(Temptation to exploit a cooperator).

Table 1: Payoffs in a 2-player social dilemma.

Cooperate Defect

Cooperate (R,R) (S,T )

Defect (T, S) (P,P)

This matrix game is deﬁned as a social dilemma

if the four payoffs verify the following inequalities

(Macy and Flache, 2002):

1. R > P

: Mutual cooperation is better than mutual

defection

2. R > S

: Mutual cooperation is better than exploita-

tion

3. At least one of these two inequalities:

• T > R: Greed (3a)

• P > S: Fear (3b)

4. R >

(S + T )

: Mutual cooperation is better than

equiprobable different choice (4)

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

294

The last condition (4) is relevant in the iterated

version of the game to avoid that the rotation Coop-

erate/Defect becomes optimal. In the literature, there

are three kinds of social dilemma depending of which

incentive of inequality (3) is veriﬁed. In this paper, we

focus on the case of Prisoner’s Dilemma (where greed

(3a) and fear (3b) are veriﬁed). The often used pay-

offs

S < P < R < T

are given by

S = 0,P = 1, R = 3

and

T = 5

(Axelrod and Hamilton, 1981). This par-

ticular game admits one Nash Equilibrium which is

(Defection, Defection) whereas the optimal outcome

is (Cooperation, Cooperation).

2.2 Continuous Prisoner’s Dilemma

The classic PD can be extended to a continuous ver-

sion by extrapolating a payoff with the four values of

Table 1. Let us say that two players A and B play

a dilemma. Instead of choosing a discrete action be-

tween Cooperate and Defect, they now can choose a

continuous cooperation degree

a ∈ [0,1]

and

b ∈ [0,1]

(

for total defection and

for total cooperation). (Ver-

hoeff, 1998) proposes to extrapolate the values of S, P,

R and T as by the gain function G follows:

G : [0,1] × [0, 1] → R

G(x,y) = xyR + (1 − x)(1 − y)P + x(1 − y)S + (1 − x)yT

(1)

We then deﬁne the payoffs of a continuous Pris-

oner’s Dilemma between two players A and B choos-

ing respectively actions

and

= V (a,b)

with:

V : [0, 1] × [0,1] → R × R

V (a,b) = G(a, b),G(b,a)

(2)

For clarity, we can check that with discrete actions

(i.e.

a,b ∈ {0,1}

), we ﬁnd the four payoffs in the

discrete case given in the Table 1:

• V (0,0) = P,P

• V (1,0) = S,T

• V (0,1) = T, S

• V (1,1) = R,R

3 RELATED WORK

Social dilemmas, and in particular the Prisoner’s

Dilemma, have been studied for decades. They have

their roots in the Nash notion of non-cooperative

games (Nash, 1951) and then have been properly

introduced in the Axelrod’s tournament of Iterated

Prisoner’s Dilemmas (Axelrod and Hamilton, 1981).

The winner of this seminal tournament was the

Tit-for-Tat strategy (Rapoport et al., 1965), a rather

simple strategy basically consisting in reproducing the

opponent choice. Then, numerous improvements have

been proposed to the original TFT: (Wu and Axelrod,

1995) tried to cope with the noise of TFT in IPD,

(Beauﬁls et al., 2001) proposed a memory-based TFT.

Other novel strategies similar to the TFT have been

introduced e.g. win-stay and lose-shift (Nowak and

Sigmund, 1993). Reinforcement Learning techniques

have also been adopted to train agents to face the

IPD: (Matignon et al., 2012) conducted a study on

decentralized multi-agent Q-learning in cooperative

and non-cooperative games, (Matignon et al., 2007)

proposed the hysteretic Q-learning to cope with

non-stationarity of non-cooperative agents. More

recently, (Lin et al., 2020) conducted a very complete

tournament of bandits, RL and TFT agents.

Moreover, variants of Prisoner’s Dilemma have

emerged: (Verhoeff, 1998) introduced the continuous

PD and some corresponding adapted strategies of

TFT ; (Hamburger, 1973) proposed a formalism of N-

Iterated Prisoner Dilemmas (NIPD) in which payoffs

of players are based on the number of cooperators.

Some experiments have been conducted on NIPD

(Yao, 1996), and in particular with Reinforcement

Learning (Agudo and Fyfe, 2011). Some studies

also tackled the problem of graphs with Prisoner’s

Dilemmas (Ashlock, 2007),(Luo et al., 2010). Their

models simulate situations of multiple players placed

in a (undirected) graph in which they can play a

PD only with their neighbors. Our approach differs

greatly in a sense that maximal authorized cooperation

between players is given by a directed and weighted

graph. Thus, the cooperation between each pair

of players is directed and weighted (in particular

non-existent) and can enable non-symmetrical and

even circular situations.

To ﬁnish, recently social dilemmas have known a

new interest with the emergence of deep RL: (Leibo

et al., 2017) introduced sequential social dilemmas in

the form of more realistic games in which RL agents

are trained to cooperate between each other. (Lerer

and Peysakhovich, 2017) showed empirically that RL

agents fall in non-optimal Nash Equilibrium, and that

TFT was necessary to help RL policies to mutually

cooperate and maintain cooperation. The solution mix-

ing TFT strategies and RL policies they brought is

very promising, however their solution doesn’t cover

asymmetric and circular situations.

Towards Circular and Asymmetric Cooperation in a Multi-player Graph-based Iterated Prisoner’s Dilemma

295

4 GRAPH-BASED ITERATED

PRISONER’S DILEMMA

In this section, we propose to extend the

-player

Iterated Prisoner’s Dilemma with a graph structure.

The main idea is that maximal authorized coopera-

tion within each ordered pair of players is given by a

weighted directed graph.

4.1 N-player Prisoner’s Dilemma

In this section, we describe the model used for the

-player PD, that we deﬁne here without graph exten-

sion. We consider a decentralized model, i.e. the

players play one continuous PD between each other:

each player

chooses a continuous cooperation degree

i j

∈ [0,1]

towards every other player

(

i j

= 0

for

total defection and

i j

= 1

for total cooperation). In

other words, each player

chooses a vector of coop-

eration

−→

= (c

i j

)

j∈J1,NK

and all decisions of players

form the matrix

C = (c

i j

) ∈ [0,1]

N×N

. Note that we

adopt the convention that one player cannot cooperate

with oneself:

∀i,c

= 0

. After the decision of coop-

eration degrees, the

N(N − 1)/2

continuous PD made

simultaneously within each pair of players

(i, j)

give to

them the payoffs given by 2.2. Therefore, each player

i receives the total payoff:

∑

j6=i

i j

R + (1 −c

i j

)(1 − c

)P + c

i j

(1 − c

+(1 − c

i j

(3)

4.2 Graph-based Iterated Prisoner’s

Dilemma (GIPD)

We introduce our formalism of GIPD that we deﬁne

by :

• a number N of players

•

a weighted directed graph

max

of maximal coop-

eration deﬁned by a weighted adjacency matrix

max

∈ [0, 1]

N×N

•

a vector

max

∈ (R

)

of maximal cooperation

effort

• a number of steps (or rounds) T

max

In this game, at each step

, each agent

can choose

N − 1

cooperation degrees

i j

with two constraints:

ﬁrst, the maximal value for

i j

is ﬁxed by the graph

max

, and secondly its outgoing ﬂow cannot exceed

max

∑

j6= j

i j

≤ D

max

[i]

. In practice, the ﬁrst

constraint is veriﬁed by clipping the total choice matrix

= (c

i j

)

by the adjacency matrix of maximal cooper-

ation graph

max

← min(C

max

)

. It means for

example that if

max

[a,b] = 0

, player

cannot cooper-

ate with

, so even if

chooses a degree

= 1

, the

effective degree will in fact be equal to 0. To ensure

the second constraint, each row

−→

is normalized by

the factor

min(1,

max

[i]

)

. When the effective matrix

= (c

i j

)

is computed, the agents receive the payoffs

determined by the formulation 3.

In this game, we assume that all players can observe

the full effective choice matrix of the previous step

t−1

, that they have the knowledge of

max

and

max

but

max

is unknown to them. This formalism of so-

cial dilemma allows to model the classic prisoner’s

dilemma (Figure 1a) as well as what we call circu-

lar dilemmas i.e. the presence of a cyclic ﬂow in the

weighted directed graph of maximal cooperation

max

(e.g. Figures 2c or 2d). For better intuition, we pro-

vide in Figure 2 some real examples related to the

cooperation graphs represented in Figure 1.

4.3 Examples

Although applications of this formalism are out of

scope of the paper, we nevertheless provide below

(Figure 2) some didactic examples of dilemmas related

to the GIPD presented in Figure 1. The edge weights

of the maximal cooperation graphs can be roughly

viewed in this case as proportional to the payoffs sum

of the helper and the ”receiver”.

The above example of dilemmas represents the

numerous situations where multiple actors can share

some items (or services) to homogenize their resources

(or energy) by mutually giving their surplus to others.

5 GRAPH-BASED Tit-for-Tat

In this section, we update the classic Tit-for-Tat algo-

rithm to adapt it to the GIPD (deﬁned in 4.3). We start

by recalling the principle of the classic Tit-for-Tat al-

gorithm, in particular in a continuous version, and then

we detail the novel Graph-based Tit-for-Tat algorithm

we propose.

5.1 Deﬁnition of Tit-for-Tat

We assume that a TFT function

T FT

with

steps of

memory is a function indicating at each time step

what a player A (facing a player B) should choose

as cooperation degree

∈ [0, 1]

according to the

previous cooperation degrees:

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

296

1.0 1.0

∞

1 2

1.0

0.5

1.0

3 2

1.0

∞

1.0

3 2

1.0

(a)

1.0 1.0

∞

1 2

1.0

0.5

1.0

3 2

1.0

∞

1.0

3 2

1.0

(b)

1.0 1.0

∞

1 2

1.0

0.5

1.0

3 2

1.0

∞

1.0

3 2

1.0

(c)

1.0 1.0

∞

1 2

1.0

0.5

1.0

3 2

1.0

∞

1.0

3 2

1.0

(d)

Figure 1: Some examples of Graph-based Prisoner’s Dilemmas: (1a) is the classic

-player PD. (1b) is a

-player full version of

PD. (1c) is a

-player circular PD and (1d) is a

-player circular PD with an alternative with four

-player cycles of cooperation

(less optimal : ﬂow of 0.5 instead of 1.0). The values of maximal cooperation effort of D

max

are indicated in gray.

(a)

(b)

(c)

(d)

Figure 2: A game where

players can decide to cooperate by sharing their items or defect by keeping them. The items have a

decreasing marginal utility (e.g.

N − k + 1

for the

same item) thereby conferring the game a dilemma property: the optimal

outcome is the mutual cooperation which is exchanging equitably items, but greed and fear lead to the non-optimal mutual

defection. According to the topology of resources of agents, circular situations can emerge (2c and 2d).

T FT

: N × [0,1]

→ [0, 1]

T FT

(t, a

t−1

,...,a

t−k

) = a

(4)

The majority of TFT algorithms needs only the

previous step (

k = 1

) but some approaches needs more

steps, like the gradual behavior with memory proposed

by (Beauﬁls et al., 2001) and we can theoretically

envisage the case

k = +∞

with the use of models

learning the history (Recurrent Neural Networks).

For example, the original Tit-for-Tat with discrete

choice (cooperation/defection i.e. a cooperation de-

gree in

{0,1}

) is deﬁned by cooperating on the ﬁrst

move (cooperation equal to

) then doing whatever the

other player did on the previous move. For better un-

derstanding of our notations, we detail the formalism

of the classic TFT:

TFT : N × {0, 1} → {0,1}

TFT(t, b

t−1

) =

(

1, if t = 0,

t−1

, if t > 0.

(5)

5.2 Continuous Tit-for-Tat

To address the continuous version of an IPD (deﬁned in

2.2), some continuous versions of Tit-for-Tat exist. We

gather propositions of (Verhoeff, 1998) and (Le Gl

eau

et al., 2020) as well as a contribution (the stochastic

incentive) in the following expression:

TFT

α,β,γ,r

: N × [0,1]

→ [0, 1]

TFT

α,β,γ,r

(t, a

t−1

),r











if t = 0

αa

t−1

+ (1 − α)(r

t−1

+ (1 − r

t−1

+ β(b

t−1

− a

t−1

)]

+ r

if t > 0

(6)

In this expression,

is an inertia coefﬁcient to

smooth reaction.

is a coefﬁcient to incentivize co-

operation (

is the initial value of

is the adap-

tive coefﬁcient to make r

dynamic: it increases (resp.

decreases) when partner cooperation increases (resp.

decreases). The objective of that adaptive coefﬁcient

is to gain safety. At last,

is a Bernoulli variable

of probability

, it means that

is equal to

with

probability

and

otherwise. This stochastic parame-

ter allows to stimulate incentive in case of null value of

for all players. At last, for our simulations, we use

an null initial degree

= 0.0

. To sum up the notations,

we consider three kinds of TFT functions:

•

TFT alpha: we omit adaptive and stochastic pa-

rameters (β = γ = 0), i.e. the incentive coefﬁcient

is constant r

= r

• TFT beta: we omit stochastic parameter (γ = 0)

• TFT gamma: we use all parameters

Towards Circular and Asymmetric Cooperation in a Multi-player Graph-based Iterated Prisoner’s Dilemma

297

5.3 Graph-based Tit-for-Tat

We introduce the Graph-based Tit-for-Tat

. The goal

of this algorithm is to extend the classic TFT in par-

ticular to cope with asymmetry and the existence of

cycles of cooperation. Our idea relies on viewing the

cooperation graph as a ﬂow network (Ford Jr, 1956)

and ﬁnding the maximum ﬂow which makes a cycle.

We detail our algorithm denoted GRAPHTFT for the

point of view of player

. The principle is that

GRAPHTFT(

) has inner variables that it updates at

each step: a cooperation graph

, a graph which al-

lows to penalize defectors and a source ﬂow

, an

amount of cooperation that it is ready to provide. In

the following, we consider that the algorithm uses a

TFT function

T FT

: [0, 1] × [0,1] → [0, 1]

such that

t+1

= f

T FT

)

. This function allows to update

over time a coefﬁcient

according to an observed

coefﬁcient

fulﬁlling the objectives of TFT spirit.

GRAPHTFT(

) is divided into several phases, at each

step:

For each other player

, update

[k, j]

with

T FT

according to the difference between what

”re-

ceived” and what he ”gave” at previous step.

Update the source ﬂow

with

T FT

according

to the difference between what

(oneself) ”has

received” and what

(oneself) ”had given” at pre-

vious step.

Create a ﬂow network

, whose capacities are

given by

with a source vertex directed towards

the vertex of

(oneself) with capacity

and all

edges of

initially directed towards vertex

ar-

tiﬁcially redirected towards a sink vertex. Thus,

we have a ﬂow network allowing to ﬁnd the max-

imum cyclic ﬂow (i.e. from

). For better

understanding, see Figure 3.

Compute the maximum ﬂow

, i.e. a sub-

graph in

and extract the next choice of coopera-

tion

−→

← R [k,:]

5.3.1 Max Flow Problem

To ﬁnd the maximum cyclic ﬂow of cooperation, our

algorithm converts its inner cooperation graph into a

ﬂow network (Figure 3), and ﬁnds the maximal ﬂow.

We use two kinds of algorithms with polynomial com-

plexity (

O(∆N

)

where

∆

is the discretization num-

ber):

•

Ford-Fulkerson algorithm (Ford and Fulkerson,

1956): ﬁnd the maximal ﬂow (but with shortest

path)

For reproducibility, the code has been made available:

https://github.com/tlgleo/graph based TFT

Algorithm 1: GRAPHTFT (for agent k).

Input: Max cooperation graph C

max

and max

source ﬂow D

max

given by the game and a

TFT function f

T FT

Initialize: C

← C

max

, D

← D

max

[k]

First step: Choose

∀ j 6= k,

[ j] ← f

T FT

(t = 0)

for t ∈ [1, T

max

] do

for each other agent j do

From C

t−1

, compute outgoing ﬂow of

cooperation of j : (C

t−1

)

Execute a TFT on j :

k j

= f

T FT

t−1

k j

,(C

t−1

)

Modify the inner cooperation graph:

[k, j] ← c

k j

max

end

From

t−1

, compute the incoming ﬂow of

cooperation for k : (C

t−1

)

−

Update by TFT the next source ﬂow:

← f

T FT

,(C

t−1

)

−

)

Generate a new ﬂow network F from k to

k with a source of capacity D

and

capacities given by C

(see Figure 3)

From F , extract the sub-graph R of

maximum ﬂow of cooperation

Choose cooperation degrees from max

ﬂow:

−→

← R [k,:]

end

•

Min-cost max ﬂow (Orlin, 1997): a variant of Ford-

Fulkerson, with a minimization of a certain cost per

chosen edge (for the cost, we choose the inverse of

cooperation so that the ﬂow search prefers longest

cycles.)

6 METHODS

In this section, we deﬁne and detail some methodolog-

ical points such as our designed metrics as well as the

agents and tournaments we use in our simulations.

6.1 Metrics

Let

agents denoted

π = (π

)

acting for the

play-

ers of a tournament

during

max

steps. We denote

(T ,

π)(t)

the

max

payoffs received by the player

and

(T ,

π)

the sum of its

max

payoffs. Moreover,

we deﬁne the social welfare

SW (T ,

π,t)

as the sum of

payoffs of the

agents at time

. In the following, we

succinctly deﬁne the ﬁve metrics we design (adapted

from (Lerer and Peysakhovich, 2017)).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

298

0.5

1 2

1.0

0.6

0.5

1.0

0.6

0.5

𝐷

1 2

1.0

0.6

0.4

0.0

𝐶

= 0.6

𝐶

= 1.0𝐶

= 1.0

𝐶

= 1.0

1.0

(a) Step 1:

Tit-for-Tat

0.5

1 2

1.0

0.6

0.5

1.0

0.6

0.5

𝐷

1 2

1.0

0.6

0.4

0.0

𝐶

= 0.6

𝐶

= 1.0𝐶

= 1.0

𝐶

= 1.0

1.0

(b) Step 2: Transformation of the graph 3a into a

ﬂow network

0.5

1 2

1.0

0.6

0.5

1.0

0.6

0.5

𝐷

1 2

1.0

0.6

0.4

0.0

𝐶

= 0.6

𝐶

= 1.0𝐶

= 1.0

𝐶

= 1.0

1.0

sub-graph

Figure 3: Steps to ﬁnd a cyclic sub-graph of max ﬂow from player 1 in the graph (3a). The graph is transformed into a ﬂow

network regarding player 1 with a source s and a sink t in step (3b) and the max ﬂow is extracted in (3c).

First, the Utilitarian metric

measures how close

the social welfare is from the optimum which is mutual

cooperation (

) compared to the mutual defection (

and the speed

measures how fast the Utilitarian

metric reaches its maximal value. Then the incentive-

compatibility

is destined to measure the capacity

to incentivize cooperation within other players. We

deﬁne the incentive-compatibility of the agent

by the

difference between what one agent (

i = 0

) receives by

cooperating with all other agents

compared to what

it would have received by defecting. The safety

S f

measures the risk an agent takes by preferring

rather

than defection face to defectors ; let us note that since

defection is dominant (by deﬁnition of dilemma), this

metric is always non positive: the higher it is, the more

the agent is safe. At last, the forgiveness

measures

how the social welfare is impacted when a ”repentant

defector” R begins to cooperate only after

steps. For

the sake of clarity, we denote

1 = (x)

the constant

joint policy of N or N − 1 agents choosing x.

U(T ,π,t) =

SW (T ,π

1,t) − SW (T , D

1,0)

SW (T ,C

1,0) − SW(T , D

1,0)

, Sp(T ,π) =

τU

max

U(T ,π,t)dt

IC(T ,π) =

(T ,(C,π

1)) −V

(T ,(D, π

1))

(T ,C

1) −V

(T ,D

, S f (T , π) =

(T ,(π, D

1)) −V

(T ,D

1) −V

(T ,(C,D

1))

Fg(T ,π) =

max

− τ

max

−1

∑

t=τ

SW (T ,(R,π, ...,π),t) − SW(T , D

1,τ

)

SW (T ,C

1,τ

) − SW(T , D

1,τ

)

6.2 Agents and Tournaments

In our simulations, we compare several agents of TFT.

We use as baseline the vanilla continuous TFT and we

compare the different graph algorithms of our novel

GRAPHTFT. Moreover, we also compare the choice

of the TFT function in our algorithm and evaluate the

addition of our improvements (Alpha, Beta, Gamma).

For our simulations, we created two kinds of tourna-

ments of

N > 2

players with some patterns of circu-

larity. One is purely circular that we denote CIRC(

the weight of edge

(i, j)

is equal to

1.0

j = (i + 1)

mod N

and

0.0

otherwise. The other one is double

circular DOUBLE(

), the same with an alternative co-

operation edge (to study the case when one defector

breaks the cooperation cycle): the weight of edge

(i, j)

is equal to

1.0

j = (i + 1) mod N

j = (i + 2)

mod N and 0.0 otherwise.

7 RESULTS AND DISCUSSION

In this section, we present the results of some simula-

tions where we compare our extension of TFT suited

for the GIPD compared to the classic TFT. We ﬁrst

study the relevance of the graph structure of our GTFT

and then the impact of the choice of the TFT function.

7.1 Impact of the Graph-processing

Algorithm

First, we focus on the necessity of adding a graph-

processing algorithm and study the impact of the cho-

sen algorithm. The three cases we study are:

•

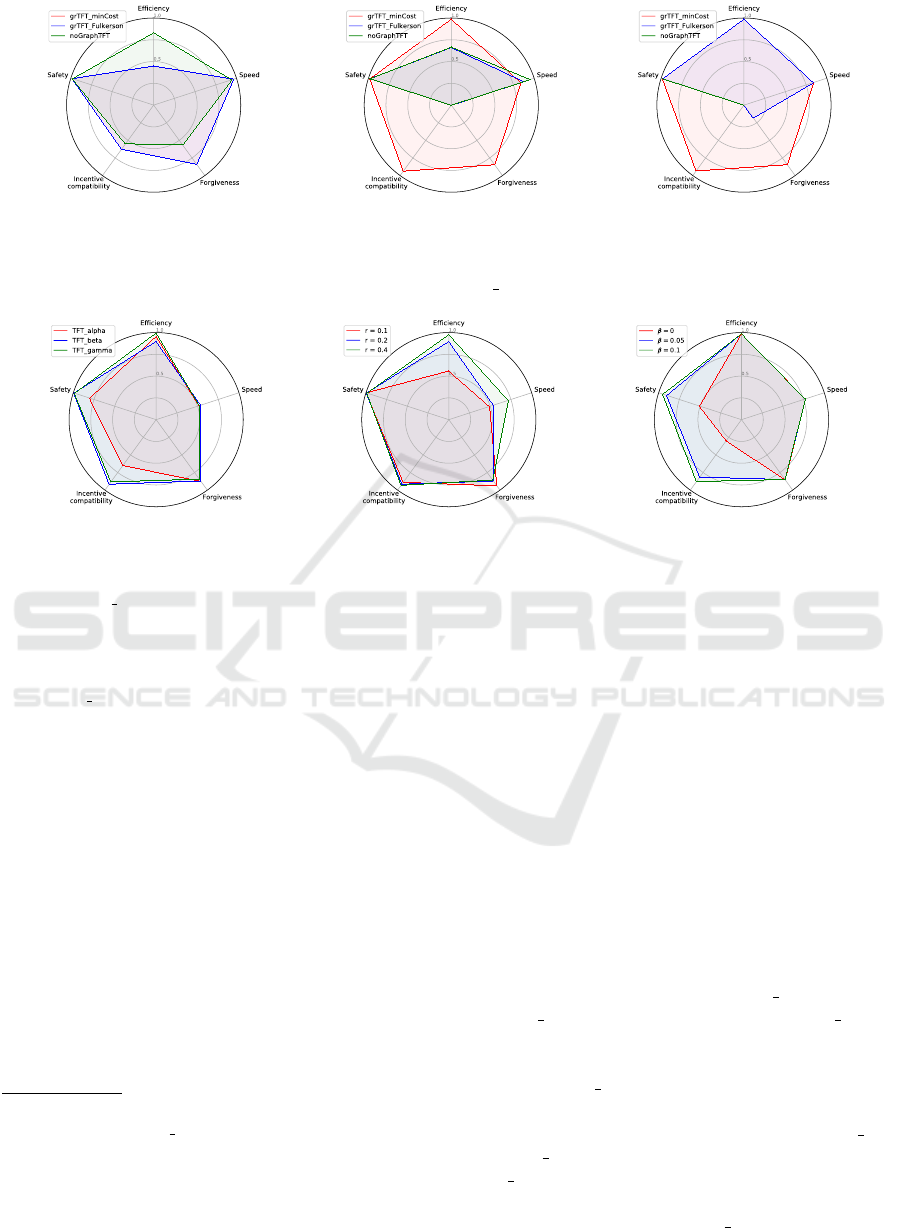
noGraphTFT: classic continuous TFT with no

graph processing.

•

grTFT Fulkerson: our GRAPHTFT (algo 1) with

Towards Circular and Asymmetric Cooperation in a Multi-player Graph-based Iterated Prisoner’s Dilemma

299

(a) Double Circular

3 players

(b) Double Circular

4 players

6 players

Figure 4: Impact of the choice of graph processing in the double circular tournament with 3, 4 and 6 players. The Tit-for-Tat

algorithm used for all agents of that simulation is the algorithm TFT beta with parameters (α = 0.6, β = 0.6, r

= 0.7)

(a) Impact of type (b) Impact of incentive r

Figure 5: Impact of the choice of TFT function on DOUBLECIRC(6) with GRAPHTFT (with min cost approach). We compare

the three kinds of TFT (Figure 5a), then the impact of the initial incentive

(Figure 5b) and the adaptive coefﬁcient

(Figure

5c) on the TFT beta algorithm.

a Ford-Fulkerson algorithm to ﬁnd the maximum

ﬂow.

•

grTFT minCost: our GRAPHTFT (algo 1) with

a min-cost max ﬂow approach: it searches the

max ﬂow but with constraint of maximal circulated

ﬂow (cooperation through maximum number of

players).

We simulate these three kinds of agents in the

games DOUBLECIRC with 3, 4 or 6 players and com-

pare the results of the metrics in Figure 4.

The observations conﬁrm the intuition that the lack

of graph processing in circular situations totally de-

feats the classic TFT in the 6-player game since there

is no possibility of symmetrical cooperation. In the

4-player game, the classic TFT can ﬁnd a less optimal

solution since it exists two less optimal 2-player cy-

cles. At last, the classic TFT can address the 3 players

DOUBLECIRC because a symmetrical alternative is

possible but a bit less optimal. Regarding the choice

A simulation of the cycle issue with 3 players: https:

//youtu.be/VHhEZ8Wu XQ or with 5 players: https://youtu.

be/J-weuvOkkBc

A simulation with 4 players: https://youtu.be/

s08j24LMr0U

A simulation with 6 players: https://youtu.be/

AL29LFbh3n8

of graph processing, the best one is the approach with

min cost because it allows to select the most pro-social

cycles of cooperation (unlike the Ford-Fulkerson al-

gorithm). It is therefore more suited to incentivize

cooperation and is safer to defection. However, when

it exists several equivalent optimal cycles (e.g. with

3 or 5 players), both GTFT agents naturally hardly

synchronize themselves.

7.2 Impact of Choice of Tit-for-Tat

Function

We study here the choice of Tit-for-Tat function

T FT

used in our GRAPHTFT (algo 1). We ﬁrst evalu-

ate the impact of the choice of TFT among the de-

scribed algorithms in section 5.2 (TFT alpha with iner-

tia, TFT beta with adaptive incentive and TFT gamma

with stochastic incentive). We then study the impact of

initial incentive coefﬁcient

and adaptive coefﬁcient

β with the TFT beta.

In Figure 5a, we can observe that the adaptive

coefﬁcient

is interesting since it makes TFT beta

and TFT gamma safer and more incentive compatible.

TFT gamma seems to be a bit more efﬁcient in a sense

that the outcome is more optimal. Regarding the im-

pact of parameters of the TFT beta, we can remark

that a higher initial incentive coefﬁcient

allows to

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

300

reach a more optimal outcome more rapidly without re-

ducing safety and incentive-compatibility. Regarding

the impact of adaptive coefﬁcient

, we can observe

that a tiny non-null coefﬁcient is sufﬁcient to make the

agent safer and more incentive compatible.

7.3 Results Summary

Although our GTFT is not perfectly optimal in am-

biguous situations (with multiple optimal cycles), we

can conclude that the key point of our experiments is

the importance of a graph-processing algorithm. The

min-cost max ﬂow is the best approach since it is

more incentive-compatible. Regarding the choice of

TFT function, the TFT beta function is clearly safer

than TFT alpha while TFT gamma is slightly more

efﬁcient.

8 CONCLUSION

In this paper, we introduced a novel paradigm for the

-player Prisoner’s Dilemma where maximal coopera-

tion between agents is induced by a weighted directed

graph. This new model is particularly suited to address

the asymmetry of cooperation and in particular the cir-

cular social dilemmas: a speciﬁc situation of dilemma

where players can form a cycle of cooperation in which

no player can cooperate with its ”helper”. We showed

that classic solutions like Tit-for-Tat strategies can-

not solve properly this speciﬁc issue, we therefore

also proposed in the paper a Graph-based Tit-for-Tat

which generalizes the classic TFT with a ﬂow network

approach. We evaluated this new algorithm in some

scenarios and compare it to some baselines. As ma-

jor conclusions, we can observe that adding a graph

processing in the TFT is relevant since our GTFT out-

performs the original TFT in most of situations. As

further works, it could be very interesting to address

the ambiguous cases with multiple equivalent optimal

cycles.

We recall our main contributions:

•

We introduced and formalized a novel Graph-

based Iterated Prisoner’s Dilemma: a formalism

able to generalize the

-player IPD involving

asymmetrical or circular cooperation.

•

We designed and formalized several social metrics

adapted to this GIPD.

•

We constructed a novel Graph-based Tit-for-Tat

able to cope with circular cooperation, it is based

on continuous TFT and max-ﬂow algorithms.

We are convinced that this new GTFT paradigm

which solves circular dilemmas should offer a lot of

perspectives particularly in addition to the recent tech-

niques mixing RL and TFT. Finally, in view of the

expectations regarding the digital sobriety and the eth-

ical stakes of artiﬁcial intelligence, we reiterated the

importance of focusing urgently on non-cooperative

games, and striving to include this kind of paradigm

in the design of our future intelligent systems.

REFERENCES

Agudo, J. E. and Fyfe, C. (2011). Reinforcement learning

for the n-persons iterated prisoners’ dilemma. In 2011

Seventh International Conference on Computational

Intelligence and Security, pages 472–476. IEEE.

Ashlock, D. A. (2007). Cooperation in prisoner’s dilemma

on graphs. In 2007 IEEE Symposium on Computational

Intelligence and Games, pages 48–55. IEEE.

Axelrod, R. and Hamilton, W. D. (1981). The evolution of

cooperation. science, 211(4489):1390–1396.

Beauﬁls, B., Delahaye, J.-P., Mathieu, P., et al. (2001).

Adaptive behaviour in the classical iterated prisoner’s

dilemma. In Proc. Artiﬁcial Intelligence & Simul. Be-

haviour Symp. on Adaptive Agents & Multi-Agent Sys-

tems. Citeseer.

Flood, M. M. (1958). Some experimental games. Manage-

ment Science, 5(1):5–26.

Ford, L. R. and Fulkerson, D. R. (1956). Maximal ﬂow

through a network. Canadian journal of Mathematics,

8:399–404.

Ford Jr, L. R. (1956). Network ﬂow theory. Technical report,

Rand Corp Santa Monica Ca.

Hager, G. D., Drobnis, A., Fang, F., Ghani, R., Greenwald,

A., Lyons, T., Parkes, D. C., Schultz, J., Saria, S.,

Smith, S. F., et al. (2019). Artiﬁcial intelligence for

social good. arXiv preprint arXiv:1901.05406.

Hamburger, H. (1973). N-person prisoner’s dilemma. Jour-

nal of Mathematical Sociology, 3(1):27–48.

Izquierdo, S. S., Izquierdo, L. R., and Gotts, N. M. (2008).

Reinforcement learning dynamics in social dilemmas.

Journal of Artiﬁcial Societies and Social Simulation,

11(2):1.

Jaques, N., Lazaridou, A., Hughes, E., Gulcehre, C., Ortega,

P., Strouse, D., Leibo, J. Z., and De Freitas, N. (2019).

Social inﬂuence as intrinsic motivation for multi-agent

deep reinforcement learning. In International Confer-

ence on Machine Learning, pages 3040–3049. PMLR.

Le Gl

eau, T., Marjou, X., Lemlouma, T., and Radier, B.

(2020). Game theory approach in multi-agent resources

sharing. In 25th IEEE Symposium on Computers and

Communications (ISCC).

Leibo, J. Z., Zambaldi, V., Lanctot, M., et al. (2017). Multi-

agent reinforcement learning in sequential social dilem-

mas. In Proceedings of the 16th Conference on Au-

tonomous Agents and MultiAgent Systems, pages 464–

473.

Lerer, A. and Peysakhovich, A. (2017). Maintaining cooper-

ation in complex social dilemmas using deep reinforce-

ment learning. arXiv preprint arXiv:1707.01068.

Towards Circular and Asymmetric Cooperation in a Multi-player Graph-based Iterated Prisoner’s Dilemma

301

Lin, B., Bouneffouf, D., and Cecchi, G. (2020). Online

learning in iterated prisoner’s dilemma to mimic human

behavior. arXiv preprint arXiv:2006.06580.

Luo, L., Chakraborty, N., and Sycara, K. (2010). Prisoner’s

dilemma in graphs with heterogeneous agents. In 2010

IEEE Second International Conference on Social Com-

puting, pages 145–152. IEEE.

Macy, M. W. and Flache, A. (2002). Learning dynamics in

social dilemmas. Proceedings of the National Academy

of Sciences, 99(suppl 3):7229–7236.

Matignon, L., Laurent, G. J., and Le Fort-Piat, N. (2007).

Hysteretic q-learning: an algorithm for decentral-

ized reinforcement learning in cooperative multi-agent

teams. In 2007 IEEE/RSJ International Conference on

Intelligent Robots and Systems, pages 64–69. IEEE.

Matignon, L., Laurent, G. J., and Le Fort-Piat, N. (2012).

Independent reinforcement learners in cooperative

markov games: a survey regarding coordination prob-

lems. Knowledge Engineering Review, 27(1):1–31.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,

J., Bellemare, M. G., Graves, A., Riedmiller, M., Fidje-

land, A. K., Ostrovski, G., et al. (2015). Human-level

control through deep reinforcement learning. nature,

518(7540):529–533.

Nash, J. (1951). Non-cooperative games. Annals of mathe-

matics, pages 286–295.

Nowak, M. and Sigmund, K. (1993). A strategy of win-stay,

lose-shift that outperforms tit-for-tat in the prisoner’s

dilemma game. Nature, 364(6432):56–58.

Orlin, J. B. (1997). A polynomial time primal network sim-

plex algorithm for minimum cost ﬂows. Mathematical

Programming, 78(2):109–129.

Rapoport, A., Chammah, A. M., and Orwant, C. J. (1965).

Prisoner’s dilemma: A study in conﬂict and coopera-

tion, volume 165. University of Michigan press.

Soroos, M. S. (1994). Global change, environmental security,

and the prisoner’s dilemma. Journal of Peace Research,

31(3):317–332.

Verhoeff, T. (1998). The trader’s dilemma: A continuous

version of the prisoner’s dilemma. Computing Science

Notes, 93(02).

Wu, J. and Axelrod, R. (1995). How to cope with noise in

the iterated prisoner’s dilemma. Journal of Conﬂict

resolution, 39(1):183–189.

Yao, X. (1996). Evolutionary stability in the n-person iter-

ated prisoner’s dilemma. BioSystems, 37(3):189–197.

Zheng, S., Trott, A., Srinivasa, S., Naik, N., Gruesbeck, M.,

Parkes, D. C., and Socher, R. (2020). The ai economist:

Improving equality and productivity with ai-driven tax

policies. arXiv preprint arXiv:2004.13332.

APPENDIX

Theoretical Approach

Our conclusions were mainly experimental. In this

section, we propose to study some properties of our

policy TFT in a cycle of players (CIRC(K)).

Proposition 1.

(Efﬁciency) Let a cycle of

players (CIRC(K)) who all follow the policy

TFT

α,β,0,r

. Then,

∀i ∈ [0,K − 1], with j =

i + 1 mod K, we have ∀t, c

i j

= c

→

where

→

deﬁned by :

→

= 1 − Q

(1 − c

)

avec Q = α + (1 − α)(1 − r

)

(7)

Proof.

For the

players, the policy of the incom-

ing ﬂow of cooperation is the same as its outgoing

ﬂow, so we have the same function of cooperation

degree for all players :

∀i ∈ [0,K − 1], with j = i +

1 mod K, we have ∀t, c

i j

= c

→

. First, let us focus

. Since

β(c

t−1

(i−1)i)

− c

t−1

i(i+1)

) = β(c

t−1

→

− c

t−1

→

) = 0

and

γ = 0.0

, we have

∀t, r

= r

. We can rewrite the

expression of the sequence c

→

= TFT

α,β,0,r

(t, c

t−1

→

t−1

→

)

= αc

t−1

→

+ (1 − α)(r

+ (1 − r

t−1

→

)

= [α +(1 − α)(1 − r

)]c

t−1

→

+ (1 − α)r

= Qa

t−1

+ R

with Q = α + (1 − α)(1 − r

) and R = (1 − α)r

(8)

It is an arithmetico–geometric sequence of com-

mon ratio

and common difference

. If we note

W =

1−Q

, the solution of c

→

is given by:

→

= Q

−W) +W (9)

Let us compute the value of W :

W =

1 − Q

(1 − α)r

1 − (α +(1 − α)(1 − r

))

(1 − α)r

(1 − α)(1 −(1 − r

))

= 1

(10)

Therefore, the ﬁnal expression of c

→

is given by:

→

= 1 − Q

(1 − c

)

with Q = α + (1 − α)(1 − r

)

(11)

Proposition 2.

(Safety) Let a player A, using the TFT

function

TFT

α,β,0,r

to choose

, he is facing a pure

defector B (∀t, b

= 0.0).

β ≥

(1−α)

, then it exists

such that

∀t ≥ τ, r

= 0.0

and therefore lim

t→+∞

= 0

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

302

Proof. First, we have :

= αa

t−1

+ (1 − α)(r

+ (1 − r

t−1

)

= αa

t−1

+ (1 − α)r

≥ αa

t−1

(12)

With this geometric sequence, we can ﬁnd a lower

bound for a

∀t, a

≥ a

(13)

Let us ﬁnd an upper bound for r

= r

t−1

+ β(b

t−1

− a

t−1

)

= r

t−1

− βa

t−1

≤ r

t−1

− βa

t−1

(14)

Hence,

∀u ≥ 1, r

− r

u−1

≤ −βa

u−1

(15)

We can add up the terms:

∀t ≥ 1,

∑

u=1

− r

u−1

≤ −βa

∑

u=1

u−1

⇐⇒ r

− r

≤ −βa

1 − α

⇐⇒ r

≤ r

− βa

1 − α

(16)

Then, the condition

β ≥

(1−α)

is a sufﬁcient

condition such that it exists

for which

∀t ≥ τ, r

= 0

Finally,

∀t ≥ τ, a

= a

(t−τ)

and therefore

lim

t→+∞

= 0

Towards Circular and Asymmetric Cooperation in a Multi-player Graph-based Iterated Prisoner’s Dilemma

303