Identifying Problematic Gamblers using Multiclass and Two-stage

Binary Neural Network Approaches

Kurt Dylan Buttigieg

, Mark Anthony Caruana

and David Suda

University of Malta, Malta

Keywords: Artificial Neural Networks, Bayesian Neural Networks, Problematic Gambling.

Abstract: Responsible gaming has gained traction in recent years due to the harmful nature of compulsive online

gambling and the increased awareness on the unfavourable consequences arising from this type of gambling.

In Malta, legislation passed in 2018 places the onus of responsibility on online gaming companies has made

studying this problem even more important. The focus of this research paper is to apply multistage and two-

stage artificial neural networks (ANN), and two-stage Bayesian neural networks (BNN), to the responsible

gaming problem by training models that can predict the gambling-risk of a player as a multiclass classification

problem. The models are trained using data from gambling session histories provided by a gaming company

based in Malta. These models will then be compared using different performance metrics. It is shown that,

while all approaches considered have their strengths, multiclass artificial neural networks perform best in

terms of overall accuracy while the two-stage Bayesian neural network model performs best in classifying the

most important class, the one where the players have a high risk of becoming problematic gamblers, and also

second best at classifying the medium risk class.

1 INTRODUCTION

The inception of the internet introduced new issues to

the gambling industry. Due to the harmful nature of

online gambling, responsible gaming gained

popularity in recent years, together with the

awareness regarding the unfavourable consequences

arising from gambling, especially the addiction of

gambling. Griffiths (2003) was amongst the first to

study gamblers’ behaviours in both traditional and

online forms of gambling. The paper studies the

accessibility, anonymity, affordability, and

convenience of internet gambling and noted that

problematic gamblers use the internet to further

satisfy their addiction. The author also mentions that

online gambling is incredibly dangerous considering

its convenient nature. Peller et al. (2008) mentioned

that to broaden studies on problematic online

gambling behaviour and the effect it has on one’s

health, one needs to study actual player data. Griffiths

et al. (2009) suggest that it may be more likely that

online gambling leads to problematic gambling rather

https://orcid.org/0000-0002-7861-7479

https://orcid.org/0000-0002-9033-1481

https://orcid.org/0000-0003-0106-7947

than offline gambling such as casinos. Hayer and

Meyer (2010) suggested, from preliminary scientific

evidence, that online gamblers are at greater risk of

becoming problematic gamblers than ordinary casino

or betting parlour gamblers. They argued that more

research should be conducted and favoured an

increase in effective measures which protect

gamblers. Furthermore, they concluded that

temporary self-exclusion measures to online

gambling sites yield positive psycho-social effects. A

study by McCormack & Griffiths (2012) showed that

even players themselves feel that the online element

of gambling, when compared to offline gambling,

causes more obsession and this form of gambling

increases social problems. Hubert & Griffiths (2018)

concluded that, although there were some

resemblances, online compulsive gamblers

demonstrate different characteristics when compared

to offline compulsive gamblers. The latter are more

prone to depression, feel more emotional while

gambling and experience frequent suicidal thoughts.

336

Buttigieg, K., Caruana, M. and Suda, D.

Identifying Problematic Gamblers using Multiclass and Two-stage Binary Neural Network Approaches.

DOI: 10.5220/0010821100003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 336-342

ISBN: 978-989-758-547-0; ISSN: 2184-433X

There have been a number of studies that made

use of machine learning techniques in the field of

responsible gaming. Braverman (2010) used a k-

means cluster analysis approach to identify clusters in

a dataset of 48,114 people who opened an account

with an online betting service provider. The analysis

identified four subgroups, in which one of the groups

is a cluster of gamblers that are at a higher risk for

reporting gambling-related problems. Philander

(2013) compared different data mining procedures,

with the aim of identifying gamblers at a high risk of

becoming problematic gamblers. A sample of online

live action sports betting data was used and different

classification and regression algorithms were applied

to identify which methods are better at achieving the

objective. Percy et al. (2016) applied logistic

regression, Bayesian networks, neural networks and

random forests to predict self-exclusion – these

models had very comparable results after applying

data balancing, with Bayesian networks being the

most superior in terms of accuracy and sensitivity.

Furthermore, Ukhov et al. (2020) utilise a gradient

boosting approach to identify the most important

traits of the casino and sports gambling groups,

finding distinct traits between the two. To the

authors’ knowledge, Bayesian neural networks

(BNN) has not been used for the identification of

problematic gamblers, though these have been used

in a variety of other applications. The aim is to see if

this approach yields any added benefits to the

standard ANN approach.

In this study, the problem will be tackled using

two-stage artificial neural networks, both in their

classical and Bayesian form. These techniques shall

be used to create models that can predict whether a

gambler is problematic or has a high risk of becoming

a problematic gambler by using historical session

data. The aim is to classify gamblers using 4-level

multiclass classifiers: minimal-risk, low-risk,

medium-risk and high-risk. As defined by Braverman

(2010) and Percy et al. (2016), there are four variables

which assist in classifying a player as problematic or

not: the number of bets, the amount of money bet, the

total winnings, and the number of active days. These

variables then yield the four important factors that,

depending on their degree, signify the extent of

problematic gambling behaviour, which are the

trajectory (total amount bet), frequency (days active),

intensity (how regularly the gambler places bets on

active days), and variability (the standard deviation of

the amount of money gambled) of the gambler. These

https://github.com/buttigiegkurt/responsible-gaming-

paper/blob/main/variablelist.pdf

four factors, together with similar behavioural

variables to those mentioned by Adami et al. (2013)

and Ukhov et al. (2020), and several other variables,

will be included in the analysis. In total 74 variables

are considered (see link in footnote

2 METHODOLOGY

In the methodology, multiclass artificial neural

networks and two-stage artificial and Bayesian neural

networks are considered. To keep a similar

framework throughout, only one hidden layer shall be

considered in the models. Artificial neural networks

(ANN) need no introduction. An important parameter

that shall require considering for ANN is the penalty

parameter for L

-norm regularisation 𝜑 which is

intended to regulate overfitting: 𝜑=0 means no

regularisation while larger values correspond to more

regularisation. Further theoretical detail on ANN can

be found in Courville et al. (2015). For ANN variable

selection shall also be implemented through variable

importance in some of the models. For variable

importance, Gevrey et al. (2003) introduced a method

which calculates the variable importance depending

on the absolute value of the weights. This method

gives the importance of a variable expressed in terms

of a percentage, with the most important variable

having an importance of 100%, and shall be used in

the application for calculating the importance of the

variables in the neural network models. In the

application, only variables with importance higher

than 50% will be kept.

The Bayesian approach to neural networks shall

also be considered. BNN offer automatic complexity

control, that is, regularisation coefficients which are

selected using data, and also the possibility of using

prior information for the hyperparameters. Automatic

complexity control helps in avoiding overfitting even

with highly complex models – this was tested by

Sharaf et al. (2020) where the authors concluded that

while there was the danger of overfitting the data with

ANN, the problem as not present in BNN. In this

paper, the focus shall be on the binary BNN setup

found in Liang et al. (2018). Consider the indicator

variables defined by

𝐼



()

=

if connection from input unit 𝑖 to hidden unit 𝑟 exists

otherwise

𝐼



()

=

if connection from hidden unit 𝑟 to output unit exists

otherwise

𝐼



()

=

if connection from input unit 𝑖 to output unit exists

otherwise

Identifying Problematic Gamblers using Multiclass and Two-stage Binary Neural Network Approaches

337

Then the neural network can be written as:

𝑦



(

𝒙,𝒘

)

=𝜓

()



∑

𝐼



()

𝑤



𝑥







∑

𝐼



()

𝑤



𝑧









(1)

where 𝑝 is the number of input variables, 𝐷 is the

number of nodes in the hidden layer, and 𝑧



𝜓

()



∑

𝐼



()

𝑤



𝑥







. Note that in equation (1), the

term

∑

𝐼



()

𝑤



𝑥







which is not typically present in

ANN includes the connections from the input to the

output units thus skipping the hidden layer. Also note

that the bias terms have been included as part of the

summations, by starting the summations from 0 rather

than 1. In this case, 𝑥



=1.

Next, the sets which specifies the structure and

weights of the Bayesian neural network can be

defined. Let

𝛤=𝐼



()

,𝐼



()

,𝐼



()

:𝑖=0,1,…,𝑝,𝑟=1,2,…,𝐷

denote the set which specify the structure of the

Bayesian neural network and let

𝛩

𝚪

={𝑤



,𝑤



,𝑤



:𝐼



(



)

=1,𝐼



(



)

=1,𝐼



(



)

=1: 𝑖

=0,1,…,𝑝,𝑟=1,…,𝐷}

denote the set which specifies the connection weights

associated with the BNN. Let

𝛤

denote the network

size, that is, the number of connections which have

their indicator equal to 1. Then the prior for 𝛩



is a

normal distribution with a zero vector mean and

covariance matrix 𝑉



, which has dimension

𝛤

, and the prior for 𝛤 is the probability mass

function

𝜋

(

𝛤

)

of 𝛤 satisfying

𝜋

(

𝛤

)

∝ 𝜆





(

1−𝜆



)









𝐼

(

1≤

𝛤

≤𝑟̅



,𝛤∈𝒢

)

(2)

where 𝑛 is the number of observations in the training

set, 𝐾



(

𝑝+1

)(

𝐷+1

)

+𝐷 is the total number of

connections between all the units in the neural

network when all the indicator variables are equal to

1, 𝑟̅



is the maximum network size allowed in

simulation,

𝜆



is the optimal prior hyperparameter

and 𝒢 is the set of all valid neural networks. In other

words, (2) can be considered to be Binomial with

parameters 𝐾



and 𝜆



For variable selection, Liang et al. (2018) made

use of the marginal inclusion probability approach.

The marginal inclusion probability approach,

explained in Barbieri et al. (2004), is a measure of

how likely a variable is in the true model. The

marginal inclusion probability approach can also be

used when selecting the network connections. The

same theory applies and all those connections which

have a marginal probability greater than 0.5 are

included in the BNN model. The actual number of

connections in the network, as well as the

corresponding number of hidden units, shall be

calculated automatically using the marginal inclusion

probability criterion. Furthermore, the optimal prior

hyperparameter 𝜆



is determined by specifying a

candidate set of 𝑚 values, and using K-fold cross-

validation. The 𝜆



for which the best likelihood is

obtained is then chosen. Finally, the algorithm for

generating posterior samples is an MCMC type

algorithm called the pop-SAMC algorithm.

This

algorithm operates by fine-tuning a parameter 𝜽

based on previous samples. By doing so, the

algorithm penalizes the most visited subregions and

rewards the ones less visited and thus escapes from

local traps, in which the Gibbs and the Metropolis-

Hastings algorithms are known to be vulnerable for.

The Pop-SAMC Algorithm, first published in Liang

et al. (2018), is now presented.

Pop-SAMC Algorithm:

Let 𝔊 be the sample space of 𝛩



and 𝑘 a constant.

Suppose that the posterior mass function of the BNN

can be written as ℎ

(

𝛩



)

=𝑘𝛶

(

𝛩



)

, where 𝛶

(

∙

)

is a

function of the connection weights. Partition 𝔊 into 𝑠

partitions defined as 𝑃𝑎𝑟



,𝑃𝑎𝑟



,…,𝑃𝑎𝑟



. Let 𝝎=

(

𝜔



,𝜔



,…,𝜔



)

denote the sampling frequencies for

each of the subregions, which satisfy the constraints

𝜔



>0 ∀𝑖 and

∑

𝜔







=1 . Let 𝜩



𝛩





()

,…,𝛩





()

 denote the population of samples

simulated at iteration 𝑡, where 𝑁 is the population

size. Let 𝜏∈[1,2), 𝜏



∈(0,1) and denote

{

𝑎



:𝑡=

1,2,…

}

as a positive and non-increasing sequence

which satisfies the following conditions:

𝑎







=∞,

𝑎



−𝑎



𝑎



=𝑂

(

𝑎





)



𝑎









√

𝑡





<∞.

In general, set 𝑎









for some 𝑡



>0 and 0.5 <

𝜍<1. One iteration of the algorithm consists of the

following two steps:

1. (Population Sampling) For 𝑙=1,…,𝑁,

simulate a sample 𝛩





()

by running, for one

step, the Metrapolis-Hastings algorithm

which starts with 𝛩





()

and admit the

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

338

stationary distribution ℎ





(

𝛩



)

∝

∑



(





)







,



𝐼

(

𝛩



∈𝑃𝑎𝑟



)





, where 𝜃



𝜃

,

,…,𝜃

,

 is the working parameter.

Denote the population of the new samples by

𝜩



=𝛩





()

,…,𝛩





()

.

2. ( 𝜃-updating) Firstly denote a vector 𝜻



()

made up of 𝑠 indicators 𝜻



(



)



𝐼𝛩





(



)

∈

𝑃𝑎𝑟



,…,𝐼𝛩





(



)

∈𝑃𝑎𝑟







, and let

𝑯

(

𝜃



,𝜩



)

∑

𝜻



(



)

𝝎





. Now, set

𝜃



= 𝜃



+𝑎



𝑯

(

𝜃



,𝜩



)

In this study, apart from considering a multiclass

ANN approach, a two-stage ANN and BNN approach

shall also be implemented, particularly to check

whether these yield better predictions. In particular,

the BNN that will be studied can only be implemented

in a binary setting, and hence the two-stage approach

for tackling the multiclass problem is essential. This

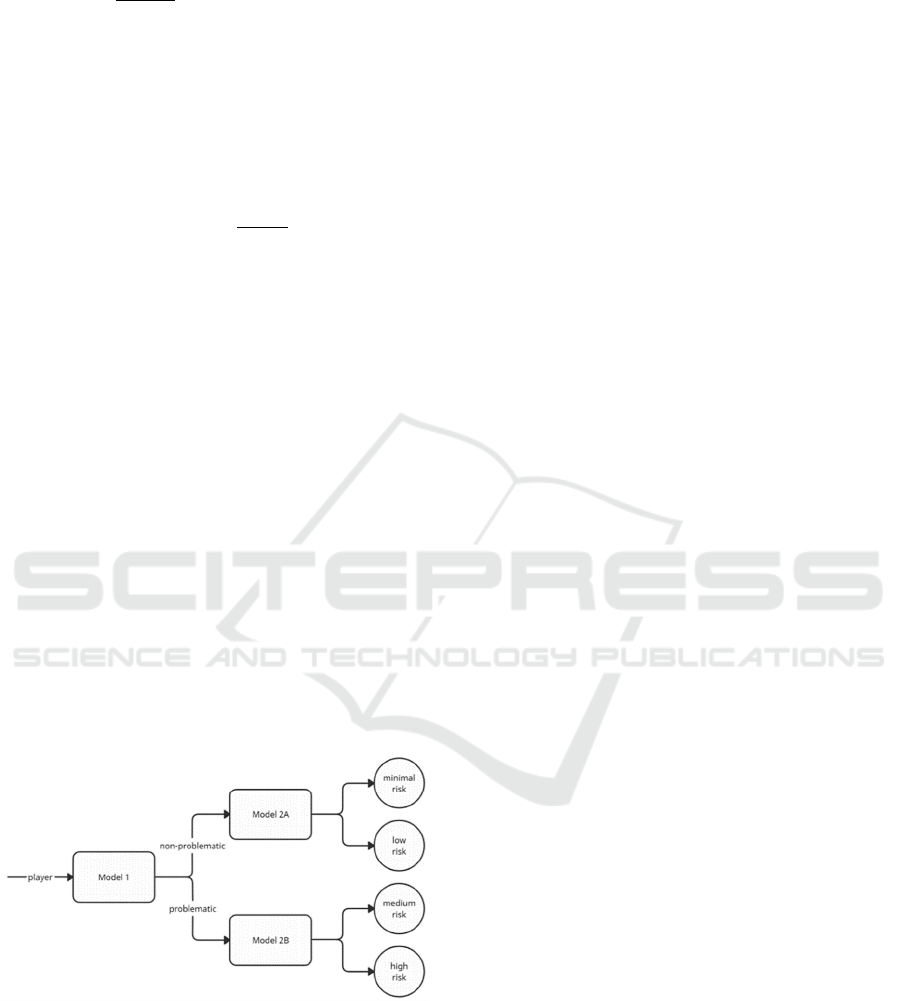
approach is described as follows. Initially, a model is

trained, denoted Model 1, which will predict whether

a gambler is classified as problematic or non-

problematic. Then, another independent model is

trained, denoted Model 2A, which classifies a non-

problematic gambler as minimal-risk or low-risk by

taking the actual class of the gamblers as reference,

i.e., only observations which have an actual class of

minimal-risk or low-risk are taken for training.

Similarly, a new model denoted Model 2B is trained,

which classifies a problematic gambler as medium-

risk or high-risk. A graphical representation of this is

given by Figure 1.

Figure 1: A graphical representation of the two-stage binary

model.

In the next section, the procedure of implementing

two-stage binary ANN and BNN, and multiclass

ANN to the responsible gambling problem shall be

described.

3 APPLICATIONS

The dataset considered consists of 30706

observations. It was discovered that a number of

observations had the same player ID due to the fact

that the same player can be assessed multiple times

by a responsible gaming agent. These duplicate

observations were removed, keeping the observations

with lowest number of days since last activity. A total

of 1829 duplicate observations have been removed,

leaving 28877 observations in the dataset.

Since the dataset used for this analysis consists of

both categorical and continuous data, SMOTE-NC

will be used to oversample the minority classes in the

training set. Python’s imblearn library (see Lemaître

et al., 2017) has been designed to deal with

imbalanced datasets and will be used for data

balancing since it has SMOTE-NC available. For

more information on SMOTE-NC, see Chawla et al.

(2002). It is known that neural networks perform

better with standardized data - see e.g. Shanker et al.

(1996). Thus, before creating the models, the data

used for both for all models has been centred and

scaled. The programming language R was used for

the data analysis, where the nnet package (see Ripley

and Venables., 2021) was used to implement artificial

neural networks and the BNN package (see Jia et al.,

2018) was used for implementing Bayesian neural

networks. To assess the performance of the models,

the MAE (the average absolute distance between the

predicted category and the actual category for

multiclass problems) and accuracy shall be used.

For ANN, the two-stage binary model uses the

sigmoid function for both the hidden and output

activation functions, the cross-entropy function as the

error function and the BFGS algorithm as the

optimisation algorithm to minimise this error

function. For further reading on the BFGS algorithm,

see Kelley (1999). This is done for all the three

models, that is, models 1, 2A and 2B. The same grid

search method will be used to find the optimal

parameters. The three models will be considered

separate and the grid search shall be used separately

for the three models. The sets specifying the different

number of hidden units 𝐷 and penalty parameter 𝜑

will be taken as {1,2,3,…,24,35} and

{0,0.1,0.2,…,0.9,1} respectively. This gives a total

of 35 × 11 = 385 different models for each of model

1, model 2A and model 2B. For each of these models,

5-fold cross validation will be used, where the

distributions of the classes over the different folds

will be kept equal. The optimal model for model 1 is

the one with 33 hidden units and a weight decay of

0.9, giving an MAE of 0.1539. The optimal model for

Identifying Problematic Gamblers using Multiclass and Two-stage Binary Neural Network Approaches

339

model 2A is the one with 23 hidden units and a weight

decay of 0.9, giving an MAE of 0.1458. The optimal

model for model 2B is the one with 35 hidden units

and a weight decay of 1, giving an MAE of 0.0886.

Next, the optimal model for model 1 shall be used to

predict gamblers on the testing set, which are then

predicted as minimal-risk, low-risk, medium-risk or

high-risk using the optimal models for 2A and 2B,

depending on their predicted class in model 1. The

two-stage binary model achieved an MAE of 0.5107

and an accuracy of 61.28%.

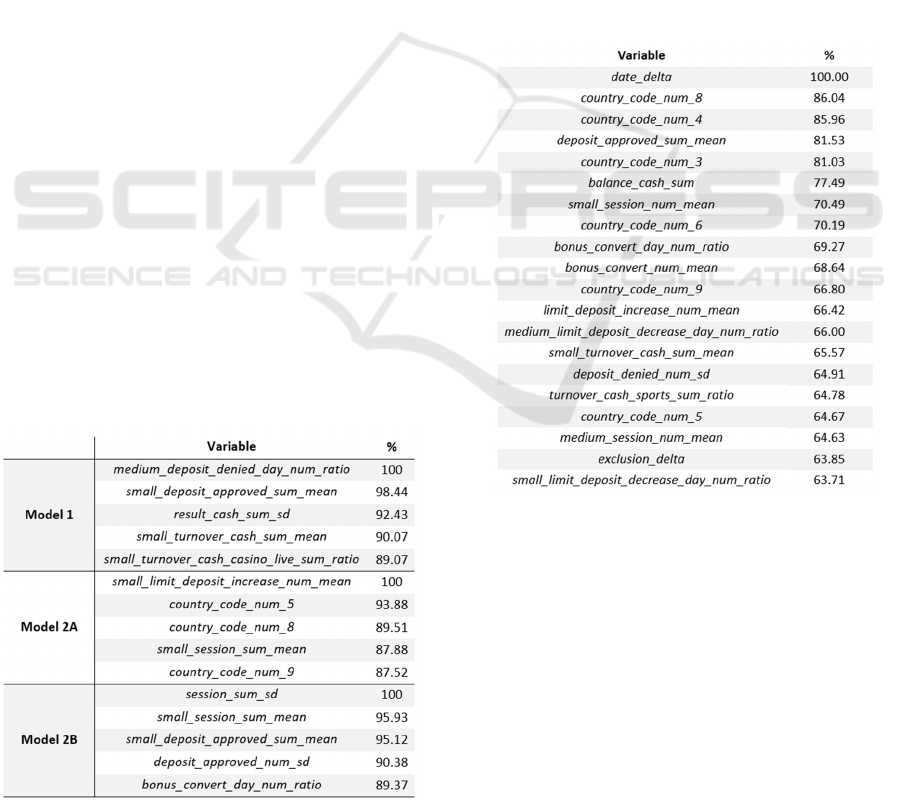
Variable importance is also considered on each of

the three optimal models, new models shall be trained

using just the variables with an importance greater

than 50%. The ratio of the number of days with at

least one denied deposit over the total number of

active days in the past thirty days was the most

important feature for model 1. For models 2A and 2B,

the average of the number of increases in the deposit

limit per active day for the last seven days and the

standard deviation of the total daily session time per

active day are the most important variables

respectively. For the top 5 most important variables

for each model refer to Table 1. The two-stage binary

model with variable selection has an accuracy of

62.06% and an MAE of 0.5035, a marginal

improvement in performance over the model without

variable importance. This shows that although

variable importance reduces the number of variables

in the models, better accuracy can still be obtained,

possibly due to further reducing overfitting in the

models.

Table 1: The five most important variables for each of the

three models in the two-stage binary artificial neural

network model (refer to variables list for full description of

each variable).

For the multiclass version of ANN, the sigmoid

function shall be used as the hidden activation

function and the softmax function for output

activation. In this case, 𝐷 shall be selected from

{1,2,3,…,24,40} and 𝜑 from

{0,0.1,0.2,…,0.9,1}. 5-fold cross validation will be

used once again. The best model is attained at 39

hidden units with a weight decay of 0.7, giving an

MAE of 0.3709. An MAE of 0.5164 is obtained, with

an accuracy of 61.7%. When considering variable

importance, this model is refitted and an MAE of

0.4919 and accuracy of 62.95% is obtained. In this

case, the variable representing the lowest number of

days since the last activity was the most important

one. For the top 20 most important variables refer to

Table 2.

Table 2: The twenty most important variables in the

multiclass artificial neural network model

(refer to variables

list for full description of each variable).

The two-stage binary model using BNN is finally

assessed. The two-stage binary BNN model uses the

tanh function as the hidden activation function and

the sigmoid function as the output. The 𝜆



’s

evaluated for each model will be from the set

{0.005,0.01,…,0.05} for each of models 1, 2A and

2B. For model 1, the optimal 𝜆



is found to be 0.015,

while for model 2A and 2B it is found to be 0.01 and

0.005 respectively. The best performing model with

25000 iterations, 5000 iterations and 50000 iterations

for models 1, 2A and 2B respectively – this yields an

MAE or 0.536 and an accuracy of 60.2%.

The MAE and accuracy for the different models

are summarised in Table 3 - it can be seen that the

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

340

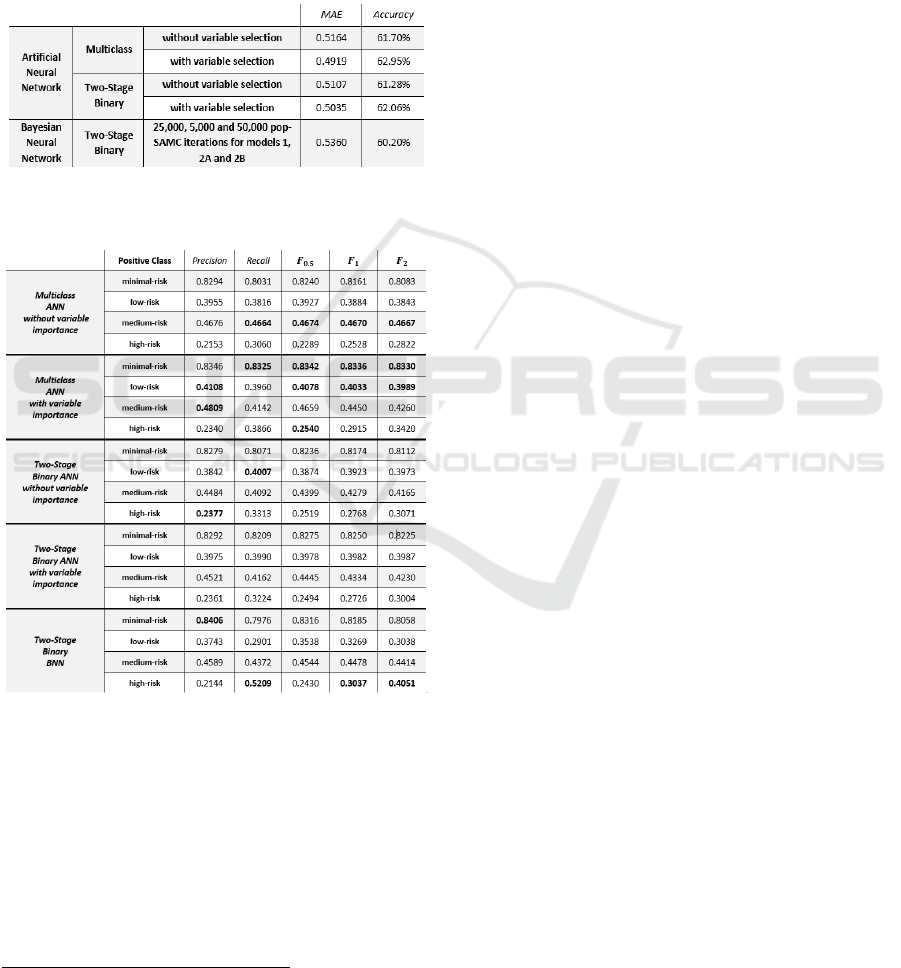
multiclass neural network model with variable

selection performed best in both. The two-stage

binary model with variable selection obtained close

results to the multiclass model, indicating that the

models with variable selection are better than the ones

without, showing that overfitting may be an issue.

Two-stage BNN’s performance is slightly inferior to

ANN, though not considerably.

Table 3: Comparing models in terms of MAE and accuracy.

Table 4: Testing model performance metrics using the one-

vs-all approach.

However, in these types of problems, accuracy is

not necessarily the most important measure, and what

needs to be considered is how well the models predict

higher risk categories, including the higher risk

classes, in particular the high-risk class. For this

reason, a one-vs-all approach is implemented to

check the performance of multiclass classifiers, i.e.,

setting a class as the positive class while setting the

other classes as the negative class. This reduces the

problem to a binary one, and thus binary performance

https://github.com/buttigiegkurt/responsible-gaming-pa

per/blob/main/variableimportance.pdf

metrics can be used such as precision, recall and the

𝐹



metrics – these are presented in Table 4. The

multiclass ANN model with variable selection

performed best in most of the metrics for the minimal

and low risk classes. However, the multiclass ANN

without variable selection performed best in

classifying the medium risk class, with BNN ranking

second best. The BNN model performed considerably

better than other models in classifying the high-risk

class, as a recall score of 0.5209 was obtained. This is

further shown by 𝐹



and 𝐹



metrics as the BNN

model obtained the best score with values of 0.3037

and 0.4051 respectively. This is of particular interest,

as detection of the high-risk class is of utmost

importance, while falsely classified lower risk

gamblers are less problematic.

4 CONCLUSIONS

In this study, it is concluded that BNN have been

more successful for predicting higher risk categories,

while multiclass ANN have performed better for

overall accuracy. Variable selection through

evaluating variable importance has, in the majority of

cases, been useful in improving accuracy. While this

has to be done via an extra procedure in ANN, this is

automatic in BNN where any unuseful connections

are automatically severed (see link in footnote for the

variables used in the BNN

). BNN have also proved

to be quite a computationally intensive procedure to

run, especially to determine the optimal 𝜆



’s, which

in total took more than 400 hours to run on a

workstation with an i7vPro 8

Gen processor. One

limitation which was experienced in the modelling is

the use of only single hidden layer neural networks in

the BNN package. The effect of the addition of extra

hidden layers could thus not be studied.

ACKNOWLEDGEMENTS

We wish to express our gratitude to LeoVegas

Gaming PLC in Sliema (Malta) for providing the data

in this study and, in addition, their support and their

insightful perspectives on the research topic.

Identifying Problematic Gamblers using Multiclass and Two-stage Binary Neural Network Approaches

341

REFERENCES

Adami, N., Benini, S., Boschetti, A., Canini, L., Maione, F.,

Temporin, M. (2013). Markers of unsustainable gaming

for early detection of at-risk online gamblers.

International Gambling Studies. 13, 188-204.

Barbieri, M., Berger, J. (2004). Optimal predictive model

selection. Annals of Statistics. 32(3), 870-897.

Braverman, J., Shaffer, H. (2010). How do gamblers start

gambling: identifying behavioural markers for high-

risk internet gambling. European Journal of Public

Health. 22, 273-278.

Chawla, N., Bowyer, K., Hall, L., & Kegelmeyer, P. (2002).

SMOTE: Synthetic minority over-sampling technique.

Journal of Artificial Intelligence Research, 16, 321-

357.

Courville, A., Goodfellow, I., Bengio, Y. (2015). Deep

Learning, The MIT Press. London, 2

edition.

Gevrey, M., Dimopoulos, I., Lek, S. (2003). Review and

comparison of methods to study the contribution of

variables in artificial neural network models.

Ecological Modelling. 160(30), 249-264.

Griffiths, M. (2003). Internet gampling: issues, concerns,

and recommendations. Cyber Psychology and

Behaviour. 6(6), 557-568.

Griffiths, M., Wardle, H., Orford, J., Spreston, K., Erems,

B. (2009). Sociodemographic correlates of internet

gambling: Findings from the 2007 British ambling

prevalence survey. Cyber Psychology and Behaviour.

12(2), 199-202.

Hayer, T., Meyer, G. (2010). Self-exclusion as a harm

minimization strategy: evidence for the casino sector

from selected European countries. Journal of Gambling

Studies. 27(4), 685-700.

Hubert, P., Griffiths, M. (2018). A comparison of online

versus offline gambling harm in Portuguese

pathological gamblers: An empirical study.

International Journal of Mental Health Addiction. 16,

1219-1237.

Jia, B., Liang F., Gentleman, R., Ihaka, R., The R Core

Team. (2018). Package ‘BNN’ (Version 1.0.2). CRAN

R-Project.

Kelley, C. T. (1999). Iterative Methods for Optimization.

Frontiers in Applied Mathematics, 18, 71-86.

Lemaître, G., Nogueira, F., Aridas, C. K. (2017).

Imbalanced-learn: a python toolbox to tackle the curse

of imbalanced datasets in machine learning. The

Journal of Machine Learning Research. 18(1), 559–

563.

Liang, F., Li, Q., Zhou, L. (2018). Bayesian neural

networks for selection of drug sensitive genes. Journal

of the American Statistical Association. 113(523), 955-

972.

McCormack, A., Griffiths, M. D. (2012). Motivating and

inhibiting factors in online gambling behavior: A

grounded theory study. International Journal of Mental

Health and Addiction. 10, 39-53.

Percy, C., Franca, M., Dragicevic, S., Garcez, A. (2016).

Predicting online gambling self-exclusion: An analysis

of the performance of supervised machine learning

methods. International Gambling Studies. 16(2), 1-18.

Peller, A., Laplante, D., Shaffer, H. (2008). Parameters for

safer gambling behaviour: examining the empirical

research. Journal of Gambling Studies. 24, 519-534.

Ripley, B., Venables, W. (2021). Package ‘nnet’ (Version

7.3-16). CRAN R-Project.

Philander, K. (2013). Identifying high-risk online gamblers:

a comparison of data mining procedures. International

Gambling Studies. 14(1), 53-63.

Shanker, M., Hu, M. Y., & Hung, M. S. (1996). Effect of

data standardization on neural network training.

Omega, 24, issue 4, 385–397.

Sharaf, T., Williams, T., Chehade, A., Pokhrel, K. (2020).

BLNN: An R package for training neural networks

using Bayesian inference. SoftwareX. 11, 100432.

Ukhov, I., Bjurgert,, J., Auer, M., Griffiths, M. (2020).

Online problem gambling: a comparison of casino

players and sports bettors via predictive modelling

using behavioral tracking data. Journal of Gambling

Studies. 37, 887-897.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

342