Moving Gap Solitons in Semilinear Coupled Bragg Gratings with a
Phase Mismatch
Shuvashis Saha and Javid Atai
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Australia
Keywords:
Moving Gap Solitons, Bragg Gratings, Phase Mismatch, Dual-core System.
Abstract:
We consider the existence and stability of the moving gap solitons in a semilinear coupler where one core
has Kerr nonlinearity and the other is linear and both cores are equipped with a Bragg grating with a phase
mismatch between them. We analyze the effect of the phase mismatch and the soliton velocity on the existence
and stability of moving gap solitons. It is found that larger phase mismatch leads to the expansion of the
stability region of the moving gap solitons.
1 INTRODUCTION
Nonlinear photonic structures equipped with fiber
Bragg gratings (FBGs) have attracted much interest
due to their potential applications in the slow light
applications (Aceves and Wabnitz, 1989; de Sterke
and Sipe, 1994; Sukhorukov and Kivshar, 2006). One
of the most interesting features of FBGs is that there
is a band gap in their linear spectrum where no lin-
ear waves can propagate. Moreover, a strong effec-
tive dispersion is generated due to the cross-coupling
between forward and backward propagating waves
(de Sterke and Sipe, 1994). This strong effective dis-
persion can be counterbalanced by the nonlinearity of
the medium when the pulse intensity is sufficiently
high giving rise to solitary waves known as gap soli-
tons (GSs). A very important property of GSs is that
they can propagate with any velocities ranging from
zero to the speed of light in the medium (Aceves and
Wabnitz, 1989). Experimentally GSs were observed
in a ∼ 6cm−long FBGs (Eggleton et al., 1996). Thus
far, moving gap solitons with a velocity in excess of
23% of the speed of light in the medium have been
observed experimentally (Mok et al., 2006).
The properties of GSs have been studied theo-
retically for different photonic structures and non-
linear media such as cubic-quintic nonlinear media
(Dasanayaka and Atai, 2013; Islam and Atai, 2014),
photonic crystals (Skryabin, 2004; Atai et al., 2006;
Neill and Atai, 2007), nonuniform Bragg gratings
(Atai and Malomed, 2005; Ahmed and Atai, 2017),
waveguide arrays (Mandelik et al., 2004; Dong et al.,
2011) and dual-core fibers with gratings in one or both
cores (Mak et al., 1998; Atai and Malomed, 2005;
Baratali and Atai, 2012).
Semilinear coupled systems exhibit superior
switching characteristics and support a wide range
of GSs (Chowdhury and Atai, 2017). It has been
demonstrated that very slow GSs can be generated in
a grating-assisted semilinear coupler (Atai and Mal-
omed, 2000; Shnaiderman et al., 2011). In the case
of dual-core systems made of coupled identical Bragg
gratings, both symmetric and asymmetric GSs exist in
the system (Mak et al., 2004). However, in the pres-
ence of a finite phase shift between the gratings, the
symmetric GSs are transformed into quasi-symmetric
ones (Tsofe and Malomed, 2007).
In this paper we analyze the existence and dynam-
ics the moving GSs in a semilinear coupled system
where both cores are equipped with a BG but there is
a phase mismatch between the gratings and one core
is linear while other one has Kerr type nonlinearity.
2 THE MODEL
The system model which was introduced in Ref.
(Saha and Atai, 2021) is given by the following cou-
pled partial differential equations:
iu
t
+ iu
x
+

|v|
2
+
1
2
|u|
2

u+ v+ κφ = 0
iv
t
− iv
x
+

|u|
2
+
1
2
|v|
2

v+ u+ κψ = 0
iφ
t
+ icφ
x
+ ψe
iθ/2
+ κu = 0
iψ
t
−icψ
x
+ φe
−iθ/2
+ κv = 0
(1)
38
Saha, S. and Atai, J.
Moving Gap Solitons in Semilinear Coupled Bragg Gratings with a Phase Mismatch.
DOI: 10.5220/0010819900003121
In Proceedings of the 10th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2022), pages 38-41
ISBN: 978-989-758-554-8; ISSN: 2184-4364
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

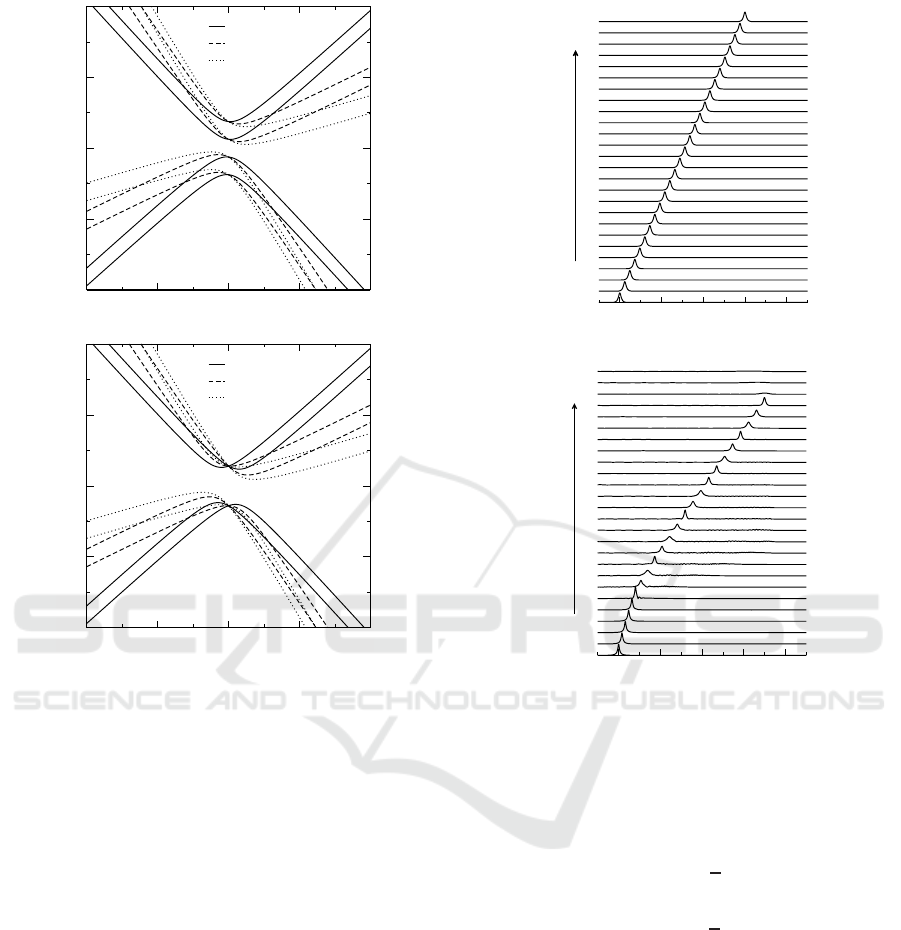
-8 -4 0 4 8
k
-8
-4
0
4
8
Ω
δ = 0.10
δ = 0.50
δ = 0.70
(a)
-8 -4 0 4 8
k
-8
-4
0
4
8
Ω
δ = 0.10
δ = 0.50
δ = 0.70
(b)
Figure 1: Examples of the spectra generated by the disper-
sion relation for κ = 0.5, c = 1, and different values of soli-
ton velocity δ; (a) θ = 0 and (b) θ = 2π.
where u and v represent the forward and backward
waves in the nonlinear core and φ and ψ are their
counterparts in the linear core. κ accounts for the
linear coupling coefficient between two cores. Rel-
ative group velocity in the nonlinear core is set to 1
and c denotes the relative group velocity mismatch.
The phase mismatch between two Bragg gratings is
denoted by θ.
To determine the moving GS solutions, Eqs.
(1)
need to be transformed to the moving frame using
the transformation
{X,T} = {x− δt,t}. δ accounts
for the normalized velocity of moving solitons (δ = 1
corresponds to velocity of light in the medium).
The transformation gives rise to the following set of
partial differential equations in the moving reference
frame:
-80 -40 0 40 80
x
(a)
0
t
1200
0
t
-80 -40 0 40 80
x
800
0
t
(b)
Figure 2: Examples of the evolution of moving gap soli-
tons for zero phase mismatch (θ = 0). (a) Stable soliton
corresponding to Ω = 0.20 and (b) Unstable soliton corre-
sponding to Ω = −0.45. The other parameters are κ = 0.5,
c = 1.0 and δ = 0.1. Only the u components are shown.
iu
T
+ i (1 − δ)u
X
+

|v|
2
+
1
2
|u|
2

u+ v+ κφ = 0
iv
T
− i (1 + δ)v
X
+

|u|
2
+
1
2
|v|
2

v+ u+ κψ = 0
iφ
T
+ i (c− δ) φ
X
+ ψe
iθ/2
+ κu = 0
iψ
T
− i (c+ δ) ψ
X
+ φe
−iθ/2
+ κv = 0
(2)
To determine the linear spectrum in which the
moving soliton solutions may reside, we substitute the
plane wavesolutions of {u,v, φ,ψ} ∼ exp(ikX − iΩT)
into the linearized form of Eqs.
(2), which gives the
following dispersion relation:
Ω
4
+4Ω
3
δk−Ω
2
c
2
k
2
+6Ω
2
δ
2
k
2
−Ω
2
k
2
−2Ω
2
+k
2
−2Ω
2
κ
2
−2Ωc
2
δk
3
+4Ωδ
3
k
3
−2Ωδk
3
−4Ωδkκ
2
Moving Gap Solitons in Semilinear Coupled Bragg Gratings with a Phase Mismatch
39

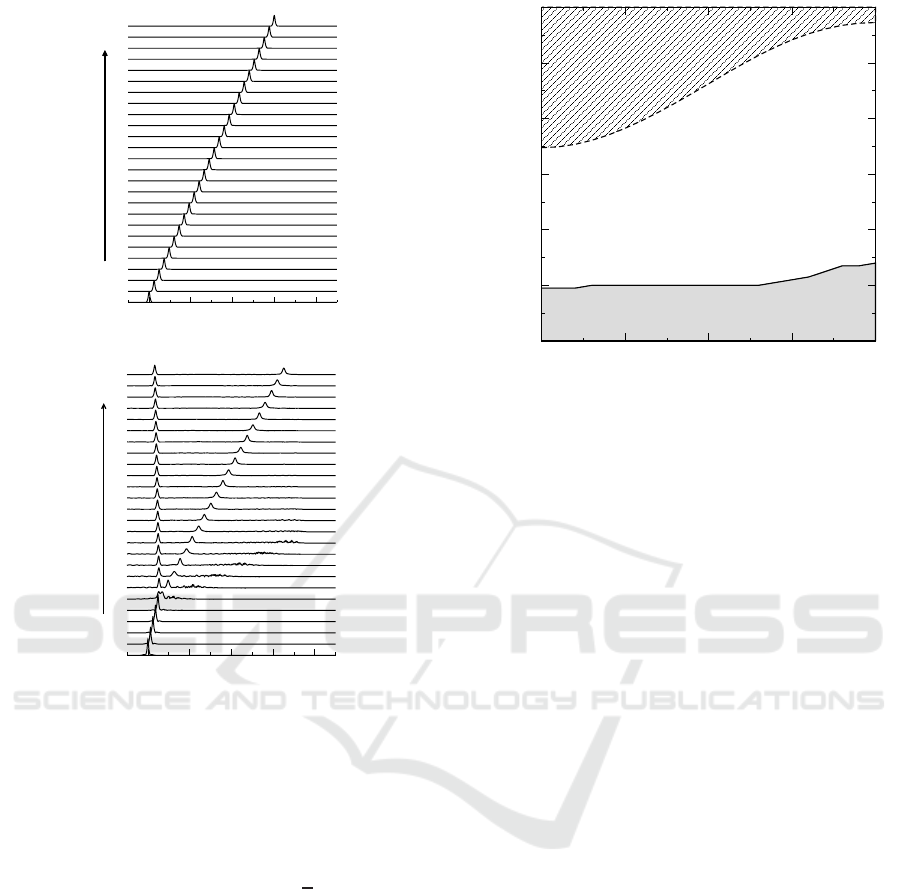
-80 -40 0 40 80
x
(a)
0
t
1200
0
t
-80 -40 0 40 80
x
600
0
t
(b)
Figure 3: Examples of the evolution of moving gap solitons
for θ = 2π. (a) Stable soliton corresponding to Ω = 0.20
and (b) Unstable soliton corresponding to Ω = −0.70. The
other parameters are κ = 0.5, c = 1.0 and δ = 0.1. Only the
u components are shown.
−4Ωδk−c
2
δ
2
k
4
+c
2
k
4
+c
2
k
2
−2ck
2
κ
2
+δ
4
k
4
+κ
4
−δ
2
k
4
− 2δ
2
k
2
κ
2
− 2δ
2
k
2
− 2cos

θ
2

κ
2
+ 1 = 0,
(3)
where k denotes the wave number and Ω is the fre-
quency detuning in the moving reference frame and it
is related to the frequency detuning (ω) in the station-
ary frame by Ω(k) = ω(k) −δk.
Fig. 1 shows the dis-
persion relation curves for different values of δ, when
c = 1, κ = 0.5 for θ = 0 and 2π. From straightforward
mathematical analysis of Eq.
(3), it is concluded that
when c = 1, the moving GS solutions exist only in
the central band gap. However, there exists a critical
value of soliton velocity, δ
cr
< 1 for which the central
band gap completely closes.
0
0.5
1
1.5
2
θ/π
-0.2
0
0.2
0.4
0.6
0.8
1
Ω
No Soliton Solution
Stable
Unstable
Figure 4: Stability diagram of the moving gap solitons in
the (θ,Ω) plane for κ = 0.5, c = 1.0 and δ = 0.10.
3 STABILITY OF MOVING
SOLITONS
To obtain the moving soliton solutions, Eqs. (2) were
solved numerically using a relaxation algorithm. We
then utilized the split-step Fourier method to investi-
gate the stability of moving GS solutions through di-
rect simulation of Eqs. (1). Figs. 2 and 3 show some
examples of the evolution of stable and unstable mov-
ing GSs for θ = 0 and 2π, respectively. Our analysis
shows that the model supports stable moving solitons
for values of θ in the range 0 ≤ θ ≤ 2π. A noteworthy
finding is that in the absence of the phase shift, i.e.
θ = 0, the unstable solitons may either decay com-
pletely (Fig. 2(b)) or shed some energy in the form
of radiation and evolve to another stable moving soli-
ton. However, as is shown in Fig. 3(b), when θ = 2π,
an unstable soliton loses energy upon propagationand
then splits and evolves into a quiescent and a moving
soliton.
Fig. 4 summarizes the result of stability diagram
on the (θ,Ω) plane when c = 1, κ = 0.50 and δ =
0.1. A notable finding is that, increasing θ leads to
the expansion of the stability region. The interplay of
θ and other parameters and their effect on the stability
of solitons is currently under investigation.
4 CONCLUSIONS
We have investigated the existence and stability of
moving GSs in a semilinear dual-core system where
one core has Kerr nonlinearity and the other is lin-
PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology
40

ear and both cores are equipped with BGs but there
is phase shift between them. We have focused on
the effect of phase mismatch and soliton velocity on
the existence and stability of moving GSs. A notable
finding is that the higher phase mismatch leads to the
expansion of the stable regions for the moving GSs.
Another finding is that for certain parameters unsta-
ble solitons may evolve into a quiescent and a moving
soliton. This outcome and its prevalence is currently
under investigation.
REFERENCES
Aceves, A. B. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Phys. Lett. A, 141:37–42.
Ahmed, T. and Atai, J. (2017). Bragg solitons in systems
with separated nonuniform bragg grating and nonlin-
earity. Phys. Rev. E, 96:032222.
Atai, J. and Malomed, B. A. (2000). Bragg-grating soli-
tons in a semilinear dual-core system. Phys. Rev. E,
62:8713.
Atai, J. and Malomed, B. A. (2005). Gap solitons in bragg
gratings with dispersive reflectivity. Phys. Lett. A,
342:404 – 412.
Atai, J., Malomed, B. A., and Merhasin, I. M. (2006). Sta-
bility and collisions of gap solitons in a model of a
hollow optical fiber. Opt. Commun., 265:342–348.
Baratali, B. H. and Atai, J. (2012). Gap solitons in dual-core
bragg gratings with dispersive reflectivity. J. Opt.,
14:065202.
Chowdhury, S. A. M. S. and Atai, J. (2017). Moving bragg
grating solitons in a semilinear dual-core system with
dispersive reflectivity. Sci. Rep., 7:1–12.
Dasanayaka, S. and Atai (2013). Stability and collisions of
moving bragg grating solitons in a cubic-quintic non-
linear medium. J. Opt. Soc. Am. B, 30:396–404.
de Sterke, C. M. and Sipe, J. E. (1994). Gap solitons. Prog.
Optics, 33:203–260.
Dong, R., R¨uter, C. E., Kip, D., Cuevas, J., Kevrekidis,
P. G., Song, D., and Xu, J. (2011). Dark-bright gap
solitons in coupled-mode one-dimensional saturable
waveguide arrays. Phys. Rev. A, 83:063816.
Eggleton, B. J., Slusher, R. E., Krug, P. A., and Sipe, J. E.
(1996). Bragg grating solitons. Phys. Rev. Lett.,
76:1627–1630.
Islam, M. J. and Atai, J. (2014). Stability of gap solitons
in dual-core bragg gratings with cubic-quintic nonlin-
earity. Laser Phys. Lett., 12:015401.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (1998).
Solitary waves in coupled nonlinear waveguides with
Bragg gratings. J. Opt. Soc. Am. B, 15:1685–1692.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (2004).
Symmetric and asymmetric solitons in linearly cou-
pled bragg gratings. Phys. Rev. E, 69:066610.
Mandelik, D., Morandotti, R., Aitchison, J. S., and Silber-
berg, Y. (2004). Gap solitons in waveguide arrays.
Phys. Rev. Lett., 92:093904.
Mok, J. T., de Sterke, C. M., Littler, I. C. M., and Eggle-
ton, B. J. (2006). Dispersionless slow light using gap
solitons. Nature Phys., 2:775–780.
Neill, D. R. and Atai, J. (2007). Gap solitons in a hollow
optical fiber in the normal dispersion regime. Phys.
Lett. A, 367:73–82.
Saha, S. and Atai, J. (2021). Effect of phase mismatch be-
tween the bragg gratings on the stability of gap soli-
tons in semilinear dual-core system. In Proceedings of
the 9th International Conference on Photonics, Optics
and Laser Technology- PHOTOPTICS, pages 36–39.
Shnaiderman, R., Tasgal, R. S., and Band, Y. B. (2011).
Creating very slow optical gap solitons with a grating-
assisted coupler. Opt. Lett., 36:2438–2440.
Skryabin, D. V. (2004). Coupled core-surface solitons in
photonic crystal fibers. Opt. Express, 12(20):4841–
4846.
Sukhorukov, A. A. and Kivshar, Y. S. (2006). Slow-light
optical bullets in arrays of nonlinear bragg-grating
waveguides. Phys. Rev. Lett., 97:233901.
Tsofe, Y. J. and Malomed, B. A. (2007). Quasisymmetric
and asymmetric gap solitons in linearly coupled bragg
gratings with a phase shift. Phys. Rev. E, 75:056603.
Moving Gap Solitons in Semilinear Coupled Bragg Gratings with a Phase Mismatch
41