Clustering Quality of a High-dimensional Service Monitoring

Time-series Dataset

Farzana Anowar

1,2 a

, Samira Sadaoui

1 b

and Hardik Dalal

University of Regina, Regina, Canada

Ericsson Canada Inc., Montreal, Canada

Keywords:

High-dimensional Time-series Dataset, Clustering Quality, Data Clustering, Data Imputation, Deep Learning.

Abstract:

Our study evaluates the quality of a high-dimensional time-series dataset gathered from service observability

and monitoring application. We construct the target dataset by extracting heterogeneous sub-datasets from

many servers, tackling data incompleteness in each sub-dataset using several imputation techniques, and fusing

all the optimally imputed sub-datasets. Based on robust data clustering approaches and metrics, we thoroughly

assess the quality of the initial dataset and the reconstructed datasets produced with Deep and Convolutional

AutoEncoders. The experiments reveal that the Deep AutoEncoder dataset’s performances outperform the

initial dataset’s performances.

1 INTRODUCTION

In industry, an incredible amount of data is produced

on a daily basis (Anowar and Sadaoui, 2021a; Anowar

and Sadaoui, 2020). Sometimes, data are not appro-

priately captured, which may be caused by human er-

rors, or sensor malfunction, resulting in data incom-

pleteness (i.e., missing values). Additionally, in the

presence of high dimensionality in the data, the train-

ing process becomes complicated for Machine Learn-

ing Algorithms (MLAs), leading to the model over-

ﬁtting and lowering the predictive performance (Jin-

dal and Kumar, 2017), (Anowar and Sadaoui, 2021b).

These two issues become more critical for time-series

datasets since the latter are collected over large time

frames. As a consequence, there are much more

chances of having missing values and high dimen-

sionality, which necessitate special attention from the

experts when dealing with these data (Rani and Sikka,

2012).

Based on an industrial application, we construct

a new End-to-End (E2E) service monitoring time-

series dataset so that users (developers, DevOps engi-

neers, IT managers, and site reliability engineers) can

respond to system-wide performance changes, mon-

itor the services’ availability, and optimize the re-

source utilization. For this purpose, we ﬁrst collect

https://orcid.org/0000-0002-1535-7323

https://orcid.org/0000-0002-9887-1570

data from multiple sub-servers over six weeks. How-

ever, the collected sub-datasets are heterogeneous in

terms of feature spaces and sizes. Before merging

the sub-datasets, we address the issue of data in-

completeness for each sub-dataset separately. We

tackle missing values with several imputation tech-

niques carefully and keep the optimally imputed sub-

datasets only. Subsequently, we fuse the imputed

sub-datasets based on the time-stamp feature to pro-

duce the ﬁnal time-series service monitoring dataset.

The latter is unlabelled, temporal, and high dimen-

sional. Since the dataset is new and complex, we

need to evaluate its quality before using it for any

decision-making task. This study compares several

clustering techniques on this very high-dimensional

dataset and its reconstructed equivalent datasets. To

this end, ﬁrst, we handle the high dimensionality is-

sue and second adopt data clustering methods, in-

cluding two conventional and two recent time series-

based algorithms, in which the dataset is divided into

several optimal groups. Since high dimensional data

brings computational challenges for developers, we

use Deep and Convolutional Autoencoders to improve

our dataset’s quality and then assess the quality of

the reconstructed datasets using the same clustering

methods.

Many efﬁcient dimensionality reduction methods

reduce the feature space effectively; however, they are

unable to recover the original data (Anowar et al.,

2021). In contrast, the AutoEncoders are effective

Anowar, F., Sadaoui, S. and Dalal, H.

Clustering Quality of a High-dimensional Service Monitoring Time-series Dataset.

DOI: 10.5220/0010801400003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 183-192

ISBN: 978-989-758-547-0; ISSN: 2184-433X

183

not only in lowering the dimensionality but also in

reconstructing the original data. We also make sure

not to lose much information while reconstructing

the data. Lastly, we thoroughly compare the qual-

ity of the initial and reconstructed datasets based on

the optimal clusters using several quality metrics to

show the efﬁcacy of the reconstructed datasets. The

obtained best clusters will be used for any further

decision-making tasks in the ML domain. We uti-

lize AutoEncoders to showcase that the reconstructed

feature space yields better clustering than the orig-

inal dataset. Our experimental results demonstrate

that the clustering performances of the reconstructed

dataset with Deep AutoEncoder (DAE) increased sig-

niﬁcantly over the clustering performances with the

initial dataset. To the best of our knowledge, no prior

research provided a thorough analysis of the cluster-

ing quality of a high-dimensional time-series dataset

that comes with missing values.

We structure the paper as follows. Section 2 dis-

cusses recent data clustering methods for assessing

the quality of high dimensional datasets. Section 3

presents the preprocessing and the fusion process to

build the target datasets. Section 4 describes the clus-

tering approaches and their quality evaluation metrics.

Section 5 develops two deep learning methods to re-

construct the dataset. Section 6 and Section 7 perform

several experiments to assess the clustering quality of

the initial and reconstructed datasets. Section 8 com-

pares all the clustering quality results. Section 9 con-

cludes our work with future work.

2 RELATED WORK

We examine notable studies that utilized diverse data

clustering methods to deal with high-dimensional

datasets speciﬁcally and reduce their complexity. For

instance, the authors in (Dash et al., 2010) combined

the dimensionality reduction method named Princi-

pal Component Analysis (PCA) and the data clus-

tering technique K-means. First, to make K-means

more effective, they proposed to utilize the instances

that have the maximum squared Euclidian distance

(among all the instances) as the initial centroids for

the clustering task. Next, they compared the perfor-

mances of the original K-means and the new pro-

posed approach using the reduced PCA dataset. They

showed that the results produced with the proposed

centroid selection method are more accurate, easy to

visualize, and the time complexity was substantially

decreased.

Any feature selection technique for high dimen-

sional datasets is assessed from two perspectives

(Song et al., 2011): efﬁciency and effectiveness,

where efﬁciency is related to the time required to

obtain the optimal sub-group of features, and ef-

fectiveness concerns the quality of this sub-group.

A fast clustering-based feature selection approach is

proposed in (Song et al., 2011), which operates in

two phases. Firstly, all the features are partitioned

into clusters based on the ”graph-theoretic cluster-

ing” technique to select the subsets of features, and

secondly, from each cluster, the most relevant fea-

ture that is closely connected to the target variable

is chosen again to provide the best selection of fea-

tures. The authors adopted the clustering method

called ”Minimum-Spanning Tree” to prove the com-

petence of the proposed method and carried out ex-

periments to evaluate the performances between the

proposed method and several existing feature selec-

tion algorithms. The experiments demonstrated that

the proposed approach returned reduced subsets of

features and improved the performances of the clas-

siﬁcation task.

For tackling the data dimensionality, Feature Se-

lection Algorithms (FSAs) were mainly adopted in

the literature. However, FSAs fail for large-scale fea-

ture spaces. Hence, the authors in (Chormunge and

Jena, 2018) addressed this problem by integrating a

clustering technique with a correlation measure to

generate a good subset of features. They ﬁrst elim-

inated the insigniﬁcant features using K-means clus-

tering, and later, the non-redundant features are cho-

sen by utilizing the correlation metric from each clus-

ter. For the experimental purpose, they used microar-

ray and text datasets to evaluate the proposed method

and compared the performances with two other FSAs,

ReliefF and Information Gain, using the Na

ıve Bayes

classiﬁer. The experimental results showed that the

most representative features were chosen by varying

the number of relevant features and provided better

accuracy than the other two FSAs.

Detecting outliers is an essential ML task because

outliers may carry important information. However,

in the case of high-dimensional datasets, outliers may

lead to worse performances. Therefore, the authors

in (Messaoud et al., 2019) developed a hybrid frame-

work named ‘Inﬁnite Feature Selection DBSCAN’

(InFS-DBSCAN) to decrease the dimensionality of

datasets and identify outliers efﬁciently using cluster-

ing techniques. They ﬁrst removed insigniﬁcant fea-

tures by selecting the k-most relevant features from

the high dimensional data space and then adopted

the DBSCAN algorithm to detect outliers. Two real-

world datasets were used for the experiments to com-

pare the performances of the proposed approach with

DBSCAN and FS-DBSCAN clustering in terms of the

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

184

clustering accuracy and error rate. For both datasets,

the proposed approach outperformed the other meth-

ods.

3 TIME-SERIES DATASET

CONSTRUCTION

The data we use for the experiments was collected

through Prometheus from October 26 to December

03, 2020, every 15 seconds for many available ser-

vices. The data is extracted from a monitoring service

that comes with three critical characteristics:

1. By nature data is high dimensional and temporal

(time series).

2. Data was collected from different sub-servers, so

it is stored and processed separately.

3. Data has many missing values due to the nature

of the applications hosted on the servers and net-

work/hardware/software failures.

More precisely, we retrieve data from 48 sub-

servers (in CSV format). The extracted sub-datasets

possess different sizes and sets of features. Af-

ter examining all the data, we found two types:

Counter and Gauge. The Counter type indicates a

single monotonically growing counter whose value

can either increase or be reset to zero on restart

(Prometheus, 2021). The Gauge type denotes a single

numerical value that can arbitrarily go up and down

(Prometheus, 2021).

3.1 Handling Missing Values in Each

Sub-server Data

Nevertheless, all the sub-server ﬁles contain missing

values. There are several options to tackle those val-

ues, such as imputation, removal of data with miss-

ing values (good option only when missing values are

rare), replacement with constant values (i.e. 0 or 1).

The last two options are not practical if many miss-

ing values are present, like in some of our sub-servers

ﬁles. Hence, we choose three imputation techniques:

(1) KNN Imputation, (2) MissForest Imputation, and

(3) SimpleImputer using the mean value. KNN im-

putation is easy to implement and fast, MissForest

can handle mixed data type (numerical and categori-

cal) and works efﬁciently with high-dimensional data,

and SimpleImputer performs much faster and can also

tackle mixed data. (Jadhav et al., 2019), (Pedregosa

et al., 2011), (Stekhoven and B

uhlmann, 2012).

We apply the three techniques to each sub-server

dataset separately to obtain relevant imputed values.

Table 1: Silhouette-Index Scores for Data Imputation.

Sub-server SimpleImputer KNN MissForest

#1 0.996663641 0.996662706 0.995631504

#3 0.932876262 0.932890974 0.932648194

#4 0.493330594 0.523756138 0.549322423

Furthermore, we utilize the “Silhouette Index” to as-

sess the new values. The imputation method that re-

turns the best (higher) Silhouette score is selected for

each ﬁle. Table 1 reports the Silhouette scores for

three sub-servers, as examples. For different sub-

server ﬁles, different methods are needed to achieve

the best data quality. Indeed, we obtain 31 opti-

mally imputed sub-datasets with SimpleImputer, 4

optimally imputed data with KNN imputation, and

13 optimally imputed data with MissForest. We

may note that MisssForest necessitated more compu-

tational time than the two others.

3.2 Fusing Heterogeneous Sub-server

Datasets

As mentioned earlier, we obtain 48 optimally imputed

sub-datasets. Subsequently, we conduct the “Inner

Join” procedure to merge the many heterogeneous

sub-datasets by considering the time-stamp column

as the key component. This procedure keeps the in-

stances from the participating ﬁles as long as there

is a match between the key columns. It returns all

the rows where the key component (here time-stamp)

of one ﬁle is equal to the key records of another ﬁle.

As a result, we produce the ﬁnal E2E service moni-

toring dataset consisting of 3,100 features and 53,953

instances over 6 weeks (39 days). This dataset is of a

large scale and highly dimensional.

We use a simple example to explain the Inner

Join procedure (Figure 1) where we have two sepa-

rate databases: Product and Customer. After apply-

ing Inner Join to both ﬁles using the ProductID as

the key column, we obtain only 1 row (with 10 fea-

tures) as the two ﬁles have only one common value

(101). Also, notice that the attribute City is present

in both databases, and Inner Join produces 2 different

attributes (City x and City y) for the ﬁnal output, as

the ﬁrst one denotes the product’s warehouse location

and the second one is the delivery location.

Figures 2 and 3 plot two features named ‘Re-

quests1’ and ‘Responses1’ (selected randomly) from

the E2E service monitoring dataset. In Figure 2, data

has either went up or is set to 0, which implies that

the feature ‘Request1’ contains Counter-type data. In

Figure 3, data has gone up and down arbitrarily, which

shows that the feature ‘Responses1’ is of the Gauge

type.

Clustering Quality of a High-dimensional Service Monitoring Time-series Dataset

185

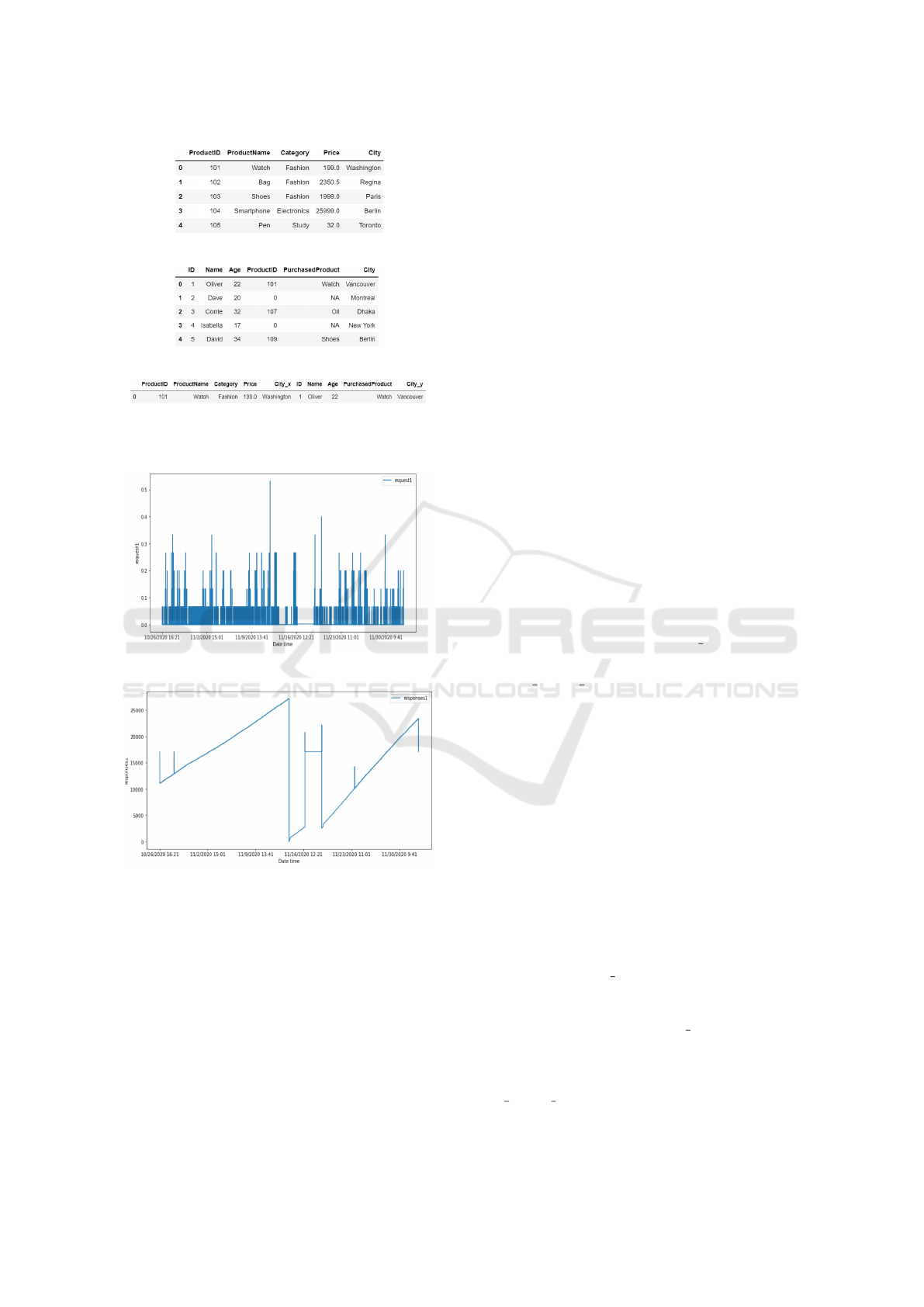
(a) Product DB.

(b) Customer DB.

Figure 1: Concept of Inner Join.

Figure 2: Feature ‘Request1’ (Counter Type).

Figure 3: Feature ‘Responses1’ (Gauge Type).

3.3 Normalizing the New Feature Space

After examining the ﬁnal dataset, we observe that

most features (80.64%) have quite small values, and

19.36% of features have very high values. The big

value disparities between features require to re-scale

the entire dataset. Using the min-max scaler in

Python, we try multiple ranges, including [0-1], [0-

10], [0-50], [0-100] for the AutuEncoders’ loss opti-

mization, and obtain [0-1] is the best range to re-scale

the dataset for the experiment.

4 CLUSTERING APPROACHES

AND METRICS

We assess the quality of the new dataset through un-

supervised learning using data clustering since it is

unlabeled. It is critical for any unsupervised ML task

to obtain high-quality clusters in order to ﬁnd the hid-

den patterns or unknown correlations in a dataset (Wu

et al., 2020). To this end, we select different clus-

tering techniques: partition-based, time-series-based,

and density-based, described below:

• K-means is a widely employed clustering

technique in the literature (Niennattrakul and

Ratanamahatana, 2007), (Aghabozorgi et al.,

2015).

• TS-Kmean and TS-Kshape are both designed ex-

plicitly for time series with a high dimensionality

(Tavenard et al., 2020). The specialty about TS-

Kmean is that it can weigh the time-stamps au-

tomatically based on the time-span’s signiﬁcance

during the clustering operation (Huang et al.,

2016). TS-Kshape computes the distance mea-

sure and centroids using the normalized cross-

correlation of two time series for each iteration,

and update the assignments of the clusters (Pa-

parrizos and Gravano, 2015). Both methods have

only one hyper-parameter (max iter).

• HDBSCAN has one hyper-parameter

(min cluster size) compared to other density-

based methods. It can handle highly dense data,

like ours. Besides, it can tackle the varying den-

sity issue, which the standard DBSCAN method

cannot (Saul, 2017). Additionally, HDBSCAN

does not require knowing the count of clusters

beforehand, unlike the three previous methods

(McInnes and Healy, 2017).

A well-known fact about K-means is that it

takes more time to converge for large-scale datasets

(Prabhu and Anbazhagan, 2011), like ours. To ﬁx

this issue, we utilize K-means++ as the initializer in-

side the K-means algorithm to make the convergence

much faster. For utilizing TS-Kmean and TS-Kshape,

we ﬁrst import ‘tslearn’, a Python machine learn-

ing package for time-series datasets. Also, for TS-

Kmean, we set max iter to 50 and include the ini-

tializer K-means++ as well, and for the cluster as-

signments, we use the Euclidean distance. More-

over, for TS-Kshape, we set max iter to 100. For the

three ﬁrst methods, we search for the optimal number

of clusters using Elbow, Silhouette Coefﬁcient, and

Caliniski-Harabasz (CH) Index. Lastly, we allocate

min cluster size to 2000 for HDBSCAN, as we be-

lieve out of 53,953 data, the minimum 2000 data (≈

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

186

26%) for a cluster is good enough.

To assess the quality of the produced clusters by

the four methods, we utilize the following quality

metrics, described below:

• Sum of Squared Error (SSE) that identiﬁes how

internally coherent each cluster is. The lower the

SSE, the better the cluster is (Pedregosa et al.,

2011).

• Davies-Bouldin (DB) Index that deﬁnes the aver-

age similarity of each cluster, i.e., the intra-cluster

distance should be minimum. Hence the lower,

the better (Pedregosa et al., 2011).

• Variance Ratio Criterion (VRC) that quantiﬁes the

ratio of “between-cluster dispersion” and “within-

cluster dispersion”. The higher the VRC, the bet-

ter the cluster is (Zhang and Li, 2013).

We compute the performances of all the opti-

mal clusters for the initial dataset and reconstructed

datasets. To this end, we utilize SSE, DB, and VRC

for K-means, TS-Kmean and TS-Kshape, and only

DB and VRC for HDBSCAN, as the latter doesn’t

have the SSE object in Python.

5 RECONSTRUCTED DATASETS

WITH AUTOENCODERS

Since numerous services run on the servers’ side,

data are generated at high speed and with soaring

dimensionality. Consequently, we adopt two self-

supervised deep-learning methods to improve the data

quality: Deep AutoEncoder (DAE) and Convolutional

AutoEncoder (ConAE). AutoEncoders uses encoder

and decoder layers. The former uses a latent space

to compress the inputs, and the later reconstructs the

original dataset as closely as possible from this com-

pressed data(Wang et al., 2016). Autoencoders learn

from the data while back-propagating the neural net-

work by disregarding insigniﬁcant data during encod-

ing, resulting in a better-reconstructed dataset (Law-

ton, 2020). Furthermore, the goal of training Au-

toEncoders is to minimize the reconstruction loss; the

lower the reconstruction loss, the more similar the

reconstruction of the original data can be generated

(Wang et al., 2016). Thanks to these methods, we do

not worry about reducing the high feature space opti-

mally.

The main challenge is determining the optimal ar-

chitecture for our complex service monitoring dataset.

We ﬁrst develop the DAE using a deep, fully con-

nected neural network. We try several rigorous com-

binations of hidden layers, loss function, weight op-

timizer, activation functions, epochs and batch sizes.

(a)

(b)

Figure 4: Loss for Different Combinations of DAE.

For instance, if we utilize 10 hidden layers for both

encoder and decoder, MSE as the loss function, Adam

as the optimizer, Relu as the activation function, batch

size of 256 with 3500 epochs, the obtained loss is high

(more than 0.45) as shown in Figure 4 (a). On the

other hand, if we use only one hidden layer for both

encoder and decoder, SGD as the optimizer, Sigmoid

as the activation function, batch size of 512 with 50

epochs, we obtain a negative loss as depicted in Fig-

ure 4 (b).

The best architecture that we attain for DAE com-

prises 6 hidden layers for both encoder and decoder,

1032 for batch size, Adadelta as the optimizer, Relu

for all the hidden layers, Sigmoid for the output layer

as activation function, and MSE as the loss function.

More precisely, for the encoder part, we sequentially

provide 3100 (original), 2500, 1650, 1032, 500, 100

and 5 features using six hidden layers, and again, we

reconstruct the features from 5, 100, 500, 1032, 1650,

2500 and 3100.

Regarding ConAE, we build a sequential neu-

ral network with two hidden layers for both encoder

and decoder. For the encoder layers, we utilize the

Conv1D class with 128 and 16 ﬁlters, and for the de-

coder layers, Conv1D with 16 and 128 ﬁlters; the ker-

nel size of all the ﬁlters is 3. For the encoding layers,

we use MaxPooling1D with a pool size of 2 to down-

sample the input representation. We adopt UpSam-

pling1D with size of 2 for the decoder to upsample

the input representation from the encoder. Also, keep

in mind that the output of ConAE is a 3D array; hence,

it needs to be converted to a 2D array before using it

for subsequent experiments.

Besides, we use ﬁve consecutive epochs with no

reduction by 0.0001 as the stopping criterion for train-

ing, and the reconstruction error for DAE is 0.0016

with the 75th epoch out of 100 epochs. However,

Clustering Quality of a High-dimensional Service Monitoring Time-series Dataset

187

(a)

(b)

Figure 5: Loss Graph for DAE (a) and ConAE (b).

while implementing ConAE, the critical challenge is

the computational complexity. Thus, instead of 5

consecutive epochs, we choose 3 without reducing

loss by 0.0001 as the stopping criterion. We obtain

the reconstruction error of 0.0021 and optimal epoch

of 74. Here, for both DAE and ConAE, the iter-

ations stop at 75th and 74th epochs respectively as

they meet the stopping criterion. We present the loss

graphs for DAE and ConAE in Figure 5 where the loss

curve goes steep down drastically after three epochs

for DAE in Figure 5(a) and gradually goes down for

ConAE in Figure 5(b). Furthermore, Figures 6 and

7 illustrate the reconstructed datasets with the ﬁrst

two features that we obtain after utilizing DAE and

ConAE models. In Figure 6, data are scattered across

the distribution, and in contrast, in Figure 7, data are

more densely located in similar positions.

Nevertheless, one crucial question raises while

compressing the initial dataset with DAE and ConAE

is that how much information was lost. For this pur-

pose, we employ the reconstruction error to measure

the information loss. As mentioned earlier, we obtain

the reconstruction error of 0.0016 and 0.0021, respec-

tively, for the reconstructed datasets using DAE and

ConAE, which are very minimal. Hence, we can con-

clude that with deep-learning methods, we lost a very

minimum amount of information.

Figure 6: Reconstructed Dataset using DAE.

Figure 7: Reconstructed Dataset using ConAE.

6 CLUSTERING QUALITY OF

INITIAL DATASET

First, we utilize Elbow method, Silhouette coefﬁcient

and CH Index to search for the best number of clus-

ters for the initial dataset, as presented in Table 2, and

Elbow, Silhouette and CH Index are described below:

1. Elbow method: One of the most popular tech-

niques for identifying the optimal number of clus-

ters. It is based on the calculation of “Within-

Cluster-Sum of Squared (WSS)” errors for a dif-

ferent number of clusters (k). It iterates over the k

and calculates the WSS errors (Yuan and Yang,

2019). Small values indicate that clusters are

more likely to be convergent, and after reaching

the optimal cluster’s number, WSS error starts de-

clining (Yuan and Yang, 2019).

2. Silhouette coefﬁcient: This metric calculates

the cluster’s cohesion and separation (Pedregosa

et al., 2011). It measures how well an instance

ﬁts into its corresponding cluster. The values of

the Silhouette coefﬁcient range between -1 and 1

(Pedregosa et al., 2011). A high (close to 1) sil-

houette score indicates that data are closer to their

assigned clusters than others. A score close to 0

means that data is very close to or on the deci-

sion boundary between two neighboring clusters.

A score close to -1 means that data is probably as-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

188

Table 2: Optimal Cluster Numbers.

Dataset

Optimal Clustering

Initial Dataset

Elbow Silhouette CH

5 5 4

Reconstructed Dataset

with DAE

Elbow Silhouette CH

5 6 14

Reconstructed Dataset

with ConAE

Elbow Silhouette CH

5 5 5

signed to a wrong cluster (Kaoungku et al., 2018).

3. CH Index: The basic idea of CH index is that

clusters that are very compact and well-separated

from each other are good clusters. This index is

a metric that compares how similar a cluster’s in-

stance is to that than other clusters (Wang and Xu,

2019).

Then, we fed the optimal number of clusters from

Table 2 to the three clustering methods (K-means, TS-

Kmeans and TS-Kshape). We do not supply the num-

ber of clusters to HDBSCAN, as by default it pro-

duces this number (which is 6). We report the per-

formances of the four clustering methods in Table 3,

with a tally of 20 results. We attain the minimum SSE

(0.004348) with TS-Kshape using 5 clusters, the min-

imum DB (0.61332) with K-means using 4 clusters.

K-means with 4 clusters provides the maximum VRC

(103431.341). However, the data performance with

HDBSCAN is not satisfactory. Due to the high data

density, we present the 3-D visualization of two ex-

amples of optimal clusters in Figure 8 to have a much

better graphical representation where x, y ans z axes

represent the ﬁrst three dimensions: dimension#1, di-

mension#2, and dimension#3.

Table 3: Optimal Clustering Quality of Initial Dataset.

K-means

5 clusters 4 clusters

SSE DB VRC SSE DB VRC

245568.441 0.613830 102604.2395 313075.295 0.61332 103431.341

TS-Kmean

5 clusters 4 clusters

SSE DB VRC SSE DB VRC

4.9938 0.613830 102604.2395 5.80274 0.7040410 97865.0800

TS-Kshape

5 clusters 4 clusters

SSE DB VRC SSE DB VRC

0.004348 2.243981 75912.984 0.00716 0.70334 62285.962

HDBSCAN with 6 clusters

DB VRC

1.3517 80707.7806

7 CLUSTERING QUALITY OF

RECONSTRUCTED DATASETS

Table 2 exposes the optimal clustering for the recon-

structed datasets. For the ConAE dataset, all the tech-

niques (Elbow, Silhouette and CH) return the same

number, unlike for the DAE dataset. Elbow tech-

nique yields the same optimal clustering for the three

datasets. However, CH recommends different cluster-

ing numbers, especially for the DEA datasets. Most

of the numbers are close by, except one (14), and

among the nine results, six return the number 5. Since

the reconstructed DAE dataset is sparsely separated

over the feature-space, CH Index returns a higher ra-

tio of between and within cluster sums of squares, re-

sulting in a higher (14) optimal clustering.

Next, Table 4 evaluates the optimal cluster qual-

ity for the DEA reconstructed dataset, with a tally of

20 results. We obtain the lowest SSE of 0.0019202

with TS-Kshape using 14 clusters, the minimum DB

of 0.05016857 with K-means and TS-Kmeans using

6 clusters, and the highest VRC of 30,312,918.2572

with K-means using 14 clusters. A higher VRC score

implies that the clusters are dense (minimized intra-

cluster distance) and well separated (maximized inter-

cluster distance) (Pedregosa et al., 2011). Table 5 as-

sesses the quality of the ConAE reconstructed dataset.

The lowest SSE of 0.004682736 is achieved with

TS-Kshape, the minimum DB with of 0.61332691

with both K-means and TS-Kmean, and the highest

VRC of 95738.59064 with K-means. Across the three

datasets, HDBSCan under-performs.

(a) K-means with Four Clusters.

(b) TS-Kshape with Five Clusters.

Figure 8: Two Examples of Optimal Clusters of Initial

Dataset.

Clustering Quality of a High-dimensional Service Monitoring Time-series Dataset

189

Table 4: Quality of DAE Reconstructed Dataset.

Kmeans

Elbow-5 clusters Silhouette-6 clusters CH-14 clusters

SSE DB VRC SSE DB VRC SSE DB VRC

16807.5332 0.181151753 1510548.891 1252.5371 0.05016857 16349947.76 259.94039 0.5234089 30312918.2572

TS-Kmean

Elbow-5 clusters Silhouette-6 clusters CH-14 clusters

SSE DB VRC SSE DB VRC SSE DB VRC

0.31155592 0.18115175 1510548.89 0.023216931 0.05016857 16349947.76 0.00497385071 0.482265234 28591306.875589

TSKshape

Elbow-5 clusters Silhouette-6 clusters CH-14 clusters

SSE DB VRC SSE DB VRC SSE DB VRC

0.002113596 0.4164552564 50036.65944 0.0019847939 0.43711877 315043.8333 0.0019202 0.4703590 16066475.8277

HDBSCAN-6 clusters

DB VRC

1.026604381 12825430.68

Table 5: Quality of ConAE Reconstructed Dataset (5 Clus-

ters).

K-means

SSE DB VRC

270260.4375 0.61332691 95738.59064

TS-Kmean

SSE DB VRC

6.316888253 0.61332691 73127.0153677

TS-Kshape

SSE DB VRC

0.004682736 1.7982134 71203.693461

HDBSCAN-5 clusters

DB VRC

1.18025933 76806.51995

8 COMPARISON

Table 6 compares the clustering performances be-

tween the initial dataset and the two reconstructed

datasets. All the metric results of the DAE recon-

structed dataset outperform the outcome attained with

the initial dataset due to the non-linear properties

of the activation functions. The gap between the

SSE values equals 0.0024 (minimal), between the

DB values 0.56316 (high), and between VRC values

30,209,486.919 (very high).

In contrast, for the ConAE reconstructed dataset,

we observe that all performance metrics are under-

performing due to the convolutional layer that could

not handle the non-linear time-series dataset. Nev-

ertheless, the ConAE metrics are pretty close to the

metrics obtained with the initial dataset.

In conclusion, the DEA dataset possesses the

highest quality. Moreover, for the SSE metric, the

TS-Kshape is the dominant clustering method across

the three datasets. For the DB and VRC metrics, K-

means is the most performing method. Also, 14 rep-

resents the best cluster number. For conducting the

subsequent decision-making tasks, the DEA dataset

based on K-means with 14 clusters will be provided to

the industrial partner, as the latter provides a large gap

between the VRC values. Furthermore, we visualize

all the best clustering performances for the DEA re-

constructed dataset in Figure 9 where each cluster ori-

entation is different from others for TS-Kshape, TS-

Kmeans and K-means.

9 CONCLUSIONS AND FUTURE

WORK

Our study ﬁrst constructed a high-dimensional time-

series dataset. However, this new dataset should

be of high quality as it will be utilized for essen-

tial decision-making tasks by the industrial partner.

We jointly addressed two signiﬁcant problems of this

dataset: data incompleteness and high dimensional-

ity. We thoroughly assessed the quality of the initial

dataset and reconstructed datasets produced with self-

supervised deep learning networks using several data

clustering approaches. The experiments showed a

higher quality for the reconstructed dataset with DAE

when using a higher number of clusters.

A crucial research direction of our study is to ex-

plore clustering-based outlier detection of the recon-

structed datasets.

ACKNOWLEDGEMENTS

We cordially thank the Observability team for grant-

ing us access to the data.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

190

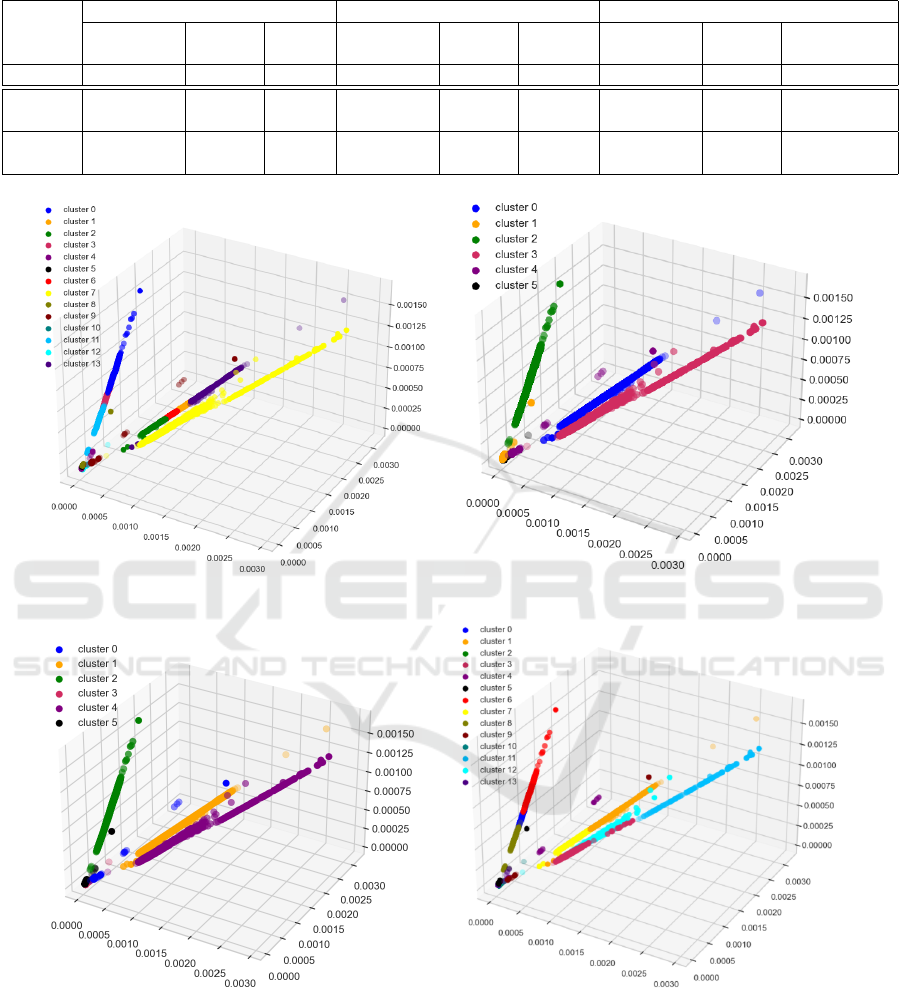
Table 6: Comparison based on Clustering Performances.

Dataset

Metric 1 Metric 2 Metric 3

Clustering

Algo.

Cluster

No.

SSE

Clustering

Algo.

Cluster

No.

Clustering

Algo.

Cluster

No.

VRC

Initial TS-Kshape 5 0.0043 K-means 4 0.61332 K-means 4 103431.341

DAE TS-Kshape 14 0.0019

K-means

TS-Kmean

6 0.05016 K-means 14 30312918.26

ConAE TS-Kshape 5 0.0046

K-means

TS-Kmean

5 0.61336 K-means 5 95738.59

(a) TS-Kshape with 14 clusters. (b) TS-Kmean with 6 clusters.

Figure 9: Optimal Clusters for DEA Reconstructed Dataset.

REFERENCES

Aghabozorgi, S., Shirkhorshidi, A. S., and Wah, T. Y.

(2015). Time-series clustering–a decade review. In-

formation Systems, 53:16–38.

Anowar, F. and Sadaoui, S. (2020). Incremental neural-

network learning for big fraud data. In 2020 IEEE

International Conference on Systems, Man, and Cy-

bernetics (SMC), pages 3551–3557.

Anowar, F. and Sadaoui, S. (2021a). Incremental learn-

ing framework for real-world fraud detection environ-

Clustering Quality of a High-dimensional Service Monitoring Time-series Dataset

191

ment. Computational Intelligence, 37(1):635–656.

Anowar, F. and Sadaoui, S. (2021b). Incremental learning

with self-labeling of incoming high-dimensional data.

In The 34th Canadian Conference on Artiﬁcial Intel-

ligence, pages 1–12.

Anowar, F., Sadaoui, S., and Selim, B. (2021). Conceptual

and empirical comparison of dimensionality reduction

algorithms (pca, kpca, lda, mds, svd, lle, isomap, le,

ica, t-sne). Computer Science Review, 40:1–13.

Chormunge, S. and Jena, S. (2018). Correlation based

feature selection with clustering for high dimensional

data. Journal of Electrical Systems and Information

Technology, 5(3):542–549.

Dash, B., Mishra, D., Rath, A., and Acharya, M. (2010). A

hybridized k-means clustering approach for high di-

mensional dataset. International Journal of Engineer-

ing, Science and Technology, 2(2):59–66.

Huang, X., Ye, Y., Xiong, L., Lau, R. Y., Jiang, N., and

Wang, S. (2016). Time series k-means: A new k-

means type smooth subspace clustering for time series

data. Information Sciences, 367:1–13.

Jadhav, A., Pramod, D., and Ramanathan, K. (2019). Com-

parison of performance of data imputation methods

for numeric dataset. Applied Artiﬁcial Intelligence,

33(10):913–933.

Jindal, P. and Kumar, D. (2017). A review on dimension-

ality reduction techniques. International journal of

computer applications, 173(2):42–46.

Kaoungku, N., Suksut, K., Chanklan, R., Kerdprasop, K.,

and Kerdrasop, N. (2018). The silhouette width crite-

rion for clustering and association mining to select im-

age features. International journal of machine learn-

ing and computing, 8(1):1–5.

Lawton, G. (2020). Autoencoders’ example

uses augment data for machine learning.

https://searchenterpriseai.techtarget.com/feature/

Autoencoders-example-uses-augment-data-for-

machine-learning. Last accessed 15 November

2021.

McInnes, L. and Healy, J. (2017). Accelerated hierarchical

density based clustering. In 2017 IEEE International

Conference on Data Mining Workshops (ICDMW),

pages 33–42. IEEE.

Messaoud, T. A., Smiti, A., and Louati, A. (2019). A

novel density-based clustering approach for outlier

detection in high-dimensional data. In International

Conference on Hybrid Artiﬁcial Intelligence Systems,

pages 322–331. Springer.

Niennattrakul, V. and Ratanamahatana, C. A. (2007). On

clustering multimedia time series data using k-means

and dynamic time warping. In 2007 International

Conference on Multimedia and Ubiquitous Engineer-

ing (MUE’07), pages 733–738. IEEE.

Paparrizos, J. and Gravano, L. (2015). k-shape: Efﬁcient

and accurate clustering of time series. In 2015 ACM

SIGMOD International Conference on Management

of Data, pages 1855–1870.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Prabhu, P. and Anbazhagan, N. (2011). Improving the per-

formance of k-means clustering for high dimensional

data set. International journal on computer science

and engineering, 3(6):2317–2322.

Prometheus (2021). From metrics to insight.

https://prometheus.io/docs/concepts/metric types/.

Last accessed 15 November 2021.

Rani, S. and Sikka, G. (2012). Recent techniques of cluster-

ing of time series data: a survey. International Journal

of Computer Applications, 52(15):1–9.

Saul, N. (2017). How hdbscan works.

https://hdbscan.readthedocs.io/en/latest/

how hdbscan works.html. Last accessed 15 Novem-

ber 2021.

Song, Q., Ni, J., and Wang, G. (2011). A fast clustering-

based feature subset selection algorithm for high-

dimensional data. IEEE transactions on knowledge

and data engineering, 25(1):1–14.

Stekhoven, D. J. and B

uhlmann, P. (2012).

Missforest—non-parametric missing value im-

putation for mixed-type data. Bioinformatics,

28(1):112–118.

Tavenard, R., Faouzi, J., Vandewiele, G., Divo, F., Androz,

G., Holtz, C., Payne, M., Yurchak, R., Rußwurm, M.,

Kolar, K., et al. (2020). Tslearn, a machine learning

toolkit for time series data. Journal of Machine Learn-

ing Research, 21(118):1–6.

Wang, X. and Xu, Y. (2019). An improved index for cluster-

ing validation based on silhouette index and calinski-

harabasz index. IOP Conference Series: Materials

Science and Engineering, 569(5):1–7.

Wang, Y., Yao, H., and Zhao, S. (2016). Auto-encoder

based dimensionality reduction. Neurocomputing,

184:232–242.

Wu, W., Xu, Z., Kou, G., and Shi, Y. (2020). Decision-

making support for the evaluation of clustering algo-

rithms based on mcdm. Complexity, 2020:1–17.

Yuan, C. and Yang, H. (2019). Research on k-value se-

lection method of k-means clustering algorithm. J,

2(2):226–235.

Zhang, Y. and Li, D. (2013). Cluster analysis by vari-

ance ratio criterion and ﬁreﬂy algorithm. International

Journal of Digital Content Technology and its Appli-

cations, 7(3):689–697.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

192