Incremental Online Reconstruction of Locally Quadric Surfaces

Josua Bloeß

and Dominik Henrich

University of Bayreuth, Chair for Applied Computer Science III, (Robotics and Embedded Systems),

Universitaetsstrasse 30, 95447 Bayreuth, Germany

Keywords:

Reconstruction, Segmentation, Point Cloud, Surface Fitting, Quadrics, Online Computation.

Abstract:

Representing surfaces of a digital 3D model using high level geometric information is key to lots of geometric

processing and other use cases. In order to obtain these 3D models, various scanning methods have been

proposed. We contribute a method for incremental reconstruction of surfaces from a series of point clouds.

For this, we use a robust over-segmentation technique on a point cloud and build a memory efﬁcient graph

structure upon it. Over time, we expand this graph structure as global representation. We also propose a fast

ﬁtting algorithm for quadric surface patches to the graph structure. We validate the overall performance in our

experiments.

1 INTRODUCTION

Digital reconstruction of real world objects from point

clouds is an avid and ever evolving ﬁeld of research.

Some of its various use cases are grasp planning in

robotics (Makhal et al., 2018), manifacturing (Vem-

pati et al., 2018) or creation of models for entertain-

ment (Beraldin et al., 2005). The process of digital re-

construction is a challenging task and requires special

hardware and speciﬁcally trained personal. In order

for the result to be useful in an industrial environment,

it must be compatible with established CAD con-

cepts and software. This in turn requires the geom-

etry of the digital reconstruction to be represented by

high level information like geometrical primitives or

Splines in contrast to low abstraction representations

like triangle meshes. The process of CAD reconstruc-

tion usually involves two steps: data acquisition and

a computationally expensive analysis for high level

geometric features (Buonamici et al., 2018). Due to

this separation, it is important that the data acquisi-

tion is done thoroughly and ﬂawlessly. Otherwise,

it can take multiple iterations of data acquisition and

analysis until a sufﬁcient result is achieved. An al-

ternative approach is an incremental reconstruction

where the analysis of point clouds is done online dur-

ing data acquisition, e.g. (Newcombe et al., 2011).

With incremental reconstruction, a user can react to

the online computed intermediate result and adapt

https://orcid.org/0000-0001-8636-3168

https://orcid.org/0000-0003-0250-2728

the data acquisition accordingly, e.g. by re-capturing

poorly scanned areas of the object. However, exist-

ing approaches for online reconstruction usually pro-

duce results with low abstraction like triangle meshes

or approximated signed distance functions. Few ap-

proaches have been proposed for incremental CAD

reconstruction. These are limited in the range of de-

tectable geometric shapes geometric primitives, e.g.

(Denker et al., 2013).

For incremental CAD reconstruction, two impor-

tant aspects have to be considered: 1. Depth images

must be accumulated in an incrementally expandable

data structure. 2. Geometric features must be ex-

tracted from this data structure online. Both aspects

must enable a responsive overall system. We consider

1 Hz a sufﬁcient frame rate as motivated by a system

with similar premises (Sand, 2019). In this paper, we

consider incremental CAD reconstruction of quadric

surfaces and contribute to both of the aforementioned

aspects: 1. A memory-efﬁcient expandable segment

graph of over-segmented point clouds. 2. A region-

merging algorithm that allows fast quadric ﬁtting on

this graph.

To our best knowledge, this is the ﬁrst approach

to combine reconstruction of general quadric surface

from a series of point clouds with a computational ef-

ﬁciency that allows an incremental online execution.

Bloeß, J. and Henrich, D.

Incremental Online Reconstruction of Locally Quadric Surfaces.

DOI: 10.5220/0010795100003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

155-162

ISBN: 978-989-758-555-5; ISSN: 2184-4321

155

2 RELATED WORK

An extensive survey of techniques for reconstruction

of shapes from point clouds is given in (Kaiser et al.,

2019). According to this survey, RANSAC based ap-

proaches promise computational efﬁciency and ro-

bustness to outliers.

RANSAC (Random Sample Consensus) is a tech-

nique where a parameterized model of a shape is ﬁtted

to a point cloud. A small number of points is ran-

domly drawn from the point cloud so that all model

parameters can be determined. This is repeated until

a shape is found that ﬁts the point cloud with a high in-

lier ratio (Fischler and Bolles, 1981). The RANSAC

concept has the advantage of being robust towards

outliers and also being time efﬁcient for the task of

ﬁnding the best ﬁtting shape for a given point cloud.

However, if the points for each shape have to be deter-

mined ﬁrst, RANSAC becomes more computationally

expensive (Gotardo et al., 2003). Hierarchical sam-

pling and lazy cost evaluation can be used to speed

up the process signiﬁcantly, still the computation time

exceeds multiple seconds (Schnabel et al., 2007). For

the planar case, the algorithm was adapted to paral-

lelization on GPUs, which speeds up the computation

to a frame rate of 7 Hz (Alehdaghi et al., 2015). In

RANSAC, prior deﬁned models limit the reconstruc-

tion to shapes of these speciﬁc models (Oesau et al.,

2016). Some works have extended RANSAC for gen-

eral quadrics (Frahm and Pollefeys, 2006). Point nor-

mals have been used as additional constraint to lower

the number of required points and thus increasing the

computational performance (Birdal et al., 2019).

Other techniques ﬁnd the parameters of a shape

model using ﬁtting methods from linear algebra. A

key requirement to this approach is that each point can

be embedded into a space where the model param-

eters have linear inﬂuence on a cost function. Then

solving an Eigenvalue problem of the scatter matrix

of the points, after said embedding, yields an alge-

braic solution (Taubin, 1991), (Luk

acs et al., 1998).

This embedding is possible for quadrics (Andrews

and S

equin, 2013). We explain this in more detail in

Section 3.3.1. These techniques can be enhanced with

knowledge about prior probabilities in order to im-

prove the ﬁtting result when only small point clouds

are available (Beale et al., 2016). The normals of each

point can be used to increase the robustness of the ﬁt

(Tasdizen et al., 1999). Strict type constraints can be

applied to the problem to force the result to be some

desired type of quadric (Andrews and S

equin, 2013).

Segmentation of point cloud is a key component

of surface reconstruction. Segmentation is the pro-

cedure of partitioning the points from a point cloud

into segments with some criterion of homogeneity.

This criterion can be based on some prior knowl-

edge about object shapes so that each segment corre-

sponds to a real-world object (Kim et al., 2012). For

general scene reconstruction, this prior information is

not available, and techniques that are based on point

feature similarity are more suitable for segmentation.

A set of point features is proposed with the point

feature histogram (Rusu et al., 2009). Point feature

based segmentation techniques produce a locally cor-

rect segmentation since point features are computed

from the local neighbourhood of a point. Smooth-

ness can be used as local homogeneity criterion to

compute an over-segmentation of a point cloud (Pa-

pon et al., 2013). In order to obtain a ﬁnal segmenta-

tion from this over-segmentation, a homogeneity cri-

terion between segments is required. Principal curva-

tures and normal similarity of segments can be used to

merge them (Arbeiter et al., 2014). Another possibil-

ity is a global criterion using a priori knowledge about

shapes occurring in the scene. For many approaches

this a priori knowledge is the assumption that a scene

consists of a small set of parameterizable primitives

(Vanco and Brunnett, 2002) . We take a similar ap-

proach, but we assume general quadrics and use an ac-

cording model to impose our homogeneity criterion.

The typical process for reconstruction from point

clouds consists of a phase of data acquisition fol-

lowed by segmentation and model extraction (Buon-

amici et al., 2018). This comes with a computa-

tional load of processing all the acquired data at once,

which makes these systems unsuitable for online ap-

plications. An alternative approach is to use vol-

umetric representations where point clouds reﬁne a

signed distance function (SDF). The SDF is deﬁned

across the whole volume of the scene and implicitly

deﬁnes a surface at its zero-level. It can be repre-

sented by a voxel-grid of function values (Newcombe

et al., 2011). Hence, memory consumption limits the

volume of reconstruction for these techniques. Us-

ing GPU-accelerated computations, these techniques

reach high frame rates of more than 40 Hz. More so-

phisticated representations of the SDF, like octrees,

have been used to lower memory consumption (Whe-

lan et al., 2012).

For limited sets of primitives, online, incremental

reconstruction concepts have been proposed. Planar

boundary representations can be built incrementally

from the data of a hand-held device with 2 Hz (Sand,

2019). A spatial partitioning and aggregation of point

features can be used to reconstruct planes, cylinder

and spheres (Denker et al., 2013).

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

156

Figure 1: A schematic overview of our approach showing control ﬂow in green arrows

and intermediate results.

Figure 2: Seg-

mentation (top)

and an over-

segmentation

(bottom).

Figure 3: Fitting

without (top)

and with (bot-

tom) normal

constraints.

3 CONCEPT

In this section, we present our approach towards in-

cremental reconstruction of quadric surfaces.

Given is a series of point clouds (P

, P

, ...). Each

is a set of points. For a point p, its position is

denoted as POS(p) ∈ R

. We assume that the extrinsic

parameters of the depth sensor are known, e.g. by

using a robot manipulator. Our goal is to ﬁnd a set

of quadrics {q

, q

, ...} that reconstructs the surface

captured by (P

, P

, ...) with a low geometrical error.

A quadric q is a quadratic polynomial

q(x, y, z) := C

θ(x, y, z).

(1)

with

= (c

, ..., c

)

∈ R

(2)

θ(x, y, z) := (x

, y

, z

, xy, xz, xy, x, y,z, 1) (3)

Each quadric q deﬁnes a surface

:= {(x, y, z) ∈ R

|q(x, y, z) = 0} (4)

An overview of our approach is given in Figure

1. These are the individual steps, following sections

explain them in more detail:

a) a point cloud is recorded

b) build local segment graph from over-

segmentation

c) expand a global segment graph using the local

segment graph

d) incrementally accumulate point clouds in global

segment graph

e) region-merging ﬁts quadric surfaces

3.1 Over-segmentation

Given a point cloud P, let S

∗

= {P

∗

, P

∗

, ...}, P

∗

⊆ P

be the segmentation of P where each segment P

∗

can

be ﬁtted by one quadric surface. The direct computa-

tion of S

∗

is a hard problem. In this work, we reduce

the complexity of this problem by ﬁrst computing

an over-segmentation of S

∗

. An over-segmentation

S = {P

, P

, ...} of S

∗

is a segmentation of P where

∀P

∈ S∃P

∗

∈ S

∗

: P

⊆ P

∗

. (5)

An example of over-segmentation is visualized in Fig-

ure 2.

We use supervoxel clustering (Papon et al., 2013)

to compute S. The algorithm selects seed points in

P using a uniform grid (parameter s

size

governs the

cell size of the grid). Clusters are formed by assign-

ing each point to the respectively nearest seed using a

metric that considers spatial distance and similarity of

the estimated surface normal in a point. Afterwards,

the seed of each cluster is updated to the mean po-

sition and normal of all points in the cluster. These

steps are repeated until the clusters converge, ﬁve it-

erations are suggested (Papon et al., 2013).

3.2 Segment Graph

We deﬁne a segment graph G = (V, E). Vertices V are

segments from an over-segmentation of point clouds

and edges E indicate whether two segments are spa-

tially neighbored.

For each point cloud P

in a series (P

, P

, ...),

we build a local segment graph G

using an over-

segmentation of P

. We incrementally build a global

segment graph G

by merging G

t−1

and G

Incremental Online Reconstruction of Locally Quadric Surfaces

157

We start with G

= (

0). An over-segmentation

S of P

is computed according to Section 3.1, G

computed from S. For t = 1, we set G

:= G

. For

t > 1, over-segmentation of P

is modiﬁed:

• the nearest point in P

to the center of each seg-

ment from G

t−1

is selected as seed. Points se-

lected by the uniform grid are only used as seeds,

if there is not already another seed withing dis-

tance s

size

• only centers of clusters not initialized by the uni-

form grid are updated. Centers of clusters initial-

ized by segments from G

t−1

are static.

Effects of these modiﬁcations are shown in Figure 4.

The incremental update is done by merging

t−1

= (V

t−1

, E

t−1

) and G

= (V

, E

) to G

, E

We denote V

the set of all segments in G

t−1

that

initialized a cluster in the over-segmentation of P

For all P

∈ V

, we denote α(P

) ∈ V

the segment

whose seed center was used to select the seed of P

First, segments in V

are updated with the respective

points from V

∗

:= {P

∪ α(P

)|P

∈ V

} (6)

Segments of the next global segment graph are

formed by

:= V

∗

∪ (V

t−1

) ∪ (V

\ α(V

)) (7)

Edges E

are the union of E

and E

t−1

considering

segments P

and α(P

) as equivalent.

3.3 Fitting

A region-merging algorithm is used on the global seg-

ment graph G

with a homogeneity criterion based on

the Taubin Fit (Taubin, 1991).

3.3.1 Taubin Fit

Given a set of points P, the Taubin Fit (Taubin, 1991)

can be used to compute a quadric q

with minimal

average approximated squared distance of the points

in P to S

. The ﬁtting quadric q

minimizes

d(q, P) :=

∑

p∈P

q(POS(p))

∑

p∈P

k∇q(POS(p))k

(8)

for q with

∑

p∈P

θ(POS(p))θ(POS(p))

(9)

∑

p∈P

∇θ(POS(p))∇θ(POS(p))

(10)

Finding q

can then be stated as the generalized

Eigenvalue problem

= argmin

(11)

From Equation 8, for two point sets P

, P

, the

Taubin Fit of P

∪ P

can be stated as

d(q, P

∪ P

) =



+ M





+ N



(12)

This means that it is sufﬁcient to store M

and N

for points P in a segment of the segment graph. No

explicit representation of P is required. In this repre-

sentation, the union of two point sets P

∪ P

is com-

puted as:

∪P

= M

+ M

∪P

= N

+ N

(13)

3.3.2 Region Merging

Since a segment graph G = (V, E) represents an over-

segmentation, segments have to be merged to use the

Taubin Fit for quadric ﬁtting. We deﬁne a homogene-

ity criterion between sets of segments, i.e. regions,

⊆ V and R

⊆ V :

HOM(R

, R

)

:= max

d(q

∪

), d(q

∪

)

with

[

∈R

and

[

∈R

(14)

Region merging proceeds as follows: We initialize a

set of 1-segment regions by R ← {{P

}|P

∈V }. Then,

we iteratively unify the pair of neighboring regions

and R

that minimizes HOM(R

, R

) as long as this

value does not exceed a user-deﬁned threshold t

err

Finally, we use the Taubin Fit to ﬁnd the best

ﬁtting general quadric for each region R

∈ R. We

also use constrained Taubin Fit (Andrews and S

equin,

2013) to ﬁnd the best ﬁtting plane for R

. As long as

the Taubin error for the plane is below t

err

, we prefer

the plane ﬁt over the general ﬁt.

Even though, quadrics in general position have a

smooth surface, an edge of e.g. a cube can be approx-

imated with arbitrary precision using a quadric. Our

algorithm often ﬁts a common quadric to two sides of

an edge. We put an additional constraint on the edges

E. We only keep edges between vertices whose av-

erage point normals are roughly the same. We use a

threshold of 0.7 for the dot product of the normals of

two segments. The effect is depicted in Figure 3.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

158

(a) G

t−1

and P

before segmentation

(b) seeds for over-segmentation (c) result of over-segmentation

Figure 4: Segments from seeds selected by vertices of G

t−1

are centered around these vertices. Segments initialized by

additional seeds (green) move during supervoxel clustering.

large a medium a small a

large b medium b small b

Figure 5: Images of the scenes used for our data set.

4 EXPERIMENTS

We evaluate our concept in terms of accuracy and

computational efﬁciency. For this, we use public and

custom-made data sets (Section 4.1) and compare our

results to existing approaches (Section 4.2). We also

analyze the inﬂuence of the parameters of our ap-

proach.

4.1 Data Sets and Evaluation Methods

Our custom-made data set compromises six scenes

(see Figure 5). For each scene, we captured 15 point

clouds from different poses using an Ensenso N10

depth sensor mounted on a robotic manipulator for

extrinsic calibration. Each point cloud consists of

752×480 = 360, 960 points. We also evaluate our ap-

proach for single view reconstruction on the ITODD

data set (Drost et al., 2017) as well as a subset of the

redwood data set (Choi et al., 2016).

We build a ground truth set of quadrics for each

data set by manually segmentation and Taubin Fit. We

refer to (Andrews and S

equin, 2013) for an analysis of

the accuracy of Taubin Fit itself. In order to compare

a set of ground truth quadrics Q

∗

= {q

∗

, q

∗

, ...} to a set

of reconstructed quadrics Q = {q

, q

, ...} we deﬁne a

similarity relation ∼

QUAD

: Q

∗

× Q → {TRUE, FALSE}.

For the evaluation of q

∗

∼

QUAD

q we test the type,

shape and pose of q and q

∗

for similarity. We obtain

the shape of a quadric q as the three Eigenvalues of the

upper left 3× 3 matrix of the matrix representation of

q. For evaluation we deﬁne the following sets:

true positives = {q ∈ Q|∃q

∗

∈ Q

∗

: q

∗

∼

QUAD

false positives = {q ∈ Q|@q

∗

∈ Q

∗

: q

∗

∼

QUAD

false negatives = {q

∗

∈ Q

∗

|@q ∈ Q : q

∗

∼

QUAD

4.2 Results

We investigate the inﬂuence of following parameters:

• t

err

: error threshold for quadric ﬁt in Section 3.3

• s

size

: grid size for seed selection in Section 3.1

• v

size

: size of a voxel grid used by (Papon et al.,

2013) to downsample a point cloud

Table 1 shows hand optimized for these parame-

ters for our data set. According to this, s

size

depends

on the size of the objects in the scene and v

size

can be

set to

size

= 10. Figure 6 shows the reason for false

positives with small objects: Segments like 409 mis-

takenly cross the border between 400 and 398, which

causes the two planar surfaces to be merged into one

quadric. The errors in the medium and large data sets

can mostly be attributed to partially scanned objects.

Small connected components in the segment graph

can often be ﬁtted by a plane, even if the underlying

surface is curved, see Figure 7a. Table 1 shows the

results for primitive ﬁtting using RANSAC (Schnabel

et al., 2007). RANSAC fails to respect surface bound-

aries or ﬁts large spheres to planar surfaces, see Figure

7b.

We sample values for each parameter around the

optimal value for medium b, see Figure 9. False pos-

itives, false negatives and true positives show that

err

= 5 · 10

is a good value. For lower values,

the algorithm many small surfaces. For higher val-

ues, surfaces are merged mistakenly, see Figure 8a.

Incremental Online Reconstruction of Locally Quadric Surfaces

159

Table 1: Results of RANSAC (Schnabel et al., 2007) and

ours with true positives (tp), false positives (fp) and false

negatives (fn) and hand optimized parameter values.

ours RANSAC

err

size

tp fp fn tp fp fn

large a 1·10

−5

0.08 0.008 6 0 0 3 2 3

medium a 5·10

−6

0.04 0.004 6 1 1 2 1 5

small a 5·10

−6

0.02 0.002 8 3 1 3 3 6

large b 1·10

−5

0.08 0.008 5 0 2 1 0 6

medium b 1·10

−5

0.04 0.004 6 0 0 1 4 5

small b 1.5·10

−6

0.02 0.002 6 2 3 4 5 5

Figure 6: Results for small b (left and middle) with false

negative quadrics (orange), false positive quadrics (red)

and true positive quadrics (green) and the local over-

segmentation of the points causing the false positives

(right).

All metrics are optimal for s

size

= 0.04. Computa-

tion time decreases from s

size

= 0.012 to s

size

= 0.04,

because computation time of ﬁtting depends on the

number of segments (see Section 3.3). For higher

values, the computation time increases again. This

is caused by the implementation details of (Papon

et al., 2013). Figure 8b shows that with s

size

0.08 over-segmentation cannot preserve the border

between cone and side of the cuboid. For s

size

= 0.02,

each segment is supported by too few points, some

segments lie on the cuboid’s edges. Figure 9 shows

that low values for v

size

cause quantization errors.

We compare computation time for a series of point

(a) Results for medium a (left) and input data (right)

(b) RANSAC (left) and ours (right) on large a

Figure 7: False negative quadrics (orange), false positive

quadrics (red) and true positive quadrics (green).

(a) Results for t

err

= 5·10

−7

, 5·10

−6

, 2·10

−5

(b) Over-segmentation with s

size

= 0.02, 0.04, 0.08

size

= 0.004, 0.008

Figure 8: Inﬂuence of different parameters on data set

medium b, values respectively from left to right.

clouds using our approach and RANSAC (Schnabel

et al., 2007). We incrementally reconstruct the data

set medium b using our approach and measure the

time for processing of each point cloud. We compare

this to RANSAC operating on increasing numbers of

merged point clouds of this data set, see Figure 10 for

results.

Figure 11 shows the numbers of correctly detected

cylinders by RANSAC and our approach for each

of the 15 point clouds from ITODD data set. The

point clouds contain increasing numbers of cylinders.

Our approach performs well for small numbers of

shapes (≤ 4) and slightly outperforms RANSAC in

this range. For > 9 cylinders, small connected com-

ponents in the segment graph cannot be merged by

region merging, see Figure 12.

We compare our approach to 4P-RANSAC (Birdal

et al., 2019). We use the following data from red-

wood data set (Choi et al., 2016): Rugby Ball (a), Pi-

lates Ball (b), Big Globe (c), Apple (d), Orange Ball

(e). Figure 13 compares our results to those stated in

(Birdal et al., 2019). 4P-RANSAC outperforms our

system for most data sets. Our algorithm is less suited

to deal with clutter in the scene. Figure 13 shows the

false negative (orange) for the Apple data set and the

segment graph (magenta edges and black vertices).

The segment graph connects points of the hand hold-

ing an apple to the points of the apple, which causes

our algorithm to fail ﬁnding the apple as a quadric.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

160

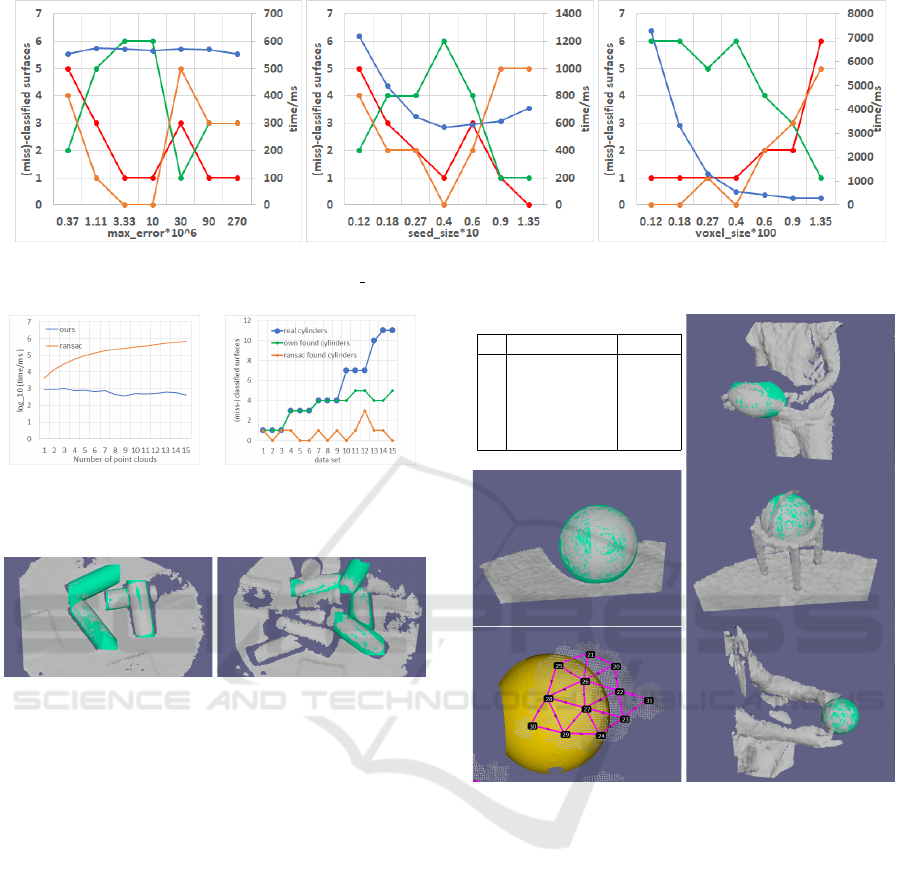
Figure 9: Average runtime per point cloud (blue), true positives (green), false positives (red) and false negatives (orange) for

different parameter values on the data set medium b.

Figure 10: Runtime of

RANSAC and ours for in-

creasing number of points.

Figure 11: Per scene metrics

for ours and (Schnabel et al.,

2007) on ITODD.

Figure 12: Cylinder detected by our approach in a scene of

4 real cylinders (left) and in a scene of 10 cylinders (right).

5 DISCUSSION AND PROSPECTS

In this paper, we present a novel technique for incre-

mental reconstruction of a piecewise quadric surface

from a series of point clouds. Our experiments show

that our memory representation of segments in a seg-

ment graph allows for fast ﬁtting of quadric surfaces

to these segments. We show that our approach can

operate at a frame rate of 1 Hz for point clouds of

> 300, 000, which is by magnitudes faster than ex-

isting RANSAC based approaches with similar accu-

racy for scenes consisting of quadric surfaces. Fu-

ture improvements can be made on the ﬁtting proce-

dure on our segment graph. Fitting is the only part

of our technique whose computation time depends on

the number of previously processed point clouds. We

plan to use an incremental ﬁtting approach that only

recomputes the surface patches associated with seg-

ments that have been inﬂuenced by the current point

cloud. Furthermore, nodes from our segment graph

that belong to a quadric surface can be used to com-

4P-RANSAC Ours

a 100% 80.2%

b 100% 100%

c 90.7% 87.1%

d 99.6% 38.8%

e 93.3% 94.4%

b c

d e

Figure 13: Accuracy for detecting an ellipsoid within a

point cloud of the data set of (Choi et al., 2016) with ours

and 4P-RANSAC (Birdal et al., 2019).

pute an approximation of the surface’s boundary to

form a more accurate reconstruction that could also

be used for common CAD exchange formats.

ACKNOWLEDGEMENTS

This work has partly been supported by the Deutsche

Forschungsgemeinschaft (DFG) under grant agree-

ment He2696/16 HandCAD.

REFERENCES

Alehdaghi, M., Esfahani, M. A., and Harati, A. (2015).

Parallel RANSAC: Speeding up Plane Extraction in

Incremental Online Reconstruction of Locally Quadric Surfaces

161

RGBD Image Sequences using GPU. In 5th Interna-

tional Conference on Computer and Knowledge Engi-

neering, pages 295–300. IEEE.

Andrews, J. and S

equin, C. H. (2013). Type-Constrained

Direct Fitting of Quadric Surfaces. Computer-Aided

Design and Applications, 11(1):107–119.

Arbeiter, G., Fuchs, S., Hampp, J., and Bormann, R. (2014).

Efﬁcient Segmentation and Surface Classiﬁcation of

Range Images. In IEEE International Conference on

Robotics and Automation, pages 5502–5509. IEEE.

Beale, D., Yang, Y.-L., Campbell, N., Cosker, D., and Hall,

P. (2016). Fitting quadrics with a Bayesian prior.

Computational Visual Media, 2(2):107–117.

Beraldin, J.-A., Picard, M., El-Hakim, S. F., Godin, G.,

Valzano, V., and Bandiera, A. (2005). Combining 3D

technologies for cultural heritage interpretation and

entertainment. In Beraldin, J.-A., El-Hakim, S. F.,

Gruen, A., and Walton, J. S., editors, Videometrics

VIII, volume 5665, page 108.

Birdal, T., Busam, B., Navab, N., Ilic, S., and Sturm, P.

(2019). Generic Primitive Detection in Point Clouds

Using Novel Minimal Quadric Fits. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

pages 1–1.

Buonamici, F., Carfagni, M., Furferi, R., Governi, L., Lap-

ini, A., and Volpe, Y. (2018). Reverse engineering

modeling methods and tools: a survey. Computer-

Aided Design and Applications, 15(3):443–464.

Choi, S., Zhou, Q.-Y., Miller, S., and Koltun, V. (2016).

A Large Dataset of Object Scans. arXiv:1602.02481,

pages 1–7.

Denker, K., Hagel, D., Raible, J., Umlauf, G., and Hamann,

B. (2013). On-Line Reconstruction of CAD Geome-

try. In 2013 International Conference on 3D Vision,

pages 151–158. IEEE.

Drost, B., Ulrich, M., Bergmann, P., Hartinger, P., and Ste-

ger, C. (2017). Introducing MVTec ITODD — A

Dataset for 3D Object Recognition in Industry. In

2017 IEEE International Conference on Computer Vi-

sion Workshops (ICCVW), volume 2018-Janua, pages

2200–2208. IEEE.

Fischler, M. a. and Bolles, R. C. (1981). Random Sample

Paradigm for Model Consensus: Applications to Im-

age Analysis and Automated Cartography. Communi-

cations of the ACM, 24(6):381–395.

Frahm, J.-M. and Pollefeys, M. (2006). RANSAC for

(Quasi-)Degenerate data (QDEGSAC). In 2006 IEEE

Computer Society Conference on Computer Vision

and Pattern Recognition - Volume 1 (CVPR’06), vol-

ume 1, pages 453–460. IEEE.

Gotardo, P., Bellon, O., and Silva, L. (2003). Range Im-

age Segmentation by Surface Extraction using an Im-

proved Robust Estimator. In IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion, volume 2. IEEE Comput. Soc.

Kaiser, A., Ybanez Zepeda, J. A., and Boubekeur, T. (2019).

A Survey of Simple Geometric Primitives Detection

Methods for Captured 3D Data. Computer Graphics

Forum, 38(1):167–196.

Kim, Y. M., Mitra, N. J., Yan, D.-M., and Guibas, L.

(2012). Acquiring 3D Indoor Environments with Vari-

ability and Repetition. ACM Transactions on Graph-

ics, 31(6):1.

Luk

acs, G., Martin, R., and Marshall, D. (1998). Faith-

ful Least-squares Fitting of Spheres, Cylinders, Cones

and Tori for Reliable Segmentation. In Computer Vi-

sion - ECCV’98, 5th European Conference on Com-

puter Vision, volume 1.

Makhal, A., Thomas, F., and Gracia, A. P. (2018). Grasping

Unknown Objects in Clutter by Superquadric Repre-

sentation. In Second IEEE International Conference

on Robotic Computing, pages 292–299. IEEE.

Newcombe, R. A., Izadi, S., Hilliges, O., Molyneaux, D.,

Kim, D., Davison, A. J., Kohli, P., Shotton, J., Hodges,

S., and Fitzgibbon, A. (2011). KinectFusion: Real-

time dense surface mapping and tracking. 2011 10th

IEEE International Symposium on Mixed and Aug-

mented Reality, ISMAR 2011, pages 127–136.

Oesau, S., Lafarge, F., and Alliez, P. (2016). Planar Shape

Detection and Regularization in Tandem. Computer

Graphics Forum, 35(1):203–215.

Papon, J., Abramov, A., Schoeler, M., and Worgotter, F.

(2013). Voxel Cloud Connectivity Segmentation -

Supervoxels for Point Clouds. Proceedings of the

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition, pages 2027–2034.

Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast Point

Feature Histograms (FPFH) for 3D registration. In

2009 IEEE International Conference on Robotics and

Automation, pages 3212–3217. IEEE.

Sand, M. (2019). Inkrementelle Rekonstruktion von

planaren Volumenmodellen mit handgehaltenen

Tiefenkameras (German). PhD thesis, University of

Bayreuth, Bayreuth.

Schnabel, R., Wahl, R., and Klein, R. (2007). Efﬁcient

RANSAC for Point-Cloud Shape Detection. Com-

puter Graphics Forum, 26(2):214–226.

Tasdizen, T., Tarel, J. P., and Cooper, D. B. (1999). Al-

gebraic curves that work better. Proceedings of the

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition, 2(February):35–41.

Taubin, G. (1991). Estimation of Planar Curves, Sur-

faces, and Nonplanar Space Curves Deﬁned by Im-

plicit Equations with Applications to Edge and Range

Image Segmentation. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 13(11):1115–

1138.

Vanco, M. and Brunnett, G. (2002). Direct Segmentation

for Reverse Engineering. In First International Sym-

posium on Cyber Worlds, 2002. Proceedings., pages

24–31. IEEE Comput. Soc.

Vempati, A. S., Kamel, M., Stilinovic, N., Zhang, Q.,

Reusser, D., Sa, I., Nieto, J., Siegwart, R., and Beards-

ley, P. (2018). PaintCopter: An Autonomous UAV for

Spray Painting on Three-Dimensional Surfaces. IEEE

Robotics and Automation Letters, 3(4):2862–2869.

Whelan, T., Kaess, M., and Fallon, M. (2012). Kintinuous:

Spatially extended kinectfusion. RSS Workshop on

RGB-D: Advanced Reasoning with Depth Cameras,

page 7.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

162