Using ConvNet for Classiﬁcation Task in Parallel Coordinates

Visualization of Topologically Arranged Attribute Values

Piotr Artiemjew

1 a

and Sławomir K. Tadeja

2 b

Faculty of Mathematics and Computer Science, University of Warmia and Mazury in Olsztyn, Poland

Institute of Applied Computer Science, Jagiellonian University in Krak

ow, Poland

Keywords:

Classiﬁcation, Parallel Coordinates, Convnet, Pattern Recognition.

Abstract:

In this work, we assess the classiﬁcation capability of visualized multidimensional data used in the decision-

making process. We want to investigate if classiﬁcation carried out over a graphical representation of the

tabular data allows for statistically greater efﬁciency than the dummy classiﬁer method. To achieve this, we

have used a convolutional neural network (ConvNet) as the base classiﬁer. As an input into this model, we used

data presented in the form of 2D curves resulting from the Parallel Coordinates Plot (PCP) visualization. Our

initial results show that the topological arrangement of attributes, i.e., the shape formed by the PCP curves

of individual data items, can serve as an effective classiﬁer. Tests performed on three different real-world

datasets from the UCI Machine Learning Repository conﬁrmed that classiﬁcation efﬁciency is signiﬁcantly

higher than in the case of dummy classiﬁcation. The new method provides an interesting approach to the

classiﬁcation of tabular data and offers a unique perspective on classiﬁcation possibilities. In addition, we

examined relevant information content potentially helpful in building hybrid classiﬁcation models, e.g., in the

classiﬁer committee model. Moreover, our method can serve as an enhancement of the PCP visualization

itself. Here, we can use our classiﬁcation technique as a form of double-checking for the pattern identiﬁcation

task performed over PCP by the users.

1 INTRODUCTION

The amount of data we currently encounter is vast and

growing. Moreover, these datasets are continuously

increasing in terms of the total number of items con-

tained within them and the number of dimensions per

item. Consequently, there is an increasing need for

swift and effective tools to process complex, multi-

variate datasets.

A widely used approach for data analysis is

preparing an appropriate data visualization to un-

ravel new insights about a given dataset. In the case

of highly-dimensional data, we can use well-known

and popular

Parallel Coordinates Plot (PCP) (Insel-

berg, 1985; Inselberg, 2009; Heinrich and Weiskopf,

2013). PCP allows to simultaneously present the en-

tire dataset without the need of using dimension re-

duction (van der Maaten and Hinton, 2008) for 2D/3D

visualization. In PCP, each multidimensional data

https://orcid.org/0000-0001-5508-9856

https://orcid.org/0000-0003-0455-4062

As of 11 May 2021, the Google Scholar search of PCP

results in more than 2 million entries.

item is presented as a curve composed of line seg-

ments connecting values of attributes in each dimen-

sion marked on parallel axes (see Fig. 1).

A typical task that we want to carry out when us-

ing PCP is to identify patterns understood as a group-

ing of similar data items across all the dimensions

(see Fig. 1) as judged by the user (Tadeja et al., 2019;

Tadeja et al., 2021). However, the PCP visualization

has its own caveats. For instance, the readability of

the PCP decreases with the number of visualized data

items. For instance, a high concentration of data may

cause visual clutter, obfuscation, or occlusion on the

main plot (Artero et al., 2004; Dang et al., 2010). As

such, a range of enhancements was proposed to at

least partially remedy this issue. These methods in-

clude stacked, density and frequency versions of the

PCP (Artero et al., 2004; Dang et al., 2010) or their

translation into 3D immersive environments (Tadeja

et al., 2019; Tadeja et al., 2021).

In this context, we propose to reformulate the pat-

tern recognition task as a form of classiﬁcation. From

this perspective, we can apply machine learning clas-

siﬁcation on visualized tabular data presented as PCP.

Artiemjew, P. and Tadeja, S.

Using ConvNet for Classiﬁcation Task in Parallel Coordinates Visualization of Topologically Arranged Attribute Values.

DOI: 10.5220/0010793700003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 167-171

ISBN: 978-989-758-547-0; ISSN: 2184-433X

167

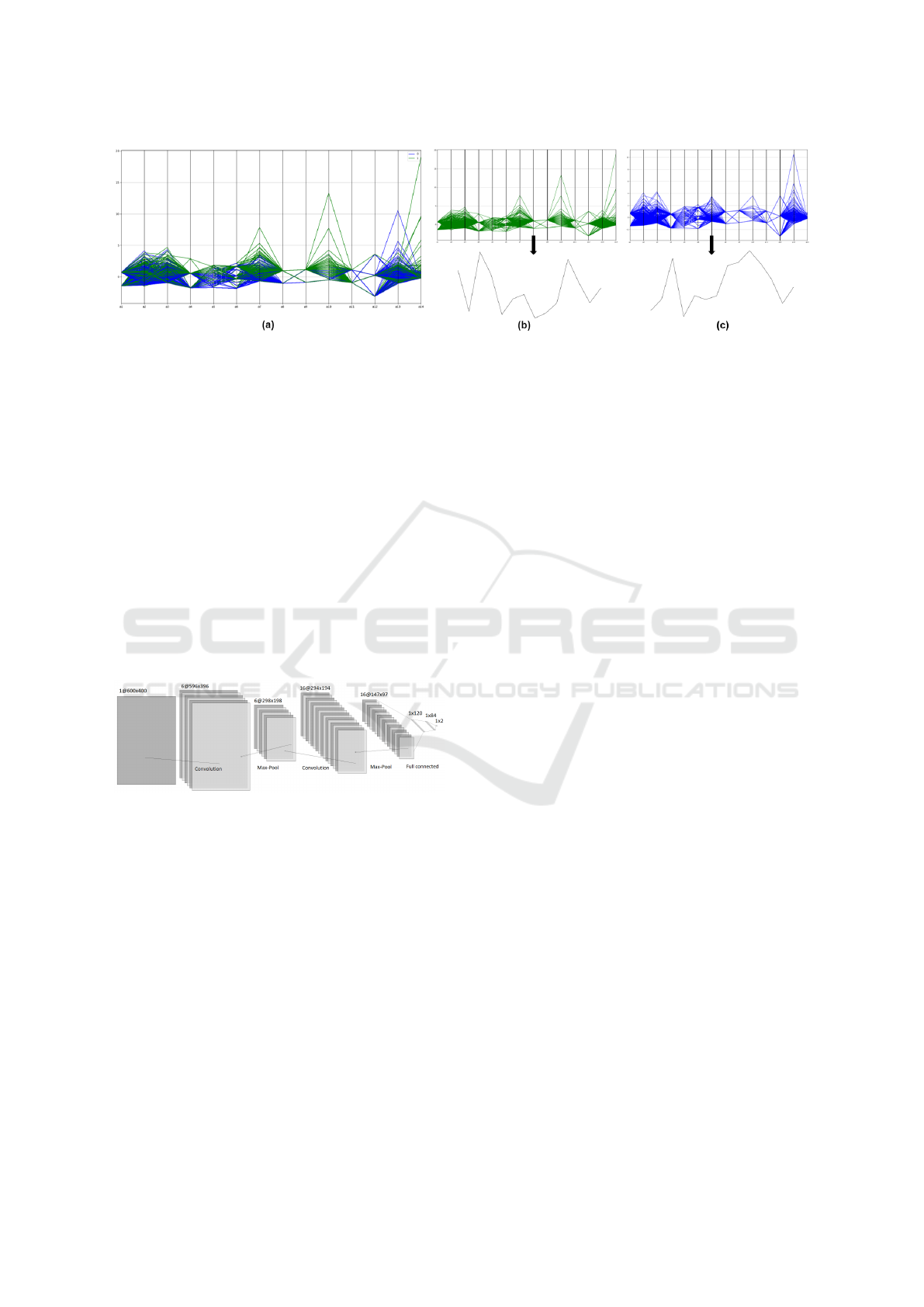
Figure 1: (a) Parallel Coordinates visualization of the Australian Credit dataset split into (b) class 0, and (c) class 1 respec-

tively. Bottom plots in (b) and (c) show one item from each class that, for readability, was not scaled to the PCP window.

As such, we evaluate the effectiveness of convolu-

tional neural network (ConvNet) with visualized tab-

ular data represented in the form of individual PCP

data items (see Fig. 1). Our goal was to validate the

efﬁcacy of visual classiﬁcation using a graphical rep-

resentation of the tabular data. We wanted to ascer-

tain if it would allow for greater efﬁciency than the

dummy classiﬁer method.

This work is also a ﬁrst step towards designing

potential enhancement of the PCP technique, further

uncovering its full potential for multidimensional data

visualization.

2 ARCHITECTURE

Figure 2: The LeNet (LeNail, 2019) architecture of our

ConvNet.

Our primary aim was to verify the experimental

effectiveness of classiﬁcation based on tabular data

visualized as a topological arrangement of attribute

values using PCP. We show the architecture of the

used network in Fig. 2. As a reference classiﬁer we

have chosen the LeNet (Lecun et al., 1998; Good-

fellow et al., 2016; Almakky et al., 2019) type Con-

vNet (Goodfellow et al., 2016; Lou and Shi, 2020).

The visualization of results was performed using

Matplotlib (Hunter, 2007) library. We scaled images

to 400 × 600 pixels to ensure the same size of the

input for the network. We also randomly divided

datasets into training and testing sets in an 80/20 ra-

tio. We fed the three-layered network with data after

two alternating convolutional and max-pooling steps.

We used max-pooling because it is the most effec-

tive technique for reducing the sizes of images, which

works well with neural network models. Such an ap-

proach turned out to be better in practice than average

pooling (Brownlee, 2019). The convolutional layers

extract features from images before they are fed into

the network.

The activation function of hidden layers was

ReLU, and the output layer had raw values. The loss

function took the form of categorical cross-entropy.

Thus, it could be higher than one. These layers can be

seen in Fig. 2. To train the neural network, we used

RGB color channels and applied the Adam optimizer

(Kingma and Ba, 2015). We carried out the train-

ing for Australian Approval Credit and Heart Disease

datasets over 20 epochs. The batch size was 50, and

the learning rate was 0.001. For the Diabetes dataset,

we used 30 epochs, batch size equal to 10, and a learn-

ing rate of 0.0001. We ﬁtted the above parameters

experimentally.

3 EXPERIMENTS

In the experimental part, we wanted to verify whether

the geometric arrangement of attribute values with

PCP can be successfully used in the classiﬁcation pro-

cess using real decision systems. This type of so-

lution for symbolic attributes is possible after con-

verting their values to dummy variables. As the data

characteristics allowed us to, we treated attributes as

numeric in our tests. We prepared the data for PCP

visualization using the StandardScaler tool from the

sklearn.preprocessing library. For the experiments,

we selected three distinctly different datasets from

the UCI repository (Dua and Graff, 2017) containing

mainly numerical data:

(i) Australian Credit (dims.: 15, items: 690);

(ii) Heart Disease (dims.: 14, items: 270);

(iii) Pima Indians Diabetes (dims.: 9, items: 768).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

168

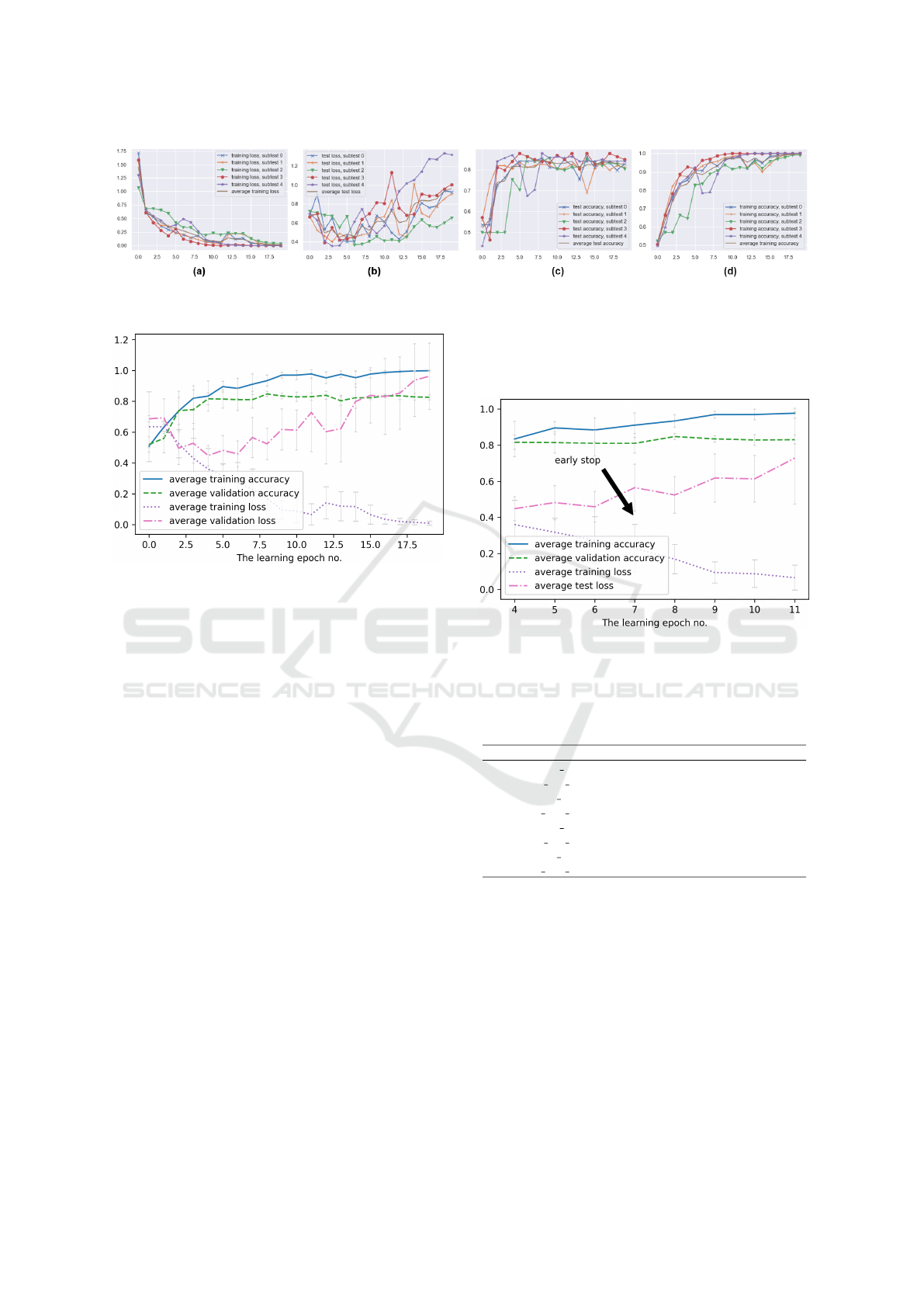
Figure 3: Accuracy for 20 iterations of ConvNet training and corresponding cross-entropy loss for the Australian Credit

dataset.

Figure 4: Summary of average results for 20 iterations over

the (i) Australian Credit Approval dataset.

Fig. 1 shows PCP-based visualization of the two

classes contained in the Australian Credit Approval

dataset. One of the classes denotes credit approval,

whereas the other marks rejected cases.

We used a LeNet-type ConvNet (Lecun et al.,

1998; Goodfellow et al., 2016; Almakky et al., 2019)

as a reference classiﬁer. In the deep neural network

classiﬁcation experiments, we divided the image sets

into a training subset and the validation test set with

an 80/20 split. To estimate the quality of the classiﬁ-

cation, we used the Monte Carlo Cross Validation (Xu

and Liang, 2001; Goodfellow et al., 2016) technique

(MCCV5, i.e., ﬁve times train and test), presenting

average results. In the experiments, the test (vali-

dation) system is applied in a given iteration to the

model to check the ﬁnal efﬁciency and observe the

overﬁtting level. By evaluating in each iteration of

learning an independent validation set (not affecting

the network’s learning process), we can determine the

degree of generalization of the model. The result is

objective when there is no process of overtraining,

i.e., a clear discrepancy between the loss during net-

work training and that resulting from testing the val-

idation set. In evaluating experiments, accuracy in a

balanced version is often recommended, i.e., the aver-

age accuracy of all classes classiﬁed (Brodersen et al.,

2010). Such an approach addresses the problem of

unbalanced classes. In our experiments, we use the

Coss Entropy Loss version, which can exceed a value

of 1, to clearly indicate where the model is malfunc-

tioning.

Figure 5: A close-up of the area of iterations where the

model begins to overlearnfor the (i) Australian Approval

Credit dataset.

Table 1: Detailed average accuracy results corresponding to

the Fig. 5 and (i) Australian Approval Credit. dataset.

parameter ep5 ep6 ep7 ep8 ep9

training acc 0.895 0.884 0.911 0.934 0.970

training acc sd 0.035 0.066 0.068 0.035 0.019

training loss 0.318 0.273 0.229 0.169 0.094

training loss sd 0.077 0.130 0.132 0.081 0.059

validation acc 0.814 0.810 0.810 0.848 0.835

validation acc sd 0.059 0.071 0.054 0.017 0.018

validation loss 0.482 0.459 0.565 0.524 0.618

validation loss sd 0.095 0.084 0.130 0.102 0.133

4 RESULTS

We performed all the experiments in a similar fash-

ion. Thus, our results show how the MCCV5 method

works in each learning epoch and present the results

of ﬁve internal tests and the average result.

The accuracy of classiﬁcation and entropy loss of

a given variant–for ﬁve subtests–is shown for the Aus-

tralian Credit Approval dataset in Fig. 3. We also offer

the combined average results by adding the standard

deviation in the form of vertical lines in individual

Using ConvNet for Classiﬁcation Task in Parallel Coordinates Visualization of Topologically Arranged Attribute Values

169

epochs in Fig. 4. We calculated the standard devia-

tion from individual subtests of the MCCV5 method.

Finally, we present a close-up of the area where we

propose the stopping point of the learning process for

each dataset (i-iii) in Fig. 5, 6 and 7. We omit detailed

results for systems (ii) and (iii). However, we have

left a close-up of the areas of learning of most interest

to us (see Fig. 5, 6 and 7).

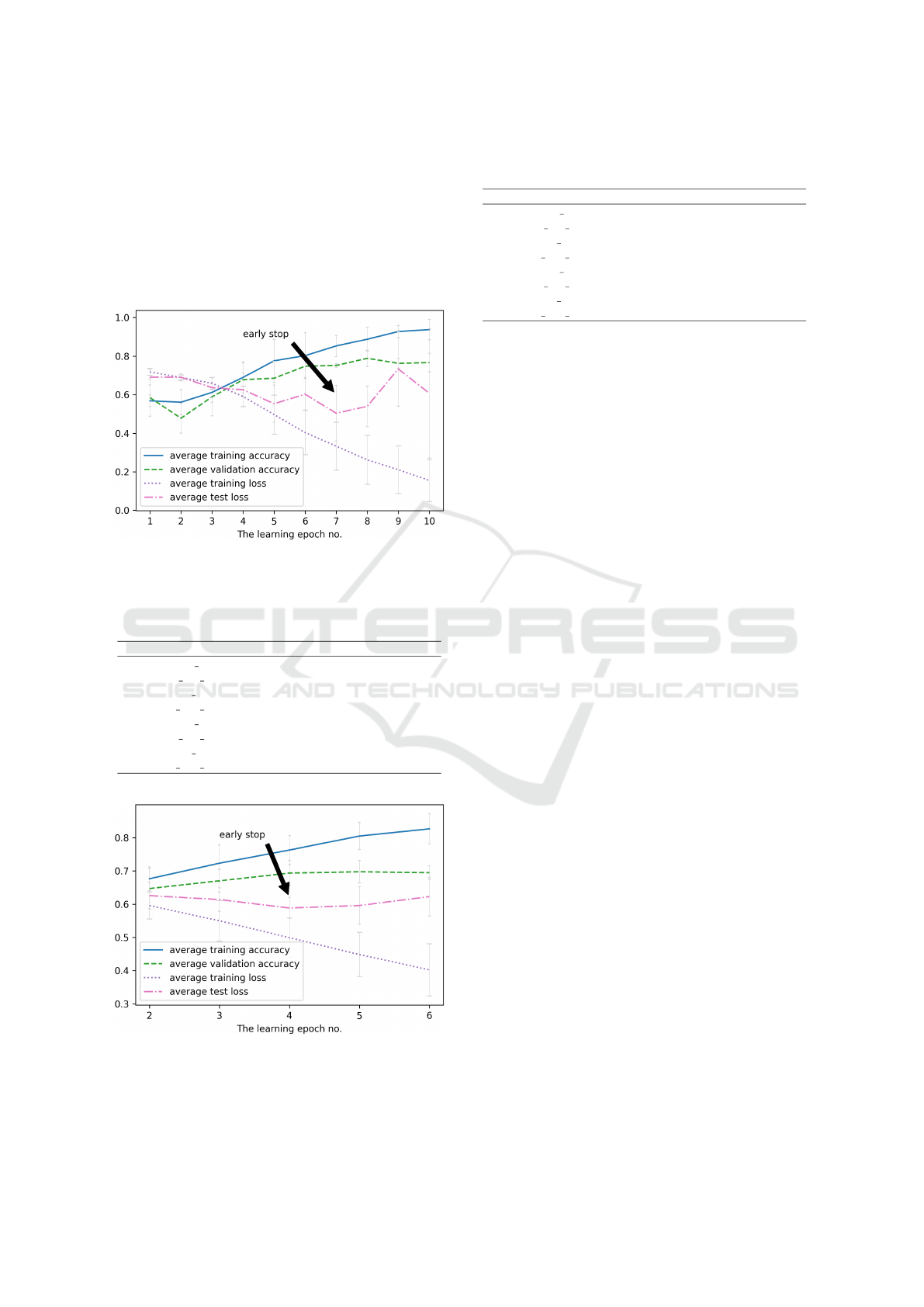
Figure 6: A close-up of the area of iterations where the

model begins to overlearnfor the (ii) Heart Disease dataset.

Table 2: Detailed average accuracy results corresponding to

the Fig. 6 and (ii) Heart Disease dataset.

parameter ep5 ep6 ep7 ep8 ep9

training acc 0.776 0.803 0.853 0.888 0.928

training acc sd 0.111 0.119 0.055 0.061 0.031

training loss 0.497 0.403 0.333 0.262 0.211

training loss sd 0.101 0.115 0.124 0.127 0.123

validation acc 0.685 0.748 0.752 0.789 0.763

validation acc sd 0.088 0.058 0.009 0.042 0.025

validation loss 0.553 0.603 0.504 0.540 0.734

validation loss sd 0.096 0.082 0.144 0.105 0.192

Figure 7: A close-up of the area of iterations where the

model begins to overlearnfor the (iii) Pima Indians Diabetes

dataset.

Table 3: Detailed average accuracy results corresponding to

the Fig. 7 and the (iii) Pima Indians Diabetes dataset.

parameter ep2 ep3 ep4 ep5 ep6

training acc 0.677 0.723 0.763 0.805 0.826

training acc sd 0.036 0.055 0.043 0.041 0.045

training loss 0.596 0.550 0.499 0.448 0.402

training loss sd 0.041 0.061 0.059 0.066 0.078

validation acc 0.647 0.670 0.694 0.697 0.695

validation acc sd 0.061 0.034 0.038 0.034 0.021

validation loss 0.626 0.614 0.588 0.596 0.623

validation loss sd 0.039 0.035 0.032 0.057 0.058

5 DISCUSSION

We conducted two classiﬁcation tests: based on ran-

domly arranged attributes and with axes sorted with

respect to the correlation with the decision attribute.

The results were comparable, and we tentatively con-

clude that the order of the attributes does not mat-

ter when classifying PCP-visualized items using Con-

vNet. However, complete veriﬁcation requires testing

a selected group of combinations without repeating

the attribute arrangement and multiple testing with

statistical conﬁrmation.

For all the datasets we show the scores narrowed

to the areas where models started to overlearn in Fig.

5, 6, and 7 together with accompanying Tab. 1, 2,

and 3 respectively. Based on this outcome, we can

conclude that the classiﬁcation based on PCP visu-

alization gives signiﬁcantly different results from the

performance of the dummy classiﬁer (i.e., random ef-

fectiveness). We further veriﬁed the stability of the

results by presenting the standard deviations of the re-

sults. Furthermore, we can successfully halt the mod-

els using the early stop method, as shown in Fig. 5, 6

and 7. Moreover, conducted tests suggest that for our

method, the order of the attributes does not matter as

conducted tests with varying arrangements yield com-

parable efﬁciency. The technique allows us to use the

topological arrangement of attributes to capture vi-

sual features that are prototypical patterns of learned

classes. These results will have to be further extended

to test the properties of the developed methodology in

detail.

6 CONCLUSION

In this ongoing work, we veriﬁed that the topolog-

ical arrangement of the attribute values of a tabular

decision system could allow effective classiﬁcation

using deep neural networks. We used a ConvNet of

the LeNet type (Lecun et al., 1998; Goodfellow et al.,

2016; Almakky et al., 2019) as a reference network.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

170

As an efﬁciency evaluation model, we applied the

Monte Carlo Cross-Validation (MCCV5) method (Xu

and Liang, 2001; Goodfellow et al., 2016).

To conduct the experiments, we selected three real

datasets from the UCI Repository (Dua and Graff,

2017). Our results indicate that classiﬁcation using

a visual representation of tabular decision systems–

in our case, PCP visualization–is possible and does

not differ signiﬁcantly from a classic form of deci-

sion systems. This work opens new research avenues

and promises a potentially handy enhancement of the

PCP technique itself.

In the future, we plan to investigate how a com-

mittee of classiﬁers based on the researched technique

behaves. Furthermore, we will also test other methods

for a visual representation of multidimensional deci-

sion systems in terms of classiﬁcation and try our ap-

proach on 3D PCP. Other threads we are planning are

to see which transformations of the original PCP visu-

alization positively impact classiﬁcation. Finally, we

will also consider the application of model explain-

ability techniques by determining which visual fea-

tures inﬂuence the classiﬁcation process.

REFERENCES

Almakky, I., Palade, V., and Ruiz-Garcia, A. (2019). Deep

convolutional neural networks for text localisation in

ﬁgures from biomedical literature. In 2019 Interna-

tional Joint Conference on Neural Networks (IJCNN),

pages 1–5.

Artero, A., de Oliveira, M., and Levkowitz, H. (2004). Un-

covering clusters in crowded parallel coordinates vi-

sualizations. In IEEE Symposium on Information Vi-

sualization, pages 81–88.

Brodersen, K. H., Ong, C. S., Stephan, K. E., and Buhmann,

J. M. (2010). The balanced accuracy and its posterior

distribution. In Proceedings of the 2010 20th Interna-

tional Conference on Pattern Recognition, ICPR ’10,

page 3121–3124, USA. IEEE Computer Society.

Brownlee, J. (2019). A gentle introduction to deep learn-

ing for face recognition. Deep Learning for Computer

Vision.

Dang, T. N., Wilkinson, L., and Anand, A. (2010). Stack-

ing graphic elements to avoid over-plotting. IEEE

Transactions on Visualization and Computer Graph-

ics, 16(6):1044–1052.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

Heinrich, J. and Weiskopf, D. (2013). State of the Art of

Parallel Coordinates. In Sbert, M. and Szirmay-Kalos,

L., editors, Eurographics 2013 - State of the Art Re-

ports. The Eurographics Association.

Hunter, J. D. (2007). Matplotlib: A 2d graphics environ-

ment. Computing in Science Engineering, 9(3):90–95.

Inselberg, A. (1985). The plane with parallel coordinates.

The Visual Computer, 1(2):69–91.

Inselberg, A. (2009). Parallel coordinates: Visual multidi-

mensional geometry and its applications. ACM SIG-

SOFT Software Engineering Notes, 35(3).

Kingma, D. P. and Ba, J. (2015). Adam: A method for

stochastic optimization. CoRR, abs/1412.6980.

Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

LeNail, A. (2019). Nn-svg: Publication-ready neural net-

work architecture schematics. J. Open Source Softw.,

4:747.

Lou, G. and Shi, H. (2020). Face image recognition based

on convolutional neural network. China Communica-

tions, 17(2):117–124.

Tadeja, S., Kipouros, T., and Kristensson, P. O. (2019). Ex-

ploring parallel coordinates plots in virtual reality. In

Brewster, S. and Fitzpatrick, G., editors, CHI EA’19

: extended abstracts of the 2019 CHI Conference on

Human Factors in Computing Systems. Association

for Computing Machinery, New York.

Tadeja, S., Kipouros, T., Lu, Y., and Kristensson, P. O.

(2021). Supporting decision making in engineering

design using parallel coordinates in virtual reality.

AIAA Journal, pages 1–15.

van der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of Machine Learning Research,

9(86):2579–2605.

Xu, Q.-S. and Liang, Y.-Z. (2001). Monte carlo cross vali-

dation. Chemometrics and Intelligent Laboratory Sys-

tems, 56(1):1–11.

Using ConvNet for Classiﬁcation Task in Parallel Coordinates Visualization of Topologically Arranged Attribute Values

171