Coordinated Collision-free Movement of Groups of Agents

svancara

, Marika Ivanov

a and Roman Bart

Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic

Keywords:

Coordinated Movement, Multi-agent, Path Finding, SAT Model.

Abstract:

Coordinating the movement of groups of autonomous agents in a crowded environment is a vital problem with

application areas such as warehousing, computer games, or drone art. In this paper, we study the problem of

ﬁnding collision-free paths for groups of agents such that the groups are kept together like a ﬂock, a ﬁsh school,

or a military unit. Speciﬁcally, we analyze the properties of the problem, propose a SAT formulation based

on network ﬂows, and perform a numerical experimental evaluation on various instance types. The results

suggest that it is a challenging problem with promising research and application potential. Furthermore, we

demonstrate the functionality of our solution method on real educational robots.

1 INTRODUCTION AND

MOTIVATION

In this paper, we introduce the Connected Colored

MAPF problem that consists of multiple teams of

agents deployed in a shared, fully observable environ-

ment with possible static obstacles. The agents then

move in a coordinate collision-free manner towards

given target locations. For each team, the number of

target locations equals the number of agents in the

team. Agents within one team are interchangeable,

that is, an agent aims to reach any of the targets as-

sociated with its team. A goal state occurs as soon as

every agent reaches any of its relevant targets.

Individual teams do not compete or harm each

other. They may cooperate in reaching their respec-

tive targets, for example, by waiting and letting an-

other agent pass. The agents within one team are re-

quired to remain close to each other at any time during

their movement. Such coordination ensures, e.g., the

possibility to communicate with each other in a multi-

hop fashion.

Practical applications of Connected Colored

MAPF include but are not limited to the video

game industry, drone formation control, or ware-

house robots. In real-time strategic games, individ-

ual military units are sometimes required to preserve

a speciﬁc formation when relocating to a given area

in the environment. Multi-UAV (unmanned aerial

https://orcid.org/0000-0002-6275-6773

https://orcid.org/0000-0002-6717-8175

vehicle) cooperative formation ﬂight is to arrange

drones with autonomous ﬂight functions according

to the designed three-dimensional space structure so

that the drones keep a stable formation during the

ﬂight and can change the formation shape accord-

ing to mission needs and environmental changes (Li

et al., 2020). Drone art shows may enhance the au-

dience’s aesthetic experience during musical perfor-

mances. Applications involving multiple robots mov-

ing in a crowded environment may require communi-

cation maintenance among the robots.

1.1 Relevance to Other Problems

Multi-Agent Path Finding (MAPF) is a rapidly devel-

oping and widely studied area dealing with ﬁnding

collision-free paths from initial to target locations for

a set of agents from moving in a given environment.

In the classical MAPF problem, each agent is asso-

ciated with a unique destination. However, there are

applications where the agents need to move to spe-

ciﬁc areas, but the exact locations of agents in these

areas are not important. An example of such situation

is when warehouse robots of the same type need to

relocate to uniform charging stations at the end of a

shift. This variant of MAPF is known as Anonymous

MAPF.

A generalized version of Anonymous MAPF, re-

ferred to as Colored MAPF, assumes multiple groups

of agents with speciﬁed areas of destinations for each

group. Colored MAPF problems can be found in

computer games, where armies of bots are moving to

Švancara, J., Ivanová, M. and Barták, R.

Coordinated Collision-free Movement of Groups of Agents.

DOI: 10.5220/0010789100003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 26-33

ISBN: 978-989-758-547-0; ISSN: 2184-433X

locations speciﬁed by the player (Ma et al., 2017). Po-

sitions of individual bots are not distinguished, but the

groups should reach their destinations. There are sim-

ilar situations in transportation problems, for exam-

ple, in warehouses (Ma and Koenig, 2016). Anony-

mous MAPF can be solved makespan-optimally in

polynomial time (Yu and LaValle, 2012); however,

ﬁnding a makespan-optimal solution to MAPF is NP-

hard (Surynek, 2010; Ratner and Warmuth, 1990).

As (Connected) Colored MAPF is a generalization of

classical MAPF, where each agent has its destination,

the NP-hardness result applies to (Connected) Col-

ored MAPF as well.

There exist both imperative and declarative

methods for ﬁnding a makespan-optimal solution

to Colored MAPF. Conﬂict-Based Min-Cost-Flow

(CBM) (Ma and Koenig, 2016) is based on algorithm

Conﬂict-Based Search (CBS) (Sharon et al., 2012).

Reduction-based methods using Boolean satisﬁabil-

ity and integer linear programming formulation have

also been developed (Bart

ak et al., 2021).

The Connected Colored MAPF problem we in-

vestigate here is a variant of Colored MAPF, where

agents within individual groups must be kept together.

Connectivity was introduced in classical

MAPF (Queffelec et al., 2020). Communication

maintenance was also studied in the Area Protection

Problem (Ivanov

a et al., 2018), which can be viewed

as a MAPF with an adversarial element. Unlike in

Connected Colored MAPF, the agents in the Area

Protection Problem (Ivanov

a et al., 2018) are not

required to keep adjacent locations. Instead, they

need to remain within a deﬁned communication

vicinity of each other, which allows them to distance

themselves up to a given diameter while obstacles are

not transparent. Connected Colored MAPF has never

been studied before, and we introduce the problem

here.

The paper is organized as follows. We will ﬁrst

formally introduce the Connected Colored MAPF

Problem and discuss some of its properties. Then, we

will present the SAT model of the problem with two

possible encodings of the connectivity constraints. Fi-

nally, we will empirically evaluate the behavior of

the solver and present an application that allows the

demonstration of the results on real education robots.

2 FORMAL DEFINITION

Let A = {1, . . . , n} be a set of n agents and G = (V, E)

be an un-directed graph with vertices V and edges E.

Agents are initially staying at some vertices, which is

described by initial conﬁguration S : A → V , where

S(a) is the initial position of agent a. The ﬁnal con-

ﬁguration is given by a set of vertices T ⊂ V such that

|T | = |A|.

Anonymous MAPF problem is given by a quadru-

ple (G, A, S, T ) and its solution is a set of collision-

free plans. A plan π

for an agent a is a sequence

of vertices such that π

[1] = S(a) and for each t ei-

ther π

[t] = π

[t + 1] (agent waits at a vertex) or

(π

[t], π

[t + 1]) ∈ E (agent moves to a neighboring

vertex). Let m

be the length of plan for agent a, then

we deﬁne π

[t] = π

] for each t > m

(agents even-

tually stay in their ﬁnal vertices). Note, however, that

if an agent reaches one of its targets at time t < m

, it

can still leave the target and perhaps give way to an-

other agent. Let M = max

a∈A

be a makespan of the

plans. We require agents to reach the ﬁnal conﬁgura-

tion: ∀v ∈ T ∃a ∈ A : π

[M] = v, and the plans to be

collision free: ∀a

, a

∈ A, a

̸= a

, ∀t : π

[t] ̸= π

[t]

(no vertex collision) and ∀a

, a

∈ A, a

̸= a

, ∀t :

[t] ̸= π

[t + 1] ∨ π

[t + 1] ̸= π

[t] (no swapping

collision).

Colored MAPF (also known as Team MAPF

or TAPF) with k groups of agents is then

given as (G, (A

, S

, T

), . . . , (A

, S

, T

)), where each

(G, A

, S

, T

) is anonymous MAPF (Solovey and

Halperin, 2014). A solution of Colored MAPF is a

union of solutions of individual anonymous MAPF

problems such that the plans across the groups are

also collision-free.

Let V

= {π

[t] : a ∈ A

} be the set of vertices

occupied by agents from A

at time step t. The

Connected Colored MAPF is a variant of Colored

MAPF that additionally requires the graph induced

by V

to be connected at each time step t, i.e., ∀c ∈

{1, . . . , k}, ∀t : G[V

] = (V

, E

) is connected.

3 PROBLEM PROPERTIES

Experimental evaluation of Colored MAPF reveals

that adding an agent and a target to an existing team

can, in fact, decrease the minimum makespan (Bart

et al., 2021), contrary to the classic MAPF, in which

adding an agent never leads to an improvement of

minimum makespan. Intuitively, this can be ex-

plained by a new goal being placed in a more favor-

able position for a particular agent. This phenomenon

can occur in the Connected Colored MAPF problem

as well, as illustrated in Fig. 1. The instance on the left

has a minimum makespan of 9 because the agents are

forced to traverse in a train-like movement around the

obstacle to keep connected. When we add three more

agents and targets as depicted on the right, the mini-

mum makespan decreases to 5 as there is now enough

Coordinated Collision-free Movement of Groups of Agents

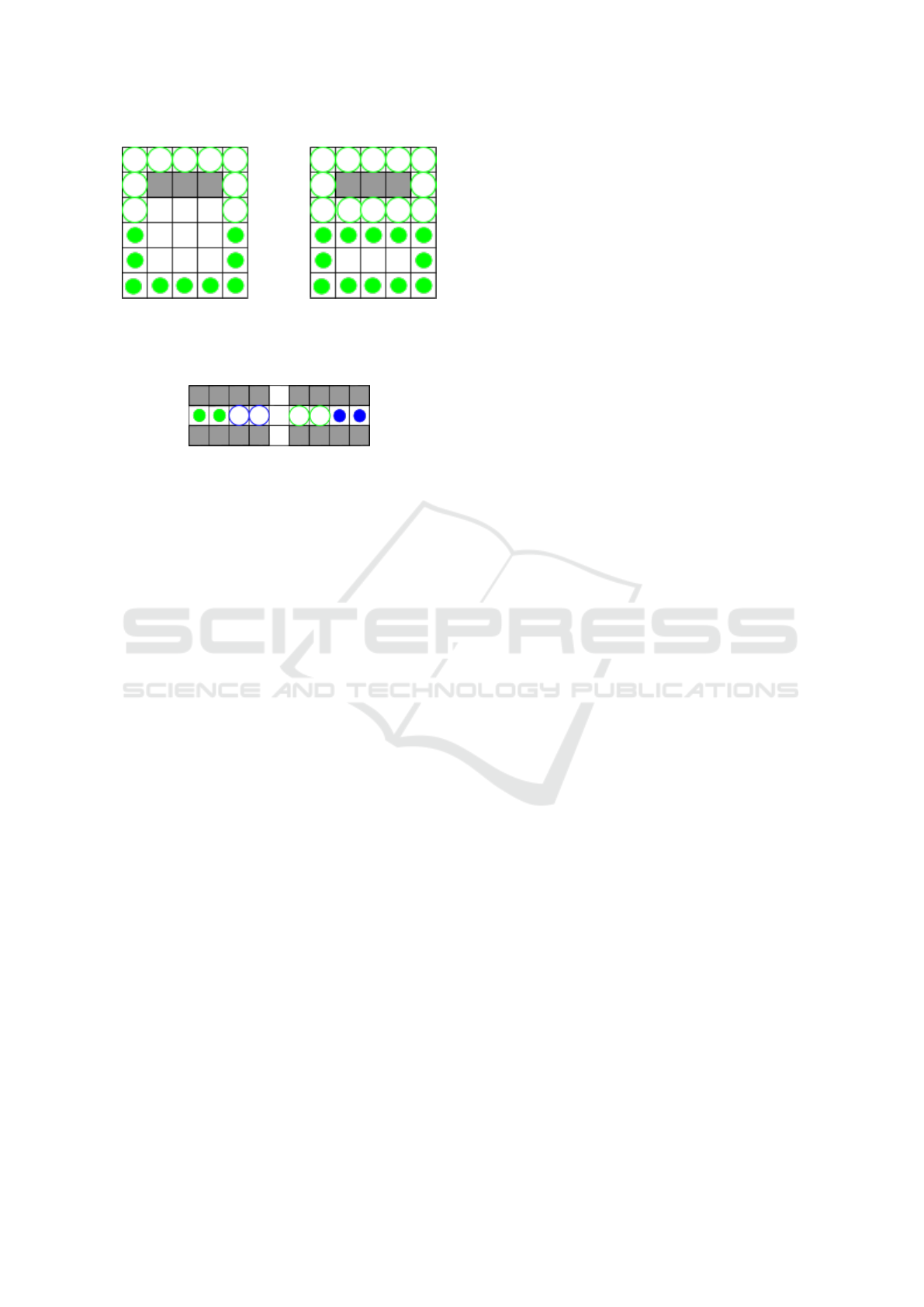
Figure 1: An example of how increasing the number of

agents can improve a makespan. Green and white circles

are agents of one team and their targets, respectively. Grey

blocks represent obstacles.

Figure 2: An instance of Colored MAPF for which there ex-

ists a solution. When connectivity is required, this instance

becomes unsolvable. The color of target matches the color

of agents.

agents to maintain connectivity: all agents make one

step up, and subsequently, all agents except the top

three in the middle make another four steps to ﬁll

the target locations along the border. Note, however,

that the depicted instance is somewhat artiﬁcially de-

signed, and improvement of makespan rarely happens

in our experimental scenarios.

Figure 1, the instance on the left, is also an exam-

ple of an instance where the connectivity constraint

increases the optimal makespan. As was mentioned,

under the Connected Colored MAPF, this instance

has an optimal makespan of 9, while under Colored

MAPF, this instance is solvable with a makespan of

5, as the agents may disconnect and approach the tar-

gets from both sides.

Furthermore, adding the connectivity constraint

can cause an instance that would be solvable as a

Colored MAPF to become unsolvable as a Connected

Colored MAPF. It typically happens in crowded in-

stances when initial and target locations overlap, but

there are cases when there is no solution, even with

disjoint initial and target locations. An example of

such an instance can be seen in Figure 2. Indeed,

in Colored MAPF, a solution is for the green agents

to move out of the way to the very top and bot-

tom vertices to let the blue agents pass. Then, they

can navigate to their target positions. This solution

(or any other) is not possible under Connected Col-

ored MAPF since any solution requires either the two

green agents or the two blue agents to disconnect.

4 SOLUTION METHODS

Our approach to tackling Connected Colored MAPF

is to propose a Boolean satisﬁability (SAT) formu-

lation that extends an existing model for Colored

MAPF (Bart

ak et al., 2021). This reduction-based

technique uses a spatial-temporal layered graph of a

certain number of layers in which the agents move.

Each layer of the graph corresponds to a single time

step. The layered graph is a directed acyclic graph,

and can be regarded as multiple copies of the orig-

inal graph with removed edges. Consecutive layers

are then connected by oriented edges that represent

a movement along an edge or staying at a vertex in

the original graph. Initially, the number of layers in

the spatial-temporal graph equals some lower bound

on the makespan. In the beginning, agents are placed

in the ﬁrst layer at their initial locations. The SAT

solver then tries to ﬁnd paths for each agent to a tar-

get associated with its team. If there is a solution,

it means the minimum makespan equals the current

number of layers. Otherwise, the number of available

layers increases by one, and the path-ﬁnding process

is repeated.

4.1 SAT Model for Colored MAPF

The existing SAT formulation of Colored MAPF uses

the following two sets of variables:

At(t, a, v) =

(

1 agent a is at node v at time step t,

0 otherwise,

Pass(t, a, v, u) =

(

1 a passes via arc (v, u) at time t,

0 otherwise,

and constraints on these variables imposing move-

ment rules and goal conditions in accordance with the

deﬁnition of Colored MAPF.

∀a ∈ ∪

c=1

: At(S(a), a, 0) = 1 (1a)

∀c ∈ {1, . . . k}, ∀a ∈ A

∑

v∈T

At(M, a, v) = 1 (1b)

∀v ∈ V, ∀t ∈ {0, . . . , M} :

∑

a∈∪

c=1

At(t, a, v) ≤ 1

(1c)

∀(v, u) ∈ E, ∀t ∈ {0, . . . , M − 1} :

∑

a∈∪

c=1

Pass(t, a, v, u) + Pass(t, a, u, v) ≤ 1 (1d)

∀v ∈ V, ∀a ∈ ∪

c=1

, ∀t ∈ {1, . . . , M} :

At(t, a, v) =

∑

(u,v)∈E

Pass(t −1, a, u, v) (1e)

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

∀v ∈ V, ∀a ∈ ∪

c=1

, ∀t ∈ {0, . . . , M − 1} :

At(t, a, v) =

∑

(v,u)∈E

Pass(t, a, v, u) (1f)

The constraints have the following interpretation:

1. Initial location of each agent is set (1a).

2. Each agent from a group c eventually arrives in

exactly one node in T

(1b).

3. Each node is occupied by at most one agent at a

time (avoidance of node collisions) (1c).

4. Two agents cannot pass through the same edge in

opposite directions at the same time (avoidance of

swapping collisions) (1d).

5. An agent is at a node if and only if it arrived

via an inbound edge, and left via an outbound

edge (waiting is enabled by the existence of

loops) (1e),(1f).

4.2 Multi-commodity Model for

Connectivity

The main idea that helps to coordinate the agents’

movement in a connected manner is based on

the multi-commodity network ﬂow (MCF) problem.

Consider positions V

of agents from each team A

at every time step t and the induced graph G[V

We are looking for a MCF in each G[V

]. Next, for

each team A

, let us select a representative agent a

whose location acts as a source of the MCF. The re-

maining agents’ locations are sinks for commodities

associated with the corresponding agents. Intuitively,

the ﬂow of commodity associated with agent a passes

through some of the agents’ current locations and is

absorbed once it reaches the current position of a. The

existence of a MCF in each G

ensures the existence

of a path from the source a

to every agent from A

and thus the connectivity of agents within one team.

We therefore extend the model by another set of

variables representing MCF. For each team c, time

step t, agent a ∈ A

and edge {u, v} ∈ E

, there is

a variable f

uva

such that

uva

(

1 ﬂow of agent a passes (u, v) at time t,

0 otherwise.

The variables are Boolean, and so the resulting as-

signment found by a SAT solver represents paths from

) to π

(a) for each a ∈ A

. Additional constraints

are derived from a standard formulation of MCF.

∀c ∈ {1, . . . , k}, ∀a ∈ A

\ {a

∀t ∈ {1, . . . , M − 1}, u = π

[t] :

∑

(u,v)∈E

uva

= 1 (2a)

∀c ∈ {1, . . . , k}, ∀a ∈ A

\ {a

∀t ∈ {1, . . . , M − 1}, v ∈ V

\ {π

[t], π

[t]} :

∑

(u,v)∈E

uva

∑

(v,u)∈E

vua

(2b)

∀c ∈ {1, . . . , k}, ∀a ∈ A

\ {a

∀t ∈ {1, . . . , M − 1}, v = π

[t] :

∑

(u,v)∈E

uva

= 1 (2c)

∀c ∈ {1, . . . , k}, ∀a ∈ A

\ {a

∀t ∈ {1, . . . , M − 1}, ∀(u, v) ∈ E

, v ̸= π

[t], :

uva

≤

∑

a∈A

At(t, a, v) (2d)

The sets of constraints (2a)-(2c) are ﬂow conser-

vation constraints on sources π

, intermediate nodes

and sinks, respectively. By (2d) we then express the

relation between the variables. It is sufﬁcient to de-

ﬁne these ﬂow constraints for time steps 1,. . . , M −1,

because the connectivity in initial and target conﬁg-

uration is already guaranteed by the admissibility of

tested instances. We shall refer to this model as an

MCF model.

Let us note that the induced graph G[V

] is not

a part of the input, but changes dynamically as the

agents progress towards their target locations, i.e.,

sources and sinks change in each time step accord-

ing to the position of the corresponding agents. When

implementing, one has to keep in mind that the ﬂow

constraints are conditional.

4.3 Single-commodity Model for

Connectivity

The previous model for connectivity treats each agent

in a group as a single commodity. This approach cre-

ates many variables since for each agent in a group,

we require a set of variables describing all of the

edges in the graph. An idea that may save some

variables treats a single group as a single commod-

ity and is based on a single commodity ﬂow (SCF).

The drawback of this model is that the domain of

the variables is not a Boolean but rather a range in

{0, . . . , |A

|}. This is not natural for a SAT solver but

can be managed with a log-encoding of the variables.

We will describe the implementation details in a later

section.

We again extend the colored MAPF model by an-

other set of variables representing SCF. For each team

c, time step t, and edge {u, v} ∈ E

, there is a vari-

able f

such that f

∈ {0, . . . , |A

|}. A representative

Coordinated Collision-free Movement of Groups of Agents

agent a

is again selected from each team A

to act as

the source of the ﬂow. The following constraints im-

posing connectivity are added to the Colored MAPF

model (1a)-(1f):

∀c ∈ {1, . . . , k}, ∀t ∈ {1, . . . , M − 1}, u = π

[t] :

∑

(u,v)∈E

= |A

| − 1 (3a)

∀c ∈ {1, . . . , k}, ∀t ∈ {1, . . . , M − 1},

v ∈ V

\ {π

[t]} :

∑

(u,v)∈E

= 1 +

∑

(v,u)∈E

(3b)

∀c ∈ {1, . . . , k}, ∀t ∈ {1, . . . , M − 1}, ∀(u, v) ∈ E

≤ |A

| ∗

∑

a∈A

At(t, a, v) (3c)

The sets of constraints (3a) and (3b) represent the

ﬂow. The representative agent a

initiates a ﬂow of

size |A

|−1, and every other agent consumes one unit

of the ﬂow, and forwards the rest of the received ﬂow

to its outgoing edges. By (3c) we then express the

relation between the ﬂow variables and the variables

modeling the presence of an agent at a node. We shall

refer to this model as an SCF model.

The reasoning why this is sufﬁcient to model

agents’ connectivity is as follows. Consider a ﬂow

network created from the induced graph G[V

] by

adding a source connected to the location of a

with

a capacity of |A

| and a sink connected to each of the

vertices in V

with a capacity of 1. The maximum

ﬂow will be equal to |A

| only if the graph G[V

] is

connected. This network is equivalent to the proposed

SCF model, but rather than adding a source and a sink,

we generate the ﬂow at the positions of a

and each

agent consumes a ﬂow of size one. The name of the

model reﬂects this reasoning.

5 EXPERIMENTAL EVALUATION

In order to assess the performance of the proposed

model, we conducted numerical experiments on sce-

narios suitable for the studied problem. In the follow-

ing, we provide a detailed explanation that facilitates

the reproducibility of the tests.

5.1 Implementation

The described model has been implemented using

the Picat programming language (Picat language and

compiler version 2.7b7), which is a logic-based pro-

gramming language similar to Prolog. The main ad-

vantage, and the reason this tool was used, is that the

constraints are easily represented and then automati-

cally translated to a propositional formula. See Figure

3 for a snipped of Picat code that models the Colored

MAPF. Adding constraints in Figure 4 or in Figure 5

creates a model for Connected Colored MAPF. Notice

the similarity between constraints (2a) – (2d), (3a) –

(3c) and the code itself.

Figure 3: A snippet of Picat code. These constraints model

the Colored MAPF problem for a given makespan M.

5.2 Instances

To test the implemented model, we create random

grid instances inspired by the benchmarks often used

in classical MAPF setting (Stern et al., 2019). We

pick three different sizes: 8 by 8, 16 by 16, and 32 by

32. For each size, we consider two options, either no

obstacles are present at all (maps empty) or 20% of

random vertices are marked as an impassable obsta-

cle (maps random). The number of agents in a single

team is ﬁxed at 5 and 10. The number of teams in-

creases from 1 to a point so that the total number of

agents present in the graph is 100 (40 in the case of

the grids of size 8 by 8). The start and goal locations

of agents are placed randomly in such a way that the

start and goal locations of a single team always form a

connected graph. However, note that based on the ex-

ample in Figure 2 this does not necessarily guarantee

that the instance has a solution. Each of the settings is

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Figure 4: A snippet of Picat code. Adding these constraints

to the ones from Figure 3 model the Connected Colored

MAPF via the MCF model.

created 5 times. This gives us a total of 720 instances.

5.3 Results

Each of the created instances was run on a PC with an

AMD Ryzen 7 4700U CPU running at 2.00 GHz with

16 GB of RAM. We used a time limit of 300 seconds

per problem instance.

First, we compare the two models for navigating

agents in a connected manner. The ratio of solved in-

stances in the given time limit is shown in Table 1 for

the MCF model and in Table 2 for the SCF model. We

split the results based on the size of the grid, the num-

ber of agents present in a single team, and whether

there are obstacles present in the grid. Based on the

presented results it can be clearly seen that the MCF

model outperforms the SCF model in all of the set-

tings. Furthermore, with the increasing size of the

grid, the problem becomes much harder. Only around

10% of instances on the largest grids are solved by

the MCF model and these correspond to the instances

with the least number of agents. The best perfor-

mance is achieved in the smallest grids. Both adding

obstacles and increasing the number of agents per

team negatively inﬂuence the success ratio. The rea-

Figure 5: A snippet of Picat code. Adding these constraints

to the ones from Figure 3 model the Connected Colored

MAPF via the SCF model.

soning behind these results is that with the increasing

size of the grid and the number of agents, the number

of variables entering the solver increase as well. Fur-

thermore, on larger grids, the average traveling dis-

tance also increases which further increases the num-

ber of variables. The traveling distance also increases

when obstacles are present.

Table 1: The ratio of instances that were solved within a

given time limit divided by the number of agents per one

team and by the grid type. Results for MCF model.

agents per team grid type

size 5 10 empty random

8 0.85 0.65 0.9 0.66

16 0.37 0.14 0.34 0.25

32 0.14 0.1 0.13 0.12

Table 2: The ratio of instances that were solved within a

given time limit divided by the number of agents per one

team and by the grid type. Results for SCF model.

agents per team grid type

size 5 10 empty random

8 0.62 0.31 0.53 0.5

16 0.14 0.06 0.12 0.11

32 0.09 0.02 0.05 0.07

We further investigate the instances on grids 8 by

8 with obstacles, since they seem to provide the most

interesting results. Comparison of runtimes of Con-

nected Colored MAPF via MCF and SCF, and Col-

Coordinated Collision-free Movement of Groups of Agents

Figure 6: Comparison of runtime of Connected Colored

MAPF and Colored MAPF on the same instances.

ored MAPF is shown in Figure 6. The instances

are ordered by their runtime, on the x-axis is shown

the instance number and on the y-axis, the runtime

is shown. This graph represents the number of in-

stances solvable in a given time limit. The lower the

line, the better. We can clearly see that the Colored

MAPF is easier to solve. This is caused only by the

added constraints and not by an increase in makespan

in which the instance is solvable (recall that adding

the connectivity requirement can cause the makespan

to increase). The case that the makespan increased

occurred only in 6 cases out of 60 instances and each

time the makespan increased by 1.

6 PRACTICAL

DEMONSTRATION

To visualize the proposed algorithm, we created a

software OzoMorph that allows the user to build a

(Connected) Colored MAPF instance, solve it with a

provided solver, see a simulation of the solution, and

even produce a code that is executable on a real robot

Ozobot. The application is written in Java so that it

can run on various platforms.

Figure 7: The user interface of OzoMorph that allows its

user to create and solve an instance of Connected Colored

MAPF.

The user interface is shown in Figure 7. First,

the user can specify the dimensions of the underly-

ing grid graph. We are working with grid graphs as

it is the most common in MAPF instances and the

easiest to apply to real robots. The user also has

the option to print the deﬁned graph on paper. Then,

choosing a color and clicking on vertices on the left-

hand side, the initial locations for that color (team) are

chosen. Similarly, by clicking on the vertices on the

right-hand side, the target locations are chosen. The

software automatically checks whether the instance

is consistent. By clicking on the Morph button, the

software creates an instance for the solver and runs

the solver. We use the solver described in the previ-

ous section; however, the users can provide their own

solver given that the input and output formats are the

same.

Figure 8: Simulation window of the OzoMorph software.

If the instance has a solution, the simulation win-

dow (see Figure 8) pops up. The simulation aims to

show the actual continuous positions of real robots

that would execute the given instance instead of

the sequence of vertices produced by the theoretical

model (Bart

ak et al., 2019). The properties (moving

and turning speeds) can be adjusted in the main user

interface of OzoMorph. Videos of the instance de-

ﬁned in Figure 7 solved in both Connected Colored

and Colored way can be found at a repository together

with the source codes and experimental data from the

previous section

If desired, the found plan can be exported into a

ﬁle that can be uploaded into Ozobot robots (Evol-

lve, Inc., 2018). An instance of Connected Colored

MAPF executed on Ozobots is shown in Figure 9.

The size of the grid in the simulation window is ad-

justable, so the execution of the robots can be done on

a ﬂat screen or tablet rather than on a printed grid to

verify that the simulation corresponds to reality.

https://github.com/svancaj/Connected-colored-MAPF

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Figure 9: An instance of Connected Colored MAPF run on

robots Ozobot (Evollve, Inc., 2018).

7 DISCUSSION AND FUTURE

WORK

The additional requirement for connectivity makes

the Colored MAPF problem signiﬁcantly more chal-

lenging for designing efﬁcient declarative models.

Our formulation is proper on relatively small in-

stances, which we demonstrated with real physical

robots Ozobots. The solution time for large instances

becomes prohibitively long, which suggests substan-

tial room for improvement of the model. Another op-

tion of potential future research is to develop both op-

timal and inexact imperative algorithms. The adap-

tation of the existing CBM algorithm that solves

Colored MAPF to solve Connected Colored MAPF

seems complicated, as repairing conﬂicts arising from

unsatisﬁed connectivity within a group would lead to

substantial branching factors.

There is a natural generalization of Connected

Colored MAPF, in which the agents do not need to

be adjacent to each other but need to keep within a

vicinity given by a deﬁned distance. In our case, we

considered this distance to be 1, but this can be gen-

eralized to any value.

ACKNOWLEDGMENTS

This research is supported by the Czech-USA Co-

operative Scientiﬁc Research Project LTAUSA19072

and by the project 19-02183S of the Czech Science

Foundation.

REFERENCES

Bart

ak, R.,

Svancara, J.,

Skopkov

a, V., Nohejl, D., and

Krasi

cenko, I. (2019). Multi-agent path ﬁnding on real

robots. AI Communications, 32(3):175–189.

Bart

ak, R., Ivanov

a, M., and

Svancara, J. (2021). Colored

multi-agent path ﬁnding: Solving approaches. The In-

ternational FLAIRS Conference Proceedings, 34.

Evollve, Inc. (2018). Ozobot — Robots to code, create, and

connect with. Accessed Nov. 20, 2020.

Ivanov

a, M., Surynek, P., and Nguyen, D. T. N. (2018).

Maintaining ad-hoc communication network in area

protection scenarios with adversarial agents. In

Brawner, K. and Rus, V., editors, Proceedings of

the Thirty-First International Florida Artiﬁcial Intel-

ligence Research Society Conference, FLAIRS 2018,

Melbourne, Florida, USA. May 21-23 2018, pages

348–353. AAAI Press.

Li, L., Sheng, W., and Hu, C. (2020). Research on forma-

tion keeping of multi-rotor UAVs based on improved

virtual structure method. Journal of Physics: Confer-

ence Series, 1631:012106.

Ma, H. and Koenig, S. (2016). Optimal target assignment

and path ﬁnding for teams of agents. In Proceedings

of the 2016 International Conference on Autonomous

Agents & Multiagent Systems, Singapore, May 9-13,

2016, pages 1144–1152.

Ma, H., Yang, J., Cohen, L., Kumar, T. K. S., and Koenig, S.

(2017). Feasibility study: Moving non-homogeneous

teams in congested video game environments. In

Magerko, B. and Rowe, J. P., editors, Proceedings of

the Thirteenth AAAI Conference on Artiﬁcial Intelli-

gence and Interactive Digital Entertainment (AIIDE-

17), October 5-9, 2017, Snowbird, Little Cottonwood

Canyon, Utah, USA, pages 270–272. AAAI Press.

Queffelec, A., Sankur, O., and Schwarzentruber, F. (2020).

Conﬂict-Based Search for Connected Multi-Agent

Path Finding. arXiv e-prints, page arXiv:2006.03280.

Ratner, D. and Warmuth, M. K. (1990). Nxn puzzle

and related relocation problem. J. Symb. Comput.,

10(2):111–138.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.

(2012). Conﬂict-based search for optimal multi-agent

path ﬁnding. In Hoffmann, J. and Selman, B., editors,

Proceedings of the Twenty-Sixth AAAI Conference on

Artiﬁcial Intelligence, July 22-26, 2012, Toronto, On-

tario, Canada. AAAI Press.

Solovey, K. and Halperin, D. (2014). k-color multi-robot

motion planning. I. J. Robotics Res., 33(1):82–97.

Stern, R., Sturtevant, N. R., Felner, A., Koenig, S., Ma, H.,

Walker, T. T., Li, J., Atzmon, D., Cohen, L., Kumar,

T. K. S., Bart

ak, R., and Boyarski, E. (2019). Multi-

agent pathﬁnding: Deﬁnitions, variants, and bench-

marks. In Proceedings of the Twelfth International

Symposium on Combinatorial Search, SOCS 2019,

Napa, California, 16-17 July 2019, pages 151–159.

Surynek, P. (2010). An optimization variant of multi-robot

path planning is intractable. In Proceedings of the

Twenty-Fourth AAAI Conference on Artiﬁcial Intelli-

gence, AAAI 2010, Atlanta, Georgia, USA, July 11-15,

2010.

Yu, J. and LaValle, S. M. (2012). Multi-agent path plan-

ning and network ﬂow. In Algorithmic Foundations

of Robotics X - Proceedings of the Tenth Workshop on

the Algorithmic Foundations of Robotics, WAFR 2012,

2012, pages 157–173.

Coordinated Collision-free Movement of Groups of Agents