Optimal 1-Request Insertion for the Pickup and Delivery Problem with

Transfers and Time Horizon

Jos

e-L. Figueroa, Alain Quilliot, H

ene Toussaint and Annegret Wagler

LIMOS INP, Universit

e Clermont Auvergne, France

ﬁ

Keywords:

Pickup and Delivery Problem with Transfers, 1-Request Exact Insertion, Constrained Shortest Path, Constraint

Propagation, Time Expanded Networks.

Abstract:

In this paper, we deal with a subproblem of the Pickup and Delivery Problem with Transfers (PDPT) where

a ﬁnite set of transportation requests has been assigned to a homogeneous ﬂeet of limited capacity vehicles,

while satisfying some constraints imposed by a set of pre-scheduled tours. Then, a new transportation request

appears, and we also have to serve it. For that, we can modify the current tours by performing a ﬁnite sequence

of changes allowing to pick up, transport, transfer or deliver this new request. The resulting tours must serve

all the requests and satisfy the original constraints, but within a given time horizon. To solve this problem, we

present an empirical Dijkstra algorithm that computes tentative solutions whose consistence is checked through

constraint propagation, and an exact algorithm which is an adaptation of the well-known A* algorithm for

robot planning, that performs an exhaustive search in a tree of partial solutions and reduces the combinatorial

explosion by pruning some unfeasible/redundant tree nodes. We conclude by comparing the performance of

both algorithms.

1 INTRODUCTION

In this ﬁrst section, we give an informal description

of the problem that we are going to treat in this paper,

which is about the way that one additional request can

be inserted into the current solution of a pickup and

delivery instance, and we survey brieﬂy some litera-

ture related to this problem which we call 1-Request

Insertion PDPT. This problem will be presented for-

mally in Section 2. In Section 3, we will describe two

algorithms for dealing with it. Finally, in Section 4

we compare the quality of the found solutions and the

performance of both algorithms over several data sets

of pseudorandom instances.

A standard Pick up and Delivery Problem (PDP)

most often involves a ﬁnite set V of identical vehi-

cles with capacity c, which must be scheduled in or-

der to perform a set of Pick and Delivery tasks inside

some network G. Time windows may be involved,

but, in most cases, a time horizon [0,T

max

] is imposed

for the whole schedule. Vehicles must meet a set R

of requests: a request r ∈ R consists in an origin o

, a

destination d

and a load ℓ

, and r has to be served

by exactly one vehicle. In the PDP with transfers

(PDPT), a request may be served by several vehicles,

in the sense that load ℓ

may start from origin o

with

some vehicle v

, and next shift to some vehicle v

some relay vertex x, and so on, until reaching destina-

tion d

into some vehicle v

. Depending on the con-

text, a transfer from v

to v

may take different forms:

one may impose either vehicles to meet (strong syn-

chronization constraint) at relay vertex x, or only for-

bid vehicle v

from leaving x before the arrival of v

(weak synchronization constraint). In other words, a

weak synchronization constraint implies that v

and

are obliged to meet only when v

arrives ﬁrst to the

relay vertex x.

In this last case, a convenient way to model PDPT

is through the use of time expanded networks (see, for

example, (Gouveia et al., 2019) and (Bsaybes et al.,

2019)). We construct a network (see Figure 1) whose

vertex set consists of a dummy source vertex s, a

dummy sink vertex p, and a copy (x,t

) of every ver-

tex x of G and for any time value t

∈ [0,T

max

] (note

that in practice, we usually consider only a ﬁnite set

of relevant time values t

). We represent any feasible

move along an arc of G, from a vertex x to a vertex y

between time t

and time t

+δ (where δ ≥ 0), by some

arc



(x,t

),(y,t

+ δ)



. If x = y then such a move be-

comes a waiting move. Then, we represent vehicles

circulation by a unique integral ﬂow vector F indexed

over the set A of the expanded network arcs, and re-

Figueroa, J., Quilliot, A., Toussaint, H. and Wagler, A.

Optimal 1-Request Insertion for the Pickup and Delivery Problem with Transfers and Time Horizon.

DOI: 10.5220/0010787000003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 17-27

ISBN: 978-989-758-548-7; ISSN: 2184-4372

quests circulation comes as a multi-commodity ﬂow

{ f

: A → R,r ∈ R}, such that for every arc a ∈ A of

the expanded network, the sum Σ

r∈R

(a) is less than

or equal to the value F

of vector F on arc a.

(y, 0)

(x, 0) (x, 1) (x, t

)

(y, t

+δ)

(x, T

max

)

(y, T

max

)

Figure 1: A Time Expanded Network.

Still, resulting models are not very well-ﬁtted to

numerical handling, both because of their size and be-

cause PDP tends to arise in dynamic contexts, with re-

quests not completely known in advance, and which

must be managed in a ﬂexible way. It comes that most

often, PDPT is handled in a heuristic way and a com-

mon strategy is to rely on an insertion (or build &

destroy) approach: requests are successively inserted

into some current schedule, and possibly removed and

reinserted in order to improve the related cost.

According to this paradigm, the key issue be-

comes the related insertion process. In case no trans-

fer is allowed, the insertion is trivial in the sense that

it can be performed through enumeration. It is not

the case when transfers are allowed. As a matter of

fact, inserting a request r becomes then signiﬁcantly

more difﬁcult than simply searching for some path

from origin o

to destination d

inside some ad hoc

network (or even time expanded network) because

synchronization (strong or weak) constraints require-

ments tend to impact the whole current schedule.

So the purpose of this work is to thoroughly study

the one request insertion problem that occurs as a

part of the Pickup and Delivery Problem with Trans-

fers (with time horizon), and that we will denote by

1-Request Insertion PDPT. We are ﬁrst going to solve

it in an exact way, without imposing any restriction

neither on the number of transfers nor on the charac-

teristics on the transfer parameters, through a combi-

nation of constraint propagation techniques and an A*

like algorithm.

Let us recall that A* algorithm (see (Nilsson,

1980) or (Dechter and Pearl, 1985)) is an artiﬁcial in-

telligence oriented version of Dijkstra’s algorithm for

shortest path, designed in order to deal with huge net-

works whose nodes represent the possible states of a

system.

Next, in order to ﬁt with the purpose of practical

use in realistic dynamic contexts, we shall describe a

heuristic algorithm, which also relies on the use of Di-

jkstra’s algorithm, augmented with a “closure” mech-

anism.

Finally, we shall observe the behavior of the algo-

rithms once we impose some common sense restric-

tions to the way that transfers can be performed.

Related Works

Surveys for Pickup and delivery problems can be

found, for example, in (Berbeglia et al., 2007),

(Berbeglia et al., 2010), and (Ho et al., 2018).

The notion of PDP with transfers was introduced

by (Laporte and Mitrovi

c-Mini

c, 2006) in the so-

called Pickup and Delivery Problem with Time Win-

dows and Transshipment, which is a PDP character-

ized for the presence of transshipment points, where

the vehicles can drop some objects or split their loads

to allow other vehicles to pick them up later.

An exact method for some PDPT was presented

by (Contardo et al., 2010). In their paper, the authors

construct a complex mixed-integer linear program-

ming formulation, and they conﬁrm that it works cor-

rectly by solving an example instance with a method

based on Benders decomposition.

In (Bouros et al., 2011), the authors address the

dynamic PDPT and propose a graph-based formu-

lation that treats each request independently as a

constrained shortest path problem. They compare

this approach against a relatively conventional local

search algorithm based on insertion heuristics and

tabu search, and conclude that their method is sig-

niﬁcantly faster with the inconvenience that solutions

quality is marginally lower.

The computational complexity of checking the

feasibility for the insertion of one request in the PDPT

was studied by (Lehu

e et al., 2013). In this work,

the authors determined that if we perform some pre-

processing of the current state of a PDPT network,

we can test the feasibility of insertions in constant

time, and the complexity to update the preprocessed

information after insertion/deletion of one request is

quadratic in the size of the network.

Above-mentioned contributions (Bouros et al.,

2011) and (Lehu

e et al., 2013) are the closest ones

to our contribution. Both rely on the construction of

auxiliary graphs, which represent the current state of

vehicle paths together with some speciﬁc constraints

related to transfers. Still (Bouros et al., 2011) does

not care of time’s feasibility (i.e. time windows) nor

the impact of restrictions imposed to the transfers.

At the opposite, (Lehu

e et al., 2013), is a theoret-

ical contribution which focuses on the complexity of

testing the feasibility of an insertion (with one trans-

fer at most), after some preprocessing that allows the

management of slack time variables. Our contribu-

tion lays in between: while we also rely on precom-

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

putation of length path values, we relax the restric-

tions on the transfer vertices, impose no restriction on

the number of transfers, and propose both exact and

heuristic algorithms for the computation of a best fea-

sible insertion for a given request. Then we analyze

through numerical experiments, the impact on both

the behavior of the algorithms and the nature of the

solutions.

2 FORMAL MODEL

We ﬁrst suppose that we are provided with a ﬁnite set

X of “points” representing physical locations, given

together with:

• A distance function d : X × X → R

, such that

for any x,y ∈ X, the value d(x,y) means the time

required for a vehicle to move in X from x to y

according to a shortest path strategy.

• A function µ : X × X → X is going to be involved

in order to determine “relay vertices”, that means

the points where two vehicles v

, v

will meet in

order to perform some transfer. Intuitively, for

any (x

) ∈ X × X, the element u = µ(x

)

corresponds to a place that is more or less at

the same distance from x to y and minimizes the

sum d(x

,u) + d(u,x

). For example, if X con-

tains points from a Euclidean space, we can deﬁne

u = µ(x

) as an element in X with minimal dis-

tance to the midpoint of the segment from x

to x

2.1 PDPT Problem

A PDPT instance consists of a ﬁnite set of points X

together with the two functions d : X × X → R

and

µ : X × X → X that we have just deﬁned, a ﬁnite set

of vehicles V with a homogeneous capacity c ∈ R

, a

time horizon [0,T

max

], and a ﬁnite set R ⊂ X ×X × R

of requests r = (o

,ℓ

). The point o

is the origin

of r, the point d

is the destination of r, and ℓ

is the

load of r. Also, each vehicle v ∈ V has assigned two

distinguished points: one starting depot point D

∈ X

and one ending depot point D

∈ X. Figure 2 shows

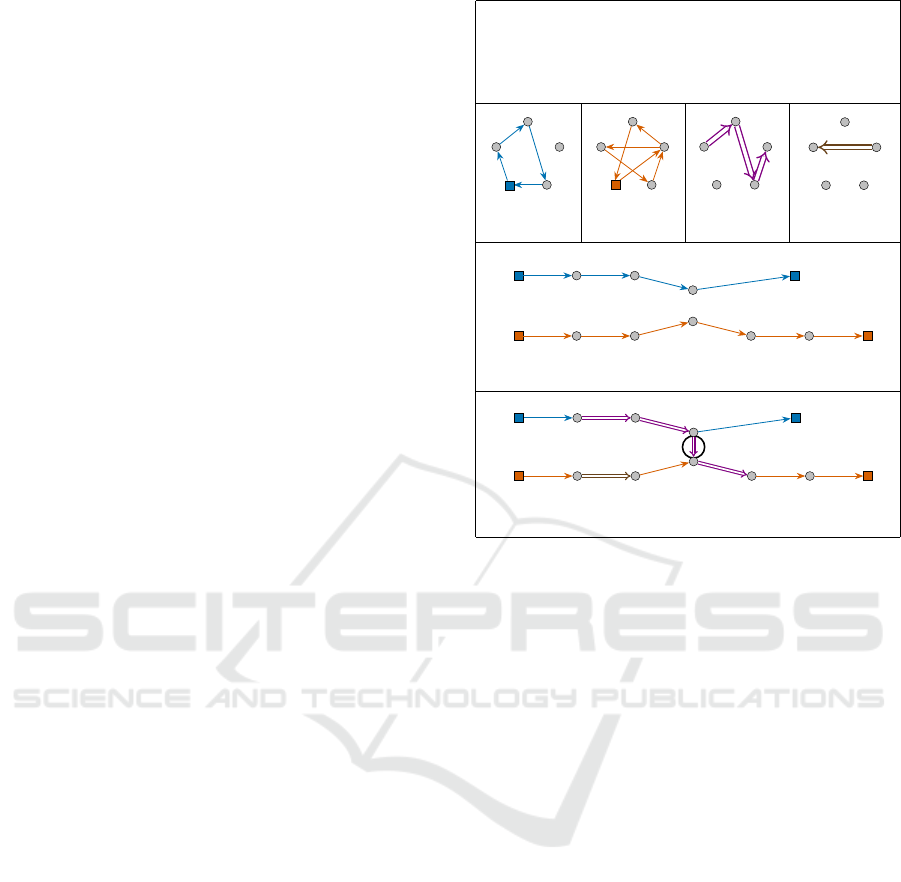
an example of PDPT instance.

Now we will brieﬂy describe the PDPT. We are

not going to deal here with the whole problem, how-

ever, for completeness reasons it is important to give

at least some intuition and clarify some details in-

volved. This will set the stage later to present our

formal model for the insertion subproblem.

The PDPT consists in ﬁnding a schedule for the

vehicles ﬂeet, allowing to transport the requests from

their origins to their destinations. Vehicles capac-

A B C D E













A 0 1 2 2 1

B 1 0 1 2 2

C 2 1 0 1 2

D 2 2 1 0 1

E 1 2 2 1 0

A B C D E













A A A B E A

B A B B C A

C B B C C D

D E C C D D

E A A D D E

(a) (b)

(e)

(c)

(d)

X ={A,B,C,D, E}

V = {v, w}, c = 10, T

max

= 15,

= D

= A



=(o

=B,d

=D,`

=5),

=(o

=D,d

=B,`

=2)



Figure 2: An example of PDPT instance. (a) The set X =

{A,B,C, D, E} of points. (b) A symmetric matrix whose

entries deﬁne the distance function d. (c) A matrix deﬁning

the function µ. (d) The set of vehicles V = {v, w}, the capac-

ity c, the upper limit of the time horizon [0, T

max

], and the

starting and ending depot points of vehicles. (e) The set R

of requests consisting of r

= (B, D, 5) and r

= (D, B, 2).

ity must be respected at any moment, however, vehi-

cles are allowed to transfer requests to other vehicles

through a weak synchronization mechanism. This is,

if a vehicle v is transferring a load ℓ

to another vehi-

cle w at a relay vertex z, and the receiving vehicle w

arrives ﬁrst to z, then w has to wait for the arriving of v

with the load ℓ

. The time duration for traversing ev-

ery path in the schedule (considering waiting times),

must be within the given time horizon.

Depending on the context, there can be several

ways to deﬁne the cost of such schedules. Here, we

put the focus on the point of view of the users, and

consider that the cost of a schedule is the sum of

the distances traversed by the requests, and then we

aim to ﬁnd a minimal cost schedule. This choice is

not particularly restrictive because the algorithms that

we will present can be adapted to handle other types

of costs (e.g. total mileage covered by the vehicles/

requests, or the time when they achieve their respec-

tive trips).

In the following subsection, we proceed to de-

scribe our formal model for the insertion problem in-

volved in the PDPT.

2.2 Formal Description of a PDPT

Feasible Solution

Let G

be the directed graph whose set of vertices is

X and whose set of arcs is {(x,y) ∈ X × X, x ̸= y}.

According to the above deﬁnition of a PDPT in-

stance, we deﬁne a solution (Γ,Π) for the PDPT in-

stance, which we also call a PDPT schedule as

• A collection Γ =



Γ(v), v ∈ V



of paths on G

where Γ(v) = (x

,.. .,x

|Γ(v)|−1

) is the path fol-

lowed by vehicle v in G

Optimal 1-Request Insertion for the Pickup and Delivery Problem with Transfers and Time Horizon

• A collection Π =



Π(r), r ∈ R



, of paths on G

The directed path Π(r) = (y

,.. .,y

|Π(r)|−1

) is

the path followed by load ℓ

when moving from

its origin o

to its destination d

. Points y

belong

to the set



: v ∈ V,0 ≤ i ≤ |Γ(v)| − 1



and we

may distinguish two classes of moves for request

– If y

and y

q+1

are related to two consecutive

vertices of path Γ(v), then they have to be con-

secutive in Π(r) and so we talk about vehicle

move inside vehicle v.

– If y

= x

and y

q+1

= x

are related to two dis-

tinct paths Γ(v) and Γ(w), then they refer to the

same vertex in X, and so we talk about transfer

move from vehicle v to vehicle w.

Denoting by X(Γ) the set



(v,i) : v ∈ V, 0 ≤ i ≤

|Γ(v)|−1



, we see that such a solution induces an ori-

ented graph structure G(Γ,Π) on the vertex set X(Γ),

with arc set A(Γ,Π) deﬁned as follows

• With any v ∈ V and any 0 ≤ i ≤ |Γ(v)| − 1, we

associate a vehicle arc e = ((v, i), (v,i + 1)), with

length d

(e) = d(x

i+1

). Following paths Π(r)

allows the computation of the load ℓ

of this arc,

which is the sum of loads ℓ

for requests r which

move through this arc. Of course ℓ

does not have

to exceed the capacity c (Load Constraints).

• With any r ∈ R and 1 ≤ q ≤ |Π(r)| − 1, such that

moving from y

= x

to y

q+1

= x

corresponds

to a transfer move from vehicle v to vehicle w,

we associate a transfer arc e = ((v,i), (w, j)), with

length d

(e) = d(y

q+1

) = 0 (because in this

case, y

and y

q+1

correspond to the same place).

We denote by A

′

the set of those transfer arcs.

Figure 3 shows an example of solution (Γ,Π) for

the instance deﬁned in Figure 2, and the associated

graph G(Γ,Π).

Feasibility of (Γ,Π): As we just told, (Γ, Π) must

meet the above Load Constraints. Also it must satisfy

time consistency constraints deﬁned as follows:

• With any vertex (v, i) in the graph G(Γ,Π) we as-

sociate a time value t

which represents the ear-

liest time when vehicle v may leave vertex (v, i).

Then we see that

– For any vehicle arc ((v,i), (v,i + 1)), we have

that t

i+1

≥ t

+ d(x

i+1

– Weak synchronization implies that t

≥ t

for

any transfer arc ((v, i),(w, j)).

They can be summarized as: (E1: Time Consistency

Constraints)

• For any arc e = ((v, i),(w, j)) in the graph

G(Γ,Π), we have that t

≥ t

+ d

(e).

(a)

A E

(b)

(c)

(d) (e)

(f)

(g)

arc in A

(w,0) (w,1) (w,2) (w,4) (w, 5) (w,6)

(v,0) (v,1) (v, 2)

(w,3)

Π(r

)

Γ =

Γ(v) = (x

= A, x

= B, x

= C, x

= E, x

= A),

Γ(w) = (x

= A, x

= D, x

= B, x

= E, x

= D, x

= C, x

= A)

 

Π =

Π(r

) = (y

= x

, y

= x

, y

= x

, y

= x

, y

= x

Π(r

) = (y

= x

, y

= x

)

 

A E

Γ(v)

Γ(w)

Π(r

)

(v,0) (v,1) (v, 2)

(w,0) (w,1) (w,2)

(w,3)

(w,4) (w,5) (w,6)

Γ(v)

Γ(w)

= o

= y

= o

= y

Π(r

)

Π(r

)

(v,3)

(v,4)

Figure 3: (a) An example of solution for the instance de-

ﬁned in Figure 2. (b)-(e) Subgraphs of G

edge-induced

by the paths Γ(v), Γ(w), Π(r

) and Π(r

), respectively.

(f) The paths on the directed graph G(Γ,Π) correspond-

ing to the directed paths Γ(v) and Γ(w) of G

. (g) The

directed graph G(Γ, Π). We have also depicted with dou-

ble arrows the directed paths corresponding to Π(r

) and

Π(r

). Numbers indicate positive loads traversing through

arcs in A(Γ,Π) \ A

′

• Due to the time horizon [0,T

max

], for any (v,i) we

have that 0 ≤ t

≤ T

max

They impose that: (E2: No Cycles Constraint)

• Arc set A(Γ, Π) does not contain any cycle.

If (Γ,Π) satisﬁes those constraints, we can asso-

ciate, with every (v,i) in G(Γ, Π), some time windows

[Min

, Max

] related to variables t

, constrained by

(E1).

Cost of a Solution (Γ, Π): As we said in 2.1, we

are going to deﬁne the cost of a solution as the sum of

the distances traversed by the requests.

2.3 The 1-Request Insertion PDPT

Model

Those preliminaries allow us to deﬁne in a formal way

the 1-Request Insertion PDPT, about the insertion of

a new request into a current feasible PDPT schedule

(Γ,Π). So we start from such a feasible schedule

(Γ,Π), and from an additional request r = (o

,ℓ

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

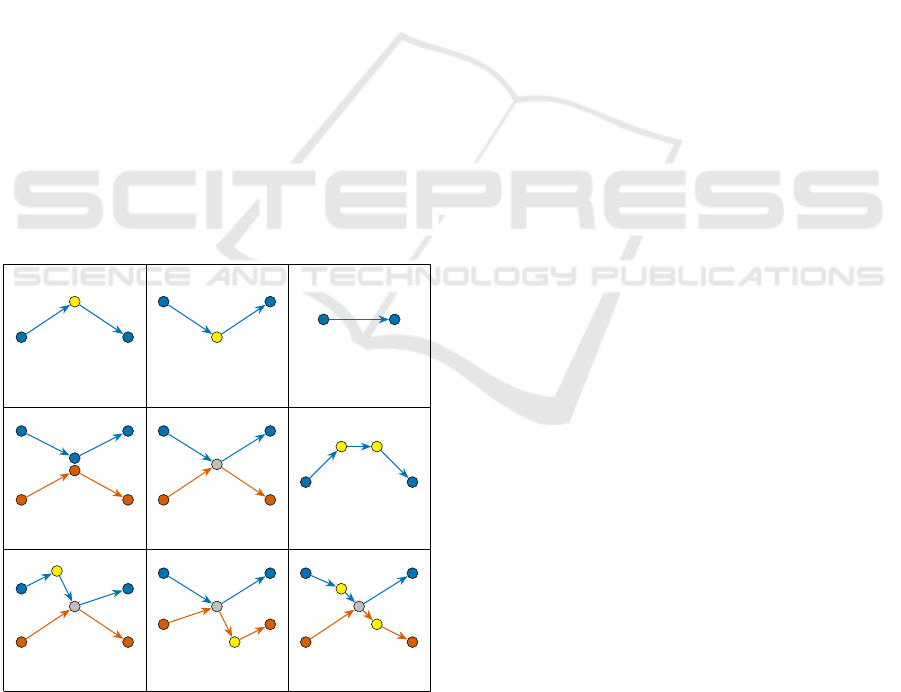
Intuitively, inserting request r means building a suit-

able sequence of the following ﬁve types of moves:

(1) Start from o

and enter into some path Γ(v) at the

level of some vertex (v, i + 1), and so imposing

vehicle v to make a deviation between (v,i) and

(v,i + 1). Such a move will be performed once as

the initial move (See Figure 4 (a)).

(2) Leave some path Γ(w) at the level of some vertex

(v,i) in order to reach d

, and so impose a vehicle

to make a deviation between (v, i) and (v,i + 1).

Such a move will be performed once as the ﬁnal

move (See Figure 4 (b)).

(3) Keep on inside vehicle v, while moving from

some (v,i) to its successor (v, i + 1). Such a type

of move will be possibly performed several times

(See Figure 4 (c)).

(4) Move from vehicle v to vehicle w while using

some arc ((v, i),(w, j)) of A

′

and some shared

point x

= x

. Such a type of move will be possi-

bly performed several times (See Figure 4 (d)).

(5) Move from vehicle v to vehicle w while getting

out of v while running between some vertex (v, i)

and its successor and entering into w at the level

of some vertex (w, j), and while w is moving from

(w, j − 1) to its successor. Such a move will be

possibly performed several times (See Figure 4

(e)).

(v, i) (v, i + 1)

(v, i − 1)

(v, i)

(v, i + 1)

= x

(w, j − 1)

(w, j)

(w, j + 1)

(v, i) (v, i + 1)

(w, j − 1) (w, j)

(v, i) (v, i + 1)

(w, j − 1) (w, j)

(v, i) (v, i + 1)

(w, j − 1) (w, j)

(v, i) (v,i + 1)

(w, j − 1) (w, j)

(a) (b) (c)

(d) (e) (f)

(g) (h) (i)

Figure 4: Types of vehicle’s moves for transporting a re-

quest r = (o

,ℓ

Remark: For simplicity, in this work we are go-

ing to restrict our study to these 5 types of moves.

However, we note that it is also possible to combine:

(6) moves of types (1) and (2), in such a way that r

is inserted through a simple deviation of a vehicle

v between two successive vertices of Γ(v). This

is, while traversing Γ(v), vehicle v performs a de-

viation from (v,i) to transport the load ℓ

from o

directly to d

, and then v returns to its original path

at the level of vertex (v,i + 1) (See Figure 4 (f)).

(7) movements of types (1) and (5), in such a way

that, request r starts from o

in a vehicle v and

then is transferred directly to another vehicle w at

some relay vertex z, while v is moving from (v, i)

to (v,i +1), and while w is moving from (w, j − 1)

to (w, j) (See Figure 4 (g)).

(8) movements of types (2) and (5), in such a way

that r leaves some path Γ(v) (at the level of a ver-

tex (v,i)), to be transferred from v to w at some

relay vertex z. Then r reaches d

directly from z

in vehicle w. The ﬁrst part of this process happens

while v is moving from (v, i) to (v, i + 1), and the

second one while w is moving from (w, j − 1) to

(w, j) (See Figure 4 (h)).

(9) moves of types (1), (2) and (5), in such a way that

r starts from o

in a vehicle v, then r is transferred

directly to another vehicle w at some relay vertex

z, and ﬁnally r reaches d

directly from z inside

vehicle w, while v is moving from (v, i) to (v, i +

1), and while w is moving from (w, j − 1) to (w, j)

(See Figure 4 (i)).

While moves of types 1, 2, 3, and 4 are easy to

understand, we need to better explain the moves of

type 5. Clearly, a move of type 5 involves some relay

vertex z: both vehicle v and w are going to perform a

deviation through z, vehicle v will drop load ℓ

in z,

and vehicle w will take it as soon as possible. In order

to identify z, we use function µ and we take:

z = µ



µ(x

),µ(x

i+1

j−1

)



. (E3)

Please notice that (E3) restricts our freedom to

choose the relay vertex, and so it has to be considered

as a hypothesis of the model.

Now, given a PDPT schedule (Γ,Π) and one ad-

ditional request r, we deﬁne the following graph

H(Γ,Π,r)

• Vertices of H(Γ,Π,r) are vertices of G(Γ, Π),

plus two vertices o

and d

• Arcs of H(Γ,Π, r) are

– In-arcs: they have the form e = (o

,(v,i)), with

0 ≤ i < |Γ(v)| − 1, length d

(e) = d(o

i+1

and such that ℓ

+ ℓ

≤ c.

– Out-arcs: with the form e = ((w, j), d

), with

1 ≤ j ≤ |Γ(w)| − 1, length d

(e) = d(x

and such that ℓ

+ ℓ

≤ c.

Optimal 1-Request Insertion for the Pickup and Delivery Problem with Transfers and Time Horizon

– Vehicle-arcs: arcs e = ((v, i),(v,i + 1)) in

G(Γ,Π), with length d

(e) = d

i+1

), and

such that ℓ

+ ℓ

≤ c.

– A

′

-arcs: the arcs e = ((v,i),(w, j)) ∈ A

′

, with

length d

(e) = d

(e) = 0.

– Transfer-arcs: with the form e = ((v,i), (w, j)),

length d

(e) = d(x

,z) + d(z,x

) where z is

deﬁned as in (E3). These arcs are such that

ℓ

+ ℓ

≤ c and ℓ

j−1

+ ℓ

≤ c.

Let π be a path from o

to d

in H(Γ,Π,r). Note

that π may be interpreted as a sequence of moves

of types (1, ... ,5) allowing to transport the request

r from o

to d

If t

denotes the time when vehicle v leaves vertex

(v,i), then every in-arc, out-arc and transfer-arc of π

is going to impose additional constraints, to be added

to constraints (E1)

• An in-arc



,(v,i)



imposes one additional con-

straint t

i+1

≥ t

+ d(x

) + d(o

i+1

). (E4)

• An out-arc



(w, j), d



imposes one additional

constraint t

j+1

≥ t

+d(x

)+d(d

j+1

). (E5)

• A transfer-arc



(v,i),(w, j)



imposes three addi-

tional constraints (here, z is taken as in (E3) )

1. t

i+1

≥ t

+ d(x

,z) + d(z, x

i+1

). (E6.1)

(Deviation for vehicle v)

2. t

≥ t

j−1

+ d(x

j−1

,z) + d(z, x

). (E6.2)

(Deviation for vehicle w)

3. t

≥ t

+ d(x

,z) + d(z, x

). (E6.3)

(Weak Synchronization)











(E6)

Then a path π in H(Γ,Π, r) is going to be time-

consistent if it allows the existence of time vectors

= (t

,.. .,t

|Γ(v)|−1

), v ∈ V , which meet constraints

(E1) and additional constraints (E4, E5, E6) related to

π. Notice that if π is given, checking the time con-

sistence of π can be performed through a simple con-

straint propagation process.

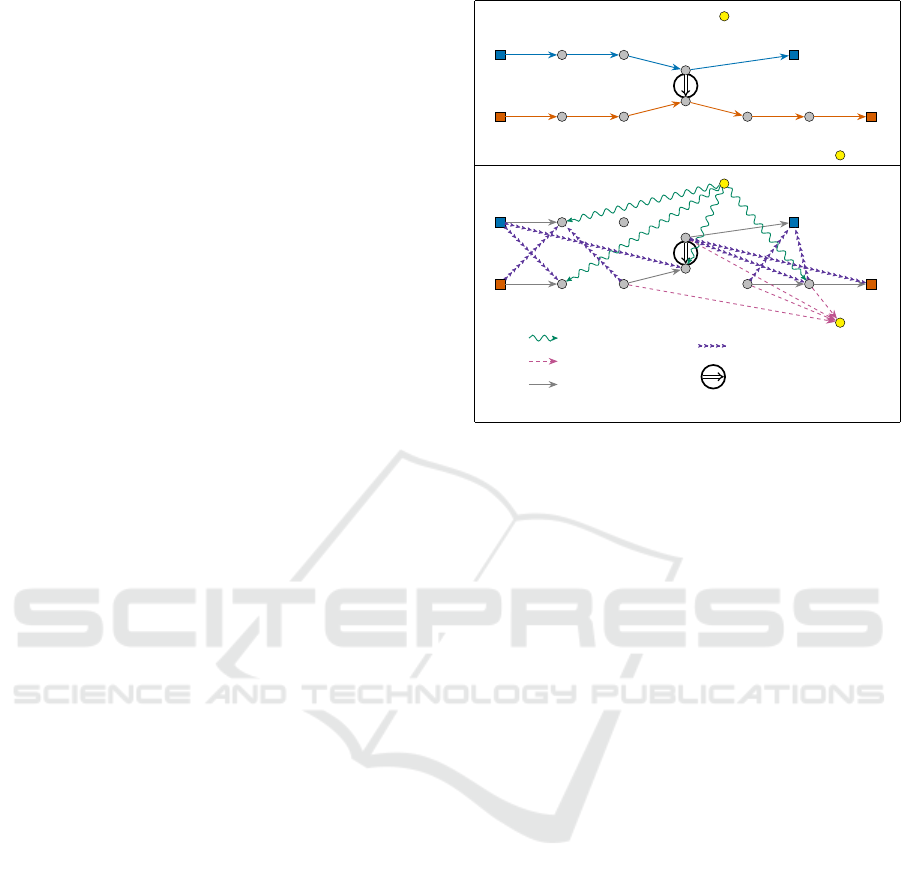
Figure 5 shows an example of construction of the

graph H(Γ,Π, r) from a PDPT schedule (Γ,Π) and

one additional request r = (o

,ℓ

The 1-Request Insertion PDPT can be summa-

rized as follows:

1-Request Insertion PDPT: Given a PDPT sched-

ule (Γ, Π) and one request r = (o

,ℓ

), compute

a shortest (in the sense of length function d

) time-

consistent path π from o

to d

in the graph H(Γ,Π,r).

Legend

In-Arc

Out-Arc

Vehicle-Arc

(a)

(b)

(v,0) (v,1) (v,2)

(v,3)

(v,4)

(w,0) (w,1)

(w,3)

(w,4) (w,5) (w,6)

0 2

0 0

arc in A

(v,0) (v,1)

(v,2)

(v,3)

(v,4)

(w,0) (w,1)

(w,2)

(w,3)

(w,4)

(w,5)

(w,6)

Transfer-arc

-arc

(w,2)

Figure 5: Deriving graph H(Γ,Π,r) from the PDPT sched-

ule (Γ, Π) corresponding to Figure 3, and one additional

request r = (o

= D, d

= B, ℓ

= 9). (a) The graph G(Γ,Π)

and the additional request r = (o

,ℓ

). (b) The graph

H(Γ,Π, r). Notice that the capacity requirement forbids

some vehicle-arcs of G(Γ,Π).

3 ALGORITHMS

We are ﬁrst going to work (in 3.1 and 3.2) con-

sidering all the transfers-arcs with enough capac-

ity to handle the given request. However, we can

notice that the number of transfer-arcs increases as

∑

v,w∈V,v̸=w

|Γ(v)| · |Γ(w)|, and then we shall adapt

in 3.3 the algorithms described in 3.1 and 3.2 in

such a way that they consider only well-ﬁtted eligi-

ble transfer-arcs.

3.1 An Exact A*-like Algorithm

The A* algorithm was introduced in (Hart et al.,

1968) as an adaptation of Dijkstra’s algorithm in order

to deal with search path in very large state networks,

like those that one may have to handle in robotics. It

is our case here since at any time during the resolution

process, we shall deal not only with a current vertex

(v,i) of the graph H(Γ,Π, r), but also with time win-

dows related to vectors t

, v ∈ V .

We suppose that we are provided, as consequence

of some constraint propagation preprocess, with

• For any pair



(v,i),(w, j)



of vertices of G(Γ,Π),

the length Φ



(v,i),(w, j)



of a longest path

from (v,i) to (w, j) in the graph G(Γ,Π); vari-

ables t

and t

are constrained by t

≥ t



(v,i),(w, j)



ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

• For any vertex u in the graph H(Γ,Π, r), the

length ω

of a shortest path from u to destination

vertex d

in H(Γ,Π,r). In case u ∈ V (Γ(v)) for

some v ∈ V we are also provided with a time win-

dow [Min

, Max

] derived from constraints (E1).

Then, as in standard A*, we perform a Breadth

First Search (BFS) process, driven by some list LS of

states, according to the algorithmic scheme described

in Algorithm 1.

Algorithm 1: A* 1-PDPT algorithmic scheme.

input : Graph H(Γ,Π,r), request

r = (o

,ℓ

output: A time-consistent (o

, d

)-path with

best cost or a failure message.

1 LS ←{(o

,0,0, 0, Nil)} [Initialize LS] ;

2 Success ← False ;

3 while LS Not empty and Not Success do

4 (u,λ, δ, ω, S )←Head(LS) [Current state];

5 Remove Head(LS) from LS;

6 if u ̸= d

then

7 Expand current state (u, λ, δ, ω, S ) (I1);

8 else

9 Success ← True;

10 end

11 end

12 if Not Success then

13 Print “No path found”;

14 else

return: Path retrieved from current state.

15 end

State’s Deﬁnition: Every element s of LS is a

state, that means a 5-uple s = (u,λ,δ, ω,S ), where

• u is a vertex of the graph H(Γ,Π, r).

• λ ∈ R is the value of the current length of the path

π(u) from origin o

to u which has been achieved.

• δ ∈ R is a lower bound on the arriving time to u. In

case u = (v,i) ∈ V (Γ(V )) for some v ∈ V , we will

write δ

instead of δ; feasibility of state s implies

that Min

≤ δ

≤ Max

• ω ∈ R is the sum ω

+λ, that is a lower bound for

any path π which would extend current path π(u);

LS remains sorted in increasing order according to

ω values.

• S is a list of transfer-arcs



(v,i),(w, j)



which

have been involved in π(u), together with lower

bounds δ

,δ

i+1

,δ

j−1

,δ

, on t

, t

i+1

, t

j−1

, and t

respectively.

Domination Rule: Let π(u) and π(u

′

) be time-

consistent paths retrieved from two different states

s = (u,λ,δ, ω,S ) and s

′

= (u

′

,λ

′

,δ

′

,ω

′

), respec-

tively. For any v ∈ V , let t

, t

′

, respectively, be

the lexicographically smallest time vectors (meeting

E1 and E4-E6) related to π(u) and π(u

′

). Let V

{v ∈ V : V (π(u)) ∩ V (Γ

) ̸=

0} and V

′

= {v ∈ V :

V (π(u

′

)) ∩V (Γ

) ̸=

0}.

We say that the state s dominates the state s

′

if u =

′

, λ < λ

′

, δ ≤ δ

′

, V

⊆ V

′

and for all v ∈ V

∩V

′

have that max{ j : (v, j) ∈ V (π(u))} ≤ max{ j : (v, j) ∈

V (π(u

′

))}, and for every v ∈ V we have that t

≤ t

′

This rule can be used to remove some redundant states

when we are exploring the BFS tree of states.

Expand Mechanism (I1) : Expanding state s =

(u,λ,δ, ω,S ), means consider the arcs e = (u, v) of

H(Γ,Π,r) with tail u and, for any such an arc, com-

puting resulting state s

′

= (v,λ

′

= λ + d(e), δ

′

,ω

′

+ ω

′

), where δ

′

and S

′

derive from δ and S ,

respectively, after propagation of constraints E1, E4,

E5, E6. If the path π(v), retrieved from s

′

, is time-

consistent and s

′

is not dominated by any state in LS,

then we insert s

′

into LS and possibly remove from

LS any state dominated by s

′

. Note that, the con-

straint propagation mechanism which yields δ

′

and S

′

is induced by the transfer-arcs which have been used

in order to reach u, and which are contained into the

list S .

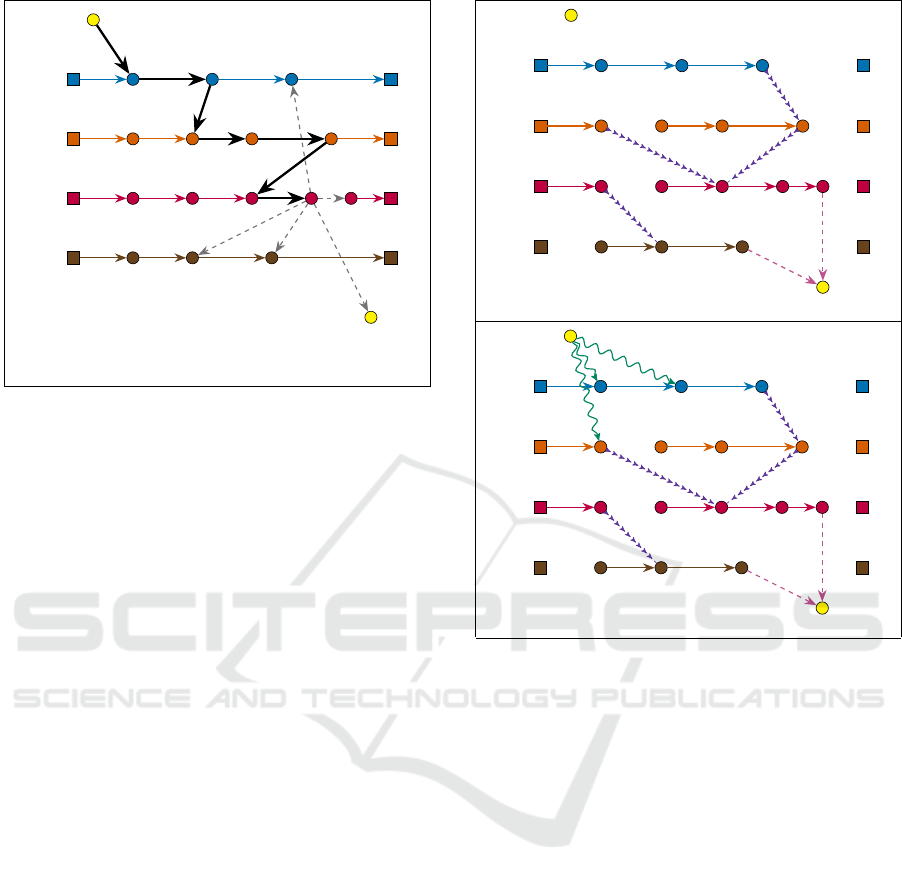
Figure 6 contains a representation of a state from

a list LS and gives some intuition about the expanding

mechanism (I1).

Now, we note that

• The A* algorithm performs an exhaustive search

on the tree of states corresponding to time-

consistent paths.

• A path which is not time-consistent cannot be ex-

tended into a time-consistent one.

• The domination rule removes only redundant

states.

Hence we have the following.

Proposition 1. Above A* 1-PDPT solves 1-Request

Insertion PDPT in an exact way (taking into account

the (E3) hypothesis), in a time which does not exceed



∆

(H(Γ,Π,r))



m+1

· Size(H(Γ,Π, r))



where

∆

(H(Γ,Π,r)) is the maximum outdegree of a vertex

in H(Γ,Π,r), and where m is the maximum number

of arcs in a path π(u) retrieved from a state s = (u, λ,

δ, ω, S ) that was involved in LS.

Remark: The complexity of the 1-Request Inser-

tion PDPT remains an issue. Still, in the case we

impose a small constant (e.g. 3 or 5) as a bound on

the number of transfer-arcs of the constructed paths,

a simple counting argument can show that it becomes

time-polynomial.

Optimal 1-Request Insertion for the Pickup and Delivery Problem with Transfers and Time Horizon

,0) (v

,1) (v

,2) (v

,3) (v

,4)

,0) (v

,1)

,2)

,3) (v

,4) (v

,5)

,0) (v

,1) (v

,2)

,3)

,4)

,0) (v

,1) (v

,2)

,3)

,4)

,5)(v

,6)

S =





,2),(v

,2)





,4),(v

,3)



, δ



Γ(v

)

Γ(v

)

Γ(v

)

Γ(v

)

Figure 6: Representation of a particular state s =



u =

,4),λ, δ, ω, S



from a list LS. Bold arcs indicate the cor-

responding path π(u) from origin o

to u which has been

achieved. The information stored in S allow us to determine

which vertices are involved in path π(u), and also give us

estimations for the arriving times to those vertices. Dashed

arcs allow extending the current path π(u), so they corre-

spond to new states that can be derived from s via the ex-

panding mechanism (I1).

3.2 A Practical Dijkstra-like Algorithm

Since our problem is likely to arise in a dynamic con-

text, we must try to propose approaches which are less

time consuming than the previous one. In order to

do it, we ﬁx some integer parameter m > 0, and next

for every (v,i) with v ∈ V , i ∈ {0,. . .,|Γ(v)| − 1}, we

compute shortest paths π(v,i), in the graph H(Γ,Π, r),

from vertex (v,i) to destination d

, while using Di-

jkstra’s algorithm (see Figure 7 (a)). We denote by

ω(v,i) the length of π(v,i). Notice that such computa-

tions are involved in A* 1-PDPT algorithm, in order

to provide us with ω values involved in Algorithm 1.

Then, we close those computed paths π(v,i)

(see Figure 7 (b)) to obtain (o

, d

)-paths π

∗

(v,i) =

,(v,i)) + π(v, i) (i.e. we create a path from o

to d

whose ﬁrst arc is the in-arc (o

,(v,i)) and

the remaining arcs are the ones of path π(v, i)).

For each constructed path π

∗

(v,i), we compute the

value d



,(v,i)



+ ω(v,i), and then we select the m

paths π

∗

),.. .,π

∗

) with the lowest values



,(v,i)



+ ω(v, i). Finally, we check for every se-

lected path π

∗

), 1 ≤ k ≤ m, the consistence of

the additional constraints induced by the in-arc, the

out-arc and the transfer-arcs of π

∗

), and we keep

the path π

∗

which meets this consistence test and

which is related to the smallest d



,(v,i)



+ ω(v, i)

value. This process is summarized in Algorithm 2.

(a)

(b)

,0)

,1)

,2) (v

,3) (v

,4)

,0)

,1)

,2) (v

,3) (v

,4) (v

,5)

,0) (v

,1) (v

,2)

,3)

,4) (v

,5)(v

,6)

,0) (v

,1)

,2)

,3) (v

,4)

Γ(v

)

Γ(v

)

Γ(v

)

Γ(v

)

,0)

,1)

,2) (v

,3) (v

,4)

,0)

,1)

,2) (v

,3) (v

,4) (v

,5)

,0) (v

,1) (v

,2)

,3)

,4) (v

,5)(v

,6)

,0) (v

,1)

,2)

,3) (v

,4)

Γ(v

)

Γ(v

)

Γ(v

)

Γ(v

)

Figure 7: Deriving solutions from a Dijkstra’s shortest path

computation. (a) A subgraph Ψ of a graph H(Γ,Π, r) ob-

tained by Dijkstra’s algorithm while computing a shortest

path π(v, i) from every vehicle vertex (v, i) to d

. (b) Graph

Ψ is extended by adding some in-arcs from H(Γ, Π, r)

(wavy arrows). Every path from o

to d

in the resulting

graph gives rise to a solution for handling request r, and the

time feasibility of such a solution is then checked through

constraint propagation.

3.3 Controlling Transfer-arcs Number

As mentioned at the beginning of Section 3, the num-

ber of transfer-arcs is an issue, since most arcs of

H(Γ,Π,r) are transfer-arcs, while at the end, the best

time-consistent paths usually contain very few of such

arcs. In order to deal with the number of transfer-arcs

issue, we impose to transfer-arcs some eligibility re-

quirement, which depends on a threshold parameter

ε ≥ 0.

ε-eligibility of a transfer-arc



(v,i),(w, j)



: we

say that transfer-arc e =



(v,i),(w, j)



is ε-eligible if

d(x

) ≤ ε and the intersection of time windows

[Min

+d(e), Max

+d(e)] and [Min

, Max

] is non-

empty.

By ﬁxing ε and imposing transfer-arcs in both

A* 1-PDPT and Dijkstra 1-PDPT algorithms to be ε-

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

Algorithm 2: Dijkstra 1-PDPT.

input : Directed graph H(Γ,Π,r) together

with the distance function d

output: A time-consistent (o

, d

)-path π

∗

, or

a failure message.

1 π

∗

← Nil ;

2 For every (v,i) with v ∈ V and

i ∈ {0,. . .,|Γ(v)| − 1}, compute through

Dijkstra’s algorithm, shortest paths π(v, i)

from (v,i) to destination d

, together with

their corresponding length ω(v,i) in the

graph H(Γ,Π,r);

3 Close every path π(v,i) computed in step 2 by

adding the corresponding in-arc



,(v,i)



and select the m resulting paths

∗

),.. .,π

∗

) with best



,(v,i)



+ ω(v,i) values;

4 For every path π

∗

),1 ≤ k ≤ m selected

in step 3, test its time-consistence (through

constraint propagation) and keep as π

∗

the

time-consistent path π

∗

) with best



,(v

)



+ ω(v

) value;

5 if π

∗

= Nil then

6 Print “No path found”;

7 else

return: π

∗

8 end

eligible, we become able to control running times. As

Section 4 will show, this control is not usually going

to induce any signiﬁcant loss in solutions quality.

4 NUMERICAL EXPERIMENTS

Purpose: We have been performing experiments to

1. Analyze the performance of both A* 1-PDPT and

Dijkstra 1-PDPT algorithms from the point of

view of running costs and, in the case of Dijkstra

1-PDPT, of gap to optimality.

2. Evaluate the impact of the ε-eligibility on those

algorithms.

3. Estimate the potential interest of transfers,

through both the number of transfer-arcs involved

in an optimal path π, and the gain induced by

those arcs.

Technical Context: Points of X are randomly

generated on an integral grid with size n × n, distance

function dist is the upper rounding of the Euclidean

distance (indicated by E) or the Manhattan distance

(indicated by M). The upper limit of the time hori-

zon [0,T

max

] is indicated by T

max

and is generated as

a linear function of n, also we will consider a ﬁxed

capacity c = 10.

While designing the paths, we follow several

strategies

• Strategy F: For every v, w ∈ V we that D

= D

. This is, all of the vehicles start and end

their paths in a common depot point. Paths Γ(v)

are generated in a pseudorandom way.

• Strategy C: For every v,w ∈ V we have D

= D

and D

= D

. This is, every vehicle start and end

its path in a same depot point, but different ve-

hicles can have distinct depot points. Paths Γ(v)

are generated by following some linear or circular

orientation.

• Strategy O: Every vehicle v starts its path in a de-

pot point D

and ends its path in a depot point

(possibly different of D

); furthermore, differ-

ent vehicles can have distinct origin depot points

and different destination depot points. Paths Γ(v)

are generated by following some linear or circular

orientation.

The designed paths have around ten arcs on av-

erage, and the arcs loads are generated in a uni-

form random way by choosing elements from the set

{1,2,. .., 10}.

Another important path feature is the mean ratio

ρ =

∑

v∈V

max

Length(Γ(v))

which gives us an approximate idea about the difﬁ-

culty of an instance.

The sets of arcs A

′

are created in the following

way: for every (v,i) ∈ Γ(v) and every (w, j) ∈ Γ(w),

such that x

= x

and



(w, j), (v, i)



/∈ A

′

we create an

arc



(v,i),(w, j)



and we add it to A

′

with a probability

of 0.5 if the resulting graph is acyclic and does not

imply exceeding the time horizon.

Requests are also generated in a random way, for

this, we have selected two different points o

and d

from X, and a random load value ℓ

from the set

{1,2,3, 4,5}.

Instances: We have that, an instance is sum-

marized by the following characteristics: the side’s

length n of the squared integer grid, the number |X|

of points, the distance function dist (E= Euclidean, or

M= Manhattan), the number of vehicles |V |, the num-

ber |A

′

| of arcs in A

′

, the upper limit T

max

of the time

horizon, the mean ratio ρ, the path generation strategy

St, and a request (o

,ℓ

) ∈ X × X × {1, 2,3,4, 5}.

Instances which are going to be used here are sum-

marized by the rows of Table 1. Note that every in-

stance with an odd index k (i.e. the number in the Id

column), shares all of its elements, up to the distance

Optimal 1-Request Insertion for the Pickup and Delivery Problem with Transfers and Time Horizon

function and the mean ratio ρ, with the instance with

index k + 1.

Table 1: Instance characteristics.

Id n |X | dist |V | |A

′

| T

max

ρ St ℓ

1 25 80 M 3 1 75 1.75 F 3

2 25 80 E 3 1 75 1.90 F 3

3 30 90 M 4 1 90 1.20 C 2

4 30 90 E 4 1 90 1.34 C 2

5 35 100 M 5 2 105 1.43 O 4

6 35 100 E 5 2 105 1.82 O 4

7 40 110 M 6 4 120 1.31 F 5

8 40 110 E 6 4 120 1.53 F 5

9 45 120 M 7 3 135 1.22 C 2

10 45 120 E 7 3 135 1.41 C 2

11 50 130 M 8 4 150 1.41 O 4

12 50 130 E 8 4 150 1.64 O 4

13 55 140 M 9 5 165 1.26 F 3

14 55 140 E 9 5 165 1.52 F 3

15 60 150 M 10 3 180 1.18 C 1

16 60 150 E 10 3 180 1.38 C 1

17 65 160 M 11 6 195 1.41 O 4

18 65 160 E 11 6 195 1.67 O 4

19 70 170 M 12 7 210 1.26 F 3

20 70 170 E 12 7 210 1.49 F 3

Outputs: For any instance we compute

1. The value VA* computed by A* 1-PDPT, to-

gether with related running time TA* in seconds

and without including preprocessing, the number

TrA* of transfer arcs of the solution.

2. The value VD computed by Dijkstra 1-PDPT, to-

gether with related running time TD in seconds

and without including preprocessing, the number

TrD of transfer arcs of the solution.

3. The value NTr of the solution obtained through

enumeration when forbidding the transfer-arcs.

4. The same values VA*(ε), TA*(ε), TrA*(ε),

VD(ε), TD(ε), TrD(ε) obtained while taking the

eligibility threshold ε as

Experiments were performed on a computer

with a 2.3GHz Intel Core i5 processor and 16GB

1333MHz RAM. The implementations were built in

C++ 11 by using the Apple Clang compiler. Note that

some values are not available due to the absence of

solutions.

Results and Comments: We note that the associ-

ated running times of both algorithms are all less than

two seconds. However, these results must be taken

carefully: although it is well known that Dijkstra’s

algorithm has a time complexity that is always poly-

nomially bounded on the size of the input, for the A*

1-PDPT this is not the case; as a matter of fact, we

have found manually an unfeasible instance with 12

vehicles, similar to instances 19 and 20 of Table 1,

where the A* 1-PDPT needs to explore many states

and takes around 9 seconds to assert infeasibility.

More extensive computational studies should con-

ﬁrm the exponential nature of the A* 1-PDPT com-

plexity (here, we mean complexity in the worst case),

and the polynomial complexities that can be achieved

by limiting the number of transfer-arcs of the con-

structed paths.

Regarding the solutions quality we can verify that,

most of the time Dijkstra’s algorithm has found an

optimal or close to optimal solution. However, for

instances 11 and 19 of Table 2, and instances 9, 11,

and 13 of Table 3 it was not able to ﬁnd any feasible

solution.

Table 2: Behavior of A* 1-PDPT and Dijkstra 1-PDPT

without any eligibility restriction.

Id VA* TA* TrA* VD TD TrD NTr

1 52 0.0022 0 52 0.0006 0 52

2 43 0.0106 0 43 0.0006 0 43

3 24 0.0036 0 24 0.0008 0 24

4 21 0.0034 0 21 0.0008 0 21

5 60 0.0157 1 60 0.0007 1 66

6 52 0.0397 1 52 0.0007 1 55

7 50 0.1937 0 50 0.0011 0 50

8 41 0.2045 0 41 0.0011 0 41

9 83 0.0488 1 83 0.0013 1 130

10 64 0.1753 0 64 0.0013 0 64

11 93 0.0195 0 0.0019 93

12 81 0.1108 0 81 0.0012 0 81

13 92 0.0028 1 92 0.0024 1 110

14 69 1.3397 1 69 0.0015 1 74

15 68 0.1309 0 68 0.0019 0 68

16 57 0.3576 0 57 0.0019 0 57

17 78 0.1754 0 78 0.0016 0 78

18 70 0.4568 0 72 0.0017 0 70

19 99 0.0340 2 0.0017

20 72 0.3319 1 72 0.0018 1 107

5 CONCLUSION

We have been analyzing transfer mechanisms for PDP

problems, while proposing exact and heuristic algo-

rithms for the 1-Request Insertion PDPT case related

to the insertion process. We could check that, while

allowing transfers is often useful, the number of trans-

fers is usually small (see the 4th and the 7th columns

of Table 2 and Table 3), and that it is important to

a priori ﬁlter transfer moves which are allowed. As

open issues, remain the case of strong synchroniza-

tion (both vehicles which perform a transfer must

meet at the time when the transfer occurs), and the

problem of ensuring the robustness of a schedule in

case some vehicle involved in an exchange is late.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

Table 3: Behavior of A* 1-PDPT and Dijkstra 1-PDPT with

eligibility threshold ε =

Id VA*(ε) TA*(ε) TrA*(ε) VD(ε) TD(ε) TrD(ε) NTr

1 52 0.0010 0 52 0.0006 0 52

2 43 0.0057 0 43 0.0008 0 43

3 24 0.0019 0 24 0.0007 0 24

4 21 0.0029 0 21 0.0008 0 21

5 62 0.0024 1 62 0.0006 1 66

6 52 0.0108 1 52 0.0010 1 55

7 50 0.1508 0 50 0.0011 0 50

8 41 0.1841 0 41 0.0011 0 41

9 100 0.0130 2 0.0013 130

10 64 0.0927 0 64 0.0013 0 64

11 93 0.0045 0 0.0016 93

12 81 0.0433 0 81 0.0012 0 81

13 98 0.0135 1 0.0021 110

14 69 0.6883 1 69 0.0015 1 74

15 68 0.0321 0 68 0.0019 0 68

16 57 0.1828 0 57 0.0018 0 57

17 78 0.1052 0 78 0.0026 0 78

18 70 0.2830 0 72 0.0016 0 70

19 0.0291 0.0025

20 87 0.0061 4 87 0.0025 4 107

ACKNOWLEDGEMENTS

This work was supported by the French National

Research Agency in the Framework of the LabEx

IMobS3 and the R

egion Auvergne-Rhone-Alpes.

REFERENCES

Berbeglia, G., Cordeau, J.-F., Gribkovskaia, I., and Laporte,

G. (2007). Static pickup and delivery problems: A

classiﬁcation scheme and survey. TOP: An Ofﬁcial

Journal of the Spanish Society of Statistics and Oper-

ations Research, 15:1–31.

Berbeglia, G., Cordeau, J.-F., and Laporte, G. (2010). Dy-

namic pickup and delivery problems. European Jour-

nal of Operational Research, 202(1):8–15.

Bouros, P., Dalamagas, T., Sacharidis, D., and Sellis, T.

(2011). Dynamic pickup and delivery with transfers.

Proceedings of the 12th International Symposium on

Spatial and Temporal Databases.

Bsaybes, S., Quilliot, A., and Wagler, A. K. (2019). Fleet

management for autonomous vehicles using ﬂows in

time-expanded networks. TOP.

Contardo, C., Cort

es, C., and Matamala, M. (2010). The

pickup and delivery problem with transfers: Formula-

tion and a branch-and-cut solution method. European

Journal of Operational Research, 200:711–724.

Dechter, R. and Pearl, J. (1985). Generalized best-ﬁrst

search strategies and the optimality of a*. J. ACM,

32:505–536.

Gouveia, L., Leitner, M., and Ruthmair, M. (2019). Lay-

ered graph approaches for combinatorial optimiza-

tion problems. Computers & Operations Research,

102:22–38.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE Transactions on Systems Science and

Cybernetics, SSC-4(2):100–107.

Ho, S. C., Kuo, Y.-H., Leung, J. M., Petering, M., Szeto,

W., and Tou, T. W. (2018). A survey of dial-a-

ride problems: Literature review and recent develop-

ments. Transportation Research Part B: Methodolog-

ical, 111:395–421.

Laporte, G. and Mitrovi

c-Mini

c, S. (2006). The pickup and

delivery problem with time windows and transship-

ment. INFOR: Information Systems and Operational

Research, 44(3):217–227.

Lehu

e, F., Masson, R., and P

eton, O. (2013). Efﬁcient

feasibility testing for request insertion in the pickup

and delivery problem with transfers. Operations Re-

search Letters, 41(3):211–215.

Nilsson, N. J. (1980). Principles of Artiﬁcial Intelligence.

Morgan Kaufmann, San Francisco (CA).

Optimal 1-Request Insertion for the Pickup and Delivery Problem with Transfers and Time Horizon