ERQA: Edge-restoration Quality Assessment for Video Super-Resolution

Anastasia Kirillova

, Eugene Lyapustin

, Anastasia Antsiferova

and Dmitry Vatolin

Lomonosov Moscow State University, Moscow, Russia

Keywords:

Video Super-Resolution, Quality Assessment, Video Restoration.

Abstract:

Despite the growing popularity of video super-resolution (VSR), there is still no good way to assess the quality

of the restored details in upscaled frames. Some VSR methods may produce the wrong digit or an entirely

different face. Whether a method’s results are trustworthy depends on how well it restores truthful details.

Image super-resolution can use natural distributions to produce a high-resolution image that is only somewhat

similar to the real one. VSR enables exploration of additional information in neighboring frames to restore

details from the original scene. The ERQA metric, which we propose in this paper, aims to estimate a model’s

ability to restore real details using VSR. On the assumption that edges are signiﬁcant for detail and character

recognition, we chose edge ﬁdelity as the foundation for this metric. Experimental validation of our work is

based on the MSU Video Super-Resolution Benchmark, which includes the most difﬁcult patterns for detail

restoration and veriﬁes the ﬁdelity of details from the original frame. Code for the proposed metric is publicly

available at https://github.com/msu-video-group/ERQA.

1 INTRODUCTION

As a fundamental image- and video-processing task,

super-resolution remains a popular research topic.

It has a wide range of applications, from low-

complexity encoding

to old-ﬁlm restoration and

medical-image enhancement. Trends in quality as-

sessment of upscaled videos and images are favoring

estimation of statistical naturalness in combination

with ﬁdelity. But restoration ﬁdelity is much more

important than statistical naturalness for some tasks:

small-object recognition (e.g., license-plate numbers)

in CCTV recordings, text recognition, and medical-

image reconstruction.

With the development of deep-learning-based ap-

proaches, many super-resolution models produce vi-

sually natural frames but lose important details. For

example, the rightmost image in Figure 2, upscaled by

TDAN (Tian et al., 2020), is perceptually better than

the leftmost one, upscaled by RRN-10L (Isobe et al.,

2020), but the shape of the shiny thread in the left-

most image is closer to ground truth (GT, center). Oc-

casionally, such models can even change the context

https://orcid.org/0000-0002-0799-3135

https://orcid.org/0000-0002-2515-9478

https://orcid.org/0000-0002-1272-5135

https://orcid.org/0000-0002-8893-9340

https://www.lcevc.org/

Figure 1: Example of changing context in an upscaled

video: two characters from source frame (GT, leftmost) mix

to yield a new one during video upscaling.

Figure 2: Example of upscaled images that vary in detail-

restoration quality. The rightmost image is visually more

natural, but the shape of the details in the leftmost image is

closer to the original.

in an image by, for example, producing an incorrect

number, character, or even human face without de-

creasing traditional-metric values. In Figure 1, Real-

ESRGAN (Wang et al., 2021) mixed two letters from

low-resolution images to form a completely different

letter (center). In Figure 4, RPBN (Haris et al., 2019)

added horizontal lines to the bottom-right character,

but all three models score the same on traditional met-

Kirillova, A., Lyapustin, E., Antsiferova, A. and Vatolin, D.

ERQA: Edge-restoration Quality Assessment for Video Super-Resolution.

DOI: 10.5220/0010780900003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

315-322

ISBN: 978-989-758-555-5; ISSN: 2184-4321

315

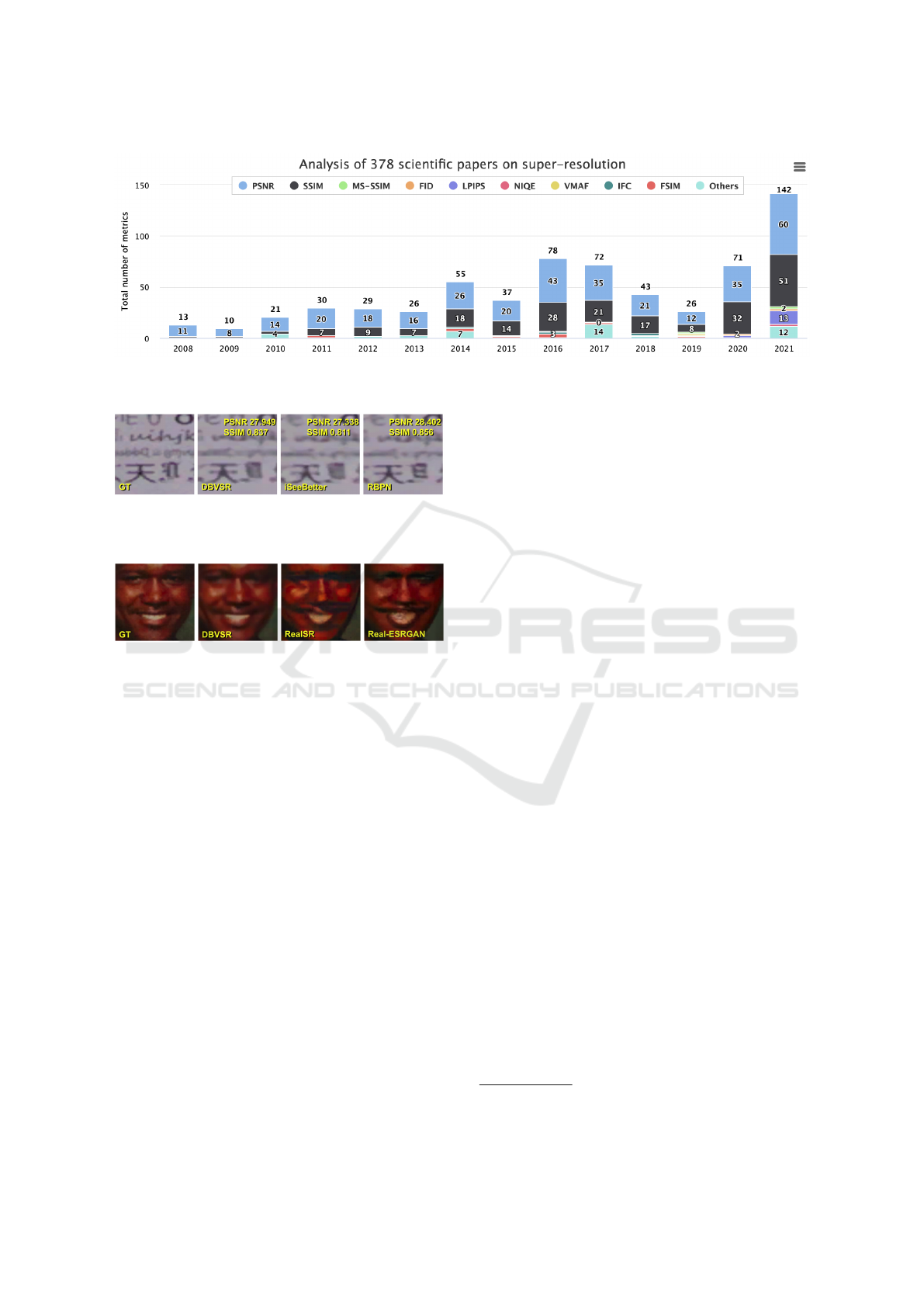
Figure 3: Metrics for estimating super-resolution quality cited in papers proposing new methods, by year. PSNR and SSIM

(Wang et al., 2004) are the most popular; LPIPS (Zhang et al., 2018) saw wide use in 2020 and 2021.

Figure 4: Example of changing context in an upscaled

video: RBPN (Haris et al., 2019) has changed a character

in the rightmost image.

Figure 5: Example of changing context in an upscaled

video: unnatural faces are the result here, differing consid-

erably from the source one (GT, leftmost).

rics. In Figure 5, Real-ESRGAN (Wang et al., 2021)

and RealSR (Ji et al., 2020) produced unnatural faces

that greatly differ from the source one.

The examples in Figures 1–2, 4–5 demonstrate

that assessment of detail-restoration quality for image

and video super-resolution is difﬁcult. The best way

to estimate restoration ﬁdelity is to conduct a subjec-

tive comparison; it’s the most precise approach but is

time consuming and expensive. Another way involves

reference quality metrics. Traditional similarity met-

rics such as PSNR and SSIM (Wang et al., 2004) are

often used to evaluate super-resolution models, but

they yield poor results and are unstable when deal-

ing with shifts and other common super-resolution ar-

tifacts. LPIPS (Zhang et al., 2018) is increasingly

popular for this task, but it originally aimed to as-

sess perceptual similarity rather than ﬁdelity. The new

DISTS (Ding et al., 2020a) metric is an improvement

on LPIPS, but it also focuses on perceptual similarity.

Our research focuses on analyzing super-

resolution algorithms, particularly their restoration

ﬁdelity. When we started working on a benchmark

for video super-resolution

, including a test for

restoration-quality assessment, we discovered that

existing metrics work ﬁne for other tests (restoration

naturalness and beauty) but have a low correlation

with subjective detail-quality estimation. In this

paper, therefore, we introduce a new method for

evaluating information ﬁdelity. Experiments reveal

that our metric outperforms other super-resolution

quality metrics in assessing detail restoration.

The main contributions of our work are the fol-

lowing:

1. A video-super-resolution benchmark based on a

new dataset containing the most difﬁcult patterns

for detail restoration.

2. A subjective comparison examining the ﬁdelity of

details from the original frame, instead of tradi-

tional statistical naturalness and beauty.

3. A new metric for assessing the detail-restoration

quality of video super-resolution.

2 RELATED WORK

PSNR and SSIM (Wang et al., 2004) are common

metrics for assessing super-resolution quality. We an-

alyzed 378 papers that propose super-resolution meth-

ods and found that since 2008, PSNR and SSIM have

remained the most popular metrics. But both have

been shown to exhibit a low correlation with subjec-

tive scores. LPIPS (Zhang et al., 2018) has grown in

popularity over the last two years; other metrics re-

main less popular (Figure 3).

Several full-reference metrics for assessing super-

resolution visual quality have emerged. (Wan et al.,

2018) used four features (gradient magnitude, phase

congruency, anisotropy, and directionality complex-

https://videoprocessing.ai/benchmarks/video-super-

resolution.html

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

316

Table 1: A comparison of datasets using for testing super-resolution quality assessment approaches.

Dataset # references # SR images # SR algorithms Subjective type

C. Ma et al.’s (Ma et al., 2017) 30 1620 9 MOS

QADS (Zhou et al., 2019) 20 980 21 Pairwise comparison

SupER (K

ohler et al., 2019) 14 3024 20 Pairwise comparison

SRIJ (Beron et al., 2020) 32 608 7 MOS

SISRSet (Shi et al., 2019) 15 360 8 MOS

ECCV (Yang et al., 2014) 10 540 6 MOS

SRID (Wang et al., 2017) 20 480 8 MOS

ity) to calculate the perceptual structure measure-

ment (PFSM) in both the upscaled and original high-

resolution frames. Similarity function applied to PF-

SMs showed more-consistent results than previous

approaches with regard to visual perception on their

dataset. (Zhou et al., 2021) calculated structural ﬁ-

delity and statistical naturalness, fused these coefﬁ-

cients into a weighted sum, and achieved good cor-

relation on the QADS image database(Zhou et al.,

2019).

Another popular approach is to extract structure or

texture features from LR and upscaled (SR) images,

compare them separately, and fuse the resulting simi-

larity indices (Yeganeh et al., 2015; Fang et al., 2019).

Metrics based on this idea achieve a Spearman rank

correlation coefﬁcient (SRCC) coefﬁcient of 0.69 to

0.85 on various datasets. (Yang et al., 2019) trained

a regression model using statistical features extracted

from LR and SR images, obtaining a correlation simi-

lar to that of other top metrics on the dataset from (Ma

et al., 2017). (Shi et al., 2019) proposed another ap-

proach for reduced-reference assessment that uses the

visual-content-prediction model to measure the struc-

ture of the reference and SR images. This method out-

performs previous ones on the SISRSet dataset (Shi

et al., 2019).

A number of no-reference metrics are also used

for video super-resolution. (Ma et al., 2017) trains

regression models on statistical features extracted

from upscaled frames, achieving high value of SRCC

on their dataset. (Zhang et al., 2021) proposed a

no-reference metric, based on features extracted us-

ing a pretrained neural network—VGGNet. (Wang

et al., 2018) trained SVM using extracted features

and obtained results similar to those of other met-

rics. (Greeshma and Bindu, 2020) proposed the

SRQC metric, which estimates structure changes and

quality-aware features. This metric exhibits good re-

sults, but they consider only a few images and four

SR methods for the test dataset.

Edges have a strong inﬂuence on the human vi-

sual system. Furthermore, edge ﬁdelity is a base cri-

terion for assessing detail-restoration quality. Sev-

eral methods thus consider edge features as the ba-

sis for quality assessment. Some calculate edge fea-

tures, including number, length, direction, strength,

contrast, and width, and compare them using the sim-

ilarity measure to estimate image or video quality (At-

tar et al., 2016; Ni et al., 2017). Nevertheless, these

metrics achieve on their datasets almost the same cor-

relation as traditional PSNR and SSIM. In (Xue and

Mou, 2011), the authors detected edges in both ref-

erence and distorted images and compared them by

calculating recall. (Chen et al., 2011) used histogram

analysis for edge comparison. These metrics deliver

a slightly greater correlation than PSNR and SSIM.

Liu et al. (Liu et al., 2019) proposed using the F1

score to evaluate edge ﬁdelity, but they declined to

conduct a comparison with other metrics and kept

their code under wraps. Our method is based on the

same edge-comparison idea, but it’s robust for small

local and global edge shifts, which appear during

super-resolution but are unessential for detail recogni-

tion. It yielded much better results than other quality-

assessment approaches.

A number of datasets are used for testing super-

resolution quality assessment (Table 1), but not for

detail restoration, because they lack difﬁcult patterns

for that task as in Figure 6 (text, numbers, QR codes,

faces, complex textures). Therefore, we built a dataset

for assessing super-resolution quality that includes the

most challenging content for detail restoration.

Summarizing the above analysis, few metrics

aim to assess and compare detail-restoration quality.

Some that use edge features have emerged, but no one

uses them for super-resolution, which involves pecu-

liar artifacts. Therefore, it’s important to obtain an

objective metric that correlates highly with human es-

timation of detail-restoration quality and that allows

comparison of super-resolution models, not only for

naturalness but also for information ﬁdelity.

ERQA: Edge-restoration Quality Assessment for Video Super-Resolution

317

3 PROPOSED METHOD

3.1 Dataset

To analyze a VSR model’s ability to restore real de-

tails, we built a test stand containing patterns that are

difﬁcult for video restoration (Figure 6).

To calculate metrics for particular content types

and to verify how a model works with different inputs,

we divide each output frame into parts by detecting

crosses:

Part 1. “Board” includes a few small objects and pho-

tos of human faces

. Our goal is to obtain re-

sults for the model operating on textures with

small details. The striped fabric and balls of

yarn may produce a Moire pattern (Figure 7).

Restoration of human faces is important for

video surveillance.

Part 2. “QR” comprises multiple QR codes of differ-

ing sizes; the aim is to ﬁnd the size of the

smallest recognizable one in the model’s out-

put frame. A low-resolution frame may blend

QR-code patterns, so models may have difﬁ-

culty restoring them.

Part 3. “Text” includes two kinds: handwritten and

typed. Packing all these difﬁcult elements into

the training dataset is a challenge, so they are

each new to the model as it attempts to restore

them.

Part 4. “Metal paper” contains foil that was vigor-

ously crumpled. It’s an interesting example

because of the reﬂections, which change peri-

odically between frames.

Part 5. “Color lines” is a printed image with numer-

ous thin color stripes. This image is difﬁ-

cult because thin lines of similar colors end

up mixing in low-resolution frames.

Part 6. “License-plate numbers” consists of a set of

car license plates of varying sizes from differ-

ent countries

. This content is important for

video surveillance and dashcam development.

Part 7. “Noise” includes difﬁcult noise patterns.

Models cannot restore real ground-truth

noise, and each one produces a unique pattern.

Part 8. “Mira” contains a resolution test chart with

patterns that are difﬁcult to restore: a set of

straight and curved lines of differing thick-

nesses and directions.

Photos were generated by https://

thispersondoesnotexist.com/

The license-plate numbers are generated randomly and

printed on paper.

Figure 6: Test stand for the proposed VSR benchmark. The

size of the stand 3, 456 × 3, 456 pixels in a source video and

1, 280 × 1, 280 pixels in a ground truth video.

Figure 7: Example of a Moire pattern on the “Board.” There

is a zoomed result on the right.

We captured the dataset using a Canon EOS 7D

camera. We quickly took a series of 100 photos and

used them as a video sequence. The shots were from

a ﬁxed point without a tripod, so the video contains

a small amount of random motion. We stored the

video as a sequence of frames in PNG format, con-

verted from JPG. The camera’s settings were ISO

4000, aperture 400, and resolution 5184 × 3456.

The source video also has a resolution of 5184 ×

3456 and was stored in the sRGB color space. We

degraded it using bicubic interpolation to generate a

ground truth of resolution 1920 × 1280. This step is

essential because many open-source models lack the

code to process a large frame; processing large frames

is also time consuming. We further degraded the input

video from ground truth, again using bicubic interpo-

lation, to 480 × 320 to test the models for 4× upscal-

ing. The output of each model is also a sequence of

frames, which we compare with the ground-truth se-

quence to verify the model’s performance.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

318

3.2 Subjective Comparison

We used 21 super-resolution algorithms in our quality

assessment. We also added a ground-truth video, so

the experimental validation involves 22 videos. We

cut the sequences to 30 frames and converted them

to 8 frames per second (fps). This length allows sub-

jects to easily consider details and decide which video

is better. We then cropped from each video 10 snip-

pets that cover the most difﬁcult patterns for restora-

tion and conducted a side-by-side pairwise subjective

evaluation using the Subjectify.us service, which en-

ables crowd-sourced comparisons.

To estimate information ﬁdelity, we asked partici-

pants in the subjective comparison to avoid choosing

the most beautiful video, but instead choose the one

that shows better detail restoration. Participants are

not experts in this ﬁeld thus they do not have profes-

sional biases. Each participant was shown 25 paired

videos and in each case had to choose the best video

(“indistinguishable” was also an option). Each pair of

snippets was shown to 10-15 participants until con-

ﬁdence interval stops changing. Three of pairs for

each participant are for veriﬁcation, so the ﬁnal re-

sults exclude their answers. All other responses from

1400 successful participants are used to predict sub-

jective scores using the Bradley-Terry (Bradley and

Terry, 1952).

3.3 Edge Restoration Quality

Assessment Method

On the basis of the hypothesis that edges are signif-

icant for detail restoration, we developed the edge-

restoration quality assessment (ERQA) metric, which

estimates how well a model can restore edges in a

high-resolution frame. Our metric compensates for

small global and local edge shifts, assuming they

don’t complicate detail recognition.

Figure 8: The content part ”Board” cropped from a GT

frame (left) along with edges of this frame highlighted with

the Canny algorithm (Canny, 1986) with chosen parameters

(right).

First, we ﬁnd edges in both the output and ground-

truth frames. Our approach uses an OpenCV imple-

Figure 9: Crop from an upscaled frame (left), crop from

the source frame (right) and visualization of ERQA metric

(center). White = true positive, blue = false negative, red =

false positive.

mentation

of the Canny algorithm (Canny, 1986).

The threshold for initially identifying strong edges is

200, and the threshold for linking edges is 100. These

coefﬁcients allow us to highlight the edges of all ob-

jects, even small ones, while skipping lines, which are

unimportant (Figure 8).

Having found the edges in the ground-truth and

distorted frames as binary masks, we compare them

using the F1 score:

precision =

T P

T P + FP

, recall =

T P

T P + FN

, (1)

= 2

precision · recall

precision + recall

, (2)

where TP (True Positive) is a number of pixels de-

tected as edge in both ground-truth and distorted

frames, FP (False Positive) is a number of pixels de-

tected as edges only in distorted frame, FN (False

Negative) is a number of pixels detected as edges only

in ground-truth frame (Figure 9).

Some models can generate frames with a global

pixel shift relative to ground truth, so we checked the

integer pixel shifts [−3, 3] along both axes and chose

the one with the maximum PSNR value. Compensat-

ing for this global shift aids our metric considerably

(Table 4).

During an upscaling, models may also shift edge

pixels locally, which in many cases is insigniﬁcant to

human perception of information. To compensate for

local single-pixel edge shifts, we consider as true pos-

itive any pixels on the output edges, which are not on

the ground-truth edges but are near (on the difference

of one pixel) with the edge of GT.

We then noticed that some models produce a

wider edge compared with the ground truth, and our

method with local compensation (ERQAv1.0) marks

these edges as fully true positive. To correct this

shortcoming, ERQAv1.1 considers each point on a

ground-truth edge as corresponding to true positive

only once. The overall pipeline of Edge Restoration

Quality Assessment method:

https://docs.opencv.org/3.4/dd/d1a/group imgproc

feature.html#ga04723e007ed888ddf11d9ba04e2232de

ERQA: Edge-restoration Quality Assessment for Video Super-Resolution

319

Edge Restoration Quality Assessment pipeline

Input: GT, image

Algorithm: shifted img = global compensation

(GT, image)

GT edge = Canny(GT)

edge = Canny(shifted img)

TP, FP, FN = local compensation

(GT edge, edge)

Output: ERQA = F1 score(TP, FP, FN)

4 EXPERIMENTAL VALIDATION

4.1 Ablation Study

To verify the signiﬁcance of the global- and local-

shift compensation, we conducted a basic edge com-

parison without compensation, with only global com-

pensation, with both global and local compensation

(v1.0), and with penalization of wide edges (v1.1).

All consistently increased both the PLCC and SRCC

(Table 4).

We also tried our compensation scheme with

Sobel, Robert(Roberts, 1963), and Prewitt(Prewitt,

1970) operators. Although there are some exceptions,

in general ERQA shows a better correlation when us-

ing the Canny operator. Different thresholds for the

Canny algorithm give metrics with high correlation

with each other. Thus to avoid overﬁtting we empir-

ically chose the theresholds 100 and 200 to highlight

only important edges.

We also veriﬁed our metric on the QADS dataset

(Zhou et al., 2019). Although the mean correlation

is lower than that of a few other metrics, the reason

is that this dataset was developed for another test case

(visual perception). In some situations, an image with

lower visual perception looks more like the original

one than does an image with higher visual perception.

At the same time, working with images closer to our

test-case ERQA yields good results.

4.2 Comparison with Other Metrics

We conducted a study of existing metrics for video-

quality assessment and found that some work well

for naturalness and beauty, but none works well for

restoration. We calculated several well-known met-

rics on a new dataset: PSNR, SSIM (Wang et al.,

2004), MS-SSIM (Wang et al., 2003), VMAF

, the

recently developed LPIPS (Zhang et al., 2018), which

https://github.com/Netﬂix/vmaf

showed good results when assessing super-resolution

imaging, its improvement DISTS (Ding et al., 2020b)

and metric for SR assessment (Ma et al., 2017).

Our metric outperforms all others in both the PLCC

and SRCC. LPIPS places second. A popular met-

ric for video-quality assessment, VMAF, exhibits

poor results even compared with the traditional SSIM

for this case. Multiscale structural similarity (MS-

SSIM), which usually delivers better results than sim-

ple structural similarity (SSIM), ranked last on super-

resolution.

We tried our global-shift-compensation scheme in

an attempt to improve the performance of these met-

rics. Nearly all metrics (except VMAF) were better

as a result (Table 3).

Because metrics can work differently on different

content types, we separately considered the correla-

tion of metric values with subjective assessment on

all crops and then calculated the mean correlation.

Despite its simple and straightforward construction,

ERQA delivers more-consistent results with subjec-

tive assessment and outperforms all other metrics in

both the PLCC and SRCC (Table 2) coefﬁcients when

assessing information ﬁdelity.

5 CONCLUSION AND FUTURE

WORK

In this paper, we proposed a new full-reference ERQA

metric for assessing detail restoration by video super-

resolution. It compares edges in reference and target

videos to analyze how well a VSR model restores the

source structure and details. We also created a spe-

cial dataset for assessing VSR quality and used it to

analyze our metric through subjective comparisons.

ERQA shows a high correlation with human detail

perception and overall better results than traditional

as well as state-of-the-art VQA methods. It approved

that edge restoration are signiﬁcant for human percep-

tion of detail restoration. The concept underlying our

metric allows it to serve for similar restoration tasks,

such as deblurring, deinterlacing, and denoising.

ACKNOWLEDGEMENTS

Dataset preparation and subjective comparison were

supported by Russian Foundation for Basic Re-

search under Grant 19-01-00785 a. Metric devel-

opment was supported by Foundation for Assistance

to Small Innovative Enterprises under Grant UMNIK

16310GU/2021. Anastasia Antsiferova and Eugene

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

320

Table 2: Spearman rank correlation coefﬁcient (SRCC) of metrics with subjective assessment on all test cases. Metrics

calculated on each test case compared with subjective score on the same test case. Mean value of correlation coefﬁcients is

also presented.

Metric Lego Toy Faces Yarn QRs Text-1 Text-2 Car-1 Car-2 Mira Mean

ERQAv1.0 0.87 0.72 0.85 0.85 0.66 0.85 0.89 0.86 0.79 0.38 0.77

ERQAv1.1 0.87 0.66 0.89 0.84 0.65 0.85 0.91 0.92 0.88 0.41 0.79

SSIM* 0.68 0.20 0.81 0.33 0.52 0.57 0.63 0.86 0.86 0.29 0.58

PSNR* 0.36 -0.05 0.66 0.14 0.40 0.40 0.54 0.82 0.72 0.06 0.41

LPIPS 0.70 0.79 0.52 0.79 0.68 0.88 0.63 0.67 0.67 0.75 0.71

LPIPS* 0.78 0.81 0.56 0.84 0.69 0.88 0.65 0.72 0.71 0.75 0.74

DISTS 0.6 0.35 0.69 0.65 0.54 0.84 0.79 0.74 0.72 0.58 0.65

DISTS* 0.6 0.35 0.72 0.71 0.58 0.86 0.88 0.87 0.81 0.56 0.694

MS-SSIM 0.38 0.30 0.59 0.20 0.32 0.48 0.47 0.56 0.59 0.39 0.43

MS-SSIM* 0.77 0.19 0.68 0.35 0.48 0.53 0.6 0.82 0.81 0.25 0.55

VMAF 0.36 0.35 0.61 0.33 0.36 0.52 0.53 0.55 0.60 0.48 0.47

VMAF* 0.33 0.36 0.57 0.38 0.34 0.52 0.48 0.56 0.58 0.47 0.46

VMAF (clip) 0.36 0.35 0.60 0.33 0.36 0.52 0.53 0.55 0.59 0.49 0.47

VMAF (clip)* 0.33 0.36 0.56 0.38 0.34 0.52 0.48 0.56 0.57 0.47 0.46

Ma et al. 0.47 0.88 -0.28 0.62 0.71 — — — — — 0.48

Table 3: Performance comparison of all metrics with and without global compensation shifts.

Metric

Without compensation With global pixel shift compensation

PLCC SRCC PLCC SRCC

LPIPS 0.8103 0.7077 0.8352 (+0.0249) 0.7377 (+0.0300)

DISTS 0.8094 0.6513 0.8278 (+0.0184) 0.6931 (+0.0418)

MS-SSIM 0.2796 0.4282 0.5992 (+0.3196) 0.5484 (+0.1202)

VMAF 0.2998 0.4692 0.2644 (-0.0354) 0.4572 (-0.012)

VMAF(not clipped) 0.3428 0.4706 0.2999 (-0.0429) 0.4586 (-0.012)

Table 4: An ablation study of the proposed method.

Stage PLCC SRCC

Without compensation (baseline) 0.5035 0.4745

+ Compensation of global shift 0.7395 (+0.2360) 0.6342 (+0.1597)

+ Compensation of local shift (v1.0) 0.8243 (+0.0848) 0.7383 (+0.1041)

+ Penalize false wide edges (v1.1) 0.8316 (+0.0540) 0.7519 (+0.0486)

Lyapustin were supported by the Fellowship from

Non-commercial Foundation for the Advancement of

Science and Education INTELLECT.

REFERENCES

Attar, A., Shahbahrami, A., and Rad, R. M. (2016). Image

quality assessment using edge based features. Multi-

media Tools and Applications, 75(12):7407–7422.

Beron, J., Benitez-Restrepo, H. D., and Bovik, A. C. (2020).

Blind image quality assessment for super resolution

via optimal feature selection. IEEE Access, 8:143201–

143218.

Bradley, R. A. and Terry, M. E. (1952). Rank analysis of in-

complete block designs: I. the method of paired com-

parisons. Biometrika, 39(3/4):324–345.

Canny, J. (1986). A computational approach to edge de-

tection. IEEE Transactions on Pattern Analysis and

Machine Intelligence, PAMI-8(6):679–698.

Chen, X., Zhang, R., and Zheng, S. (2011). Image quality

assessment based on local edge direction histogram.

In 2011 International Conference on Image Analysis

and Signal Processing, pages 108–112. IEEE.

Ding, K., Ma, K., Wang, S., and Simoncelli, E. P. (2020a).

Image quality assessment: Unifying structure and tex-

ture similarity. arXiv preprint arXiv:2004.07728.

Ding, K., Ma, K., Wang, S., and Simoncelli, E. P. (2020b).

Image quality assessment: Unifying structure and tex-

ture similarity. CoRR, abs/2004.07728.

Fang, Y., Liu, J., Zhang, Y., Lin, W., and Guo, Z. (2019).

Reduced-reference quality assessment of image super-

resolution by energy change and texture variation.

Journal of Visual Communication and Image Repre-

sentation, 60:140–148.

Greeshma, M. and Bindu, V. (2020). Super-resolution qual-

ERQA: Edge-restoration Quality Assessment for Video Super-Resolution

321

ity criterion (srqc): a super-resolution image quality

assessment metric. Multimedia Tools and Applica-

tions, 79(47):35125–35146.

Haris, M., Shakhnarovich, G., and Ukita, N. (2019).

Recurrent back-projection network for video super-

resolution. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

pages 3897–3906.

Isobe, T., Zhu, F., Jia, X., and Wang, S. (2020). Revisiting

temporal modeling for video super-resolution. arXiv

preprint arXiv:2008.05765.

Ji, X., Cao, Y., Tai, Y., Wang, C., Li, J., and Huang, F.

(2020). Real-world super-resolution via kernel esti-

mation and noise injection. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition Workshops, pages 466–467.

ohler, T., B

atz, M., Naderi, F., Kaup, A., Maier, A., and

Riess, C. (2019). Toward bridging the simulated-to-

real gap: Benchmarking super-resolution on real data.

IEEE transactions on pattern analysis and machine

intelligence, 42(11):2944–2959.

Liu, S., Peng, X., and Liu, Z. (2019). Image quality as-

sessment through contour detection. In 2019 IEEE

28th International Symposium on Industrial Electron-

ics (ISIE), pages 1413–1417. IEEE.

Ma, C., Yang, C.-Y., Yang, X., and Yang, M.-H. (2017).

Learning a no-reference quality metric for single-

image super-resolution. Computer Vision and Image

Understanding, 158:1–16.

Ni, Z., Ma, L., Zeng, H., Chen, J., Cai, C., and Ma, K.-K.

(2017). Esim: Edge similarity for screen content im-

age quality assessment. IEEE Transactions on Image

Processing, 26(10):4818–4831.

Prewitt, J. M. (1970). Object enhancement and extraction.

Picture processing and Psychopictorics, 10(1):15–19.

Roberts, L. G. (1963). Machine perception of three-

dimensional solids. PhD thesis, Massachusetts Insti-

tute of Technology.

Shi, G., Wan, W., Wu, J., Xie, X., Dong, W., and Wu, H. R.

(2019). Sisrset: Single image super-resolution subjec-

tive evaluation test and objective quality assessment.

Neurocomputing, 360:37–51.

Tian, Y., Zhang, Y., Fu, Y., and Xu, C. (2020). Tdan:

Temporally-deformable alignment network for video

super-resolution. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recog-

nition, pages 3360–3369.

Wan, W., Wu, J., Shi, G., Li, Y., and Dong, W. (2018).

Super-resolution quality assessment: Subjective eval-

uation database and quality index based on perceptual

structure measurement. In 2018 IEEE International

Conference on Multimedia and Expo (ICME), pages

1–6. IEEE.

Wang, G., Li, L., Li, Q., Gu, K., Lu, Z., and Qian, J.

(2017). Perceptual evaluation of single-image super-

resolution reconstruction. In 2017 IEEE International

Conference on Image Processing (ICIP), pages 3145–

3149. IEEE.

Wang, G., Zhu, F., Lu, Z., Yuan, X., and Li, L.

(2018). No-reference quality assessment of super-

resolution reconstructed images by incorporating do-

main knowledge. J. Inf. Hiding Multim. Signal Pro-

cess., 9(2):496–505.

Wang, X., Xie, L., Dong, C., and Shan, Y. (2021).

Real-esrgan: Training real-world blind super-

resolution with pure synthetic data. arXiv preprint

arXiv:2107.10833.

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.

(2004). Image quality assessment: from error visi-

bility to structural similarity. IEEE transactions on

image processing, 13(4):600–612.

Wang, Z., Simoncelli, E. P., and Bovik, A. C. (2003). Mul-

tiscale structural similarity for image quality assess-

ment. In The Thrity-Seventh Asilomar Conference on

Signals, Systems & Computers, 2003, volume 2, pages

1398–1402. Ieee.

Xue, W. and Mou, X. (2011). An image quality assessment

metric based on non-shift edge. In 2011 18th IEEE

International Conference on Image Processing, pages

3309–3312. IEEE.

Yang, C.-Y., Ma, C., and Yang, M.-H. (2014). Single-image

super-resolution: A benchmark. In European confer-

ence on computer vision, pages 372–386. Springer.

Yang, L., Sheng, Y., and Chai, L. (2019). A machine

learning based reduced-reference image quality as-

sessment method for single-image super-resolution.

In 2019 Chinese Control Conference (CCC), pages

3571–3576. IEEE.

Yeganeh, H., Rostami, M., and Wang, Z. (2015). Ob-

jective quality assessment of interpolated natural im-

ages. IEEE Transactions on Image Processing,

24(11):4651–4663.

Zhang, K., Zhu, D., Li, J., Gao, X., Gao, F., and Lu, J.

(2021). Learning stacking regression for no-reference

super-resolution image quality assessment. Signal

Processing, 178:107771.

Zhang, R., Isola, P., Efros, A. A., Shechtman, E., and Wang,

O. (2018). The unreasonable effectiveness of deep

features as a perceptual metric. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 586–595.

Zhou, F., Yao, R., Liu, B., and Qiu, G. (2019). Visual qual-

ity assessment for super-resolved images: Database

and method. IEEE Transactions on Image Process-

ing, 28(7):3528–3541.

Zhou, W., Wang, Z., and Chen, Z. (2021). Image

super-resolution quality assessment: Structural ﬁ-

delity versus statistical naturalness. arXiv preprint

arXiv:2105.07139.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

322