
Privacy-preserving Parallel Computation of Shortest Path Algorithms
with Low Round Complexity
Mohammad Anagreh
1,2
, Peeter Laud
2
and Eero Vainikko
1
1
Institute of Computer Science, University of Tartu, Narva maantee 18, 51009 Tartu, Estonia
2
Cybernetica, M
¨
aealuse 2/1, 12618 Tallinn, Estonia
Keywords:
Privacy-preserving Computation, Secure Multi-party Computation (SMC), Shortest Path Problem, Single-
Instruction-Multiple-Data (SIMD), Breadth-first Search, Sharemind.
Abstract:
Reducing the round complexity in secure multiparty computation (SMC) protocols is a worthy goal due to the
latency of the network. The SIMD approach is considered an efficient strategy to reduce the round complexity
of an SMC protocol. This paper studies the secure multiparty computation (SMC) protocol for the shortest
path problem in sparse and dense graphs, building upon the breadth-first search algorithm. The sensitivity of
operations in processing the algorithms led us to produce two different structural algorithms for computing
the shortest path. We present state-of-the-art parallel privacy-preserving shortest path algorithms for weighted
and unweighted graphs based on the breadth-first search. We have implemented the proposed algorithms on
top of the Sharemind SMC protocol set and tested it for different graphs, dense and sparse, represented as the
adjacency matrix.
1 INTRODUCTION
The shortest path algorithms are often used in dif-
ferent fields of computer science, such as social net-
work analysis, bioinformatics, geographical informa-
tion systems, transportation optimization, and other
computations. The shortest path problem requires
finding a path between two vertices in the graph such
that the sum of the weights of the edges on the path
is minimum. There are many algorithms for solving
this problem. Each of them has a somewhat different
performance profile.
Among the most important algorithms for solving
the single-source shortest distance (SSSD) problem is
Bellman-Ford (Bellman, 1958) and Dijkstra (Dijkstra
et al., 1959) algorithms. The Bellman-Ford algorithm
works to find the SSSD for a general graph with time
complexity O(nm), where n is the number of vertices
and m the number of edges of the graph. It’s also
considered the best option for sparse graphs (Black,
2019). The Dijkstra algorithm also finds shortest dis-
tances for general graphs with time complexity O(n
2
),
and it’s the best option for dense graphs (Goldberg,
1984).
There are different algorithms for All-Pairs Short-
est Distance (APSD), such as Johnson (Johnson,
1977) and Floyd-Warshall (Floyd, 1962) algorithms.
The time complexity of the Floyd-Warshall is O(n
3
)
while for Johnson is O(nm + n
2
logn). In differ-
ent cases and applications, researchers are interested
in finding efficient techniques to find the shortest
path in a privacy-preserving manner (Brickell and
Shmatikov, 2005); such a method can handle different
parties holding different private parts of the graph.
This work aims to find the single-source shortest
distance for the weighted and unweighted graphs in
a privacy-preserving manner, using SMC protocols.
We keep the attributes of vertices and edges private,
while the number of edges and vertices is public. We
build our protocols upon the Sharemind three-party
protocol set (Bogdanov et al., 2012), which provides
passive security against one party. The protocol set
implements protocols for the arithmetic and boolean
operations that we use. The security of our proto-
cols is conveniently analyzed (Laud, 2015b) in the
Arithmetic Black box (ABB) model (Damg
˚
ard and
Nielsen, 2003), which abstracts from the details of the
underlying SMC protocol set.
The protocols for most of the arithmetic and
boolean operations involve message exchanges be-
tween the three computing parties. Hence the latency
of the network may significantly affect the perfor-
mance of the SSSD protocol if the algorithm imple-
mentation causes it to have a high round complexity.
Anagreh, M., Laud, P. and Vainikko, E.
Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity.
DOI: 10.5220/0010775700003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 37-47
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
37

Consequently, the network latency in SMC protocol is
a challenge to many researchers. How can the round
complexity of private computation in the SMC plat-
form be reduced?(Katz et al., 2003; Katz and Koo,
2007; Boyle et al., 2018). One of the most efficient
strategies for reducing the round complexity in secure
multiparty computation is parallel calculation (Laud,
2015a; Boyle et al., 2015; Cohen et al., 2017).
Our strategy to reduce the round complexity of
the SMC platform is to apply the Single-Instruction-
Multiple-Data (SIMD) paradigm as much as possi-
ble, using the SecreC high-level language (Bogdanov
et al., 2014) for expressing algorithms making use of
the Sharemind protocol set. We use the Breadth-First
Search (BFS) algorithm (Beamer et al., 2012) to pro-
duce the privacy-preserving shortest path algorithms
for weighted and unweighted graphs. The possibil-
ity of accelerating the BFS algorithm through paral-
lel computing in shared and distributed memory is
discussed by Murphy et al. (Murphy et al., 2010).
The container-centric and vertex-centric approaches
are two types of parallel BFS algorithms in shared
memory (Berrendorf and Makulla, 2014). The par-
allel BFS algorithm in one-dimensional distributed
memory is presented for random big graphs in (Yoo
et al., 2005). Later, the parallel BFS algorithm in
2D-partitioning is proposed with two communication
phases (Buluc¸ and Madduri, 2011). The algorithmic
structure of the conventional serial BFS algorithm is
more fit to be parallelized by the SIMD approach. The
two for-loops in the serial version of the BFS algo-
rithm can also be executed in parallel by modeling the
sources and neighbors vertices as private vectors. The
new formation of vertices and their edges into vectors
can be efficiently processed using one single instruc-
tion with low round complexity.
The complexity of accessing memory at private
addresses has a high effect on the total running time
of the operations. This complexity led us to reduce
the processes in our proposed privacy-preserving
breadth-first search algorithm to avoid the linear cost
of the private memory access over the private vec-
tors. This also has the effect of noticeably reduc-
ing the round complexity of the algorithm. Hence,
we introduce two structurally different algorithms for
privacy-preserving breadth-first search for computing
the shortest path. One of the privacy-preserving short-
est path algorithms is for weighted graphs, and the
other is for unweighted graphs. Both proposed al-
gorithms have the same functionality, and both are
based on breadth-first search. In this work, various
graphs are used to benchmark the two proposed algo-
rithms for computing the shortest path, both dense and
sparse. Regardless of the graphs’ types, all the graphs
have the same data structure as the adjacency ma-
trix. Researchers have recently proposed algorithms
for computing the shortest paths over a planar graph,
and such algorithms are adapted to privacy-preserving
computations (Henzinger et al., 1997; Fakcharoen-
phol and Rao, 2006; Klein et al., 2010; Mozes and
Wulff-Nilsen, 2010).
Motivationally, the breadth-first search algorithm
is a basic algorithm used in various computational
graph algorithms, such as maximum flow algorithms
and kernel algorithms in the Graph500 benchmark.
Accordingly, producing a privacy-preserving version
of the BFS algorithms would be usable in various al-
gorithms as a related subroutine.
The paper is organized as follows. Section 1
briefly introduces the work in general. Section 2
briefly presents the related work. Section 3 shows
the secure multi-party computation. Section 4 gives
an overview of the breadth-first search. Section 5
presents the Parallel privacy-preserving BFS algo-
rithms. Section 6 presents the benchmarking results.
Finally, Section 7 concludes the paper, discussing the
results and the future work.
2 RELATED WORK
The main feature of the secure multiparty computa-
tion (SMC) protocol is the computational indistin-
guishability from some ideal functionality. The proto-
col is secure if it does not leak any information during
private computation besides what is given out by the
ideal functionality (Laud, 2015b; Canetti, 2000). Our
work in this paper does not leak any information from
the arithmetic black box (ABB). All the computations
are securely conducted in the ABB. The contribution
in this work focuses on optimizing the private com-
putation by parallel calculation to reduce the round
complexity while performing the SMC protocol over
the platform.
Recently, many researchers have been working on
optimizing the computation in the privacy-preserving
parallel computation for different combinatorial al-
gorithms. Researchers have targeted the minimum
spanning tree and shortest path algorithms in their
privacy-preserving research. The parallel privacy-
preserving minimum spanning tree algorithm for
sparse graph (Laud, 2015a) is proposed based on the
Werbach and Shiloach algorithm with time complex-
ity O(log
2
n). The same paper also presented an effi-
cient protocol for private reads and writes.
The privacy-preserving parallel computation of
minimum spanning tree for dense graphs is proposed
based on Prim’s algorithm (Anagreh et al., 2021b).
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
38

The algorithm contains a declassification for the ver-
tices u, but it is still secure. The algorithm securely
shuffles the rows and columns of their adjacency ma-
trix to mask the real identities of the vertices and their
connected edges.
In the paper (Rao and Singh, 2020), two privacy-
preserving minimum spanning tree algorithms in
the semi-honest model are proposed. The privacy-
preserving MST algorithms are implemented on top
of Yao’s protocols (Yao, 1982), which is based on
a garbled circuit (Demmler et al., 2015; Liu et al.,
2015). Both algorithms have sequential computation.
This paper focuses on a parallel privacy-
preserving shortest path algorithm for weighted and
unweighted graphs using the serial version of the
breadth-first search. Many researchers have been
working on privacy-preserving shortest path algo-
rithms. The privacy-preserving shortest path proto-
cols based on Dijkstra and Bellman-Ford are pro-
posed in (Aly et al., 2013). Also, they proposed proto-
cols for privacy-preserving computation of the maxi-
mum flow problems. Their proposed work has a high
round complexity causing a significant running time
even on small graphs.
In the paper (Aly and Cleemput, 2017), an obliv-
ious data abstraction that improves the protocol of
computing the privacy-preserving SSSD in (Aly and
Van Vyve, 2014) is conducted. There are no more
complex cryptographic techniques such as Oblivious
RAM in this protocol, and it is secure against both
semi-honest and malicious adversaries. However, the
proposed protocol is running sequentially, and it has
high round complexity.
The privacy-preserving Dijkstra’s algorithm is im-
plemented on the sparse graph using garbled circuits
and employing oblivious priority queues to increase
efficiency in (Liu et al., 2015). The running time
of their proposed privacy-preserving Dijkstra’s algo-
rithm is too high, so it’s not a fit for a large graph.
Blanton et al. (Blanton et al., 2013) presented sev-
eral data-oblivious algorithms, breadth-first search,
single-source shortest path, minimum spanning tree,
and maximum flow. Theoretically, they introduced
the data-oblivious algorithms without actual imple-
mentation shown.
Recently, a new parallel method for comput-
ing privacy-preserving shortest path based on the
radius-stepping algorithm was proposed (Anagreh
et al., 2021c). In general, the radius-Stepping algo-
rithm is an improved version of the ∆-Stepping algo-
rithm (Meyer and Sanders, 2003). The ∆-Stepping
and Radius-Stepping algorithms are parallel single-
source shortest path algorithms solving this problem
efficiently. The SIMD approach implements to effi-
ciently parallelize the algorithm as the same technique
in our work. The round complexity of the SMC proto-
col is reduced into different round complexities based
on the value of radii in the algorithm. The results
show that the parallel method is efficient; the speed-
up is hundreds of times faster than the standard ver-
sion of the algorithm and the results of the previous
works. In the implementations, the paper presented
the running time of the computation for sparse, dense,
and planar weighted graphs. The unweighted graph is
also implemented with the best speed-up of the algo-
rithm.
The secure multiparty computation protocol for
single-source shortest distance and All-pairs short-
est distances in sparse and dense graphs are stud-
ied (Anagreh et al., 2021a). The state-of-the-art
privacy-preserving implementations of Bellman-Ford
and Dijkstra SSSD algorithms have been presented
and Floyd-Warshall and Johnson APSD algorithms as
well. In the implementation, using single-instruction
multiple-data (SIMD) operations reduces the round
complexity of SMC protocols. In general, they copied
the vertices and edges elements of the private graph
into vectors, then performed the single instruction
for the entire vectorised data. Interestingly, using
the SIMD operations let proposed algorithms perform
the computation, which has a high round complex-
ity (with enormous vertices and edges) in low run-
ning time. This is done because of reducing the
round complexity in using SIMD. In both SSSD al-
gorithms have declassification for some private val-
ues. To achieve privacy preservation, masking some
private values with randomness generated during the
protocol is already done. The implementation of the
Johnson ASPD algorithm is used the Laud’s Proto-
col for private reading (Laud, 2015a), the evaluation
of the ASPD algorithm is not similar to any previ-
ous work. The privacy-preserving Bellman-Ford and
Dijkstra SSSD algorithms are secure with low round
complexity but are not the lowest round complexity
than our work.
3 SECURE MULTI-PARTY
COMPUTATION
Secure Multi-party Computation (SMC) is a technol-
ogy that enables a set of n parties with their private
input x
0
,x
1
,...,x
n−1
to jointly compute a private black
box function y
0
,y
1
,...,y
n−1
= f (x
0
,x
1
,...,x
n−1
), and
distribute the output to the parties, without knowing
the private inputs by other parties in the system. The
goal of this private model is that the cryptographic
techniques assure the security, the integrity of the
Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity
39

storage, the operations in the black box, and the com-
munication between the participants if the adversary
has corrupted a not-too-large fraction of them.
The Arithmetic Black Box (ABB) is the con-
fidential environment where the complex privacy-
preserving computation is to be securely calculated
and detailed without leaking the details of the arith-
metic operation of protocols and with private data of
the parties. The private data of the parties and the
whole arithmetic operations in the ABB are private
toward the parties themselves even if they are a par-
ticipant in this computation. In general, the ABB is
an instrumental abstraction of secure multiparty com-
putation (Laud, 2015b).
In the privacy-preserving platform, the general-
purpose model for analyzing cryptographic proto-
col with efficient security properties is called the
universally composable security (UC) framework of
MPC (Canetti, 2001). The main features in UC are
guaranteeing security properties that it remains secure
if it is arbitrarily composed with other protocols se-
cure in UC. The processing of the private function
f is performed in a privacy-preserving manner (Laur
and Pullonen-Raudvere, 2021) by applying one of the
different approaches, secret-sharing (Damg
˚
ard et al.,
2009), homomorphic encryption (Henecka et al.,
2010) or garbled circuit (Yao, 1982).
Our proposed privacy-preserving breadth-first
search for finding the shortest path is built on the
top of the ABB. In the algorithm description below,
we use the notation JvK to denote that value v is pri-
vate, which is stored in the ABB. The notation J~vK
denotes the private vector (v
0
,v
1
,...,v
n−1
), which is
also stored in the ABB. In our algorithms below, we
use the for-loop to denote that assign-operation in the
body of the function is performed in parallel using the
SIMD framework.
4 BREADTH-FIRST SEARCH
Let V and E refer to the sets of the vertices and edges
in private graph G respectively. The size of the vertex
set is n = |V | and the size of the edge set is m = |E|.
An undirected graph G = (V,E) is a graph that doesn’t
have directions for the edges. The edges indicate a
two-direction relationship between two vertices u ∈ V
and v ∈ V . Each edge e can traverse among two ver-
tices in both directions (from u to v and vice versa)
with the same weight w. The weight of edge is de-
noted as w(e), w(u,v) or (v,u). A Path from source
vertex u to target vertex v is a sequence of edges
(u
0
,v
1
),(u
1
,v
2
),...,(u
n−1
,v
n
) ∈ E, where u = u
0
and
v = v
n
. The length of the path is the sum of the
weights of the edges in the path. The shortest path
between two vertices is the path with minimum length
between them.
The undirected graph G = (V, E) can be repre-
sented in the memory as an adjacency matrix, which
is a matrix with size n × n, where the elements of the
matrix are the weights w(u,v) for the vertices u and
v. A dense graph is a graph G where the number of
edges in the graph is close to the possible maximal
number of the edges n(n − 1)/2, where n number of
the vertices |V |. A sparse graph is a graph G = (V,E)
where the number of the edges in the graph is close
to the number of vertices. A planar graph is a special
case of the sparse graph. In planar graphs, the number
of edges is at most 3n − 6. An unweighted graph is a
graph whose adjacency matrix is a symmetric matrix
of zeros and ones.
Data: Adjacency matrix G ∈ Z
n×n
Data: Source vertex s
Result: The graph distance δ(·) from s
begin
forall v ∈ V do δ(v) ← +∞
δ[s] ← 0,level ← 0
FS ← {},NS ← {}
push(s,FS)
while FS 6= {} do
foreach u ∈ FS do
foreach neighbour v of u do
if δ[v] ← ∞ then
push(v,NS)
δ[v] ← level
end
end
end
FS := NS
NS := {}
level := level + 1
end
return δ(·)
end
Algorithm 1: Serial breadth-first search.
The serial version of the Breadth-First Search al-
gorithm is presented in Alg. 1. The main feature in
this algorithm is traversing over all vertices in the
graph using two stacks FS and NS to store the visited
vertices. The stack FS is to store the visited vertices
while the stack NS is to store the next frontier of the
visited vertices. The frontier has some distances for
vertices from the source vertex s; distances are called
level. The neighbors of this vertex have to be ex-
plored, some of which are not explored yet. The BFS
algorithm discovers these vertices and stores them in
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
40

the next frontier, and so on until all vertices in the
graph will be already stored in the stack FS. In the
outer while-loop, the number of the iterations (Iter)
is completely bounded by the distances of the longest
shortest distance from source vertex s to any vertex in
the whole graph G. The two for-loops can be executed
in parallel, either in shared or distributed memory us-
ing some parallel framework.
This work uses the same algorithmic structure of
the breadth-first search algorithm to perform the par-
allel calculation of the BFS using Single-instruction-
multiple-data. The elements of the two sets of ver-
tices u, v ∈ V will be vectorized in two private vectors
J~vK and J~uK. Then, using the SIMD instructions, the
algorithm can traverse over all vertices in the graph
simultaneously, then update the distances, eventually
finding the shortest distances in the given graph.
5 PRIVACY-PRESERVING
SHORTEST PATHS
This section presents the privacy-preserving single-
source shortest distance algorithm that works effi-
ciently for an unweighted graph. The breadth-first
search algorithm is a good fit for computing the short-
est distances in weighted and unweighted graphs,
where the graph is an undirected connected graph.
The sensitivity of the private data in secure multi-
party computation requiring several round-trips be-
tween the computing parties for each operation af-
fects the implementation. The shortest distances in
a weighted graph can be computed by applying fewer
operations than computing the shortest path for un-
weighted graphs. Therefore, we present another ver-
sion of the algorithm for computing the shortest dis-
tances in the weighted graphs that will be faster. The
first algorithm is the privacy-preserving single-source
shortest distances for unweighted graphs (UBFS), and
the other is privacy-preserving single-source short-
est distances in weighted graphs (WBFS). The algo-
rithms are parallel, making use of the SIMD frame-
work, and based on the BFS.
5.1 Privacy-preserving UBFS
The breadth-first search algorithm relaxes the edges
with the same starting vertex in parallel. Each iter-
ation of the algorithm relaxes the edges of the fron-
tier vertices. We use the dense representation of the
graph. The adjacency matrix gives the weights of
edges with size n × n, weight
00
∞
00
is used to denote
the lack of an edge in the adjacency matrix. Although
we use the adjacency matrix as a data structure to
fit our proposed algorithm, we use different graphs
in our benchmarks, dense and sparse. Our privacy-
preserving implementation of the Breadth-first search
for finding the shortest path in an unweighted graph
is presented in Alg. 2.
Data: Adjacency matrix JGK ∈ Z
n×n
Data: Source vertex s
Result: The graph distance δ(·) from s
begin
δ[s] ← 0
J
~
δK ← JG[s, ∗]K
forall u ∈ {0,1,..., n − 1} do
Jδ
r
[u]K ← JδK
end
repeat
forall v ∈ {0,1,..., n − 1} do
Jδ
c
[v]K ← JδK
end
J
~
CK ← (J
~
δ
c
K 6= ∞)
J
~
MK ← (J
~
δ
c
K + J~eK)
J
~
δ
0
K := choose(J
~
CK, J
~
MK,J
~
δ
r
K)
J
~
δK ← min(J
~
δ
0
K,n)
until declassify(all(JδK 6= ∞))
return Jδ(·)K
end
Algorithm 2: Privacy-preserving UBFS for un-
weighted graph.
In detail, the algorithm works as follows: the
input data is a private unweighted undirected graph
G = (V,E) represented in an adjacency matrix, and the
second input is the source vertex. The return value is
the distance J
~
δK which is a private vector with size n.
We vectorized the data structure of the adjacency ma-
trix to be a good fit for our proposed parallel method.
Two private vectors are initialized to get the edges’
weights; both with size n
2
. The first vector J
~
δ
r
K con-
tains the rows of the matrix, and the second vector
contains J
~
δ
c
K the columns.
The initial values are, storing the first row in the
adjacency matrix JG[s, ∗]K into distance vector J
~
δK, and
source vertex. It’s important to note that the adjacency
matrix is already vectorized into a vector J~eK (the vec-
torization is column by column) with size n
2
. The two
vectors J
~
δ
r
K and J
~
δ
c
K allows to traverse over the ver-
tices in order to relax their edges via sets. Therefore,
there is no need to use the foreach-loops (in Alg 1).
This new algorithmic structure reduces the total
round complexity of the algorithm. The initial val-
ues of weights sets are given in parallel, the vector
J
~
δ
r
K gets the elements of the u-row , the vector J
~
δ
c
K
also gets the elements of v-column, u, v ∈ V . Getting
the indices J
~
δ
r
K happens only once, out of the repeat-
loop, while getting the indices of J
~
δ
c
K must take place
Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity
41

at each iteration inside the repeat-loop for updates.
The algorithm has one repeat-loop, which starts by
gathering the edges’ weights of columns J
~
δ
c
K in par-
allel.
All elements of column vector J
~
δ
c
K will be in com-
putation, regardless if there is an edge, or there is
no edge (denoted by
00
∞
00
). To discriminate this, the
condition J
~
CK will be labeling the indices of existing
edges by Boolean values. The element in the vec-
tor is true if its index will be in computation. If the
value is false, this index will be ignored. The size
of the Boolean vector is n
2
, which is similar to the
adjacency matrix JGK. This adjacency matrix can be
vectorized easily, and then the SIMD technology can
be efficiently applied to the algorithm. Next step, the
elements of the columns vector J
~
δ
c
K and the elements
of J~eK will be summed and then stored in the vector
J
~
MK. The algorithm uses the SIMD approach because
all elements are summed in a single parallel instruc-
tion.
The protocol of the vectorized operation choose
from Sharemind’s protocol set will take place in
UBFS’s algorithm. The result of this operation is a
vector, each element of which is either an element of
J
~
MK if the condition J
~
CK contains true in the corre-
sponding place, or an element of the rows vector J
~
δ
r
K
if J
~
CK is false in the corresponding place. The result
of choose is stored in J
~
δ
0
K. The currently shortest dis-
tances δ(·) from source vertex s to all vertices in the
graph are among the values stored in the vector J
~
δ
0
K.
The last operation is to get these minimum val-
ues (the shortest distances) for each vertex separately.
The operation min takes two arguments, the first of
which is a vector of private values, and the second
is a public integer n. It replaces each sequence of n
elements of the input vector with a single value, the
minimum of these n values. All operations mentioned
in the UBFS’s algorithm can be applied to vectors
of values stored in the ABB. The parameters (which
are private) to the operation are required to have the
same length. This feature of the operations satisfies
the SIMD approach.
5.2 Privacy-preserving WBFS
The feature of the sequential breadth-first search al-
gorithm can be ideally exploited to create a parallel
version of the BFS. The frontier’s data structure stores
the vertices at the same distance from the source ver-
tex s. This feature can be parallelized, which will
reduce the amount of layer-traversal. Therefore, the
given weighted graph can compute the shortest path a
bit easier than unweighted in the sense of fewer op-
erations. This section presents another version of the
privacy-preserving shortest path algorithm by BFS for
a weighted graph with fewer operations. This has a
positive effect on reducing the running time of the al-
gorithm. The privacy-preserving BFS’s shortest path
for the weighted graph is presented in Alg. 3.
Data: Adjacency matrix JGK ∈ Z
n×n
Data: Source vertex s
Result: The graph distance δ(·) from s
begin
J
~
δK ← JG[s, ∗]K
repeat
forall u ∈ {0,1,..., n − 1} do
Jδ
r
[u]K ← J
~
δK
end
J
~
δ
0
K ← min((J
−→
δ
r
K + Je(v, u)K),N(v))
J
~
DK := J
~
δK
J
~
δK := J
~
δ
0
K
until declassify(all(J
~
δ
0
K = J
~
DK))
return Jδ(·)K
end
Algorithm 3: Privacy-preserving WBFS for weighted
graph.
The data input is source vertex s, and the private
adjacency matrix has the vertices and their edges’
weights. The output data is the shortest path from the
source vertex s to all other vertices of the given graph
JGK from the source vertex s. The initial value in the
algorithm is, putting the first row in the given graph
JGK (with source vertex s) into the shortest distances
vector J
~
δK that will get an update during running the
algorithm until all vertices are already handled.
The algorithm has only one repeat-loop, starts
by assigning all rows of the given graph JGK into
rows vector J
~
δ
r
K. It’s important to note that we use
forall-loop in our algorithms to denote that all assign-
operations in that loop are already performed in paral-
lel. Later, the adjacency matrix of the given graph JGK
is already vectorized into vector J~eK, and we have vec-
torized this by storing column by column. The main
operation in the algorithm is the summation of the two
vectors J
~
δ
r
K and J~eK, and then finding the minimum
distance for each vertex using min-operation. The last
operation in the algorithm is swapping the vectors that
will be arranged to make the updates. The aim is
to check that all vertices are already handled. The
equality check at the end of the loop returns a vec-
tor of Boolean values. The values of J
~
δ
0
K and J
~
DK are
not leaked by the all-operation. This algorithm has no
specific known number of iterations. It is based on the
number of connected edges. The algorithm behaves
perfectly when the edges are close to the maximum
possible number, i.e., dense graph or like-dense.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
42

5.3 Round Complexity
In general, our proposed algorithms reduce the round
complexity of the shortest distances computation.
Round complexity is based on the size of the adja-
cency matrix. The communication-related complex-
ities of the secure multiparty computation have two
sides, round complexity, which is the number of com-
munication among the machines of the SMC platform
and bandwidth, the number of bits that will be trans-
mitted among computation parties. Let n denote the
number of the vertices in the graph, and m is the num-
ber of the edges. Theoretically, the round complex-
ity is less than O(log n) times, but it can be realistic in
bandwidth. If the vectors’ size in computations is big-
ger than bandwidth, the actual number of rounds com-
plexity will be increased based on the number of data
packets (which split because the vector’s size is big-
ger than bandwidth). The algorithm relaxes all ver-
tices’ edges in fewer iterations if the graph is dense,
with low running time. All elements of the adjacency
matrix will be taken in computation. Regardless, ei-
ther there is an edge between two vertices or no edge
(weight is
00
∞
00
).
5.4 Security and Privacy
Our implementation is built on top of a universally
composable ABB of the SMC protocol. The im-
plementation is privacy-preserving if it doesn’t have
any declassification operation. The condition of the
repeat-iteration has declassification. Otherwise, the
declassified values cannot be directly discovered with
the public parameters of the implementation. It’s a
subset of a Boolean vector that signs unhandled ver-
tices. In other words, the arrangement of unhandled
vertices depends on the values of the shortest dis-
tances and the number of iterations. The identity of
the vertices (regardless of, it is handled or not) and
their connected edges with their weights are still pri-
vate. Such declassified values are not directly helping
the semi-honest or malicious adversaries. Our imple-
mentation of the proposed protocol with its two ver-
sions is privacy-preserving.
6 EXPERIMENTAL RESULTS
6.1 Benchmarking Results
We evaluate and benchmark our results with the best
previous results conducted on top of three-party SMC
protocols in the state of art. Recently, the benchmark-
ing results for the state-of-the-art privacy-preserving
shortest path algorithms have been reported (Aly and
Cleemput, 2017). The proposed work is an oblivi-
ous data abstraction that improves the yield in (Aly
et al., 2013) (Aly and Van Vyve, 2014). The result has
shown that the running time on a 32-vertex graph is
around 5 seconds. The permutation operation is also
used to mask the real identity of the vertices, which
will increase the total running time. It is an efficient
way to keep privacy, but at the same time, it’s an extra
operation that will increase the whole running time of
computation. The presented result doesn’t show the
scalability, or it has more running time. The size of
the graph used in their experimentation is small.
In contrast, our work has no extra operations for
permutation or other steps. As well as, our proto-
col is scalable; we used different sizes of graphs in
our benchmarking. The result shows that our work is
faster than the previous work, around 50 times.
The most state of the art conducted work for
privacy-preserving SSSD is based on the radius-
stepping algorithm (Anagreh et al., 2021c). The re-
sult shows that the algorithm is more efficient than
the previous work and others, and because of the nov-
elty in this work, we use it to evaluate our work with
it. This algorithm also has an extra operation, radii,
which does not exist in classical shortest path algo-
rithms. Thus, our proposed protocol has pure pro-
cesses for finding the shortest distances without any
extra operations. The empirical tests for our protocol
show that the acceleration is 3 to 4 times more than in
the best radii case of the radius-stepping algorithm.
Extensive benchmarking results for privacy-
preserving SSSD Dijkstra and bellman-Ford algo-
rithms are documented in (Anagreh et al., 2021a).
These results are benchmarked with our BFS’s results
in Section 6.2.
6.2 Breadth-first Search Experiments
In this work, we have implemented our proposed
protocol of the privacy-preserving shortest distances
with its two versions on the Sharemind SMC plat-
form (Bogdanov et al., 2008; Bogdanov et al., 2012).
The computation was performed on the Sharemind
Cluster of three computers connected with a three-
party protocol set secure against one passively cor-
rupted party. The SIMD framework under SecreC
high-level language is used to write the code of all
implementations. The three workstations of the clus-
ter have a 12-core 3 GHz CPU with Hyper-Threading
running Linux and 48 GB of RAM. An Ethernet lo-
cal area network connects the workstations with a link
speed of 1 Gbps. Although our algorithm fits dense
graphs, we use different graphs in the implementa-
Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity
43
tions on the top of the SMC protocol set, sparse and
dense ones, with varying sizes. Among the sparse
graphs, we consider graphs whose number of edges is
similar to planar graphs, i.e., either two or three times
the number of the vertices. Using different kinds of
graphs is for the benchmarking of the two versions of
our privacy-preserving BFS algorithm. We reported
the running time of our experiments in seconds. Suf-
fix K denotes the multiplication by 1000, while the M
denotes the multiplication by 1000000. The paral-
lel codes of the implementation are written using the
SIMD framework; after vectorization of the given ad-
jacency matrices, there is no use of the multiple cores
of the Sharemind SMC platform. Among the three
workstations of the Sharemind cluster, the adjacency
matrix data is represented in secret-shared manners
for both inputs and outputs.
Table 1: Running times (in seconds) of privacy-preserving
WBFS and radius-stepping algorithms for various graphs.
Graphs Parallel Radius Parallel WBFS Speed-up
Radii = rnd Radii = ∞ BFS vs.
k n m Iter. Time Iter. Time Iter. Time rnd ∞
25 100 8 0.33 6 0.24 5 0.07 5.0x 3.6x
50 400 7 0.78 5 0.52 4 0.13 6.1x 4.1x
100 900 14 4.67 6 2.05 5 0.47 10.0x 4.4x
200 1k 33 41.4 11 13.8 10 2.98 13.9x 4.6x
500 5k 38 275 12 86.9 11 21.5 12.8x 4.1x
750 10k 58 916 9 142 8 35.4 25.9x 4.0x
1k 10k 94 2620 14 392 13 98.9 26.5x 4.0x
1k 40k 41 1141 8 224 7 56.6 20.2x 4.0x
Sparse
3k 100k 147 36.4k 11 2724 10 685 53.0x 4.0x
3k 1M 44 10.9k 7 1733 6 429 25.4x 4.0x
5k 1M 95 41.8k 7 4778 6 1198 34.8x 4.0x
5k 5M 31 14.1k 5 3459 4 852 16.5x 4.1x
10k 15M 51 91.3k 6 16.5k 5 4090 22.2x 4.0x
50 1225 5 0.56 4 0.43 3 0.11 5.0x 3.8x
100 4950 8 2.67 6 1.99 5 0.44 6.0x 4.5x
200 19.9k 9 11.3 5 6.35 4 1.45 7.8x 4.4x
750 280k 16 254 6 94.9 5 23.5 10.8x 4.0x
1k 499k 20 560 5 140 4 35.3 15.9x 4.0x
Dense
5k 12.4M 21 14.4k 5 3419 4 852 16.9x 4.4x
6k 17.9M 28 17.7k 6 5953 5 1465 12.0x 4.1x
10k 49.9M 27 48.9k 5 13.7k 4 3377 11.9x 4.1x
50 100 11 1.14 9 1.01 8 0.24 4.8x 4.3x
50 150 11 0.98 7 0.69 5 0.16 6.2x 4.4x
100 200 21 6.93 10 3.31 9 0.72 9.6x 4.6x
100 300 21 7.08 8 2.72 7 0.61 11.7x 4.5x
500 1k 146 1056 11 79.9 10 19.8 53.0x 4.0x
Like-Planar
500 1500 105 759 15 108 14 26.9 28.2x 4.0x
1k 2k 245 6834 14 271 13 61.5 111x 4.4x
1k 3K 169 4713 15 285 13 61.6 77.3x 4.6x
We report the running times of the privacy-
preserving WBFS’s algorithm for different kinds of
weighted graphs, sparse dense and like-planar, with
various sizes in Table. 1. This table presents the
benchmark for the privacy-preserving parallel ver-
sions of the WBFS and Radius-stepping algorithms.
In the implementations of the radius-stepping algo-
rithm, we use the best two cases of the radii, which
are random (rnd) and infinity (
00
∞
00
). The table shows
the number of possible iterations (Iter) for each al-
gorithm with their total running time. It is impor-
tant to note that we use a function to generate ran-
dom graphs. Therefore, the number of iterations in
all implementations can differ based on the weights
of edges and which vertices are connected by edges.
Anyway, the number of iterations in WBFS’s algo-
rithms is smaller than in both versions of the radius-
steeping algorithm in all experiments. The empiri-
cal test clearly shows that WBFS’s algorithm is faster
than the radius-stepping algorithm in two considered
cases of radii. Moreover, the efficiency shows how
much WBFS’s algorithm is faster than the best case
of radii (which is
00
∞
00
) — between 3 and 5 times.
Although, the number of Iter in WBFS is one time
less than the number of Iter in the ∞-radii version
(with some exceptions). For rnd-radii, the speed-up
of WBFS is 50 times or more. Lastly, we note that the
number of iterations in running the algorithm using
dense graphs (regardless of the sizes) is less than the
number of iterations in running the algorithm using
sparse graphs. The number of iterations is decreased
by increasing the number of edges in the given graphs.
Thus, the BFS algorithm is an efficient algorithm over
dense graphs with low running time. The algorithm
is still more efficient for other graphs than radius-
stepping and other algorithms in previous works. The
implementations of our proposed privacy-preserving
parallel computation of UBFS’s algorithm for an un-
weighted graph are presented in Table. 2.
Table 2: Running times (in seconds) of privacy-preserving
radius-stepping and UBFS algorithms over Sharemind.
K
Size Parallel Radius Parallel UBFS
Level Efficiency
n m Iter Time Iter Time
50 400 3 0.32 1 0.07 3 4.8x
100 2k 3 1.02 1 0.21 3 4.9x
150 750 5 3.59 3 0.71 4 5.1x
200 1k 5 6.28 3 1.25 4 5.0x
500 20k 3 21.9 1 4.02 3 5.5x
Sparse
750 10k 4 63.5 2 13.1 4 4.8x
1k 20k 4 113 2 23.5 4 4.8x
1k 100k 3 84.9 1 15.5 3 5.5x
3k 5k 3 762 1 136 3 5.6x
10K 15M 3 8425 1 1524 3 5.5x
50 1225 3 0.33 1 0.06 3 5.2x
100 4950 3 1.04 1 0.21 3 5.5x
200 19.9k 3 3.78 1 0.69 3 5.5x
500 124k 3 22.1 1 3.96 3 5.6x
750 280k 3 48.5 1 9.01 3 5.4x
Dense
1k 499k 3 85.1 1 15.7 3 5.4x
3k 4.49M 3 758 1 135 3 5.6x
5k 12.4M 3 2091 1 374 3 5.6x
10k 49.9M 3 8312 1 1490 3 5.6x
50 100 6 0.62 4 0.15 6 4.2x
50 150 5 0.55 3 0.11 5 5.0x
100 200 6 1.95 4 0.41 6 4.7x
100 300 5 1.72 3 0.36 6 4.8x
500 1k 10 72.6 8 18.1 10 4.0x
Like-Planar
500 1500 6 43.5 4 10.0 6 4.0x
1k 2k 9 250 7 62.4 9 4.0x
1k 3k 7 195 5 49.9 7 4.2x
We have benchmarked our algorithm with a
privacy-preserving radius-stepping algorithm for un-
weighted graphs. Different kinds of graphs were
used in the implementations, sparse, dense, and like-
planar, with various sizes. The running time in sec-
onds is reported for both algorithms. The benchmark
of the radius-stepping algorithm is noted for the ∞-
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
44
radii case, which is considered the most efficient case
of radii. In both algorithms, the result shows the pos-
sible iterations (Iter) based on the number of given
edges. The results also show the number of vertices
with the exact distances (levels) for both algorithms.
In general, the results show the running times of the
UBFS’s algorithm and its speed-up in comparison to
the radius-stepping algorithm. This speed-up is be-
tween 4 and 5.6 times.
The algorithm has the lowest possible number of
iterations in experiments with dense graphs, regard-
less of the size. The number of iterations is decreased
by increasing the number of edges in the given graph.
Thus, until reaching the maximal possible number of
edges in the dense graph. Indeed, the number of it-
erations will be only one. This is the significance of
our work, that’s, for the maximal possible number of
edges, the round complexity is constant.
Table 3: Running times (in seconds) and Bandwidth of dif-
ferent rounds for the privacy-preserving versions of BFS.
K Size WBFS UBFS
n m r / Iter. Time Band. r / Iter Time Band.
50 400 1/4 0.07 0.8 MB 1/1 0.08 0.7 MB
50 400 2/4 0.09 1.3 MB - - -
50 400 3/4 0.12 1.7 MB - - -
50 400 4/4 0.14 2.1 MB - - -
500 5k 1/11 3.9 43.9 MB 1/3 4.20 49.3 MB
500 5k 2/11 5.7 83.3 MB 2/3 6.11 102.7 MB
500 5k 3/11 7.42 109.0 MB 3/3 8.31 146.2 MB
Sparse
500 5k 7/11 14.4 277.9 MB - - -
500 5k 11/11 21.5 429.4 MB - - -
1k 40k 1/7 14.9 176.1 MB 1/2 16.2 197.7 MB
1k 40k 2/7 22.0 319.2 MB 2/2 24.5 399.1 MB
1k 40k 3/7 28.9 492.0 MB - - -
100 4950 1/4 0.20 2.0 MB 1/1 0.21 2.6 MB
100 4950 4/4 0.41 7.2 MB - - -
500 124k 1/4 3.87 49.7 MB 1/1 4.24 55.8 MB
500 124k 2/4 5.73 90.7 MB - - -
500 124k 4/4 9.32 164.4 MB - - -
Dense
1k 499k 1/5 14.7 190.8 MB 1/1 15.6 226 MB
1k 499k 5/5 43.4 562.7 MB - - -
2k 1.9M 1/5 56.9 753 MB 1/1 61.2 899 MB
2k 1.9M 5/5 164 3.2 GB - - -
5k 12.4M 1/4 362 4.5 GB 1/1 391 5.6 GB
5k 12.4M 4/4 868 16.0 GB - - -
50 100 1/7 0.07 0.5 MB 1/4 0.07 0.8 MB
50 100 2/7 0.10 1.0 MB 2/4 0.10 1.2 MB
50 100 7/7 0.22 3.1 MB 4/4 0.16 2.3 MB
50 150 1/5 0.07 0.8 MB 1/3 0.07 0.8 MB
100 200 1/9 0.21 1.9 MB 1/4 0.22 2.0 MB
Like-Planar
100 300 1/7 0.21 2.2 MB 1/3 0.22 2.2 MB
500 1k 1/12 3.84 44.7 MB 1/8 4.04 50.5 MB
500 1k 12/12 23.1 471.8 MB 8/8 17.9 391 MB
1k 2k 1/12 14.7 158.8 MB 1/9 15.8 200 MB
1k 2k 12/12 91.6 1.8 GB 9/9 76.4 1.7 GB
The performance of the secure multiparty compu-
tation protocols feature is measured by two parame-
ters — the round complexity and the bandwidth. Ta-
ble. 3 presents the running time and the bandwidth
for two versions of the algorithm with different data
inputs. We performed the computation over the pre-
ferred network, which has high bandwidth and low
latency. The table shows the running time and band-
width for each number of rounds (r) separately and
how many possible iterations there are for the entire
computation, given by r/Iter. In general, the number
of Iter is somewhat larger. These cause a higher band-
width and running time. The running time and band-
width for first-round r = 1 is similar in both dense and
sparse graphs (those have the same number of ver-
tices). When the number of rounds r starts increas-
ing, both running time and bandwidth scalably in-
creased. Thus, until computation reach the last round
(r = Iter). In the dense graph, the computation fin-
ishes early, while in the sparse graph, iterating un-
til the last round in computation. This causes round
complexity and bandwidth for a given graph.
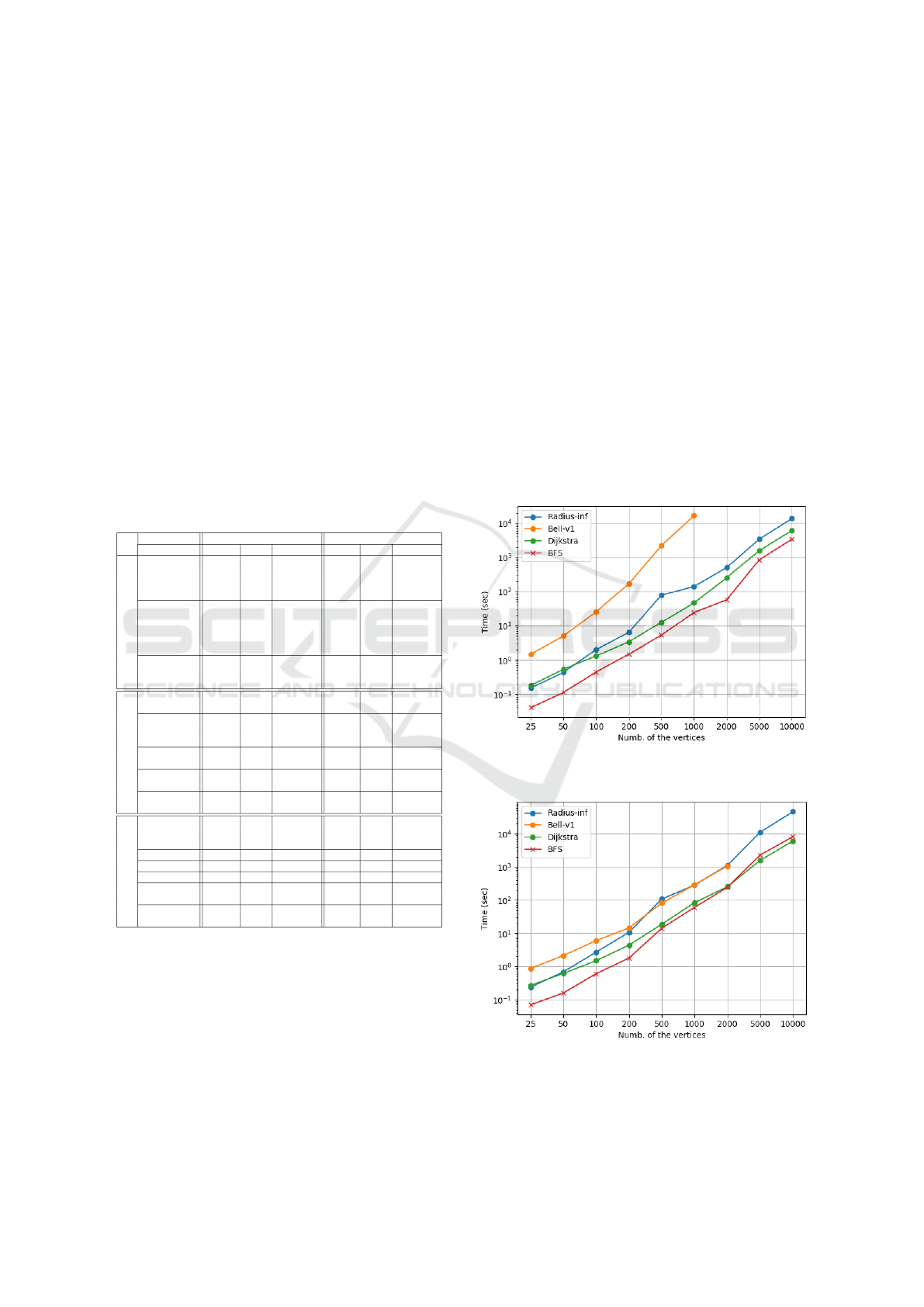
In Figure. 1, the benchmark results for the four
SSSD algorithms in privacy preservation over dense
graphs are presented. In contrast, the privacy-
preserving SSSD Algorithms for the sparse graph is
presented in Figure. 2. The number of the edges in
the sparse graphs is three times number of the ver-
tices, given by m = 3n.
Figure 1: Running time of the privacy-preserving SSSD al-
gorithms over the dense graphs in different sizes.
Figure 2: Running time of the privacy-preserving SSSD al-
gorithms over the sparse graphs in different sizes.
Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity
45

7 CONCLUSIONS
We have presented the state-of-the-art privacy-
preserving computation of the single-source shortest
distances for the weighted and unweighted graphs.
The proposed protocol is built based on a breadth-
first search algorithm. We have designed our proto-
col using SIMD to reduce the round complexity of
the SMC protocol. The protocol perfectly processes a
subset of the vertices and their edges in the possible
lower number of iterations, thus relaxing all edges.
We have benchmarked this protocol using different
graphs of various sizes. As well as, we evaluated our
work with a privacy-preserving shortest path by the
radius-stepping algorithm with its the best two cases
of radii. The result shows that our protocol is efficient.
Its running time was never achieved before by other
such work, especially for the dense graph. The fu-
ture work is studying other classical SSSD and APSD
algorithms in privacy and using different techniques
for finding the shortest path like path algebra com-
putation. As well as the ability to use our proposed
method as related work in other techniques in com-
binatorial graph algorithms such as maximum follow
algorithms. In general, our work can be considered
an example of how using SIMD is beneficial in de-
signing new computational protocols with low round
complexity. Such work using such a parallel strat-
egy makes the whole privacy-preserving computation
more usable due to reducing network latency, which
is considered the most critical challenge of the SMC
protocol set.
ACKNOWLEDGEMENT
We want to thank Dr Alisa Pankova from Cybernetica
for her constructive suggestions on bandwidth issues.
This research received funding from the European Re-
gional Development Fund through the Estonian Cen-
tre of Excellence in ICT Research-EXCITE.
REFERENCES
Aly, A. and Cleemput, S. (2017). An improved protocol for
securely solving the shortest path problem and its ap-
plication to combinatorial auctions. Cryptology ePrint
Archive, Report 2017/971. https://ia.cr/2017/971.
Aly, A., Cuvelier, E., Mawet, S., Pereira, O., and Van Vyve,
M. (2013). Securely solving simple combinatorial
graph problems. In International Conference on Fi-
nancial Cryptography and Data Security, pages 239–
257. Springer.
Aly, A. and Van Vyve, M. (2014). Securely solving classi-
cal network flow problems. In International Confer-
ence on Information Security and Cryptology, pages
205–221. Springer.
Anagreh, M., Laud, P., and Vainikko, E. (2021a). Parallel
privacy-preserving shortest path algorithms. Cryptog-
raphy, 5(4):27.
Anagreh, M., Vainikko, E., and Laud, P. (2021b). Paral-
lel privacy-preserving computation of minimum span-
ning trees. In ICISSP, pages 181–190.
Anagreh, M., Vainikko, E., and Laud, P. (2021c). Parallel
privacy-preserving shortest paths by radius-stepping.
In 2021 29th Euromicro International Conference on
Parallel, Distributed and Network-Based Processing
(PDP), pages 276–280. IEEE.
Beamer, S., Asanovic, K., and Patterson, D. (2012).
Direction-optimizing breadth-first search. In SC’12:
Proceedings of the International Conference on High
Performance Computing, Networking, Storage and
Analysis, pages 1–10. IEEE.
Bellman, R. (1958). On a routing problem. Quarterly of
applied mathematics, 16(1):87–90.
Berrendorf, R. and Makulla, M. (2014). Level-synchronous
parallel breadth-first search algorithms for multicore
and multiprocessor systems. In Nygard, T., editor, Fu-
ture Computing 2014, The Sixth International Confer-
ence on Future Computational Technologies and Ap-
plications. Venice, Italy, May 25-29, 2014, pages 26 –
31. ThinkMind.
Black, P. E. (2019). Bellman-ford algorithm. in Dictionary
of Algorithms and Data Structures (online), Paul E.
Black, ed.
Blanton, M., Steele, A., and Alisagari, M. (2013). Data-
oblivious graph algorithms for secure computation
and outsourcing. In Proceedings of the 8th ACM
SIGSAC symposium on Information, computer and
communications security, pages 207–218.
Bogdanov, D., Laud, P., and Randmets, J. (2014). Domain-
polymorphic programming of privacy-preserving ap-
plications. In Proceedings of the Ninth Workshop on
Programming Languages and Analysis for Security,
pages 53–65.
Bogdanov, D., Laur, S., and Willemson, J. (2008). Share-
mind: A framework for fast privacy-preserving com-
putations. In European Symposium on Research in
Computer Security, pages 192–206. Springer.
Bogdanov, D., Niitsoo, M., Toft, T., and Willemson, J.
(2012). High-performance secure multi-party com-
putation for data mining applications. International
Journal of Information Security, 11(6):403–418.
Boyle, E., Chung, K.-M., and Pass, R. (2015). Large-
scale secure computation: Multi-party computation
for (parallel) ram programs. In Annual Cryptology
Conference, pages 742–762. Springer.
Boyle, E., Jain, A., Prabhakaran, M., and Yu, C.-H. (2018).
The bottleneck complexity of secure multiparty com-
putation. In 45th International Colloquium on Au-
tomata, Languages, and Programming (ICALP 2018).
Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
46

Brickell, J. and Shmatikov, V. (2005). Privacy-preserving
graph algorithms in the semi-honest model. In Inter-
national Conference on the Theory and Application of
Cryptology and Information Security, pages 236–252.
Springer.
Buluc¸, A. and Madduri, K. (2011). Parallel breadth-first
search on distributed memory systems. In Proceed-
ings of 2011 International Conference for High Per-
formance Computing, Networking, Storage and Anal-
ysis, pages 1–12.
Canetti, R. (2000). Security and composition of multiparty
cryptographic protocols. Journal of CRYPTOLOGY,
13(1):143–202.
Canetti, R. (2001). Universally composable security: A new
paradigm for cryptographic protocols. In Proceedings
42nd IEEE Symposium on Foundations of Computer
Science, pages 136–145. IEEE.
Cohen, R., Coretti, S., Garay, J., and Zikas, V.
(2017). Round-preserving parallel composition of
probabilistic-termination cryptographic protocols. In
44th International Colloquium on Automata, Lan-
guages, and Programming (ICALP 2017). Schloss
Dagstuhl-Leibniz-Zentrum fuer Informatik.
Damg
˚
ard, I., Geisler, M., Krøigaard, M., and Nielsen, J. B.
(2009). Asynchronous multiparty computation: The-
ory and implementation. In International workshop
on public key cryptography, pages 160–179. Springer.
Damg
˚
ard, I. and Nielsen, J. B. (2003). Universally com-
posable efficient multiparty computation from thresh-
old homomorphic encryption. In Annual International
Cryptology Conference, pages 247–264. Springer.
Demmler, D., Schneider, T., and Zohner, M. (2015). Aby-
a framework for efficient mixed-protocol secure two-
party computation. In NDSS.
Dijkstra, E. W. et al. (1959). A note on two problems
in connexion with graphs. Numerische mathematik,
1(1):269–271.
Fakcharoenphol, J. and Rao, S. (2006). Planar graphs, nega-
tive weight edges, shortest paths, and near linear time.
Journal of Computer and System Sciences, 72(5):868–
889.
Floyd, R. W. (1962). Algorithm 97: shortest path. Commu-
nications of the ACM, 5(6):345.
Goldberg, A. V. (1984). Finding a maximum density sub-
graph. University of California Berkeley.
Henecka, W., K
¨
ogl, S., Sadeghi, A.-R., Schneider, T., and
Wehrenberg, I. (2010). Tasty: tool for automating se-
cure two-party computations. In Proceedings of the
17th ACM conference on Computer and communica-
tions security, pages 451–462.
Henzinger, M. R., Klein, P., Rao, S., and Subramanian,
S. (1997). Faster shortest-path algorithms for pla-
nar graphs. journal of computer and system sciences,
55(1):3–23.
Johnson, D. B. (1977). Efficient algorithms for shortest
paths in sparse networks. Journal of the ACM (JACM),
24(1):1–13.
Katz, J. and Koo, C.-Y. (2007). Round-efficient secure
computation in point-to-point networks. In Annual
International Conference on the Theory and Appli-
cations of Cryptographic Techniques, pages 311–328.
Springer.
Katz, J., Ostrovsky, R., and Smith, A. (2003). Round ef-
ficiency of multi-party computation with a dishonest
majority. In International Conference on the Theory
and Applications of Cryptographic Techniques, pages
578–595. Springer.
Klein, P. N., Mozes, S., and Weimann, O. (2010). Shortest
paths in directed planar graphs with negative lengths:
A linear-space o (n log2 n)-time algorithm. ACM
Transactions on Algorithms (TALG), 6(2):1–18.
Laud, P. (2015a). Parallel oblivious array access for secure
multiparty computation and privacy-preserving mini-
mum spanning trees. Proc. Priv. Enhancing Technol.,
2015(2):188–205.
Laud, P. (2015b). Stateful abstractions of secure multi-
party computation. In Laud, P. and Kamm, L., edi-
tors, Applications of Secure Multiparty Computation,
volume 13 of Cryptology and Information Security Se-
ries, pages 26–42. IOS Press.
Laur, S. and Pullonen-Raudvere, P. (2021). Foundations
of programmable secure computation. Cryptography,
5(3):22.
Liu, C., Wang, X. S., Nayak, K., Huang, Y., and Shi, E.
(2015). Oblivm: A programming framework for se-
cure computation. In 2015 IEEE Symposium on Secu-
rity and Privacy, pages 359–376. IEEE.
Meyer, U. and Sanders, P. (2003). δ-stepping: a paralleliz-
able shortest path algorithm. Journal of Algorithms,
49(1):114–152.
Mozes, S. and Wulff-Nilsen, C. (2010). Shortest paths in
planar graphs with real lengths in o (nlog 2 n/loglogn)
time. In European Symposium on Algorithms, pages
206–217. Springer.
Murphy, R. C., Wheeler, K. B., Barrett, B. W., and Ang,
J. A. (2010). Introducing the graph 500. Cray Users
Group (CUG), 19:45–74.
Rao, C. K. and Singh, K. (2020). Securely solving pri-
vacy preserving minimum spanning tree algorithms in
semi-honest model. International Journal of Ad Hoc
and Ubiquitous Computing, 34(1):1–10.
Yao, A. C. (1982). Protocols for secure computations. In
23rd annual symposium on foundations of computer
science (sfcs 1982), pages 160–164. IEEE.
Yoo, A., Chow, E., Henderson, K., McLendon, W., Hen-
drickson, B., and Catalyurek, U. (2005). A scal-
able distributed parallel breadth-first search algorithm
on bluegene/l. In SC’05: Proceedings of the 2005
ACM/IEEE Conference on Supercomputing, pages
25–25. IEEE.
Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity
47
