
Multi Robot Surveillance and Planning in Limited Communication
Environments
Vibhav Inna Kedege
1,2
, Aleksander Czechowski
1
, Ludo Stellingwerff
2
and Frans. A. Oliehoek
1
1
Department of Intelligent Systems, Delft University of Technology, Delft, The Netherlands
2
Almende B. V., Rotterdam, The Netherlands
Keywords:
Agents, Autonomous Systems, Artificial Intelligence, Multi-agent Systems, Robotic Exploration, Planning.
Abstract:
Distributed robots that survey and assist with search & rescue operations usually deal with unknown en-
vironments with limited communication. This paper focuses on distributed & cooperative multi-robot area
coverage strategies of unknown environments, having constrained communication. Due to restricted commu-
nication there is performance loss for the multi-robot team, in terms of increased number of steps to cover an
area. From simulation results, it is shown that enabling partial communication amongst robots can recover a
significant amount of performance by decreasing the number of steps required for area coverage. Additionally
it is found that partially communicating robots that predict the paths of peers do not perform significantly
different from robots that are only partially communicating. This is found due to predictions spreading the
robots away from one another, which reduces meeting times and instances of inter-robot data sharing.
1 INTRODUCTION
When multiple robots or agents are deployed to sur-
vey or map an indoor disaster zone, the area to be
mapped or covered is often unknown and has re-
stricted communication. Figure 1 shows such a sit-
uation where a fleet of aerial robots navigate and map
a previously unknown environment that is cluttered,
radio-hampered and GPS-denied. Such a setting leads
to reduced inter-robot data sharing, a decrease in co-
operative behaviour and a possible increase in redun-
dant area coverage, with the same sub-region of the
environment being covered by multiple robots. An
increase in redundant coverage increases survey time
which leads to delay in search, rescue and disaster
containment efforts. To deal with the problem of re-
dundant area coverage, many researchers have used
communication to synchronize robot knowledge/data.
However, as described this may not always be avail-
able in disaster environments.
Thus, the goal of this paper is to evaluate the per-
formance of area coverage algorithms and techniques
that deal with unknown limited communication envi-
ronments. To do this, a distributed multi-robot team
is simulated on different communication scenarios to
perform surveillance or area coverage. First, agents
are simulated in a full communication scenario where
the Monte Carlo Tree Search (MCTS) algorithm used
Figure 1: Four aerial robots surveying an environment that
has restricted communication.
in (Hyatt et al., 2020) is used for multi-robot area cov-
erage. Following this, No Communication is simu-
lated where agents have no possibility for communi-
cation. The third scenario is partial communication,
where robots can communicate when within a com-
munication range. In the fourth scenario, in addition
to partial communication robots can predict the paths
of peers using a heuristic that is inspired by (Claes
et al., 2017). By following this approach, the con-
tributions made by this work are to extend the study
on Coverage Path Planning by (Hyatt et al., 2020) to
an environment of limited communication and extend
the heuristic prediction model introduced by (Claes
et al., 2017) to robotic area coverage and where the
global state of the environment is unknown.
Kedege, V., Czechowski, A., Stellingwerff, L. and Oliehoek, F.
Multi Robot Surveillance and Planning in Limited Communication Environments.
DOI: 10.5220/0010775500003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 139-147
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
139

The rest of the paper is organised as follows. Sec-
tion 2 mentions relevant methods used previously to
perform multi-robot area coverage and introduces the
method used to perform the same in this paper. Sec-
tion 3 elaborates on the main approach taken in this
paper. Following this, Section 4 presents experimen-
tal results. Section 5 draws important inferences and
also reflects on the limitations of the approach taken.
Finally, Section 6 draws key conclusions and provides
directions for future work.
2 RELATED WORK
Prior literature/methods have been considered to se-
lect a suitable baseline for the approach and ex-
periments. One of the earliest methods in multi-
robot area coverage is robots dispersing in the en-
vironment (Howard et al., 2002), (Damer et al.,
2006), (Pang et al., 2019). The methods following
this approach however do not allow robots to share
data and work together, thereby reducing coopera-
tion. Frontier based area coverage utilised in (Umari
and Mukhopadhyay, 2017), (Nair and Givigi, 2019),
(Dadvar et al., 2020), (Bautin et al., 2012), (Bena-
vides et al., 2016) aims at directing robots to posi-
tions at the boundaries of known and unknown re-
gions. Most methods however are either centralised
or assume unrestricted communication to exist in
the environment, where robots can share information
with one another, irrespective of physical limitations.
Environment partitioning utilised by (Lopez-Perez
et al., 2018), (Jain et al., 2020) attempts to reduce
redundant coverage by dividing the region amongst
robots. However, this approach too assumes unre-
stricted communication. Game theory based multi-
robot mapping in (Meng, 2008), (Ni et al., 2020) at-
tempts to find suitable positions for agents based on
the computation of a Nash Equilibrium using a pre-
defined utility measure. This approach however as-
sumes some prior information of the environment as
well as unrestricted communication.
In comparison to these methods, the Monte Carlo
Tree Search (MCTS) algorithm used by Hyatt et al
(Hyatt et al., 2020) allows robots to simulate the paths
of peers, which brings in cooperation and reduces re-
dundant coverage. The algorithm also plans an action
based on future rewards, which helps robots avoid
getting stuck in cluttered regions. One drawback
however is that the approach assumes an unrestricted
communication environment. However, as the ap-
proach is distributed, cooperative and can explore un-
known maps by looking ahead, it has been chosen as
the baseline. Apart from robot area coverage, MCTS
has also been used for other multi-robot applica-
tions like warehouse commissioning, (Li et al., 2019),
(Czechowski and Oliehoek, 2020), (Claes et al., 2017)
and active object recognition (Best et al., 2019). In
(Claes et al., 2017), robots additionally have the capa-
bility to predict the paths of peers, which could also
be useful in a limited communication setting.
3 APPROACH
The experiments of this paper are based on an area
coverage setting with multiple cooperative robots.
The setting is modelled by a simulation where robots
are represented as software agents that can communi-
cate with one another according to set rules of com-
munication. Based on the level of communication
between agents, four different settings or communi-
cation scenarios are created and described further in
3.3.1 to 3.3.4. The first setting implemented is the
Full Communication scenario, where agents have no
restrictions on their communication capability. Fol-
lowing this is the No Communication scenario where
agents cannot communicate with one another. In the
third setting of Partial Communication, agents can
share information when within a predefined commu-
nication range. Agents are also given the capability
to predict the paths of peers in the fourth setting of
Partial Communication with Prediction. Compared to
the first (baseline) setting, the remaining settings are
expected to take larger time-steps for area coverage.
This increase in time-steps is referred to as perfor-
mance loss in this work. The goal of the partial com-
munication setting variants are to recover this loss.
3.1 Simulation Environment
In each communication scenario, every agent only
knows the size of the region that the entire team
is required to cover and the number of agents
in the team. Each agent divides the region
into grid-cells that can take one of the values of
{Covered,Unexplored, Obstacle}. Initially, all grid-
cells are assumed to be Unexplored. A grid-cell tran-
sitions from Unexplored to Covered when an agent
moves over it. Agents can also only observe their
local surroundings. This can be understood by con-
sidering Figure 2 where the agent’s environment po-
sition can be seen in subfigure 2a, while what the
agent perceives of the environment can be seen in
subfigure 2b. Further, each agent can take up posi-
tions in the grid-world which is represented as a tu-
ple (x, y, yaw). The position (x, y) refers to the x and
y coordinates in the grid-world, while yaw refers to
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
140

(a) Agent’s Environment
Position
(b) Agent’s Environment
Belief
Figure 2: Local observability - The
colours {Green, Blue, Red} correspond to
{Covered,U nexplored, Obstacle} respectively.
the heading angle of the agent with respect to the
horizontal axis. Each agent can execute one of the
actions {FORWARD, RIGHT, LEFT }, where the ac-
tion FORWARD moves an agent one grid-cell ahead
based on the yaw value, while RIGHT and LEFT ac-
tions only rotate the agent by 90
◦
.
3.2 Algorithm
Algorithm 1: MCTS for Area Coverage.
Ensure: Area Coverage by N Agents (A
1
, A
2
..A
N
)
1: while CoverageGoal is Not Met do
2: for i ← 1, .., N do
3: A
i
.Map ← A
i
.Sensing
4: DataSharing()
5: A
i
.Action ← A
i
.MCT SPlanning
6: end for
7: ActionExecution(A
1
, A
2
..A
N
)
8: end while
Algorithm 1 describes the steps that are common
to all settings. The approach consists of each agent
sequentially executing four major steps of Environ-
ment Sensing, Data Sharing (if possible), MCTS Path
Planning and Action Execution. These steps are ex-
ecuted until a predefined CoverageGoal is achieved
by the whole team. In every setting, each agent of
the team first senses the environment to update its
knowledge/map about the environment. Following
this is the Data Sharing step which differs in every
setting and thus indicated in a box. In the Predic-
tion scenario, there is additionally the function of
peer prediction at this step. Utilising information ob-
tained from sensing & sharing or by prediction, an
agent begins the path planning step where it utilises
MCTS to plan the next action from the action set
{FORWARD, RIGHT, LEFT }. The above steps are
performed by each agent, after which the planned ac-
tion of every agent of the team is executed.
3.2.1 Data Sharing
The data sharing step is required for each agent to
share its grid-world position, its surveyed map and its
most recently computed plans. This data is shared
only with a selection of agents, based on the setting.
Using surveyed map information of peer agents, an
agent updates its own knowledge of the overall region
to explore. The computed plans of peer agents are
then executed on this updated knowledge map during
the MCTS planning step, as will be explained further.
By using the updated knowledge map, an agent can
plan paths away from already covered environment
portions, which minimises redundant coverage plans
and reduces the number of coverage steps by the team.
3.2.2 MCTS Planning
The planning step utilises MCTS to plan an action. In
the search method, an agent uses Monte Carlo Sim-
ulations to construct a tree of future states of the en-
vironment. The tree consists of nodes that represents
the state of the environment and branches which cor-
respond to actions {FORWARD, RIGHT, LEFT }. A
single iteration of MCTS planning consists of four
parts (Browne et al., 2012). The first part is where
the tree is traversed using a tree policy (selection).
A new action is sampled and a new node is created
based on the resulting environment state (expansion).
A heuristic policy/ default policy is then executed for
a predefined number of time-steps (roll-out). Finally,
a reward is computed which is stored in the visited
nodes (back-propagation). This is also the technique
followed by (Hyatt et al., 2020). While the Tree Pol-
icy used is the same as this work (Upper confidence
bound for trees, UCT1), there are modifications made
in the Default Policy. The Default Policy utilised by
(Hyatt et al., 2020) does not handle the case of being
completely surrounded by Covered grid-cells. The
Default Policy implemented here considers this and
directs planning towards one of the Covered grid-cells
in a semi-random manner.
The Reward function is the TotalReward which is
given by,
TotalReward = w
LR
× LocalReward+
w
GR
× GlobalReward
(1)
w
GR
and w
LR
are the weights given to the global
and local rewards respectively. In the above equation
GlobalReward is given by the relation:
GlobalReward = −
N(UnexploredCells)
N(TotalCells)
(2)
In the above equation N(UnexploredCells) refers to
the number of unexplored grid-cells in the gridmap
Multi Robot Surveillance and Planning in Limited Communication Environments
141

and N(TotalCells) refers to the total number of grid-
cells present in the gridmap. The LocalReward is
given by equation 3,
LocalReward =
T
∑
t=1
"
1
(t + 1)
2
(C
cov
−C
hit
)
#
(3)
In the above equation C
cov
and C
hit
are hyper-
parameters that determine the simulation result.
C
cov
> 0 if the robot lands up on a newly discovered
grid cell at time step t and ”covers” it, else C
cov
= 0.
C
hit
> 0 if the robot encounters an obstacle or another
robot at time step t, else it remains 0. The normalisa-
tion using the (t +1)
2
term is used to decay the reward
overtime.
Overall, in every MCTS algorithm iteration the
agent first simulates the plans of peer agents on its
own simulator/knowledge map of the environment.
This simulation is only possible if the agent has
information obtained via Data Sharing or through
prediction. During rollout, the agent simulates its
own plan using the default policy and computes the
LocalReward for a predefined number of time-steps
(T ). The GlobalReward and TotalReward are then
computed, which is back-propagated until the root of
the tree. This process is repeated for a predefined
number of iterations. The root of the tree represents
the starting of the planning and the action that results
in the largest accumulated reward at the root is exe-
cuted. Thus, while planning happens for the future T
time-steps, only the one action that gives the highest
TotalReward is executed.
3.3 Communication Scenarios
As seen in algorithm 1, each setting differs in the Data
Sharing step. This will be discussed below.
3.3.1 Full Communication (FULLCOMM or
FC)
Algorithm 2: FC Data Sharing for Agent i (A
i
).
1: for j ← 1, .., N and j ̸= i do
2: A
i
.Map ← MapMerge(A
i
.Map, A
j
.Map)
3: A
i
.Position
A
j
← A
j
.Position
4: A
i
.PathPlan
A
j
← A
j
.PathPlan
5: end for
Algorithm 2 shows the specific portion of data
sharing for an Agent i (A
i
) during the FULLCOMM
scenario. As there is unrestricted data sharing, A
i
shares and receives information from every peer of
the team of size N at anytime. A
i
updates its map
by merging its current knowledge of the world with
map information from peers. The current position and
most recent path plans or the best path plans in the
previous time-step of all peers is also recorded (Hy-
att et al., 2020). This is used in the subsequent step
of MCTS Planning in Algorithm 1. As agents know
the positions and plans of peers at all times in FULL-
COMM, there is reduced redundant coverage. This
leads to the least area coverage time amongst the four
settings.
3.3.2 No Communication (NOCOMM or NC)
During NOCOMM, A
i
has no possibility for commu-
nication and the data sharing step in algorithm 1 is
skipped. When calculating plans, A
i
only simulates
its own actions but still computes TotalReward. As
the agents of the team make plans without taking into
account the plans of one another, redundant coverage
is the highest and area coverage takes the maximum
number of steps.
3.3.3 Partial Communication (PARCOMM or
PC)
Algorithm 3: PC Data Sharing for Agent i (A
i
).
1: A
i
.Neighbours ← A
i
.CommRangeSensing
2: for j ← 1, .., A
i
.Neighbours do
3: A
i
.Map ← MapMerge(A
i
.Map, A
j
.Map)
4: A
i
.Position
A
j
← A
j
.Position
5: A
i
.PathPlan
A
j
← A
j
.PathPlan
6: end for
Algorithm 3 explains data sharing in the partial
communication scenario where A
i
shares data with
neighbouring peers that are within a predefined com-
munication range. The list of neighbouring peers
(A
i
.Neighbours) is obtained via the step of sens-
ing peers that are within a pre-defined communica-
tion range (A
i
.CommRangeSensing). The data shared
between A
i
with neighbours is the same as FULL-
COMM. During MCTS planning, A
i
simulates the
path of neighbouring peers and subsequently com-
putes the TotalReward. As there is some amount
of sharing in PARCOMM, agents can avoid redun-
dant coverage at several instances of time, resulting
in area coverage steps lying in between NOCOMM
and FULLCOMM.
3.3.4 Partial Communication with Prediction
(PARCOMM PRED or PCPD)
Algorithm 4 illustrates PARCOMM PRED that
builds over PARCOMM. In this, A
i
predicts the paths
of agents outside communication range. As A
i
knows
the total number of team members, it can extract
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
142

Algorithm 4: PARCOMM PRED Data Sharing and Predic-
tion for Agent i (A
i
).
1: A
i
.Neighbours ← A
i
.CommRangeSensing
2: for j ← 1, .., N and j ̸= i do
3: if A
j
in A
i
.Neighbours then
4: A
i
.Map ← MapMerge(A
i
.Map, A
j
.Map)
5: A
i
.Position
A
j
← A
j
.Position
6: A
i
.PathPlan
A
j
← A
j
.PathPlan
7: else
8: A
i
.PathPlan
A
j
← A
i
.PeerPrediction(A
j
)
9: end if
10: end for
agents that are not present in A
i
.Neighbours (Non-
Neighbours). To make predictions, A
i
uses the most
recent plans that it knows about Non-Neighbours.
The plan obtained by A
i
(A
i
.PathPlan
A
j
) is a finite list
of actions that a peer agent executes, for a predefined
number of time steps in the default policy of MCTS.
When this list gets exhausted, A
i
predicts the path of
peer agents using a Coverage-by-Step Heuristic met-
ric. This metric is used for any instance in the list
A
i
.PathPlan
A
j
that is unknown. In this metric, A
i
pre-
dicts the actions of peer agents by computing the re-
ward for the eight grid-cells around the predicted/last
seen position of the peer agent. This can be under-
stood by considering the scenario of Figure 3. In the
scenario, Agent 0 computes a heuristic for each of the
eight neighbouring grid-cells (within the yellow box
in subfigure 3c) of Agent 1 in order to predict its next
position and action.
(a) Environment
(b) Agent Position
(c) Peer Belief
Figure 3: Coverage-by-Step Heuristic Computation -
Amongst the two agents in subfigure 3a, Agent 0 (top) pre-
dicts the next action of Agent 1 (bottom) using a heuristic
reward of the surrounding eight gridcells as shown in sub-
figure 3c.
The heuristic reward (Reward
heur
) is computed for
each zone. Equation (4) shows this reward compu-
tation, where R
cov
denotes the coverage reward of
the particular zone and N
min steps
gives the minimum
number of steps that the belief agent is required to
move from its current position to the zone position.
Reward
heur
=
R
cov
N
minsteps
(4)
The value of R
cov
is given by the equation
R
cov
=
+2, if zone is Unexplored
+1, if zone is Covered
0, if zone is Obstacle
(5)
It is important to note that due to an unknown en-
vironment, predictions are not always correct. The
number of correct predictions decreases with time
since the last meeting between agents. When pre-
dictions are correct, agents spread out in the environ-
ment that potentially leads to a reduction in the area
coverage steps by the team. With wrong predictions
however, a particular sub-region may remain unex-
plored as each agent may assume that the other ex-
plores it. This increases the area coverage steps over-
time. A method to solve this is inspired by the do-
it-yourself (DIY) reward presented by Claes et al in
(Claes et al., 2017) where agents have a certain bias
to perform tasks on its own. This idea is incorpo-
rated into the rollout step of the MCTS planner, where
the agent simulates the actions of solely the Neigh-
bour agents before making its own plans. Once the
agent has planned its own path, it simulates the plans
of Non-Neighbours. This helps override the plans
of peers for which it has less information about. To
ensure that plans of Non-Neighbours are still consid-
ered during MCTS planning, the agent still computes
the GlobalReward. As PARCOMM PRED includes
the aspect of partial communication, the area cover-
age steps lies between FULLCOMM & NOCOMM.
Compared to PARCOMM however, there is no signif-
icant difference in coverage steps, as will be observed
and discussed further.
4 EXPERIMENTS
The experiments for each communication scenario
were implemented on a simulation environment de-
veloped in Python. The experiments involved spawn-
ing a team of robots on a gridmap and recording the
number of steps taken by the team for area cover-
age. The experiments were run on 40x40 gridmaps
with 10% obstacle density. All experiments were con-
ducted on five different gridmaps for 10 times each,
thereby resulting in 50 simulations for each setting.
The goal of each simulation was 95% area cover-
age. 100% area coverage was not considered, due
to the high variance of results that was caused when
agents would cover far off single grid-cells. By de-
fault, the sensor and communication range was set to
one. With a sensor range of one, agents could sense
the status of nearby eight grid-cells as explained in
Figure 2. A communication range of one implied
Multi Robot Surveillance and Planning in Limited Communication Environments
143
that agents could share information with those agents
present in the eight surrounding grid-cells. Further,
simulations terminated when the team of agents com-
pleted the area coverage. The hyper-parameters that
were utilised are listed in Table 1.
Table 1: Hyper-parameter Values.
Hyper-parameter Description Value
C cov Coverage Reward 5
C hit Collision Penalty 2
lw Local Reward Weight 1
gw Global Reward Weight 1
T horizon Rollout steps 30
MCTS iter MCTS Loop Iterations 100
C p UCT1 Exploration 0.707
As discussed previously, PARCOMM and PAR-
COMM PRED are created to recover the lost per-
formance when moving from FULLCOMM to NO-
COMM. In the experiments, this is measured using a
recovery performance metric. Equation 6 shows this
metric for the PARCOMM case,
Recovery
PC
=
N
NC
− N
PC
N
NC
− N
FC
× 100 (6)
In this equation N
NC
, N
PC
and N
FC
are the number
steps for area coverage for NOCOMM, PARCOMM
and FULLCOMM respectively. Equation 6 measures
the recovered number of steps for PARCOMM as
a percentage of the original lost performance when
moving to NOCOMM. A larger value of Recovery
PC
indicates a larger difference between NOCOMM
& PARCOMM, and PARCOMM moves closer to
FULLCOMM performance. A similar computation
is also made for PARCOMM PRED by replacing the
numerator with N
NC
− N
PCPD
, where N
PCPD
is the
number of steps for the PARCOMM PRED setting.
4.1 Area Coverage v/s Team Size
In this experiment, the number of steps for area cov-
erage is studied for increasing team size and for each
communication scenario.
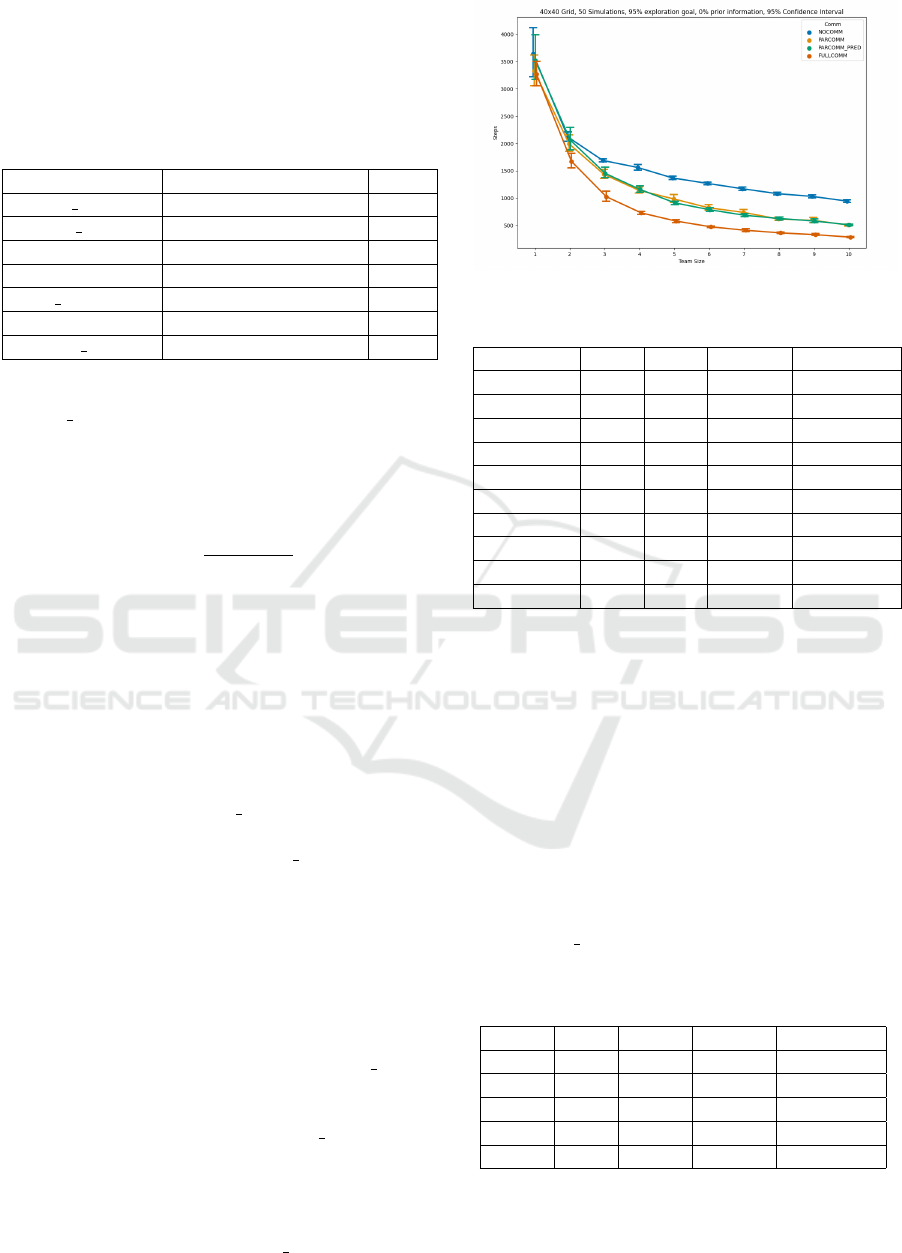
From Figure 4, it can be seen that the perfor-
mance of both PARCOMM and PARCOMM PRED
lies in between NOCOMM and FULLCOMM. Due
to the overlapping confidence intervals, the difference
between PARCOMM and PARCOMM PRED is not
significant for any team size. From the values indi-
cated in Table 2, the recovery provided by each set-
ting increases with the increase in team-size. In the
10 agent scenario, recovery increases upto 66% for
both PARCOMM and PARCOMM PRED.
Figure 4: 40x40 Map.
Table 2: 40x40 Map Data.
Team Size FC NC PC Rec PCPD Rec
1 3265 3637 83 33
2 1674 2118 28 12
3 1028 1691 38 36
4 733 1562 50 48
5 582 1371 49 58
6 477 1271 56 61
7 414 1174 57 64
8 367 1084 65 63
9 334 1034 63 64
10 289 948 66 66
4.2 Area Coverage v/s Communication
Range
In this experiment, a team of three agents is spawned
into the arena. The communication range is varied
to take one of the values in the set {1, 2, 3, 4, 5}. A
communication range of N indicates that an agent can
communicate with up-to N grid-cells around it in all
directions. Due to the high variance in the case of
smaller number of agents, each of the communica-
tion scenarios are run for 400 simulations (instead of
50) and the recovery provided by the PARCOMM and
PARCOMM PRED is measured using Equation 6.
Table 3: Area Coverage v/s Communication Range, 3
agents - Data (NC - 1717, FC - 1077).
Range PC PCPD PC Rec PCPD Rec
1 1435 1418 44 43
2 1358 1360 47 59
3 1312 1278 62 73
4 1248 1220 73 79
5 1187 1182 77 81
In the case of a smaller number of agents (three
in this case) spawned into an arena, it can be seen
from Figure 5 that area coverage steps of PARCOMM
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
144
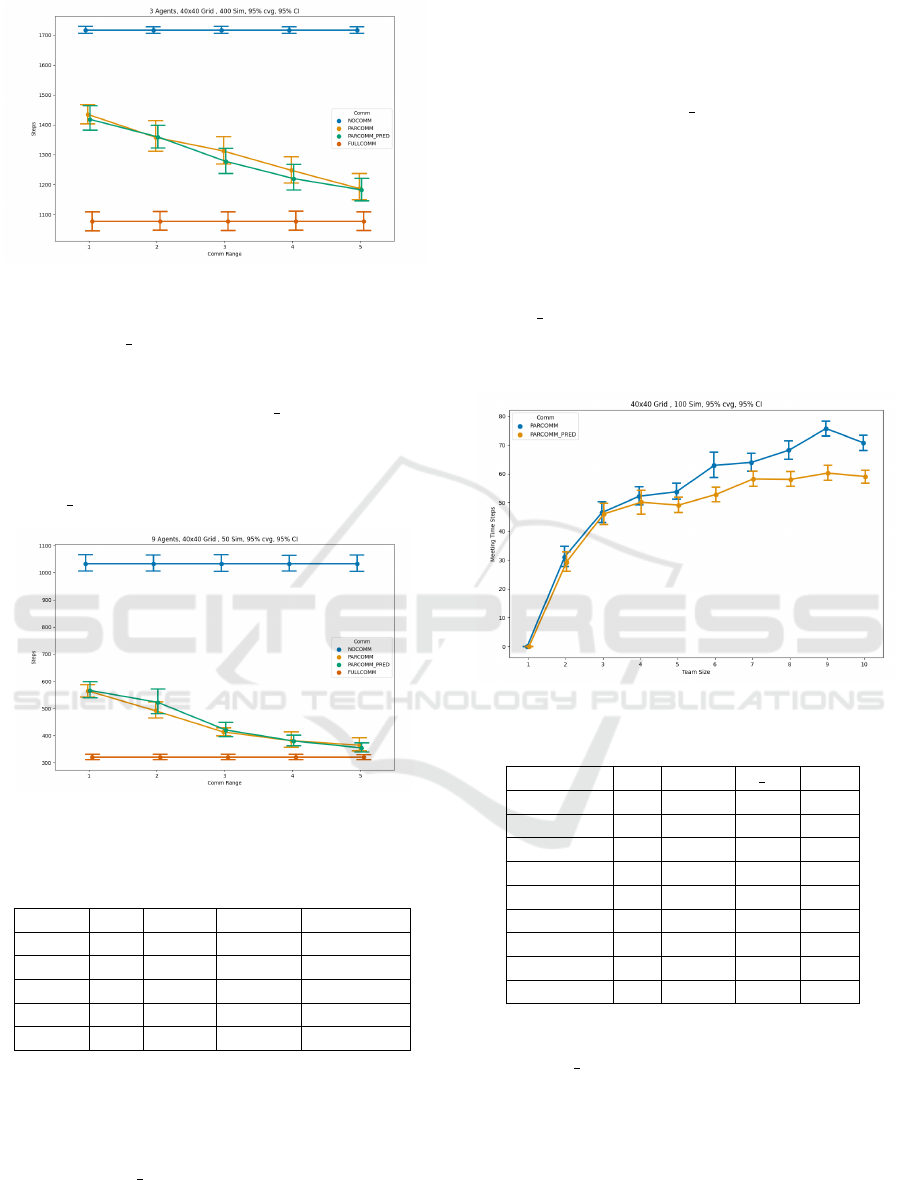
Figure 5: Area Coverage v/s Communication Range, 3
agents - Graph.
& PARCOMM PRED approach FULLCOMM level
with an increase in communication range. The over-
lapping confidence intervals indicate no significant
difference between PARCOMM PRED and PAR-
COMM. From Table 3, it can be seen that increas-
ing the communication range from one till five can
increase the percentage of recovery to 81% for PAR-
COMM PRED and 77% for PARCOMM.
Figure 6: Area Coverage v/s Communication Range, 9
agents - Graph.
Table 4: Area Coverage v/s Communication Range, 9
agents - Data (NC - 1034, FC - 321).
Range PC PCPD PC Rec PCPD Rec
1 565 567 66 66
2 491 522 76 72
3 413 421 87 86
4 382 380 92 92
5 365 355 94 95
The same experiment was repeated with larger
number of agents (nine) for 50 simulations and the
coverage performance was studied. Figure 6 shows
overlap in the confidence intervals of PARCOMM
and PARCOMM PRED, indicating no significant dif-
ference. From Table 4, the percentage recovery in
the case of communication range of five is as high
as 95%.
4.3 Meeting Time Steps v/s Team Size
In the previous sections, it was observed that there
is no statistical significant difference between PAR-
COMM and PARCOMM PRED. This experiment
aims at providing reasoning to this observed be-
haviour by studying the number of time steps where
agents meet one another for varying team sizes.
The number of meeting times is considered as it
is the moment when agents can share information,
thereby knowing each one’s plans and updating its
own knowledge about the environment coverage.
This is performed for both PARCOMM & PAR-
COMM PRED and the meeting time steps metric is
the average of the total number of time steps that
agents of a team spend in meeting a peer.
Figure 7: Meeting Time Steps v/s Team Size - Graph.
Table 5: Meeting Time Steps v/s Team Size - Data.
Team Size PC PCPD p val Sig?
2 31 29 0.46 No
3 47 46 0.85 No
4 52 50 0.44 No
5 54 49 0.02 Yes
6 63 53 0 Yes
7 64 58 0.01 Yes
8 68 58 0 Yes
9 76 60 0 Yes
10 71 59 0 Yes
From Figure 7, it can be seen that agents under
PARCOMM PRED meet less often as compared to
PARCOMM. From Table 5 this difference is found to
be statistically significant (using t-tests) for team sizes
greater than five.
Multi Robot Surveillance and Planning in Limited Communication Environments
145

5 DISCUSSION
From the experiments conducted, it is seen that partial
communication results in high performance recovery.
This recovery increases with increase in team size
and communication range, which indicates the ben-
efit of increased meeting times and information shar-
ing amongst agents for the overall exploration perfor-
mance. It is also found that enabling agents to predict
the plans of peers does not provide additional bene-
fit to area coverage, due to reduced number of meet-
ing times. We discuss these inferences in more detail
here.
5.1 Merit of Information Sharing
The strategy that each agent follows is sensing, in-
formation sharing and MCTS planning. Sharing of
information is observed to be highly beneficial for
overall region exploration. Subsections 4.1 & 4.2 in-
dicate this, where increasing team size and commu-
nication range decreases the area coverage steps. Af-
ter an agent obtains shared information, it first sim-
ulates the plans of peers and then plans its own path.
This leads to paths that can avoid redundant coverage.
Subsection 4.3 also shows information sharing bene-
fit. Even though PARCOMM PRED spreads robots
away, the coverage steps is similiar to PARCOMM
due to the increase in redundant coverage, resulting
from reduced information sharing.
5.2 Large Partial Communication
Recovery
Subsections 4.1 and 4.2 indicate that increasing team
size and communication range can increase the per-
formance recovery of PARCOMM. The performance
recovery with nine agents in PARCOMM is as high
as 63% and raising the communication range to five
grid-cells further increases this recovery to 94%. This
can be attributed to increased information sharing in-
stances. It is also important to note that in the physi-
cal world, communication range is not as tightly con-
trolled with gridcells and robots can communicate
through a larger range. Thus when deployed in re-
alistic situations, PARCOMM is likely to further be
closer to the performance of FULLCOMM. This in-
dicates that certain multi-robot coverage algorithms
that rely on unrestricted communication, can be de-
ployed into limited communication environments and
possibly achieve almost unchanged performance lev-
els.
5.3 Limited Benefit of Peer Prediction
PARCOMM and PARCOMM PRED perform in a
similar manner as seen from subsections 4.1 and 4.2.
Predictions causes a robot to spread away from peers
and reduces data sharing instances, where robots
share important map coverage information. This in-
formation enables an agent avoid already covered re-
gions. Thus, reducing meeting times results in higher
chances of redundant area coverage. Subsection 4.3
also shows the effect where the difference in the meet-
ings between agents in PARCOMM PRED and PAR-
COMM is significant for large team sizes. This is due
to increased number of misprediction corrections for
robots in larger team sizes. When this occurs, correct
predictions about peer paths increases which leads to
further dispersion and reduced meeting times.
5.4 Limitations
While the approach and experiments do provide re-
sults that can be translated to a real-world setting,
there are some limitations. One limitation is the map,
where grid-cells are of the same size as the robot.
While grid-cells do provide a rough estimate of obsta-
cles, they may not always be coarse enough to model
every obstacle. In terms of the MCTS algorithm, due
to the finite amount of computation, 100% coverage
of the area is difficult and additional mechanisms to
handle isolated far off unexplored grid-cells are re-
quired. In the experiments, currently termination oc-
curs when the whole team covers the grid and not
when each individual agent senses termination. This
leads to a type of centralised termination which is not
desirable, especially if robots are expected to return
to the base station after they are done mapping.
6 CONCLUSIONS
In this work, strategies that enable multi-robot sur-
veying or area coverage in unknown limited commu-
nication environments have been studied. An existing
baseline method that used Monte Carlo Tree Search
(Hyatt et al., 2020) was implemented first. The com-
munication dependency of this work was completely
removed and strategies to recover the lost efficiency
were studied. As seen from the experiments, provid-
ing robots the ability to communicate when within a
communication range can regain a significantly high
percentage of lost efficiency. By increasing the com-
munication range this percentage can be further in-
creased. It is also found that peer predictions can
spread out robots in the arena, but do not significantly
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
146

reduce area coverage time due to the reduced num-
ber of information sharing instances. Some directions
for future work are strategies on ensuring less varying
100% area coverage and experiments avoiding cen-
tralised termination.
ACKNOWLEDGEMENTS
This work is part of the COMP4DRONES project
(https://www.comp4drones.eu/) and has received
funding from the ECSEL Joint Undertaking (JU) un-
der the grant agreement No 826610.
Vibhav Inna Kedege, Aleksander Czechowski,
and Frans A. Oliehoek were also supported by the
European Research Council (ERC) under the Euro-
pean Union’s Horizon 2020 research and innovation
programme (grant agreement No. 758824 —INFLU-
ENCE).
REFERENCES
Bautin, A., Simonin, O., and Charpillet, F. (2012). Minpos
: A novel frontier allocation algorithm for multi-robot
exploration. In Su, C.-Y., Rakheja, S., and Liu, H.,
editors, Intelligent Robotics and Applications, pages
496–508.
Benavides, F., Monz
´
on, P., Carvalho Chanel, C. P., and
Gramp
´
ın, E. (2016). Multi-robot cooperative sys-
tems for exploration: Advances in dealing with con-
strained communication environments. In 2016 XIII
Latin American Robotics Symposium and IV Brazilian
Robotics Symposium (LARS/SBR), pages 181–186.
Best, G., Cliff, O. M., Patten, T., Mettu, R. R., and Fitch, R.
(2019). Dec-mcts: Decentralized planning for multi-
robot active perception. Int. J. Robotics Res., 38(2-3).
Browne, C., Powley, E., Whitehouse, D., Lucas, S., Cowl-
ing, P., Rohlfshagen, P., Tavener, S., Perez Liebana,
D., Samothrakis, S., and Colton, S. (2012). A survey
of monte carlo tree search methods. IEEE Transac-
tions on Computational Intelligence and AI in Games,
4:1:1–43.
Claes, D., Oliehoek, F., Baier, H., and Tuyls, K. (2017). De-
centralised online planning for multi-robot warehouse
commissioning. In Proceedings of the 16th Confer-
ence on Autonomous Agents and MultiAgent Systems,
AAMAS ’17, page 492–500, Richland, SC. Interna-
tional Foundation for Autonomous Agents and Multi-
agent Systems.
Czechowski, A. and Oliehoek, F. A. (2020). Decentralized
mcts via learned teammate models. Proceedings of the
Twenty-Ninth International Joint Conference on Arti-
ficial Intelligence.
Dadvar, M., Moazami, S., Myler, H. R., and Zargarzadeh,
H. (2020). Exploration and coordination of comple-
mentary multi-robot teams in a hunter and gatherer
scenario. https://arxiv.org/abs/1912.07521.
Damer, S., Ludwig, L., LaPoint, M. A., Gini, M., Pa-
panikolopoulos, N., and Budenske, J. (2006). Disper-
sion and exploration algorithms for robots in unknown
environments. In Gerhart, G. R., Shoemaker, C. M.,
and Gage, D. W., editors, Unmanned Systems Tech-
nology VIII, volume 6230, pages 251 – 260. SPIE.
Howard, A., Matari
´
c, M. J., and Sukhatme, G. S. (2002).
Mobile sensor network deployment using potential
fields: A distributed, scalable solution to the area cov-
erage problem. In Proceedings of the International
Symposium on Distributed Autonomous Robotic Sys-
tems, pages 299–308.
Hyatt, P., Brock, Z., and Killpack, M. D. (2020).
A versatile multi-robot monte carlo tree search
planner for on-line coverage path planning.
https://arxiv.org/abs/2002.04517.
Jain, U., Tiwari, R., and Godfrey, W. (2020). A hybrid evsa
approach in clustered search space with ad-hoc parti-
tioning for multi-robot searching. Evolutionary Intel-
ligence, 13.
Li, M., Yang, W., Cai, Z., Yang, S., and Wang, J. (2019).
Integrating decision sharing with prediction in decen-
tralized planning for multi-agent coordination under
uncertainty. In Proceedings of the Twenty-Eighth In-
ternational Joint Conference on Artificial Intelligence,
IJCAI-19, pages 450–456. International Joint Confer-
ences on Artificial Intelligence Organization.
Lopez-Perez, J., Hernandez-Belmonte, U., Ramirez-
Paredes, J.-P., Contreras-Cruz, M., and Ayala, V.
(2018). Distributed multirobot exploration based on
scene partitioning and frontier selection. Mathemati-
cal Problems in Engineering, 2018:1–17.
Meng, Y. (2008). Multi-robot searching using game-theory
based approach. International Journal of Advanced
Robotic Systems, 5(4):44.
Nair, M. and Givigi, S. (2019). The impact of communica-
tions considerations in multi-robot systems. In 2019
International Conference on Communications, Signal
Processing, and their Applications (ICCSPA), pages
1–6.
Ni, J., Tang, G., Mo, Z., Cao, W., and Yang, S. X. (2020).
An improved potential game theory based method for
multi-uav cooperative search. IEEE Access, 8:47787–
47796.
Pang, B., Song, Y., Zhang, C., Wang, H., and Yang, R.
(2019). A swarm robotic exploration strategy based
on an improved random walk method. J. Robotics,
2019:6914212:1–6914212:9.
Umari, H. and Mukhopadhyay, S. (2017). Autonomous
robotic exploration based on multiple rapidly-
exploring randomized trees. In 2017 IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems (IROS), pages 1396–1402.
Multi Robot Surveillance and Planning in Limited Communication Environments
147
