Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free

mmWave Massive MIMO

Yu Zhao

, Ignas Niemegeers

and Sonia Heemstra de Groot

Department of Electrical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands

Keywords:

Cell-free Massive MIMO, Deep Reinforcement Learning, Deep Q-Network, Power Allocation.

Abstract:

Numerical optimization has been investigated for decades to solve complex problems in wireless communi-

cation systems. This has resulted in many effective methods, e.g., the weighted minimum mean square error

(WMMSE) algorithm. However, these methods often incur a high computational cost, making their applica-

tion to time-constrained problems difﬁcult. Recently data-driven methods have attracted a lot of attention due

to their near-optimal performance with affordable computational cost. Deep reinforcement learning (DRL) is

one of the most promising optimization methods for future wireless communication systems. In this paper,

we investigate the DRL method, using a deep Q-network (DQN), to allocate the downlink transmission power

in cell-free (CF) mmWave massive multiple-input multiple-output (MIMO) systems. We consider the sum

spectral efﬁciency (SE) optimization for systems with mobile user equipment (UEs). The DQN is trained

by the rewards of trial-and-error interactions with the environment over time. It takes as input the long-term

fading information and it outputs the downlink transmission power values. The numerical results, obtained for

a particular 3GPP scenario, show that DQN outperforms WMMSE in terms of sum-SE and has a much lower

computational complexity.

1 INTRODUCTION

Massive multiple-input multiple-output (MIMO)

(Larsson and Edfors, 2014) and the use of mmWave

spectrum, have been widely recognized as key to in-

creasing the system capacity by an order of magnitude

compared to present sub-6 GHz networks (Busari and

Huq, 2018). This is because of the larger band-

width available in the mmWave spectrum and the

signiﬁcantly higher spectral efﬁciency (SE) that can

be achieved with massive MIMO (Andrews and G.,

2014).

In massive-MIMO, a base station (BS), equipped

with a very large antenna array, serves simultaneously

multiple user-equipments (UEs), using the same time-

frequency resource. The number of antennas should

signiﬁcantly exceed the number of UEs. Further gains

can be obtained by spreading the antennas over multi-

ple geographically distributed access points (APs), in-

stead of concentrating them in a single BS. This leads

to the concept of cell-free (CF) massive MIMO, intro-

duced in (Q and Ashikhmin, 2017). The APs jointly

https://orcid.org/0000-0002-5639-4470

https://orcid.org/0000-0002-2560-4746

https://orcid.org/0000-0003-2270-727X

and coherently provide service to the UEs. CF mas-

sive MIMO still has the beneﬁts of centralized mas-

sive MIMO, e.g., favorable propagation and channel

hardening, provided there are multiple (e.g., 5 to 10)

antennas at each AP (Chen and Bj

ornson, 2018). Fa-

vorable propagation means that the UE’s channel vec-

tors are almost orthogonal. Channel hardening means

that the beamforming transforms the fading multi-

antenna channel into an almost deterministic scalar

channel. These properties simplify the signal process-

ing and resource allocation. The additional advan-

tages of such an architecture, compared to centralized

massive MIMO are that (1) because the antennas are

geographically distributed, transmissions are less af-

fected by shadow fading and (2) the average distance

from a UE to its nearest AP is smaller. The drawback

is the need for an optical or wireless fronthaul to con-

nect the APs with a central controller (CC), see Fig.1.

Since the sub-6 GHz radio spectrum is highly

congested, mmWave massive MIMO systems have

increasingly attracted attention (Gonz

alez-Coma and

Rodr

ıguez-Fern

andez, 2018; Yu and Shen, 2016;

Alonzo and Buzzi, 2019). However, the operation in

the mmWave domain poses different and new chal-

lenges for CF massive MIMO systems:

Zhao, Y., Niemegeers, I. and Heemstra de Groot, S.

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO.

DOI: 10.5220/0010617300330045

In Proceedings of the 18th International Conference on Wireless Networks and Mobile Systems (WINSYS 2021), pages 33-45

ISBN: 978-989-758-529-6

(1) The full beneﬁt of massive MIMO is obtained

by providing each antenna with its own RF chain,

which includes the DACs, mixers, etc. (I and H,

2018); this is called full-digital beamforming. Hard-

ware constraints prevent the realization of full-digital

beamforming at mmWave frequencies (Alkhateeb and

Mo, 2014). Thermal problems, due to the density

of the hardware components and the high cost of

RF chains, make full-digital beamforming, for the

time being, an uneconomical solution. Therefore,

one resorts to the more practical hybrid beamform-

ing, which has much less RF chains, that each drive

an analog beamforming antenna array (Alkhateeb and

Mo, 2014). This, however, degrades the system per-

formance in terms of achievable SE. Several studies,

e.g., (O. and S., 2014; F and W., 2016; Lin and Cong,

2019), addressed techniques to decrease this degrada-

tion.

(2) Power allocation is another challenge in

CF mmWave massive MIMO systems (Alonzo and

Buzzi, 2019). Because different UEs are simultane-

ously served by the same time-frequency block, con-

trolling the inter-UE interference is important. In

principle, the suppression of the inter-UE interference

could be achieved by using zero-forcing (ZF) beam-

forming. However, due to the geographical spreading

of the antennas, this is not feasible. The ZF algorithm

would require the channel state information (CSI) for

each channel in the network to be available at the CC,

implying an unaffordable control message overhead

between APs and the CC and the associated timing

issues. Therefore, the conjugate beamforming (CB)

or normalized CB (NCB) (Polegre and Palou, 2020),

which can be processed locally in APs, are used in

CF massive MIMO. Because the inter-UE interfer-

ence cannot be suppressed by CB or NCB, power al-

location is the key to optimize the downlink perfor-

mance in terms of SE (Bj

ornson and Hoydis, 2017;

Hamdi and Driouch, 2016). In this paper we focus

on the problem of power allocation to maximize the

downlink sum-SE, which requires the solution of a

non-convex optimization problem.

Although many existing heuristic algorithms have

shown excellent performance for solving non-convex

problems, their application in real systems faces se-

rious obstacles because of their computational com-

plexity (Sun and Chen, 2018). For example, the popu-

lar weighted minimum mean square error (WMMSE)

algorithm requires complex operations such as ma-

trix inversion and bisection in each iteration (Shi and

Razaviyayn, 2011). Even when the power allocation

is performed at the CC and is done on the large-scale

fading time scale (milliseconds for mmWave) (Q and

Ashikhmin, 2017), it is still challenging to make an

Fronthaul

CC=central controller UE=user equipment AP=access point

Backhaul

Core network

Figure 1: Cell-free massive MIMO system.

implementation that meets the real-time constraints.

Recently deep-learning (DL) data-driven ap-

proaches have been tried for power allocation in wire-

less communication systems, achieving near-optimal

performance with affordable computational cost, e.g.,

(Sun and Chen, 2018) and (Chien and Canh, 2020;

Nikbakht and Jonsson, 2019; Nasir and Guo, 2019;

Meng and Chen, 2020). There are three main

branches of DL, namely supervised learning, unsu-

pervised learning, and deep reinforcement learning

(DRL). DRL is characterized by how agents ought to

take actions in an environment such that the cumu-

lative reward is maximized (Mnih and Kavukcuoglu,

2013). DRL has been applied to solve power op-

timization problems in non-massive-MIMO cellular

networks, e.g., (Nasir and Guo, 2019) used a four-

layer DQN and (Meng and Chen, 2020) a ﬁve-layer

DQN for different network conﬁgurations.

In this paper we propose a DRL method to op-

timize the power allocation in CF mmWave massive

MIMO. The reason is that it has a low computational

complexity, which, as we will see, is needed to meet

certain real-time constraints. Unlike supervised learn-

ing, which requires a huge training dataset gener-

ated by a computationally complex algorithm, DRL

is trained by the rewards of trial-and-error interac-

tions with its environment over time. It requires only

a small number (e.g., 4 in our case) of matrix mul-

tiplications to perform the power allocation. More-

over, we will show that its performance, in terms of

the downlink sum-SE it achieves, is competitive com-

pared with the WMMSE algorithm.

We consider a CF mmWave massive MIMO sys-

tem that serves several mobile UEs. The objective

function of the power allocation is the downlink sum-

SE. We assume NCB because it can be performed

locally at each AP, which implies that there is no

overhead for sending CSI from the APs to the CC

via the fronthaul. In addition, NCB can be easily

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

implemented in a hybrid beamforming architecture,

since in each RF chain only a phase-shift of the data

signal is required in each antenna path (Interdonato

and Ngo, 2016). The analysis is carried out using

Monte Carlo simulations for a 3GPP indoor mixed-

ofﬁce scenario (3GPP, 2018) with the well-adopted

extended Saleh-Valenzuela (S-V) channel model to

describe the mmWave propagation (C and K, 2013).

Imperfect CSI and pilot contamination are considered

in our analysis. The main contributions of this paper

are:

1. A closed-form formalization of the down-

link sum-SE maximization problem for CF mmWave

massive MIMO with multi-antenna APs and single-

antenna UEs, taking into account imperfect CSI and

pilot contamination.

2. A DRL-based power allocation method, using

a deep Q-network (DQN). The inputs to the DQN are

the normalized large-scale fading between transmit-

ters and receivers, and the outputs are the downlink

transmission powers.

3. An evaluation of the downlink sum-SE ob-

tained by DRL-based power allocation, comparing it

with the WMMSE algorithm for a 3GPP indoor mixed

ofﬁce scenario with mobile UEs. The simulation re-

sults show that DRL outperforms WMMSE in terms

of downlink sum-SE and has a much lower computa-

tional complexity.

The rest of the paper is structured as follows. Sec-

tion 2 describes the system models and power allo-

cation problem. Section 3 describes the DRL based

power allocation. Section 4 shows the simulation re-

sults and their interpretation. Finally, Section 5 draws

the conclusions.

2 SYSTEM MODEL

Consider a CF mmWave massive MIMO system

where N APs serve K UEs. Each AP has M anten-

nas, whereas each UE has a single antenna (K <<

MN). All APs are connected to a CC through a fron-

thaul (Fig.1). We assume the system is driven by

= K RF chains to enable K UEs being served

simultaneously by the same time-frequency resource

block. We do not address the possible limitations the

fronthaul links may introduce. As discussed in (Q

and Ashikhmin, 2017), these limitations degrade the

system performance in terms of achievable SE and

should be quantiﬁed in further studies. We assume

the system operates in TDD mode and the uplink and

downlink channels are reciprocal. We focus on the

downlink.

Typically, the length of the time-frequency re-

source block is chosen to be the coherence time τ

i.e., the time during which small-scale fading has an

insigniﬁcant effect on the signals. The time-interval

of a time-frequency resource block, is divided in two

phases: the uplink channel estimation phase and the

downlink data transmission phase. During the up-

link channel estimation, the UEs send pilots to the

APs and each AP estimates the corresponding chan-

nels. During the downlink data transmission, the esti-

mated channels are used to perform beamforming and

transmit the payload data. The duration of the up-

link channel estimation phase is denoted by τ

, where

< τ

and the duration of the downlink data trans-

mission phase is then τ

−τ

. The beamforming, used

during the data transmission phase and based on the

CSI values collected, will be valid for approximately

the coherence time. This implies that there are real-

time constraints on the computation of the beamform-

ing: the results should be available before the start of

each data transmission phase. If one has the bene-

ﬁt of channel hardening, i.e., small-scale fading can

be neglected, due to the spatial diversity created by

the large number of antennas (Chen and Bj

ornson,

2018), power allocation can be done on a longer time

scale, commensurate with the large-scale time τ

. τ

is deﬁned as the time during which the effect of large-

scale fading can be considered to be constant. It typi-

cally is around 40 times the coherence time τ

(Q and

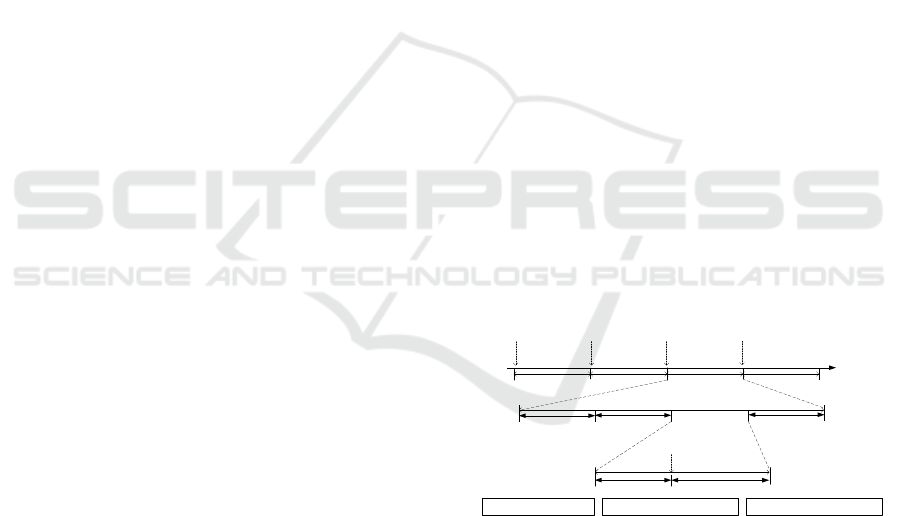
Ashikhmin, 2017; Mai and Ngo, 2020). Fig.2 shows

the time scales for beamforming and power alloca-

tion.

Coherence

Time

Coherence

Time

Coherence

Time

…

Coherence

Time

Uplink Channel

Estimation

Downlink Data

Transmission

-τ

…

Time Flow

Large-Scale

Time

Large-Scale

Time

Large-Scale

Time

Large-Scale

Time

Power

Allocation

Power

Allocation

Power

Allocation

Beamforming

Time Flow

Power

Allocation

Power

Allocation

Power

Allocation

Power

Allocation

Uplink:

Downlink

:τ

-τ

Beamforming

Large-Scale Time:

Coherence Time :

Channel Estimation Time:

Figure 2: Time scales for beamforming and power alloca-

tion.

2.1 Channel Model

We use the extended S-V channel model to describe

the propagation of the mmWave signals. One could

also choose other channel models such as the IEEE

802.11ad or the IEEE 802.15.3c models, which

are similar to the extended S-V model (C and K,

2013). The channel vector from AP n to UE k can be

formulated as follows (Busari and Huq, 2018):

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO

n,k

∑

l=1

n,k

(ψ

n,k

l,r

,θ

n,k

l,r

(ψ

n,k

l,r

,θ

n,k

l,t

) (1)

where L is the number of propagation paths from AP

n to UE k, α

n,k

is the pathloss of the l-th path, ψ

n,k

l,r

and θ

n,k

l,r

are the azimuth and elevation angle of the

angle of arrival (AoA) of path l, where subscript r

stands for reception, ψ

n,k

l,t

and θ

n,k

l,t

are the azimuth

and elevation angle of the angle of departure (AoD)

of path l, where subscript t stands for transmission,

and f

(ψ

n,k

l,r

,θ

n,k

l,r

) and f

(ψ

n,k

l,t

,θ

n,k

l,t

) are the receive and

transmit antenna array response vectors with dimen-

sions equal to the number of receive and transmit an-

tennas respectively. The antenna response vectors f

depend on the particular antenna design and array

conﬁguration. In our downlink analysis we assume

the transmission antenna is a uniform planar array

(UPA) with U

×U

elements. For this case, the re-

sponse vector f

(ψ

n,k

l,t

,θ

n,k

l,t

) has U

×U

elements and

takes the following form (O. and S., 2014):

UPA

(ψ,θ) =

√

[1,...,e

j2π

sin(ψ)sin(θ)+u

cos(θ))

,...,e

j2π

((U

−1)sin(ψ)sin(θ)+(U

−1)cos(θ))

]

(2)

where u

= [1, 2, . . . , U

], u

= [1, 2, . . .U

], d is the

antenna spacing and λ is the wavelength. In our case

we choose U

√

M. Since we assume that all

UEs are equipped with a single omnidirectional an-

tenna, the reception response vector f

(ψ

n,k

l,r

,θ

n,k

l,r

) in

(2), reduces to a scalar with value 1.

2.2 Uplink Channel Estimation

By using the minimum mean-square error (MMSE)

estimation (Bj

ornson and Hoydis, 2017), the estimate

n,k

includes M i.i.d. Gaussian components. The

mean-square of the m-th component is denoted by

n,k

, given by:

n,k

∑

n,k

|φ

+ 1

(3)

where p

is the normalized pilot power, φ

is the pi-

lot sequence transmitted by UE k, β

n,k

represents the

large-scale fading between AP n and UE k.

2.3 Downlink Data Transmission and

Spectral Efﬁciency

Based on the estimated channels, the APs employ

NCB to transmit signals to UEs. UE k will receive the

superposition of the signals of all APs in the whole

system:

∑

n=1

∑

√

n,k

∗

n,k

Mγ

n,k

+ w

(4)

where p

n,k

is the normalized downlink transmission

power from AP n to user k

satisfying p

n,k

≤ p

max

is the power transmission limit and q

is the in-

tended signal to UE k

. w

∼C N (0,1) is the additive

noise at UE k. The downlink SE for user k, is given

by (6) in the next page (Bj

ornson and Hoydis, 2017).

2.4 Max sum-SE Power Allocation

We use the max sum-SE power allocation policy,

which can be formulated as follows:

max

n,k

∑

k=1

s.t. p

n,k

≤ p

max

,∀n,k

(5)

This is a non-convex and NP-hard optimization

problem, since the computational complexity in-

creases exponentially as N and K increase. A well-

adopted method to solve (5) is the WMMSE heuris-

tic, which converts the sum-SE maximization prob-

lem to an equivalent minimization problem of the

mean square error in the data detection (Shi and Raza-

viyayn, 2011). Speciﬁcally, the algorithm (Algorithm

I) works as follows.

From an initial point {v

n,k

} satisfying the con-

straints, the optimal power allocation is obtained

by updating {v

n,k

} in an iterative manner,

where v

n,k

are optimization variables. The

variables {v

n,k

}, for all n, k in iteration I,

are updated using (7) (8) and (9), where (9) implies

that the variable v

n,k

should be in the range from 0

√

max

. The details of the WMMSE algorithm in

solving (5) are given by Algorithm1. The algorithm

stops when the condition w

n,k

< ε is fulﬁlled. The

value of ε depends on the convergence behavior of

the WMMSE algorithm. Similarly to (Shi and Raza-

viyayn, 2011) we set ε = 0.01.

The computational complexity mainly lies in steps

3 and 6. The calculation of γ

n,k

has a complexity of

O(K). For the denominator of (7) and (9), the com-

plexity is O(NK

). So for the updating of p

n,k

, the

complexity is O(INK

), where I represents the num-

ber of iteration for WMMSE to converge. Finally, the

total complexity to update NK links is O(IN

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

= (1 −

)log

(1 +

∑

n=1

√

n,k

)

∑

6=k

(

∑

n=1

√

n,k

)

|φ

∑

n=1

n,k

+ 1

) (6)

n,k

√

l−1

n,k

√

n,k

∑

(

∑

l−1

√

)

|φ

∑

l−1

)

+ 1

(7)

n,k

1 −u

l−1

n,k

Mγ

n,k

l−1

n,k

(8)

n,k

= min(max(

n,k

Mγ

n,k

∑

)

Mγ

,0),

√

max

) (9)

Algorithm 1: Pseudo Code of WMMSE for (5).

1: Initialize v

n,k

such that (v

n,k

)

≤ p

max

,∀k, n

2: Set I = 1, repeat:

3: Update the variables u

n,k

for all n,k, by (7).

4: Update the variables w

n,k

for all n,k, by (8).

5: Update the variables v

n,k

for all n,k, by (9).

6: Set I = I + 1.

7: Until w

n,k

< ε.

8: Output: p

n,k

= (v

n,k

)

3 DQN BASED POWER

ALLOCATION

In this section we propose a DQN to perform the

power allocation, combining reinforcement learning

with a deep neural network (Mnih and Kavukcuoglu,

2013). This method has low computational complex-

ity: it only requires a small number of layers of sim-

ple operations such as matrix or vector multiplications

(Sun and Chen, 2018).

3.1 Background of DQN

Deep reinforcement learning (or deep Q-learning) is

a category of machine learning where an agent learns

by interacting with its dynamic environment through

a repeated sequence of observations, actions and re-

wards (Mnih and Kavukcuoglu, 2013). After each

action, the agent observes the effect on the environ-

ment and receives a reward which depends on the ex-

tent to which the observations get closer to a target.

The agent maximizes the cumulative reward along the

course of interacting with its environment.

Through trial and error, an agent keeps learning,

making this technology ideal for dynamic environ-

ments that keep changing. The ’deep’ in DQN refers

to the fact that the neural network has multiple (deep)

internal layers.

The deep reinforcement learning is a discrete-time

system. At time step t, by observing the state s

the agent takes action a

∈ A

A according to a certain

policy π, then gets the reward r

from the environ-

ment and enters the next state s

t+1

. The policy π(s, a)

is the probability of taking action a conditioned on

the current state s. The experience sequence, deﬁned

as e

= (s

t+1

), describes a single interaction

with the environment. The goal of the agent is to se-

lect actions that maximize the future cumulative re-

ward:

= r

+ ωr

t+1

+ ω

t+2

+ ... (10)

where ω ∈ [0,1) is a discount factor that trades off

the importance of immediate and future rewards. The

action-value (also know as Q function) deﬁnes the ex-

pected reward once action a is taken in state s under

policy π:

(s,a) = E

= s,a

= a} (11)

The basic idea behind reinforcement learning is

to estimate the optimal action-value function by the

Bellman equation (N and H, 1989):

∗

(s,a) = E{r

+ ωmax

∗

t+1

)|s,a} (12)

where Q

∗

(s,a) represents the action-value of the op-

timal policy. It is common to use a function approxi-

mator to estimate the action-value function, typically

a lookup table or a linear function. If this approxima-

tor is a DNN, it is called DQN. The DQN is deﬁned as

Q(s,a,ξ

ξ) where ξ

ξ represents the parameters (weights

between neurons). The DQN is trained to estimate

the optimal action-value function, i.e., the vector ξ

ξ is

updated to estimate Q

∗

(s,a). The agent stores the ex-

periences in a data set D = {e

,. . . e

}, which is

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO

used to train the DQN by the gradient descent algo-

rithm (LeCun and Bengio, 2015). Ideally the training

of DQN should use all data in each iteration, however,

this is very expensive when the training set is huge.

An efﬁcient way is to use a random subset of the train-

ing set, called mini batch, to evaluate the gradients in

each iteration (M and T., 2014). The loss function of

the DQN for a random mini-batch D

(random sample

over D) at time step t is:

L(ξ

) =

∑

e∈D

(r + ωmax

Q(s

ξ) −Q(s, a,ξ

))

(13)

where e = (s, a,r, s

ξ represents the network param-

eters to compute the target at time step t, which is

only updated every C steps, see details in (Mnih and

Kavukcuoglu, 2013). Finally the stochasitc gradient

descent algorithm is used to update ξ

ξ over the mini-

batch D

3.2 DQN Power Allocation

Typically, DQNs are very suitable to solve problems

that can be modeled as Markov decision processes,

where the goal of the agent is to maximize the cumu-

lative rewards (Mnih and Kavukcuoglu, 2013). The

power allocation in CF mmWave massive MIMO, ac-

cording to the policy formulated in (5), can be seen

as such a Markov decision process: the large-scale

fading changes according to the mobility of UEs over

time, which, in our case, can be modeled as a Markov

process (see Section 4). For a non-Markov process,

due to the high correlations between the current state

and previous several states, the updates of the DQN

have large variances, leading to an inefﬁcient training

(Mnih and Kavukcuoglu, 2013). How to reduce the

variance of the DQN update is an open issue in case

of non-Markovian problems.

To use the DQN solving the power allocation

problem in CF mmWave massive MIMO, we deﬁne

the duration of each time step t as the large-scale time

in Fig.2. In scenarios with ﬁxed position UEs, the dis-

count factor ω was suggested to be zero (Meng.F and

P., 2019). However, in our case, since we consider

mobile UEs, we determine ω by trial-and-error, see

Section 4.2.

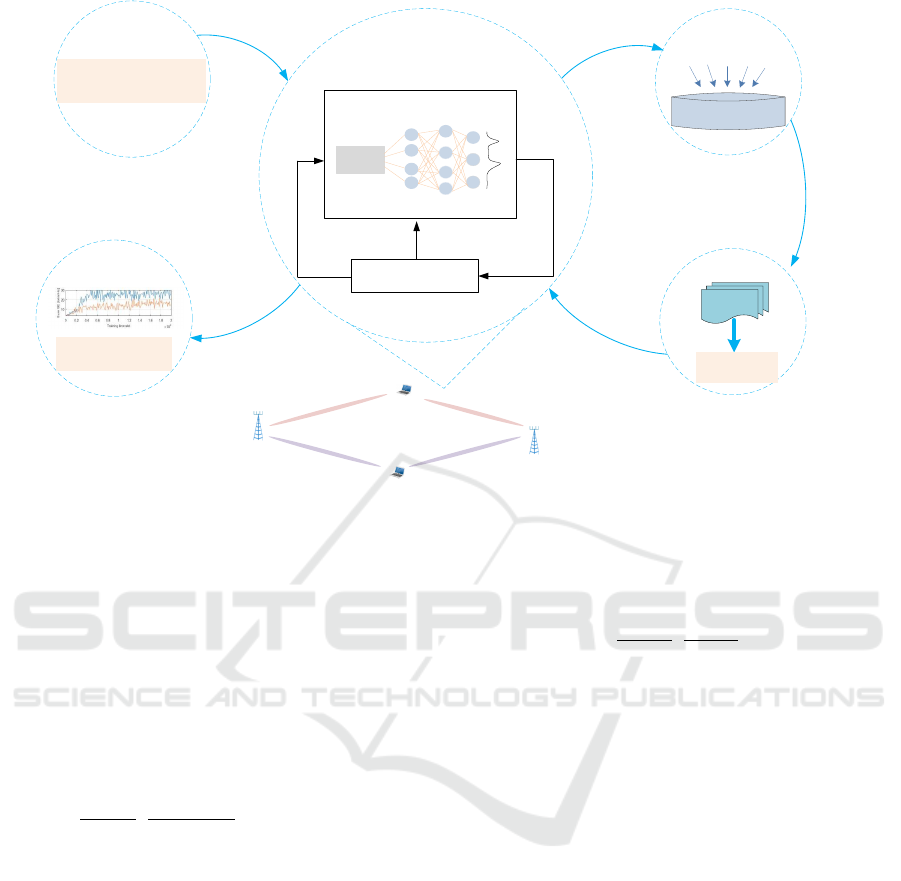
As in (Nasir and Guo, 2019) and (Meng and

Chen, 2020), we deﬁne for each AP-UE link an agent,

thus the power allocation is performed by a multi-

agent system, where each agent contains a DQN. The

agents interact with the environment to collect data

t+1

) and store it in a dataset at the CC, then

by mini-batch sampling the DQN is trained using the

gradient descent algorithm, as shown in Fig.3. Since

the learning is done off-line, the overhead cost of the

data collection does not affect the operational phase.

It is unnecessary to have ‘real-time’ training in off-

line learning mode. The training time, however, could

be considerable. We also should clarify that for the

off-line learning mode, the DQN is trained by a sufﬁ-

cient dataset, the size depends on the convergence of

the sum-SE. Once the training is ﬁnished, the DQN

is used to perform the power allocation. No further

training is needed. However, when there are signif-

icant changes in the network conﬁguration, e.g., the

number of active APs, or in the temporal and spatial

trafﬁc characteristics, the DQN should be retrained.

When that should happen and what impact it would

have on the operation of the system has not been ad-

dressed yet and requires further study.

There is a total of NK agents in the whole system.

At time step t, each agent (n,k) allocates power from

AP n to UE k. One should note that all agents use the

same DQN parameters, i.e., after the DQN is trained

by the experience of all agents, the DQN shares its

parameters with all other agents to allocate power.

We deﬁne e

n,k

= (s

n,k

t+1

n,k

) as the experi-

ence sequence of agent (n,k) at time step t. The DQN

is trained by the dataset D = {e

1,1

1,2

,. . . ,e

n,k

. . . },

which describes the agents’ relation with their envi-

ronment. The key to using the DQN for solving (5)

is to model the decision variables as the action of

agents. Obviouly the normalized downlink transmis-

sion power p

n,k

is the decision variable for SE, there-

fore the action of agent (n,k) is p

n,k

. We deﬁne p

n,k

the action of agent (n,k) at time step t. The agent (n,k)

takes action according to the current state s

n,k

, which

features the independent variables. From (4) we ﬁnd

that the large-scale fading is the independent variable

for SE, therefore the large-scale fading matrix at time

step t,







1,1

1,2

... β

1,K

2,1

2,2

... β

2,K

... ... ... ...

N,1

N,2

... β

N,K







(14)

is a key element for s

n,k

. The objective function,

which describes the target of the agents, is deﬁned

as the reward, i.e., the downlink sum-SE, achieved in

each time step. Based on the above analysis, the el-

ements of the experience etnk for CF mmWave mas-

sive MIMO power allocation are deﬁned as following:

1) State s

n,k

: The signal-to-interference-plus-

noise ratio (SINR) is the key element of the SE.

The signal in SINR of UE k comes from the agent

set {(1,k), (2,k),. . . ,(N,k)}, while the interference in

SINR for agent (n, k) mainly comes from the agent

set {(n,1), (n,2),. . . ,( n,K)}. Therefore, for agent (n,

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

link (n,k)

UE k

AP n

Environment

Reward

Action

State

Agent(n,k)

State

DQN

Parameter θ

Policy

π(s,a)

2. Interaction with environment

3. Dataset

Parameters

4. Training

1. Initialization

Design of the DQN

and parameter selection

UE k-1

AP n-1

link (n,k-1)

Record

Sampling

link (n-1,k-1)

link (n-1,k)

5. Testing

Parameters

=(s

, a

, r

, s

t+1

)

D={e

, e

,… e

}

Mini-batch

Gradient

descent

New

parameters

Performance and

execution time

Figure 3: Illustration of the proposed multi-agent deep reinforcement learning system.

k) only the n-th row and k-th column of β

are rel-

evant. We normalize these elements by β

n,k

as data

preprocessing. It has been determined experimentally

that some auxiliary information can improve the sum-

SE performance of DQN. Like in (Nasir and Guo,

2019) and (Meng and Chen, 2020), we consider two

auxiliary information elements, namely the sum-SE

∑

t−1

and the power allocation p

t−1

n,k

at time step

t-1. Finally, s

n,k

is formalized as follows:

n,k

= {

(n,:)

n,k

(:,k)

/β

n,k

, p

t−1

n,k

∑

t−1

} (15)

where β

(n,:), β

(:,k) represent the n-th row and k-th

column of β

, respectively. The numerator of the sec-

ond term in s

n,k

removes a redundant β

n,k

. Therefore

the size of s

n,k

, i.e., the input dimension of the DQN,

is N + K + 1. One remark is that

∑

t−1

in (15)

is the sum-SE at time step t −1. Each UE measures

its SE and then sends it to the APs by the uplink at

time step t −1. Then the CC collects this information

as the input of the DQN at time step t. The process

of sending SE values can be neglected in the power

allocation process, since it occurs on the time scale of

large-scale fading, similar to the β

collection. In ad-

dition, compared to the β

matrix (KNelements), there

are only K elements of the SE information i.e., the SE

of K UEs.

2) Action a

n,k

: The allocated power is a continu-

ous variable, however, for the action space of DQN,

the dimension must be ﬁnite. Therefore we discretize

the power as follows:

A = {0,

max

A|−1

max

A|−1

,..., p

max

} (16)

where |A

A| represents the number of power levels.

3) Reward r

n,k

: The target is to maximize the sum-

SE. Therefore, the reward is the sum-SE at time step

n,k

∑

k=1

(17)

3.3 Complexity of the Proposed DQN

The computational complexity considers the opera-

tional phase, i.e., the time period that a trained DQN

performs the power allocation. Therefore the com-

putational complexity of the DQN is only determined

by the DNN. The computational complexity of a neu-

ral network depends on the number of neurons and

layers. Speciﬁcally, for a fully-connected neural net-

work, the complexity is O(νµ

), where ν is the num-

ber of layers and µ is the number of neurons for

the widest layer, i.e., the layer with the most neu-

rons. Typically, the number of neurons in each layer

depends on the dimension of the input layer, i.e.,

O(µ)=O(N +K + 1) in our case. The number of layers

for a DQN is independent of the scale of the problem.

Therefore the computational complexity of DQN is

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO

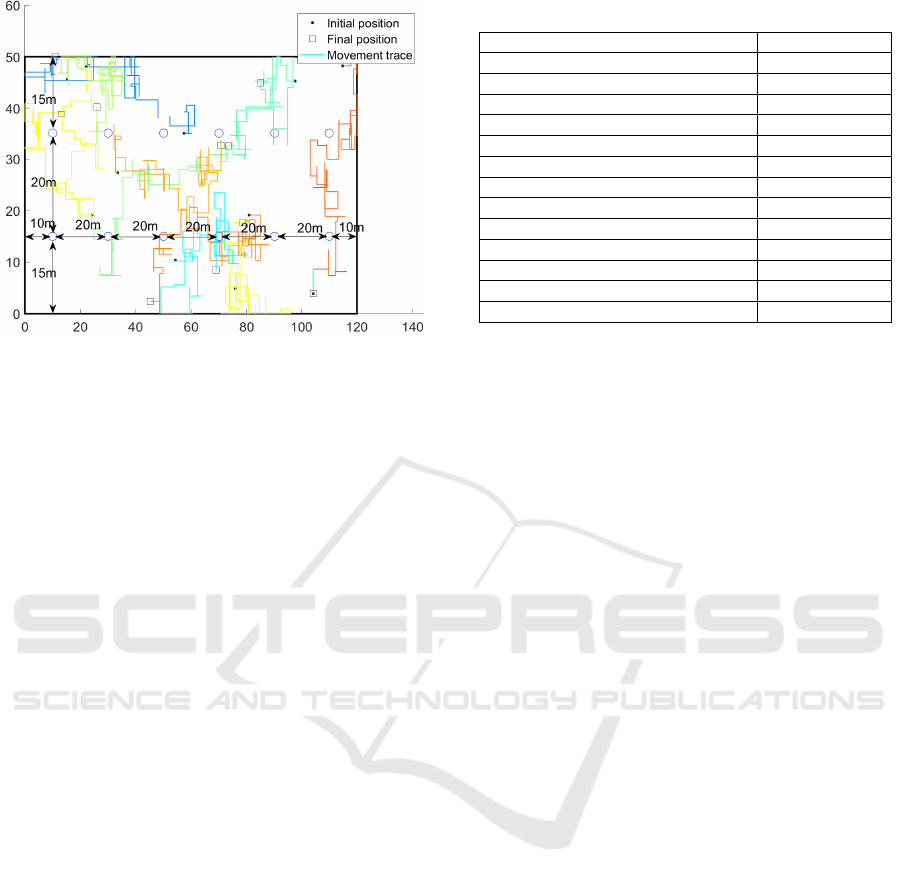
Figure 4: Example of UE movement traces in a 3GPP TR

38.901 scenario for 100 seconds.

O(N

+ K

). Compared to the WMMSE algorithm

O(IN

) in Section 2.4, the DQN has a much lower

computational complexity.

4 SIMULATION RESULTS

In this section we show by simulations that the

DQN-based power allocation in CF mmWave mas-

sive MIMO is competitive in terms of performance

and complexity.

4.1 Scenario and Conﬁguration

We consider the 3GPP TR 38.901 indoor mixed of-

ﬁce scenario (120m×50m×3m) (3GPP, 2018) with

12 APs. Each AP contains 9 antennas in a horizon-

tally mounted and downward radiating 3×3 UPA at a

height of 3m. We assume K=10 single-antenna UEs

moving within the coverage area. Each UE moves in

a random direction (up, down, left, and right) with

a randomly chosen velocity distributed uniformly be-

tween 0 and 1m/s. We consider a discrete time system

where the duration of each time step is 0.2s, corre-

sponding to the large-scale time (40 coherence times),

as discussed in Section 3.2. The carrier frequency is

29 GHz, the bandwidth is 200 MHz. For a UE ve-

locity of 1m/s, the channel coherence τ

is about 5

ms, calculated as τ

= λ/2v, where λ is the wave-

length and v is the velocity (Marzetta and Ngo.H.Q,

2016). Each UE maintains its speed and direction in

each second before selecting a new speed and direc-

tion. The initial positions of the UEs at time t=0, are

uniformly distributed over the coverage area (Fig.4).

We model the large-scale fading as the combination

of pathloss and shadowing, as in (3GPP, 2018).

Table 1: Parameters used in simulations.

Parameter value

Coverage volume 120m×50m×3m

K, number of UEs 10

M, number of antennas per AP 9

N, number of APs 12

max

, maximum power constraint 13 dBm

, pilot power 20 dBm

, length of coherence time in symbols 200

, length of pilot in symbols 5

Carrier frequency 29 GHz

Bandwidth 200 MHz

Noise power -74dBm

Distribution of UE velocity U(0, 1) m/s

Timeslot duration 0.2s

The maximum power constraint p

max

is 13 dBm

and the noise power is assumed to be -74 dBm. The

uplink pilot power is 20 dBm. We set the coher-

ence time to 200 modulation symbols as in (Q and

Ashikhmin, 2017). We assume the length of the up-

link pilot, used to determine the CSI, is 5 symbols. As

discussed in (Q and Ashikhmin, 2017), when τ

< K

some pilot sequences are reused, hence the simula-

tions take pilot contamination into consideration. The

parameters used in the simulations are listed in Table

4.2 DQN Parameter Selection

We adopted a four-layer fully connected neural net-

work, where the number of neurons in the two hid-

den layers are 128 and 64, respectively. This choice

was based on what was proposed and worked well in

(Nasir and Guo, 2019) and (Meng and Chen, 2020).

We did not investigate whether different values for

these hyperparameters would lead to better results.

This may be a topic for further study. The number of

neurons in the input layer is N +K + 1 as discussed in

(20), i.e., 22 in our case. We set the number of power

levels equal to 10; therefore, the number of neurons

in the output layer is 10.

It is worth pointing out that ﬁnding the best DQN

parameters can be seen as an optimization problem

in its own right. For a given problem, the training

should be based on the particular network conﬁgura-

tion and the usage scenarios to be expected. In this

subsection we tried several parameters to ﬁnd the best

choice, i.e., those that give us the highest sum-SE dur-

ing training. We studied the impact of the discount

factor ω, the training interval C, the initial adaptive

learning rate lr and the adaptive ε-greedy algorithm

on the training of the DQN.

Adaptive learning means that the learning rate

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

decays with the number of training time steps. Gen-

erally, a large learning rate allows the model to learn

faster but may end up with a sub-optimal ﬁnal set of

weights. A smaller learning rate may allow the model

to learn a more optimal or even globally optimal

set of weights but may take signiﬁcantly longer.

Adaptive learning balances the training time and

performance. The ε-greedy algorithm is a learning

method that makes use of the exploration-exploitation

tradeoff, in which the agent takes a random action

(choosing a power level) with probability ε or takes

the DQN output with probability 1-ε. A random

action may lead the training ‘jumps’ out of a local

optimum and explores new convergence regions.

In the adaptive ε-greedy algorithm the value of ε

decays each training time step. A large ε avoids

the training ending up in local optima during the

intial training time steps, a small value of ε makes

sure that the training will converge in the later

training time steps. Referring to the literatures,

we choose ω ∈ {0.1,0.3,0.5,0.7, 0.9}(Meng.F

and P., 2019), C ∈ {10,50,100, 200,500}(Nasir

and Guo, 2019; Mnih and Kavukcuoglu,

2013), lr ∈ {0.001,0.005, 0.01,0.05,0.1}(Chien

and Canh, 2020; Nasir and Guo, 2019),

ε ∈ {0.1,0.3,0.5, 0.7,0.9}(Mnih and Kavukcuoglu,

2013; Meng.F and P., 2019) to ﬁnd the optimal

conﬁgurations.

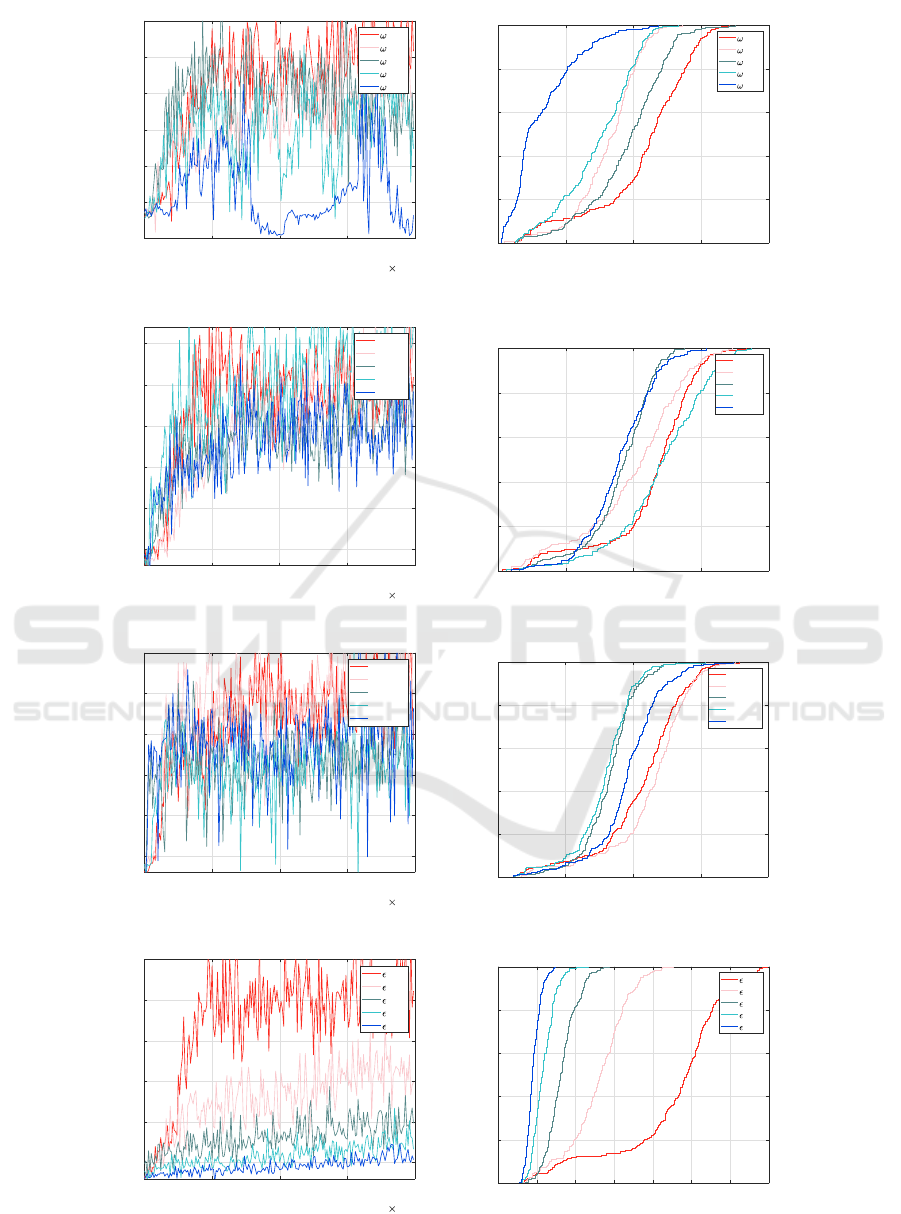
Fig.5 shows the effect of different parameters on

the training process. The graphs on the left show the

sum-SE as a function of time over a period of 20000

time steps. The corresponding graphs on the right

show the empirical CDF of the sum-SE. In each of

the ﬁgures we vary one parameter, while keeping the

others constant.

Fig.5(a) shows the effect of the discount factor ω.

Although the differences are not pronounced, we see

that the sum-SE for ω=0.1 is always larger than for

ω=0.9, by observing that the red line is to the right

of the the blue line in the empirical CDF graph. The

ﬂuctuations of the sum-SE as a function of the train-

ing time, is due to the random mobility of the UEs,

which leads to a variation of the large-scale fading.

Fig.5 (b) shows the effect of the training interval

C. Similar observations can be found as in Fig.5(a),

the differences between the lines are not pronounced.

Nevertheless we ﬁnd that C=100 achieves the highest

sum-SE, by observing the light blue line in the empir-

ical CDF graph.

Fig.5(c) shows the effect of the initial learning rate

lr. The differences between the lines are not obvious,

but we still see that the sum-SE for lr=0.005 achieves

the highest sum-SE, by observing the light red line is

to the right of other lines in the empirical CDF graph.

Fig. 5(d) shows the effect of ε-algortihm. We ﬁnd

that for different values of ε, the values of sum-SE

are very different. It is obvious that ε=0.1 achieves

the highest sum-SE, by observing the red line in both

training process and empirical CDF graphs.

Based on the above observations, we choose the

parameters ω=0.1, C=100, lr=0.005 and ε=0.1 to train

the DQN. The length of the training period we choose

is determined by the time it takes for the time-average

of the sum-SE to converge to a stable value, i.e., a

longer training period does not result in a signiﬁcantly

different time-average. In our case 30000 time steps,

appears to be sufﬁciently long, as can be observed

from Fig.6.

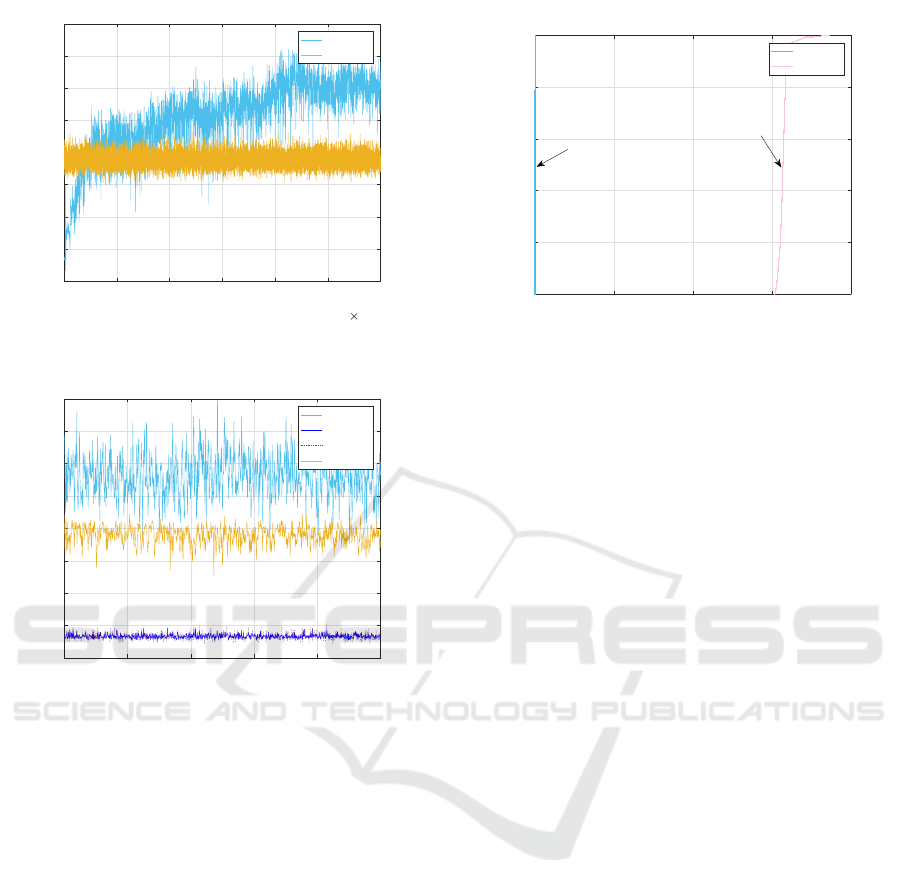
Observe that DQN achieves sum-SE values ﬂuctu-

ating around 23 bit/s/Hz around 5,000th training time

steps. Afterward the average rises slowly and ﬁnally

converges to around 30 bit/s/Hz after 20,000 training

time steps. This is obviously better than the value

obtained by the WMMSE algorithm, which is also

shown in the ﬁgure as a reference benchmark. The

random mobility of UEs causes the ﬂuctuations of the

sum-SE for both methods. It is clear that the DQN

method, after sufﬁcient training, achieves signiﬁ-

cantly better average sum-SE values than WMMSE.

4.3 Sum-SE Performance

We have used three benchmark algorithms to evalu-

ate the performance of the DNQ based-power alloca-

tion. The ﬁrst benchmark is the WMMSE algorithm

described in Section 2.4, which is well-adopted and

has been shown to perform well in cases studied in

the literature (Sun and Chen, 2018; Nasir and Guo,

2019; Meng.F and P., 2019). The second benchmark

is random power allocation where p

n,k

∼U(0, p

max

)

for all n and k. The third one is full power allocation,

i.e.,p

n,k

= p

max

for all n and k. We use the DQN that

has been trained for 30000 time steps, as described

in Fig.6 and run it for 1000 time steps. Fig.7 shows

the sum-SE of the four methods over a period of 1000

time steps.

As expected, WMMSE and DQN have much bet-

ter performance than random and full power alloca-

tion. In addition, the DQN method performs sig-

niﬁcantly better than WMMSE. The DQN method

achieves around 10 bit/s/Hz higher sum-SE than the

WMMSE algorithm.

4.4 Computational Complexity

Comparison

To get an indication of the difference in computational

complexity of DQN and WMMSE, we measured the

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO

0 0.5 1 1.5 2

Training time step

Sum SE [bit/s/Hz]

=0.1

=0.3

=0.5

=0.7

=0.9

0 10 20 30 40

Sum SE[bit/s/Hz]

0.2

0.4

0.6

0.8

F(x)

Empirical CDF

=0.1

=0.3

=0.5

=0.7

=0.9

(a) Discount factor ω selection with training interval C = 10, initial learning rate lr = 0.001, ε = 0.1.

0 0.5 1 1.5 2

Training time step

Sum SE [bit/s/Hz]

C=10

C=20

C=50

C=100

C=200

0 10 20 30 40

Sum SE[bit/s/Hz]

0.2

0.4

0.6

0.8

F(x)

Empirical CDF

C=10

C=20

C=50

C=100

C=200

(b) Training interval C selection with discount factor ω = 0.1, initial learning rate lr = 0.001, ε = 0.1.

0 0.5 1 1.5 2

Training time step

Sum SE [bit/s/Hz]

lr=0.001

lr=0.005

lr=0.01

lr=0.05

lr=0.1

0 10 20 30 40

Sum SE[bit/s/Hz]

0.2

0.4

0.6

0.8

F(x)

Empirical CDF

lr=0.001

lr=0.005

lr=0.01

lr=0.05

lr=0.1

0 0.5 1 1.5 2

Training time step

Sum SE [bit/s/Hz]

=0.1

=0.3

=0.5

=0.7

=0.9

0 5 10 15 20 25 30 35

Sum SE[bit/s/Hz]

0.2

0.4

0.6

0.8

F(x)

Empirical CDF

=0.1

=0.3

=0.5

=0.7

=0.9

(d) ε selection with discount factor ω = 0.1, training interval C=10, initial learning rate lr = 0.001.

Figure 5: Effect of different parameters on the training process.

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

0 0.5 1 1.5 2 2.5 3

Training time step

Sum SE [bit/s/Hz]

DQN

WMMSE

Figure 6: Training process of DQN with ω = 0.1,C =

100,lr = 0.005,ε = 0.1.

0 200 400 600 800 1000

Time slot

Sum SE[bit/s/Hz]

DQN

Full

Random

WMMSE

Figure 7: Comparison of sum-SE of DQN with the bench-

mark power allocation schemes over 1000 time steps, where

DQN is trained with ω = 0.1,C = 100, lr = 0.005, ε = 0.1.

execution time in each of the 1000 time steps. We ran

the algorithms on a 4 core Intel Core i5-7300 CPU

with 2.6 GHz frequency. The programs are coded in

Python 3.7.2 (DQN with Tensorﬂow 1.13.1). Fig.8

shows the empirical CDF of the execution times that

we recorded for the two methods.

From Fig.8 it is obvious that DQN requires much

less processing time than WMMSE and has less varia-

tion. It is around 0.6 ms for DQN while for WMMSE

the execution time ranges from 600 ms to 750 ms.

Recall that the power allocation is performed within

each large-scale time, namely 0.2s in our case. It is

obvious the DQN method meet this time constraint,

while the WMMSE does not.

In addition, for DQN, the number of calculations

is constant, as the number of neurons and layers does

not change. Although it is invisible in Fig.8, there

are still some slight ﬂuctuations of execution time,

which come from the calculation of different ﬂoating-

point numbers and the inaccuracy of reading the sys-

tem time. For WMMSE, the time ﬂuctuation mainly

0 200 400 600 800

Execution time[ms]

0.2

0.4

0.6

0.8

F(x)

Empirical CDF

DQN

WMMSE

The median:626.8

The median:0.63

Figure 8: Execution time for DQN and WMMSE.

comes from different initializations, i.e., a different

initial point of the algorithm can make a large dif-

ference in the time needed to ﬁnd the optimum. So

we can conclude that the DQN method is expected to

meet the requirements of real-time power allocation

in a real implementation. One should note that the ex-

ecution times shown in Fig.8 do not take into account

the overhead for the information exchange between

the APs and the CC via the fronthaul.

5 CONCLUSION

In this paper, we studied the use of DQN to allo-

cate transmission power for maximizing the down-

link sum-SE in CF mmWave massive MIMO systems

with mobile UEs in an indoor scenario. Imperfect CSI

and uplink pilot contamination were considered in the

analysis. Unlike supervised learning that needs a huge

dataset generated by other algorithms, the DQN is

trained by interacting with the environment. The ob-

jective function, i.e., the sum-SE, is used as the re-

ward to train the DQN. The sum-SE obtained by the

DQN is signiﬁcantly higher than the one achieved by

the well-adopted WMMSE algorithm. In addition, the

time-complexity of the DQN method is very low. The

numerical results show that the DQN is expected to

satisfy the stringent time constraints of power alloca-

tion in CF mmWave massive MIMO. There are still

open issues to be addressed:

1. Online learning, which is expected to be pro-

cessed in the real deployment of DQN, should be fur-

ther studied to accommodate the scenarios with real

measurements of channels and mobility of real UEs.

2. Different power allocation objective function,

e.g., max-min policy, should be studied.

3. We assumed a Markovian UE mobility model.

The mobility of real UEs is non-Markovian, which

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO

might lead to an inefﬁcient training of the DQN. This

should be further investigated.

4. When, during operation, signiﬁcant changes in

the network conﬁguration, e.g., the number of active

APs, or in the temporal and spatial trafﬁc characteris-

tics, occur, the DQN should be retrained. When that

should happen and what impact it would have on the

operation of the system has not been addressed yet

and requires further study.

5. For the hyper-parameters of the DQN, i.e., the

number of layers and neurons, we used values taken

from the literature. One could investigate whether

these hyper parameters could be optimized to get bet-

ter results in terms of the achieved sum-SE.

REFERENCES

3GPP (2018). Study on channel model for frequencies from

0.5 to 100 GHz (Release 15). In IEEE 21st Interna-

tional Workshop on Computer Aided Modelling and

Design of Communication Links and Networks. 3GPP.

Alkhateeb, A. and Mo, J. (2014). MIMO precoding and

combining solutions for millimeter-wave systems. In

IEEE Communications Magazine. IEEE.

Alonzo, M. and Buzzi, S. (2019). Energy-efﬁcient power

control in cell-free and user-centric massive MIMO

at millimeter wave. In IEEE Transactions on Green

Communications and Networking. IEEE.

Andrews and G., J. (2014). What will 5G be? In IEEE

Journal on Selected Areas in Communications. IEEE.

ornson, E. and Hoydis, J. (2017). Massive MIMO

Networks: Spectral, Energy, and Hardware Efﬁ-

ciency. Foundations and Trends in Signal Processing,

Hanover.

Busari, S. A. and Huq, K. M. S. (2018). Millimeter-wave

massive MIMO communication for future wireless

systems: A survey. In IEEE Communications Surveys

& Tutorials. IEEE.

C, G. and K, H. (2013). On mm-wave multipath cluster-

ing and channel modeling. In IEEE Transactions on

Antennas and Propagation. IEEE.

Chen, Z. and Bj

ornson, E. (2018). Channel hardening

and favorable propagation in cell-free massive MIMO

with stochastic geometry. In IEEE Transactions on

Communications. IEEE.

Chien, T. V. and Canh, T. N. (2020). Power control in cellu-

lar massive MIMO with varying user activity: A deep

learning solution. In IEEE Transactions on Wireless

Communications. IEEE.

F, S. and W., Y. (2016). Hybrid digital and analog beam-

forming design for large-scale antenna arrays. In

IEEE Journal of Selected Topics in Signal Processing.

IEEE.

Gonz

alez-Coma, J. P. and Rodr

ıguez-Fern

andez, J. (2018).

Channel estimation and hybrid precoding for fre-

quency selective multiuser mmWave MIMO systems.

In IEEE Journal of Selected Topics in Signal Process-

ing. IEEE.

Hamdi, R. and Driouch, E. (2016). Resource allocation in

downlink large-scale MIMO systems. In IEEE Access.

IEEE.

I, A. and H, K. (2018). A survey on hybrid beamforming

techniques in 5G: Architecture and system model per-

spectives. In IEEE Communications Surveys & Tuto-

rials. IEEE.

Interdonato, G. and Ngo, H. Q. (2016). On the performance

of cell-free massive MIMO with short-term power

constraints. In IEEE 21st International Workshop on

Computer Aided Modelling and Design of Communi-

cation Links and Networks. IEEE.

Larsson, E. G. and Edfors, O. (2014). Massive MIMO for

next generation wireless systems. In IEEE Communi-

cations Magazine. IEEE.

LeCun and Bengio (2015). Deep learning. In Nature. Na-

ture.

Lin and Cong, J. (2019). Hybrid beamforming for millime-

ter wave systems using the MMSE criterion. In IEEE

Transactions on Communications. IEEE.

M, L. and T., Z. (2014). Efﬁcient mini-batch training for

stochastic optimization. In Proceedings of the 20th

ACM SIGKDD international conference on Knowl-

edge discovery and data mining. ACM.

Mai, T. C. and Ngo, H. Q. (2020). Downlink spectral

efﬁciency of cell-free massive MIMO systems with

multi-antenna users. In IEEE Transactions on Com-

munications. IEEE.

Marzetta and Ngo.H.Q (2016). Fundamentals of massive

MIMO. Cambridge University Press, Cambridge.

Meng, F. and Chen, P. (2020). Power allocation in multi-

user cellular networks: Deep reinforcement learning

approaches. In IEEE Transactions on Wireless Com-

munications. IEEE.

Meng.F and P., C. (2019). Power allocation in multi-user

cellular networks with deep Q learning approach. In

IEEE International Conference on Communications.

IEEE.

Mnih and Kavukcuoglu (2013). Human-level control

through deep reinforcement learning. In Nature. Na-

ture.

N, B. E. and H, I. (1989). The Bellman equation for min-

imizing the maximum cost. In Nonlinear Analysis:

Theory, Methods & Applications.

Nasir, Y. S. and Guo, D. (2019). Multi-agent deep rein-

forcement learning for dynamic power allocation in

wireless networks. In IEEE Journal on Selected Ar-

eas in Communications. IEEE.

Nikbakht, R. and Jonsson, A. (2019). Unsupervised-

learning power control for cell-free wireless systems.

In IEEE 30th Annual International Symposium on

Personal, Indoor and Mobile Radio Communications.

IEEE.

O., E. A. and S., R. (2014). Spatially sparse precoding in

millimeter wave MIMO systems. In IEEE transac-

tions on wireless communications. IEEE.

Polegre, A. . and Palou, F. R. (2020). New insights on chan-

nel hardening in cell-free massive MIMO networks. In

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

2020 IEEE International Conference on Communica-

tions Workshops. IEEE.

Q, N. H. and Ashikhmin (2017). Cell-free massive MIMO

versus small cells. In IEEE Transactions on Wireless

Communications. IEEE.

Shi, Q. and Razaviyayn, M. (2011). An iteratively weighted

MMSE approach to distributed sum-utility maximiza-

tion for a MIMO interfering broadcast channel. In

IEEE Transactions on Signal Processing. IEEE.

Sun, H. and Chen, X. (2018). Learning to optimize: Train-

ing deep neural networks for interference manage-

ment. In IEEE Transactions on Signal Processing.

IEEE.

Yu, X. and Shen, J. (2016). Alternating minimization al-

gorithms for hybrid precoding in millimeter Wave

MIMO systems. In IEEE Journal of Selected Topics

in Signal Processing. IEEE.

Deep Reinforcement Learning for Dynamic Power Allocation in Cell-free mmWave Massive MIMO