Proof-of-Forgery for Hash-based Signatures

Evgeniy Kiktenko

1,2 a

, Mikhail Kudinov

1,2 b

, Andrey Bulychev

and Aleksey Fedorov

1,2 c

Russian Quantum Center, Skolkovo, Moscow 143025, Russia

QApp, Skolkovo, Moscow 143025, Russia

Keywords:

Hash-based Signatures, Lamport Signature, Winternitz Signature, Crypto-agility.

Abstract:

In the present work, a peculiar property of hash-based signatures allowing detection of their forgery event

is explored. This property relies on the fact that a successful forgery of a hash-based signature most likely

results in a collision with respect to the employed hash function, while the demonstration of this collision

could serve as convincing evidence of the forgery. Here we prove that with properly adjusted parameters

Lamport and Winternitz one-time signatures schemes could exhibit a forgery detection availability property.

This property is of signiﬁcant importance in the framework of the crypto-agility paradigm since the considered

forgery detection serves as an alarm that the employed cryptographic hash function becomes insecure to use

and the corresponding scheme has to be replaced.

1 INTRODUCTION AND

PROBLEM STATEMENT

Today, cryptography is an essential tool for protecting

the information of various kinds. A particular task

that is important for modern society is to verify the

authenticity of messages and documents effectively.

For this purpose, one can use so-called digital signa-

tures. An elegant scheme for digital signatures is to

employ one-way functions, which are one of the most

important concepts for public-key cryptography. A

crucial property of public-key cryptography based on

one-way functions is that it provides a computation-

ally simple algorithm for legitimate users (e.g., for

key distribution or signing a document), whereas the

problem for malicious agents is extremely computa-

tionally expensive. It should be noted that the very

existence of one-way functions is still an open con-

jecture. Thus, the security of corresponding public-

key cryptography tools is based on unproven assump-

tions about the computational facilities of malicious

parties.

Assumptions on the security status of crypto-

graphic tools may change with time. For example,

breaking the RSA cryptographic scheme is at least as

hard as factoring large integers (Rivest et al., 1978).

https://orcid.org/0000-0001-5760-441X

https://orcid.org/0000-0002-8555-4891

https://orcid.org/0000-0002-4722-3418

This task is believed to be extremely hard for classi-

cal computers, but it appeared to be solved in poly-

nomial time with the use of a large-scale quantum

computer using Shor’s algorithm (Shor, 1997). A full-

scale quantum computer that is capable of launching

Shor’s algorithm for realistic RSA key sizes in a rea-

sonable time is not yet created. At the same time,

there are no identiﬁed fundamental obstacles that pre-

vent from development of quantum computers of a

required scale. Thus, prudent risk management re-

quires defending against the possibility that attacks

with quantum computers will be successful.

A solution for the threat of creating quantum com-

puters is the development of a new type of crypto-

graphic tools that strive to remain secure even under

the assumption that the malicious agent has a large-

scale quantum computer. This class of quantum-safe

tools consists of two distinct methods (Wallden and

Kasheﬁ, 2019). The ﬁrst is to replace public-key cryp-

tography with quantum key distribution, which is a

hardware solution based on transmitting information

using individual quantum objects. The main advan-

tage of this approach is that the security relies not

on any computational assumptions, but on the laws of

quantum physics (Gisin et al., 2002). However, quan-

tum key distribution technologies today face a num-

ber of important challenges such as secret key rate,

distance, cost, and practical security (Diamanti et al.,

2016).

Another way to guarantee the security of com-

Kiktenko, E., Kudinov, M., Bulychev, A. and Fedorov, A.

Proof-of-Forgery for Hash-based Signatures.

DOI: 10.5220/0010579603330342

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 333-342

ISBN: 978-989-758-524-1

333

munications is to use so-called post-quantum (also

known as quantum-resistant) algorithms, which use a

speciﬁc class of one-way functions that are believed

to be hard to invert both using classical and quan-

tum computers (Bernstein and Lange, 2017). The

main criticism of post-quantum cryptography is the

fact that they are again based on computational as-

sumptions so that there is no strict proof that they are

long-term secure.

In our work, we consider a scenario, where an

adversary ﬁnds a way to violate basic mathematical

assumptions underlying the security of a particular

cryptographic primitive. Thus, the adversary becomes

able to perform successful attacks on information pro-

cessing systems, which employ the vulnerable crypto-

graphic primitive in their workﬂow. At the same time,

it is in the interests of the adversary that the particu-

lar cryptographic primitive be in use as long as possi-

ble since its replacement with another one eliminates

an obtained advantage. Thus, the preferable strategy

of an attacker is to hide the fact that the underlying

cryptographic primitive has been broken. It can be re-

alized by performing attacks in such a way that their

success could be explained by some other factors (e.g.

user negligence, hardware faults, and etc.), but not the

underlying cryptographic primitive. An illustrative

example of such a strategy is hiding the information

about the successes of the Enigma system cryptoanal-

ysis during World War II.

Broadly speaking, the question we address in the

present work is as follows: Is it possible to supply a

new generation of post-quantum cryptographic algo-

rithms with some kind of alarm indicating that they

are broken? We argue that the answer to this ques-

tion is partially positive, and the property, which we

refer to as a forgery detection availability, can be real-

ized by properly designed hash-based signatures. The

intuitive idea behind this property is that a forgery

of a hash-based signature most likely results in ﬁnd-

ing a collision with respect to the underlying crypto-

graphic hash function (see Fig. 1), and so the demon-

stration of this collision can serve as convincing evi-

dence of the forgery and corresponding vulnerability

of the employed cryptographic hash function. We re-

fer to the mathematical scheme for the evidence of

the forgery event as a proof-of-forgery concept. We

also would like to emphasize the fact that some of

widespread hash functions have been compromised

after their publication (Dobbertin, 1998; Black et al.,

2006; Stevens et al., 2017), therefore the considered

problem is more than just of academic interest.

In the present work, we illustrate the forgery de-

tection availability property for Lamport (Buchmann

et al., 2009; Lamport, ) and Winternitz (Buchmann

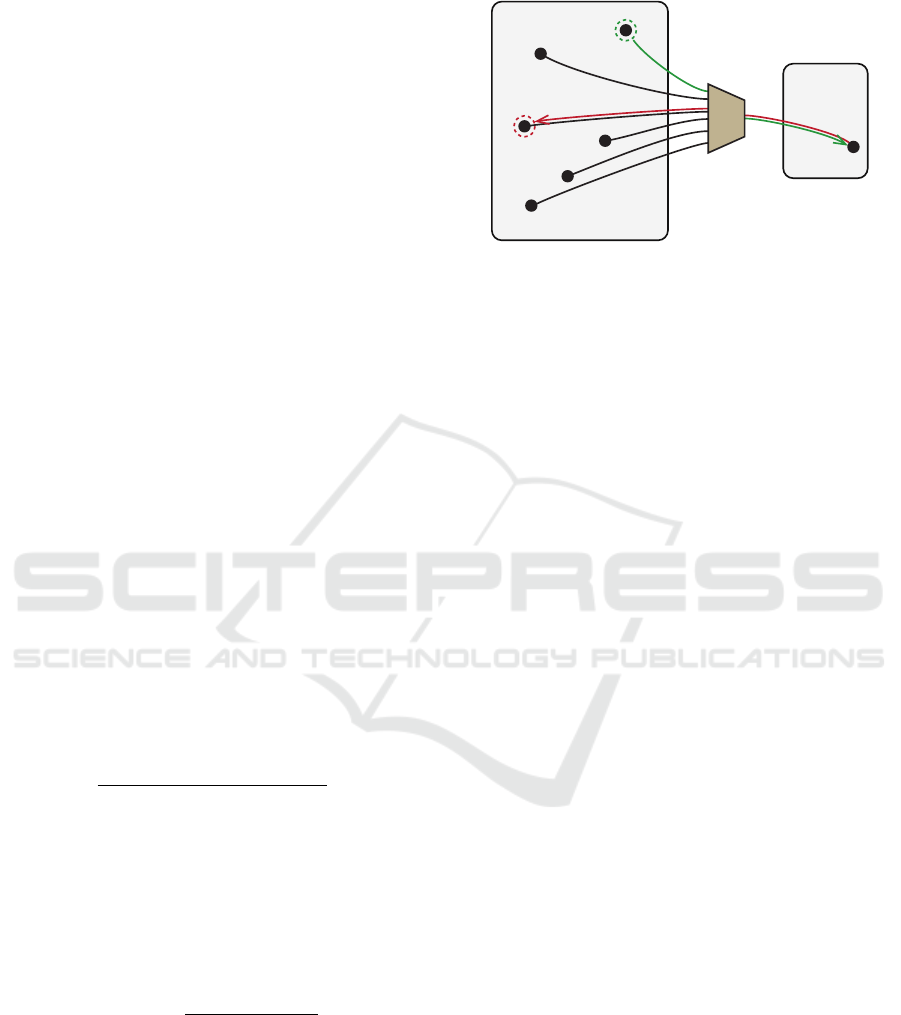
Space of images

Space of pre-images

of finite length

original

preimage

reconstructed

preimage

Figure 1: Demonstration of the idea behind proving the fact

of the hash-based signature forgery. In order to forge the

signature, an adversary ﬁnds a valid preimage for a given

image of a cryptographic hash function. If the size of the

preimages space is large enough then the preimage obtained

adversary is most likely different from the legitimate user’s

one. Disclosing the colliding preimage could serve as evi-

dence that a particular hash function is vulnerable.

et al., 2009) one-time signatures schemes. First, we

consider the Lamport scheme, which is paradigmat-

ically important: It is the ﬁrst and the simplest al-

gorithm among hash-based schemes. However, the

Lamport scheme is not widely used in practice. Then

we analyze the Winternitz scheme, particularly the

variant presented in Ref. (H

ulsing, 2013), which can

be considered as a generalization of the Lamport

scheme that introduced a size-performance trade-off.

Variations of the Winternitz scheme are used as build-

ing blocks in a number of modern hash-based sig-

natures, such as LMS (McGrew and Curcio, 2016),

XMSS (Huelsing et al., 2018), SPHINCS (Bernstein

et al., 2016) and its improved modiﬁcations (Bern-

stein et al., 2017; Aumasson and Endignoux, 2017),

as well as applications such as IOTA distributed

ledger (IOT, ).

The paper is organized as follows. In Sec. 2, we

give a short introduction to the scope of hash-based

signatures. In Sec. 3, we provide a general scheme of

detecting signature forgery event and deﬁne a prop-

erty of the ε-forgery detection availability (ε-FDA).

In Sec. 4, we consider the ε-FDA property for the

generalized Lamport one-time signature (L-OTS). In

Sec. 5, we consider the ε-FDA property for the Win-

ternitz one-time signature (W-OTS

). We summarize

the results of our work in Sec. 6.

2 HASH-BASED SIGNATURES

Hash-based digital signatures (Bernstein and Lange,

2017; Bernstein et al., 2009) are one of the post-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

334

quantum alternatives for currently deployed signature

schemes, which have gained a signiﬁcant deal of in-

terest. The attractiveness of hash-based signatures is

mostly due to low requirements to construct a secure

scheme. Typically, a cryptographic random or pseu-

dorandom number generator is needed, and a func-

tion with some or all of preimage, second-preimage,

and collision resistance properties, perhaps, in their

multi-target variety (Bernstein et al., 2017; H

ulsing

et al., 2016; Buchmann et al., 2009). Some schemes

for hash-based signatures require a random oracle as-

sumption (Koblitz and Menezes, 2015) to precisely

compute their bit security level (Katz, 2016).

Up to date known quantum attacks based on

Grover’s algorithm (Grover, 1996) are capable to ﬁnd

a preimage and a collision with time growing sub-

exponentially with a length of hash function out-

put (Boyer et al., 1999; Brassard et al., 1998). Specif-

ically, it is proven that in the best-case scenario

Grover’s algorithm gives a quadratic speed-up in a

search problem (Grover, 1996). While this area is a

subject of ongoing research and debates (Bernstein,

2009; Banegas and Bernstein, 2018; Chailloux et al.,

2017), hash-based signatures are considered resilient

against quantum computer attacks. Meanwhile, the

overall performance of hash-based digital signatures

makes them suitable for the practical use, and several

algorithms have been proposed for standardization by

NIST (SPHINCS

(Bernstein et al., 2017), Gravity-

SPHINCS (Aumasson and Endignoux, 2017)) and

IETF (LMS (McGrew and Curcio, 2016), XMSS

(Huelsing et al., 2018)).

We note that the hash-based digital signature

scheme can be instantiated with any suitable crypto-

graphic hash function. In practice, standardized hash

functions, such as SHA, are used for this purpose

since they are presumed to satisfy all the necessary re-

quirements. The availability of changing a core cryp-

tographic primitive without a change in the function-

ality of the whole information security system ﬁts a

paradigm of crypto-agility, which is the basic princi-

ple of modern security systems development with the

built-in possibility of component replacement.

3 PROVING THE FACT OF A

FORGERY

Here we present a general framework for the investi-

gation of the proof-of-forgery concept. We start our

consideration by introducing a generic deterministic

digital signature scheme.

Deﬁnition 1 (Deterministic Digital Signature

Scheme). A deterministic digital signature scheme

(DDSS) S = (Kg, Sign,Vf) is a triple of algorithms

that allows performing the following tasks:

• S.Kg(1

) → (sk,pk) is a probabilistic key genera-

tion algorithm that outputs a secret key sk, aimed

at signing messages, and a public key pk, aimed at

checking signatures validity, on input of a security

parameter 1

• S.Sign(sk,M) → σ is a deterministic algorithm

that outputs a signature σ under secret key sk for

a message M.

• S.Vf(pk,σ,M) → v is a veriﬁcation algorithm that

outputs v = 1 if the signature σ of the signed mes-

sage M is correct under the public key pk, and

v = 0 otherwise.

We note that the deterministic property of the DDSS

is deﬁned by the fact that for a given pair (sk,M) the

algorithm S.Sign(sk,M) always generates the same

output.

The standard security requirement for digital sig-

nature schemes is their existential unforgeability un-

der chosen message attack (EU-CMA). The chosen

message attack setting allows the adversary to choose

a set of messages that a legitimate user has to sign.

Then the existential unforgeability property means

that the adversary should not be able to construct

any valid message-signature pair (M

,σ

), where the

message M

is not previously signed by a legitimate

secret key holder. In the present work, we limit our-

selves to the case of one-time signatures, so the ad-

versary is allowed to obtain a signature for a single

message only. The generalization to the many-time

signature schemes is left for future research.

In the present work, we consider a stronger secu-

rity requirement known as strong unforgeability un-

der chosen message attack (SU-CMA). A DDSS is

said to be SU-CMA if it is EU-CMA, and given sig-

nature σ on some message M, the adversary cannot

even produce a new signature σ

∗

6= σ on the message

M. We note that SU-CMA schemes are used for con-

structing chosen-ciphertext secure systems and group

signatures (Boneh et al., 2006; Steinfeld and Wang,

2007). The security is usually proven under the as-

sumption that the adversary is not able to solve some

classes of mathematical problems, such as integer fac-

torization, discrete logarithm problem, or inverting a

cryptographic hash function. Here we consider the

case where this assumption is not fulﬁlled.

Let us discuss the following scenario involving

three parties: An honest legitimate signer S, an hon-

est receiver R , and an adversary A. At the be-

ginning (step 0) we assume that S possesses a pair

(sk,pk) ← S.Kg, while R and A have a public key

Proof-of-Forgery for Hash-based Signatures

335

pk of S , and they have no any information about the

corresponding secret key sk (see Table 1).

At step 1 A forces S to sign a message M of

A’s choice. In the result, A obtains a valid message-

signature pair (M, σ). At this step, R may or may not

know about the fact of signing M by S .

Then at step 2 A performs an existential forgery

by producing a new message-signature pair (M

,σ

)

with M

6= M. Below we introduce a formal deﬁni-

tion of the signature forgery and specify two different

cases.

Deﬁnition 2 (Signature Forgery and Its Types). A

signature σ

is called a forged signature of the mes-

sage M

under the public key pk and the signature

scheme S if S.Vf(pk,σ

) → 1, where the message

has not been signed by the legitimate sender pos-

sessing secret key sk corresponding to pk. The follow-

ing two cases are possible.

• A pair (M

,σ

) is called a forgery of type I if

the signature σ

has been previously generated by

the legitimate user a signature for some message

other than M

. That is, there is a message M with

S.Sign(sk,M) → σ

previously signed by a legiti-

mate user.

• A pair (M

,σ

) is called a forgery of type II if the

signature σ

has not been previously generated by

the legitimate user. That is, there has not been a

message with signature σ

, signed by the legiti-

mate user.

The type I forgery can take place if the signature algo-

rithm S.Sign calculates a digest of an input message

and then computes a signature of the corresponding

digest. In this case, the adversary A may ﬁnd a col-

lision of the digest function, and then force the legit-

imate user to sign a ﬁrst colliding message by using

it as M, and automatically obtain a valid signature for

the second colliding message (use it as M

An example of type II forgery is the reconstruc-

tion of the sk from pk using an efﬁcient algorithm (in

analogy to the use of Shor’s algorithm on a quantum

computer for the RSA scheme). We note that in our

consideration it is assumed that the only way for the

adversary A to forge the signature for M

is to em-

ploy advanced mathematical algorithms and/or unex-

pectedly powerful computational resources. In other

words, we do not consider any side-channel attacks

or other forms of secret key “stealing”, such as social

engineering and others.

Coming back to the considered scenario, at the

step 2, A sends a pair (M

,σ

) to R claiming that M

was originally signed by S . If the signature is success-

fully forged by the adversary A, then this could be the

end of the story.

However, we suggest accomplishing this scenario

by the following next steps. At the step 3, R sends a

message (M

,σ

) directly to S in order to request an

additional conﬁrmation. Then S observes a valid sig-

nature σ

of the corresponding message M

, which

was not generated by him. The concrete issue we

address in the present work is whether S is able to

prove the fact of a forgery event. Here we formally

introduce a proof-of-forgery concept, which is mathe-

matical evidence that someone cheats with signatures

by employing computational resources or advanced

mathematical algorithms.

Deﬁnition 3 (Proof-of-Forgery of Type I). A set E =

(pk,σ

,M, M

) is called a proof-of-forgery of type I

(PoF-I) for a DDSS S if for M 6= M

there is a valid

signature σ

for these two messages, i.e. the following

relations hold:

S.Vf(pk,σ

) → 1, S.Vf(pk,σ

,M) → 1. (1)

Obviously, if the adversary A performs the type I

forgery, then S is able to prove this fact by demon-

strating M to R at step 4. Thus, S and R have the

complete PoF-I set E = (pk,σ

,M, M

), and they are

sure that someone has an ability to break SUF-CMA

property (Brendel et al., 2020), which is typically

beyond the consideration in standard computational

hardness assumptions. Moreover, they can use the set

E to prove the fact of the forgery event to any third

party since E contains a public key pk. We also note

that it is possible to prove the fact of a forgery of type

I for any DDSS. The situation in the PoF-II case is

more complicated.

Deﬁnition 4 (Proof-of-Forgery of Type II) . A set

E = (pk,

,σ

) is called a proof-of-forgery of

type II (PoF-II) for a DDSS S if for a message M

there are distinct valid signatures

6= σ

, i.e. the

following relations hold:

S.Vf(pk,

) → 1, S.Vf(pk,σ

) → 1.

The ability of the adversary A to perform a forgery of

type II depends on a particular deterministic signature

scheme S. Suppose that A has succeeded in obtaining

sk from pk (e.g. by using Shor’s algorithm and RSA-

like scheme), then it is impossible for S to convince

R that (M

,σ

) was not generated by S . However, if

the adversary A has succeeded in obtaining a valid,

but different secret key sk

6= sk, then the legitimate

sender S is able to construct the corresponding PoF-II

set by calculating Sign(sk,M

) →

with

6= σ

As we show below this scenario is the case for

properly designed hash-based signatures. We con-

sider particular examples of Lamport and Winternitz

one-time signatures schemes. We show that under

SECRYPT 2021 - 18th International Conference on Security and Cryptography

336

Table 1: Message-signature pairs and keys available to involved parties on each step of the scenario, where the adversary

A makes a successful CMA obtaining a signature σ for some message M, and forges a signature σ

for some new message

6= M under the public key pk of the signer S. However, the signer S is able to construct the corresponding proof-of-forgery

message E in order to convince the receiver R that the forgery event happened. Square brackets correspond to the optional

message-signature transmission.

Signer S Adversary A Receiver R

Step 0 sk, pk pk pk

Step 1 sk, pk, (M,σ) pk, (M,σ) pk, [(M,σ)]

Step 2 sk, pk, (M,σ) pk, (M,σ), (M

,σ

) pk, [(M,σ)], (M

,σ

)

Step 3 sk, pk, (M,σ), (M

,σ

) pk, (M,σ), (M

,σ

) pk, [(M,σ)], (M

,σ

)

Step 4 sk, pk, (M,σ), (M

,σ

), E pk, (M,σ), (M

,σ

), [E] pk, [(M,σ)], (M

,σ

), E

favourable circumstances S’s signature

of the cor-

responding message M

is different from A’s signa-

ture σ

, and S can send it as part of PoF-II to R at step

4. Thus, the PoF-II set is successfully constructed, so

legitimate parties are aware of the break of the used

DDSS.

Here, we introduce a deﬁnition of an adversary

who successfully forged, which allows proving their

forgery.

Deﬁnition 5 (ε-Forgery Fetection Availability). ε-

forgery detection availability (ε-FDA) for a one-time

DDSS S is deﬁned by the following experiment.

Experiment. Exp

FDA

S,n

(A)

(sk,pk) ← S.Kg(1

)

,σ

) ← A

Sign(sk,·)

Let (M,σ) be the query-answer pair of Sign(sk,·).

Return 1 iff S.Sign(sk,M

) → σ

S.Vf(pk,σ

) → 1, and M

6= M.

Then the DSS scheme S has ε-FDA if there is no

adversary A that succeeds with probability ≥ ε.

Remark 1. In our consideration, we implicitly as-

sume that the parties are able to communicate with

each other via authentic channels, e.g. when R sends

a request to S at step 3. One can see that in order

to enable the detection of the forgery event, the au-

thenticity of the channel should be provided with some

different primitives rather than employed signatures.

For example, one can use message authentication

codes (MACs), which can be based on information-

theoretical secure algorithms and symmetric keys.

Remark 2. In the considered scheme honest users

only become aware of the fact of forgery event. How-

ever, the scheme does not allow determining who ex-

actly in this scenario has such powerful computa-

tional capabilities. Indeed, S is not sure whether the

signature σ

is forged by R or by A. That is why it is

advisable for S also to send evidence E to A as well.

At the same time, R is not sure, who is the original

n bits

n + δ bits

Figure 2: Basic principle of the public key construction in

the (n,δ)-L-OTS scheme.

author of σ

. It is a possible case that S has forged

its own signature (say, obtained two messages M and

with a same signature σ = σ

), and sent a mes-

sage M to A, who then just forwarded it R . It may

be in the interest of a malicious S to reveal M

at the

right moment and claim that it was a forgery.

4 ε-FDA FOR LAMPORT

SIGNATURES

Here we start with a description of a general-

ized Lamport single bit one-time DDSS. Consider a

cryptographic hash function H : {0, 1}

∗

→ {0, 1}

The (n, δ)-Lamport one-time signature ((n,δ)-L-OTS)

scheme for single bit message M ∈ {0, 1} has the fol-

lowing construction.

Key Pair Generation Algorithm: ((sk,pk) ← (n, δ)-L-

OTS.Kg). The algorithm generates secret and public

keys in a form (sk

,sk

) and (pk

,pk

), with sk

←

{0,1}

n+δ

and pk

:= H(sk

) (see Fig. 2). Here and

after

← stands for uniformly random sampling from

a given set.

Signature Algorithm: (σ ← (n,δ)-L-

OTS.Sign(sk, M)). The algorithm outputs half

of the secret key as a signature: σ := sk

Veriﬁcation Algorithm: (v ← (n,δ)-L-

OTS.Vf(pk, σ,M))). The algorithm outputs v := 1, if

H(s) = pk

, and its output is 0 otherwise.

The security of the (n, δ)-L-OTS scheme is based

on the fact that in order to forge a signature for a bit

M it is required to invert the used one-way function H

for a part of the public key pk

, that is traditionally

Proof-of-Forgery for Hash-based Signatures

337

assumed to be computationally infeasible.

In our work, we particularly stress the importance

of inequality between space sizes of secret keys and

public keys. Speciﬁcally, we demonstrate that for suf-

ﬁciently large δ even if an adversary ﬁnds a correct

preimage sk

, such that H(sk

) = pk

, the obtained

value is different from the original sk

used for calcu-

lating pk

by the legitimate user. Then the signature

of an honest user is different from a forged signature,

and so the forgery event can be revealed.

Before turning to the main theorem, we prove the

following Lemma.

Lemma 1. Consider a function f : {0,1}

n+δ

→

{0,1}

with n  1 and δ ≥ 0 taken at random from

the set all functions from {0,1}

n+δ

to {0,1}

. Let

= f (x

) for x

taken uniformly at random from

{0,1}

n+δ

. Deﬁne a set

Inv(y

) := {x ∈ {0, 1}

n+δ

| f (x) = y

} (2)

of all preimages of y

under f . Consider a randomly

taken preimage X

← Inv(y

). Then the probability to

obtain the original preimage X = x

has the following

lower and upper bounds:

a) Pr(X = x

) > exp(−2

);

b) Pr(X = x

) < 5.22 × 2

−δ

Proof. Let N := |Inv(y

)| be a number of preimages

of y

under f . Due to the random choice of f , it is

given by N = 1 +

N , where

N is a random variable

having binomial distribution Bin(2

−n

n+δ

− 1) with

the success probability 2

−n

and number of trials equal

to 2

n+δ

−1. Then the corresponding probability that a

randomly chosen element X from Inv(y

) is equal to

is as follows:

Pr(X = x

) =

n+δ

−1

∑

N=1

Pr(N = N). (3)

In order to obtain the lower bound for Pr(X = x

), we

consider only the ﬁrst term in Eq. (3) and arrive at the

following inequality:

Pr(X = x

) > Pr(N = 1) =



1 − 2

−n



n+δ

−1



1 − 2

−n



n+δ

' exp(−2

), (4)

where we use the fact that (1 − 2

−n

)

' exp(−1) for

n  1. This proves part a) of Lemma 1.

In order to obtain the upper bound for Pr(X = x

we split the sum in Eq. (3) into following two parts:

Pr(X = x

) =

∑

N=1

Pr(N = N)+

−1

∑

N=N

Pr(N = N) (5)

where N

:= k2

≥ 1 for some k ∈ (0,1). The ﬁrst part

can be bounded as follows:

∑

N=1

Pr(N = N) ≤ Pr(N ≤ N

)

≤

n+δ

− N

−n

− N

)

−δ

(k − 1)

(6)

where we use a bound for the cumulative binomial

distribution function (Feller, 1968). For the second

part we consider the following bound:

−1

∑

N=N

Pr(N = N) <

−1

∑

N=N

Pr(N = N)

−δ

(7)

By combining Eq. (6) with Eq. (7) and setting k :=

0.36, which corresponds to a minimum of Pr(X = x

we obtain Pr(X = x

) < 5.22 × 2

−δ

. This proves part

b) of Lemma 1.

Remark 3. The bound for commutative binomial dis-

tribution employed in (6) is rather rough, however, it

is quite convenient for the purposes of further discus-

sion. Tighter bound can be obtained, e.g. using the

technique from Ref. (Zubkov and Serov, 2013).

Next we assume that the number of (n + δ)-bit

preimages for H(x) with x

← {0,1}

n+δ

behaves in the

same way as for a random function from {0, 1}

n+δ

{0,1}

. The main result on the FDA property of the

(n,δ)-L-OTS scheme can be formulated as follows:

Theorem 1 . (n,δ)-L-OTS scheme has ε-FDA with

ε < 5.22 × 2

−δ

Proof. Consider an adversary who successfully

forged a signature σ

for message M

. From the con-

struction of the signature scheme we have H(σ

) =

. According to part b) of Lemma 1, the probabil-

ity that the obtained value σ

coincides with the orig-

inal value sk

is bounded by 5.22 × 2

−δ

. It follows

from the fact that sk

is generated uniformly ran-

domly from the set {0,1}

n+δ

. Therefore, with proba-

bility at least 1 − 5.22 × 2

−δ

the legitimate user’s sig-

nature sk

← (n,δ)-L-OTS.Sign(sk,M

) is different

from the adversary’s signature σ

and the presence of

the forgery event is then proven.

Remark 4 . We note that it is extremely important to

employ true randomness in the Kg algorithm in or-

der to provide the independence between the results

of the adversary and the original value of sk. For this

SECRYPT 2021 - 18th International Conference on Security and Cryptography

338

purpose, one can use, for example, certiﬁed quantum

random number generators.

Remark 5. We see that ε-FDA property appears only

for high enough values of δ. Meanwhile it follows

from part a) of Lemma 1 that for a common case of

δ = 0 the probability for the adversary to obtain the

original value sk

is at least exp(−1) ≈ 0.368 that is

non-negligible.

5 ε-FDA FOR THE WINTERNITZ

SIGNATURE SCHEME

Here we consider an extension of L-OTS scheme

which allows signing messages of L-bit length. We

base our approach on a generalization of the Winter-

nitz one-time signature (W-OTS) scheme presented in

Ref. (H

ulsing, 2013), known as W-OTS

, and used in

XMSS (H

ulsing et al., 2016), SPHINCS (Bernstein

et al., 2016) and SPHINCS

(Bernstein et al., 2017).

We note that W-OTS

is SU-CMA scheme (H

ulsing,

2013). We refer our scheme (n,δ, L,ν)-W-OTS

and

construct it as follows.

Let us introduce the parameter ν ∈ {1,2,. ..}

deﬁning blocks length in which a message is split

during a signing algorithm, where we assume that

L is a multiple of ν. Let us introduce the follow-

ing auxiliary values: w := 2

, l

:= dL/νe, l

blog

(w − 1))/νc +1, l := l

+ l

. Then we con-

sider a family of one-way functions:

(i)

: {0,1}

n+δ(w−i)

→ {0,1}

n+δ(w−i−1)

, (8)

where i ∈ {1,.. .,w − 1} and a parameter r belongs to

some domain D. The employ of this parameter can

correspond to XORing the result of some hash func-

tion family with a random bit-mask, as it considered

in Ref. (H

ulsing, 2013)). We assume that f

(i)

sat-

isﬁes the random oracle assumption for a uniformly

randomly chosen r from D.

We then introduce a chain function F

(i)

, which we

deﬁne recursively in the following way:

(0)

(x) = x,

(i)

(x) = f

(i)

(i−1)

(x)) for i ∈ {1,. .., w − 1}.

(9)

The algorithms of (n,δ,L, ν)-W-OTS

scheme are the

following:

Key Pair Generation Algorithm: ((sk,pk) ←

(n,δ,L,ν)-W-OTS

.Kg). First the algo-

rithm generates a secret key in the following

form: sk := (r, sk

,sk

,... ,sk

), with sk

←

{0,1}

n+δ(w−1)

and r

← D (see Fig. 3). Then a

(w-1)

(1)

...

(w-1)

(1)

...

n bits

n + δ bits

n + (w - 1) δ bits

n + (w - 2) δ bits

Figure 3: Basic principle of the public key construction in

the (n,δ,L,ν)-W-OTS

scheme.

public key composed of the randomizing parameter

r and results of the chain function employed to

as follows: pk := (r,pk

,pk

,... ,pk

) with

:= F

(w−1)

(sk

Signature Algorithm: (σ ← (n,δ, L,ν)-W-

OTS

.Sign(sk,M)). First the algorithm com-

putes base w representation of M by splitting

it into ν-bit blocks (M = (m

,... ,m

), where

∈ {0,. .. ,w − 1}). We call it a message

part. Then the algorithm computes a checksum

C :=

∑

i=1

(w − 1 − m

) and its base w representa-

tion C = (c

,... ,c

). We call it a checksum part.

Deﬁne an extended string B = (b

,... b

) := MkC

as the concatenation of message and checksum

parts. Finally, the signature is generated as follows:

σ := (σ

,σ

,... ,σ

) with σ

:= F

)

(sk

Veriﬁcation Algorithm: (v ← (n, δ,L,ν)-W-

OTS

.Vf(pk,σ,M))). The idea of the algorithm

is to reconstruct a public key from a given signature

σ and then to check whether it coincides with the

original public key pk. First, the algorithm computes

a base w string B = (B

,... ,B

) in the same way as

in the signature algorithm (see above). Then for each

part of the signature σ

the algorithm computes the

remaining part of the chain as follows:

check

:= f

(w−1)

◦ ... ◦ f

+1)

(σ

), (10)

where ◦ stands for the standard functions composi-

tion. If pk

check

= pk

for all i ∈ {1, ...,l}, then the

algorithm outputs v := 1, otherwise v := 0.

The main result on the FDA property of the

(n,δ,L,ν)-W-OTS

scheme can be formulated as fol-

lows:

Theorem 2 . The (n,δ, L,ν)-W-OTS

scheme has the

ε-FDA property with ε < 5.22 × 2

−δ

Proof. Consider a scenario of successful CMA on

the (n,δ,L, ν)-W-OTS

scheme, in which an adver-

sary ﬁrst forces a legitimate user with public key

pk = (r,pk

,... ,pk

) to provide him a signature σ =

(σ

,... ,σ

) for some message M, and then generate

a valid signature σ

= (σ

,... ,σ

) for some mes-

sage M

6= M. Let (m

,... ,m

) and (m

,... ,m

)

Proof-of-Forgery for Hash-based Signatures

339

...

n bits

n + (w - 1) δ bits

n + (w - b

- 1) δ bits

n + (w - b

- 1) δ bits

Figure 4: Illustration of the principle of PoF-II construction

for the (n,δ,L,ν)-W-OTS

scheme.

be the w-base representations of M and M

corre-

spondingly. Consider extended w-base strings B =

,... ,b

) and B

= (b

,... ,b

) generated by adding

checksum parts. It easy to see that for any distinct M

and M

there exists at least one position j ∈ {1,... ,l}

such that b

< b

. Indeed, even if for all positions

i ∈ {1,.. .,l

} it happened that m

> m

, from the def-

inition of checksum it follows that there exists a po-

sition j ∈ {l

+ 1,... ,l

} in checksum parts such that

< b

Since σ

is a valid signature for M

we have

(w−1)

◦ ... ◦ f

+1)

(σ

) = pk

. (11)

One can see that forgery event will be detected if the

part of the legitimate user’s signature of M

is dif-

ferent from the forged one (see also Fig. 4), so that:

:= F

)

(sk

) 6= σ

. (12)

Consider two possible cases. The ﬁrst is that the con-

dition (11) is fulﬁlled, but the following relation holds

true:

)

◦ ... ◦ f

+1)

(σ

) 6= σ

. (13)

In this case we obtain

6= σ

with unit probability

since

= f

)

◦...◦ f

+1)

(

) 6= f

)

◦...◦ f

+1)

(σ

(14)

In the second case we have the following identity:

)

◦ ... ◦ f

+1)

(σ

) = σ

, (15)

which automatically implies the fulﬁlment of

Eq. (11). Consider the function

F := f

)

◦ ... ◦ f

+1)

: {0,1}

∗

+δ ∆

→ {0,1}

∗

(16)

where ∆ := b

− b

≥ 1 and n

∗

:= n + δ(w − b

− 1).

This function satisﬁes random oracle assumptions,

since each of { f

(k)

}

k=b

do. The random oracle as-

sumption implies that the number of preimages of F is

the distributes in the same way as for random random

function. Moreover, due to the fact that the values of

are generated uniformly at random, the inputs for

F are also uniformly distributed over the correspond-

ing domains. So, according to part b) of Lemma 1, we

have the probability of the adversary to obtain σ

is bounded by ε < 5.22 × 2

−δ ∆

≤ 5.22 × 2

−δ

Remark 6. One can see that the excess of the preim-

age space size over the image space size, given by δ,

is a crucial condition for the FDA property both for L-

OTS and W-OTS

schemes. We also note that in the

case of the W-OTS

scheme it is important to have

such excess for all the elements of the employed one-

way chain.

Remark 7. One can imagine a situation where an

attacker is able to compute sk

6= sk

for some i ∈

{1,... ,l}, such that F

(w−1)

(sk

) = pk

. This means

that the chain collides somewhere on the way to pk

As long as an attacker reveals forgeries only above

this collision, there is no way for the legitimate user

to present a different signature on the same message.

However, in line with our proof, the probability of

such a scenario is limited by ε.

In WOT S

scheme consider an attacker who is

able to compute some value sk

6= sk

, such that

w−1

(sk

) = pk

for one of the public-key chunks pk

this means that the chain collides somewhere on the

way to pk

. One can notice that as long as an attacker

reveals forgeries only above this collision, there is no

way for the legitimate user to present a different sig-

nature on the same message. But following our proof,

this situation is limited by ε.

6 CONCLUSION

In this work, we have considered the ε-FDA property

of DDSS that allows detecting a forgery event gen-

erated by advanced mathematical algorithms and/or

unexpectedly powerful computational resources. We

have shown that this property is fulﬁlled for properly-

designed hash-based signatures, in particular, for L-

OTS and W-OTS

schemes with properly tuned pa-

rameters. As we have noted, the probability of the

successful demonstration of the DDSS forgery event

depends on an excess of preimage space sizes over

image space sizes and using true randomness in the

generation of secret keys in hash-based DDSS. The

important next step is to study this property for other

types of hash-based signatures.

Our observation is important in the view of the

crypto-agility paradigm. Indeed, the considered

forgery detection serves as an alarm that the employed

SECRYPT 2021 - 18th International Conference on Security and Cryptography

340

cryptographic hash function has a critical vulnerabil-

ity and it has to be replaced. We note that a simi-

lar concept has been recently considered for detecting

brute-force attacks on cryptocurrency wallets in the

Bitcoin network (Kiktenko et al., 2019). Namely, it

was considered the alarm system that detects the case

of stealing coins by ﬁnding a secret-public key pair

for standard elliptic curve digital signature algorithm

(ECDSA) used in the Bitcoin system, such that a pub-

lic key hash of adversary equals a public key hash of

a legitimate user. This kind of alarm system can be

of particular importance in view of the development

of quantum computing technologies (Fedorov et al.,

2018).

ACKNOWLEDGEMENTS

We thank A.I. Ovseevich, A.A. Koziy, E.K. Alekseev,

L.R. Akhmetzyanova, and L.A. Sonina for fruitful

discussions. This work is partially supported by Rus-

sian Foundation for Basic Research (18-37-20033).

REFERENCES

IOTA project website: www.iota.org.

Aumasson, J.-P. and Endignoux, G. (2017). Improving

stateless hash-based signatures.

Banegas, G. and Bernstein, D. (2018). Low-communication

parallel quantum multi-target preimage search. In Se-

lected Areas in Cryptography – SAC 2017, page 325.

Bernstein, D. (2009). Cost analysis of hash collisions: Will

quantum computers make sharcs obsolete. In Proceed-

ings of Workshop Record of SHARCS 2009: Special-

Purpose Hardware for Attacking Cryptographic Sys-

tems, page 51.

Bernstein, D., Buchmann, J., and Dahmen, E. (2009). Post-

Quantum Cryptography. Springer-Verlag, Berlin Hei-

delberg.

Bernstein, D., D. Hopwood, A. H., Lange, T., Niederhagen,

R., Papachristodoulou, L., Schneider, M., Schwabe,

P., and Wilcox-O’Hear, Z. (2016). Sphincs: Practical

stateless hash-based signatures. Lect. Notes Comp.

Sci, 9056:368.

Bernstein, D., Dobraunig, C., Eichlseder, M., Fluhrer, S.,

Gazdag, S.-L., H

ulsing, A., Kampanakis, P., K

olbl,

S., Lange, T., Lauridsen, M., Mendel, F., Niederha-

gen, R., Rechberger, C., Rijneveld, J., and Schwabe,

P. (2017). SPHINCS+.

Bernstein, D. and Lange, T. (2017). Post-quantum cryptog-

raphy. Nature, 549:188.

Black, J., Cochran, M., and Highland, T. (2006). A study

of the md5 attacks: Insights and improvements. Lect.

Notes Comp. Sci., 4047:262.

Boneh, D., Shen, E., and Waters, B. (2006). Unforgeable

signatures are used for constructing chosen-ciphertext

secure systems and group signatures. Lect. Notes

Comp. Sci., 3958:229.

Boyer, M., Brassard, G., Hoeyer, P., and Tapp, A. (1999).

Tight bounds on quantum searching. Fortschr. Phys.,

46:493.

Brassard, G., Høyer, P., and Tapp, A. (1998). Quantum

cryptanalysis of hash and claw-free functions. Lect.

Notes Comp. Sci., 1380:163.

Brendel, J., Cremers, C., Jackson, D., and Zhao, M. (2020).

The Provable Security of Ed25519: Theory and Prac-

tice.

Buchmann, J., Dahmen, E., and Szydlo, M. (2009). Hash-

based digital signature schemes. In Post-Quantum

Cryptography. Springer-Verlag Berlin Heidelberg.

Chailloux, A., Naya-Plasencia, M., and Schrottenloher, A.

(2017). An Efﬁcient Quantum Collision Search Algo-

rithm and Implications on Symmetric Cryptography.

Diamanti, E., Lo, H.-K., and Yuan, Z. (2016). Practical

challenges in quantum key distribution. npj Quant.

Inf., 2:16025.

Dobbertin, H. (1998). Cryptanalysis of md4. J. Crypt.,

11:253.

Fedorov, A., Kiktenko, E., and Lvovsky, A. (2018). Quan-

tum computers put blockchain security at risk. Nature,

563:465.

Feller, W. (1968). An Introduction to Probability Theory

and Its Applications. Wiley, USA, 3rd edition.

Gisin, N., Ribordy, G., Tittel, W., and Zbinden, H. (2002).

Quantum cryptography. Rev. Mod. Phys., 74:145.

Grover, L. (1996). A fast quantum mechanical algorithm

for database search. In Proceedings of 28th Annual

ACM Symposium on the Theory of Computing, vol-

ume 212, page 261, New York, USA.

ulsing, A. (2013). W-ots+ – shorter signatures for hash-

based signature schemes. In Progress in Cryptology -

AFRICACRYPT 2013, volume 7918, page 173–188.

Springer.

ulsing, A., Rijneveld, J., and Song, F. (2016). Mitigating

multi-target attacks in hash-based signatures. Lect.

Notes Comp. Sci., 9614:387.

Huelsing, A., Butin, D., Gazdag, S.-L., Rijneveld, J., and

Mohaisen, A. (2018). eXtended Merkle Signature

Scheme. RFC 8391, Internet-Draft.

Katz, J. (2016). Analysis of a proposed hash-based signa-

ture standard. Lect. Notes Comp. Sci., 10074:261.

Kiktenko, E., Kudinov, M., and Fedorov, A. (2019). Detect-

ing brute-force attacks on cryptocurrency wallets. In

Business Information Systems Workshops. BIS, page

373. Lecture Notes in Business Information Process-

ing.

Koblitz, N. and Menezes, A. (2015). The random oracle

model: a twenty-year retrospective. Des. Codes Cryp-

togr., 77:587.

Lamport, L. Constructing digital signatures from a one-way

function. Technical Report SRI-CSL-98, SRI Interna-

tional Computer Science Laboratory.

McGrew, D. and Curcio, M. (2016). Hash-Based Signa-

tures. RFC 8554, Internet-Draft.

Rivest, R., Shamir, A., and Adleman, L. (1978). A method

for obtaining digital signatures and public-key cryp-

tosystems. Commun. ACM, 21.

Proof-of-Forgery for Hash-based Signatures

341

Shor, P. (1997). Polynomial-time algorithms for prime fac-

torization and discrete logarithms on a quantum com-

puter. SIAM J. Comput., 26:1484.

Steinfeld, R. and Wang, J. P. H. (2007). How to strengthen

any weakly unforgeable signature into a strongly

unforgeable signature. Lect. Notes Comp. Sci.,

4377:357.

Stevens, M., Bursztein, E., Karpman, P., Albertini, A., and

Markov, Y. (2017). The ﬁrst collision for full sha-1.

Lect. Notes Comp. Sci., 10401:570.

Wallden, P. and Kasheﬁ, E. (2019). Cyber security in the

quantum era. Commun. ACM, 62:120.

Zubkov, A. and Serov, A. (2013). A complete proof of uni-

versal inequalities for the distribution function of the

binomial law. Theory Probab. Appl., 57:539.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

342