Online Facility Service Leasing Inspired by the COVID-19 Pandemic

Christine Markarian

and Peter Khallouf

Department of Engineering and Information Technology, University of Dubai, U.A.E.

Data Science - Data and IT, International University of Applied Sciences, Germany

Keywords:

Facility Location, Service Leasing, COVID-19 Pandemic, Decision-making, Online Algorithms, Optimization

Problems, Competitive Analysis.

Abstract:

In response to resource shortages caused by the COVID-19 pandemic, many communities have been leasing

health facilities such as hospitals, clinics, and other centers in order to meet the needs of their patients. The

goals have been two-folded: leasing costs had to be optimized and patients had to be served as soon as possible.

Decisions as to when to lease which services at which facility locations shaped the success of these goals. At

the heart of these decisions lies a complex optimization problem, which we call the Online Non-metric Facility

Service Leasing problem (non-metric OFSL), a generalization of the well-known Online Non-metric Facility

Leasing problem (non-metric OFL) in which facility locations are leased for different facility-time durations.

In non-metric OFSL, each facility location may provide a number of services leased for different service-time

durations. Additionally, each service is associated with a dormant fee that needs to be paid for each day at

which the service is not leased. The optimization goal is to minimize the total leasing costs, dormant fees, and

the distances between patients and the facilities they are connected to. We develop the ﬁrst online algorithm

for non-metric OFSL, evaluated using the notion of competitive analysis. The latter is a worst-case analysis

used to measure the quality of online algorithms, in which the online algorithm’s output is compared to the

optimal ofﬂine solution for all instances of the problem.

1 INTRODUCTION

The COVID-19 pandemic has put health systems

around the world under immense pressure (Vaccaro

et al., 2020; Kumari et al., 2020; Emanuel et al., 2020;

Sen-Crowe et al., 2021; Pfefferbaum and North,

2020). According to the World Health Organiza-

tion, failure to protect health care can have a long-

lasting impact on the health and well-being of pop-

ulations (WHO, 2020). A successful protection of

these systems means the ability to provide patients ac-

cess to health services as soon as needed. For most

communities, available health facilities were notably

scarce and so new measurements had to be taken.

Some sought to build new health facilities. Others

made agreements with various facilities to lease med-

ical services at their locations. Circumstances were

changing too fast and decisions had to be made on-

the-ﬂy. The lack of future knowledge in terms of the

evolution of the COVID-19 disease made decision-

making even more challenging.

Motivated by these events, we target in this pa-

per provably good decision-making in the face of the

uncertainty of the future, focusing on communities

that lease services at different facility locations, such

as hospitals, clinics, and other centers to meet the

needs of their patients. The goals here have been two-

folded: leasing costs had to be optimized and patients

had to be served as soon as possible. Decisions as

to when to lease which services at which facility loca-

tions shaped the success of these goals. The challenge

was to make immediate decisions without knowing

the future with as few regrets as possible.

More generally, consider a company trying to

serve its clients with the least possible costs while op-

timizing the distances between clients and the facility

locations they are served by. The company has made

contracts with a number of facility locations, each

willing to offer a number of services. The contract re-

quires that these facility services remain reserved for

the company for as long as the contract states. The

company has a number of lease types to choose from

when it comes to leasing services at facilities. Lease

types respect economy of scale such that longer leases

are more expensive but cheaper per unit time. More-

over, the price of leasing the same service for the same

Markarian, C. and Khallouf, P.

Online Facility Service Leasing Inspired by the COVID-19 Pandemic.

DOI: 10.5220/0010572601950202

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 195-202

ISBN: 978-989-758-522-7

195

duration may differ between one facility location and

the other. Prices vary based on how attractive a facil-

ity location is in comparison to other locations. The

company has the option not to lease a service at some

facility location for some period of time but has to

pay a dormant fee for each day at which the service is

not leased. This is to compensate for what the facility

location could have gained had there been no reserva-

tion of this service at the facility location. By holding

a service for the company, the facility is losing poten-

tial customers from other companies that could have

been interested in the service at the facility during that

period of time. Each day, a number of clients show

up, each requesting a number of services. The com-

pany needs to decide when to lease which facilities at

which facility locations in order to connect clients to

a number of facility locations jointly offering the ser-

vices requested. Its goal is reached only if each client

is served as soon as it arrives by services leased at the

time of its arrival.

At the heart of such decisions lies a complex op-

timization problem which we approach in this paper

from an online algorithmic perspective. Unlike clas-

sical ofﬂine algorithms, the input to an online algo-

rithm is not given all at once but arrives in portions

over time. The job of the online algorithm is to re-

act to each arriving portion while targeting a given

optimization goal against the entire input. Online al-

gorithms are evaluated using the notion of competi-

tive analysis. The latter is a worst-case performance

analysis in which the online algorithm’s decisions are

compared to the optimal ofﬂine decisions which could

have been made in an ideal situation should the entire

future be known.

The optimization problem at hand is called the

Online Non-metric Facility Service Leasing problem

(non-metric OFSL), a generalization of two well-

known optimization problems in the ﬁeld of Online

Algorithms (Borodin and El-Yaniv, 2005), namely, the

Online Non-metric Facility Location problem (non-

metric OFL) (Alon et al., 2006) and the Parking Per-

mit problem (PP) (Meyerson, 2005). In non-metric

OFSL, rather than leasing facilities as in (Markarian

and Meyer auf der Heide, 2019; Abshoff et al., 2016;

Nagarajan and Williamson, 2013), services are leased

at facilities for different time durations, and addition-

ally, each service is associated with a dormant fee that

needs to be paid for each day at which the service is

not leased. Such fees were not considered in previ-

ous leasing models. The goal is to minimize the total

leasing costs, dormant fees, and the distances between

clients and the facilities they are connected to. We call

these distances connecting costs.

We say r is the competitive ratio of an online algo-

rithm (or an online algorithm is r-competitive) if r is

the worst case ratio of the cost of the online algorithm

to that of the optimal ofﬂine solution, measured over

all possible instances of the problem. In this paper, we

design the ﬁrst online algorithm for non-metric OFSL

and prove that it has an O(log(n + m · l

max

)log(Lm))

competitive ratio, where:

– n is the total number of clients

– l

max

is the length of the longest lease duration

– L is the number of lease types available

– m is the total number of facility locations

Outline. The rest of the paper is structured as fol-

lows. In Section 2, we given an overview of works

related to leasing and online non-metric facility loca-

tion problems. We give a formal deﬁnition of non-

metric OFSL in Section 3 and formulate it as a graph-

theoretic problem in Section 4. In Section 5, we

present our online algorithm for non-metric OFSL

and analyze its competitive ratio in Section 6. We

present in Section 7 some concluding remarks and fu-

ture works.

2 RELATED WORK

The ﬁrst leasing model was introduced by Meyer-

son (Meyerson, 2005) with the Parking Permit prob-

lem (PP). Meyerson proposed an O(L)-competitive

deterministic algorithm and an O(logL)-competitive

randomized algorithm for PP and showed that these

ratios are the best possible competitive ratios. Many

network optimization problems were later studied fol-

lowing the leasing model of Meyerson (Anthony and

Gupta, 2007; Markarian and Kassar, 2020; Nagarajan

and Williamson, 2013; Abshoff et al., 2016). A num-

ber of extensions of the model were also known (Feld-

kord et al., 2017; Li et al., 2018; Markarian, 2018;

De Lima et al., 2017; De Lima et al., 2020).

Facility Location problems have been studied as

non-metric and metric versions. The latter version as-

sumes facilities and clients reside in a metric space

and all distances respect the triangle inequality. This

property has been used to prove the competitive ratio

of the algorithms for the metric version (Meyerson,

2001; Fotakis, 2008). In this paper, we study the non-

metric version.

Non-metric OFSL is a generalization of the non-

metric Online Facility Location problem (non-metric

OFL) (Alon et al., 2006), in which there is only one

lease type of length inﬁnity; each facility offers one

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

196

service; and dormant fees are zero. Alon et al., (Alon

et al., 2006) gave an O(log mlog n)-competitive on-

line randomized algorithm for non-metric OFL.

Non-metric OFSL generalizes the Online Set

Cover problem (OSC) (Alon et al., 2003) and the

Parking Permit problem (PPP) (Meyerson, 2005).

We can thus conclude that there is a lower bound

of Ω(logn logm + log L) on the competitive ratio

of any randomized polynomial-time algorithm for

non-metric OFSL. The latter results from the lower

bound on the competitive ratio of any randomized

polynomial-time algorithm for the Online Set Cover

problem (OSC) due to (Korman, 2005) and the lower

bound on the competitive ratio of any randomized al-

gorithm for the Parking Permit problem (PPP) due

to (Meyerson, 2005).

3 PROBLEM DESCRIPTION

In this section, we give a formal deﬁnition of the

Online Non-metric Facility Service Leasing problem

(non-metric OFSL).

Deﬁnition 1. (non-metric OFSL) We are given m fa-

cility locations and k services. Each facility location

offers a subset of the k services. These services can

be leased for L different types, each differing by a du-

ration and price. For each service at some facility

location and each time step at which the service is not

leased by the algorithm, there is a dormant fee that

needs to be paid. There are in total n clients that may

arrive. In each time step, a subset of the clients ar-

rives, each requesting a subset of the k services. The

algorithm serves a client by connecting it to a number

of facility locations jointly offering the requested ser-

vices, such that these services are leased at the time

of the client’s arrival. Connecting a client to a facility

location incurs a connecting cost which is equal to the

distance between the client and the facility location.

In each time step, the algorithm needs to decide which

services to lease at which facility locations with which

lease type in order to serve all arriving clients. The

goal is to minimize the total leasing costs, dormant

fees, and connecting costs.

4 GRAPH FORMULATION

In this section, we formulate non-metric OFSL as a

graph-theoretic problem. The latter will be the basis

of our algorithm in Section 5.

Figure 1: Interval Model.

Nodes.

– For each client which arrives, we create a node,

called actual client node.

– For each facility, we create a node, called actual

facility node.

– For each service, we create a node, called service

node.

– For each time step and facility, we create two

nodes, one client node, called virtual client node,

and another facility node, called virtual facility

node.

Edges.

– We add a directed edge from each actual client

node to each actual facility node of weight equal

to the connecting cost between the corresponding

client and facility.

– We add L directed edges from each actual facility

node to each service node, corresponding to the

L lease types, each of weight equal to the corre-

sponding cost of leasing the service at the facility.

The Interval Model below explains the choice of

Interval Model. Meyerson (Meyerson, 2005)

proved that we can assume, without affecting the

competitive ratio of the algorithm by more than

a constant factor, that leases may have a special

property in regards to their allignment and length. He

refered to the model as the interval model, deﬁned as

follows.

– leases of the same type do not overlap

– all lease lengths are power of two

Figure 1 gives an illustration of the Interval Model

using an example of four lease types denoted as l

, l

and l

. We assume in this paper that leases are in

accordance to the Interval Model. This means that at

any time step, there are exactly L different lease types

available. Hence, on any time step t, the L directed

edges correspond to the L different leases whose in-

tervals cover time step t.

– For each virtual client node corresponding to fa-

cility j, we add a directed edge from the virtual

Online Facility Service Leasing Inspired by the COVID-19 Pandemic

197

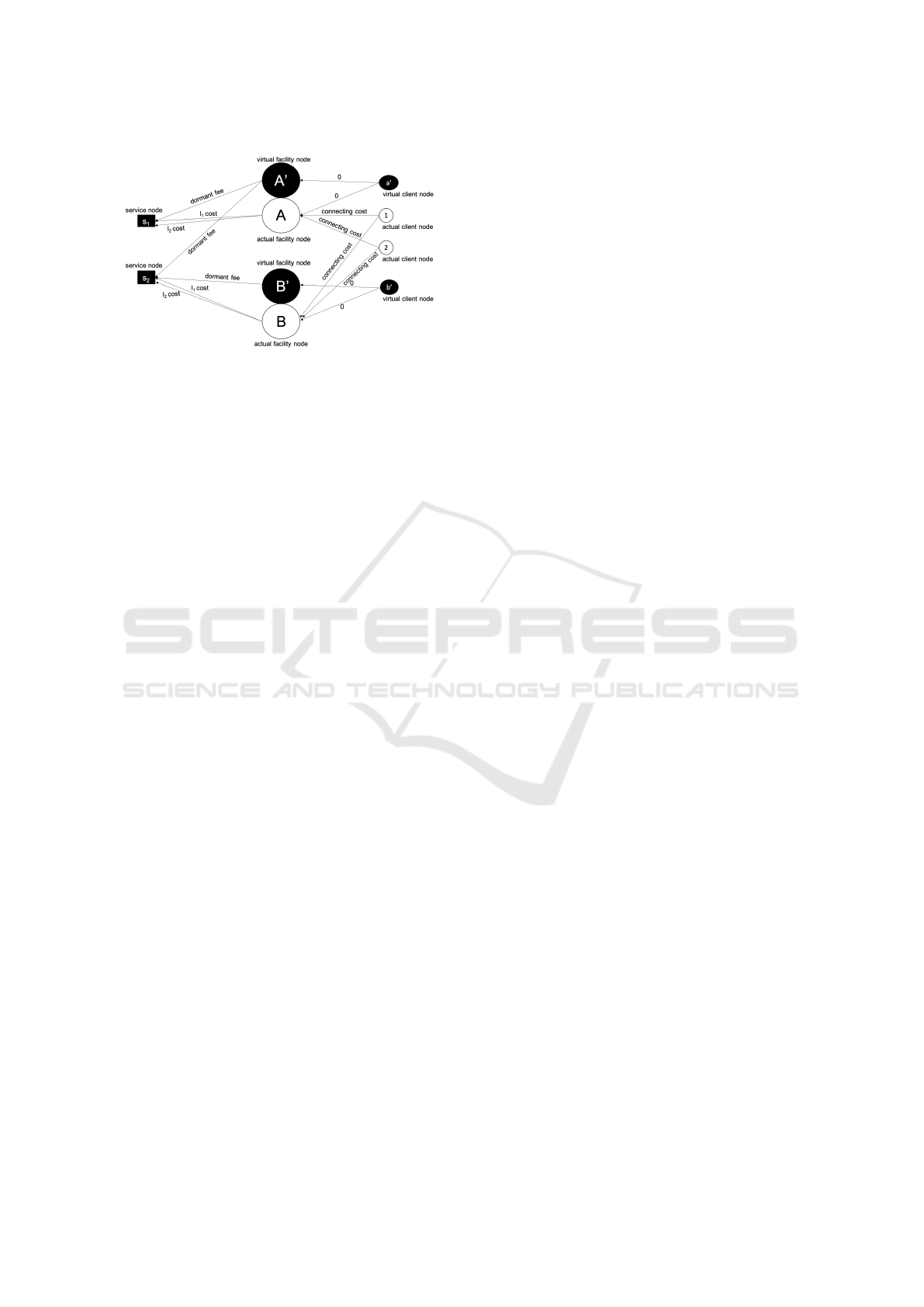
Figure 2: Graph formulation of non-metric OFSL instance.

client node to the actual facility node correspond-

ing to j and a directed edge from the virtual client

node to the virtual facility node corresponding to

j; both edges have weight equal to 0.

– We add a directed edge from each virtual facil-

ity node to each service node associated with it of

weight equal to the dormant fee associated with

the service at that facility.

Figure 2 illustrates the graph formulation using an

instance of two lease types l

and l

, two services s

and s

, two facilities A and B, and two clients, 1 and

2. Facility A offers both services s

and s

. Facility B

offers service s

. Virtual facility A

and virtual client

are created in association with facility A. Virtual fa-

cility B

and virtual client b

are created in association

with facility B. Hence, virtual facility A

has outgoing

edges to s

and s

; virtual facility B

has an outgoing

edge to s

only. The ﬁgure also shows the weights on

the edges in association with each dormant fee, con-

necting cost, and lease cost, as described earlier.

Algorithm’s Input. The algorithm initially knows

the facilities, the services, the leasing costs, the dor-

mant fees, and the maximum number of clients that

may arrive. On each time step, a number of clients

requesting different services arrive. The algorithm

will know the connecting costs of a client to all fa-

cilities at the time step of the client’s arrival. Follow-

ing the graph formulation above, the algorithm will

initially know the entire graph except for the actual

client nodes and the outgoing edges from these nodes.

These will be created upon the arrival of the clients.

Algorithm’s Output: Upon the arrival of a new

client, the algorithm needs to serve it immediately

by connecting it to a number of services jointly offer-

ing the services requested, such that these services are

leased at the time of the client’s arrival. On each time

step, the algorithm needs to decide which services to

lease at which facility locations with which lease type

in order to serve all arriving clients. Following the

graph formulation above, on each time step, the algo-

rithm needs to:

– for each arriving client i, ﬁnd a directed path from

the actual client node corresponding to i to each

service node corresponding to each service re-

quested by i.

– for each facility j, ﬁnd a directed path from the

virtual client node corresponding to j to each ser-

vice node corresponding to each service offered

by j.

Algorithm’s Decisions. By ﬁnding the aforemen-

tioned paths, the algorithm can make its decisions by

mapping the solution paths as follows.

– The virtual facility and client nodes will be used

to determine when to pay a dormant fee. For each

virtual client node and service node associated

with it, if the solution path from the virtual client

node to the service node passes through a virtual

facility node, the corresponding dormant fee of

the service at the facility is paid. This means that

the algorithm will pay the dormant fee of a ser-

vice at a facility if the algorithm hasn’t purchased

a lease for the service. This is true since there

must be at least one path from each virtual client

node to each service node associated with it.

– For each client and service it has requested, we

purchase the lease at the actual facility node as-

sociated with the edge on the solution path from

the corresponding actual client node to the ser-

vice node. This guarantees that the algorithm pur-

chases for each arriving client at least one lease

for each service requested.

5 ONLINE ALGORITHM

In this section, we propose an online randomized al-

gorithm for non-metric OFSL, based on the graph for-

mulation described above.

Before the execution of the algorithm, the facility

nodes and the service nodes along with their edges are

created. On a given time step t, the online algorithm

is given a number of clients each requesting a number

of services. For each client, an actual client node and

its edges are created. Moreover, for each facility, a

virtual client node and a virtual facility node along

with their edges are created. Weights on the edges are

added as decribed before. Let the weight of edge e be

denoted by w

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

198

To ﬁnd the solution paths, the algorithm will asso-

ciate each edge e with a value v

, initially 0. Through-

out the execution of the algorithm, the values of the

edges will increase, and on each time step, the algo-

rithm will purchase some of the edges of the graph

based on their values so as to provide a feasible solu-

tion for each time step. Recall that, a feasible solution

on a given time step means to ﬁnd for each arriving

client i, a directed path from the actual client node of

i to each service node requested by i. Moreover, the

solution needs to also include for each facility j, a di-

rected path from the virtual client node of j to each

service node offered by j.

The maximum ﬂow between two nodes will be the

smallest total values of edges which if removed would

disconnect the two nodes. These edges will be called

a minimum cut. While producing a feasible solution

on any given time step, the algorithm ignores all edges

whose corresponding leases are expired.

To decide which edges to purchase, the algorithm

will use a randomization process commonly adopted

by online algorithms (Alon et al., 2006; Markarian

and Meyer auf der Heide, 2019). The process is

rather straightforward. A random variable r is cho-

sen as the minimum among 2

log(n + m · l

max

+ 1)

independent random variables, distributed uniformly

in the interval [0, 1], where base 2 is assumed for the

logarithms. Recall that n is the total number of clients

and l

max

is the length of the longest lease. The choice

of the number of variables and the interval becomes

clear in the competitive analysis of the algorithm in

Section 6.

The solution of the online algorithm is the set of

edges purchased by the algorithm. We deﬁne a sub-

routine, called Edges-selection, that takes as input two

nodes i and s, and retuns a set of edges. These edges

will be purchased by the algorithm to guarantee a di-

rected path from i to s in the solution. As a reaction

to a given time step t, the algorithm performs two

phases, depicted in Algorithm 1 below.

6 COMPETITIVE ANALYSIS

In this section, we give a competitive analysis of our

algorithm.

We measure the cost of the total edges purchased

by the algorithm. Following the graph formulation in

Section 4 – Algorithm’s Decisions, the latter repre-

sents the cost of the algorithm. Recall that, our leases

follow the Interval Model of Meyerson, as described

in Section 4 – Edges. This means that it is enough

to measure the cost of the algorithm over the duration

associated with the longest lease duration l

max

. A sim-

Algorithm 1: Online Algorithm for non-metric OFSL.

Phase 1. For each actual client node i and each

service s requested by the client

- Run Edge-selection(i, s)

- Purchase the edges returned.

Phase 2. For each virtual client node i and each

service s associated with it

- Run Edge-selection(i, s)

- Purchase the edges returned.

Edge-selection (node i , node s)

i. If the current solution contains a directed path

from i to s, we do nothing. Else, while the maxi-

mum ﬂow between i and s is less than 1:

- We compute a minimum cut Q between i and s.

- We increase the value v

of each edge e ∈ Q

using the following equation:

← v

(1 +

) +

|Q | · w

ii. We return edge e if its value v

≥ r.

iii. If i is not connected to s, we return the edges of

a shortest-weight path from i to s.

ilar analysis has been done in (Abshoff et al., 2016;

Markarian, 2015).

Let Opt be the cost of the optimal ofﬂine solution.

The algorithm buys edges returned by Edge-selection

in the second and third steps (ii. and iii.). We analyze

each separately.

Edge-selection – Step ii. Let E

be the collection of

edges returned by Edge-selection in the second step

ii. Let Cost

be the expected cost of this collection.

An edge is returned here if its value exceeds r, the ran-

dom number selected before the execution of the algo-

rithm. We ﬁx any i : 1 ≤ i ≤ 2

log(n + m · l

max

+ 1)

and edge e. We denote by X

e,i

the indicator variable

of the event that e is returned by Edge-selection. We

denote by w

the weight of edge e and v

its value. We

can write Cost

as:

Cost

∑

e∈E

log(n+m·l

max

+1)

∑

i=1

· Exp [X

e,i

] (1)

= 2

log(n + m · l

max

+ 1)

∑

e∈E

(2)

∑

e∈E

can be compared to the optimal ofﬂine

solution as follows. Every time we compute a mini-

mum cut, there must be in the minimum cut at least

one edge that belongs to the optimal ofﬂine solution.

Online Facility Service Leasing Inspired by the COVID-19 Pandemic

199

This is true since, for any pair that we need to connect,

the optimal solution needs to also connect it through

some path p. By deﬁnition of a cut, every cut should

contain at least one edge of p.

We give in the following lemma an upper bound

on the total number of times Edge-selection computes

a minimum cut.

Lemma 1. The total number of times Edge-selection

computes a minimum cut is upper bounded by O(Opt ·

log|Q|), where |Q| is the size of the largest minimum

cut constructed.

Proof. Each optimal edge e could have appeared in

multiple minimum cuts constructed, and after some

number of times, its value becomes 1 and it won’t

belong to any future minimum cut. The algorithm

ensures that the maximum ﬂow is less than 1 be-

fore it computes any minimum cut. Thus, it becomes

easy to see that we can actually bound these number

of times by O(w

log|Q|), based on the equation in

Edge-selection for increasing the values of the edges.

Applying the same analysis to each optimal edge and

summing up over all these edges, we can conclude

that the total number of times we compute a minimum

cut is O(Opt · log|Q|), since each minimum cut must

contain at least one optimal edge.

Furthermore, the largest minimum cut |Q| con-

structed by Edge-selection can be upper bounded in

terms of L and m:

|Q| ≤ L · m (3)

The following lemma shows that the total value

increase does not exceed 2 for each minimum cut.

Lemma 2. The total value increase associated with

each minimum cut constructed does not exceed 2.

Proof. We ﬁx any minimum cut Q constructed.

Based on the equation in Edge-selection, each edge

e in Q contributes to a value increase of w



·w



. Before we make any value increase,

the maximum ﬂow is less than 1, that is,

∑

e∈Q

< 1.

Summing up over all the edges in Q, we conclude that

the total value increase does not exceed:

∑

e∈Q



· w



< 2

From Lemma 1 and Lemma 2, we imply:

∑

e∈E

≤ O(Opt · log |Lm|) (4)

Therefore,

Cost

≤ O(Opt · log(n + m · l

max

) · log |Lm|) (5)

Edge-selection – Step iii. Let E

be the collection

of edges returned by Edge-selection in the third step

iii. Let Cost

be the expected cost of this collection.

The algorithm performs this step each time it ﬁnds

out that the pair at hand is not connected in the cur-

rent solution. We deﬁne the ﬂow of a path to be the

minimum of all edge values of the path. To calculate

Cost

, we need to observe the probability that the

given pair (i, s) is not connected. The latter is upper

bounded by the probability that r exceeds the ﬂow of

each path from i to s. We ﬁx a minimum cut Q con-

structed at the end of step i. Before executing step

ii, Edge-selection ensures that the sum of ﬂows of all

paths from i to s is at least 1. Hence, the probability

that the pair is not connected is:

∏

e∈Q

(1 − v

) ≤ e

−

∑

e∈Q

≤

Computing for all i: 1 ≤ i ≤

log(n + m · l

max

+ 1)

, the probability that the

pair is not connected will be at most

(n+m·l

max

)

Each time Edge-selection ﬁnds out that the pair

(i, s) is not connected, it returns the cheapest path

from i to s. The latter is a lower bound on Opt. Hence,

Cost

be will at most (n+ m ·l

max

)·

Opt

(n+m·l

max

)

, since

there are in total l

max

virtual client nodes over an l

max

interval and n actual client nodes.

Thus, the cost is negligible on the competitive ra-

tio.

Cost

≤

Opt

n + m · l

max

(6)

Therefore, we conclude the following theorem.

Theorem 1. There is an O(log(n+m·l

max

)log(Lm))-

competitive randomized algorithm for Online Non-

metric Facility Service Leasing (non-metric OFSL),

where n is the total number of clients, l

max

is the

length of the longest lease duration, L is the number

of lease types available, and m is the total number of

facility locations.

7 DISCUSSION & FUTURE

WORK

Inspired by resource shortages during the COVID-19

pandemic, we have presented in this paper an opti-

mization model for leasing services at facility loca-

tions. It is important to note here that the latter is not

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

200

speciﬁc to only health services but can be applied to

any type of facility-service-leasing scenario.

Our model aims to minimize the leasing costs

while optimizing the distances between clients and

the facilities they are served by. Moreover, it requires

a dormant fee for each day a service is kept dormant.

As a future work, it would be interesting to study

other variations such as assuming different fees for

different dormant times. For example, a one-month

dormant fee of a service could be cheaper per unit

day than a one-week dormant fee, since the facility

can make use of the service over a longer period if it

knows in advance that the service will not be used for

a whole month rather than a week only.

In this paper, we have presented the ﬁrst online al-

gorithm for making on-the-ﬂy decisions about leasing

services at facilities and connecting clients to them.

Next steps would be: to achieve a better competitive

ratio by designing another algorithm or improving the

competitive analysis of our algorithm; to prove lower

bounds on the competitive ratio of any randomized

online algorithm for our problem; and to design a de-

terministic algorithm for our problem.

Another research direction is to add capacities to

the facilities and/or the services provided by them. So

far in this model, we have assumed that facilities can

serve any number of clients, since we assume that the

input sequence receives a limited number of clients

each day.

Our proposed online algorithmic approach has the

advantage of providing decisions that have a proven

guarantee. That is, even on the worst input sequence,

the algorithm can assure that the decisions are not

worse than what promised. Hence, it is worth imple-

menting the proposed algorithm ﬁrst on a simulated

environment of COVID-19 facility locations and ser-

vices, and second on a real-world community provid-

ing services to its members through leased services at

facility locations.

REFERENCES

Abshoff, S., Kling, P., Markarian, C., Meyer auf der Heide,

F., and Pietrzyk, P. (2016). Towards the price of leas-

ing online. Journal of Combinatorial Optimization,

32(4):1197–1216.

Alon, N., Awerbuch, B., and Azar, Y. (2003). The on-

line set cover problem. In Proceedings of the Thirty-

ﬁfth Annual ACM Symposium on Theory of Comput-

ing, STOC ’03, pages 100–105, New York, NY, USA.

ACM.

Alon, N., Awerbuch, B., Azar, Y., Buchbinder, N., and

Naor, J. (2006). A general approach to online net-

work optimization problems. ACM Transactions on

Algorithms (TALG), 2(4):640–660.

Anthony, B. M. and Gupta, A. (2007). Infrastructure leas-

ing problems. In International Conference on Integer

Programming and Combinatorial Optimization, pages

424–438. Springer.

Borodin, A. and El-Yaniv, R. (2005). Online computa-

tion and competitive analysis. Cambridge University

Press.

De Lima, M. S., San Felice, M. C., and Lee, O. (2017). On

generalizations of the parking permit problem and net-

work leasing problems. Electronic Notes in Discrete

Mathematics, 62:225–230.

De Lima, M. S., San Felice, M. C., and Lee, O. (2020).

Group parking permit problems. Discrete Applied

Mathematics, 281:172–194.

Emanuel, E. J., Persad, G., Upshur, R., Thome, B., Parker,

M., Glickman, A., Zhang, C., Boyle, C., Smith, M.,

and Phillips, J. P. (2020). Fair allocation of scarce

medical resources in the time of covid-19.

Feldkord, B., Markarian, C., and Meyer auf der Heide, F.

(2017). Price ﬂuctuation in online leasing. In Inter-

national Conference on Combinatorial Optimization

and Applications, pages 17–31. Springer.

Fotakis, D. (2008). On the competitive ratio for online fa-

cility location. Algorithmica, 50(1):1–57.

Korman, S. (2005). On the use of randomization in the on-

line set cover problem. Master’s thesis, Weizmann In-

stitute of Science, Israel.

Kumari, V., Mehta, K., and Choudhary, R. (2020). Covid-

19 outbreak and decreased hospitalisation of preg-

nant women in labour. The Lancet Global Health,

8(9):e1116–e1117.

Li, S., Markarian, C., and Meyer auf der Heide, F. (2018).

Towards ﬂexible demands in online leasing problems.

Algorithmica, 80(5):1556–1574.

Markarian, C. (2015). Online resource leasing. PhD thesis,

University of Paderborn, Germany.

Markarian, C. (2018). Leasing with uncertainty. In Op-

erations Research Proceedings 2017, pages 429–434.

Springer.

Markarian, C. and Kassar, A.-N. (2020). Online deter-

ministic algorithms for connected dominating set &

set cover leasing problems. In International Confer-

ence on Operations Research and Enterprise Systems

(ICORES), pages 121–128.

Markarian, C. and Meyer auf der Heide, F. (2019). On-

line algorithms for leasing vertex cover and leasing

non-metric facility location. In International Confer-

ence on Operations Research and Enterprise Systems

(ICORES), pages 315–321.

Meyerson, A. (2001). Online facility location. In Proceed-

ings 42nd IEEE Symposium on Foundations of Com-

puter Science, pages 426–431. IEEE.

Meyerson, A. (2005). The parking permit problem. In 46th

Annual IEEE Symposium on Foundations of Computer

Science (FOCS’05), pages 274–282. IEEE.

Nagarajan, C. and Williamson, D. P. (2013). Ofﬂine

and online facility leasing. Discrete Optimization,

10(4):361–370.

Online Facility Service Leasing Inspired by the COVID-19 Pandemic

201

Pfefferbaum, B. and North, C. S. (2020). Mental health

and the covid-19 pandemic. New England Journal of

Medicine, 383(6):510–512.

Sen-Crowe, B., Sutherland, M., McKenney, M., and Elk-

buli, A. (2021). A closer look into global hospital beds

capacity and resource shortages during the covid-19

pandemic. Journal of Surgical Research, 260:56–63.

Vaccaro, A. R., Getz, C. L., Cohen, B. E., Cole, B. J., and

Donnally III, C. J. (2020). Practice management dur-

ing the covid-19 pandemic. The Journal of the Amer-

ican Academy of Orthopaedic Surgeons.

WHO, W. H. O. (2020). Attacks on health care in the con-

text of covid-19.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

202