Fractional Order Tracking Control of Unmanned Aerial Vehicle in

Presence of Model Uncertainties and Disturbances

Heera Lal Maurya, Padmini Singh, Subhash Chand Yogi, Laxmidhar Behera

and Nishchal K. Verma

Department of Electrical Engineering, Indian Institute of Technology, Kanpur, U.P., 208016, India

Keywords:

Unmanned Aerial Vehicle, Fractional Calculus, Sliding Mode Control, Model Uncertainty.

Abstract:

An unmanned Aerial Vehicle (UAV) is a highly non-linear unstable system. In this work using fractional

order calculus, a novel fractional order dynamics of UAV is proposed. The concept of fractional order depicts

the more realistic behavior of UAVs. For proposed fractional order model, a fractional order sliding mode

controller (SMC) is designed such that the desired path can be achieved by the UAV in ﬁnite-time. In addition

to this model uncertainty and disturbance is considered in the system which is handled by the proposed robust

SMC. Stability analysis is given for the fractional order SMC using fractional Lyapunov method. Simulations

have been done for position and attitude tracking of UAV to demonstrate the efﬁcacy of the proposed method.

1 INTRODUCTION

Recently, UAVs are being used for wide variety of

applications some of them are transportation, survel-

liance (Aubry et al., 2014), forest trail destection

(Giusti et al., 2015), agriculture purposes (Mogili and

Deepak, 2018) etc. however to control a quadrotor is

quite challenging due to its characteristics like high

nonlinearity, underactuation propoerty and external

disturbances. From the past few years it is a subject

of interest for researchers to design a robust controller

for quadrotor UAVs.

Although there are several controllers e.g. LQR

controller (Cohen et al., 2020), Backstepping Con-

troller (Yu et al., 2019), (Liu et al., 2016) developed

and applied on the UAV, still a robust control scheme

has been an interest of research. Sliding mode control

(SMC) (R

ıos et al., 2018) is one of the most popular

and robust control technique which has the ability to

rejects disturbances and uncertainties but at the cost

of chattering (Boiko and Fridman, 2005). The chat-

tering actuates the unwanted dynamics of the system

which can deteriorate the system performance, hence

disturbance rejection at a cost of deteriorated perfor-

mance is not appreciable. Since quadrotor is a rela-

tive degree two type of system, a proper stable sliding

surface is needed for the design of controller. De-

pending upon the type of surface the convergence of

https://orcid.org/0000-0003-1879-5609

error can be asymptotic or ﬁnite-time. The asymptotic

surface (Xiong and Zhang, 2016) shows slower con-

vergence than the ﬁnite-time surface but ﬁnite-time

surface or terminal sliding surface (Weidong et al.,

2015), (Wang et al., 2016) cause singularity issue.

Most of the controllers discussed above are inte-

ger order control schemes. Recently, fractional order

controllers (Chen et al., 2019)(Cajo et al., 2019)(Hua

et al., 2019) have drawn much attention due to appli-

cation of powerful processors. The fractional order

terms provides an extra degree of freedom in terms of

controller parameters which can be adjusted for bet-

ter tracking performance. Some of the work on frac-

tional order controller on UAV are as (Oliva-Palomo

et al., 2019) presents a PI fractional order controller

for quadrotor for only attitude control. A novel

fractional controller has been proposed in (Izaguirre-

Espinosa et al., 2018) for attitude control as well as

position control of quadrotor. Conventinal SMC has

been employed in (Shi et al., 2020) for position and

attitude control of quadrotor where fractional order

switching law is proposed to compensate the uncer-

tainties on integer model of quadrotor. A fast termi-

nal SMC (FTSMC) has been presented in (Labbadi

et al., 2019) for faster convergence of tracking er-

ror however FTSMC is applied only on attitude con-

trol whereas conventional SMC is employed for posi-

tion control and thus overall scheme doesn’t provide

faster convergence. All these schemes hasve been ap-

plied on applied on the integer order model of the

274

Maurya, H., Singh, P., Yogi, S., Behera, L. and Verma, N.

Fractional Order Tracking Control of Unmanned Aerial Vehicle in Presence of Model Uncertainties and Disturbances.

DOI: 10.5220/0010554902740281

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 274-281

ISBN: 978-989-758-522-7

 2021 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

quadrotor UAV. Moreover, less attention is given to

the fractional-order based dynamics. Though we con-

sider the dynamics of the quadrotor of integer order

but practically it may not be of integer order because

there may be some fractional order term exist which

effects the dynamics of the quadrotor. Hence, a frac-

tional order controller can increase the robustness and

usability of controller if employed with the fractional

order model of the quadrotor.

Motivated from the above discussion, a fractional

order model of quadrotor has been considered in-

stead of an integer order model In this work which is

more practical and feasible with the real world model.

Thereafter, A robust control law as fractional order

sliding mode controller (SMC) has been presented for

the quadrotor model while considering the uncertain

dynamics. There is a trade-off has been done between

the asymptotic surface and ﬁnite-time time surface

using fractional order theory. Using fractional order

theory, a novel fractional sliding surface is proposed

for the quadrotor which improves the response of the

surface as well as avoids the singularity issue of the

ﬁnite-time sliding surface. Next for mitigating the

chattering issue of SMC, a power rate reaching law

along with a proportional term has been used in the

control laws for position and attitude tracking. There

are six fractional order control laws are designed for

UAV where, three are position controllers which gen-

erates the thrust required and attitude reference for

attitude controller while rest of the three are attitude

controllers. The main contribution of the paper are

summarised as follows:

1. A fractional order novel sliding surface is pro-

posed so that the region of stability increased in

left half plane.

2. A novel fractional order singularity free control

law is proposed which rejects the model uncer-

tainties present in the quadrotor.

3. Stability of the fractional sliding surface and the

controller is given using Lyapunov stability the-

ory.

4. Simulations are conducted for quadrotor position

and attitude tracking and it is shown that the pro-

posed technique is better than the existing second

order twisting controller.

Rest of the paper is organized as follows: prelim-

inaries for fractional calculus is provided in section

2 and section 3 constitutes the problem formulation.

Fractional order quadrotor model is presented in sec-

tion 4 which is followed by the controller design in

section 5 and stability analysis in section 6. Simula-

tion results slong with the comparative analysis has

been presented in section 7. Finally, conclusion and

future scope is given in section 8.

2 PRELIMINARIES

The caputo fractional derivative (Odibat, 2006) of any

function f (ϑ) is represented by:

[ f (ϑ)] =

Γ(n − β)

(n)

(τ)

(t − τ)

(β−n+1)

dτ

(1)

where, Γ(.) represents the Gamma function and n −

1 < β < n ∈ N.

Fractional order integral (Odibat, 2006) of order α >

0 can be expressed as:

[ f (ϑ)] =

Γ(α)

(t − τ)

(α−1)

f (ϑ)dτ

(2)

3 PROBLEM FORMULATION

The control architecture is shown in Fig .1 consists of

two control loops where ﬁrst one corresponds to inner

or attitude control loop which runs at high frequency,

another is position control loop which estimates the

attitude reference to the attitude controller in terms

of φ

, θ

and thrust to the quadrotor. The speed of

the rotor is regulated by the pulse width modulated

(PWM) signal.The generation of the desired PWM

signal is controlled by the output of attitude controller

i.e. torque and thrust from the position controller,

which then actuates the motors of quadrotor.

The objective is to track the desired position and at-

titude in presence of uncertainties where the desired

position x

, y

, z

and desired yaw angle ψ

are pro-

vided by the user. Here a novel fractional order slid-

ing surface is proposed which increases the stability

range of the error plane. After that a fractional order

SMC is applied on the quadrotor which rejects the un-

certainty present in the system.

So mathematically, the objective is

lim

t→∞

x → x

, lim

t→∞

y → y

, lim

t→∞

z → z

and lim

t→∞

ψ → ψ

4 QUADROTOR MODEL

Fig. 2 represents the pictorial view of quadrotors and

direction of the forces acting on the four arms. The

forces F

, F

and F

works in the upwards direc-

tion to generate the desired thrust so that the quadrotor

can ﬂy in the qpwards direction. The sum of the total

Fractional Order Tracking Control of Unmanned Aerial Vehicle in Presence of Model Uncertainties and Disturbances

275

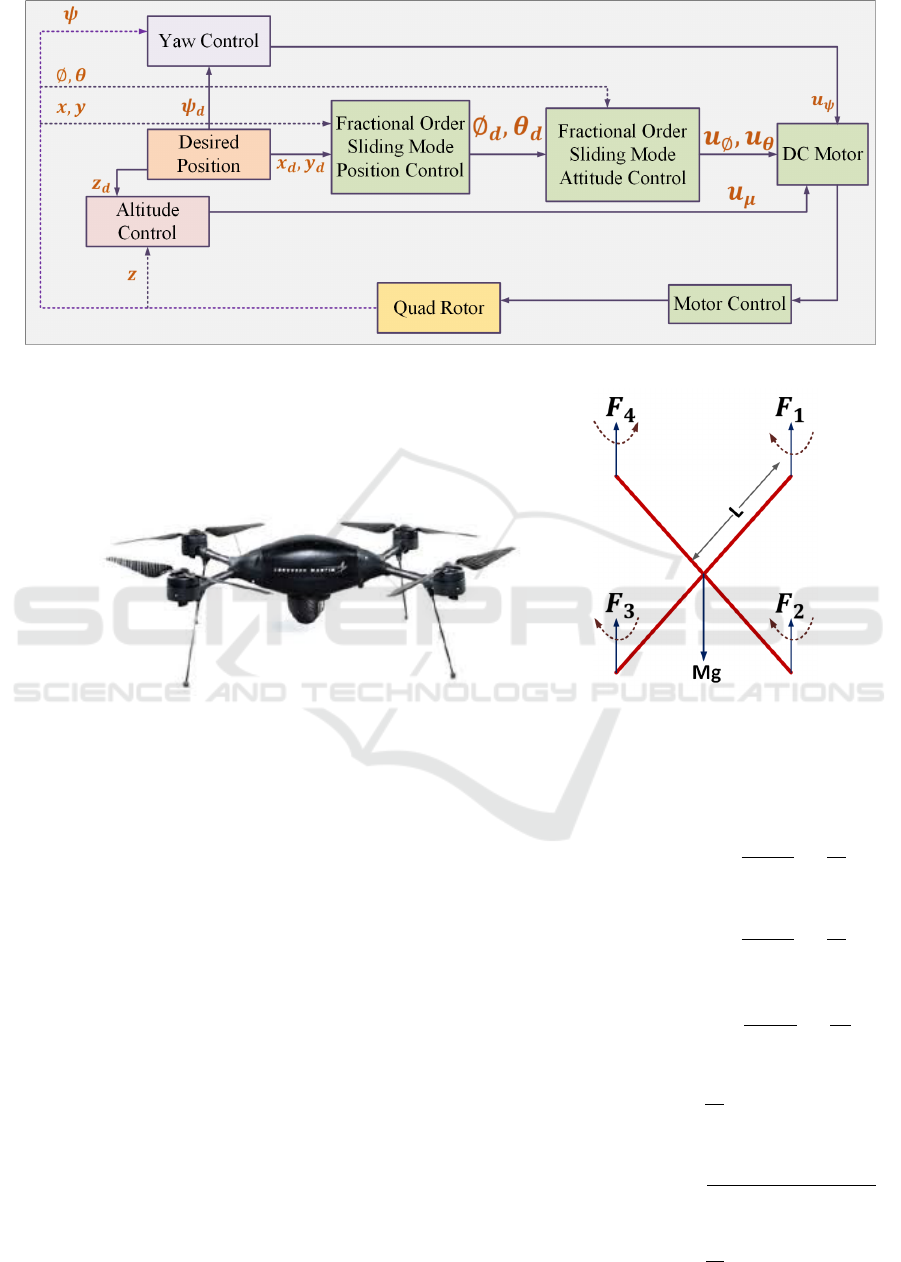
Figure 1: Control Architecture for UAV.

(a) (b)

Figure 2: (a.) Quadrotor (b.) Direction of Forces acting on Four arms.

forces u

= F

+ F

is called the total thrust

required to lift the quadrotor. The minimum thrust

required to drag the UAV in the upward direction

should be greater than the weight of the UAV. There-

fore small UAVs required small thrust compared to

big one to achieve the same height from the ground

and hence takes less power.

4.1 Quadrotor Dynamics

Generally fractional order controllers are designed for

integer order system. In (Hua et al., 2019) fractional

order sliding mode controller is designed for integer

order UAVs. It will be more realistic if one would

take the dynamics of UAVs also fractional order. The

fractional order dynamics of quadrotor in presence of

model uncertainty and external disturbance, is pre-

sented here by taking the fraction order of the model

of UAV given in (Singh et al., 2020). It is to be

noted that in this paper a novel fractional model of

the quadrotor is designed.

= φ

= δ f (φ, t) + d

(t) +

ψ(

− J

) +

= θ

= δ f (θ, t) + d

(t) +

ψ(

− J

) +

= ψ

= δ f (ψ, t) + d

(t) +

θ(

− J

) +

= z

= δ f (z, t) + d

(t) +

(CφCθ) − g

= x

= δ f (x, t) + d

(t) +

(CφSθCψ + SφSψ)

= y

= δ f (y, t) + d

(t) +

(CφSθSψ − SφCψ)

(3)

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

276

where C(.), S(.) corresponds to cos(.) and sin(.) re-

spectively, φ

, θ

, ψ

are three attitude angles i.e.

roll, pitch and yaw angles respectively whereas x

, z

are positions of the quadrotors. There are total

twelve states including angular velocities φ

, θ

, ψ

and translational velocities x

, y

, z

. All these twelve

states are controlled by four control inputs u

, u

and u

. δ f (φ,t), δ f (θ, t) , δ f (ψ,t), δ f (x, t) , δ f (y, t) ,

δ f (z, t) are model uncertainty and d

(t) , d

(t)

are external disturbances. The relation between ro-

tor forces and four control inputs is given in (Singh

et al., 2020). The dynamics of the quadrotor can be

represented as second order fractional subsystems if

the virtual control laws are selected as:

(cosφsin θcosψ + sin φsin ψ)

(cosφ sin θsin ψ − sinφcos ψ)

(cosφ cos θ) − g

(4)

Therefore,

= m

)

+ (u

)

+ (u

+ g)

(5)

After considering all the virtual control inputs the dy-

namics of the quadrotor can be decoupled using six

second order subsystems. Now objective is to design

tracking controller such that desired positions and at-

titude angles are achieved.

4.2 Error Model

In this section error dynamics of x, y, z and φ, θ, ψ is

given. Now, the second order fractional dynamics for

x position is:

= x

= δ f (x, t) + d

(t) + u

(6)

If the desired x position is x

then the error will be:

= x

− x

= x

− D

(7)

Hence, fractional order error dynamics for x position

in presence of model uncertainty and disturbance is:

= e

= δ f (x, t) + d

(t) + u

− D

2α

(8)

Like wise error dynamics for rest of the ﬁve subsys-

tems are:

= e

= δ f (y, t) + d

(t) + u

− D

2α

(9)

= e

= δ f (z, t) + d

(t) + u

− D

2α

(10)

φ1

= e

φ2

ψ(

− J

) + δ f (φ,t) + d

(t) + u

− D

2α

(11)

θ1

= e

θ2

ψ(

− J

) + δ f (θ,t) + d

(t) + u

− D

2α

(12)

ψ1

= e

ψ2

θ(

− J

) + δ f (ψ, t) + d

(t) + u

− D

2α

(13)

Now, in next section fractional order controller is

designed for the quadrotor.

5 CONTROLLER DESIGN

In this section, a novel robust fractional order SMC

has been proposed to counteract parametric uncer-

tainty, external disturbances as well as unmatched un-

certainty.

5.1 Fractional Order Sliding Surface

Design

The proposed fractional order sliding surface is:

(t) = D

α−1

+ D

α−2

(| e

| + | e

) |

) + k

(| e

| + | e

) |

) + (sign(e

1−α

)

sign(e

)

(14)

where, β ∈ (0, 1) is a positive constant. and k

and k

are positive tuning parameters. Taking the derivative

of sliding surface eq.(14), we get

˙s

(t) = D

+ D

α−1

(| e

| + | e

) |

) + k

(| e

| + | e

) |

) + (sign(e

1−α

)

sign(e

)

(15)

Fractional Order Tracking Control of Unmanned Aerial Vehicle in Presence of Model Uncertainties and Disturbances

277

After the reaching phase is achieved i.e. when ˙s

(t) =

0, eq.(15) reduces to,

= −D

α−1

(| e

| + | e

) |

) + k

(| e

) | + | e

) |

) + (sign(e

1−α

)

sign(e

)

(16)

5.1.1 Error Dynamics in Sliding Mode

From Eq. (16) and (7), fractional dynamics for x po-

sition in sliding mode can be written as :

= e

= −D

α−1

(| e

| + | e

) |

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

(17)

Likewise, error dynamics for rest of the quadrotor

states can be obtained.

5.2 Fractional Order Controller Design

Again revisiting eq.(15)

˙s

(t) = D

+ D

α−1

(| e

| + | e

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

(18)

Substituting value of D

from eq.(8) in eq.(18) and

substituting ˙s

(t) = −k

− k

| s

sign(s

) the

control law u

will be:

− k

| s

sign(s

) = δ f (x, t) + d

(t) + u

− D

2α

+ D

α−1

(| e

| + | e

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

(19)

where, γ ∈ (0, 1) is a positive constant. and k

and k

are positive tuning parameters. Further simplifying

= −k

− k

| s

sign(s

) − δ f (x, t) − d

(t)

+ D

2α

− D

α−1

(| e

| + | e

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

(20)

For rejecting the model uncertainties and disturbances

the control law is modiﬁed to,

= −k

− k

| s

sign(s

) − (δ

+ δ

)sign(s

)

+ D

2α

− D

α−1

(| e

| + | e

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

(21)

where δ

and δ

are positive tuning parameters.

Like wise control laws for rest of the position and Eu-

ler angels can be calculated. Control law for y posi-

tion tracking is:

= −k

− k

| s

sign(s

) − (δ

+ δ

)sign(s

)

+ D

2α

− D

α−1

(| e

| + | e

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

Control law for altitude z tracking is:

= −k

− k

| s

sign(s

) − (δ

+ δ

)sign(s

)

+ D

2α

− D

α−1

(| e

| + | e

) + k

(| e

| + | e

) + (sign(e

1−α

)

sign(e

)

Control law for roll φ tracking is:

= J

− k

φ3

− k

φ4

| s

sign(s

) −

ψ(

− J

)

− (δ

φ1

+ δ

φ2

)sign(s

) + D

2α

− D

α−1

φ1

(| e

φ1

) |

+ | e

φ1

) |

) + k

φ2

(| e

φ2

) | + | e

φ2

) |

) + (sign(e

φ1

)×

1−α

φ2

)

sign(e

φ2

)

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

278

Control law for pitch θ is:

= J

− k

θ3

− k

θ4

| s

sign(s

) −

ψ(

− J

)

− (δ

θ1

+ δ

θ2

)sign(s

) + D

2α

− D

α−1

θ1

(| e

θ1

+ | e

θ1

) + k

θ2

(| e

θ2

| + | e

θ2

) + (sign(e

θ1

)×

1−α

θ2

)

sign(e

θ2

)

Control law for yaw θ is:

= J

− k

ψ3

− k

ψ4

| s

sign(s

) −

θ(

− J

)

− (δ

ψ1

+ δ

ψ2

)sign(s

) + D

2α

− D

α−1

ψ1

(| e

ψ1

+ | e

ψ1

) + k

ψ2

(| e

ψ2

) | + | e

ψ2

) |

) + (sign(e

ψ1

)×

1−α

ψ2

sign(e

ψ2

6 STABILITY ANALYSIS OF

CONTROLLER

For the stability analysis, two different Lyapunov

function have been taken where one is for reaching

phase stability analysis and the other is for sliding

phase.

6.1 Reaching Phase Stability

For reaching phase we have to show that reachability

law ˙s

(t) = −k

− k

| s

sign(s

) converges to

zero. Let us take Lyapunov candidate as:

=| s

(22)

The derivative of V

= sign(s

) ˙s

(23)

Substituting derivative of sliding surface using

eq.(15) in eq.(23)

+ D

α−1

(| e

) | + | e

) |

) + k

(

| e

| + | e

) |

) + (sign(e

1−α

)

sign(e

)

× sign(s

)

(24)

After substituting the value of D

from error dy-

namics and inserting the control law u

eq.(24) will

become:

≤ −sign(s

)(k

+ k

| s

sign(s

))

(25)

Using sign(s

=| s

| and sign

= 1. The Lya-

punov derivative will become-

≤ −k

(| s

| + | s

) ≤ −k

| s

(26)

where, k

= min(k

, k

). Eq.(26) is negative deﬁnite

hence it is stable.

6.2 Sliding Phase Stability

for sliding phase stability we have to show that both

the error states of x position tracking converges to

zero. Let us take Lyapunov candidate as:

=| e

| + | e

(27)

The derivative of V

= sign(e

) ˙e

+ sign(e

) ˙e

(28)

Eq.(23) can also be written as using property of frac-

tional order theory

= sign(e

)[D

1−α

] + sign(e

)[D

1−α

]

From eq.(8) and eq.(16) substituting the values of

and D

in the above Eq.

= sign(e

)[D

1−α

] − sign(e

1−α

α−1

(| e

) | + | e

) |

) + k

(| e

) | + | e

) |

)

+ (sign(e

1−α

)

sign(e

)

(29)

After simplifying eq.(29), we get

= −

(| e

) | + | e

) + k

(| e

) | + | e

) |

which is negative deﬁnite. Hence both the reaching

phase and sliding phase of designed fractional order

controller is stable.

7 SIMULATION RESULTS

Proposed approach has been validated in MATLAB

where following set of parameters speciﬁcation has

been taken as:

Mass (m) 1.0 Kg

Inetria (I

) 1.676 × 10

−2

Inetria (I

) 1.676 × 10

−2

Inetria (I

) 2.314 × 10

−2

Fractional Order Tracking Control of Unmanned Aerial Vehicle in Presence of Model Uncertainties and Disturbances

279

The gain parameters value has been chosen by trial

and error as. k

= k

= 2, k

= k

= 2, k

= k

= 2

and k

φ1

= k

= 1.2, k

= k

= 1.2, k

= k

= 1.4.

The fractional derivatives are selected as α = 0.6 and

β = 0.7. The proposed approach has been validated

for two cases i.e. quadrotor hovering at 1.25m and

spiral trajectory tracking. A comparison has also been

provided against twisting controller (Shtessel et al.,

2017) and the superiority of presented approach is

validated.

7.1 Quadrotor Hovering

0 5 10 15 20

(d)

0.5

1.5

z (m)

Desired

Actual

0 5 10 15 20

Time(sec) (e)

0.1

0.2

0.3

ψ (rad)

Desired

Actual

0 5 10 15 20

(c)

-0.5

0.5

y (m)

Desired

Actual

0 5 10 15 20

Time(sec) (b)

-0.5

0.5

x (m)

Desired

Actual

y (m)

x (m)

0.2

0.5

0.1

z(m)

-0.2

-0.1

Desired

Actual

uncertainty

(a)

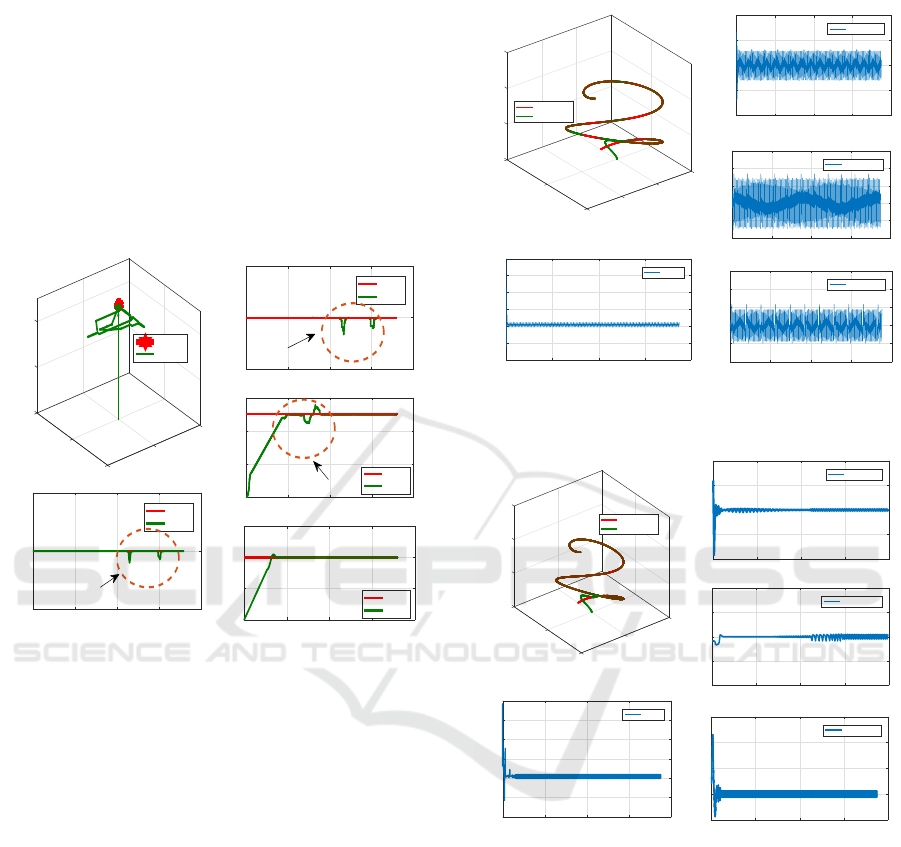
Figure 3: Hovering of UAV using proposed method.

Here, the objective is to takeoff the quadrotor to

= 1.25m and hover thereafter at this height. To

check the robustness of the proposed controller, a dis-

turbance has been added at hovering in all of the three

directions x, y and z at different time instants, the max-

imum bound on the magnitude of disturbances in all

the three directions are 0.2 ∗ sint. Disturbances are

applied in all the three directions at different instants

of time to check the robustness of the controller. The

simulation results are shown in Fig 3 where we see

that the quadrotor successfully reaches at 1.25 m and

hover as shown in 3(a) in spite of the disturbance.

Thus we can conclude from Fig 3 that the quadrotor

effectively counteract the disturbance and hover con-

tinuously at 1.25 m.

7.2 Spiral Trajectory Tracking

Now, the quadrotor is required to track the spiral

shaped trajectory which is generated as follows by

desired positions as: x

= 01 ∗ sin(0.15 ∗ t), y

2 ∗ cos(0.2 ∗ t) and z

= 1.5 ∗ t. The proposed ap-

proach is compared with (Shtessel et al., 2017) as well

and obtained results are shown in Fig 4.

z(m)

100

y(m)

x(m)

150

-1

-5

-2

Desired Path

Actual Path

0 20 40 60 80

time(sec) (b)

(N)

Thrust

0 20 40 60 80

time(sec) (c)

-10

-5

(N-m)

Roll Torque

0 20 40 60 80

time(sec) (d)

-4

-2

(N-m)

Pitch Torque

0 20 40 60 80

time(sec) (e)

-4

-2

(N-m)

Yaw Torque

(a)

Figure 4: UAV tracking spiral shaped trajectory using

Twisting controller.

z(m)

100

y(m)

x(m)

150

-5

-2

Desired Path

Actual Path

0 20 40 60 80

time(sec) (e)

-0.2

0.2

0.4

0.6

(N-m)

Yaw Torque

0 5 10 15 20

time(sec) (c)

-0.2

-0.1

0.1

0.2

(N-m)

Roll Torque

0 5 10 15 20

time (sec) (d)

-0.2

-0.1

0.1

0.2

(N-m)

Pitch Torque

0 20 40 60 80

time (sec) (b)

(N)

Thrust

(a)

Figure 5: UAV tracking spiral shaped trajectory using pro-

posed fractional order controller.

The tracking results obtained by proposed ap-

proach are shown in Fig 5. Form Fig 4(a) and 5(a),

we see that both of the approaches show good per-

formance in term of disturbance rejection. How-

ever, the control effort required for tracking is having

more chattering as shown in Fig 4(b),(c),(d) and (e)

as compared to the proposed approach in 5(b),(c),(d)

and (e). Due to the large chattering, it may actuate

the unmodelled dynamics which affects the actuator’s

performance and thus the approach (Shtessel et al.,

2017) is not feasible in real-time scenario whereas

proposed approach show less chattering and can be

implemented in real-time.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

280

8 CONCLUSION AND FUTURE

SCOPE

In the proposed work novel fractional order model is

presented for the quadrotor which is more real for

practical applications. The fractional order parame-

ters achieves the tracking accuracy of the controller.

The comparative study has been done with the pro-

posed method with the existing second twisting con-

troller in terms of chattering attenuation and con-

troller effort. The future scope of the present work

is to design controller for multiagent quadrotor sys-

tems in presence of communication bandwidth limi-

tation using fractional order theory. The present work

is just a proof of the concept to be validated on more

complex systems.

REFERENCES

Aubry, M., Maturana, D., Efros, A. A., Russell, B. C., and

Sivic, J. (2014). Seeing 3d chairs: exemplar part-

based 2d-3d alignment using a large dataset of cad

models. In Proceedings of the IEEE conference on

computer vision and pattern recognition, pages 3762–

3769.

Boiko, I. and Fridman, L. (2005). Analysis of chattering in

continuous sliding-mode controllers. IEEE transac-

tions on automatic control, 50(9):1442–1446.

Cajo, R., Mac, T. T., Plaza, D., Copot, C., De Keyser, R.,

and Ionescu, C. (2019). A survey on fractional order

control techniques for unmanned aerial and ground

vehicles. IEEE Access, 7:66864–66878.

Chen, L., Saikumar, N., and HosseinNia, S. H. (2019).

Development of robust fractional-order reset control.

IEEE Transactions on Control Systems Technology,

28(4):1404–1417.

Cohen, M. R., Abdulrahim, K., and Forbes, J. R. (2020).

Finite-horizon lqr control of quadrotors on se 2(3).

IEEE Robotics and Automation Letters, 5(4):5748–

5755.

Giusti, A., Guzzi, J., Cires¸an, D. C., He, F.-L., Rodr

ıguez,

J. P., Fontana, F., Faessler, M., Forster, C., Schmidhu-

ber, J., Di Caro, G., et al. (2015). A machine learning

approach to visual perception of forest trails for mo-

bile robots. IEEE Robotics and Automation Letters,

1(2):661–667.

Hua, C., Chen, J., and Guan, X. (2019). Fractional-

order sliding mode control of uncertain quavs with

time-varying state constraints. Nonlinear Dynamics,

95(2):1347–1360.

Izaguirre-Espinosa, C., Mu

noz-V

azquez, A.-J., S

anchez-

Orta, A., Parra-Vega, V., and Fantoni, I. (2018).

Fractional-order control for robust position/yaw track-

ing of quadrotors with experiments. IEEE Trans-

actions on Control Systems Technology, 27(4):1645–

1650.

Labbadi, M., Nassiri, S., Bousselamti, L., Bahij, M., and

Cherkaoui, M. (2019). Fractional-order fast termi-

nal sliding mode control of uncertain quadrotor uav

with time-varying disturbances. In 2019 8th Inter-

national Conference on Systems and Control (ICSC),

pages 417–422. IEEE.

Liu, H., Li, D., Zuo, Z., and Zhong, Y. (2016). Robust

three-loop trajectory tracking control for quadrotors

with multiple uncertainties. IEEE Transactions on In-

dustrial Electronics, 63(4):2263–2274.

Mogili, U. R. and Deepak, B. (2018). Review on application

of drone systems in precision agriculture. Procedia

computer science, 133:502–509.

Odibat, Z. (2006). Approximations of fractional integrals

and caputo fractional derivatives. Applied Mathemat-

ics and Computation, 178(2):527–533.

Oliva-Palomo, F., Mu

noz-V

azquez, A. J., S

anchez-Orta, A.,

Parra-Vega, V., Izaguirre-Espinosa, C., and Castillo,

P. (2019). A fractional nonlinear pi-structure con-

trol for robust attitude tracking of quadrotors. IEEE

Transactions on Aerospace and Electronic Systems,

55(6):2911–2920.

ıos, H., Falc

on, R., Gonz

alez, O. A., and Dzul, A.

(2018). Continuous sliding-mode control strategies

for quadrotor robust tracking: Real-time applica-

tion. IEEE Transactions on Industrial Electronics,

66(2):1264–1272.

Shi, X., Cheng, Y., Yin, C., Zhong, S., Huang, X., Chen,

K., and Qiu, G. (2020). Adaptive fractional-order smc

controller design for unmanned quadrotor helicopter

under actuator fault and disturbances. Ieee Access,

8:103792–103802.

Shtessel, Y. B., Moreno, J. A., and Fridman, L. M. (2017).

Twisting sliding mode control with adaptation: Lya-

punov design, methodology and application. Automat-

ica, 75:229–235.

Singh, P., Gupta, S., Behera, L., Verma, N. K., and Naha-

vandi, S. (2020). Perching of nano-quadrotor using

self-trigger ﬁnite-time second-order continuous con-

trol. IEEE Systems Journal.

Wang, H., Ye, X., Tian, Y., Zheng, G., and Christov, N.

(2016). Model-free–based terminal smc of quadro-

tor attitude and position. IEEE Transactions on

Aerospace and Electronic Systems, 52(5):2519–2528.

Weidong, Z., Pengxiang, Z., Changlong, W., and Min, C.

(2015). Position and attitude tracking control for a

quadrotor uav based on terminal sliding mode con-

trol. In 2015 34th Chinese control conference (CCC),

pages 3398–3404. IEEE.

Xiong, J.-J. and Zhang, G. (2016). Sliding mode control for

a quadrotor uav with parameter uncertainties. In 2016

2nd International Conference on Control, Automation

and Robotics (ICCAR), pages 207–212. IEEE.

Yu, G., Cabecinhas, D., Cunha, R., and Silvestre, C. (2019).

Nonlinear backstepping control of a quadrotor-slung

load system. IEEE/ASME Transactions on Mecha-

tronics, 24(5):2304–2315.

Fractional Order Tracking Control of Unmanned Aerial Vehicle in Presence of Model Uncertainties and Disturbances

281