Stiffness Modeling of Compliant Serial Manipulators based on

Tensegrity Mechanism under External Loading

Wanda Zhao

, Anatol Pashkevich

1,2

and Damien Chablat

1,3

Laboratoire des Sciences du Numérique de Nantes (LS2N), UMR CNRS 6004, Nantes, France

IMT Atlantique Bretagne Pays de la Loire, Nantes, France

Centre National de la Recherche Scientifique (CNRS), France

Keywords: Compliant Manipulator, Tensegrity Mechanism, Stiffness Analysis, Robot Buckling.

Abstract: The paper focuses on the stiffness modeling of a new type of compliant manipulator and its non-linear

behavior under external loading. The manipulator under study is a serial mechanical structure composed of

dual-triangle segments. The main attention is paid to the possible equilibriums and the manipulator stiffness

behavior under the loading for the initial non-straight configuration. It was demonstrated that there is a quasi-

buckling phenomenon for this manipulator while the external loading increasing. In the neighborhood of these

configurations, the manipulator behavior was analyzed using the enhanced Virtual Joint Method (VJM).

Relevant simulation study confirmed the obtained theoretical results.

1 INTRODUCTION

Compliant manipulators are used nowadays in many

fields due to their flexibility, modularized

construction, and low weight. A lot of new

mechanical structures were studied in this area

(Frecker, Ananthasuresh et al., 1997; Albu-Schaffer

et al., 2008; Wang and Chen, 2009; Howell, 2013),

which showed quite good performances compared

with traditional rigid robots. Recently, in literature

particular attention is paid to tensegrity mechanisms,

which are made up of a series of similar segments

composed of compressive and tensile elements

(cables or springs) (Skelton and Oliveira, 2009;

Moored, Kemp, et al., 2011). One of such structures

is studied in this paper.

Stiffness properties of some tensegrity

mechanisms have been already studied carefully. In

(Arsenault and Gosselin, 2006), the authors

considered the mechanism composed of two springs

and two length-changeable bars. They analyzed the

mechanism stiffness using the energy method,

demonstrated that the mechanism stiffness may

decrease under external loading with the actuators

locked, which may lead to the “buckling”

phenomenon. Also, in (Furet, Lettl and Wenger,

2018), the cable-driven X-shape tensegrity structures

were considered; here the authors investigated the

influence of cable lengths on the mechanism

equilibrium configurations, which may be both stable

and unstable. The relevant analysis of the equilibrium

configurations as well as the stability and singularity

study can be found in (Wenger and Chablat, 2019).

For robotics, similar to classical mechanics

dealing with the Euler column, the buckling is usually

treated as an undesirable phenomenon, because the

robot may suddenly change its shape when the

loading force exceeds some critical value. However,

such property can be useful in some fields (Yamada,

Mameda, et. al., 2010). Also, sometimes the quasi-

buckling phenomenon may occur, which changes the

robot resistance in one direction suddenly while the

external loading is increasing. It is not typical for

robotics and was rarely studied before. For this

reason, this phenomenon should be obligatory taken

into account in stiffness analysis.

This paper is an extension of our previous results

(Zhao, Pashkevich et al., 2020 & 2021), which

concentrated on the stiffness analysis of the simplest

manipulator composed of two and three segments. It

was assumed that each segment is a composition of

two rigid triangle parts, which are connected by a

passive joint in the center and two elastic edges on

each side with controllable preload. In contrast to the

previous results, here we consider a general case with

an arbitrary number of segments, and its stiffness

behavior under the loading.

254

Zhao, W., Pashkevich, A. and Chablat, D.

Stiffness Modeling of Compliant Serial Manipulators based on Tensegrity Mechanism under External Loading.

DOI: 10.5220/0010506102540262

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 254-262

ISBN: 978-989-758-522-7

Figure 1: Geometry of a dual-triangle mechanism.

Figure 2: The torque-angle curves of dual-triangle

mechanism.

2 MECHANICS OF A SINGLE

SEGMENT

Let us present first a single segment of the compliant

serial manipulator under study. It consists of two rigid

triangles connected by a passive joint whose rotation

is constrained by two linear springs as shown in

Fig. 1. It is assumed that the mechanism geometry is

described by two triangle parameters (a, b), and the

mechanism shape is defined by the central angle q,

which is adjusted through two control inputs

influencing on the springs L

and L

. Let us denote the

spring lengths in the non-stress state as

L ，and the

spring stiffness coefficient as k.

The mechanism configuration angle q

corresponding to the given control inputs

L can be

computed through the static equilibrium equation of

this mechanism, which can be easily derived using the

forces generated by the springs:

()

iiii

FkLL=−

where the lengths

are computed using the

formulas

() 2 2cos( )

Lq c

cab=+

2 q

=−

, and

atan( / )ab

. It can

be proved that the torques generated by the springs

can be obtained as the following form.

() (1 ()) sin(2 )

qkLLqc q

q k LLq c q

=+ − +

=− − −

(1)

where

denote the springs stiffness coefficients,

(q) and L

(q) are the spring lengths,

L are control

inputs, while c and

are the geometric parameters

described above (see Fig. 1). So, taking into account

the external torque M

ext

applied to the moving

platform, the static equilibrium equation for the

considered mechanism can be written as M(q)+M

ext

=0, where M(q)= M

(q)+ M

(q) and

()

2 cos(2 )sin cos( )sin( 2)Mq ckc q L q

ββ





=−





(2)

It should be noted that the static stability of this

mechanism highly depends on the equilibrium

configuration defined by q. As follows from the

relevant analysis, the function M(q) can be either a

monotonic or non-monotonic one (Fig. 2), so the

single-segment mechanism may have multiple stable

and unstable equilibriums, which are studied in detail

in (Zhao, Pashkevich et al. 2020). As follows from the

relevant analysis, the stability condition for this

mechanism can be expressed via the derivative sign

at the zero point, i.e.

()

′

, which is easy to

verify in practice. So, the relevant analytical

expression for the derivative

2cos(2 )cos cos c ))2(os(cMkc qL qq

ββ

′





=−





(3)

allows us to present the condition of the torque-angle

curve monotonicity as follows

()

21( )Lb ab>⋅−

(4)

This expression is extensively used below.

3 MECHANICS OF

MULTI-SEGMENT

MANIPULATOR

The serial manipulator considered in this paper is

composed of n similar sections connected in series as

shown in Fig. 3, where the left-hand-side is assumed

to be fixed. For the initial straight configuration, the

stiffness properties of this manipulator were studied

in our previous paper, where the buckling

Figure 3: Geometry of a multi-segment manipulator.

Stiffness Modeling of Compliant Serial Manipulators based on Tensegrity Mechanism under External Loading

255

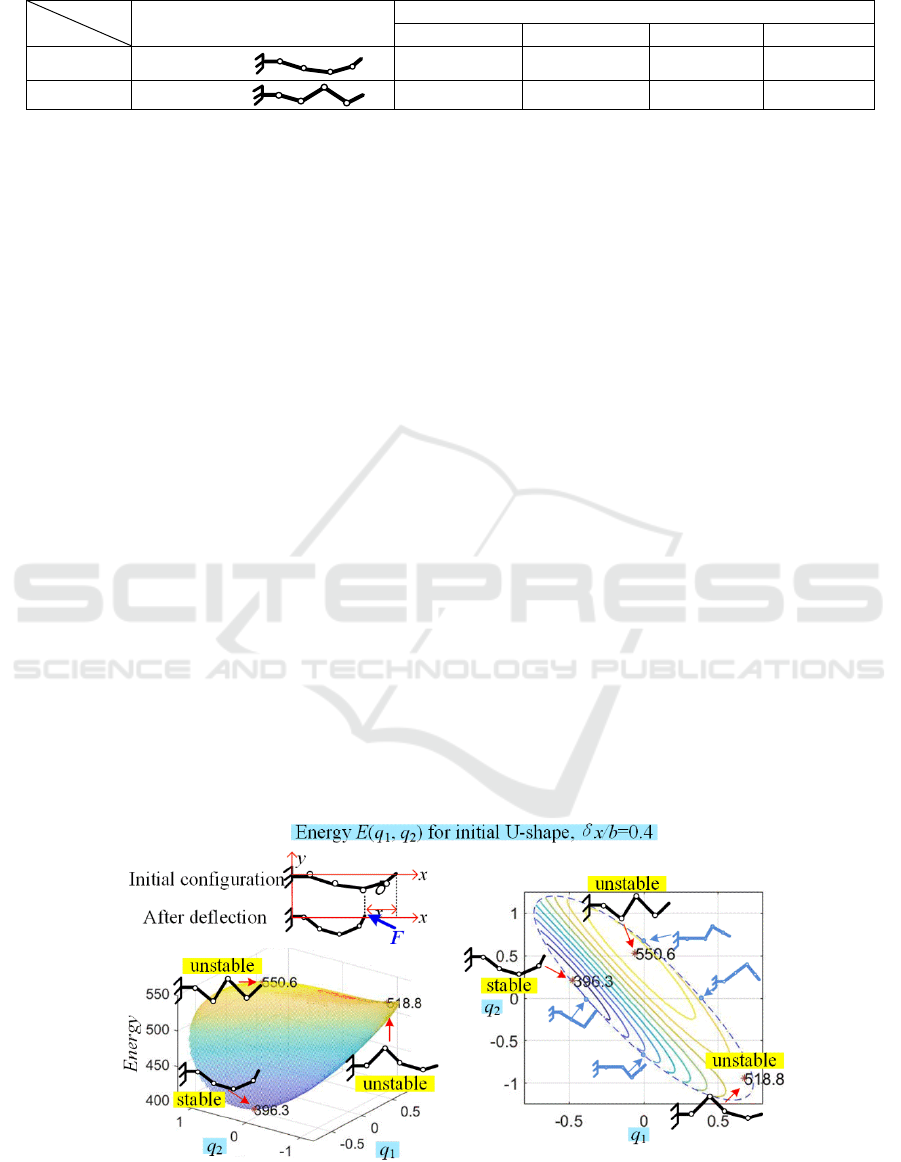
Table 1: Two typical initial configurations of the manipulator for the end-point location (x0, y0) = (7.7b, 0).

Initial shape

Initial confi

uration an

les

q1 q2 q3 q4

Case #1 U-shape:

‒0.3093 +0.1348 +0.4246 +0.2288

Case #2 Z-shape: ‒0.1136 +0.3768 ‒0.6242 +0.7869

phenomenon (similar to the Euler column) was

discovered and the critical force was computed. In

this paper, a general case is considered where the

initial shape is assumed to be non-straight, and the

stiffness analysis is carried out for the loaded mode.

Let us assumed that the initial configuration of the

n-link manipulator is a non-straight one, which

corresponds to the non-zero angles (

0, 1,2,...,

qi n≠=

) and the initial end-point

location is

(, )(2 ,0)

ynbx=⋅−Δ

with 0xΔ> . It

is assumed that the corresponding control inputs

(, ) 1,2,..,

LL i n=

are computed from the

equilibrium conditions, where

1ii

LL=−Δ

2ii

LL=+Δ

and

(causing the pre-stress). It is

clear that if

3n ≥ this manipulator is redundant with

respect to the end-effector location control in the (x,

y)-plane. So, for given

(, )

the configuration

angles

cannot be computed in a unique way. For

this reason, we will consider two typical initial shapes

of the manipulator, which in our previous paper were

referred to as the U-shape and Z-shape (Zhao,

Pashkevich et al. 2020). Examples of such initial

configurations for n=4 are shown in Table 1, and their

elastostatic properties will be carefully studied below.

First, let us investigate the force-deflection

relations

()

and

()

corresponding to the

end-effector displacement with

, i.e. from the

initial location

(, ) (2 ,0)

ynbx=⋅−Δ

to the

current one

(, ) (2 ,0)

ynbxx

=⋅−Δ−

where

the end-effector deflection caused by the external

forces

(, )

and

Δ denotes the initial

displacement of the end-effector. Let us apply the

energy method (detailed of this elastic energy were in

Zhao, 2020) allowing us to find possible equilibrium

configurations corresponding to the given

. It

should be noted that the geometric constraint coming

from the given end-effector location is

-1

11 1

-1

11 1

2 cos cos 2

2sin sin 0

ii x

ji i

bb q b q nbx

bqbq

== =



++=−Δ−











 

(5)

and allows us to reduce the number of variables in the

energy function

12 2

(, ,... )

Eq q q

−

by applying the 2-

link manipulator inverse kinematics to compute the

remaining angles

(,)

−

. Further, by detecting the

max/min and saddle points of the function

12 2

( , ,... )

Eq q q

−

, it is possible to find the

configuration angles for all possible equilibriums. To

evaluate their stability and compute the external

forces

(, )

corresponding to the end-effector

Figure 4: The energy function

(, )

and manipulator equilibriums for initial U-shape configuration (end-effector deflection

δx/b=0.4, δy=0; geometric parameters a/b=1.0; q4>0).

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

256

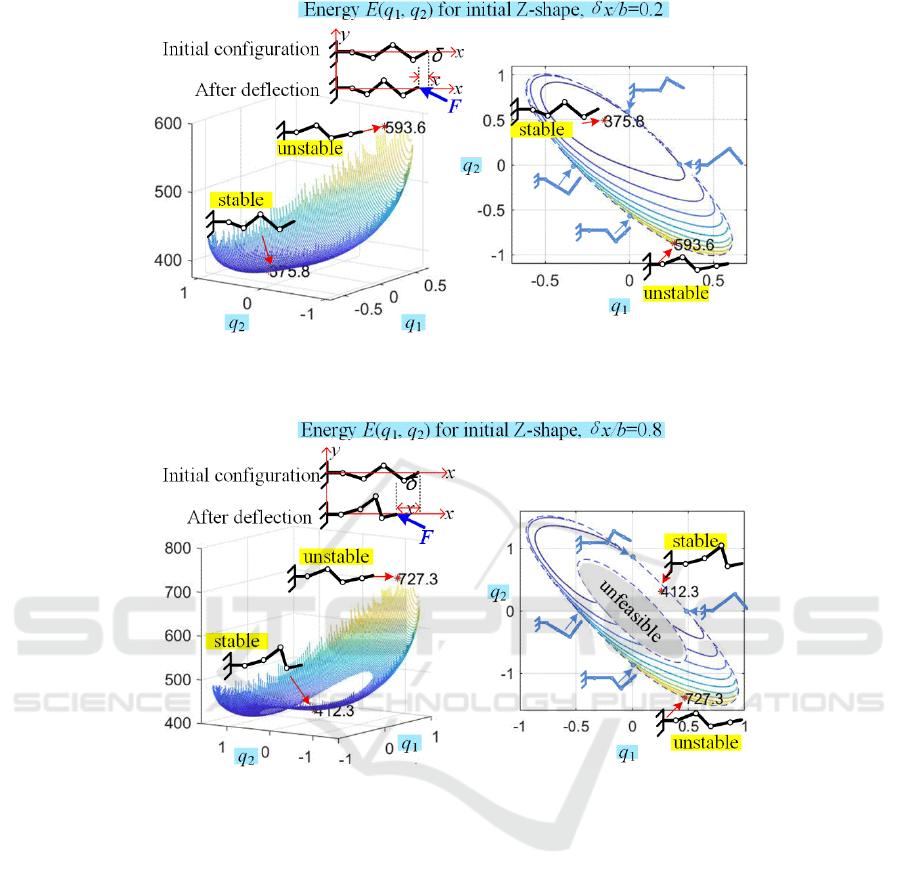
Figure 5: The energy function

(, )

and manipulator equilibriums for initial Z-shape configuration (end-effector deflection

δx/b=0.2, δy=0; geometric parameters a/b=1.0; q4>0).

Figure 6: The energy function

(, )

and manipulator equilibriums for initial U-shape configuration (end-effector deflection

δx/b=0.8, δy=0; geometric parameters a/b=1.0; q4>0).

deflection

, let us apply the Moore-Penrose

pseudo-inverse on the static equilibrium condition,

which is shown as follows,

...

−





 

=− ⋅ ⋅

 





qqq

JJJ

(6)

where both the Jacobian

and the joint torques

are computed using the configuration angles

corresponding to the stable equilibriums.

Examples of the obtained energy surfaces for n=4

are presented in Figs 4, 5 and 6, where the end-

effector elastic deflection is

{

}

0.2 , 0.4 ,0.8

bbb

∈

and the initial shapes correspond to the end-effector

displacement

0.3

bΔ=

(see Table 1). As follows

from these figures, for the initial U-shape (see Fig. 4)

there are two cases of the energy surfaces

(, )Eq q

corresponding to q

>0 and q

<0 which are

symmetrical. Totally, they have 6 critical points; each

of them contains a single maximum, a single

minimum and a single saddle point. Also, their

evolution with respect to

is continuous, their

topology remains the same while increasing the

deflection

. In contrast, for the initial Z-shape (see

Figs. 5, 6), the energy surfaces

(, )Eq q

are quite

different, their evolution with respect to

discontinuous. The latter leads to sign-changing of

some configuration angles

under the external

loading F as shown in the figures (see angle q

for

instance). Besides, if the deflection

is large

enough as in Fig. 6, the energy surfaces may contain

Stiffness Modeling of Compliant Serial Manipulators based on Tensegrity Mechanism under External Loading

257

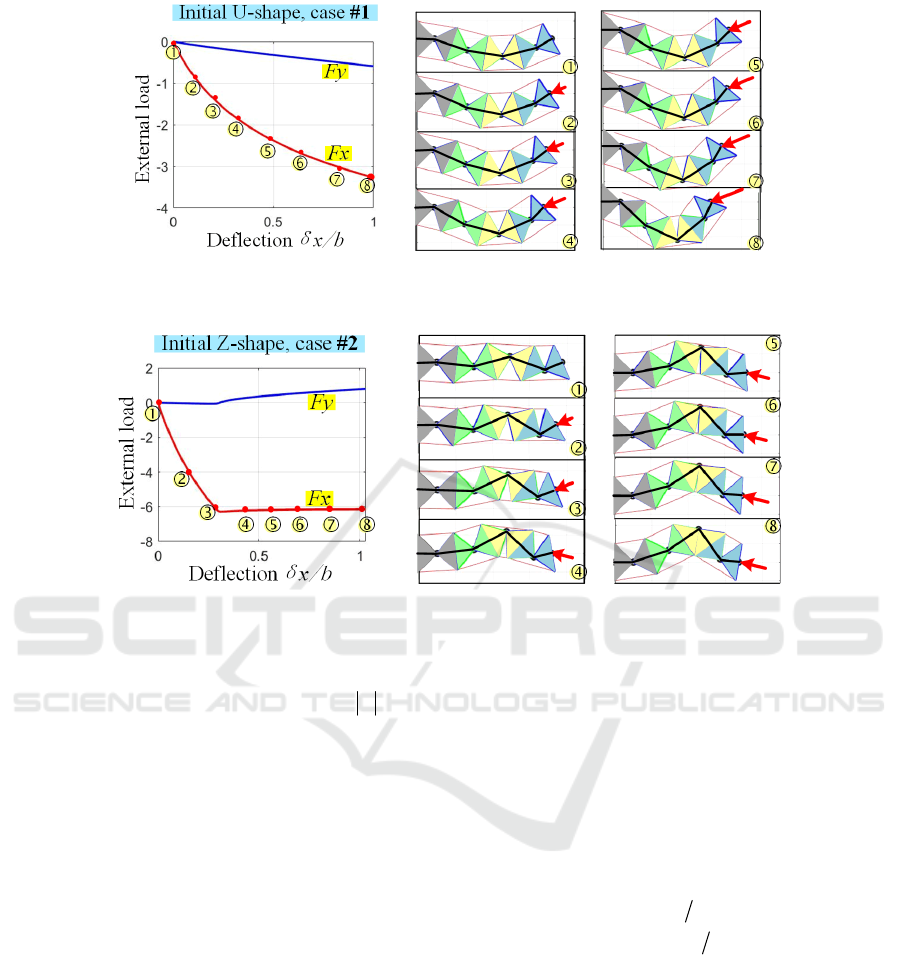
Figure 7: Force-deflection curves Fx(δx), Fy(δx) and manipulator shape changing under the loading for initial U-shape for

(x0, y0) = (7.7b, 0), geometric parameters a/b=1.0 and δy=0.

Figure 8: Force-deflection curves F

(δx), F

(δx) and manipulator shape changing under the loading for initial Z-shape for (x

) = (7.7b, 0), geometric parameters a/b=1.0 and δy=0.

a “hole”, i.e. an unfeasible area, caused by the

violation of the geometric constraints

max

qq≤

inside of the manipulator segments.

4 MANIPULATOR STIFFNESS

UNDER THE LOADING

By applying the above-presented energy method and

computing minimums of the energy function

12 2

( , ,... ) min

Eq q q

−

→

for different

, it is

possible to obtain the desired force-deflection

relations

()

and

()

describing the

manipulator stiffness properties. Examples of such

computations for n=4 are presented in Figs 7 and 8.

For the initial U-configuration (see Fig. 7), the

change of the manipulator shape is smooth, the

manipulator resistance against the external loading is

gradually increasing while the deflection

becomes larger. Also, the stiffness coefficient in the

x-direction is decreasing continuously. This tendency

is observed until the manipulator reaches its

geometric constraints.

In contrast, for the initial Z-configuration (see Fig.

8), there are two intervals of the manipulator

deformation. In the beginning when

is relatively

small the manipulator maintains its Z-shape and the

resistance against the external force is monotonically

increasing, similar to the previous case. Further, when

the deflection

is larger than some critical value,

the buckling phenomenon is occurring, and the

manipulator resistance against the external force is

not increasing anymore. Correspondingly, the

stiffness coefficient

dF dx

becomes very small,

the stiffness coefficient

dF dx

changes its sign and

the manipulator does not keep its initial Z-shape

(some of the angles

change the signs). Finally,

after the buckling, the manipulator moves in the

direction of its internal geometric constraints. Hence,

in practice, it is preferable to use the U-shape of the

manipulator if the task space obstacles (external

constraints) allows. It should be also noted that for the

Z-shape it is necessary to avoid high loadings

exceeding the critical force causing buckling.

Further, in addition to the above presented force-

deflection relations

()

and

()

derived

from the assumption of

varx

= ,

, let us

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

258

analyze the changing of the manipulator stiffness

coefficients under the loading

()

without

imposing any kinematic constraints of the end-effector

location. To obtain the desired relations it is necessary

to compute the configuration angles

( ,..., )

corresponding to the manipulator equilibriums for

different given external forces

()

. It is clear that

these angles can be found numerically by solving the

system of n independent equations





M+J F 0 (7)

describing the static equilibrium condition (by

applying Newton’s method for instance). However,

the initial guess of the angles

( ,..., )

should be

evaluated correctly, to ensure that they are in the

neighborhood of the minimum energy configuration,

because only such cases can be observed in practice.

Such initial guess can be obtained using the above-

presented energy method applied in the space

( ,..., )

with rather rough grid with large step.

Also, the desired angles corresponding to the external

()

can be found using the Matlab

function fminsearch which minimizes the sum of the

squared residuals i.e.

arg min

nn××



 

=+⋅



 



qMJF

(8)

where both the internal torques

and the Jacobian

depend on the angles

( ,..., )

. It should be also

mentioned that it is possible to simplify the problem

of the initial guess

( ,..., )

selection by gradually

increasing the forces

()

and using solutions

from the previous loaded-equilibrium as the initial

guess for the next one corresponding to

()

xy y

FFFF+Δ +Δ

. However, when the forces

()

approach the buckling point, the initial

guess from the previous step is not suitable because

the configuration angles are changing essentially and

only the straightforward energy method allows to

obtain the correct initial guess.

5 EVOLUTION OF STIFFNESS

COEFFICIENTS

If the equilibrium configuration angles

( ,..., )

corresponding to the given force

()

are

computed, it is possible to find the desired stiffness

coefficients using the formula for the loaded case,

()

−





=−





Fqqgq

KJKKJ

(9)

that includes two essential components, the first of

which

corresponds to the unloaded case, and the

second one

describes the external force influence

on the stiffness. In this expression, the

n×n matrix of

the joint elastic stiffness coefficients

( ,..., )

eq eqi

diag K K=

can be computed using the

segment torque equilibrium equation from section 2,

which yields

()

00 00

12 12

2cos

cos sin

2222

ii i

kb a q

LL qLL q

=− −

+−



−−





(10)

It should be stressed that here, the control inputs

and

are constant values, which correspond to the

initial unloaded joint angles

The second matrix

containing the stiffness

coefficients caused by the loading is symmetrical and

can be computed as

q∂∂⋅

KJ F

, which gives us

the following formula

21 11 2 1

...

... ... ...

... ...

ynxny

nx ny

FJF JFJF

FJF

−+ −+









−+









K (11)

where

denotes the element of the Jacobian matrix

with the ith row and jth colomn.

It is obvious that when the external forces are

equal to zero, the stiffness matrix expression is

reduced to the form, which is known from the

unloaded mode analysis

−





qqq

KJKJ

. It should

be also mentioned that, in contrast to the classical

link serial manipulators, here the diagonal matrix

is configuration dependent (not constant) because

each initial configuration with the angles

( ,..., )

produces its own control inputs

and

included

in the expression (10). Besides, here the unloaded

compliance matrix

can be expressed analytically

in the following way

11 1

21 2

... *

*...

qqn





















(12)

To illustrate the practical importance of the

above-presented results, they were applied to the case

Stiffness Modeling of Compliant Serial Manipulators based on Tensegrity Mechanism under External Loading

259

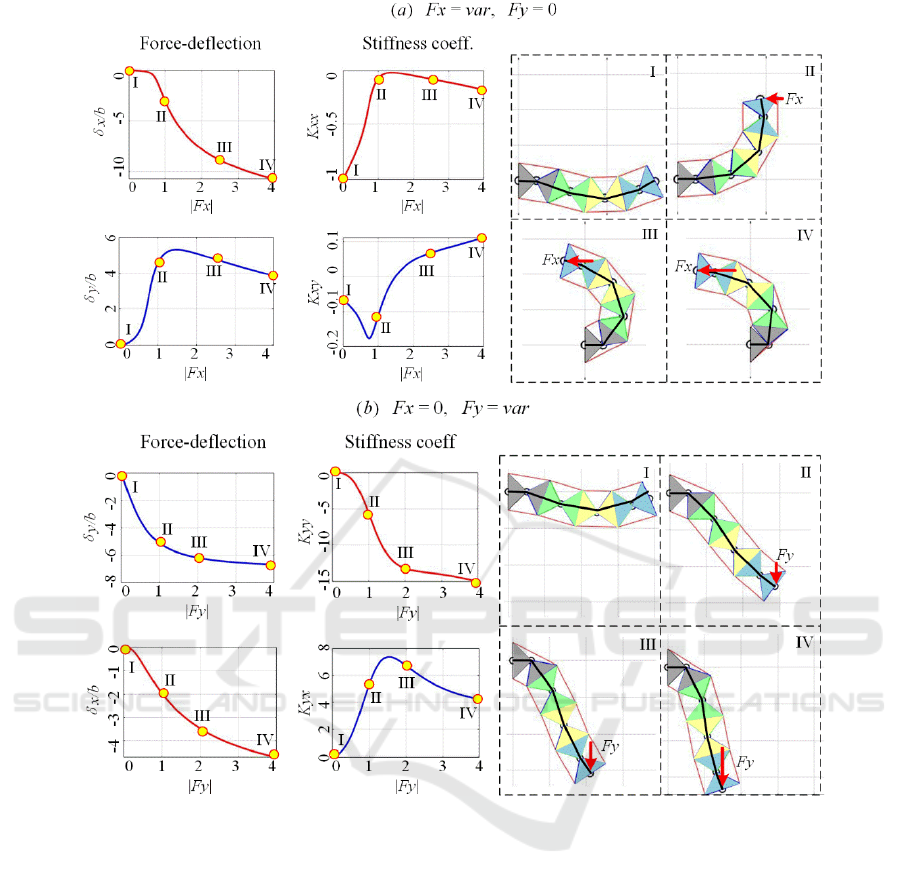
Figure 9: Stiffness coefficients under the F

- and F

-loading for initial U-shape configuration with (x

, y

) = (7.7b, 0) and

geometric parameters a/b=1.0.

n=4 assuming that the initial (unloaded) endpoint

location is

()( )

,7.7,0xy b=

, and the initial shape is

either U- or Z- one. The configuration angles under

the loading, corresponding to the external force

()

FFF=

, were computed numerically using the

technique proposed above. Relevant results of the

initial U-shape and Z-shape are presented in Figs. 9

and 10 respectively. As follows from these figures,

the manipulator stiffness essentially changes if the

external loading is applied. For the initial U-shape

case, the absolute value of the manipulator stiffness

coefficient |

| decreases first, while the force F

increasing (see Fig. 9a) , until

is reaching some

critical value when |

| is the minimum, then it

begins to increase slowly. In contrast, the stiffness

coefficient

(describing the manipulator reaction in

the

y-direction) changes its sign under the loading.

These stiffness properties can be also interpreted from

the geometrical and physical point of view, using the

right-hand side of the Fig. 9a, which shows the

evolution of the manipulator configuration under the

loading. In general, such manipulator behavior can be

treated as “

quasi-buckling”, because for certain

the stiffness in both x- and y-direction is

very small. And the manipulator rotates quickly until

one of the segment goes close to its joint limits, where

the equivalent rotational stiffness coefficient is very

low. Hence, in practice, it is necessary to avoid

applying too high loading in

x-direction causing

approaching either to the “

quasi-buckling” or the

joint limits and losing the manipulator stiffness.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

260

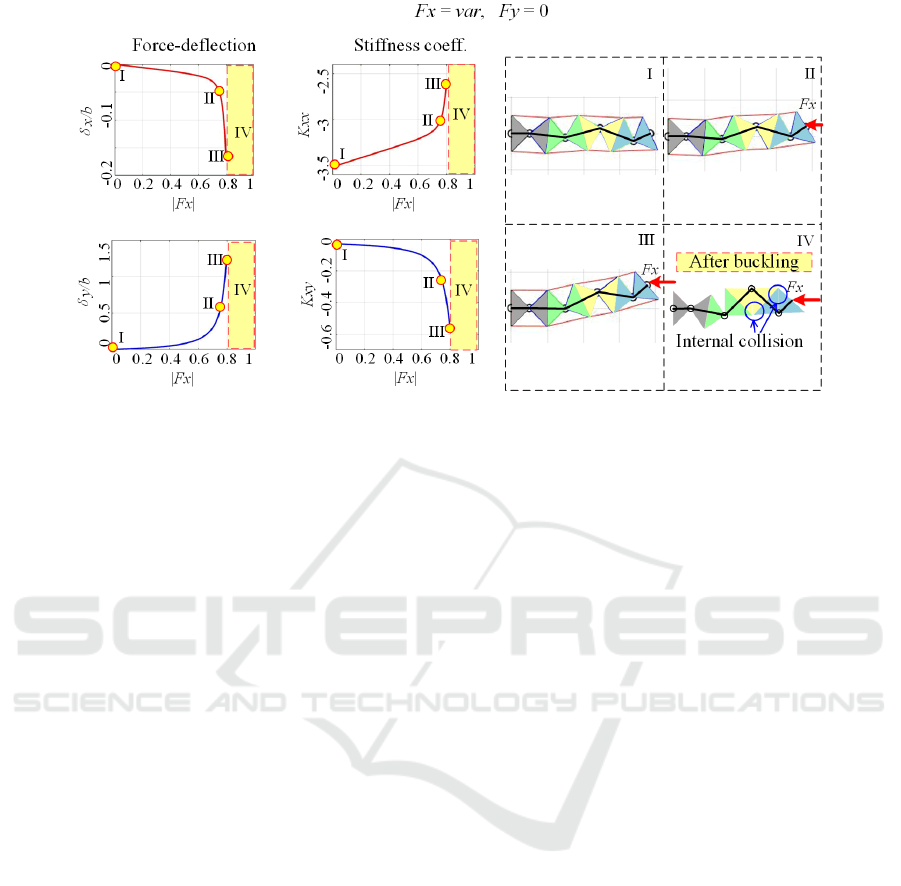
Figure 10: Stiffness coefficients under the F

-loading for initial Z-shape configuration with (x

, y

) = (7.7b, 0) and geometric

parameters a/b=1.0.

On the other side, while increasing the force F

(i.e. in the orthogonal direction), the absolute value of

the stiffness coefficient |

| is monotonically

increasing first, then it keeps the same tendency

slowly (see Fig. 9b) because of the restriction of the

geometric length of the manipulator. At the same

time, the stiffness coefficient

demonstrates non-

monotonic behavior. Such performance can be seen

from the evolution of the manipulator configuration

at the right-hand side of Fig. 9b, where the

manipulator end-point moves towards the extreme

location, as far as possible from the initial one.

Therefore, the high loading in

y-direction should be

also avoided, to prevent from the manipulator

changing its shape change to a pure straight line (see

case IV).

However, for the second case study dealing with

the initial Z-shape, the stiffness properties under the

loading are quite different compared to the U-shape

case. In particular, as follows from Fig. 10, under the

-loading, the absolute value of the stiffness

coefficient |

| decreases gradually at the beginning,

then it decrease quickly to zero. In contrast, the

absolute value of the stiffness coefficient |

increases monotonically. This phenomenon can be

also treated as “

quasi-buckling” because for certain

loading the manipulator stiffness in

x-direction is

equal to zero, and the stiffness in

y-direction is very

high. These results are illustrated geometrically by

the right-hand side of Fig. 10 showing the evolution

of the manipulator configuration under the

–

loading. It is clear that here each segment of the

manipulator tends to move close to its geometric

limits before the “

quasi-buckling” is occurring. In this

configuration, even a quite small change of the

external force may lead to large manipulator

deflection, so in practice, it is reasonable to avoid

such situations. It is worth mentioning that the case of

–loading is not presented in Fig. 10, because it is

quite similar to the U-shape case.

Hence, for the manipulator under study, the

stiffness properties are essentially non-linear with

respect to the loading force. Moreover, if the loading

exceeds a certain value, the stiffness coefficients may

become very low or even change their sign. The latter

may be treated as the

quasi-buckling, which normally

should be avoided.

6 CONCLUSIONS

The paper focuses on the stiffness analysis of a new

type of compliant serial manipulator under the

loading, which is composed of multiple dual-

triangle segments. It is a specific case of the

tensegrity mechanisms that currently are widely

used in soft robotics. The main attention is paid to

the initial non-straight configuration of the

manipulator. It was proved that under the external

loading there may be the quasi-buckling

phenomenon, which suddenly changes the

manipulator resistance in one direction of its

deflection, but may do not influence the resistance

in another direction. It was also demonstrated that

normally there are six equilibrium configurations of

this manipulator (two stable ones and four unstable

ones). But if the deflection of the end-effector is

Stiffness Modeling of Compliant Serial Manipulators based on Tensegrity Mechanism under External Loading

261

large enough some of the equilibriums may be

unfeasible due to the geometric constraints.

To find the possible equilibriums and to analyze

the manipulator shape under the loading, the energy

method was used. Further, the stiffness analysis was

based on the VJM approach allowing to find

linearized relations between the end-effector

deflection and the external force. Relevant simulation

confirmed the obtained results. In the future, this

technique will be used for the development of

relevant control algorithms and related redundancy

resolution.

ACKNOWLEDGEMENTS

This work was supported by the China Scholarship

Council (No. 201801810036).

REFERENCES

Frecker, M. I., Ananthasuresh, G. K., Nishiwaki, S.,

Kikuchi, N., & Kota, S. (1997). Topological Synthesis

of Compliant Mechanisms Using Multi-Criteria

Optimization. Journal of Mechanical Design, 119(2),

238–245. https://doi.org/10.1115/1.2826242

Albu-Schaffer, A., Eiberger, O., Grebenstein, M.,

Haddadin, S., Ott, C., Wimbock, T., Wolf, S., &

Hirzinger, G. (2008). Soft robotics. IEEE Robotics

Automation Magazine, 15(3), 20–30.

https://doi.org/10.1109/MRA.2008.927979

Wang, M. Y., & Chen, S. (2009). Compliant Mechanism

Optimization: Analysis and Design with Intrinsic

Characteristic Stiffness. Mechanics Based Design of

Structures and Machines, 37(2), 183–200.

https://doi.org/10.1080/15397730902761932

Howell, L. L. (2013). Compliant Mechanisms. In J. M.

McCarthy (Ed.), 21st Century Kinematics (pp. 189–

216). Springer. https://doi.org/10.1007/978-1-4471-

4510-3_7

Skelton, R. E., & Oliveira, M. C. de. (2009). Tensegrity

systems. Springer.

Moored, K. W., Kemp, T. H., Houle, N. E., & Bart-Smith,

H. (2011). Analytical predictions, optimization, and

design of a tensegrity-based artificial pectoral fin.

International Journal of Solids and Structures, 48(22–

23), 3142–3159. https://doi.org/10.1016/j.ijsolstr.

2011.07.008

Arsenault, M., & Gosselin, C. M. (2006). Kinematic, static

and dynamic analysis of a planar 2-DOF tensegrity

mechanism. Mechanism and Machine Theory, 41(9),

1072–1089. https://doi.org/10.1016/j.mechmachtheory.

2005.10.014

Furet, M., Lettl, M., & Wenger, P. (2019). Kinematic

Analysis of Planar Tensegrity 2-X Manipulators. In J.

Lenarcic & V. Parenti-Castelli (Eds.), Advances in

Robot Kinematics 2018 (Vol. 8, pp. 153–160). Springer

International Publishing. https://doi.org/10.1007/978-

3-319-93188-3_18.

Wenger, P., & Chablat, D. (2019). Kinetostatic analysis and

solution classification of a class of planar tensegrity

mechanisms. Robotica, 37(7), 1214–1224.

https://doi.org/10.1017/S026357471800070X.

Yamada, A., Mameda, H., Mochiyama, H., & Fujimoto, H.

(2010). A compact jumping robot utilizing snap-

through buckling with bend and twist. 2010 IEEE/RSJ

International Conference on Intelligent Robots and

Systems, 389–394. https://doi.org/10.1109/IROS.2010.

5652928

Zhao, W.; Pashkevich, A.; Klimchik, A. and Chablat, D.

(2020). Stiffness Analysis of a New Tensegrity

Mechanism based on Planar Dual-triangles.

In Proceedings of the 17th International Conference on

Informatics in Control, Automation and Robotics -

Volume 1: ICINCO, ISBN 978-989-758-442-8, pages

402-411. https://doi.org/10.5220/0009803104020411

Zhao, W., Pashkevich, A., Klimchik, A., & Chablat, D.,

2020. The Stability and Stiffness Analysis of a Dual-

Triangle Planar Rotation Mechanism. IDETC-

CIE2020. https://doi.org/10.1115/DETC2020-22076

Zhao, W., Pashkevich, A., Klimchik, A., & Chablat, D.,

(2021). Kinematic Control of Compliant Serial

Manipulators Composed of Dual-Triangles, in 2021

International Conference on Computer, Control and

Robotics (ICCCR), Jan. 2021, pp. 93–97, doi:

10.1109/ICCCR49711.2021.9349285

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

262