Soft Directional Substitutable based Decompositions for MOVCSP

Maher Helaoui

1 a

and Wady Naanaa

LIMTIC Laboratory, Higher Institute of Business Administration, University of Gafsa, Tunisia

LIMTIC Laboratory, National Engineering School of Tunis, Tunis, Tunisia

Keywords:

Multi-objective Valued Constraint Satisfaction Problems, Tractable Class, Directional Substitutable Valuation

Functions, Decomposition Scheme for General MOVCSP.

Abstract:

To better model several artiﬁcial intelligence and combinatorial problems, classical Constraint Satisfaction

Problems (CSP) have been extended by considering soft constraints in addition to crisp ones. This gave rise to

a Valued Constraint Satisfaction Problems (VCSP). Several real-world artiﬁcial intelligence and combinatorial

problems require more than one single objective function. In order to present a more appropriate formulation

for these real-world problems, a generalization of the VCSP framework called Multi-Objective Valued Con-

straint Satisfaction Problems (MOVCSP) has been proposed.

This paper addresses combinatorial optimization problems that can be expressed as MOVCSP. Despite the

NP-hardness of general MOVCSP, we can present tractable versions by forcing the allowable valuation func-

tions to have speciﬁc mathematical properties. This is the case for MOVCSP whose dual is a binary MOVCSP

with crisp binary valuation functions only and with a weak form of Neighbourhood Substitutable Valuation

Functions called Directional Substitutable Valuation Functions.

1 INTRODUCTION

Constraint Satisfaction Problems (CSP) provide a

general and convenient framework to model and solve

numerous combinatorial problems including tempo-

ral reasoning (van Beek and Manchak, 1996), com-

puter vision (Schlesinger, 2007). . . In the standard

CSP framework, the constraints are deﬁned by crisp

relations, which specify the consistent combinations

of values. With these relations, one can force some

pairs of intervals to overlap, and any plan that does

not meet this requirement is considered as inconsis-

tent even though the intervals are very close.

However, one may need to express various de-

grees of consistency in order to reﬂect the speciﬁcity

of the problem at hand. The valued constraint sat-

isfaction problems (VCSPs) approach (Schiex et al.,

1995) is intended to model such situations. A VCSP

consists of a set of variables taking values in discrete

sets called domains. A valued constraint is deﬁned

through the use of a valuation function. The role of

a valuation function is to associate a degree of desir-

ability to each combination of values. The problem is

to ﬁnd an assignment of values to variables from their

respective domains with an optimal cost.

https://orcid.org/0000-0002-4748-4773

The computational complexity of ﬁnding the optimal

solution to a VCSP has been largely studied in many

works and several classes of tractable VCSPs, that

is, VCSPs that are solvable in polynomial time, have

been identiﬁed and solved. Tractability is obtained by

limiting the set of allowed valuation functions and or

by detecting some desirable properties exhibited by

the problem structure (Cohen et al., 2008a; Cohen

et al., 2008b; Greco and Scarcello, 2011; Cohen et al.,

2012; Cooper and Zivn

y, 2011; Cooper and Zivn

2012; Helaoui and Naanaa, 2013; Helaoui et al.,

2013; Cooper et al., 2016; Carbonnel and Cooper,

2016).

However, in real-world situations like the dis-

crete time/cost trade-off problem (Vanhoucke, 2005;

Debels and Vanhoucke, 2007; Tavana et al., 2014),

one may need to express multiple objectives to opti-

mize in order to reﬂect the speciﬁcity of the problem

at hand (Greco and Scarcello, 2013).

Incorporating conﬂicting objective functions di-

vide the solution set into dominated and non-

dominated solutions. With reference to Pareto, Non

Dominated Solutions (NDS) are solutions where we

cannot improve further the attainability of one ob-

jective without degrading the attainability of another,

which means that a compromise should be found.

218

Helaoui, M. and Naanaa, W.

Soft Directional Substitutable based Decompositions for MOVCSP.

DOI: 10.5220/0010271802180225

In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 218-225

ISBN: 978-989-758-485-5

Table 1: The Π project.

Tasks Prede- choice 1 choice 2 choice 3

cessors

– (15,10) (9,25) (3,50)

(15,10) (12,30) (6,90)

(15,10) (9,35) (6,60)

(30,20) (24,50) (21,80)

(15,10) (9,30) (3,60)

(15,10) (12,58) (6,250)

Example 1. DISCRETE TIME COST TRADE OFF

PROBLEM (DE ET AL., 1997).

Let Π be a project deﬁned as follows:

Π is comprised of 6 tasks: T

, T

and T

The predecessors of each task are deﬁned by column

”Predecessor” of Table 1.

The various options of the executions times and the

relatives costs of each tasks are given in columns

3, 4 and 5. For instance, Task T

could be exe-

cuted in 15 time units with cost 10 or in 9 time units

with cost 25 or even in 3 time unit but the cost rise

to 50. Solving the problem amounts to ﬁnding, for

each task, one choice such that both global costs and

global makespan are optimized and the precedence

constraints are satisﬁed.

The multi-objectives valued constraint satisfaction

problems (MOVCSP) presented in (Ali et al., 2019) is

intended to model such situations. A Multi-objectives

VCSP consists in a VCSP where the goal is to ﬁnd an

assignment of values to variables, from their respec-

tive domains, with an optimal multi-objectives valua-

tions. Solving a problem with several multi-objective

functions is commonly referred to as multi-objective

problem. The goal is to compute the best set of com-

promise solutions called Pareto borders.

Furthermore, interchangeability and substitutabil-

ity are two techniques that have been initially intro-

duced for CSP (Freuder, 1991). In (Lecoutre et al.,

2012), Neighbourhood Substitutability has been ex-

tended to VCSP. A decomposition directional sub-

stitutability algorithm that applies when the stud-

ied problem does not satisfy the conditions of inter-

changeability or substitutability has been proposed in

(Naanaa, 2008; Naanaa et al., 2009) respectively for

CSP and CSOP : a VCSP with Crisp binary Con-

straint.

In this paper, we present tractable versions of

MOVCSP by forcing the allowable valuation func-

tions to have speciﬁc mathematical properties. This

is the case for MOVSCP whose dual is a binary crisp

MOVCSP with crisp binary valuation functions only

and with Directional Substitutable Valuation Func-

tions. We denote this MOVCSP class by L(MODS).

We also take advantage of the discovered tractable

class to conceive a decomposition scheme for general

MOVCSP.

The paper is organized as follows: the next Sec-

tion introduces MOVCSP. In Section 3 we study Soft

Directional Substitutable MOVCSP. We conclude in

Section 4.

2 MULTI-OBJECTIVE VCSP

In a MOVCSP, and as for a VCSP (Schiex et al.,

1995), for each objective j = 1,2,. .., k, we assume

a set E

of possible valuations which is a totally or-

dered with a minimal element ⊥

and a maximal ele-

ment >

. In addition, we need k monotone operators

⊕

, j : 1,. .., k. These components can be gathered in

k valuation structures each of which can be speciﬁed

as follows:

Deﬁnition 1. A valuation structure S

is the triple

= (E

,⊕

,

), where

• E

is a set of valuations for the objective function

• 

is a total order on E

;

• ⊕

is commutative, associative and monotone bi-

nary operator.

Once the valuation structure S is speciﬁed, the

multi-objective valued constraint satisfaction problem

(MOVCSP) can be deﬁned as follows:

Deﬁnition 2. A multi-objective valued constraint sat-

isfaction problem denoted (MOVCSP) is deﬁned by

the tuple (X, D,C,S ) such as:

• X is a ﬁnite set of variables;

• D is a ﬁnite set of value domain, such that D

∈ D

denotes the domain of x ∈ X.

• S = (S

,.. .,S

), where each S

is a valuation

structure of objective j;

• C is a set of valued constraints. Each constraint

is an ordered pair (σ,Φ), where σ ⊆ X is the

scope of the constraint and Φ is a k-functions

vector

,.. .,φ

, where each function φ

from Π

x∈σ

to E

The arity of a multi-objective valued constraint is the

size of its scope. The arity of a MOVCSP is the max-

imum over the arities of all its constraints.

To simplify the notation, and if there is no confu-

sion, we will denote each ⊕

by ⊕, each 

by  and

each φ

by φ.

The valuation of an assignment t that assigns val-

ues to a subset of variables V ⊆ X is obtained by

Soft Directional Substitutable based Decompositions for MOVCSP

219

Φ(t) =





(σ,φ

)∈C,σ⊆V

(t ↓ σ),. ..,

(σ,φ

) ∈ C,σ⊆V

(t ↓ σ)





(1)

Where t ↓ σ denotes the projection of t on the vari-

ables of σ. Hence, an optimal solution of a MOVCSP

on n variables is a n-tuple t such that Φ(t) is optimal

over all possible n-tuples.

In order to simplify the notation we denote

,.. .,v

|σ|

by v

Deﬁnition 3. Let t

and t

two solutions.

• We say that solution t

dominates solution t



) if, for each objective j, we have

(σ,Φ)∈C

↓ σ) 

(σ,Φ)∈C

↓ σ)

with at least one objective, we have a strict in-

equality.

• We say that t

and t

are two Non Dominated So-

lutions (NDS) if there are two objectives j and j

∈ k, such that

(σ,Φ)∈C

↓ σ) 

(σ,Φ)∈C

↓ σ) ∧

(σ,Φ)∈C

↓ σ) 

(σ,Φ)∈C

↓ σ)

This allows us to deﬁne a partial order between the

dominated solutions.

Lemma 1. 

is transitive.

Proof Lemma: According to the Deﬁnition 3, we

have:

• (i) t



if and only if for each objective j

(σ,Φ)∈C

↓ σ) 

(σ,Φ)∈C

↓ σ)

• (ii) t



if and only if for each objective j

(σ,Φ)∈C

↓ σ) 

(σ,Φ)∈C

↓ σ)

• (i) and (ii) imply that for each objective j

(σ,Φ)∈C

↓ σ) 

(σ,Φ)∈C

↓ σ)

Hence t



Example 2. We will return to the same DTCT project

Π presented in Example 1. This project Π can be

modelled as a bi-objectives VCSP P

deﬁned such

that:

1. X is a ﬁnite set of variables such that each x

is a

task i;

2. D = {v

} is a set of ﬁnite domains, where

choice

∈ D denotes the value v

choice

of the variable

;

3. S = (E,⊕,) is a fair valuation structure, where

⊕ is the sum and E the set of integers.

4. C is a set of valued constraints. Each

unary valued constraint C

is an ordered pair

(

,Φ(v

choice

) =

choice

),φ

choice

)

We get P

(X, D,S , (

,Φ))

The predecessors

of each task are deﬁned in the sec-

ond column of Table 2. The valuation functions of the

bi-objectives VCSP P

are given in columns 3, 4 and

Table 2: The bi-objectives VCSP P

= Π.

X Predecessors Φ(v

) Φ(v

)

– (15,10) (9,25) (3,50)

(15,10) (12,30) (6,90)

(15,10) (9,35) (6,60)

(30,20) (24,50) (21,80)

(15,10) (9,30) (3,60)

(15,10) (12,58) (6,250)

3 TRACTABLE CLASS FOR

MOVCSPs

If it is more easy to generalize tractability from VCSP

to MOVCSP with Soft Neighbourhood Substitutable

Valuation Functions only. What about MOVCSP with

a weak form of Soft Neighbourhood Substitutable

called Soft Directional Substitutable Valuation Func-

tions? In this section, we present tractable class for

MOVCSPs that take advantage of Soft Directional

Substitutable Valuation Functions.

3.1 The Power of a Binary Crisp

MOVCSP

We present the power of a binary MOVCSP with crisp

binary valuation functions only motivated by the fact

that

1. Any binary MOVCSP with only modular binary

functions and any crisp binary functions can be

transformed in polynomial time to an equivalent

In graph theory, the precedence constraints of P

are

satisﬁed by using RANK algorithm in order to give the vari-

ables order of execution.

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

220

binary MOVCSP with crisp binary valuation func-

tions only.

2. The dual problem of any MOVCSP is a binary

MOVCSP with crisp binary valuation functions

only.

We deﬁne a binary CSOP as a binary VCSP such that

binary valuations are only in {⊥,>}. A binary MOC-

SOP is a binary MOVCSP such that binary valuations

are only in {⊥

} for each objective j.

Let, for each objective j, φ

: D × D

−→ E

be a

binary function which is not necessarily modular. In

the following, we show that restricting the ﬁrst argu-

ment of φ

to speciﬁc subsets of D yields a family of

modular binary functions.

Deﬁnition 4. Let, for any objective j, φ

: D × D

−→

be a binary function and let a,b be in D. We say

that a and b are modular with regard to all φ

, a ∼

if and only if the restriction of all φ

to {a, b} × D

modular.

We note the class of MOVCSP with only modular bi-

nary functions and any crisp binary functions L

(M).

Note that

Φ ∈ L

(M) ⇔ a ∼

b, ∀a,b ∈ D ∧ ∀ j ∈ k

(2)

Lemma 2. Let P a binary MOVCSP. If P ∈ L

(M)

then it exists a polynomial transformation ρ such that

ρ(P ) = binary MOCSOP

Proof Lemma: By applying DECOMPOSE algo-

rithm presented in (Helaoui and Naanaa, 2013) for

each objective j to any binary MOVCSP with only

modular binary functions and any crisp binary func-

tions we get a binary MOCSOP. Since DECOMPOSE

algorithm run on O(ed) (where e is the number of

constraints, and d is the size of the largest value do-

main) and it must be called for each objective j. Then

ρ can be done on O(ked). We can conclude that ρ is

a polynomial transformation.

The dual problem of a MOVCSP is a reformula-

tion of the problem that expresses each constraint of

the original problem as a variable. The dual problems

contain only unary and binary constraints and there-

fore are binary problems. Therefore, it is possible to

apply the known algorithms for such problems.

The dual problem of a MOVCSP is a reformula-

tion of the latter which considers each constraint of

the original problem as a variable. The unary con-

straint associated with such variable speciﬁes unary

and binary costs and costs given by the unary and bi-

nary constraints of the original problem.

Binary constraints of the dual problem express

the fact that the variables common to two constraints

must have the same value.

Table 3: The valuation functions of the primal problem P

Φ 1 2

1 (α

,α

) (⊥

,⊥

)

2 (>

) (β

,β

)

Deﬁnition 5. Let P = (X, D,C,S) a MOVCSP. The

dual of P , denoted P

∗

is deﬁned by (X

∗

)

such that:

• X

∗

= C;

• D

∗

is such that D

∗

= {t ∈ D

× D

| σ(c) =

x,y

};

• S

∗

= S;

• C

∗

= C

∗1

∪C

∗2

– C

∗1

= {(

,φ) | c = (

x,y

,Φ) ∈ C} with

Φ(t) = Φ(t ↓ x) ⊕ Φ(t);

– C

∗2

= {(

,Φ) | c

∈ C ∧ σ(c

) ∩

σ(c

) 6= ∅} with

Φ(t,t

) =







(⊥

,.. .,⊥

)if(t ↓ σ(c

) ∩ σ(c

)

= t

↓ σ(c

) ∩ σ(c

))

,.. .,>

)else

where σ(c) designates the scope of the constraint c.

As can be seen from the above deﬁnition, all binary

constraints of the dual of a MOVCSP are binary crisp

constraints. Hence the following Lemma

Lemma 3. The dual of a MOVCSP is a binary MOC-

SOP.

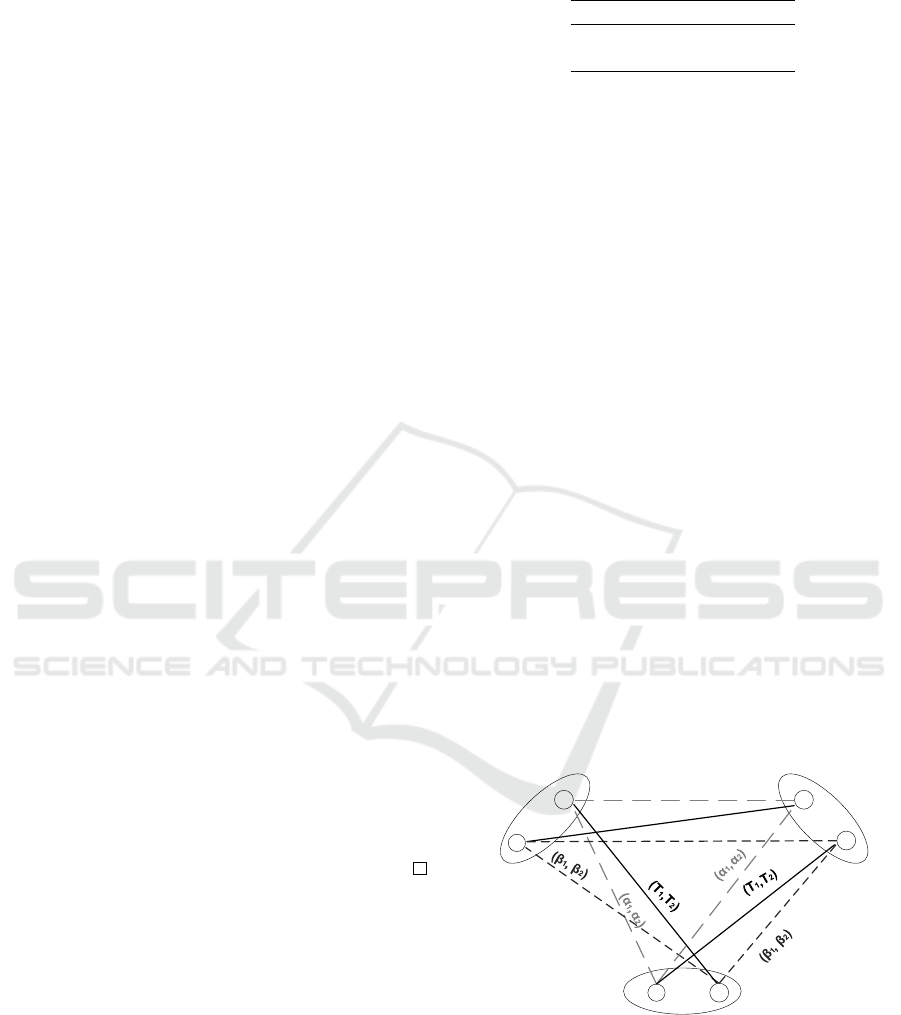
Example 3. Let P

is a binary bi-Objectives VCSP

composed of three variables x

, x

and x

. (see Fig-

ure 1). The domain D

of each variable x

is formed

1 2

(β1

(α1,α2)

, β2)

(T1,T2)

Figure 1: P

the Primal bi-objectives VCSP.

of two values D

= {1,2}. This bi-Objectives

VCSP has three constraints c

= (

,Φ), c

(

,Φ) and c

= (

,Φ) whose valuations

functions Φ are deﬁned in Table 3. Referring to Def-

inition 5, the dual of P

is a problem P

∗

deﬁned as

follows

Soft Directional Substitutable based Decompositions for MOVCSP

221

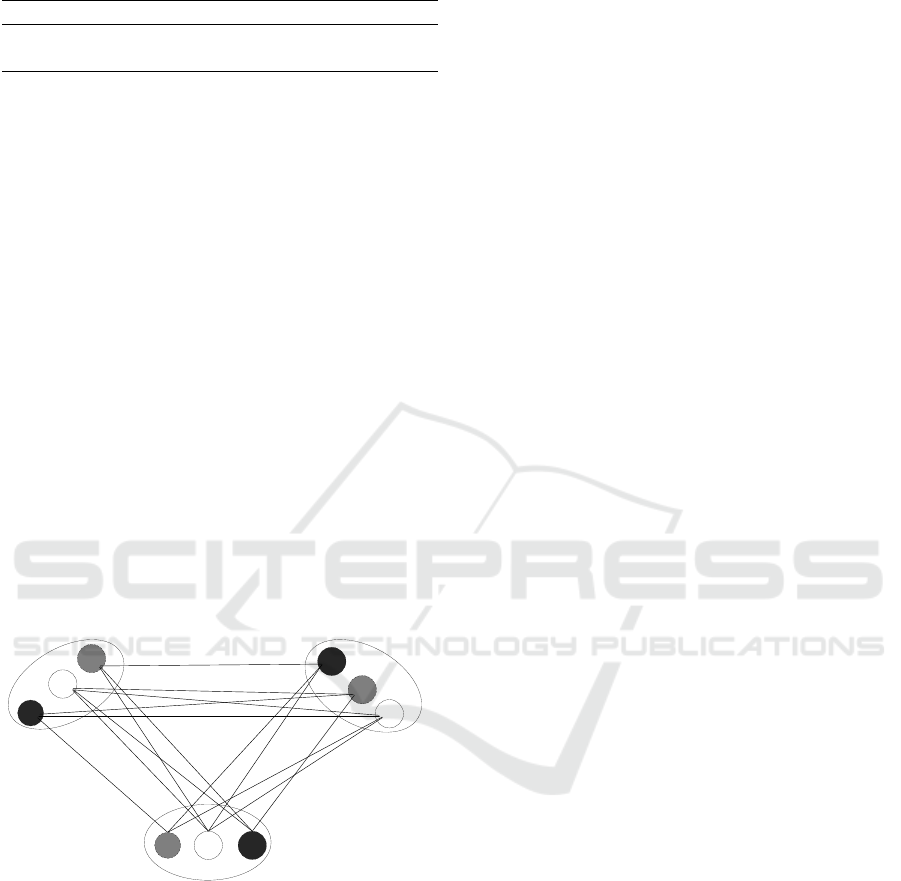
Table 4: Unary cost valuation functions of the dual problem

∗

Values (1,1) (1,2) (2,1) (2,2)

Unary- (α

,α

) (⊥

,⊥

) (>

) (β

,β

)

cost Φ

• P

∗

is a bi-objectives VCSP composed of three

variables (the constraint of P

): c

, c

and c

. (See

Figure 2).

• The domain D

of each variable c

is formed of

four tuple values

= {(1, 1),(1,2), (2,1),(2,2)}.

• Binary constraints in P

become unary constraints

in P

∗

– for each variable c

, the value (1, 1) has a

unary cost (α

,α

), the value (1, 2) has a unary

cost (⊥

,⊥

), the value (2,1) has a unary cost

) and it will be ﬁltered by applying an

arc-consistency algorithm, and the value (2, 2)

has a unary cost (β

,β

• binary constraints in P

∗

should be added Prohibit-

ing the choice of two values of the same variable

in P

. These binary constraints are crisp as they

prohibit impossible solutions for the primal prob-

lem.

As can be seen in Table 4 and Figure 2 P

∗

is a bi-

objectives CSOP.

(1,1)

(2,2)

(1,1)

(2,2)

(1,1) (2,2)

C1 C2

(1,2)

Figure 2: P

∗

the Dual of the bi-objectives VCSP.

3.2 Directional Substitutability for a

Binary MOCSOP

The Directional Substitutability (Naanaa, 2008) is

a weak form of Neighbourhood Substitutability

(Freuder, 1991). Initially, this concept has been de-

ﬁned for binary CSPs. In this paper, we generalize

the concept of directional substitutability to reﬂect

multi-objective unary cost functions involved in bi-

nary MOCSOP.

Deﬁnition 6. The multi objective inconsistency graph

of a binary MOCSOP P is a simple graph GI(P ) in

which the vertices correspond to the k values of the

variables and edges connecting pairs of vertices rep-

resenting for each objective incompatible values.

Multi Objective Directional substitution for binary

MOCSOP, in this paper, is deﬁned using, as a refer-

ence, an orientation of the multi objective inconsis-

tency graph of a binary MOCSOP.

Deﬁnition 7. An orientation A

of multi objective

inconsistency graph of binary MOCSOPs is an

assignment for each objective j of a direction to each

edge {φ

(a),φ

(b)} of graph resulting to the arc

(φ

(a),φ

(b)) or arc (φ

(b),φ

(a)).

The concept of multi-objective directional substi-

tutability is then a binary relation deﬁned, in this pa-

per, as follows

Deﬁnition 8. Let P = (X ,D,C,S) is a binary MOC-

SOP, x ∈ X and a,b ∈ D

. A value a is said

Multi Objective Directionally Substitutable (MODS)

to b with reference to A

(notation a 

b) if for

each objective j = 1,... ,k:

1. for all (

,φ) ∈ C

, we have

(a) 

(b)

2. for all (

x,y

,φ) ∈ C

et a

∈ D

, we have

(φ

(a),φ

)) ∈ A

⇒ (φ

(b),φ

)) ∈ A

∧

(a,a

) 

(b,a

)

With reference to this deﬁnition we can deﬁne Multi-

Objective Directional Substitutable Valued Constraint

Satisfaction Problem with Crisp binary Constraints as

follows

Deﬁnition 9. Let P a binary MOVCSP. P is a bi-

nary Multi-Objective Directional Substitutable Val-

ued Constraint Satisfaction Problem with only Crisp

binary Constraints P ∈ L(MODS) if and only if

for each variable x of P and for each a,b ∈ D

: a

is MODS to b or b is MODS to a a 

b ∨ b 

Given an orientation A

for each objective j of multi

objective inconsistency graph, the relation 

de-

ﬁnes a total order on the domain of each variable.

Lemma 4. 

is a total order on D

Proof Lemma: 

is trivially reﬂexive. We

prove that 

is also transitive. To this end, assume

the opposite and proceed to obtain a contradiction.

Let u,v, w ∈ D

such that for each objective j u 

v ∧ v 

w This means that u 

v ∧ v 

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

222

but ∃ j such that u 

w. This means that, for all

∈ D

, we have for each objective j

(u) 

(v) ∧ [(φ

(u),φ

)) ∈ A

⇒

(φ

(v),φ

)) ∈ A

∧ φ

(u,u

) 

(v,u

)] (3)

(v) 

(w) ∧ [(φ

(v),φ

)) ∈ A

⇒

(φ

(w),φ

)) ∈ A

∧ φ

(v,u

) 

(w,u

)] (4)

as ∃ j such that u 

w and  is a total order, it

must exists u

∈ D

such that it must exists j where:

(u) 

(w) ∨ [(φ

(u),φ

)) ∈ A

∧

(φ

(w),φ

)) /∈ A

∨ φ

(u,u

) 

(w,u

)] (5)

From (3) and (4) we get for each objective j

(u) 

(w) ∧ [(φ

(u),φ

)) /∈ A

∨

(φ

(w),φ

)) ∈ A

∧ φ

(w,u

) 

(u,u

)]

which contradicts (5).

Thus, 

is transitive.

The binary relation ∼

is deﬁned on D

as follows:

u ∼

v if and only if u 

v and v 

Lemma 5. ∼

is an equivalence relation on D

Thus, each domain D

can be divided into subsets

= D

x,1

∪ . .. ∪ D

x,s

such that the elements of

each D

x,Q

, k = 1,... ,s they are all comparable, that

is to say, that for any a,b ∈ D

x,Q

, we have a 

or b 

a. Each D

x,Q

is a chain of value totally or-

dered by 

In each chain D

x,Q

, we can distinguish the subset of

directional dominant elements denoted by D

x,Q

= {a ∈ D

x,Q

| ∀ b ∈ D

x,Q

,a 

b} (6)

3.3 Tractability of the Directional

Substitutable MOCSOP Class

In what follows, we study the tractability of binary

MOCSOP.

The following approach identiﬁes a tractable class of

binary MOCSOP which is based on the Directional

Substitutable functions.

We denote that if P is in L(MODS) then it is with

Directional Substitutable Valuation Functions only.

Theorem 1. The class of binary Multi-Objective

Directional Substitutable Valued Constraint Satis-

faction Problem with only crisp binary constraint

(L(MODS)) is tractable.

Proof Theorem 1. First we will make P arc-

consistent. Then, we show that by selecting a

dominant element (see (6)) of each domain value,

an optimal solution is obtained. This means that

any n-tuple t ∈ Π

x∈X

is an optimal solution.

Referring to the Deﬁnition 8 and the fact that the

function Φ is computable in polynomial time, this

selection can be done in polynomial time.

Suppose that t ∈ Π

x∈X

is not an optimal solution.

This means that t is inconsistent or that Φ(t) is not

dominate.

Suppose that t is inconsistent. Therefore t must

include, at least, a pair of incompatible values. Let

a ∈ D

and b ∈ D

such a pair. Since a and

b are inconsistent, for each objective j such that

(φ

(a),φ

(b)) ∈ A

{φ

(a),φ

(b)} must be an arc of

GI(P ). As a result, we must have for each objective j

(φ

(a),φ

(b)) ∈ A

or (φ

(b),φ

(a)) ∈ A

Assume without loss of generality that

(φ

(a),φ

(b)) ∈ A

, (otherwise we can reason

on φ

(b) rather than φ

(a) and obtain the same

result). It follows that (∀ j) φ

(a,b) = >

, and

since a ∈ D

then for all a

∈ D

, we must have

(∀ j) φ

,b) = >

. This means that (∀ j) b has

no support in D

and so that P is not arc-consistent,

hence a contradiction.

Suppose now that Φ(t) is not dominant, therefore

∈

x∈X

such that Φ(t

) ≺ Φ(t). Since the

values of the function Φ(t) are obtained from those

of φ(t ↓ x) using a monotone operator there must be

x ∈ X such that t ↓ x = a ∧ t

↓ x = a

and ∃ j such

that φ

) ≺

(a). It follows that a /∈ D

), hence

a contradiction.

3.4 Usefulness of Directional

Substitutable MOVCSP Class

Given a MOVCSP P not in a Directional Substi-

tutable MOVCSP class (L(MODS)), is-it possible to

use L (MODS) class to solve P ? A problem decom-

Function ORDER

(φ,D

,v, A

) : ¯v

← D

\ v

¯v ← ∅

while D

u ← MINCOST(φ,D

)

← D

\ u

Order ← true

for u

∈ D do

for v ∈ ¯v do

for j ∈ k do

(v,u

) 

(u,u

)∧φ

(v) 

(u) ∨ φ

(v,u

) 

(u,u

) ∧ φ

(v) 

(u) then

Order ← false

break

if Order then ¯v ← ¯v ∪ {u}

Soft Directional Substitutable based Decompositions for MOVCSP

223

position scheme for MOVCSPs that takes advantage

of Directional Substitutable Valuation Functions even

when the studied problem is not limited to these Func-

tions can be solved within a backtrack-based search.

The Algorithm DS–MOEDAC

1. computes P

the dual of P (line 1)

2. computes the subset of directional dominant ele-

ments denoted by D

(line 2)

3. in order to update the Pareto set of non dominated

solution s

∗

, according to Deﬁnition 3 and Lemma

1, if a solution s dominates one solution s

from

∗

, deletes s

from s

∗

and adds s to s

∗

(lines 3, 4).

4. calls the Function ORDER

to identify in O(ked

)

(where k the number of objectives and e is the

number of constraints) a tractable sub-problem P

of P

such that P

is in L (MODS). (line 5) For a

value v there may be more than one ¯v partitions.

As a result, we can use any partition strategy. For

example, the partition that promotes values which

minimize cost.

5. calls the Function MOEDAC

∗

presented in (Ali

et al., 2019) to compute Pareto-based Soft Arc

Consistency.

This decomposition scheme can be distinguished by

the possibility of instantiating variables by assigning

to each one of them a subset of values in L (MODS)

instead of single values for the P

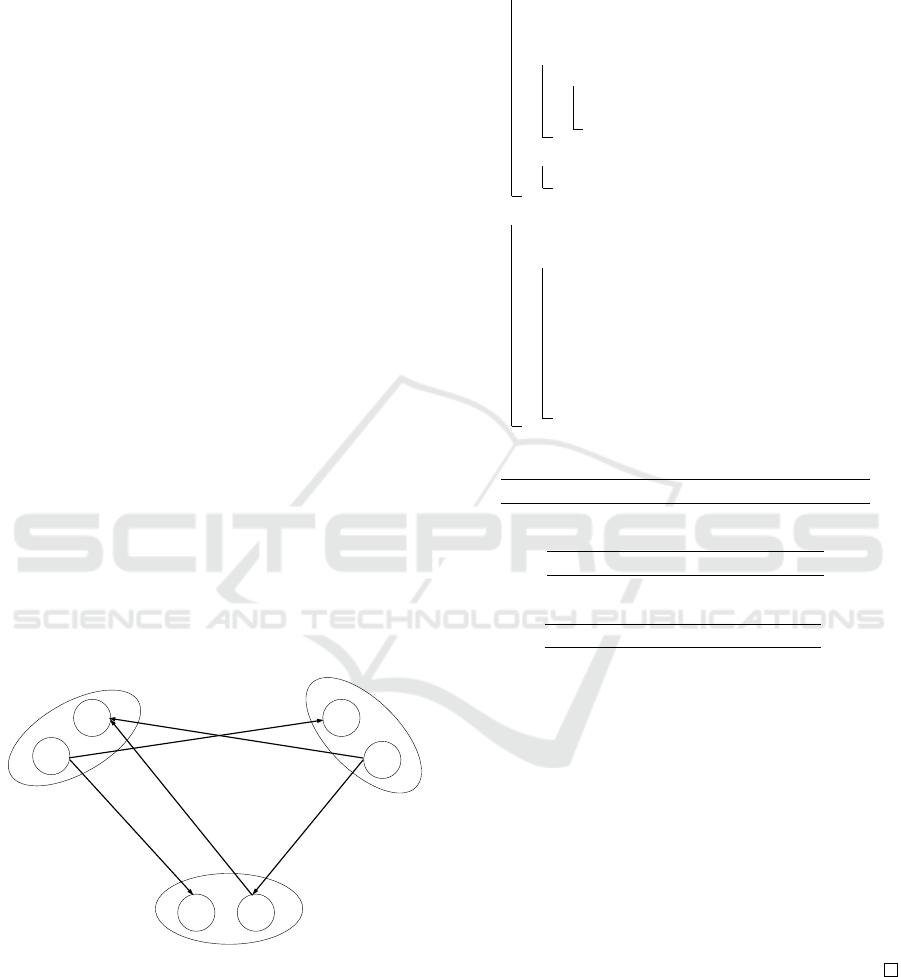
Example 4. Let P

is a bi-Objectives binary VCSP

composed of three variables x

, x

and x

. (see Fig-

ure 3). The domain D

of each variable x

is formed

(α1,α2)

(β1,β2)

(α1,α2) (β1,β2)

Figure 3: P

in a bi-objectives L (MODS) class.

of two values D

= {a,b}. This bi-Objectives

VCSP has three constraints c

= (

,Φ), c

(

,Φ) and c

= (

,Φ) whose valuations

functions Φ

are deﬁned in Table 5. We suppose that

for the both objectives j = 1,2 α

 β

Referring

to the Deﬁnition 9 P

is in a bi-objectives L (MODS).

Referring to the orientation A given in Figure 3 and

referring to the proof of Theorem 1, if we affect the

Algorithm 1: DS–MOEDAC

∗

(P,Y,s

∗

) : s

∗

1 P

← DUAL(P)

if Y

= ∅ then

2 s ← D

)

ADD ← FALSE

for ∀s

∈ s

∗

if s ≺

then

3 s

∗

← s

∗

\ s

ADD ← TRUE

if ADD then

4 s

∗

← s

∗

∪ s

else

x ← SELECT(Y

)

while true do

v ← MINCOST(φ, D

)

5 ¯v ←ORDER

(φ,D

,v, A

)

← D

\ ¯v

← P

6 P

← MOEDAC

∗

)

if ∅ ∈ D then break

else s

∗

← DS–MOEDAC

∗

,Y \ {x},s

∗

)

Table 5: The valuation functions of P

φ(v

) = φ(v

) a b

a (⊥

,⊥

) (>

)

b (>

) (⊥

,⊥

)

φ(v

) a b

a (⊥

,⊥

) (⊥

,⊥

)

b (⊥

,⊥

) (>

)

φ(v

i=1,2,3

) a b

(α

,α

) (β

,β

)

value a to each variable x

we get the optimal solution

of P

since for each variable x

: a 

Let P a MOVCSP. We deduce the tractability of

MOVCSPs through their duals.

Corollary 1. The MOVCSP P is tractable if

Dual(MOVCSP) = P

∈ L(MODS)

Proof Corollary 1. From Lemma 3 the

Dual(MOVCSP) is MOCSOP. By Theorem 1 we

have that L (MODS) is a tractable class of MOCSOP.

This means that the MOVCSP P such that Dual(P ) =

∈ L(MODS) is tractable.

4 CONCLUSION

In this paper we have proposed a Soft Directional

Substitutable based Decompositions for MOVCSP.

Despite the NP-hardness of MOVCSP we have pre-

sented a tractable classes by forcing the allowable val-

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

224

uation functions to have speciﬁc mathematical prop-

erties. This is the case of MOVCSP classes MOVC-

SPs with Directional Substitutable Valuation Func-

tions only (L(MODS)). As usefulness of L(MODS)

MOVCSP class even when the studied problem is not

limited to these functions, we have proposed a Direc-

tional Substitutable decomposition algorithm. As a

natural extension of this work, in order to validate the

practical use of L (MODS), we will compare a prob-

lem decomposition scheme for MOVCSPs that uses

Pareto-based Soft Arc Consistency only with a de-

composition scheme witch, in addition, takes advan-

tage of L(MODS).

REFERENCES

Ali, L. B., Helaoui, M., and Naanaa, W. (2019). Pareto-

based soft arc consistency for multi-objective val-

ued csps. In Rocha, A. P., Steels, L., and van den

Herik, H. J., editors, Proceedings of the 11th In-

ternational Conference on Agents and Artiﬁcial In-

telligence, ICAART 2019, Volume 2, Prague, Czech

Republic, February 19-21, 2019, pages 294–305.

SciTePress.

Carbonnel, C. and Cooper, M. C. (2016). Tractability in

constraint satisfaction problems: a survey. Constraints

An Int. J., 21(2):115–144.

Cohen, D. A., Cooper, M. C., Creed, P., Marx, D., and Sala-

mon, A. Z. (2012). The tractability of CSP classes

deﬁned by forbidden patterns. J. Artif. Intell. Res.,

45:47–78.

Cohen, D. A., Cooper, M. C., and Jeavons, P. (2008a). Gen-

eralising submodularity and horn clauses: Tractable

optimization problems deﬁned by tournament pair

multimorphisms. Theor. Comput. Sci., 401(1-3):36–

51.

Cohen, D. A., Jeavons, P., and Gyssens, M. (2008b). A uni-

ﬁed theory of structural tractability for constraint sat-

isfaction problems. J. Comput. Syst. Sci., 74(5):721–

743.

Cooper, M. C., Duchein, A., Mouelhi, A. E., Escamocher,

G., Terrioux, C., and Zanuttini, B. (2016). Broken

triangles: From value merging to a tractable class of

general-arity constraint satisfaction problems. Artif.

Intell., 234:196–218.

Cooper, M. C. and Zivn

y, S. (2011). Hybrid tractability

of valued constraint problems. Artif. Intell., 175(9-

10):1555–1569.

Cooper, M. C. and Zivn

y, S. (2012). Tractable triangles and

cross-free convexity in discrete optimisation. J. Artif.

Intell. Res., 44:455–490.

De, P., Dunne, E. J., Ghosh, J. B., and Wells, C. E. (1997).

Complexity of the discrete time-cost tradeoff problem

for project networks. Oper. Res., 45(2):302–306.

Debels, D. and Vanhoucke, M. (2007). A decomposition-

based genetic algorithm for the resource-constrained

project-scheduling problem. Oper. Res., 55(3):457–

469.

Freuder, E. C. (1991). Eliminating interchangeable values

in constraint satisfaction problems. In Dean, T. L. and

McKeown, K. R., editors, Proceedings of the 9th Na-

tional Conference on Artiﬁcial Intelligence, Anaheim,

CA, USA, July 14-19, 1991, Volume 1, pages 227–233.

AAAI Press / The MIT Press.

Greco, G. and Scarcello, F. (2011). Structural tractabil-

ity of constraint optimization. In Lee, J. H., editor,

Principles and Practice of Constraint Programming -

CP 2011 - 17th International Conference, CP 2011,

Perugia, Italy, September 12-16, 2011. Proceedings,

volume 6876 of Lecture Notes in Computer Science,

pages 340–355. Springer.

Greco, G. and Scarcello, F. (2013). Constraint satisfac-

tion and fair multi-objective optimization problems:

Foundations, complexity, and islands of tractability.

In Rossi, F., editor, IJCAI 2013, Proceedings of the

23rd International Joint Conference on Artiﬁcial In-

telligence, Beijing, China, August 3-9, 2013, pages

545–551. IJCAI/AAAI.

Helaoui, M. and Naanaa, W. (2013). Modularity-based de-

compositions for valued CSP. Ann. Math. Artif. Intell.,

67(2):165–187.

Helaoui, M., Naanaa, W., and Ayeb, B. (2013).

Submodularity-based decomposing for valued CSP.

Int. J. Artif. Intell. Tools, 22(2).

Lecoutre, C., Roussel, O., and Dehani, D. E. (2012). WCSP

integration of soft neighborhood substitutability. In

Milano, M., editor, Principles and Practice of Con-

straint Programming - 18th International Conference,

CP 2012, Qu

ebec City, QC, Canada, October 8-12,

2012. Proceedings, volume 7514 of Lecture Notes in

Computer Science, pages 406–421. Springer.

Naanaa, W. (2008). A domain decomposition algorithm for

constraint satisfaction. ACM J. Exp. Algorithmics, 13.

Naanaa, W., Helaoui, M., and Ayeb, B. (2009). A do-

main decomposition algorithm for constraint satisfac-

tion and optimization. In JFPC 2009 - Actes des Cin-

quiemes Journees Francophones de Programmation

par Contraintes.

Schiex, T., Fargier, H., and Verfaillie, G. (1995). Valued

constraint satisfaction problems: hard and easy prob-

lems. In In Proceedings of the 14

IJCAI, 631–637,

Montr

eal, Canada.

Schlesinger, D. (2007). Exact solution of permuted sub-

modular minsum problems. In Yuille, A. L., Zhu,

S. C., Cremers, D., and Wang, Y., editors, Energy Min-

imization Methods in Computer Vision and Pattern

Recognition, 6th International Conference, EMM-

CVPR 2007, Ezhou, China, August 27-29, 2007, Pro-

ceedings, volume 4679 of Lecture Notes in Computer

Science, pages 28–38. Springer.

Tavana, M., Abtahi, A., and Damghani, K. K. (2014).

A new multi-objective multi-mode model for solv-

ing preemptive time-cost-quality trade-off project

scheduling problems. Expert Syst. Appl., 41(4):1830–

1846.

van Beek, P. and Manchak, D. W. (1996). The design and

experimental analysis of algorithms for temporal rea-

soning. J. Artif. Intell. Res., 4:1–18.

Vanhoucke, M. (2005). New computational results for the

discrete time/cost trade-off problem with time-switch

constraints. Eur. J. Oper. Res., 165(2):359–374.

Soft Directional Substitutable based Decompositions for MOVCSP

225