
The Impact of Information Geometry on the Analysis of the Stable
M/G/1 Queue Manifold
Ismail A. Mageed and Demetres D. Kouvatsos
Department of Computer Science, Faculty of Engineering and Informatics,
University of Bradford, Bradford, BD7 1DP, U.K.
Keywords: Stable M/G/1 Queue, Maximum Entropy (ME), Information Geometry (IG), Statistical Manifold (SM), Queue
Manifold (QM), Ricci Curvature (RC), Riemannian Metric (RM), Fisher Information Matrix (FIM),
Kullback’s Divergence (KD), J-divergence (JD), Information Matrix Exponential (IME).
Abstract: Information geometry (IG) provides the characterization of the structure of statistical models from a
differential geometric point of view. By considering families of probability distributions as manifolds with
coordinate charts determined by the parameters of each individual model, the tools of differential geometry,
such as divergences and metric tensors, provide effective means of studying their characteristics. The research
undertaken in this paper presents a novel approach to the modelling study of information geometrics of a
queueing system. In this context, the manifold of stable M/G/1queue is characterised from the viewpoint of
IG, the Kullback’s divergence (KD) and J-divergence (JD) are determined. Also, it is revealed that the stable
M/G/1 queue manifold has a zero 0 -Gaussian curvature a non-zero Ricci Curvature Tensor (RCT). Unifying
IG with Queueing Theory enables the study of dynamics of queueing system from a novel Riemannian
Geometry (RG) point of view, leading to the analysis of the stable M/G/1 queue, based on Theory of Relativity
(TR).
1 INTRODUCTION
Information geometry (IG) has been widely applied
in many research fields such as statistical inference,
stochastic control and neural networks (c.f., Amari,
1985) In other words, IG aims to apply the techniques
of differential geometry (DG) to statistics. This
means that IG’s main idea is to apply methods and
techniques of non-Euclidean geometry to stochastic
processes and probability theories. IG indicates that
the use of an Euclidian geometry technique is useful
to think of a family of probability distributions as a
statistical manifold (SM). Moreover, IG has been
adopted for the study of statistical manifolds (SMs),
where the geometric metrics gave a new description
of the probability density function which plays an
important role in SM and can be regarded as the
coordinate system.
A manifold (c.f., Škoda, 2019) is a topological
finite dimensional Cartesian space, ℝ
, where one
has an infinite-dimensional manifold. ℝ
could be
described merely as topological space (may be
defined as a set of points, along with a set of
neighbourhoods for each point, satisfying a set of
axioms relating points and neighbourhoods). In
addition, IG supports reasoning intuitively the
description of SMs. Note that although figures can be
visualised (i.e., plotted in coordinate charts), they
should be thought of as purely abstract figures,
namely, geometric figures. One may have a higher
level of appreciation of the significant importance of
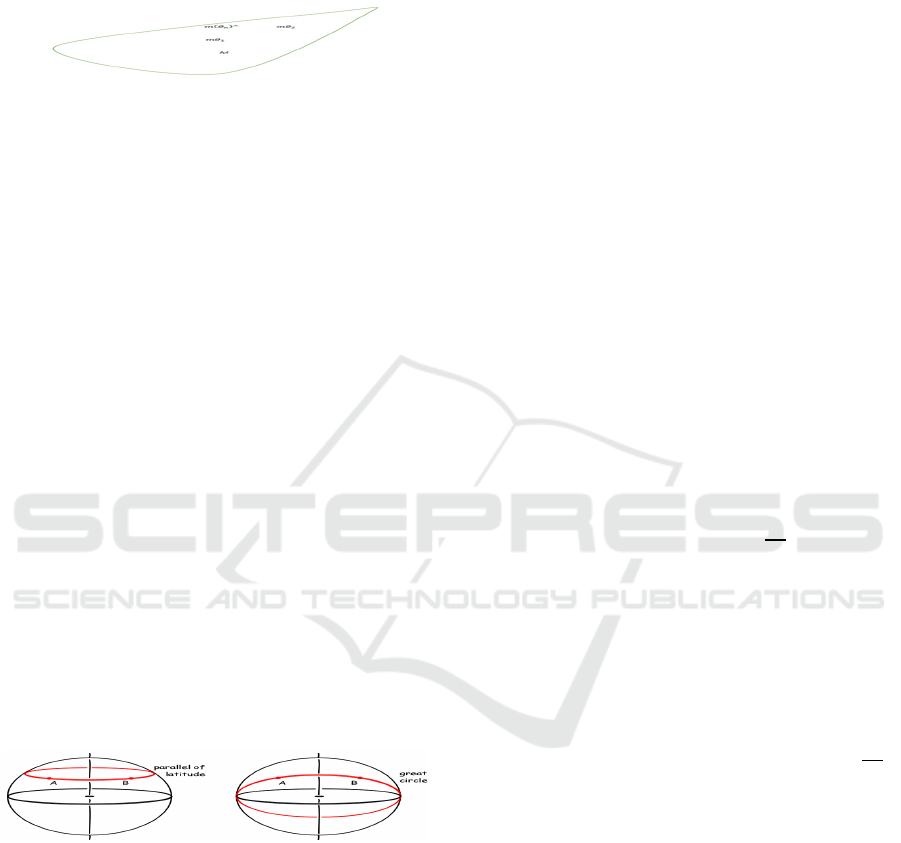
IG (c.f., Nielsen, 2018). In Figure 1, the parameter
inference 𝜃
∧
of a model from data can be interpreted
as a decision-making problem: One has to decide
which parameter of a family of models 𝑀={𝑚
}
suits “best’’ the data, where Θ is the set of parameters
{𝜃
,𝜃
,..,𝜃
} of the probability density function of
the distribution of the geometric manifold. IG
provides a differential-geometric manifold
structure 𝑀 that is useful for developing decision
rules. In (Amari, 1985), the exponential distribution
families were investigated whilst (Dodson, 1999)
studied some special exponential distributions such as
the bivariate normal distribution, the Gamma
distribution, the McKay distribution and the Frund
distribution and revealed their geometric structures.
In this paper, a study is undertaken of the
geometric structure of the stable M/G/1 queue
A. Mageed, I. and Kouvatsos, D.
The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold.
DOI: 10.5220/0010206801530160
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 153-160
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
153
manifold (QM) as well as finding its information
matrix exponential (IME). The (IME) is a matrix on
square matrices analogous to the ordinary exponential
function.
Figure1: Parametrization of a SM (c.f., Nielsen, 2018).
It is used to solve systems of linear differential
equations. In addition to that, the matrix exponential
plays a crucial role in the theory of Lie groups (c.f.,
Hall, 2015). To our knowledge, there is only one
research paper (c.f., Nakagawa, 2002), which studied
the IG of a stable M/D/1 queues, where a geometric
structure was introduced on the set of M/D/1 queues
by employing the properties of queue length paths.
This point of view motivated the novel track of the
research of this paper linking IG with information
matrix theories towards a new re-interpretation of the
stable M/G/1 queue. In this context, by analogy to
information theory (IT), the geometric approach
adopted in this paper enables the study of invariance
and equivariance of figures in a coordinate-free
approach (n.b., by equivariance as a concept, it is
meant when there is a group acting on a pair of spaces
and there is a map from functions on one to the
functions on the other (c.f., Kondor and Trivedi,
2018). In the context of this paper, Ricci curvature
(c.f., Nielsen, 2020) measures the deviation of the
Riemannian metric (RM) from the standard
Euclidean metric (EM) and how scalar curvature
measures the deviation in the volume of a geodesic
ball from the volume of an Euclidean ball of the same
radius (c.f., Figure 2).
Figure 2: Geometric representation of geodesics on curved
surfaces (c.f., Norton, 2020).
In IG, the Fisher information metric (FIM) is a
particular Riemannian metric (RM), which can be
defined on a smooth statistical manifold (i.e., a
smooth manifold whose points are probability
measures defined on a common probability space). It
can be used to calculate the informational difference
between measurements. The FIM measures closeness
of the shape between two distribution functions, it is
also proportional to the amount of information that
the distribution function contains about the parameter
of the probability density function of the SM. The
focus of this work is foundational with the following
list of its contributions:
i) The FIM and its inverse as well as the FIM for the
stable M/G/1 QM are introduced.
ii) A novel 𝛼 (or ∇
(
)
)-connection (the 𝛼−
connection
(
c.f.,Dodson,2005
)
,maps each co
ordinate 𝜃
𝑜f 𝜃,𝑖=1,2,3,…,𝑛 to a value. In
particular, the 1-connection (or, ‘exponential
connection’) and the (-1) – connection (or,
‘mixture connection’) of a stable M/G/1 queue
manifold are devised. iii) The KD and the JD of a
stable M/G/1 queue are determined. iv)The stable
M/G/1 queue’s manifold could be considered to
be incompressible or solenoidal, in which case
any closed surface has no net flux across it (n.b.,
A flux is a vector quantity, describing the
magnitude and direction of the flow of a substance
or property c.f., Divergence Theorem by (c.f.,MIT
Open Course Ware, 2010), which is the second 3-
dimensional analogue of Green’s Theorem stating
that ‘If F is a vector field with continuous
derivatives defined on a region D ⊆ 𝑅
with
boundary curve C, then, the flux of F across C is
equal to the integral of the divergence over its
interior’). v) The exponential of the FIM for the
stable M/G/1 queue is shown to be a solution of a
differential equation of the form
= Ax, where x
is an n-dimensional vector and A is an nxn matrix.
This paper is a major extension of a short paper by
(Mageed and Kouvatsos, 2019) with the following
contributions:
• The determination of the Kullback Divergence
and the J-divergence of the stable M/G/1 QM.
• The proof that the exponential of the Fisher
information matrix of the stable M/G/1 QM is a
solution of a differential equation of the form
=
Ax.
The main original contributions of this paper are
described below.
• The inclusion of the definitions of Gaussian and
Ricci curvatures and their physical
interpretations;
• The proposed novel approach for the pioneer
visualization of queueing systems via
computational information geometry;
• The development of a new quantitative approach
(which hadn’t been discovered at the time we
presented our UKPEW 2019;
• The determination of new important links
between classical queueing theory and other
mathematical disciplines, such as IG, matrix
theory Riemannian geometry and the Theory of
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
154

Relativity by providing for first time i) The full
detailed derivations of the Gaussian curvature ii)
The Ricci curvature tensor and iii) The full
physical as well as the geometric interpretation of
these new results;
• The provision of a novel link between Ricci
Curvature (RCT) and the stability analysis of the
stable M/G/1 QM.
The rest of this paper is organised as follows:
Section 2 presents preliminary definitions associated
with (IG). The FIM and its inverse as well as the
Fisher information metric for a stable M/G/1 queue
manifold are introduced in Section 3. The 𝛼(or ∇
()
)-
connection of a stable M/G/1 queue manifold is
obtained in Section 4. The KD and JD (c.f., Peng, Sun
and Jiu, 2007) of a stable M/G/1 QM are obtained in
Section 5. The structured proofs that the stable M/G/1
queue manifold has a non-zero Ricci Curvature
Tensor (RCT) is devised in Section 6. The
exponential matrix analysis of a stable M/G/1 queue
is obtained in Section 7. Conclusions and future
research directions are included in Section 8.
2 MAIN DEFINITIONS IN IG
Definition 2.1: Statistical Manifold (SM).
𝑀={𝑝(𝑥,𝜃)|𝜃ϵΘ} is called an SM (c.f., Li, Sun, Tao
and Jiu, 2007) if x is a random variable in sample
space 𝑋 and 𝑝(𝑥,𝜃) is the probability density
function, which satisfies certain regular conditions.
Here, 𝜃=(𝜃
,𝜃
,..,𝜃
)ϵΘ is an n-dimensional
vector in some open subset Θ⊂ℝ
, and 𝜃 can be
viewed as the coordinates on manifold M.
Definition 2.2: Potential Function. The potential
function Ψ
(
𝜃
)
(c.f., (2.1)) (c.f., Li, Sun, Tao and Jiu,
2007) is the distinguished negative function of the
coordinates alone of (ℒ
(
𝑥;𝜃
)
=𝑙𝑛𝑝
(
𝑥;𝜃
)
) and in
a sequel, it will appear in the information geometric
analysis of the M/G/1 queue manifold.
Definition 2.3: Fisher’s Information Matrix
(FIM). The FIM (or, Fisher’s metric) [ 𝑔
] (c.f.,
Dodson, 2005) is given by the Hessian (the nxn
matrix of the partial derivatives of the potential
function Ψ(𝜃) with respect to the coordinates) i.e.,
𝑔
=
∂
∂𝜃
∂𝜃
Ψ
(
𝜃
)
,𝑖,
𝑗
=1,2,..,𝑛 (2.1)
with respect to natural coordinates.
Definition 2.4: Inverse Matrix of Fisher’s
Information Matrix (FIM). Given the FIM, the
inverse matrix of [𝑔
] is defined by (c.f., Dodson,
2005).
[𝑔
]= ([𝑔
]) )
=
∆
, ∆= det𝑔
(2.2)
The FIM for the manifold M is given
in 𝜃 coordinates by the arc length function.
(𝑑𝑠)
= 𝑔
,
(𝑑𝜃
)(𝑑𝜃
)
(2.3)
Definition 2.5: 𝜶-Connection. For each 𝛼𝜖ℝ, the
𝛼(or ∇
()
)-connection (c.f., Dodson, 2005) is the
torsion-free affine connection with components:
Γ
,
()
= (
)(𝜕
𝜕
𝜕
(Ψ
(
𝜃
)
))
(2.4)
where 𝛹(𝜃) is the potential function and 𝜕
=
.
Definition 2.6: Kullback’s Divergence (KD),
𝑲
(
𝒑,𝒒
)
. Assume 𝑝𝑥;𝜃
and 𝑞𝑥;𝜃
are two
points on the manifold M, the Kullback’s divergence
𝐾
(
𝑝,𝑞
)
(c.f., Li, Sun, Tao and Jiu, 2007) is defined
by
𝐾
(
𝑝,𝑞
)
=𝐸
𝑙𝑛
;
;
=∫𝑝
𝑥;𝜃
𝑙𝑛
;
;
𝑑𝑥
(2.5)
where 𝐸
stands for the expected value and the J-
divergence is defined by
𝐽
(
𝑝,𝑞
)
=∫𝑙𝑛
𝑝𝑥;𝜃
𝑞𝑥;𝜃
;
;
𝑑𝑥
(2.6)
When the two 𝑝(𝑥;𝜃
) and 𝑞(𝑥;𝜃
) are close
enough and by using Taylor’s formula, the following
analytic (c.f., Li, Sun, Tao and Jiu, 2007) result holds:
𝐾
(
𝜃,𝜃+𝑑𝜃
)
=
𝐽
(
𝜃,𝜃+𝑑𝜃
)
=
1
2
(𝑑𝑠)
where (𝑑𝑠)
stands for the square of the arc length of
the manifold.
Definition 2.8:
1. Under the 𝜃 coordinate system, the 𝛼−
curvature Riemannian Tensors, 𝑅
()
(c.f., Li,
Sun, Tao and Jiu, 2007) are defined by
𝑅
()
=𝜕
𝛤
(
)
−𝜕
𝛤
(
)
𝑔
+𝛤
,
(
)
𝛤
(
)
−𝛤
,
(
)
𝛤
(
)
,𝑖,
𝑗
,𝑘,𝑙,𝑠,𝑡
=1,2,3,….,𝑛
(2.7)
where 𝛤
(
)
= 𝛤
,
(
)
𝑔
, i,j,k,s = 1,2,...,n
2. The 𝛼− Ricci curvatures (Ricci Tensors) 𝑅
()
are determined by (c.f., Li, Sun, Tao and Jiu,
2007).
𝑅
()
=𝑅
()
𝑔
,𝑖,
𝑗
,𝑘,𝑙=1,2,3,….,𝑛
(2.8)
3. The 𝛼−sectional curvatures 𝐾
()
are defined
by (c.f., Li, Sun, Tao and Jiu, 2007).
The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold
155

𝐾
()
=
()
(
)
(
)
,𝑖,
𝑗
=1,2,…,𝑛
(2.9)
Specifically, if 𝑛=2, the 𝛼−
sectional curvature 𝐾
(
)
= 𝐾
(
)
is called 𝛼−
Gaussian curvature and is given by (c.f., Li, Sun,
Tao and Jiu, 2007).
𝐾
(
)
=
()
(2.10)
4. The Ricci Tensor (c.f., Loveridge, 2016) is simply
a contraction of the Riemannian Tensor (c.f., Li,
Sun, Tao and Jiu, 2007).
5. The Ricci curvature Tensor (RCT) (c.f., Rudelius,
2012) of an oriented Riemannian Manifold M
means the extent to which the volume of a
geodesic ball on the surface differs from the
volume of a geodesic ball in Euclidean space.
6. The Ricci curvature (RCT) (c.f., Ollivier, 2010)
contracts the evolution of volumes under the
geodesic flow. When Ricci curvature is positive,
then according to the Bonnet Myers theorem (c.f.,
Ollivier, 2010) the Riemannian manifold is more
positively curved than a sphere and the diameter
of the manifold is smaller.
Figure 3: (RCT) describes how conical regions in the
manifold differ in volume from the equivalent conical
regions in Euclidean space (c.f., Thomas, 2015).
Definition 2.9:
1. Considering the linear system of differential
equations
=
𝐴
𝑥
(2.11)
with x is an n-dimensional vector and A is an nxn
matrix. It can be shown that (Gunawardena, 2006) the
matrix exponential
𝑒
=
∑
!
= 𝐼+
𝐴
+
!
+⋯+
!
+....
(2.12)
is the solution of (2.11).
2. If the characteristic polynomial of A is defined by
Φ
(
𝛿
)
=det
(
A−δI
)
(2.13)
then, the set of eigen values of A will is defined to be
(c.f., Gunawardena, 2006) the set of all the roots of
the equation
Φ
(
𝛿
)
=
(
𝛿
)
=det
(
A−δI
)
= 0
(2.14)
and corresponding eigen vectors x assigned to each
eigen value 𝛿 are defined to satisfy the equation:
𝐴
𝑥= 𝛿𝑥
(2.15)
Another way to represent 𝑒
will be
𝑒
=𝑇𝑒
𝑇
(2.16)
where D is the diagonal matrix of eigen values of A,
and T is matrix having of the corresponding eigen
vectors of A as its columns (c.f., Gunawardena, 2006).
3 THE FIM AND ITS INVERSE
FOR THE STABLE M/G/1 QM
According to (El-Affendi and Kouvatsos, 1983), the
maximum entropy (ME) state probability of the
generalized geometric solution of a stable M/G/1
queue (c.f., Figure. 4), subject to normalisation, mean
queue length (MQL), L and server utilisation, 𝜌(<1)
is given by
Figure 4: A Stable M/G/1 queue.
𝑝
(
𝑛
)
=
1−𝜌, 𝑛=0
(
1−𝜌
)
𝑔𝑥
,𝑛≥1
(3.1)
where 𝑔=
(
)(
)
,𝑥=
and 𝐿=
1+
(MQL of Pollaczeck-Khinchin Formula of a
stable M/G/1 queue), 𝜌 = 1 – 𝑝
(
0
)
(server utilisation)
and 𝐶
(SCV of the service times).
It clearly follows that 𝑝
(
𝑛
)
of (3.1) can be
rewritten as
𝑝
(
𝑛
)
=
⎩
⎪
⎨
⎪
⎧
1−𝜌, 𝑛=0
2𝜌(
1+𝜌𝛽
1−𝜌
−1)
(
1+𝜌𝛽
1−
𝜌
+1)
, 𝑛≥ 0 , with 𝛽= 𝐶
(3.2)
Theorem 3.1. For the stable M/G/1 queue manifold,
it holds that
(i) The FIM is given by
[𝑔
] =
()
0
0
(
)
(3.3)
(ii) The square of the arc length (i.e., Fisher
Information Metric) is determined by
(𝑑𝑠)
= (
()
)(𝑑𝜌)
-
(
)
(𝑑𝛽)
(3.4)
(iii) The inverse of Fisher Information Matrix is
given by
[𝑔
] =
∆
=
(1 − 𝜌)
0
0−(𝛽+1)
(3.5)
Proof. Following (3.2), two cases would arise.
Case I: For 𝑛=0, 𝑝
(
𝑛
)
=1−𝜌. Hence, the
coordinate system is one dimensional satisfying
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
156

ℒ
(
𝑥;𝜃
)
=𝑙𝑛𝑝
(
𝑥;𝜃
)
= 𝑙𝑛
(
1−𝜌
)
,
𝜃= 𝜃
= 𝜌
(3.6)
The potential function Ψ
(
𝜃
)
will be the standalone
part of (- ℒ
(
𝑥;𝜃
)
)involving the coordinates, i.e.,
Ψ
(
𝜃
)
=−𝑙𝑛
(
1−𝜌
)
(3.7)
Thus,
𝜕
=
𝜕Ψ
𝜕𝜌
=
1
1−𝜌
(3.8)
𝜕
𝜕
=
𝜕
Ψ
𝜕𝜌
=
1
(1−𝜌)
(3.9)
FIM is given by
[𝑔
] =
=
()
(3.10)
The inverse of the FIM is determined by
[
𝑔
]
=[𝑔
]
=
[
(1 − 𝜌)
]
(3.11)
Moreover,
Γ
,
()
= (
()
) , Γ
()
=
()
, Γ
()
=
()
(3.12)
Following the same argument, the proofs of (ii)
and (iii) follow.
4 𝐓𝐡𝐞 𝜶(OR 𝛁
(𝛂)
)-CONNECTION
OF THE M/G/1 QM
By definition (2.8), we have
Γ
,
()
=
()
()
(4.1)
Similarly, the remaining components are devised.
Furthermore, after some lengthy calculations
𝛤
11
1
(
𝛼
)
=
1−𝛼
(1−𝜌)
,𝛤
11
1
(
0
)
=
1
(1−𝜌)
(4.2)
𝛤
(
)
= −
1−𝛼
(
1+𝛽
)
,𝛤
(
)
= −
1
(1 + 𝛽)
(4.3)
The remaining components could be computed as
above. Using the above derivations, the Ricci
curvature of the stable M/G/1 QM can be devised.
5 THE KD AND THE J-D OF
STABLE M/G/1 QM
Following (2.6), KD is expressed by
𝐾
(
𝑝,𝑞
)
= 𝐸
𝑙 𝑛
;
;
=
⎩
⎪
⎨
⎪
⎧
𝒍𝒏(
𝟏−𝝆
𝒑
𝟏−𝝆
𝒒
), 𝒏 =𝟎
𝒍𝒏
𝟏−𝝆
𝒑
𝟏−𝝆
𝒒
𝟏+𝜷
𝒒
𝟏+𝜷
𝒑
[
𝝆
𝒒
(𝟐 + 𝝆
𝒒
(𝜷
𝒒
−𝟏)
𝝆
𝒑
(𝟐 + 𝝆
𝒑
(𝜷
𝒑
−𝟏)
𝟏+𝜷
𝒒
𝟏+𝜷
𝒑
]
𝑳
,𝒏≥𝟎
(5.1)
where 𝐿 is MQL of Pollaczeck-Khinchin Formula of
a stable M/G/1 QM. (5.1)
Moreover, in a similar fashion, it could be seen
that
𝐽
(
𝑝,𝑞
)
=𝐾
(
𝑝,𝑞
)
+𝐾
(
𝑞,𝑝
)
=0
(5.2)
Equation (5.2) presents a great contribution as it
shows that the stable M/G/1 QM is incompressible or
non-solenoidal, in which case any closed surface has
no net flux across it.
6 THE STABLE M/G/1 QM HAS A
NON-ZERO RICCI
CURVATURE (RCT) TENSOR
In this section, it is revealed that the stable M/G/1 QM
is developable (can be mapped onto the plane surface
without distortion of curves: any curve from such a
surface drawn onto the flat plane remains the same)
and has a non-zero Ricci curvature, shortly written as
(RCT) tensor (the M/G/1 QM is more positively
curved than a sphere and the diameter of the manifold
is smaller).
Theorem 6.1. The stable M/G/1 QM.
i) Has a zero 0-Gaussian curvature ii) Has a non-zero
Ricci tensor
Proof. Case i), by definition (2.10), part i), it is
enough to show that the 𝛼−Gaussian curvature
𝐾
(
)
=
()
= 0
(6.1)
It could be verified that,
𝑅
()
=0
(6.2)
𝑑𝑒𝑡
𝑔
= −
(
)
()
≠0. Hence, 𝐾
(
)
=
()
=0,
which proves the developability Case i) of stable
M/G/1 QM.
Case ii) To prove that the stable M/G/1 (QM)
Ricci tensor is non-zero, one needs to show that the
𝛼−RCs,𝑅
()
are given by(c.f., definition 2.8, part 2)
𝑅
𝑖𝑘
(𝛼)
= 𝑅
𝑖𝑗𝑘𝑙
(𝛼)
𝑔
𝑗𝑙
,𝑖,𝑗,𝑘,𝑙=1,2,3,….,𝑛
is non zero, which means that at least one of its
components is non-zero. By (6.1), 𝑅
11
(𝛼)
equals
𝑅
()
𝑔
+ 𝑅
()
𝑔
+ 𝑅
()
𝑔
+ 𝑅
()
𝑔
Engaging the same procedure as in (6.1), we have
𝑅
(
)
=𝑅
(
)
=𝑅
(
)
=0
(6.3)
𝑅
()
=−
(
)
(6.4)
Hence,
𝑅
()
≠0
(6.5)
This proves Case ii).
The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold
157

As 𝜌→1, 𝑅
()
→−∞. This shows the significant
impact of instability of the two dimensional M/G/1
QM. This presents a novel link between Ricci
Curvature (RCT) and the stability analysis of Queueing
Systems. It is clear that 𝑅
()
is a server utilization
dependent function. To experiment more closely the
impact of the server utilization, 𝜌 and the behaviour of
the (RCT). It is observed by Figure 5 that the stability
phase of M/G/1 QM enforces (RCT) to be a decreasing
function in 𝜌, whereas in Figure 6, it can be seen that
instability phase of M/G/1 QM enforces (RCT) to be
an increasing in 𝜌.
Figure 5. Figure 6.
7 THE EXPONENTIAL MATRIX
OF FIM OF STABLE M/G/1 QM
Theorem 7.1. The exponential matrix of the Fisher
information of the stable M/G/1 QM is a solution of a
differential equation of the form
= Ax.
Proof. It has been proved earlier (c.f. Theorem 3.1)
that the FIM of the stable M/G/1 queue manifold
𝑔
,𝑖,𝑗=1,2 is given by
𝑔
=
(
)
0
0
(
)
(7.1)
We write
[𝑔
] =
𝑎0
0 𝑏
,𝑎=
()
,𝑏=
(
)
(7.2)
It follows that
Φ
(
𝛿
)
=
(
𝛿
)
=det[𝑔
]−δI=
det
𝑎−𝛿 0
0 𝑏− 𝛿
=0
. Hence, it holds that
𝛿
−
(
𝑎+𝑏
)
𝛿+𝑎𝑏 =0,
which implies that the eigenvalues
are given by
𝛿
,
=𝑎,𝑏. The diagonal matrix D is
given by
𝐷 =
𝛿
0
0 𝛿
(7.3)
For
𝛿
,
=𝑎,𝑏 , the corresponding eigen vectors
are
,
.Hence,
T = 𝑇
=
10
01
(7.4)
Hence, the exponential matrix of the FIM of the
stable M/G/1 queue manifold is given by
𝑒
= 𝑇𝑒
𝑇
=
𝑒
0
0 𝑒
(7.5)
The result obtained in (7.5) shows that the
exponential of the FIM of the stable M/G/1 queue
manifold is a solution of a differential equation of the
form
= Ax
(7.6)
8 CONCLUSIONS AND FUTURE
WORK
The stable M/G/1 QM is characterized from the
viewpoint of IG, KD and J-D were determined.
Moreover, the matrix exponential of information of
the M/G/1 QM is devised. This paper opens a new
ground for research linking queueing theory with
many other mathematical disciplines such as
information theory, differential geometry and matrix
theory. Specifically, adding information geometric
links with queueing theory enables the study of the
dynamics of a queueing system from the Riemannian
Geometric point of view (c.f., Amari, 1985) and (c.f.,
Dodson, 1999) and in turn, enabling the analysis of a
queueing system based on the Theory of Relativity
(c.f., Norton, 2020).
This paper has introduced for the first time the
FIM and its inverse and has also obtained the Fisher
information metric for the M/G/1 QM.
Moreover, a novel expression for 𝛼 (or ∇
(α)
)-
connection of the stable M/G/1 queue manifold was
devised. In addition, the KD and the J-D of the stable
M/G/1 queue manifold were devised. In this context,
it was shown that the stable M/G/1 queue manifold
can be described as compressible or non-solenoidal,
in which case any closed surface has no net flux
across it The latter, was justified by the Divergence
Theorem of (c.f., MIT Open Course Ware, 2010),
which states that the flux of a vector field across a
closed boundary curve C is equal to the integral of the
divergence over its interior. It is implied that, when
the J-D is zero, any closed surface has no net flux
across the M/G/1 QM. Moreover, it was revealed that
the stable M/G/1 QM has a zero 0-Gaussian curvature
and a non-zero Ricci Curvature Tensor. Finally, it
was proven that the exponential of the FIM of the
stable M/G/1 queue manifold is a solution of a
differential equation of the form
𝑑𝑥
𝑑𝑡
= Ax. Specifically,
the main original contributions of this paper are
summarised below.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
158

• The proposed new approach to visualize queueing
systems via computational information geometry;
• The establishment of new links between queueing
theory and other mathematical disciplines such as
information geometry, matrix theory Riemannian
geometry and the theory of Relativity.
• Providing a novel link between Ricci Curvature
(RCT) and the stability analysis of the stable
M/G/1 QM.
• Having introduced several information geometric
concepts, we have managed for first time to
capture the M/G/1 queue as a manifold and
analysed the M/G/1 QM by using information
geometric methods. Consequently, classical
Queueing Theory can be extended to become
richer because of the application of IG.
An exponential family or mixture family of
probability distributions has a natural hierarchical
structure. Orthogonal decomposition of such a system
based (c.f. Amari, 2001) on information geometry. A
typical example is the decomposition of stochastic
dependency among a number of random variables. In
general, they have a complex structure of
dependencies. The orthogonal decomposition is given
in a wide class of hierarchical structures including
both exponential and mixture families. As an
example, we decompose the dependency in a higher
order Markov chain into a sum of those in various
lower order Markov chains.
Single-server, such as M/G/1 system is simple and
can be utilized as preliminary models (c.f., Hamasha
et al, 2016). Modelling of the systems state using
Markov chain approach and queuing models provides
a more rigid approach to better understand the
dynamics of the service delivery system, which
proposes a conceptual model using of Markov chain
approach combined with M/G/1 queuing model to
optimize general service delivery systems.
Based on the above discussion, clearly the lost
link is now uncovered by our novel approach as it
reveals the significant impact of IG on Queueing
Theory.
The stability problem (Rachev, 1989) in queueing
theory is concerned with the continuity of the
mapping F from the set U of the input flows into the
set V of the output flows. First, using the theory of
probability metrics we estimate the modulus of F-
continuity providing that U and V have structures of
metric spaces. Then we evaluate the error terms in the
approximation of the input flows by simpler ones
assuming that we have observed some functionals of
the empirical input flows distributions. This shows
the strength of our novel approach as it derives for the
first time ever the exact stability and instability
phases of the underlying M/G/1 queueing system.
The beauty of our novel approach that
revolutionizes Queueing Theory, is looking at a queue
as a manifold, in which case, 𝛼 is considered as the
parameter of curvature as well as being the connection
parameter of the underlying stable M/G/1 QM.
In other words, under a metric connection (c.f.,
Jefferson, 2018), parallel transport of two vectors
preserves the inner product, hence their significance
in Riemannian geometry. Any connection which is
both metric and symmetric is Riemannian, of which
there are generically an infinite number. However, the
natural metrics on statistical manifolds are
generically non-metric! Indeed, since only the special
case 𝛼=0 defines a Riemannian connection ∇
()
with respect to the Fisher metric (though observe that
∇
()
is symmetric for any value of 𝛼). While this may
seem strange from a physics perspective, where
preserving the inner product is of prime importance,
there’s nothing mathematically pathological about it.
Indeed, the more relevant condition, that every point
on the manifold have an interpretation as a probability
distribution. In general, (c.f., Lee, 1950),
exponentiating a matrix corresponds to
exponentiating each of its Jordan blocks. In fact, this
interpretation also holds for any analytic function 𝑓
applied to a matrix and not just 𝑒
. Also, it may be
useful to think of the matrix exponential as the
"Solution to the System of Ordinary Differential
Equations (ODEs)".
Based on the contributions of this paper, there are
several future research directions towards the new
applications of information geometric queueing
theory includes developing further advances on many
existing queueing manifolds, such as the G/G/1 queue
(c.f., Dodson, 2005 and Kouvatsos 1988) manifold
and employing information geometrics on various
statistical manifolds.
REFERENCES
Amari, S., 1985, Differential Geometrical Methods in
Statistics, Springer lecture Notes in Statistics, 28.
Skoda, Z., 2019, available online at
https://ncatlab.org/nlab/show/information+geometry
Nielsen, F., 2020, An Elementary Intrduction to
Information Geometry,Sony Computer Science
Laboratories Inc, Japan, MDPI Journal.
Dodson, C. T. J., 1999, Spatial Statistical and Information
Geometry for Parametric Statistical Models of Galaxy
Clustering, Springer Netherlands, 10.
The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold
159

Hall, B. C., 2015, The Matrix Exponential. In: Lie Groups,
Lie Algebras, and Representations. Graduate Texts in
Mathematics, vol 222. Springer, Cham.
Nakagawa, K., 2002, The geometry of M/D/1 queues on
Large Deviation, International Transactions of
Operational Research, Volume 9, Issue 2.
Kondor, R., Trivedi, S., 2018, On the Generalization of
Equivariance and Convolution in Neural Networks to
te action of Compact Groups, Proceedings of the 35
th
International Conference on Machine Learning,
Stockholm, Sweden, PMLR 80.
Norton, J. D., 2020, Non-Euclidean geometry and curved
spaces, department of history and philosophy of
science, University of Pittsburgh, available online at
https://www.pitt.edu/~jdnorton/teaching/HPS_0410/ch
apters/non_Euclid_curved/index.htm
Dodson, C. T. J., 2005, Topics in Information Geometry,
University of Manchester. Available online on
http://eprints.maths.manchester.ac.uk/131/1/InfoGeom
.pdf
MIT Open Course Ware, 2010. Online available at:
https://ocw.mit.edu/courses/mathematics/18-02sc-
ultivariable-calculus-fall-2010/4.-triple-integrals-and-
surface-integrals-in-3-space/part-b-flux-and-the-
divergence-theorem/session-84-divergence-
heorem/MIT18_02SC_MNotes_v10.1.pdf
Peng, L., Sun, H. and Jiu, L., 2007, The Geometric
Structure of the Pareto Distribution, Boletin de la
Asociación Matemática Venezolana, Vol. XIV, No 1
Mageed, I. A., Kouvatsos, D. D., 2019, Information
Geometric Structure of Stable M/G/1 Queue Manifold
and its Matrix Exponential, Proceedings of the 35th UK
Performance Engineering Workshop, School of
Computing, University of Leeds, Edited by Karim
Djemame, 16
th
of Dec.2019, p.123-135. [Online] at:
https://sites.google.com/view/ukpew2019/home
Loveridge, L.C., 7 September 2016, Physical and
Geometric interpretations of the Riemannian Tensor,
Ricci Tensor and Scalar Curvature, [Online] Available
on https://arxiv.org/pdf/gr-qc/0401099.pdf
Rudelius, T., 2012, A Geometric Understanding of Ricci
Curvature in the context of Pseudo-Riemannian
Manifold, Bachelor of Arts, Cornell University.
Ollivier, Y., 201, A visual interpretation to Riemannian
Curvatures and Some Discrete Generalizations. [Online]
www.yann-ollivier.org/rech/publs/visualcurvature.pdf
Thomas, R., 2015, Kissing the curve – manifolds in many
dimensions, online at: https://plus.maths.org/content/
kissing-curve-manifolds-many-dimensions
Gunawardena, G., 2006, Matrix Algebra for Beginners,
part III, Department of Systems Biology, Harvard
Medical School, MA02115, USA.
El-Affendi, M. A. and D.D. Kouvatsos, 1983, A Maximum
Entropy Analysis of the M/G/1 and G/M/1 Queueing
Systems at Equilibrium, Acta Informatica, 19, 339-355.
Kouvatsos, D. D., 1988, A Maximum Entropy Analysis of
the G/G/1 Queue at Equilibrium. J. Opl. Res. Soc.,
39(2), 183- 200
Amari, S., 2001, Information Geometry on Hierarchy of
Probability Distributions, IEEE Transactions on
Information Theory
Hamasha, M. M, Elsaadi, E., Hassonah, Y., Magrabi L., and
Alamudi, H., ,2016, Analysis of Service Delivery
System Using Markov Chain Approach and M/G/1
Queuing Systems, Asian Journal of Industrial
Engineering. [Online] Available at: 67518-AJIE-KR
(docsdrive.com)
Rachev, S. T., 1989, The problem of stability in queueing
theory. Queueing Syst 4, 287–317 (1989).
https://doi.org/10.1007/BF01159470
Jefferson, J. 2018, Information Geometry. [Online]
available at: https://rojefferson.blog/page/2/
Lee, J. M., 1950, Riemannian Manifolds: An Introduction
to Curvature, Graduate Texts in Mathematics, 176.
Springer-Verlag New York, Inc.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
160
