The Power Index at Infinity: Weighted Voting in Sequential Infinite

Anonymous Games

Shereif Eid

Leibniz Information Center for Science and Technology (TIB), Hannover, Germany

Keywords: Cooperative Games, Weighted Voting, Shapley-Shubik Power Index, Infinite Games, Multi-Agent Systems.

Abstract: After we describe the waiting queue problem, we identify a partially observable 2𝑛  1-player voting game with

only one pivotal player; the player at the 𝑛1 order.Given the simplest rule of heterogeneity presented in this

paper, we show that for any infinite sequential voting game of size 2𝑛 1, a power index of size 𝑛 is a good

approximation of the power index at infinity, and it is difficult to achieve. Moreover, we show that the collective

utility value of a coalition for a partially observable anonymous game given an equal distribution of weights is

𝑛



𝑛.This formula is developed for infinite sequential anonymous games using a stochastic process that yields

a utility function in terms of the probability of the sequence and voting outcome of the coalition. Evidence from

Wikidata editing sequences is presented and the results are compared for 10 coalitions.

1 INTRODUCTION

Cooperative games are used in many applications

across various domains such as collective decision

making, waste management, economics (such as

profit sharing in cooperative e-commerce

applications), dynamic robot coalition formation, and

utility allocation in open anonymous environments

(Skibski et al.,2018; Bachrach and Elind,2008;

Eryganov et al.,2020; Smirnov et al.,2019; Zhao et

al.,2018). Such cooperative games rely on coalition

formation, and in most cases, weighted voting is used

to predict the collective payoff gained through

cooperation. In weighted voting, allocation of payoff

depends on how much each agent is decisive in a

sequential voting game. Unlike non-cooperative

games which analyze the actions performed by

individual players, weighted voting is based on the

cooperative game theory which focuses on coalition

formation strategies and allocating collective payoff

based on group actions.

The Shapley-Shubik power index is the most

prominent among weighted voting models and it is

used in the majority of cooperative game

applications. The shapely value provides interesting

properties that make it more suitable for fair payoff

allocation in cooperative games such as symmetry

(identity of players should not have impact on payoff

https://orcid.org/0000-0003-0206-8095

allocation) and efficiency (all available payoff should

be distributed among players) (Skibski et al., 2018).

Because the Shapley value is equiprobable (Boratyn

et al., 2020), the existence of the grand coalition is

necessary at least as a mere assumption for tactical

reasons (Elkind et al., 2008). Moreover,

equiprobability implies that coalitions are formed

such that they represent a perfect sample of the

population. The Shapley-Shubik power index

measures the value of a coalition based on the hidden

(marginal) voting power of each member. This hidden

power can be described in terms of the marginal value

of a member based on his order in a sequence randomly

selected from the set 𝐴 which includes all agents, i.e.

the grand coalition. Given the cardinality of 𝐴 ,

assuming that players leave the grand coalition

sequentially in a random order ,each coalition is a

permutation, and the contribution of each player is the

probability of his random order in the coalition he joins

averaged over all the permutations of 𝐴 (Skibski et

al.,2018; Benati et al.,2019).

Therefore, studying coalition formation strategies

and coalitional structures is paramount and has been

an important line of research for many years (Skibski

et al.,2018).Some proposals identify a stable coalition

structure that embeds all coalitions to optimize

resource allocation and allow more than one coalition

to win (Elkind et al.,2008). Moreover, discrete-time

Eid, S.

The Power Index at Inﬁnity: Weighted Voting in Sequential Inﬁnite Anonymous Games.

DOI: 10.5220/0010178504750482

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 475-482

ISBN: 978-989-758-484-8

475

stochastic processes, such as the Chinese Restaurant

Process, have been used to model coalition formation

in the Shapley-Shubik model (Skibski et al., 2018).

For instance, in the Chinese Restaurant Process,

agents leave the grand coalition sequentially and each

new agent either forms a new partition or joins an

existing one (Skibski et al., 2018).

Unlike the Chinese Restaurant Process, in this

paper, we consider a waiting queue example where

each agent at the order 𝑛 can form a new partition

given that 𝑛1 anonymous players will form the

remaining partition. Moreover, a discrete time

stochastic process, played with a fair coin, is

modelled to discard contributions made by

consecutive voters to model heterogeneity in real-

time. Real-time heterogeneity is considered an

important prerequisite for effective coalition

formation and fair distribution of rewards in

cooperative multi-agent systems (Smirnov et al.,

2019). Nonetheless, we believe that studying

weighted voting in infinite games and creating

dependencies on future group actions, especially for

open anonymous environments, is important for

identifying the threshold beyond which cooperative

patterns may need to be refreshed or altered to a

certain extent. This means that we highlight the

possibility that cooperative patterns in infinite games

may reach a certain level of exhaustion at points in

time when they achieve the threshold at which task

requirements are satisfied.

Fundamentally, the most important condition in

the Shapley-Shubik model states that the number of

agents in a game is finite and a value function 𝑣

describes the value of the coalition by mapping subset

players to some real number such that 𝑣:2



→

𝑅.Where 𝑣 is the collective payoff which the

members of a coalition 𝑆⊆𝐴 gain through

cooperation. However, the payoff for each player

depends heavily on the player’s order in the sequence.

For instance, the Shapley value of player 𝑖 in a game

of 𝑛 players described as 𝐺𝑣,𝐴 is :

𝜑





𝑣





𝑛!

𝑣𝑅





∪



𝑖



𝑣𝑅







(1)

Therefore, the marginal voting power is

calculated over the range 𝑛! , and 𝑅





is the set of

players in the sequence 𝑄 which precede 𝑖 . The

winning coalition is the one which achieves a certain

quota concluded based on either a fuzzy rule or a pre-

identified value (for example, fuzzy rules are used to

limit cooperation by restricting payoff for some

players - see Gallardo and Jiménez-Losada

(2017)).Each sequence plays a crucial rule in

identifying the value of the coalition, however, when

the number of players is large, the Shapley value

takes a heuristic form:



𝑆





𝑑𝑠



𝑣



𝑡𝐴  𝑑𝑠



𝑣



𝑡𝐴



𝑑𝑡





(2)

Where 𝑡𝐴 is the proportionality of coalition 𝑆∈

𝐴, and 𝐴 contains a large number of players. This

latter setting matches an infinite game model in which

the identity of players does not play a crucial rule in

deducing the value of the coalition. In this paper, we

redefine the proportionality in terms of the likelihood

of occurrence of the sequence. In infinite sequential

ordered votes, each player has a minor contribution

and the game evolves as a nonlinear game wherein

the value of the coalition is more important than the

payoff obtained by each agent. In particular,

individual contributions are minor with respect to the

collective contribution of the coalition. Moreover, in

sequential infinite games, it is common to divide the

action space into finite sequential games that

approximate the utility gain in general situations

(Reeves and Wellman, 2012).

Unfortunately, much of the work produced in this

field is directed towards studying finite voting games

and less work has addressed infinite sequences. In this

paper, we obtain the likelihood of the occurrence of

any finite sequential partition 𝑡𝐴 in infinite sequential

anonymous games. Firstly, we describe the waiting

queue problem, then we identify a 2𝑛 1-player

game with only one pivotal player; the player at the

𝑛1 position.We use a stochastic game formula to

model an infinite sequence given the simplest rule of

heterogeneity in anonymous games identified in our

method. We reach an approximate of the power index

at infinity using samples of finite sequences, and we

show that it is difficult to achieve. Our method is

described in the next section. Section 3 analyses the

results. Section 4 discusses related work. Finally,

section 5 concludes the paper.

2 METHOD

Infinite sequences disproportionately influence the

voting power of players because at any position in a

sequential game the number of remaining voters is

undefined or possibly large. In this case, predicting

the proportionality of a coalition is more viable than

computing the collective payoff based on the shapely

value of each player. For instance, a voting game

𝐺𝑣,𝐴 can be represented as a vector of values 𝑊 

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

476







,…w





that represents the weights of

players and 𝑞 is the quota (Bachrach and Elind,

2008). If 𝑊 represents the weights of an infinite

number of players, the shapely value is undefined. To

reduce this problem, we assume that the weight of

each position in an infinite sequence is dependent on

the number of players yet to vote, and moreover, we

assume that every infinite game is partially

observable. By “position” we mean the order of the

player regardless of the identity of neighboring

players.

This problem resembles a waiting queue problem

in which the weight of any agent 𝑖 is dependent on the

number of agents that precede 𝑖 in the queue.

However, to deal with the problem of having an

infinite number of players, we assume that every

queue of size 𝑛 is only a partition of a larger queue of

size 2𝑛 1. if we consider a queue with size 2𝑛1

, and the function 𝑓𝑛  𝑘 identifies the waiting

time of any member 𝑖



at the 𝑘1 position

(assuming that each member corresponds to a single

unit of time), we find that 𝑓



2𝑛 10, 𝑓



2𝑛

2𝑛12𝑛  1, and we always find that 𝑓



𝑛 

𝑛  1.This is observable for any sequence of size

2𝑛 1. However, algebraically we can conclude that

𝑓





𝑛1







𝑛1



1𝑛.

In light of the previous queue problem, we define

a game 𝐺𝐴,𝑣 is a voting game with 𝐴: the set

that contains all agents (grand coalition), and 𝑣 is a

value function that maps a coalition to some real

number ; 2



→𝑅.Now consider a finite game with

size 2𝑛 1 and quota 𝑞𝑛 ,i.e.

𝐺:𝑎



,𝑎



,𝑎



….𝑎



;𝑛 where 𝑛 is any small

number. In addition, the collective utility (value)

function is identified by 𝜑





𝑣



𝑤



𝑡



where ∈0,1

, i.e. voters can only conduct a ‘yes’ or no ‘vote’ and

𝑤𝑓





𝑛



𝑛1 for any 𝑖. In this case, we find

that the only pivotal player is the player at the 𝑛1

position.

Lemma 1: Given a partially observable sequential

voting game of size 2𝑛 1 of which only an 𝑛-

player partition is observable, the player at the order

𝑘𝑛1 is pivotal for the grand coalition.

Proof: For any quota 𝑞n and 𝑄



is the

sequence identified by 𝐺𝑎



,𝑎



,𝑎



….𝑎



, we

split G into 𝐺



𝑎



,𝑎



,..𝑎



 and 𝐺





𝑎



,𝑎



,..𝑎



,𝑎



 .We the assume that only

𝐺



is observed with the assumption that ∃𝑡



∈𝑇 

1and 𝑖∈ 𝐺



,and therefore, the quota 𝑞



for 𝐺



𝑛1.Given that weights are distributed equally

among voters, we find that the player at the order 𝑘

𝑛1 is pivotal for 𝐺



.Given that 𝐺



is not

observable, we conclude that player 𝑎



is pivotal

for an infinite sequence of size 2𝑛 1.

Example 1: Consider the game 𝐺

1,1,1,1,1,0,0,0,0;4,this is a 2𝑛 1 game with 𝑛

4. If all players up to the 𝑛



position vote ‘yes’, the

quota is achieved assuming that there is at least one

player at any position 𝑘𝑛 will vote ‘yes’. In the

above example, the outcome for 𝐺



∈𝐺, where 𝐺



contains all players up to the 𝑛



position, is 4.Any

player in the remaining sequence, let’s say the one at

the order 𝑘𝑛1, can guarantee achieving the

quota if he conducts a ‘yes’ vote. In the above game,

the player at the 𝑛1 position is the one at the 5

position, therefore, the collective outcome of 𝐺 is 5.

Therefore, given a 2𝑛 1 game and an 𝑛-player

partition , at the order 𝑘𝑛, we find that there are

still 𝑛1 players yet to vote , and assuming that at

least one player in the remaining sequence will

conduct a ‘yes’ vote , we conclude that the pivotal

player in any infinite sequential game of size 2𝑛 1

is the one at the 𝑛1 position. Although the player

at the 𝑛



order guarantees achieving the quota if he

conducts a positive vote, he is not pivotal to the

coalition. Our interest here is identifying the pivotal

player that first guarantees achieving the quota,

regardless of whether the quota is exceeded, and

given that at least one player in 𝐺



will conduct a

positive vote.

Lemma 2: For an infinite sequential voting game and

a coalition of size 2𝑛 1 players, and quota 𝑞  𝑛,

the value of the coalition 𝜑



𝑣



is 𝑛



𝑛.

Proof: Consider the coalitional utility value function



→𝑅 represented by 𝜑



𝑣





∑

𝑤



𝑡



and 𝑡∈0,1

, and moreover, the function 𝑓





𝑛



𝑛1

represents the weight 𝑤



of player 𝑖 at any order

𝑘.For simplicity, we assume that ∀



𝑖



∈𝐴,𝑡



1.

For an 𝑛-player partition we get :

𝑤



𝑡









𝑛



𝑛1



 𝑛



𝑛

(3)

By revisiting example 1 above, we notice that the

collective value of the coalition should be 4



4

20.Moreover, the collective value of 𝐺



∈𝐺 is 14,

where 𝐺



contains all players up to the 𝑛



position.

In this case, the first player at the least 𝑛1 order,

i.e. the player at the 5

position, has sufficient weight

to achieve the coalitional value, however, there is

uncertainty about the state of all players at 𝑘𝑛

since 𝐺 is an infinite game.

Note

that for any game of size 2𝑛  1 there is a

The Power Index at Inﬁnity: Weighted Voting in Sequential Inﬁnite Anonymous Games

477

partition of size 𝑛, i.e an 𝑛-player game that contains

at least 2 players. This rule is violated for 𝑛

2.Consider a game with 𝑛1 and 3 players, for

example 𝐺0,0,1;1, at the 𝑛



position there

should be a number of 𝑛1 players that guarantee

achieving the quota if they all conduct a “yes’ vote.

Therefore, for a 2𝑛 1 player game with 3 players

there is no pivotal player, and the quota is not

achievable in this case.

For infinite sequential voting games, we model a

sequence of infinite games each with 𝑛1 using a

discrete-time stochastic Bernoulli process. Note that

given a Bernoulli process with 𝑛1, 𝑎



does not

affect the state transition in all cases because it is the

initial input to the process. Moreover, in anonymous

environments, heterogeneity is not observed, and

therefore, the weight is identical for any two players

𝑖 and 𝑗. Therefore, in order to model heterogeneity in

its simplest form, we assume that anonymous players

cannot conduct two consecutive votes. This rule is

described in definition 1 below:

Definition 1: In anonymous games, the simplest Rule

of Heterogeneity (RoH) states that 𝑖  𝑗 where 𝑖 and

𝑗 are the players at the positions 𝑘1 and 𝑘

respectively.

Follows from definition 1 that the total number of

votes in any fair game with an ordered sequence 𝑄 is

bounded according to Lemma 3 below:

Lemma 3: Given an infinite anonymous game with

fair distribution of votes, the sequence 𝑄



with

size 2𝑛 1 has 𝑛 number of votes.

Proof: Given a Bernoulli stochastic sequence of

games, each with a state space {0, 1}, and assuming

that all games are played using a fair coin, a sequence

of size 𝑍 contains 𝑍1 coin tosses. A sequence of

size 2𝑛 1, therefore, contains 2𝑛 coin tosses with

probability





for any selection.

To model heterogeneity, we use a discrete-time

Bernoulli stochastic game with state space 𝑎

0,𝑏1 where 𝑎 and 𝑏 are Boolean variables that

represent the satisfaction and dissatisfaction of RoH.

Moreover, 𝑆𝑡𝑟𝑎𝑡𝑒𝑔𝑦



𝑎 is the winning

strategy which occurs when RoH is satisfied, and

𝑆𝑡𝑟𝑎𝑡𝑒𝑔𝑦



𝑏 is vice versa. Thus, given that

the random variable 𝑋 has a Bernoulli distribution,

the probability of obtaining a win is 𝑃 and the

probability of obtaining a loss is 1𝑃. The game

starts at state 𝑇



with applying the biased function

𝑓



(X)𝑥; if the result is 𝑓





𝑋



𝑏 then there is a

loss and the process stays at 𝑇



, if the result is

𝑓





𝑋



𝑎 then the result is a win and there should be

a state transition to 𝑇



.Note that the function𝑓





𝑋



does not guarantee collecting 𝑛 votes because 𝑓





𝑋



is not a fair function yet it represents the likelihood of

occurrence of the best possible sample of the

population. More precisely, 𝑓





𝑋



𝑎 is the degree

to which the voting sequence is heterogeneous. Given

an infinite random game, intuitively, the probability

of obtaining 𝑛 votes should be extremely low.

Moreover, in a sequence of size 2𝑛 1 , the

probability of obtaining 𝑙 losses is 𝑃



and the

probability of obtaining 𝑤 wins is 1 𝑃



, and

𝑤2𝑛1𝑙.The higher the value of 𝑃, the less

likely two consecutive wins will occur. Now

considering the sequence Q, given that the discrete

random variable 𝑋 has a Bernoulli distribution, the

probability of obtaining 𝑄 is given by 𝑃



𝑄





𝑃



𝑋



,𝑋



,𝑋



,𝑋



,….𝑋





𝑃



1  𝑃



. The reason

Q is observed is due to the collective measure of

fairness it can provide; P(Q) is the likelihood of

occurrence of the partition 𝑡𝐴 which is a perfect

sample of the population of agents. To calculate the

power index for the k

player in the game, equation 1

is not valid because the sequence can be large enough

such that equation 1 cannot be solved in polynomial

time. Equation 2 satisfies a voting game with large

number of participants, however, it does not satisfy

an infinite game in which the identity of agents cannot

be resolved in real time. The probability of

occurrence of any sequence 𝑄 is 𝑃𝑄 and it has been

concluded as described above. Therefore, given that

the game is anonymous and with a large number of

players, it is reasonable to replace 𝑡𝐴 with P(Q),the

probability of the sequence, in equation 2 above, and

thus, the index of the 𝑘



player in the game is

calculated as follows:



𝑆





𝑑𝑠



𝑣



𝑃



𝑄





1𝑃



𝑄











𝑣



𝑃



𝑄





1𝑃



𝑄











𝑃𝑄





1𝑃𝑄





(4)

Since the contribution of each player is minor, we

have assumed that weights are distributed equally

among voters. Therefore,



𝑆





𝑑𝑠



now represents

the power index of agent 𝑎



in terms of the

marginality (hidden power) over the range 1

𝑃



𝑄



. Due to the minority of individual contributions,

the value 𝑑𝑠 now is very small and can be ignored,

hence, the value function at position 𝑘 can be reduced

to represent the power index of the 𝑘

position. This

is calculated in equation 5.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

478

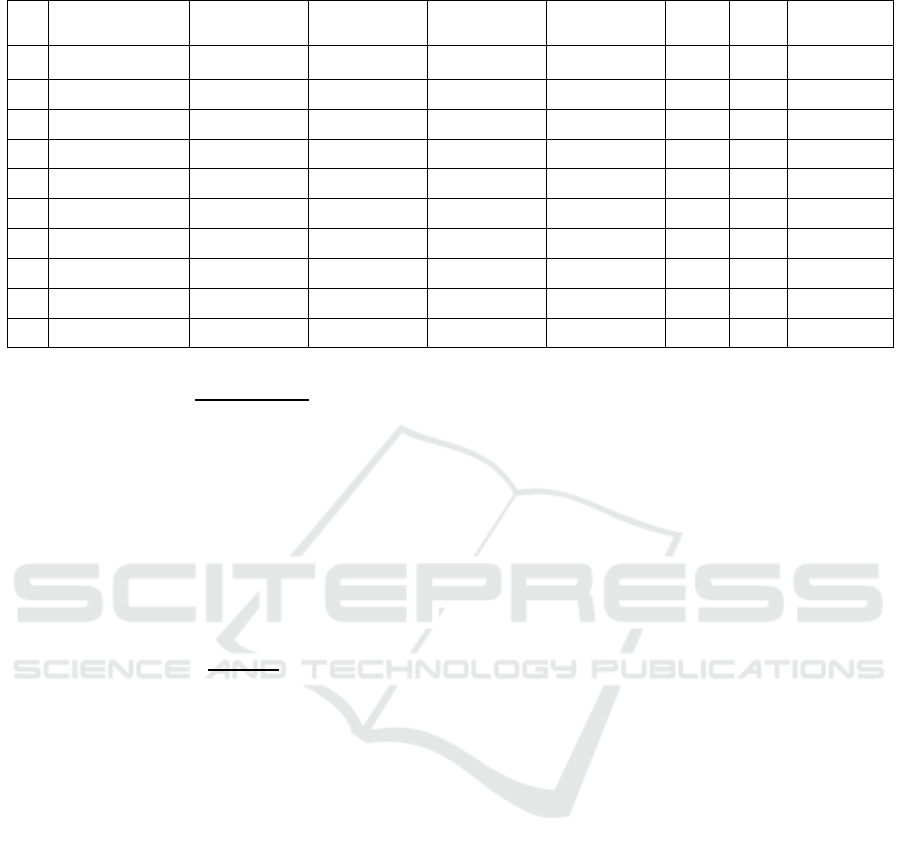
Table 1: Sample of the results of 10 coalition obtained by analysing Wikidata’s editing sequences.

𝑃 1𝑃 𝑃𝑄 1𝑃𝑄 𝑤





𝑣



𝑛



𝜑





𝑣



𝐹𝜆



𝑒



0.55465587 0.44534413 0.247012736 0.752987264 0.32804371 73 27 0.037037037

𝑒



0.58552631 0.414473684 0.242685249 0.757314751 0.320454935 65 35 0.028571429

𝑒



0.64734299 0.352657005 0.228290042 0.771709958 0.295823631 61 39 0.025641026

𝑒



0.29003021 0.709969789 0.205912688 0.794087312 0.259307364 56 44 0.022727273

𝑒



0.57142857 0.428571429 0.244897959 0.755102041 0.324324324 55 45 0.022222222

𝑒



0.27118644 0.728813559 0.197644355 0.802355645 0.246330111 38 62 0.016129032

𝑒



0.37804878 0.62195122 0.2351279 0.7648721 0.307408128 54 46 0.02173913

𝑒



0.28179551 0.718204489 0.202386801 0.797613199 0.253740537 72 28 0.035714286

𝑒



0.61940298 0.380597015 0.235742927 0.764257073 0.308460249 64 36 0.027777778

𝑒



0.178 0.822 0.14631 0.853684 0.17139363 40 60 0.016666667

𝑤





𝑣



 𝑣



𝑃



𝑄





1𝑃



𝑄







(5)

Indeed, the quota for any sequence



𝑎



,𝑎



,𝑎



,…..𝑎





is 𝑛



𝑛.Where 𝑛



is the

number of votes obtained by using the biased function

𝑓





𝑋



at the pivotal position where 𝑘𝑛1 and

𝑤





𝑣



is the marginal power at the 𝑘



position.

Moreover, there is a proximity function that measures

the degree to which the outcome of any sequence 𝑄

is close to the quota:

𝐹𝜆





𝑛 𝑛



(6)

Note that as 𝑛



gets closer to n, 𝐹



𝜆



→∞ and

𝐹𝜆



∈



0,∞



. The value of the coaltion in this case

can be concluded by updating equation 3 as follows:

𝜑





𝑣



 𝑤





𝑣



∗ 𝑛



(7)

Where 𝜑





𝑣



represents the collective utility

value of the coalition, i.e. the payoff members of the

coalition gain through cooperation. In the next

section, we use equations 6 and 7 to derive the

coalitional values for 10 Wikidata coalitions.

Furthermore, equation 6 is used to calculate the

proximity value for each coalition with respect to the

predicted output at infinity (which should precisely be

equal to ∞).

3 ANALYSIS

In this analysis we exploit the nonlinearity of

Wikidata, the largest structured crowdsourced

knowledgebase that currently exists. Wikidata

depends on a peer production service in which a large

sample of the general population, called the crowd, is

hired to perform editing tasks. Editing tasks merely

depend on individual agent preferences. Therefore,

selecting a targeted knowledge resource (entity) is a

random process, as well as selecting the time to

execute edits.

The editing process in Wikidata is a sequential

process with no bound on the amount of edits required

to complete the knowledge. Thus, editing events can

be modelled as an infinite sequential voting game

where each edit is equivalent to a single vote.

Moreover, identity of editors does not affect the

editing sequence, while in particular many of the

editing events are already performed by anonymous

users or automated group programs (bots).Therefore,

Wikidata editing events can ideally be modelled as an

infinite anonymous voting game. In this context,

editing events of many entities were analyzed. A

sample of the result is shown in table 1 above. The

editing sequence of each entity represents a

coalitional game for which the value of the coalition

at the 𝑘



position is calculated as in equation 5 and

each entity is represented by a coalition 𝑆 ⊂𝐴.

Moreover, entities are chosen such that the

assumption can be made that the progress of different

coalitions is not necessarily competitive, but distinct

games should at least be comparable. Concerning the

targeted quota, the progress of 1000 coalitions over

five iterations, was analysed, but no coalition

achieved the target quota. As expected, 𝑛 is difficult

to achieve in an infinite game. As shown in table 1

above, some coalitions came very close to 𝑛 with

proximity as low as ~0.016 , but no coalition

achieved 𝐹𝜆



 ∞ which means that 𝑛 can be

considered as the power index at infinity.

The Power Index at Inﬁnity: Weighted Voting in Sequential Inﬁnite Anonymous Games

479

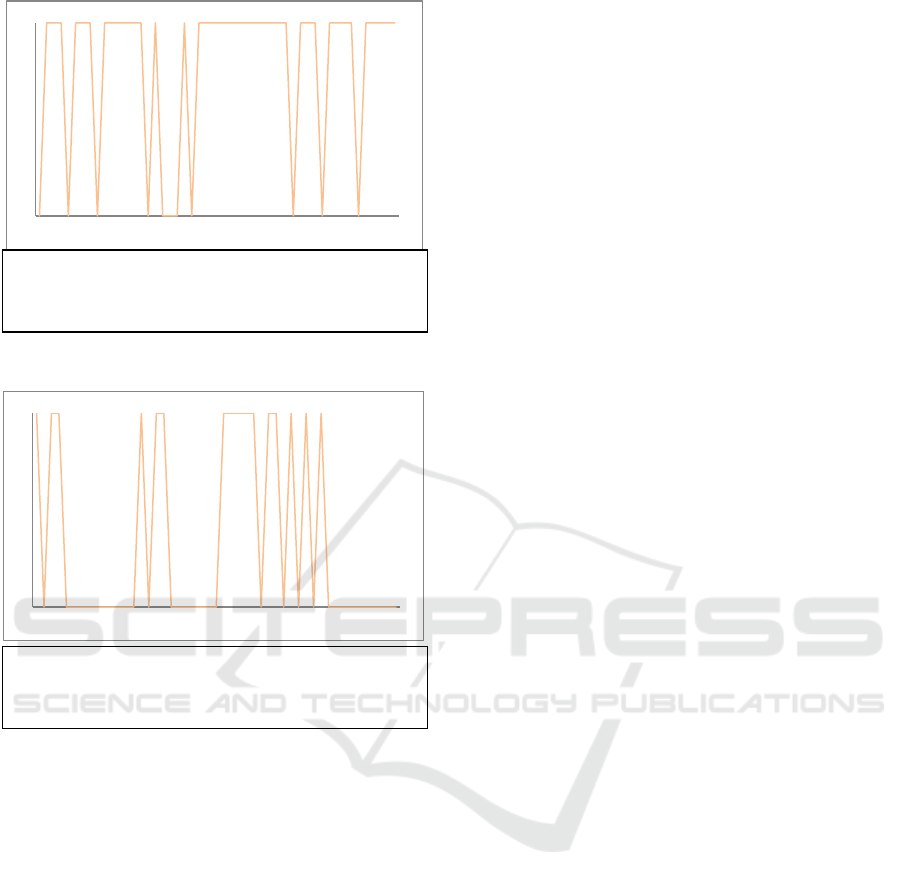
Figure 1: Voting pattern and BF for 𝑒



Figure 2: Voting pattern and BF for 𝑒



Equation 7 is used to obtain the utility value of

each coalition as shown in table 1.By examining

many entities, we noticed that there is a strong

relation between the utility function 𝜑





𝑣



and the

publicity of entities. For example, the above entities

represent a selection of higher educational

institutions, the two entities with the highest

coalitional values 62 and 60 are the most prominent

in this list. Similarly in other coalitions that belong to

comparable categories, in many cases, the value of

the coalition is related to the publicity of entities.

Because 𝜑





𝑣



also represents the quality of

cooperative patterns in terms of achieving real-time

heterogeneity (represented by the probability of the

sequence captured at certain points in time), this

result suggests that entities with higher public

awareness may have higher quality cooperative

patterns. However, the quality of cooperative patterns

should not directly relate to the quality of the content

of the corresponding Wikidata articles.

Moreover, the sequential voting scheme for

Wikidata yields a Boolean fingerprint (BF) as shown

in figures 1 and 2 above. Both figures show the BF

for the coalition with the largest gain (𝑒



) and the

coalition with the lowest gain ( 𝑒



) respectively at the

pivotal position 𝑛1 for 𝑛100 (the complete BF

for each entity is shown below each graph). However,

it should be noted that 𝑃𝑄 does not represent the

number of aggregated votes, but it represents the

probability of the sequence, and it depends on the

degree to which the voting sequence is

heterogeneous. Heterogeneity in real-time is not the

total number of players in the coalition, but it is the

number of consecutive actions performed by different

players. Therefore, on some occasions, coalitions

with lower number of players may have highly

heterogeneous patterns, hence higher quality

cooperative patterns, than coalitions with higher

number of players.

4 RELATED WORK

Skibski et al. (2018) derive the “stochastic shapely

value” by applying the Chinese restaurant process to

games with externalities .In the Chinese Restaurant

Process, each player can either form a new group with

probability 1/𝑛 or join an existing group with

probability 𝑏/𝑛 where 𝑏 is the number of existing

players. The stochastic shapely value takes into

consideration , not only the marginal power of each

player, but also the weighted average over all

partitions , which is based on the probability that the

coalition will form using the Chinese Restaurant

Process.

Benati et al. (2019) Show that stochastic

approximation can produce effective sampling of

additive exponential values in cooperative games.

This is achieved by applying probability concepts

only to the sample and reduced sum. They show that

there stochastic approximation method produces

accurate predictions equivalent to the actual value of

the game with minor standard error.

de Keijzer et al.(2010) addressed the possibility

of manipulating voting games by designing a

weighted voting game that yields a target power

index, or at least a power index that is close enough

to a certain threshold in an 𝑛-player game. This

problem is a difficult one because identifying a priori

for agent 𝑖’s position such that the coalition yields a

certain value requires examining an infinite set of

weights and calculating all permutations over the

finite set of players, and moreover, this applies to

each weighed voting game. Our method escapes this

135791113151719212325272931333537394143454749

011101111011111101000101111111111111011

101111011111010110111001000011101111111

01110111111011111010001

101100000000001011000000011111011010101

000000000000000001111001100000011100100

0001010101110011011011

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

480

restriction for two reasons: 1. there is an infinite

number of players which implies that each player has

a minor contribution to the value of the

coalition.2.players are anonymous, and given the

simplest RoH, the maximum contribution of each

player is bounded by uniformity.

However, the method represented by de Keijzer et

al. (2010) requires excluding dummy players and

identifying a superset, i.e. a super coalition that is

always winning, then iteratively identifying the

maximum-weight losing coalition. The previous

approach is close to identifying the best response

profiles in partially observable infinite games

(Reeves and Wellman, 2012). Usually, computing the

linear best response strategies in infinite games, such

as the work of Reeves and Wellman (2012), needs a

number of steps: 1.developing an algebraic formula

for predicting the utility given a strategy and a set of

parameters. 2. The action space of agents is then

partitioned, and the maximum utility action, i.e. the

action with the potential to maximize the utility

expression, is identified. This method depends

heavily on effectively identifying partitions such that

the maximum utility action is the best one for

generalization.

To study false name manipulation, Bachrach and

Elind (2008) studied a game that consists of all

players in the grand coalition, and weights are

distributed fairly among players. In addition, a value

function 𝜑





𝑣



2 describes the gain and each

player can split his weight fairly between two false

identities. For example ,in a game 𝐺:2,2,2,…;2𝑛,a

player can split his weight equally among 2 identities

resulting in the game 𝐺





2,2,…2,1,1;2𝑛



. Indeed, in

such game the shapely value for any player is 1/𝑛 (

given that this is the only permutation that

exists).Therefore, the maximum gain for the last two

players with false identities is 2𝑛/𝑛 1.Due to our

RoH we have considered the game 2,1,1;𝑛 ,and

given our stochastic process , the maximum gain of

this coalition is 𝑛1.Moreover, to model an infinite

game of this sample we have generalized our formula

to model any sequence of size 2𝑛 1.

5 CONCLUSIONS

Infinite sequential games are now important in

internet open anonymous environments, such as the

Wikidata case study presented in this paper. We have

reached the best approximation of the voting power

index at infinity for a coalition. In light of the waiting

queue problem described in this paper, we identified

a voting game with only one pivotal player. In

particular, for a partially observable sequence of size

2𝑛1, we have found that the only pivotal player is

the one at the order 𝑛1 given a utility function that

identifies the coalitional value gained through

cooperation. Moreover, we have found that 𝑛 is a

good approximation of the power index at infinity,

and it is difficult to achieve. This result is based on

the simplest rule of heterogeneity which prevents

anonymous players from conducting consecutive

votes.

We have applied our game formula to Wikidata

editing sequences of many entities and a sample of

the results has been presented. Using a discrete-time

stochastic process, we have modelled Wikidata

editing events as infinite sequential voting games.

The quality of cooperative patterns, identified in

terms of the degree of real-time heterogeneity, has

played a key role in yielding higher coalitional values.

An interesting line of research for future work is

identifying the threshold beyond which cooperative

patterns need to be refreshed to yield higher

coalitional values or to maintain a winning strategy.

ACKNOWLEDGEMENTS

The author would like to thank the anonymous

reviewers for their constructive comments which

contributed to improving the final version of the

paper.

REFERENCES

Skibski, O., Michalak, T. P., & Wooldridge, M. (2018). The

Stochastic Shapley Value for coalitional games with

externalities. Games and Economic Behavior, 108, 65-

80.

Bachrach, Y., & Elkind, E. (2008, May). Divide and

conquer: False-name manipulations in weighted voting

games. In Proceedings of the 7th international joint

conference on Autonomous agents and multiagent

systems-Volume 2 (pp. 975-982).

Eryganov, I., Šomplák, R., Nevrlý, V., Smejkalová, V.,

Hrabec, D., & Haugen, K. K. (2020). Application of

cooperative game theory in waste

management. Chemical Engineering Transactions.

Smirnov, A. V., Sheremetov, L., & Teslya, N. (2019, May).

Fuzzy Cooperative Games Usage in Smart Contracts

for Dynamic Robot Coalition Formation: Approach and

Use Case Description. In ICEIS (1) (pp. 361-370).

Zhao, W. J., & Liu, J. C. (2018). Triangular Fuzzy Number-

Typed Fuzzy Cooperative Games and Their

Application to Rural E-Commerce Regional

Cooperation and Profit Sharing. Symmetry, 10(12), 699.

The Power Index at Inﬁnity: Weighted Voting in Sequential Inﬁnite Anonymous Games

481

Benati, S., López-Blázquez, F., & Puerto, J. (2019). A

stochastic approach to approximate values in

cooperative games. European Journal of Operational

Research, 279(1), 93-106.

Boratyn, D., Kirsch, W., Słomczyński, W., Stolicki, D., &

Życzkowski, K. (2020). Average weights and power in

weighted voting games. Mathematical Social Sciences.

Elkind, E., Chalkiadakis, G., & Jennings, N. R. (2008,

July). Coalition Structures in Weighted Voting Games.

In ECAI (Vol. 8, pp. 393-397).

Kurz, S. (2012). On minimum sum representations for

weighted voting games. Annals of Operations

Research, 196(1), 361-369.

Reeves, D., & Wellman, M. P. (2012). Computing best-

response strategies in infinite games of incomplete

information. arXiv preprint arXiv:1207.4171.

de Keijzer, B., Klos, T., & Zhang, Y. (2010, May).

Enumeration and exact design of weighted voting

games. In Proceedings of the 9th International

Conference on Autonomous Agents and Multiagent

Systems: volume 1-Volume 1 (pp. 391-398).

Gallardo, J. M., Jiménez, N., & Jiménez-Losada, A. (2017).

Fuzzy restrictions and an application to cooperative

games with restricted cooperation. International

Journal of General Systems, 46(7), 772-790.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

482