
CPA Lyapunov Functions: Switched Systems vs. Differential Inclusions
Sigurdur Hafstein
Science Institute and Faculty of Physical Sciences, University of Iceland, Dunhagi 5, 107 Reykjav
´
ık, Iceland
Keywords:
Lyapunov Function, Switched Systems, Differential Inclusions, Numerical Algorithm, Artstein’s Circles.
Abstract:
We present an algorithm that uses linear programming to parameterize continuous and piecewise affine Lya-
punov functions for switched systems. The novel feature of the algorithm is, that it can compute Lyapunov
functions for switched system with a strongly asymptotically stable equilibrium, for which the equilibrium of
the corresponding differential inclusion is merely weakly asymptotically stable. For the differential inclusion
no such Lyapunov function exists. This is achieved by removing constraints from a linear programming prob-
lem of an earlier algorithm to compute Lyapunov functions, that are not necessary to assert strong stability for
the switched system. We demonstrate the benefits of this new algorithm sing Artstein’s circles as an example.
1 INTRODUCTION
We start with an informal introduction of the switched
systems and differential inclusions we will be con-
cerned with; the technical details follow later when
we concretize our setting. Keep in mind that we are
setting the stage to remove conditions on a Lyapunov
function for a switched system with a strongly asymp-
totically stable equilibrium, which is merely weakly
asymptotically stable for the corresponding differen-
tial inclusion.
We consider switched systems of the form
˙
x = f
α
(x), α : [0, ∞) → A, (1)
where for each a ∈ A the vector field f
a
: D(f
a
) → R
n
is defined on D(f
a
) ⊂ R
n
, A is a finite set equipped
with the discrete topology, and α : [0, ∞) → A is a
right-continuous switching signal. Solution trajecto-
ries of the system are continuous paths obtained by
gluing together trajectory pieces of the individual sys-
tems
˙
x = f
a
(x). Switched systems and their stabil-
ity have been intensively studied, cf. the monograph
(Liberzon, 2003; Sun and Ge, 2011). The main ques-
tions regarding the asymptotic stability of an equilib-
rium of a switched system, which we may assume is at
the origin, is if a switching can be chosen such that so-
lution trajectories are steered to the equilibrium (weak
asymptotic stability) or if trajectories are attracted to it
regardless of the switching (strong asymptotic stabil-
ity). The latter case is referred to as arbitrary switch-
ing. Both types of stability are usually dealt with us-
ing Lyapunov functions, i.e. functions from the state
space to the real numbers that are decreasing along so-
lution trajectories. In (Hafstein, 2007) an algorithm to
compute continuous and piecewise affine (CPA) Lya-
punov functions for arbitrary switched systems was
developed; we will discuss it below.
Closely related to the switched system (1) is the
differential inclusion
˙
x ∈ F(x) := co{f
a
(x) : x ∈ D(f
a
)}, (2)
where coC denotes the convex hull of the set C ⊂ R
n
.
Solution trajectories are absolutely continuous paths
t 7→ x(t) fulfilling
˙
x(t) ∈ F(x(t)) almost surely. One
speaks of weak asymptotic stability of an equilibrium
if there are solution trajectories that are asymptot-
ically attracted towards the equilibrium and strong
asymptotic stability if this is the case for all solu-
tion trajectories. In (Baier et al., 2010; Baier et al.,
2012) an algorithm for the computation of CPA Lya-
punov functions for strongly asymptotically stable in-
clusions was presented and in (Baier and Hafstein,
2014) a corresponding algorithm for the computa-
tion of control CPA Lyapunov functions for weakly
asymptotically stable differential inclusions. See also
(Baier et al., 2018) for a different approach including
semiconcavity condition into the formulation of the
optimization problem.
Let us give a short review of CPA Lyapunov func-
tions in the context of switched systems and differ-
ential inclusions. To define a CPA Lyapunov func-
tion V , first a triangulation T of its domain, a subset
of R
n
, must be fixed. The triangulation must have
the property that any two different simplices inter-
sect in a common face or not at all. The continuous
Hafstein, S.
CPA Lyapunov Functions: Switched Systems vs. Differential Inclusions.
DOI: 10.5220/0009992707450753
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 745-753
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
745
and piecewise affine function V is then defined by as-
signing it values at the vertices of the simplices of T
and linearly interpolating these values over the sim-
plices. The resulting function is affine on each sim-
plex S
ν
∈ T and thus differentiable in its interior S
◦
ν
.
In particular, its gradient is a well defined constant
vector ∇V
ν
in the interior. At the boundaries, where
two or more simplices intersect, the function V is not
differentiable and its gradient is not defined. In (Baier
et al., 2010; Baier et al., 2012; Baier and Hafstein,
2014) this was dealt with in the context of nonsmooth
analysis using the Clarke subdifferential, which can
be defined through
∂
Cl
V (x) := co{ lim
x
i
→x
∇V(x
i
) : ∃ lim
x
i
→x
∇V(x
i
)} (3)
for locally Lipschitz continuous V , cf. (Clarke, 1990).
That is, Clarke’s subdifferential ∂
Cl
V (x) ⊂ R
n
is the
convex hull of all converging sequences (∇V (x
i
))
i∈N
,
where x
i
→ x as i → ∞. The establishing of the strong
stability of an equilibrium of the differential inclusion
(2) now essentially boils down to showing, where
•
denotes the dot product of vectors and sets of vectors
N
•
M := {x
•
y : x ∈ N,y ∈ M}, that
∂
Cl
V (x)
•
F(x) < 0 (4)
in a punctuated neighbourhood of the equilibrium. In
this context < means that every element of the set on
the left-hand side is less than zero. For a CPA function
V this further simplifies to
∇V
ν
•
f
a
(x) < 0 (5)
for every ν such that x ∈ S
ν
and every a ∈ A such that
x ∈ D(f
a
). This comes as every element in ∂
Cl
V (x)
is the convex sum of such ∇V
ν
and every element of
F(x) is the convex sum of such f
a
(x). Exactly the
same condition (5) can be used to show the strong sta-
bility of the same equilibrium for the switched system
(1).
Now, even for considerably more general differ-
ential inclusions than (2), i.e. compact, convex, upper
semicontinuous F, the strong asymptotic stability of
an equilibrium was shown in (Clarke et al., 1998) to
be equivalent to the existence of a Lyapunov function
V fulfilling (4). However, there are arbitrary switched
systems with a strongly asymptotically stable equilib-
rium, such that the equilibrium is only weakly sta-
ble for the corresponding differential inclusion. We
will modify the CPA algorithm to compute Lyapunov
functions for arbitrary switched system and differen-
tial inclusions to deal with this case. Our motivating
example will be that of Artstein’s circles.
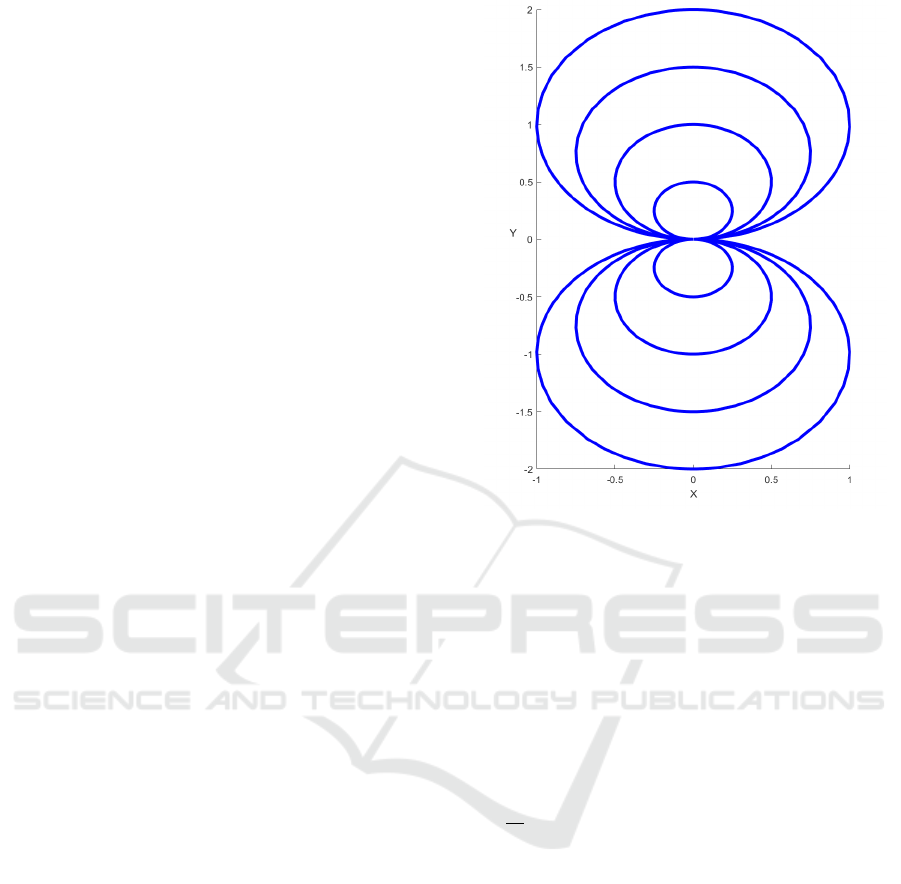
Figure 1: Trajectories of Artstein’s circles (6). For an initial
value (x
0
,y
0
) the trajectory is an arc of a circle with center
on the y-axis and passing through (0,0) and (x
0
,y
0
). Vary-
ing u changes the speed and the orientation of how the cir-
cles are traversed. For u > 0 the upper circles are traversed
clockwise and the lower circles counter-clockwise until the
equilibrium at zero is reached; for u < 0 vise versa. The
speed of the traversing is proportional to |u|.
1.1 Artsteins’s Circles
Artstein’s circles (Artstein, 1983) are given by the dif-
ferential inclusion
d
dt
x
y
∈
u
−x
2
+ y
2
−2xy
: u ∈ [−1, 1]
. (6)
See Fig. 1 for its solution trajectories. Clearly, the
equilibrium at zero is not strongly asymptotically sta-
ble for the differential inclusion, fix e.g. u = 0. How-
ever, it is clearly weakly stable because, e.g. fixing
u = −1 or u = 1, delivers an ODE with this property.
Let us define
f
+
(x,y) =
−x
2
+ y
2
2xy
(7)
and f
−
(x,y) = −f
+
(x,y). Then system (6) can be
written
˙
x ∈ co{f
−
(x),f
+
(x)} and the corresponding
switched system is
˙
x = f
α
(x), α : [0, ∞) → {−, +}, (8)
for which the origin is a weakly asymptotically stable
equilibrium, and not strongly asymptotically stable!
From now on we limit the domains of f
−
and
f
+
to D(f
−
) = (−∞,0] × R and D(f
+
) = [0,∞) × R.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
746

Then the switched system (8) has a strongly asymp-
totically stable equilibrium at the origin. The reason
for this is that the switching only has more than one
option on D(f
−
) ∩ D(f
+
) = {0} × R, and no mat-
ter which choice is made, the system state is asymp-
totically attracted to the origin. The decision only
influences whether the left- or the right trajectory
arc is traversed. Note that for the inclusion
˙
x ∈
co{f
−
(x),f
+
(x)} with these domains for f
−
(x) and
f
+
(x), the origin is weakly- but not strongly asymptot-
ically stable, because 0 ∈ co{f
−
(x),f
+
(x)} for every
x ∈ {0} × R.
It follows from the discussion above, that there
does not exists a CPA Lyapunov function V fulfilling
(5) for the switched system (8), although the equilib-
rium is strongly asymptotically stable. The condition
(5) is unnecessary strict for switched systems; it is
used to assert
limsup
h→0+
V (x + hf
a
(x)) −V (x)
h
< 0 (9)
for all f
a
such that x ∈ D(f
a
), but this may hold true
although (5) fails for some of them. To see this con-
sider two triangles, S
ν
= co{(−c, c), (0, c), (0,2c)}
and S
µ
= co{(c,c), (0, c), (0, 2c)} for c > 0, and x =
(0,3c/2) for the switched system (8). Let V be a CPA
function such that ∇V
ν
•
f
−
(x) < 0 and ∇V
µ
•
f
+
(x) < 0.
Since f
−
(x) = −f
+
(x) this implies ∇V
ν
•
f
+
(x) > 0 and
∇V
µ
•
f
−
(x) > 0, but (9) still holds true. The reason is
that f
−
(x) points into S
ν
and f
+
(x) points into S
µ
. In
our modified CPA algorithm below we systematically
remove such unnecessary constraints from the origi-
nal linear programming problem.
2 THE SETUP
For formulating our modified CPA algorithm for
switched system some preparation is needed. Let
{
S
ν
}
ν∈T
= T , T an index set, be a set of simplices
in R
n
, such that different simplices S
ν
,S
µ
∈ T inter-
sect in a common face or not at all and with D
T
=
S
ν∈T
S
ν
, D
◦
T
is a simply connected neighborhood of
the origin. The set T is the triangulation that we use
to define a CPA function V by fixing its values at the
vertices
V
T
:= {x
i
: x
i
is a vertex of a simplex S
ν
∈ T }
of the triangulation.
For each S
ν
∈ T denote by C
ν
= {x
ν
0
,x
ν
1
,...,x
ν
n
}
the set of its vertices. Thus S
ν
= coC
ν
and S
ν
∩ S
µ
=
co(C
ν
∩C
µ
). Define I
T
: R
n
⇒ T by I
T
(x) := {ν ∈
T : x ∈ S
ν
}. Thus I
T
(x) is a set of the indices of the
simplices in T containing x. The notation ⇒ denotes
a multivalued function, the values of I
T
are subsets
of T . We consider arbitrary switched systems as (1)
and corresponding differential inclusions (2) that are
adapted to the triangulation T .
For defining what adapted to the triangulation T
means some further definitions are useful: Let A be
a finite set and f
a
: D(f
a
) → R
n
be vector fields, such
that for every a ∈ A the domain D(f
a
) ⊂ R
n
of f
a
is
the union of some of the simplices in T . Thus, for
every a ∈ A we have
/
0 6= D(f
a
) = S
ν
1
∪S
ν
2
∪· ··∪ S
ν
k
,
where ν
1
,ν
2
,...,ν
k
∈ T . Define for every ν ∈ T the
set
A
ν
:= {a ∈ A : S
ν
⊂ D(f
a
)}
and assume that A
ν
6=
/
0 for all ν ∈ T . Hence, on every
simplex S
ν
∈ T at least one of the vector fields f
a
is
defined.
For a simplex S
ν
∈ T define the set
NS
ν
:= {S
µ
∈ T : S
µ
6= S
ν
and S
µ
∩ S
ν
6=
/
0}
of its neighbouring simplices in T .
Our modified CPA algorithm will eliminate un-
necessary constraints from the original linear pro-
gramming problem. For this we need to define for
every simplex S
ν
and every vector field f
a
defined on
the simplex S
ν
, i.e. every a ∈ A
ν
, the set of the essen-
tial neighbouring simplices ENS
a
ν
with respect to the
vector field f
a
. That is, ENS
a
ν
contains the simplices
S
µ
∈ NS
ν
, such that solution trajectories of
˙
x = f
a
(x)
with an initial position in x ∈ S
ν
can move into the
interior of S
µ
in an infinitesimal time. In formula, for
every S
ν
∈ T and every a ∈ A
ν
define
ENS
a
ν
:= {S
µ
∈ NS
ν
: ∃x ∈ S
ν
, ∃h > 0
s.t. x + [0,h]f
a
(x) ⊂ S
µ
},
where
x + [0,h]f
a
(x) := {x + h
0
f
a
(x) : 0 ≤ h
0
≤ h}.
Define
D
+
V (x, y) := lim sup
h→0+
V (x + hy) −V (x)
h
.
It is well known that D
+
V (x, f
a
(x) is the orbital
derivative of a locally Lipschitz V at point x along
the solution trajectories of
˙
x = f
a
(x), i.e. if t 7→ φ(t) is
the solution with φ(0) = x, then
D
+
V (x, f
a
(x)) = lim sup
h→0+
V (φ(h)) −V (x)
h
,
for a proof cf. e.g. (Marin
´
osson, 2002, Th. 1.17). Fur-
ther, CPA functions are obviously locally Lipschitz.
Lemma 2.1. For every S
µ
∈ T such that there ex-
ists an h > 0 with x + [0, h]f
a
(x) ⊂ S
µ
we have
D
+
V (x, f
a
(x)) = ∇V
µ
•
f
a
(x).
CPA Lyapunov Functions: Switched Systems vs. Differential Inclusions
747

Proof. Assume x + [0,h]f
a
(x) ⊂ S
α
∩ S
β
for two sim-
plices S
α
,S
β
∈ T . Since V is affine on both simplices
S
α
and S
β
we have for some constants a
α
,a
β
∈ R and
∇V
α
and ∇V
β
defined as above that V (y) = ∇V
α
•
y +
a
α
for all y ∈ S
α
and V (y) = ∇V
β
•
y+a
β
for all y ∈ S
β
.
In particular, we have for all y ∈ S
α
∩ S
β
that
∇V
α
•
y + a
α
= ∇V
β
•
y + a
β
.
Now substitute x + h
0
f
a
(x) for y and simplify to get
h
0
(∇V
α
− ∇V
β
)
•
f
a
(x) = a
β
− a
α
− (∇V
α
− ∇V
β
)
•
x
and note that this equation must hold true for all 0 ≤
h
0
≤ h. Since the right-hand side is constant we must
have (∇V
α
− ∇V
β
)
•
f
a
(x) = 0. The statement is now
obvious.
The next lemma justifies the nomenclature for
ENS
a
ν
: essential neighbouring simplices with respect
to the vector field f
a
Lemma 2.2. Let x ∈ D
◦
T
. Then there is a ν ∈ T such
that x ∈ S
ν
and for every a ∈ A
ν
we have
D
+
V (x, f
a
(x)) = ∇V
µ
•
f
a
(x) (10)
where µ = ν or S
µ
∈ ENS
a
ν
.
Proof. That there is a ν ∈ T such that x ∈ S
ν
follows
directly from our setup. Since simplices are convex
and closed there surely exists an h > 0 and µ ∈ T such
that x+ [0, h]f
a
(x) ⊂ S
µ
and by the definition of ENS
a
ν
necessarily S
µ
∈ ENS
a
ν
if µ 6= ν.
3 THE MODIFIED
CONSTRAINTS
We now describe how we eliminate unnecessary con-
straints from the liner programming problem in (Baier
and Hafstein, 2014). Note that this is the same linear
programming problem as for the differential inclusion
in (Baier et al., 2010; Baier et al., 2012), but when the
differential inclusion is considered, then these con-
straints are necessary. Indeed, as discussed in Sec-
tion 1.1 for Artstein’s circles, the equilibrium might
be merely weakly asymptotically stable for the differ-
ential inclusion, although it is strongly asymptotically
stable for the corresponding switched system.
The constraints to enforce ∇V
ν
•
f
a
(x) < 0 for all
x ∈ S
ν
are only verified at the vertices of the simplex
S
ν
. As a consequence one must verify ∇V
ν
•
f
a
(x
ν
i
) <
−a
i
at the vertices x
ν
i
of the simplex S
ν
for appropriate
a
i
> 0, to make sure that the inequality folds for all
x ∈ S
ν
. This motivates the following definitions.
For a set C = {x
0
,x
1
,...,x
k
} of affinely indepen-
dent vectors in R
n
and a vector field f
a
defined on coC
with components ( f
a
1
, f
a
2
,..., f
a
n
) = f
a
define
B
a
C,r,s
:= max
x∈coC
m=1,2,...,n
∂
2
f
a
m
∂x
r
∂x
s
(x)
. (11)
Further, for each (vertex) y ∈ C define
C
max
y,s
:= max
j=0,1,...,k
|e
s
•
(x
j
− y)|
and let E
a,y
C,x
i
, i = 0, 1,...,k, be constants such that
E
a,y
C,x
i
≥ (12)
1
2
n
∑
r,s=1
B
a
C,r,s
|e
r
•
(x
i
− y)|(C
max
y,s
+ |e
s
•
(x
i
− y)|).
A few comments are in order. As shown later,
the constants E
a,y
C,x
i
are defined such that if for one
fixed vertex y of the simplex S
ν
= coC
ν
∈ T , C
ν
=
{x
ν
0
,x
ν
1
,...,x
ν
n
}, we have
∇V
ν
•
f
a
(x
ν
i
) < −E
a,y
C,x
ν
i
k∇V
ν
k
1
, i = 0, 1,...,k = n,
then ∇V
ν
•
f
a
(x) < 0 for all x ∈ S
ν
.
For implementing the constraints it is of essen-
tial practical importance that E
a,y
C,x
i
is an upper bound,
which in effect means that one must not compute
the B
a
C,r,s
exactly, which can be difficult. Any upper
bound on the second order derivatives of the com-
ponents f
a
m
can be used. However, less conservative
bounds might mean that one needs smaller simplices
to fulfill the constraints.
Finally, if
E
a,y
C,x
i
≥ h
2
C
n
∑
r,s=1
B
a
C,r,s
whith h
C
= diam(C) := max
x,y∈C
kx − yk
2
, then the
estimate (12) follows. In particular one can for sim-
plicity use a uniform bound
B
a
≥ max
x∈D(f
a
)
m,r,s=1,2,...,n
∂
2
f
a
m
∂x
r
∂x
s
(x)
and set E
a,y
C,x
ν
i
= n
2
B
a
h
2
ν
, where h
ν
:= diam(S
ν
), for
/
0 6= C ⊂ C
ν
. Indeed, a little more careful analysis us-
ing that kxk
2
1
≤ nkxk
2
2
shows that using
E
a,y
C,x
ν
i
= nB
a
h
2
ν
is enough to fulfill the estimate (12), cf. e.g. (Baier
et al., 2012). However, although this more conserva-
tive formula is more pleasant to the eye, the imple-
mentation of (12) is not more involved in practice.
We therefore use the sharper estimate (12) in what
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
748

follows. Note, however, that in order to understand
the linear programming problems very little is lost if
one just considers the E
a,y
C,x
ν
i
as appropriate constants
needed to interpolate inequality conditions from ver-
tices over simplices and faces and of simplices, with-
out following the details. Computing the E
a,y
C,x
ν
i
al-
gorithmically is simple given some upper bounds on
the second order derivatives of the components of the
vector fields f
a
.
We are now ready to state our linear programming
problem to compute CPA Lyapunov functions. We
first state it as in (Baier et al., 2010; Baier et al., 2012)
and then outline a proof of why a feasible solution to it
delivers a CPA Lyapunov function for the differential
inclusion used in its construction. From the proof it
becomes clear what conditions are unnecessary when
we move from the differential inclusion (2) to the ar-
bitrary switched system (1). In Section 3.2 we then
discuss how the removing of constraints can be algo-
rithmically implemented.
3.1 The Linear Programming Problem
Consider a triangulation T as in Section 2 and,
adapted to the triangulation, the differential inclusion
(2) and the corresponding arbitrary switched system
(1). Assume that the equilibrium in question is at the
origin. For every simplex S
ν
∈ T let
C
ν
= {x
ν
0
,x
ν
1
,...,x
ν
n
}
denote its vertices, i.e. S
ν
= coC
ν
. Assume that for
every S
ν
= coC
ν
∈ T and every
/
0 6= C ⊂C
ν
and every
a ∈ A
ν
we have an upper bound B
a
C,r,s
as in (11) and
that we have fixed a vertex y of C for the definition
of E
a,y
C,x
i
. If 0 ∈ C we must choose y = 0 to avoid un-
satisfiable constraints. Note that the sets coC, where
/
0 6= C ( C
ν
, are the faces of the simplex S
ν
.
The variables of the linear programming problem
are V
x
for every x that is a vertex of a simplex in T ,
i.e. x ∈ V
T
. From a feasible solution, where the vari-
ables V
x
have been assigned values such that the lin-
ear constraints below are fulfilled, we then define a
continuous function V : D
T
→ R through parameteri-
zation using these values: for an x ∈ D
T
we can find a
simplex S
ν
= co{x
ν
0
,x
ν
1
,...,x
ν
n
} such that x ∈ S
ν
and x
has a unique representation x =
∑
n
i=0
λ
i
x
ν
i
as a convex
sum of the vertices. For x we define
V (x) :=
n
∑
i=0
λ
i
V
x
ν
i
.
If two different simplices in T intersect they do so in
a common face, hence V is well-defined and continu-
ous. By a slight abuse of notation we both write V (x
ν
i
)
for the variable V
x
ν
i
of the linear programming prob-
lem and the value of the function V at x
ν
i
, since after
we have assigned a numerical value to the former it is
the value of the function V at x
ν
i
.
There are two groups of constrains in the linear
programming problem. The first group is to assert
that V has a minimum at the origin:
Linear Constraints L1
If 0 ∈ V
T
one sets V (0) = 0. Then for all x ∈ V
T
:
V (x) ≥ kxk
2
.
Another possibility is to relax the condition of
strong asymptotic stability of the origin to practical
strong asymptotic stability. In this case one prede-
fines an arbitrary small neighbourhood of the origin
N and does not demand that V is decreasing along
solution trajectories in this set. One must then make
sure through constraints that
max
x∈∂N
V (x) < min
x∈∂D
T
V (x),
because sublevel sets of V that are closed in D
◦
T
are
lower bounds on the basin of attraction. This is not
difficult to implements and is discussed in detail in
e.g. (Hafstein, 2004; Hafstein, 2007; Baier et al.,
2012; Hafstein et al., 2015). In short, the implica-
tions of such a Lyapunov function are that solutions
enter N in a finite time and either stay in N or stay
close and enter it repeatedly.
The second group of linear constraints is to assert
that V is decreasing along all solution trajectories.
The simplest case is when A
ν
= A for all ν ∈ T and
then the appropriate constraints are:
Linear Constraints L2 (Simplest Case)
For every S
ν
∈ T , we demand for every a ∈ A
ν
and
i = 0, 1,...,n that:
∇V
ν
•
f
a
(x
ν
i
) + k∇V
ν
k
1
E
a,y
C
ν
,x
ν
i
≤ −kx
ν
i
k
2
. (13)
In the case of practical strong asymptotic stabil-
ity one disregards the constraints (13) for S
ν
⊂ N .
Note that the constrains (13) are linear in the vari-
ables V (x
ν
i
), cf. e.g. (Giesl and Hafstein, 2014, Re-
marks 9 and 10), in particular k∇V
ν
k
1
can be mod-
elled through linear constraint using auxiliary vari-
ables.
Now, let us consider how one uses the con-
straints (13) to show that D
+
V (x, f
a
(x)) ≤ −kxk
2
. By
(Marin
´
osson, 2002, Lemma 4.16) we have for a ∈ A
ν
and x =
∑
n
i=0
λ
i
x
ν
i
∈ S
ν
,
∑
n
i=0
λ
i
= 1, that
f
a
(x) −
n
∑
i=0
λ
i
f
a
(x
ν
i
)
∞
≤
n
∑
i=0
λ
i
E
a,y
C
ν
,x
ν
i
. (14)
CPA Lyapunov Functions: Switched Systems vs. Differential Inclusions
749

Hence, H
¨
older inequality, constraints (13), and the
convexity of the norm imply that
∇V
ν
•
f
a
(x) = (15)
n
∑
i=0
λ
i
∇V
ν
•
f
a
(x
ν
i
) + ∇V
ν
•
"
f
a
(x) −
n
∑
i=0
λ
i
f
a
(x
ν
i
)
#
≤
n
∑
i=0
λ
i
∇V
ν
•
f
a
(x
ν
i
) + k∇V
ν
k
1
·
n
∑
i=0
λ
i
E
a,y
C
ν
,x
ν
i
=
n
∑
i=0
λ
i
∇V
ν
•
f
a
(x
ν
i
) + k∇V
ν
k
1
E
a,y
C
ν
,x
ν
i
≤
n
∑
i=0
λ
i
(−kx
ν
i
k
2
) ≤ −k
n
∑
i=0
λ
i
x
ν
i
k
2
= −kxk
2
.
For an x ∈ S
◦
ν
we have the existence of an h > 0 such
that x + h
0
f
a
(x) ⊂ S
ν
for all 0 ≤ h
0
≤ h and we get by
Lemma 2.2 that
D
+
V (f
a
(x),x) = ∇V
ν
•
f
a
(x) ≤ −kxk
2
for all a ∈ A
ν
. For an x ∈ ∂S
ν
we cannot con-
clude this in general, because is is possible that x +
[0,h]f
a
(x) 6⊂ S
ν
for any h > 0 and we need the con-
straints (13) to hold true with ν = µ, where S
µ
is such
that x + [0,h]f
a
(x) ⊂ S
µ
for some h > 0. Note that if
a ∈ A
µ
then this is assured, therefore nothing can go
wrong if A
µ
= A for all µ ∈ T .
In (Baier et al., 2010; Baier et al., 2012) the
general case, when A
µ
6= A for some µ ∈ T , was dealt
with by adding the constraints:
Linear Constraints L2 (Old)
For every S
ν
= coC
ν
∈ T we demand for every a ∈
A
ν
, in addition to the constraints (13), that for every
S
µ
∈ NS
a
ν
such that a /∈ A
µ
we have for C = C
µ
∩C
ν
=
{x
0
,x
1
,...,x
k
} that:
∇V
µ
•
f
a
(x
i
) + k∇V
µ
k
1
E
a,y
C,x
i
≤ −kx
i
k
2
(16)
for i = 0, 1,...,k.
Note that the linear constraints (16) imply by com-
putations analog to (15) that ∇V
µ
•
f
a
(x) ≤ −kxk
2
for
every x ∈ D(f
a
), even if a /∈ A
µ
, i.e. S
µ
6⊂ D(f
a
) and
f
a
is only defined on a face of S
µ
. Just substitute n,
∇V
ν
, x
ν
i
, E
a,y
C
ν
,x
ν
i
with k, ∇V
µ
, x
i
, E
a,y
C,x
i
, respectively, in
the computations (15).
For the differential inclusion (2) these constraints
is indeed necessary to show strong asymptotic stabil-
ity of the equilibrium at the origin, or strong practical
asymptotic stability of a set N , because for a CPA
function V we have
∂
Cl
V (x) := co{∇V
µ
: x ∈ S
µ
}
and
F(x) = co{f
a
(x) : x ∈ D(f
a
(x))}.
Hence ∂
Cl
V (x)
•
F(x) ⊂ R consists of the elements
∑
µ:x∈S
µ
α
µ
∇V
µ
!
•
∑
a:x∈D(f
a
)
β
a
f
a
(x)
!
=
∑
µ: x∈S
µ
a: x∈D(f
a
)
α
µ
β
a
∇V
µ
•
f
a
(x),
for all α
µ
,β
a
≥ 0 fulfilling
∑
µ:x∈S
µ
α
µ
=
∑
a:x∈D(f
a
(x))
β
a
= 1.
In the case S
ν
⊂ D(f
a
), S
µ
6⊂ D(f
a
), and x ∈ S
ν
∩ S
µ
,
we have S
µ
∈ NS
a
ν
and the constraints (16) assure that
∇V
µ
•
f
a
(x) < −kxk
2
.
However, by Lemma 2.2, we can conclude
D
+
V (f
a
(x),x) ≤ −kxk
2
if the constraints (13) hold
for all essential neighbours S
µ
∈ ENS
a
ν
of S
ν
with
respect to the vector field f
a
. We do not need to
consider neighbouring simplices S
µ
∈ NS
a
ν
that are
not essential! The modified constraints are :
New Linear Constraints L2
For every S
ν
= coC
ν
∈ T we demand for every a ∈
A
ν
, in addition to the constraints (13), that for every
S
µ
∈ ENS
a
ν
such that a /∈ A
µ
we have for C = C
µ
∩C
ν
=
{x
0
,x
1
,...,x
k
} that:
∇V
µ
•
f
a
(x
i
) + k∇V
µ
k
1
E
a,y
C,x
i
≤ −kx
i
k
2
(17)
for i = 0, 1,...,k.
Note that the only difference between the old con-
straints and the new ones is that NS
a
ν
in the old ones
has been replaced by ENS
a
ν
in the new ones.
For algorithmically implementing the new con-
straints we need to be able to generate the sets ENS
a
ν
efficiently. In practice we can efficiently compute sets
(ENS
a
ν
)
∗
,
NS
a
ν
⊂ (ENS
a
ν
)
∗
⊂ ENS
a
ν
,
using some of the same ideas as in the computa-
tions (15). The practical implementation of New lin-
ear constraints L2 is then done by using these sets
(ENS
a
ν
)
∗
instead of the sets ENS
a
ν
. We describe the
details of how to compute the sets (ENS
a
ν
)
∗
in the next
section.
3.2 Computing Essential Neighbours
Consider a simplex S
ν
= coC
ν
∈ T , where as before
C
ν
=
x
ν
0
,x
ν
1
,...,x
ν
n
. Another way to describe the
simplex S
ν
is to define it as the intersection of n + 1
half-spaces. Recall that a half-space is defined as {x ∈
R
n
: n
•
(x−y) ≥ 0} for some vectors n,y ∈ R
n
, n 6= 0.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
750
These half-spaces for S
ν
can be constructed using the
set C
ν
as follows, see also (Hafstein, 2017).
For i = 0,1, . . .,n we construct a half-space H
ν,x
ν
i
such that S
ν
⊂ H
ν,x
ν
i
and C
ν
\ {x
ν
i
} is a subset of the
boundary ∂H
ν,x
ν
i
of H
ν,x
ν
i
in the following way:
Set y
n
:= x
ν
i
and pick an arbitrary, but fixed vector
y
0
∈ C
ν
\ {x
ν
i
}. Let {y
1
,y
2
,...,y
n−1
} = C
ν
\ {y
0
,y
n
}
and define the matrix n × n matrix
Y
ν,x
ν
i
:= (y
1
− y
0
,y
2
− y
0
,...,y
n
− y
0
)
T
.
That is, the first row in the matrix Y
ν,x
ν
i
is the vector
y
1
− y
0
, the second row is the vector y
2
− y
0
, etc.
Because the vectors y
0
,y
1
,...,y
n
are affinely in-
dependent the matrix Y
ν,x
ν
i
is non-singular and the
equation
Y
ν,x
ν
i
y = e
n
,
where e
n
is the usual n-th unit basis vector, has a
unique solution n
ν,x
ν
i
for y. Define the half-space
H
ν,x
ν
i
:= {x ∈ R
n
: n
ν,x
ν
i
•
(x − y
0
) ≥ 0}. (18)
Note that H
ν,x
ν
i
is a half-space such that S
ν
⊂ H
ν,x
ν
i
and the vertices y
1
,y
2
,...,y
n−1
of the simplex S
ν
, and
hence the face co(C
ν
\ {x
ν
i
}), are in the hyper-plane
∂H
ν,x
ν
i
dividing the space. This can be seen from
n
ν,x
ν
i
= Y
−1
ν,x
ν
i
e
n
and then, since
n
ν,x
ν
i
•
(x − y
0
) = e
T
n
Y
−T
ν,x
ν
i
(x − y
0
),
where Y
−T
ν,x
ν
i
:=
Y
−1
ν,x
ν
i
T
, and Y
−T
ν,x
ν
i
(x − y
0
) = e
k
for
x = y
k
, k = 1, 2, . ..,n, we have n
ν,x
ν
i
•
(y
k
− y
0
) = 0 if
k = 1, 2, . . . ,n − 1 and n
ν,x
ν
i
•
(y
n
− y
0
) = 1.
Every point x ∈ S
ν
can be written uniquely as a
convex combination x =
∑
n
k=0
λ
k
y
k
and thus
x − y
0
=
n
∑
k=0
λ
k
(y
k
− y
0
).
Hence,
n
ν,x
ν
i
•
(x − y
0
) = λ
n
,
from which the propositions follow. Using these re-
sults it is easily verified that
S
ν
=
n
\
i=0
H
ν,x
ν
i
. (19)
We now use this to compute a set (ENS
a
ν
)
∗
such
that ENS
a
ν
⊂ (ENS
a
ν
)
∗
⊂ NS
a
ν
. Fix an S
µ
∈ NS
a
ν
and
let
{z
1
,z
2
,...,z
r
} = C
ν
∩C
µ
and
{y
1
,y
2
,...,y
s
} = C
µ
\C
ν
.
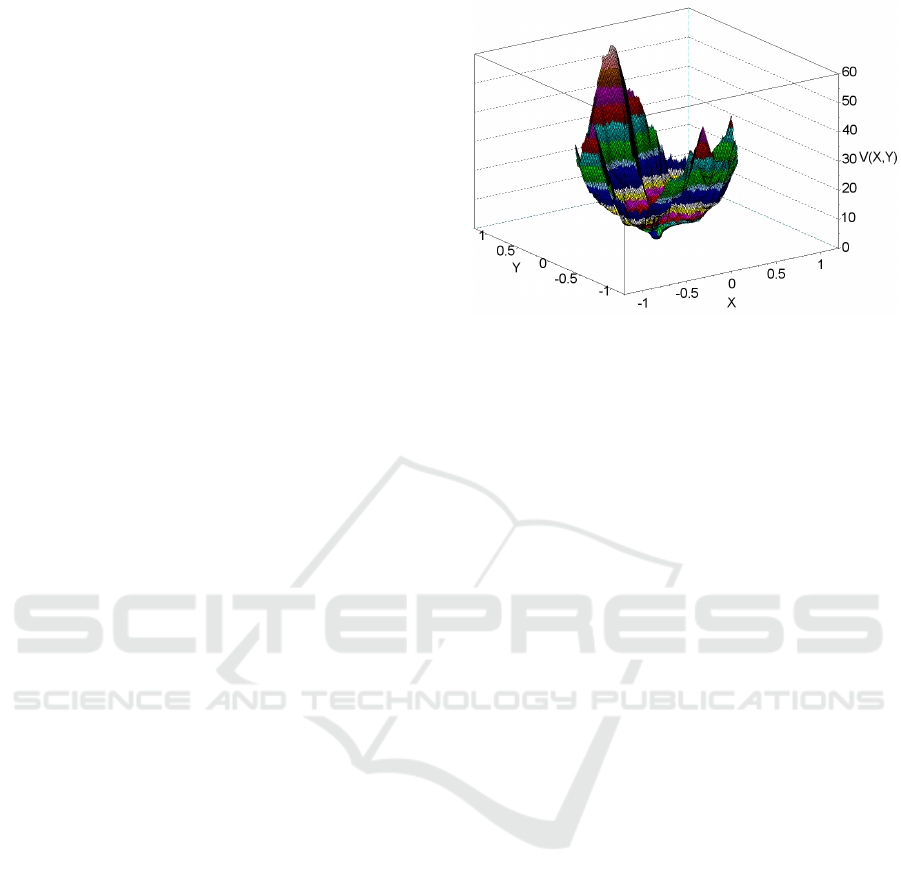
Figure 2: Continuous piecewise affine Lyapunov function
computed for Artstein’s circles with the new algorithm.
Corresponding to the half-spaces H
µ,y
j
are the vectors
n
µ,y
j
computed as above, but now for the simplex S
µ
and its vertices C
µ
⊃ {y
1
,y
2
,...,y
s
}. Assume that for
any j ∈ {1, 2, . ..,s} we have
0 > n
µ,y
j
•
f
a
(z
i
) + E
a,y
C
ν
∩C
µ
,z
i
kn
µ,y
j
k
1
(20)
for all i = 1, 2,...,r. Then, for an arbitrary convex
combination x =
∑
r
i=1
λ
i
z
i
, we have
n
µ,y
j
•
f
a
(x) =
r
∑
i=1
n
µ,y
j
•
λ
i
f
a
(z
i
)
+ n
µ,y
j
•
f
a
(x) −
r
∑
i=1
λ
i
f
a
(z
i
)
!
≤
r
∑
i=1
λ
i
n
µ,y
j
•
f
a
(z
i
) + E
a,y
C
ν
∩C
µ
,z
i
kn
µ,y
j
k
1
< 0.
In particular, because n
µ,y
j
•
(x − z
k
) = 0 as shown
above, where z
k
∈ C
ν
∩C
µ
corresponds to the vector
y
0
in (18), we have
n
µ,y
j
•
(hf
a
(x) + x − z
k
) = h
n
µ,y
j
•
f
a
(x)
< 0
for all h > 0. Hence, hf
a
(x)+ x /∈ H
µ,y
j
for any h > 0,
which, by (19), implies hf
a
(x) + x /∈ S
µ
for any h > 0.
Thus S
µ
/∈ ENS
a
ν
.
For each a ∈ A
ν
we define (ENS
a
ν
)
∗
as those S
µ
∈
NS
ν
that are not eliminated by this process. That is,
S
µ
∈ (ENS
a
ν
)
∗
if for all j = 1,2,..., s the inequality
(20) fails to hold true for at least one i ∈ {1,2,...,r}.
Note that this is easily checked algorithmically. For a
visual illustration of the sets (ENS
a
ν
)
∗
see Fig. 3.
Returning to our example of Artstein’s circles,
this new algorithm easily generates a CPA Lyapunov
function for the system (8) in a few seconds after the
domains of f
+
and f
−
have been fixed as D(f
−
) =
(−∞,0]× R and D(f
+
) = [0, ∞) × R, see Fig. 2. With
CPA Lyapunov Functions: Switched Systems vs. Differential Inclusions
751
Figure 3: The simplex S
ν
is the convex combination of the 3 = n+1 vertices 1,3,4, i.e. S
ν
= co{1,3, 4}, and S
µ
1
= co{3,4, 6},
and S
µ
2
= co{2,3, 5}. Clearly {S
µ
1
,S
µ
2
} ⊂ NS
ν
. We consider three constant f
a
(x) on S
ν
: f
1
(x) =
*
a , f
2
(x) =
*
b, and f
3
(x) =
*
c ;
depicted by arrows. Since the vector fields are constant the sets ENS
a
ν
and (ENS
a
ν
)
∗
coincide. Now S
ν
∩ S
µ
1
= co{3, 4} and
the half-space H
µ
1
,6
, with co{3,4} at its boundary and containing S
µ
1
, is depicted in blue. We have S
µ
1
∈ (ENS
1
ν
)
∗
because
f
1
(x) =
*
a points into H
µ
1
,6
for (some) x ∈ co{3, 4} but S
µ
1
/∈ (ENS
a
ν
)
∗
for a = 2, 3 because f
2
(x) =
*
b and f
3
(x) =
*
c do not
point into H
µ
1
,6
for any x ∈ co{3,4}. Similarly, S
ν
∩ S
µ
2
= {3} and the (n − 1)-faces co{2,3} and co{3, 5} of S
µ
2
contain
S
ν
∩ S
µ
2
. The half-spaces H
µ
2
,5
(blue) and H
µ
2
,2
(red) are supersets of S
µ
2
and with co{2, 3} and co{3,5} at their boundaries,
respectively, are depicted. Now S
µ
2
∈ (ENS
1
ν
)
∗
because f
1
(x) = a points into both H
µ
2
,5
(blue) and H
µ
2
,2
for x at the vertex 3,
but S
µ
2
/∈ (ENS
2
ν
)
∗
because f
2
(x) =
*
b does not point into H
µ
2
,5
and S
µ
2
/∈ (ENS
3
ν
)
∗
because f
2
(x) =
*
c does neither point into
H
µ
2
,5
nor H
µ
2
,2
.
the old algorithm or when D(f
+
) = D(f
−
) = R
2
no
such CPA Lyapunov function exists and the algo-
rithm reports that the corresponding linear program-
ming problem is infeasible.
4 CONCLUSIONS
We presented a novel algorithm that uses linear pro-
gramming to parameterize continuous and piecewise
affine Lyapunov functions asserting strong asymp-
totic stability of equilibria for arbitrary switched sys-
tems, for which the same equilibria of the correspond-
ing differential inclusion is merely weakly asymptot-
ically stable. For the differential inclusion no such
Lyapunov function can exists. This algorithm is an
adaptation of an earlier algorithm for differential in-
clusions presented in (Baier et al., 2010; Baier et al.,
2012; Baier and Hafstein, 2014). Artstein’s circles
were studied and used as motivation for the new ap-
proach in the paper.
ACKNOWLEDGEMENT
The research done for this paper was partially sup-
ported by the Icelandic Research Fund (Rann
´
ıs) grant
number 163074-052, Complete Lyapunov functions:
Efficient numerical computation, which is gratefully
acknowledged.
REFERENCES
Artstein, Z. (1983). Stabilization with relaxed controls.
Nonlinear Anal. Theory Methods Appl., 7(11):1163–
1173.
Baier, R., Braun, P., Gr
¨
une, L., and Kellett, C. (2018).
Large-Scale and Distributed Optimization, chapter
Numerical Construction of Nonsmooth Control Lya-
punov Functions, pages 343–373. Number 2227 in
Lecture Notes in Mathematics. Springer.
Baier, R., Gr
¨
une, L., and Hafstein, S. (2010). Computing
Lyapunov functions for strongly asymptotically stable
differential inclusions. In IFAC Proceedings Volumes:
Proceedings of the 8th IFAC Symposium on Nonlinear
Control Systems (NOLCOS), volume 43, pages 1098–
1103.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
752

Baier, R., Gr
¨
une, L., and Hafstein, S. (2012). Linear pro-
gramming based Lyapunov function computation for
differential inclusions. Discrete Contin. Dyn. Syst. Ser.
B, 17(1):33–56.
Baier, R. and Hafstein, S. (2014). Numerical computation
of Control Lyapunov Functions in the sense of gen-
eralized gradients. In Proceedings of the 21st Inter-
national Symposium on Mathematical Theory of Net-
works and Systems (MTNS), pages 1173–1180 (no.
0232), Groningen, The Netherlands.
Clarke, F. (1990). Optimization and Nonsmooth Analysis.
Classics in Applied Mathematics. SIAM.
Clarke, F., Ledyaev, Y., and Stern, R. (1998). Asymptotic
stability and smooth Lyapunov functions. J. Differen-
tial Equations, 149:69–114.
Giesl, P. and Hafstein, S. (2014). Revised CPA method to
compute Lyapunov functions for nonlinear systems. J.
Math. Anal. Appl., 410:292–306.
Hafstein, S. (2004). A constructive converse Lyapunov the-
orem on exponential stability. Discrete Contin. Dyn.
Syst. - Series A, 10(3):657–678.
Hafstein, S. (2007). An algorithm for constructing Lya-
punov functions, volume 8 of Monograph. Electron.
J. Diff. Eqns. (monograph series).
Hafstein, S. (2017). Efficient algorithms for simplicial com-
plexes used in the computation of Lyapunov func-
tions for nonlinear systems. In Proceedings of the
7th International Conference on Simulation and Mod-
eling Methodologies, Technologies and Applications
(SIMULTECH), pages 398–409.
Hafstein, S., Kellett, C., and Li, H. (2015). Computing con-
tinuous and piecewise affine Lyapunov functions for
nonlinear systems. Journal of Computational Dynam-
ics, 2(2):227 – 246.
Liberzon, D. (2003). Switching in systems and control.
Systems & Control: Foundations & Applications.
Birkh
¨
auser.
Marin
´
osson, S. (2002). Stability Analysis of Nonlin-
ear Systems with Linear Programming: A Lyapunov
Functions Based Approach. PhD thesis: Gerhard-
Mercator-University Duisburg, Duisburg, Germany.
Sun, Z. and Ge, S. (2011). Stability Theory of Switched Dy-
namical Systems. Communications and Control Engi-
neering. Springer.
CPA Lyapunov Functions: Switched Systems vs. Differential Inclusions
753
