
Address-bit Differential Power Analysis on Boolean Split Exponent
Counter-measure
Christophe Negre
1,2
1
DALI, Universit
´
e de Perpignan, France
2
LIRMM, Universit
´
e de Montpellier et CNRS, France
Keywords:
Side Channel Analysis, Address Bit Differential Power Analysis, Exponentiation, Randomization.
Abstract:
Current public key cryptographic algorithms (RSA, DSA, ECDSA) can be threaten by side channel analyses.
The main approach to counter-act such attacks consists in randomizing sensitive data and address bits used in
loads and stores of an exponentiation algorithm. In this paper we study a recent counter-measure ”Boolean
split exponent” (Tunstall et al. 2018) preventing differential power analysis on address bits. We show that one
of their proposed protections has a flaw. We derive an attack exploiting this flaw and we successfully apply it
on a simulated power consumption of an RSA modular exponentiation.
1 INTRODUCTION
Side channel analysis is a serious threat for devices
performing cryptographic computation. Specifically,
it can threaten exponentiation x
κ
involved in cur-
rently used cryptosystems (RSA, DSA and ECDSA).
In 1996, in a seminal work (Kocher, 1996) Kocher
showed that a statistical analysis of the computation
time can leak out the secret key used in RSA cryp-
tosystem. Afterwards, it was shown that the power
consumption can be used to extract secret informa-
tion: with simple power analysis (SPA) (Kocher et al.,
1999) one can read on the power trace the sequence of
operations (squaring/multiplication) performed dur-
ing an exponentiation and then deduce the secret ex-
ponent. In (Kocher et al., 1999) the authors introduce
the differential power analysis (DPA) which computes
differences on the power traces to determine the bits
of the key.
To counter-act these side channel analyses, the ba-
sic approach is to randomly mask sensitive data: we
can blind the point x by multiplying it by a random
element (Coron, 1999) or use randomized represen-
tation (Clavier et al., 2010), and we can use addi-
tive or multiplicative mask of the exponent (Coron,
1999; Tunstall and Joye, 2010). But this is not al-
ways sufficient, since it was shown (Itoh et al., 2003)
that the loads and stores performed during the expo-
nentiation induce a power consumption correlated to
the corresponding address bits. This can be exploited
to mount a differential power analysis on the address
bits (ADPA). Recently some strategies (Izumi et al.,
2010; Tunstall et al., 2018) were proposed to counter-
act this attack by randomizing the address bits used in
the loads and stores of the exponentiation algorithm.
Contribution. In this paper we analyse a poten-
tial flaw in the signed version of the boolean exponent
splitting approach of (Tunstall et al., 2018). We show
that the sequence of operations (squarings and multi-
plications) are not fully regular: we show that if we
can distinguish a squaring from a multiplication we
can deduce the bit used to randomize the address bits.
Then a classical differential power analysis on the ad-
dress bits can be performed to determine the secret ex-
ponent. We validate this attack by simulating power
traces based on the Hamming weight model. We pro-
vide a method for distinguishing a squaring from a
multiplication which has a high level of confidence.
Then we show that an ADPA attack can be performed
and successfully deduce the secret exponent with a
few thousand power traces.
Organization of the Paper. In Section 2 we review
power analyses on exponentiation algorithm and re-
lated counter-measures. In Section 3 we show that
there is a flaw in the counter-measures “boolean split-
ting exponent” of (Tunstall et al., 2018). In Section 4
we present our approach for power consumption sim-
ulation of modular exponentiation, and we apply an
attack on the “boolean splitting exponent” exploiting
the flaw shown in Section 3. We ends the paper in
Section 5, with a few concluding remarks.
632
Negre, C.
Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure.
DOI: 10.5220/0009891306320637
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 632-637
ISBN: 978-989-758-446-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 REVIEW OF POWER
ANALYSES
In currently used public key cryptosystems (e.g. RSA,
DSA, ECDSA), the sensitive operation is an exponen-
tiation x
κ
for x ∈ G a finite group or ring and κ a
secret exponent. With the square-and-multiply algo-
rithm one can compute x
κ
as a sequence of squarings
R ← R
2
followed by a multiplication g ← g × x when
the i-th bit κ
i
= 1. This basic approach is not secure
when considering side channel analysis. For exam-
ple, if we monitor the power consumption of an ex-
ponentiation, then, a simple power analysis (Kocher
et al., 1999) can identify on the trace the operations
performed (square or multiplication) on the device
and then deduce the secret exponent κ. To counter-
act this attack modified versions of the square-and-
multiply exponentiation are recommended for which
the sequence of computed operations is not related to
bits of the exponent κ. The most popular method is
the Montgomery ladder (Joye and Yen, 2002) which
involves two variables R
0
and R
1
, for which, during
the exponentiation, we always have R
1
= xR
0
and the
loop iteration is always a multiplication followed by
a squaring (cf. Algorithm 1).
Algorithm 1: Montgomery-ladder.
Require: x ∈ G, one n-bit integers κ =
∑
n−1
i=0
κ
i
2
i
Ensure: x
κ
1: R
0
← 1
G
; R
1
← x;
2: for i = n − 1 down to 0 do
3: R
1−κ
i
← R
κ
i
· R
¬κ
i
;
4: R
κ
i
← R
2
κ
i
;
5: return R
0
The Montgomery ladder is a good protection
against SPA, but it is not robust against attack like dif-
ferential power analysis (DPA) (Kocher et al., 1999),
collision attack (Fouque and Valette, 2003; Yen et al.,
2006). Indeed these attacks guess one or several bits
of the key and they predict the power consumption
at some iteration of the exponentation. If this predic-
tion is correct this means that the guessed bits are also
correct otherwise one can try another guess. To coun-
teract such attacks at the algorithmic level, the best
approaches randomize data in order to render power
consumption unpredictable:
• Point blinding. The strategy here is to hide the
data x and R
0
,R
1
by either multiplying x by a
random element (Coron, 1999), adding a ran-
dom mask or by randomizing the representation
of x (Clavier et al., 2010).
• Exponent masking. In this case we randomly
modify the exponent. (Coron, 1999) proposed to
add to κ a random mutiple r ×N where N is the or-
der of G. One can also (Tunstall and Joye, 2010)
randomize the exponent as κ
0
= β
−1
κ mod N and
compute x
κ
as (x
β
)
κ
0
.
Point blinding and Exponent masking counter-
measures induce an overhead which, for the later, is
important since the level of randomization have to be
larger than the longest run of 0 or 1 in κ (Smart et al.,
2008).
Point blinding approaches used alone are not suf-
ficient to counter-act DPA attack on the address bits
(ADPA (Itoh et al., 2003)). Indeed guessing a few key
bits leads to a prediction of the address bits involved
in the loads and stores performed during the expo-
nentiation. Predicting these address bits, leads to pre-
dicting the behavior of the power consumption dur-
ing the loads or stores and performing a DPA on sev-
eral power traces validates the guessed key bit or not.
Since point blinding counter-measures do not modify
the sequence of operations done during the exponen-
tiation, they do not protect the implementation from
an ADPA.
Consequently, to counter-act such DPA on address
bits, the authors in (Izumi et al., 2010) proposed a first
version of the Montgomery-ladder which randomizes
the loads and stores. This work was subsequently im-
proved in (Tunstall et al., 2018) which provides two
kinds of randomized Montgomery-ladder. In their
first approach they use one random bit a
i
to split the
key bit κ
i
= a
i
⊕ b
i
and which decides the order of
loads R
0
and R
1
for the multiplication R
0
×R
1
in Step
3 of Algorithm 1. This bit a
i
is also used to randomly
store the results of the squaring in Step 4 and the mul-
tiplication in Step 3 of Algorithm 1 done in one itera-
tion of the Montgomery ladder. This requires a bit b
0
which memorizes how the value are stored in the two
registers R
0
and R
1
at the end of a loop iteration. This
approach is shown in Algorithm 2.
Algorithm 2: Montgomery-Ladder with XOR split exponent
I (Tunstall et al., 2018).
Require: x ∈ G, two n-bit integers A =
∑
n−1
i=0
a
i
2
i
and
B =
∑
n−1
i=0
a
i
2
i
Ensure: x
κ
where κ = A ⊕ B
1: R
0
← 1
G
; R
1
← 1
G
; R
2
← 1
G
; b
0
←
R
{0,1};
R
¬b
0
← x;
2: for i = n − 1 down to 0 do
3: R
2
← R
a
i
· R
¬a
i
;
4: R
a
i
← R
2
(b
i
⊕b
0
)⊕a
i
;
5: R
¬a
i
← R
2
;
6: b
0
← b
i
;
7: return R
b
0
Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure
633

The authors in (Tunstall et al., 2018) propose a
second approach (Algorithm 3) which randomizes the
signed version of the Montgomery ladder. This algo-
rithm perform the exponentiation as a sequence of two
multiplications one between R
0
and R
1
and between
R
0
and either U
0
= x or U
1
= x
−1
. In Algorithm 3 the
addresses used in the store instructions are fixed and
then they are not correlated to the bits of the expo-
nent. The random bit a
i
(and thus b
i
= κ
i
⊕a
i
) is used
to randomize the load instructions in Step 4 and Step
5. The bit b
0
is used to memorize how the data are
placed in the registers R
0
and R
1
at the end of a loop
iteration.
Algorithm 3: Montgomery-Ladder with XOR split exponent
II (Tunstall et al., 2018).
Require: x ∈ G, two n-bit integers A =
∑
n−1
i=0
a
i
2
i
and
B =
∑
n−1
i=0
a
i
2
i
Ensure: x
κ
where κ = A ⊕ B
1: R
0
← 1
G
; R
1
← 1
G
; R
2
← 1
G
; b
0
←
R
{0,1};
R
¬b
0
← x;
2: for i = n − 1 down to 0 do
3: R
0
← R
b
i
⊕b
0
· R
(b
i
⊕b
0
)⊕a
i
;
4: R
1
← R
0
·U
b
i
;
5: b
0
← b
i
;
6: return R
b
0
3 WEAKNESSES OF BOOLEAN
SPLIT RANDOMIZATION
In (Tunstall et al., 2018) the authors claim that their
algorithm combined with a point blinding technique
has the same security level but with a lower cost as the
method based on randomizing the exponent (Coron,
1999; Tunstall and Joye, 2010). For Algorithm 2
and 3, this is not entirely true:
• Randomizing the exponent alone prevents from
the three attacks : DPA, collision and ADPA. This
approach ensure that the sequence of points R
0,i
and R
1,i
in G for i = n − 1, . . . , 0 computed dur-
ing the exponentiation are always different. This
renders impossible to predict the power consump-
tion of operation involving R
0,i
and R
1,i
and then
prevents DPA and collision attack. Randomizing
the exponent also randomly changes the bits of the
exponent, which implies that the stores and loads
are also randomized and thus unpredictable.
• Randomizing the loads and stores like it is done in
Algorithm 2 and 3 does not modify the sequence
of computed element R
0,i
and R
1,i
of G. So a cor-
rect guess of the bits of the exponent would lead
to a correct guess of R
0
and R
1
at the considered
iteration. So if we want to hide these values we
have to inject a high level of randomization oth-
erwise a small amount of leakage could be ex-
ploited and would lead to a successful DPA. The
only approach which produces a randomized and
unpredictable sequence of computed points R
0,i
and R
1,i
in the exponentiation is the point blinding
of (Coron, 1999) which multiplies x by a random
value.
The table below summarizes the strength of the
counter measures reviewed in Section 2 when they are
used alone. This table shows that exponent random-
izations are the most robust methods.
Table 1.
Counter-measure DPA and CA ADPA
Point blinding yes no
Exponent randomization yes yes
Address randomization no yes
Algorithm 3 has a more important flaw. The main
problem of Algorithm 3 is that in Step 3, a multipli-
cation of two different data R
0
and R
1
is done when
a
i
= 1 but when a
i
= 0 this multiplication is either
R
0
× R
0
or R
1
× R
1
, which are squarings done us-
ing a multiplication routine. But distinguishig such a
squaring done with multiplication routine from a gen-
uine multiplication can be detected by power analysis.
In (Hanley et al., 2011) the authors showed that the
power consumption of these operations can be distin-
guished using template methodology.
If we successfully distinguish the power trace of
R
0
× R
1
from either R
1
× R
1
or R
0
× R
0
, for unknown
R
0
and R
1
, we can deduce the value of a
i
for i = n −
1,...,0. Then the randomization of loads and stores
is broken and DPA can be conducted on the address
bits of Algorithm 3.
4 EXPERIMENTATION
In this section we present experimental results of the
proposed attack on address randomization of Algo-
rithm 3. The attack is performed on a simulated power
traces using the hamming weight leakage model.
4.1 Simulation of Power Consumption
We target an RSA modular exponentiation with an
RSA modulus N of bit length 1024. We consider an
implementation of the modular exponentiation RSA
based on a word-level Montgomery modular multi-
plication algorithm (Bosselaers et al., 1993). Then
in order to simulate the power consumption of a full
SECRYPT 2020 - 17th International Conference on Security and Cryptography
634

FAFA
FA = Full Adder
FA FA
v
31
v
30
c
31
a
31
0, ..., 0, b
31
, ..., b
0
a
30
c
30
v
1
v
0
c
0
c
1
a
0
a
1
r
63
, . . . , r
0
Figure 1: 32-Bit sequential multiplier.
modular multiplication we only need to generate the
power consumption of w-bit additions and multiplica-
tions.
32-bit multiplier and adder. We defined a circuit per-
forming multiplication of 32-bit integers and a circuit
performing addition of 32-bit integers. The multi-
plier shown in Fig. 1 is a bit sequential multiplier.
It computes r = a × b where a = (a
31
,...,a
0
)
2
and
b = (b
0
,...,b
1
)
2
as shown in the following pseudo-
code:
for i = 0 to 32 do
r ← r + 2
i
(b
i
× a)
The i-th bit r
i
is output after the i-th clock-cycle. The
additions in Fig. 1 are done through carry save adder
in order to reduce the critical path delay. This means
that the carries are not propagated and but are saved
in the flip-flops c
i
for i = 0,...,31. After the first 32
iterations the first 32 bits r
0
,...,r
31
of r are generated
and output. But it remains to perform 32 more itera-
tions, with input 0 in place of b
i
,to propate the carries
and generate r
32
,...,r
63
.
We do not provide the circuit of the 32-bit adder,
since it is a classical 32 bit adder, which can be easily
found in the literature.
To get the power consumption of one clock-cycle
of the multiplier we compute the hamming weight of
signal flowing in the wires. We split the clock cycle
into four parts P
1
,P
2
,P
3
and P
4
. We assume that at be-
ginning of a cycle there are only 0 on all wires. Then
we propagate data from the flip-flop and deduce the
simulated consumption:
• Each wire containing a signal 1 and connecting
a flip-flop and a first gate contributes to 1 on the
consumption of P
1
,P
2
,P
3
and P
4
.
• Each wire containing a 1 and connecting a first
gate and a second gate contributes to to the con-
sumption of P
2
,P
3
and P
4
.
• Each wire containing a 1 and connecting a second
gate and a third gate contributes to 1 to the con-
sumption of P
3
and P
4
.
• Each wire containing a 1 and connecting a third
gate and the flip-flop contributes to 1 to the con-
sumption of P
4
.
The above simulation of the consumption is highly
Figure 2: Power trace of a 32-bit multiplication.
simplified but we believe that it is sufficient to vali-
date the potential threat of the proposed attack on Al-
gorithm 3. We show in Fig. 2 an example of the simu-
lated power consumption of one w-bit multiplication.
Word level Montgomery modular multiplication. For
a modular multiplication we use the word level
version (Bosselaers et al., 1993) of the Mont-
gomery modular multiplication with word size w.
Given two integers A and B consisting of s words
the modular multiplication are performed as fol-
lows
1: R ← (0,. . . , 0)
2
w
2: for i = 0 to s − 1 do
3: q ← (R + A[i] × B) × N
0
mod 2
w
4: R ← (R + q × N + A[i] × B)/2
w
Step 3 consists of two w-bit multiplications and
one w-bit addition. Step 4 involves two products of
a ws-bit integer by a w-bit integer and two additions
of two ws-bit integers. Each of these operations are
computed through a sequence of w-bit multiplications
and/or additions.
4.2 Distinguishing a Square from a
Multiplication
We would like to distinguish a multiplication (A × B)
mod N from a squaring (A × A) mod N. The main
idea to get such distinguisher is that during the mul-
tiplication of (A × A) mod N for each i 6= j the same
product is done twice as A[i] × A[ j] and in reverse
operand A[ j] × A[i] in Step 3 the word level Mont-
gomery multiplication. But since these multiplica-
tions involve the same data their power trace must be
correlated.
Then we tried to compute the covariance of the
power traces of the 32-bit multiplication in order to
determine if they are correlated or not. But this strat-
egy was not successful. Probably this is due to the
non symmetric form of the considered 32-bit multi-
plier. We tried another strategy where we evaluate the
Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure
635
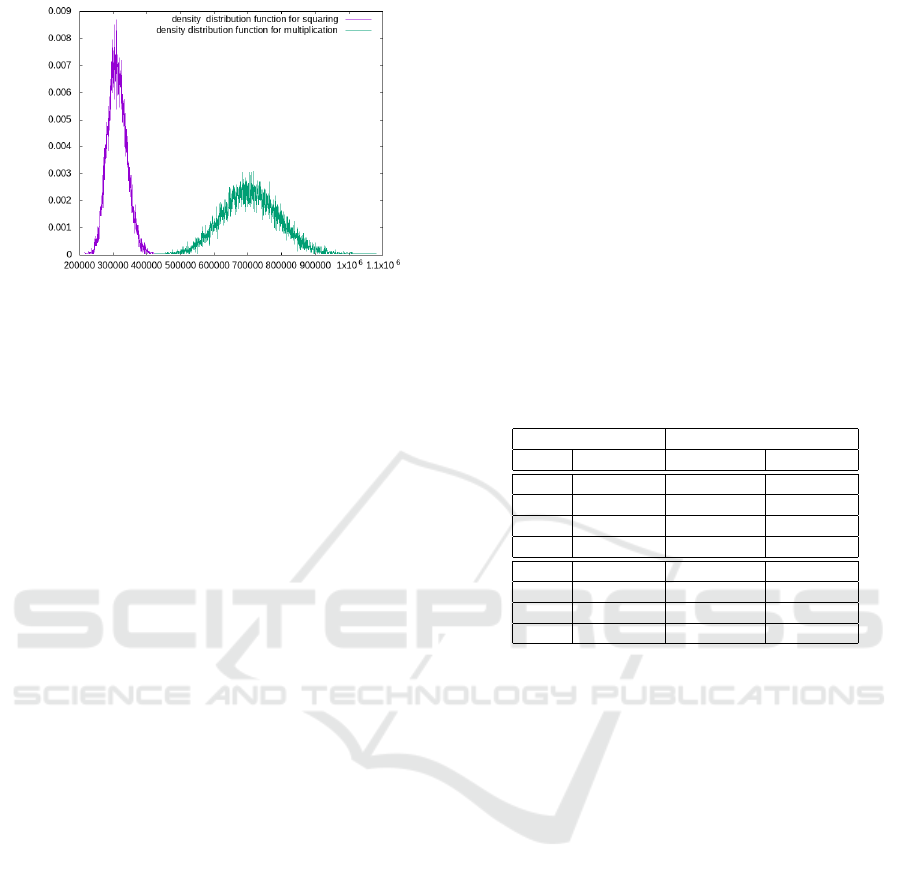
Figure 3: Square and non square repartition of power con-
sumption.
difference of the mean of the power traces:
σ
i, j
(A,B)=
|
R
Tr(Mul(A[i], B[ j])
|
−
|
R
Tr(Mul(B[i], A[ j])
|
This computed value might be low if A = B,
since, in this case, many computed bits appearing
in the multiplication Mul(A[i],A[ j]) also appear in
Mul(A[ j],A[i]) and they cancel out in the difference
of σ
i, j
(A,A). If A 6= B these bits do not cancel out re-
sulting in a higher value for σ
i, j
(A,B). This effect is
amplified if we add up σ
i, j
(A,B) over all i < j:
σ(A,B) =
∑
0≤i< j≤s
σ
i, j
(A,B).
In order to check this fact we performed the fol-
lowing experiment: for a sufficiently large number of
time (
∼
=
10000) we chose randomly A and B and com-
puted σ(A, B) and σ(A, A). We obtained the resulting
density distribution function shown in Fig. 3.
Fig. 3 clearly shows that we can easily distinguish
a squaring from a genuine multiplication. We esti-
mated the mean value m and the standard deviation d
for the two cases: squaring (S) and genuine multipli-
cation (M):
m
S
= 310000,d
S
= 28000
m
M
= 710038,d
M
= 82000
Given a power trace for a multiplication A × B
mod N, we compute σ(A,B) and we deduce that A =
B if σ(A,B) is close to m
S
and A 6= B if it is close to
m
M
. To a get an estimation of the probability of suc-
cess of this approach, we use the following inequal-
ity of Bienaym
´
e-Tchebychev for a random variable X
with mean m and standard deviation d:
P(|X −m| > kd) < 1/k
2
.
We chose k = 3 leading to a level of confidence in
our distinguisher of 1 − 1/9.This is validated by an
experiment for 5000 samples for which we get 99.5%
of success.
4.3 Final Step: ADPA
Now, since we have a reliable distinguisher, we can
proceed to the next step: finding the bits of the expo-
nent with a DPA attack on the address bits. Given a
power trace of an exponentiation x
κ
mod N we can
find the random bit a
i
used in Algorithm 3 for all
i = 0,...,n − 1. Our goal now is to find difference
of the power trace related to the address bits involved
in loads or stores. Let us analyze the loads and stores
in order to select interisting power traces and compute
a difference producing a peak if the guess is incorrect
and a flat trace if the guess is correct.
The table below shows the relation between the
(i + 1)-th iteration and i-th iteration for the operation
done in Step 5 in Algorithm 3 depending on the value
of b
0
,k
i
and a
i
.
Table 2.
(i + 1)-th iter. i-th iter.
bit Op. (Step 5) bits Op. (Step 4)
b
0
= 0 R
1
← R
0
U
0
k
i
= 0, a
i
= 0 R
1
← R
0
U
0
b
0
= 0 R
1
← R
0
U
0
k
i
= 0, a
i
= 1 R
1
← R
0
U
1
b
0
= 1 R
1
← R
0
U
1
k
i
= 0, a
i
= 0 R
1
← R
0
U
0
b
0
= 1 R
1
← R
0
U
1
k
i
= 0, a
i
= 1 R
1
← R
0
U
1
b
0
= 0 R
1
← R
0
U
0
k
i
= 1, a
i
= 0 R
1
← R
0
U
1
b
0
= 0 R
1
← R
0
U
0
k
i
= 1, a
i
= 1 R
1
← R
0
U
0
b
0
= 1 R
1
← R
0
U
1
k
i
= 1, a
i
= 0 R
1
← R
0
U
1
b
0
= 1 R
1
← R
0
U
1
k
i
= 1, a
i
= 1 R
1
← R
0
U
0
If we focus on the cases a
i
= 0 (the row in bold in
the table), we can notice that:
• Case 1: b
0
⊕ k
i
= 0. The operations in Step 5 of
the two iterations are the same. In particular the
address for U
i
is the same.
• Case 2. b
0
⊕ k
i
= 1. The operations in Step 5 of
the two iterations are different. In particular the
address bits for U
i
are different.
Consequently, we proceed by guessing the value of
g = k
i
⊕ k
i+1
. Then we select the power traces such
that a
i
= 0 and such that a
i+1
⊕ g = 0. If our guess is
correct we will have:
0 = a
i+1
⊕ g = a
i+1
⊕ k
i+1
⊕ k
i
= b
i+1
⊕ k
i
= b
0
⊕ k
i
.
This means that if the guess g is correct, then Case
1 applies, which means that computing the difference
of the power traces of loop i and i + 1 would lead to
a zero difference for the address of U
i
, and the differ-
ence will be flat. If the guess is not correct, we are in
Case 2, and the difference would be equal to the con-
sumption of the address of U
0
minus the one for U
1
.
Adding a sufficient number of such differences would
lead to a flat difference if the guess is correct and a
peak if it is not correct.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
636
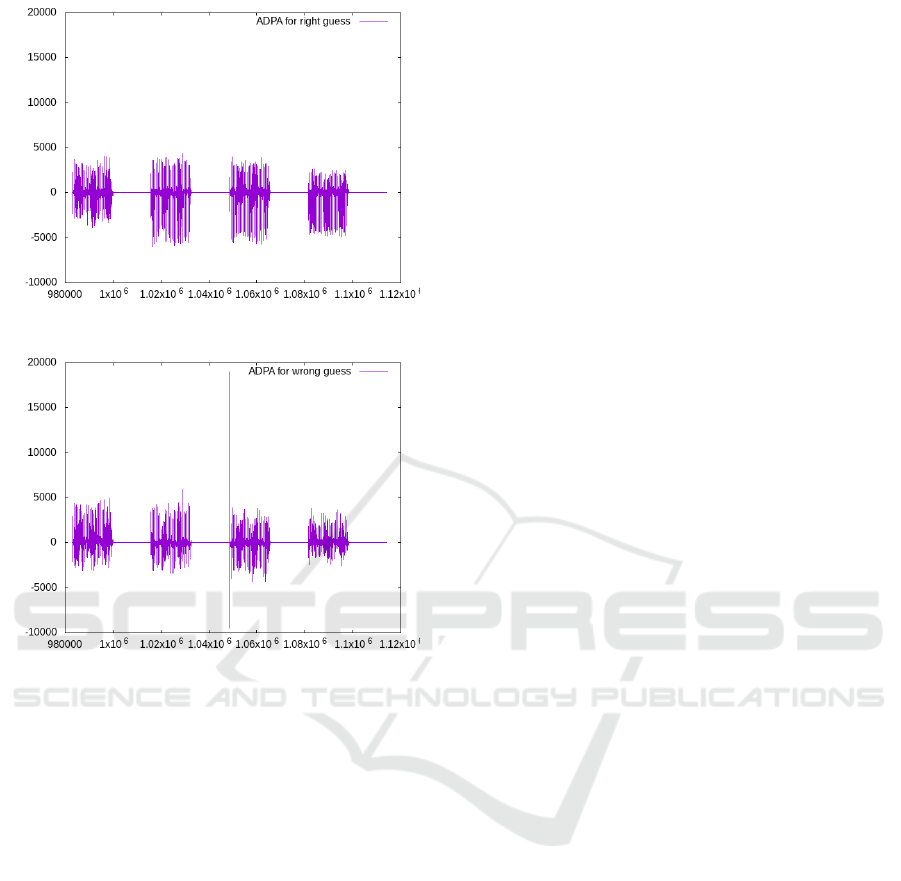
Figure 4: Difference for a correct guess on k
i+1
⊕ k
i
.
Figure 5: Difference for a wrong guess on k
i+1
⊕ k
i
.
In Fig. 4 and Fig. 5 we provide the ADPA obtained
for an RSA of size 1024 bits and using 4000 traces.
We can see the peak in Fig. 5 showing that the guess
g is not correct. There is no peak in Fig. 4 which
means that the guess is correct.
This experimentation shows that the proposed ap-
proach is effective to extract the whole key. This
means that Algorithm 3 does not provide the claimed
protection from ADPA. This attack works even if the
elements are blinded at the beginning of the expo-
nentiation, by either a randomized representation or
a multiplication with a random element.
5 CONCLUSION
In this paper we considered two exponentiation al-
gorithms (Algorithm 2 and 3) proposed in (Tunstall
et al., 2018) with randomized store and load in or-
der to counter-act address bit differential power anal-
ysis. We analyzed the security of these approaches,
and we showed that Algorithm 3 has a an important
flaw. Indeed, the operation done in Step 3 of Algo-
rithm 3 is a square or multiplication depending on
the bit used for load and store randomization. With
a simulated power consumption we showed that we
can distinguish a square from a multiplication. This
means that the randomization of loads and stores in
Algorithm 3 is not effective anymore and an ADPA
can be conducted to recover the whole secret key with
a few thousand power traces.
REFERENCES
Bosselaers, A., Govaerts, R., and Vandewalle, J. (1993).
Comparison of Three Modular Reduction Functions.
In CRYPTO’93, volume 773 of LNCS, pages 175–186.
Clavier, C., Feix, B., Roussellet, M., and Verneuil, V.
(2010). Horizontal Correlation Analysis on Exponen-
tiation. In ICICS 2010, volume 6476 of LNCS, pages
46–61.
Coron, J.-S. (1999). Resistance against Differential Power
Analysis for Elliptic Curve Cryptosystems. In CHES
1999, pages 292–302.
Fouque, P. and Valette, F. (2003). The Doubling Attack –
Why Upwards Is Better than Downwards. In CHES
2003, pages 269–280.
Hanley, N., Tunstall, M., and Marnane, W. (2011). Using
templates to distinguish multiplications from squaring
operations. Int. J. Inf. Sec., 10(4):255–266.
Itoh, K., Izu, T., and Takenaka, M. (2003). Address-Bit Dif-
ferential Power Analysis of Cryptographic Schemes
OK-ECDH and OK-ECDSA. In CHES 2002, LNCS,
pages 129–143.
Izumi, M., Ikegami, J., Sakiyama, K., and Ohta, K. (2010).
Improved countermeasure against address-bit DPA for
ECC scalar multiplication. In DATE 2010, pages 981–
984.
Joye, M. and Yen, S. (2002). The Montgomery Powering
Ladder. In CHES 2002, volume 2523 of LNCS, pages
291–302.
Kocher, P. (1996). Timing Attacks on Implementations of
Diffie-Hellman, RSA, DSS, and Other Systems. In
CRYPTO ’96, volume 1109 of LNCS, pages 104–113.
Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differential
Power Analysis. In CRYPTO’99, volume 1666 of
LNCS, pages 388–397.
Smart, N. P., Oswald, E., and Page, D. (2008). Randomised
representations. IET Inform. Security, 2(2):19–27.
Tunstall, M. and Joye, M. (2010). Coordinate Blinding over
Large Prime Fields. In CHES 2010, pages 443–455.
Tunstall, M., Papachristodoulou, L., and Papagiannopoulos,
K. (2018). Boolean Exponent Splitting. Technical
Report 2018/1226, IACR Cryptology ePrint Archive.
Yen, S., Ko, L., Moon, S., and Ha, J. (2006). Relative Dou-
bling Attack Against Montgomery Ladder. In ICISC
2005, LNCS, pages 117–128.
Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure
637
