
Bi-Objective CSO for Big Data Scientific Workflows Scheduling in the
Cloud: Case of LIGO Workflow
K. Bousselmi
1
, S. Ben Hamida
2
and M. Rukoz
2
1
Paris Nanterre University, 92001 Nanterre Cedex, France
2
Paris Dauphine University, PSL Research University, CNRS, UMR [7243], LAMSADE, 75016 Paris, France
Keywords:
Scientific Workflow, Data Intensive, Cat Swarm Optimization, Multi-Objective Scheduling, LIGO.
Abstract:
Scientific workflows are used to model scalable, portable, and reproducible big data analyses and scientific
experiments with low development costs. To optimize their performances and ensure data resources efficiency,
scientific workflows handling big volumes of data need to be executed on scalable distributed environments
like the Cloud infrastructure services. The problem of scheduling such workflows is known as an NP-complete
problem. It aims to find optimal mapping task-to-resource and data-to-storage resources in order to meet end
user’s quality of service objectives, especially minimizing the overall makespan or the financial cost of the
workflow. In this paper, we formulate the problem of scheduling big data scientific workflows as bi-objective
optimization problem that aims to minimize both the makespan and the cost of the workflow. The formulated
problem is then resolved using our proposed Bi-Objective Cat Swarm Optimization algorithm (BiO-CSO)
which is an extension of the bio-inspired algorithm CSO. The extension consists of adapting the algorithm
to solve multi-objective discrete optimization problems. Our application case is the LIGO Inspiral workflow
which is a CPU and Data intensive workflow used to generate and analyze gravitational waveforms from data
collected during the coalescing of compact binary systems. The performance of the proposed method is then
compared to that of the multi-objective Particle Swarm Optimization (PSO) proven to be effective for scientific
workflows scheduling. The experimental results show that our algorithm BiO-CSO performs better than the
multi-objective PSO since it provides more and better final scheduling solutions.
1 INTRODUCTION
Scientific applications handling big volumes of data
usually consist of a huge number of computational
tasks with data dependencies between them, which
are often referred to as scientific workflows. They
are frequently used to model complex phenomena, to
analyze instrumental data, to tie together information
from distributed sources, and to pursue other scien-
tific endeavors (Deelman, 2010). Data intensive sci-
entific workflows need from few hours to many days
to be processed in a local execution environment. In
this paper, we consider the scientific application of
Laser Interferometer Gravitational Wave Observatory
(LIGO)
1
which is a network of gravitational-wave
detectors, with observatories in Livingston, LA and
Hanford, WA. The observatories’ mission is to detect
and measure gravitational waves predicted by general
relativity Einstein’s theory of gravity in which grav-
1
https://www.ligo.caltech.edu/
ity is described as due to the curvature of the fabric
of time and space. The data collected by the dif-
ferent LIGO observatories is about Tera-octets per
hour. To analyze this huge amount of data, scien-
tists modeled their workloads using scientific work-
flows. The LIGO workflow may contain up to 100
sub-workflows and 200,000 jobs (Juve et al., 2013)
which requires many hours to be performed in a Grid
computing environment. To obtain simulation results
within acceptable timeframes, large scientific work-
loads are executed on distributed computing infras-
tructures such as grids and clouds (Brewer, 2000).
The Cloud Computing environment offers on-demand
access to a pool of computing, storage and net-
work resources through Internet that allows hosting
and executing complex applications such as scien-
tific workflows. As a subscription based computing
service, it provides a convenient platform for scien-
tific workflows due to features like application scal-
ability, heterogeneous resources, dynamic resource
provisioning, and pay-as-you-go cost model (Poola
Bousselmi, K., Ben Hamida, S. and Rukoz, M.
Bi-Objective CSO for Big Data Scientific Workflows Scheduling in the Cloud: Case of LIGO Workflow.
DOI: 10.5220/0009827106150624
In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 615-624
ISBN: 978-989-758-443-5
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
615

et al., 2014). Scheduling data intensive scientific
workflows on the Cloud environment is usually an
NP-complete problem (Guo et al., 2012). It aims
to find convenient resources for executing the work-
flow tasks and storing its data in order to meet the
user’s quality of service objectives such as minimiz-
ing the makespan or the cost of the workflow. In
the Cloud Computing environment, the overall ob-
jective of the task scheduling strategy is to guar-
antee the service-level agreements (SLAs) of allo-
cated resources to make cost-efficient decisions for
workload placement (Bousselmi et al., 2016b). In
real-life situations, there are three main QoS con-
straints that need to be considered for efficient uti-
lization of resources: (1) minimizing the execution
cost of resources, (2) minimizing the execution time
of workloads, (3) reducing the energy consumption
and at the same time meeting the cloud workload
deadline (Singh and Chana, 2015). In our context,
we focus on the objectives of reducing both the cost
and the makespan of the workflow since they are the
most important quality metrics for the workflow’s end
users (Bousselmi et al., 2016b). These metrics are
conflicted because high-performance Cloud resources
with high storage capacities are often more expansive
than others.
The scheduling problem is more challenging for
data intensive scientific workflows as they produce a
huge amount of data that should be communicated to
other tasks in order to perform their execution. Since
data storage and data transfer through the Internet is
paying, the cost and time needed for the execution of
the overall workflow can be consequent. For instance,
both Amazon S3 and EBS use fixed monthly charges
for the storage of data, and variable usage charges
for accessing the data. The fixed charges are 0.15$
per GB-month for S3, and 0.10$ per GB-month for
EBS (Berriman et al., 2010). The variable charges are
0.01$ per 1000 PUT operations and 0.01$ per 10000
GET operations for S3, and 0.10$ per million I/O op-
erations for EBS (Berriman et al., 2010).
This work is an extension of an earlier conference
publication (Bousselmi et al., 2016b). In (Bousselmi
et al., 2016b), the scheduling problem of scientific
workflows was formulated as a mono-objective op-
timization problem and we used typical workflows
for the experiments. In this paper, our objective is
to propose a scheduling solution for data intensive
scientific workflows that considers the time and cost
of data storage and transfer. The proposed exten-
sion consists on formulating our scheduling problem
as a multi-objective optimization problem dedicated
to Big Data scientific workflows. Indeed, we model
1
https://pegasus.isi.edu/application-showcase/ligo/
our scheduling problem as a bi-objective optimiza-
tion problem that aims to reduce the overall cost and
the response time of the workflow. As an optimiza-
tion technique, we propose the extension of the cat
swarm optimization algorithm (CSO) algorithm to al-
low the resolution of a multi-objective optimization
problem. We chose the CSO algorithm since it has
proven its efficiency compared to other evolutionary
algorithms such as the particle swarm optimization al-
gorithm especially in solving common NP-hard opti-
mization problems (Chu et al., 2007) Thus, the prin-
cipal contribution of our paper is the proposition of a
new multi-objective optimization solution that allows
the scheduling of Big Data scientific workflows based
on the quality metrics of time and cost.
The remainder of this paper is organised as fol-
lows. In section 2, we summarize some works that
were interested in the scheduling of scientific work-
flows in the cloud computing environment. In sec-
tion 3, we present our problem formulation as well
as the formulation of the scientific workflows and the
execution environment. Section 4 describes the CSO
algorithm and its components. In section 5, we detail
the proposed algorithm for the scheduling of scientific
workflows in the cloud. We describe our application
case, namely, the LIGO workflow in section 6. Then,
we report and discuss our experimental results before
concluding in the final section.
2 RELATED WORKS
With the development of cloud technology and ex-
tensive deployment of cloud platform, the problem
of workflow scheduling in the cloud becomes an im-
portant research topic. The challenges of the prob-
lem lie in: NP-hard nature of the task-resource map-
ping with diverse Quality of Service (QoS) require-
ments (Wu et al., 2015). Several approaches were
proposed recently to resolve this problem with con-
sidering multiple QoS metrics such as the makespan,
cost and energy consumption, others focused only on
a single-objective problem by aggregating all the ob-
jectives in one analytical function such as in (Bous-
selmi et al., 2016b). (Durillo and Prodan, 2014) pro-
posed Multi-objective Heterogeneous Earliest Finish
Time (MOHEFT) which gives better trade-off solu-
tions for makespan and financial cost when the results
are compared with SPEA2* Algorithms (Yu et al.,
2007). A multi-objective heuristic algorithm, Min-
min based time and cost trade-off (MTCT), was pro-
posed by Xu et al. in (Xu et al., 2016). As scheduling
approach, the Balanced and file Reuse-Replication
Scheduling (BaRRS) algorithm, was proposed to se-
ICSOFT 2020 - 15th International Conference on Software Technologies
616

lect the optimal solution based on makespan and cost
(Casas et al., 2017).
To reduce the cost and time of data transfer,
some scheduling strategies prefer employing the same
cloud provider for the data storage and VMs, since the
data transfer cost between inner services is free (Ber-
riman et al., 2010). However, executing too many
workloads on a single cloud will cause workloads
to interfere with each other and result in degraded
and unpredictable performance which, in turn, dis-
courages the users (Dillon et al., 2010). Only few
works were interested in the problem of reducing the
time and cost of data transfer while executing data
intensive workflows in multi-cloud environment. In
(Yao et al., 2017), the authors designed a multi-swarm
multi-objective optimization algorithm (MSMOOA)
for workflow scheduling in multi-cloud that optimizes
three objectives (makespan, cost and energy con-
sumption) with taking into consideration the structure
characteristic of cloud data center but they consid-
ered only computational-intensive workflows. Wang-
som and al. proposed in (Wangsom et al., 2019) a
multi-objective peer-to-peer clustering algorithm for
scheduling workflows where cost, makespan and data
movement are considered, but this work lacks details
in the reported results.
3 EXECUTION ENVIRONMENT
AND PROBLEM
FORMULATION
In this section, we explain how we formulate our
multi-objective combinatorial optimization problem
for scheduling big data scientific workflows in the
cloud. We start by defining the model used for the
presentation of big data scientific workflows. Then,
a model of our execution environment, namely the
cloud computing, is proposed. Finally, we present our
problem formulation.
3.1 Big Data Scientific Workflows
Modeling
Scientific workflows are usually modeled using Di-
rected Acyclic Graphs (DAG). Since our objective is
to handle big data workflows, we model a workflow
as a DAG graph where tasks are represented by nodes
and dependencies between them are represented by
links. Dependencies typically represent the dataflow
in the workflow, where the output data produced by
one task is used as input of one or multiple other tasks.
A single workflow task T
i
can be modeled using the
triplet T
i
= (D, Dt
in
, Dt
out
) with:
• Dt
in
= {Dt
in
j
| j ∈ [0..(i − 1)]} represents the
amounts of data to be processed by T
i
with Dt
in
j
is the dataset from the task j.
• D = {D
k
|k = 1. . . r} is the vector of demands of
the T
i
in terms of resource capacities with D
k
is the
minimum capacity required of the resource type k
to process the task and r the total number of re-
source types.
• Dt
out
= {Dt
out
|l = 1, . . . ,s} represents the number
of datasets generated after the completion of T
i
.
3.2 Modeling the Cloud Computing
Environment
The Cloud Computing environment can be modeled
as a set of datacenters. Each datacenter is composed
of a set of cloud clusters where each cluster is com-
posed of a set of physical machines, network devices
and storage devices. The physical machines, that we
note PM, can be used for both computing and stor-
age. PM may be a dedicated computing machine,
a set of virtual machines or a shared machine. In
this scope, we consider only physical machines that
are composed of a set of virtual machines such as
PM = {V M
i
|i = 1, . . . , m}. The communication link
between two physical machines BW (PM
i
, PM
j
) is de-
fined as the bandwidth demand or the traffic load be-
tween them. In addition, we define the quality of ser-
vice metrics used to evaluate the performances of a
virtual machine V M
i
by the vector Q
i
= (T
exe
,C, A, R)
where:
• T
exe
=
∑
k
j=1
Dt
in
j
T
u
is the execution time of a sin-
gle task assessed as the sum of times needed to
process each input data file Dt
in
j
. T
u
is assessed in
million instructions per second (MIPS).
• The cost of processing a task on a V M
i
denoted
C = T
exe
∗ C
u
, where C
u
represents the cost per
time unit incurred by using V M
i
.
• A is the availability rate of V M
i
.
• R is the reliability value of V M
i
.
In this paper, we will consider only the first two qual-
ity metrics, namely the execution time and the cost of
V M
i
.
3.3 Problem Formulation
Dispersion, heterogeneity and uncertainty of cloud re-
sources bring challenges to resource allocation, which
cannot be satisfied with traditional resource allocation
Bi-Objective CSO for Big Data Scientific Workflows Scheduling in the Cloud: Case of LIGO Workflow
617

policies. Resource scheduling aims to allocate appro-
priate resources at the right time to the right work-
loads, so that applications can utilize the resources
effectively which lead to maximization of scaling ad-
vantages (Singh and Chana, 2015). In this paper, our
objective is to propose a new multi-objective schedul-
ing approach for big data scientific workflows in the
Cloud. The proposed approach considers two QoS
metrics that can represent, according to our under-
standing, the most important QoS metrics for end
users, namely: the makepsan and the cost.
The execution of a big data workflow in the cloud
implies executing each task using the allocated virtual
machine with respect to the data-flow dependencies
among different tasks. At the end of a task execution,
generated data is transferred to one or several follow-
ing tasks to perform their execution. These data are
often massive and require additional time and cost to
be transferred to other geographically distributed vir-
tual machines. Some final or intermediary generated
data have to be stored also in dedicated storage ser-
vices to be analyzed later (Yuan et al., 2012).
We denote X
k
a realizable workflow schedule
where each task is assigned to a specific VM. Then,
the overall makespan of the schedule X
k
can be as-
sessed by the equation 1 as the sum of the data pro-
cessing and data transfer times between dependent
tasks, such as:
Makespan(X
k
) = T
(data−processing)
(X
k
)
+ T
(data−t rans f er)
(X
k
)
(1)
We argue that the time needed for data storage in
dedicated storage services (SS) can’t be assessed in
the makespan since these data could remain in SS ser-
vices even after the workflow execution end for an-
alyze requirements. Likewise, the overall cost of a
schedule solution X
k
is assessed as the sum of the data
processing cost on the allocated VMs, the overall cost
of data transfer between tasks and data storage on SS
services as follows:
Cost(X
k
) = C
(data−processing)
(X
k
)
+ C
(data−t rans f er)
(X
k
)
+ C
(data−st orage)
(X
k
)
(2)
Like in (Bousselmi et al., 2016a), to assess the
global quality metrics values of the workflow during
its execution, such as its makespan and its cost, we use
aggregation functions of different considered quality
metrics as shown in the table 1 with N is the total
number of tasks of the workflow, T
exe
i
, C
i
, DT
(i, j)
,
d
(i,i+1)
, T
rem
are respectively the data processing time
of a task i on a specific VM, its execution cost, the
data-flow transmitted between two VMs i and j cor-
responding to two consecutive tasks, the throughput
of network bandwidth between two VMs i and j and
the time during which data is remaining stored on a
specific SS. In the case of parallel tasks of the work-
flow, the operators of the aggregation function for the
execution time and data transfer time metrics are re-
placed by the maximum operator.
To sum up, our scheduling objective can be formu-
lated as a multi-objective optimization problem that
aims to reduce both the makespan and the cost of the
workflow using the following linear representation:
min makespan(X
k
)
min cost(X
k
)
(3)
The objective functions of our optimization problem
are reported by the formulas 1 and 2. In the next ses-
sion, we will introduce the CSO algorithm used for
the resolution of our formulated problem.
4 CAT SWARM OPTIMIZATION
(CSO) ALGORITHM
Biologically inspired computing has been given im-
portance for its immense parallelism and simplicity in
computation. In recent times, quite many biologically
motivated algorithms have been invented and are be-
ing used for handling many complex problems of the
real world (Das et al., 2008). Using a biologically in-
spired algorithm for the scheduling of scientific work-
flows in the cloud became an attractive research track
due to complexity of the problem of finding the best
match of task-resource pair based on the user’s QoS
requirements.
Recently, a family of biologically inspired algo-
rithms known as Swarm Intelligence has attracted the
attention of researchers working on bio-informatics
related problems all over the world (Das et al., 2008).
Algorithms belonging to this field are motivated by
the collective behavior of a group of social insects
(like bees, termites and wasps). For instance, the Cat
Swarm Optimization algorithm (CSO) aims to study
the behavior of cats to resolve complex combinatory
optimization problems. According to (Bahrami et al.,
2018), cats have high alertness and curiosity about
their surroundings and moving objects in their envi-
ronment despite spending most of their time in rest-
ing. This behavior helps cats in finding preys and
hunting them down. Compared to the time dedicated
to their resting, they spend too little time on chasing
preys to conserve their energy. The first optimization
algorithm based of the study of cat swarms was pro-
posed in 2007 by (Chu et al., 2007). The steps of
the CSO algorithms are as follows. First, the CSO
algorithm creates an initial population of N cats and
ICSOFT 2020 - 15th International Conference on Software Technologies
618
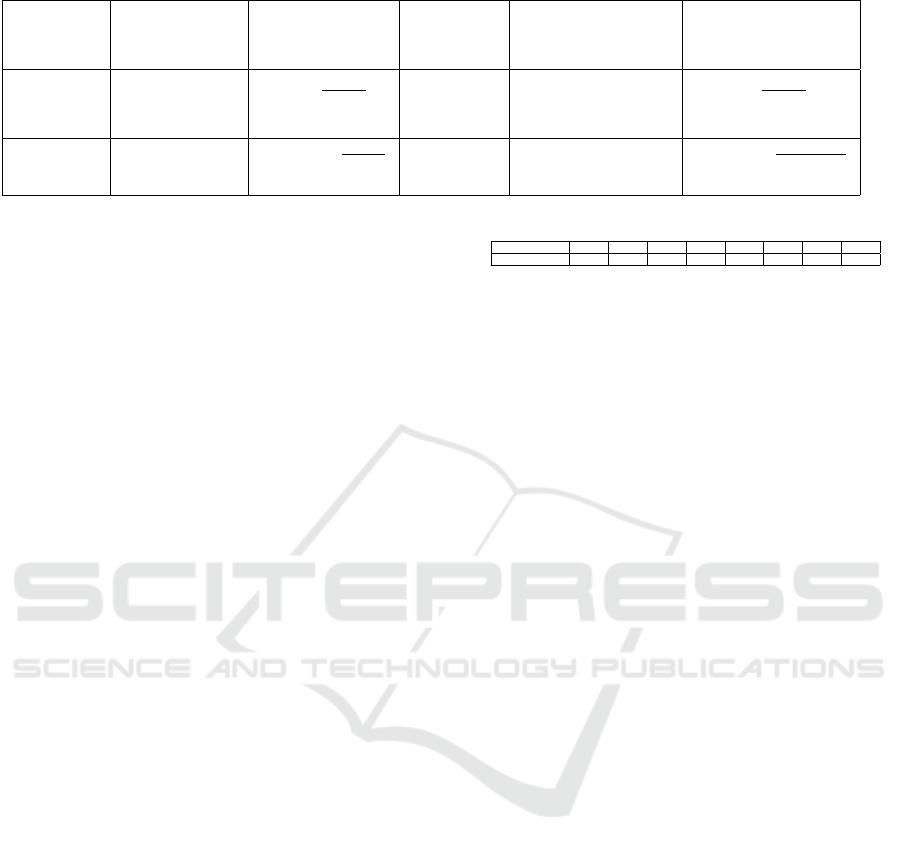
Table 1: Aggregation functions for QoS metrics.
Quality Data Data Data Data Data
metric processing Transfer processing storage transfer
time time cost cost cost
Sequential
∑
N
i=1
T
exe
i
∑
N
i=1
DT
i,i+1
d
i,i+1
∑
N
i=1
C
i
∑
N
i=1
T
rem
i
∗C
i
n
∑
i=1
DT
i,i+1
d
i,i+1
Tasks
Parallel max
1≤i≤n
T
exe
i
max
1≤i≤n
DT
i,i+1
d
i,i+1
∑
N
i=1
C
i
max
1≤i≤n
T
rem
i
∗C
i
max
1≤i≤n
DT
i,i+1
∗C
i j
d
i,i+1
Tasks
defines their characteristics. Each cat represents a so-
lution of the formulated optimization problem and its
characteristics represent the parameters of this solu-
tion, namely its fitness value, its mode (in “seeking”
or “tracing” mode), its position and its velocity. Sec-
ond, cats are organized randomly into two groups, one
group of cats is in ”Seeking mode” and the other in
”Tracing mode”. All cats are evaluated according to
the fitness function and the cat with the best fitness
value is retained. After that, if the cat is in ”Seek-
ing mode”, then the process of ”Seeking mode” is
applied, otherwise the process of ”Tracing mode” is
applied. Finally, if the stop condition has not been
reached yet, then the algorithm restarts from the sec-
ond step. The optimum solution is represented by the
cat having the best fitness value at the end of the algo-
rithm. The details of the ”Seeking mode” and ”Trac-
ing mode” procedures could be found in (Chu et al.,
2007). Four essential parameters are to be defined and
applied in the CSO algorithm, namely:
• SMP (Seeking Memory Pool): the search memory
pool that defines the size of the seeking memory
of each cat.
• SRD (Seeking Range of the selected Dimension):
the mutative ratio for the selected dimensions.
• CDC (Counts of Dimension to Change): the num-
ber of elements of the dimension to be changed.
• SPC (Self Position Consideration): a Boolean
number indicating whether the current position
is to be considered as a candidate position to be
moved on or not.
5 PROPOSED BI-OBJECTIVE
CSO (BiO-CSO) ALGORITHM
In this paper, we formulated our scheduling problem
as a multi-objective optimization problem that aims
to reduce both the overall makespan and cost of the
workflow execution in the cloud. To resolve this lat-
ter, we applied the discrete version of the CSO algo-
rithm proposed in (Bouzidi and Riffi, 2013) since our
Table 2: Example of scheduling solution representation.
Workflow’s task Task 1 Task 2 Task 3 Task 4 Task 5 Task 6 Task 7 Task 8
VM identifier 4 1 2 3 4 3 2 5
objective function uses discrete integers to model a
task-resource affectation.
We start by representing the scheduling solution
for the CSO algorithm. Then, we will detail the steps
of the proposed BiO-CSO algorithms and its tracing
and seeking mode procedures.
5.1 Mapping between Problem
Formulation and CSO
In our context, a scheduling solution is a set of N af-
fectations < task,V M > for all the tasks of the work-
flow to the available cloud VMs that can perform
these tasks. A realizable scheduling solution should
respect the order of execution of the tasks so that two
parallel tasks can’t be assigned to the same VM. We
suppose that the number of available VMs is less than
or equal to the number of tasks. The table 2 shows an
example of realizable scheduling solution of a work-
flow sample with 8 tasks. We suppose that for each
task, there are 5 candidates VMs that can perform it.
We suppose that the tasks 1,2, 3 and 4 can be per-
formed in parallel and then the tasks 5,6,7,8 are in
sequence.
As our scheduling problem is multi-objective, we
consider that the best scheduling solution is the one
having the best value of makespan and cost at the
same time than all the other solutions. All non-
dominated scheduling solutions are retained and con-
sidered as best solutions. To find these solutions we
should first map our problem formulation with the for-
malism of the CSO algorithm. In fact, in the CSO
algorithm, each cat represents a solution for the con-
sidered optimization problem. The overall objective
of the CSO is to find the cat having the optimal solu-
tion from all the population of cats, i.e. the cat with
best fitness value. Then, the mapping between our
problem formulation and the CSO algorithm can be
summarized in the following table 3.
Bi-Objective CSO for Big Data Scientific Workflows Scheduling in the Cloud: Case of LIGO Workflow
619

Table 3: Mapping between our problem formulation and
CSO.
Optimization problem formulation CSO algorithm
A scheduling solution A cat
The number of workflow tasks A cat’s position dimension
< taks,V M > affectations A cat’s position vector
The objective function The fitness value of a cat
5.2 BiO-CSO Algorithm Details
The CSO algorithm was designed for mono-objective
optimization problems (Chu et al., 2007; Bouzidi and
Riffi, 2013). We extended this algorithm to consider
multi-objective optimization problems. First, we de-
fine a vector of best solutions to store a fixed number
of non-dominated solutions along the evolution pro-
cess. Then, for each cat, we replace its fitness value
by a structure that stores the two values of our ob-
jective functions (the makespan and the cost of the
scheduling solution described by this cat). Also, we
implement additional functions to compare the new
generated solutions in order to update the vector of
best solutions. The pseudo code of the proposed al-
gorithm is given by Algorithm 1 detailed hereafter.
Algorithm 1: BiO-CSO.
Input: MaxLoopIteration :maximum number of
iterations
Variables:
CATS: population of cats (scheduling solutions)
BestParetoSet: vector of stored non-dominated so-
lutions
1: Initialize the cats’ population CATS
2: Initiate the position and velocity for each cat
3: Pick randomly a mode for each cat (CatModes)
4: for all iteration I < MaxLoopIteration do
5: for all cat in CATS do
6: fitnessValue = EvaluateFitness(cat) // evalu-
ate the makespan and cost
7: Apply BiO-Replacement(fitnessValue, Best-
ParetoSet) // Apply cat mode procedure
8: if catModes (cat) == SeekingMode then
9: Apply seekingModeProce-
dure(cat,CATS)
10: else
11: Apply TracingModeProce-
dure(cat,CATS)
12: end if
13: Re-pick randomly a mode for each cat Cat-
Modes
14: end for
15: end for
BiO-CSO works as follows. First, the algorithm
creates N cats and initialize their properties (step 1
and 2), each cat has an M dimensional position vector
that represent a realizable scheduling solution with M
is the total number of tasks per workflow. The val-
ues of the position vector represent the identifiers of
VMs affected respectively to each task of the work-
flow. The fitness value of a cat is the Bi-value vec-
tor that represents the makespan and the cost of the
represented scheduling solution. Second, BiO-CSO
randomly chooses a sequence of cats using the MR
parameter value, set them in the ‘Tracing mode’ and
set the rest of cats in ‘Seeking mode’ (step 3). Third,
it evaluates the fitness values (step 6) of each cat (the
makespan and cost of the scheduling solution repre-
sented by a cat) and keep the cat with the best fit-
ness values. The retained solutions may be several
as our problem is multi-objective. Then, we keep all
the non-dominated solution in a vector representing
the best solutions (step 7). The update of this vector
is described below (algo 2). If the cat is in ’Seeking
mode’, then the ’Seeking mode’ procedure is applied
as described in the algorithm 3, otherwise, apply the
procedure of ‘Tracing mode’ as described in the al-
gorithm 4. Forth, the algorithm re-selects a sequence
of cats, sets them to tracing mode and puts the rest of
the cats in ’Seeking mode’. Finally, if the termination
condition is reached (the maximum number of itera-
tions is reached or a desirable best solution is found),
then terminate the algorithm. If not, return to step 4.
Bi-Objective Replacement: As for most of
the multi-objective optimization algorithms (Reyes-
Sierra et al., 2006), the proposed BiO-CSO is Pareto-
based. Its purpose is to generate a Pareto solution set
with optimized maksespan and cost. The algorithm
maintains a list of best Pareto solutions that consists
of a subset of non-dominated designs found so far.
Since the number of best solutions can quickly grow
very large, the size of the Pareto list is limited. Each
cat is inserted into the Pareto set only if it is non dom-
inated as described in algorithm 2.
Tracing Mode and Seeking Mode Procedures: The
Seeking mode corresponds to the resting state of the
cats while being in continuous research of a better po-
sition. In this mode, the BiO-CSO algorithm performs
multiple copies of the cat‘s position (the scheduling
solution), then, modifies this solution using the pa-
rameter CDC for all the position copies (CDC defines
the number of values of the position to be changed).
After that, it calculates the distance between the new
position’s fitness value and the old one. According to
the distance value, the algorithm chooses the new po-
sition to assign to the cat according to its probability
value. In tracing mode, cat tries to trace targets by
ICSOFT 2020 - 15th International Conference on Software Technologies
620

updating their velocity and positions. The details of
these procedures are given in the algorithms 3 and 4.
Algorithm 2: BiO-Replacement.
Inputs:
BestParetoSet: vector of stored non-dominated so-
lutions
X: a cat (a solution)
1: if X is dominated by an other cat Y in BestPare-
toSet then
2: Replace X parameters by Y parameters
3: else
4: if X is non-dominated solution and BestPare-
toSet is not full then
5: Add X to BestParetoSet
6: else
7: Find a solution from BestParetoSet to be re-
placed by the new one X
8: end if
9: end if
Algorithm 3: Seeking Mode Procedure.
Inputs:
cat: a solution
SMP: number of cat
copies
1: Perform SMP cat position copies in Position-
sCopies
2: for all position in PositionCopies do
3: modify cat position
4: end for
5: for all cat corresponding to a position in Posi-
tionCopies do
6: Compute cat fitness
7: Calculate the distance of the new solution to
previous one
8: Move cat to the new picked position with a
given probability
9: end for
Algorithm 4: Tracing Mode Procedure.
Inputs: CATS: a set of solu-
tions
1: for all cat in CATS do
2: Update cat velocity
3: Update cat position
4: end for
6 BIG DATA SCIENTIFIC
WORKFLOWS: CASE OF LIGO
The LIGO concept built upon early work by many sci-
entists to test a component of Albert Einstein’s theory
of relativity, the existence of gravitational waves [10].
LIGO operates two gravitational wave observatories
in the USA: the LIGO Livingston Observatory in Liv-
ingston, Louisiana, and the LIGO Hanford Observa-
tory, Washington. These sites are separated by 3,002
kilometers (1,865 miles) straight line distance through
the earth, but 3,030 kilometers (1,883 miles) over the
surface [10]. Other similar observatories were built
later in other countries in the world. The workflow of
LIGO Inspiral Analysis is one of the LIGO project de-
fined workflows using scientific workflows to detect
and analyze gravitational waves produced by various
events in the universe. The LIGO Inspiral Analysis
workflow [22] is a CPU and Data intensive workflow
used to analyze the data obtained from the coalesc-
ing of compact binary systems such as binary neutron
stars and black holes. The time-frequency data from
each of the three LIGO detectors is split into smaller
blocks for analysis. For each block, the workflow
generates a subset of waveforms belonging to the pa-
rameter space and computes the matched filter output.
If a true inspiral has been detected, a trigger is gener-
ated that can be checked with triggers for the other de-
tectors. A simplified representation of the workflow is
shown in figure 1 with sub-workflows outlined below.
This workflow may contain up to 100 sub-workflows
and 200,000 jobs (Juve et al., 2013). The execution
of a sample instance of the LIGO Inspiral workflow
with 3981 tasks on a local machine runs for 1 day and
15 hours and uses more than 1 Go of input data and
more than 2 Go of output data [9].
Figure 1: Structure of the LIGO Inspiral Workflow.
Bi-Objective CSO for Big Data Scientific Workflows Scheduling in the Cloud: Case of LIGO Workflow
621

In order to establish a confident detection or mea-
surement, a large amount of auxiliary data will be
acquired (including data from seismometers, micro-
phones, etc.) and analyzed (for example, to eliminate
noise) along with the strain signal that measures the
passage of gravitational waves (Deelman et al., 2002).
The raw data collected during experiments is a collec-
tion of continuous time series at various sample rates.
The amount of data that will be acquired and cata-
loged each year is on the order of tens to hundreds
of terabytes (Deelman et al., 2002). These data are
treated in real time by the LIGO workflow, so, sev-
eral instances of this workflow should run simultane-
ously to achieve the objectives of the project. Con-
sequently, the execution environment should provide
efficient tools and enough resources for the execution
and the data storage of the LIGO workflow. Therefore
we have chosen this workflow as an application case
for our proposed algorithm BiO-CSO for its excessive
use of computing and storage resources.
7 RESULTS AND DISCUSSION
In this section, we present the execution environment
for our proposed BiO-CSO algorithm and the used
parameters for our algorithm and the PSO algorithm.
Then, we will expose our experimentation results and
discuss the performances of our proposition.
7.1 Execution Environment and
Algorithm Parameters
As a simulation environment, we used the Work-
flowSim (Chen and Deelman, 2012) on which we im-
plemented our proposed algorithm BiO-CSO. Work-
flowSim extends the CloudSim (Calheiros et al.,
2011) simulation toolkit by introducing the support
of workflow preparation and execution with an im-
plementation of a stack of workflow parser, work-
flow engine and job scheduler. It supports a multi-
layered model of failures and delays occurring in
the various levels of the workflow management sys-
tems. CloudSim is an extensible simulation toolkit
that enables modeling and simulation of Cloud com-
puting systems and application provisioning environ-
ments (Calheiros et al., 2011). We tested the LIGO
Inspiral workflow with different scales using respec-
tively 30, 100 and 1000 tasks. To compare our algo-
rithm performances, we implemented also the Multi-
objective version of the Particle swarm optimization
(PSO) algorithm. PSO is an optimization algorithm
1
https://pegasus.isi.edu/portfolio/ligo/
which is based on swarm intelligence (Tripathi et al.,
2007). It is inspired by the flocking behavior of birds,
which is very simple to simulate and has been found
to be quite efficient in handling the single objective
optimization problems. The simplicity and efficiency
of PSO motivated researchers to apply it to the MOO
problems since 2002 (Calheiros et al., 2011). For the
MOPSO algorithm, we consider c1=c2=2, and the in-
ertia weight ’w’ varying from 0.4 at the beginning to
0.9 at the end of execution of the algorithm. The table
4 illustrates the general parameters of the CSO algo-
rithm. The initial population size of cats is set to 32.
Table 4: Generic parameters of CSO algorithm.
Parameter Value
SMP 5
SRD 20
CDC 80%
MR 10%
c1 2.05
r1 [0,1]
7.2 Experimentation Results
The experiments were repeated 20 times by varying
the value of MP parameter of CSO for each workflow
instance. Average values of the output metrics are re-
ported in this section. This manipulation allowed to
generate more values of best solutions for our consid-
ered objective functions. Thus, all non-dominated so-
lutions obtained over each run are recorded in a gen-
eral Pareto set. Figure 2 shows the obtained Pareto set
for LIGO workflow with 30, 100 and 1000 tasks re-
spectively for the proposed BiO-CSO algorithm and
the MOPSO one. In the figure 2, it is clear that the
makespan and deployment cost functions are strongly
correlated with a negative slope. With respect to the
Pareto front, BiO-CSO demonstrates the ability to
generate better diversity of solutions with a uniform
distribution than MOPSO. In fact, the CSO algorithm
was designed to avoid the problem of premature con-
vergence thanks to the weighted position update strat-
egy.
It can also be seen that the Pareto fronts obtained
using BiO-CSO are superior for all the different scales
of LIGO workflow. In figure 2, the non-dominated so-
lutions generated by the BiO-CSO algorithm are bet-
ter spread over the solutions space than those of the
MOPSO algorithm which offers more choices to the
workflow end user to make cost-efficient decisions.
In figure 3, we can see that the BiO-CSO al-
gorithm achieves better average values for both
Makespan and Cost for all the LIGO workflow in-
stances. For the Makespan, the BiO-CSO allows
ICSOFT 2020 - 15th International Conference on Software Technologies
622
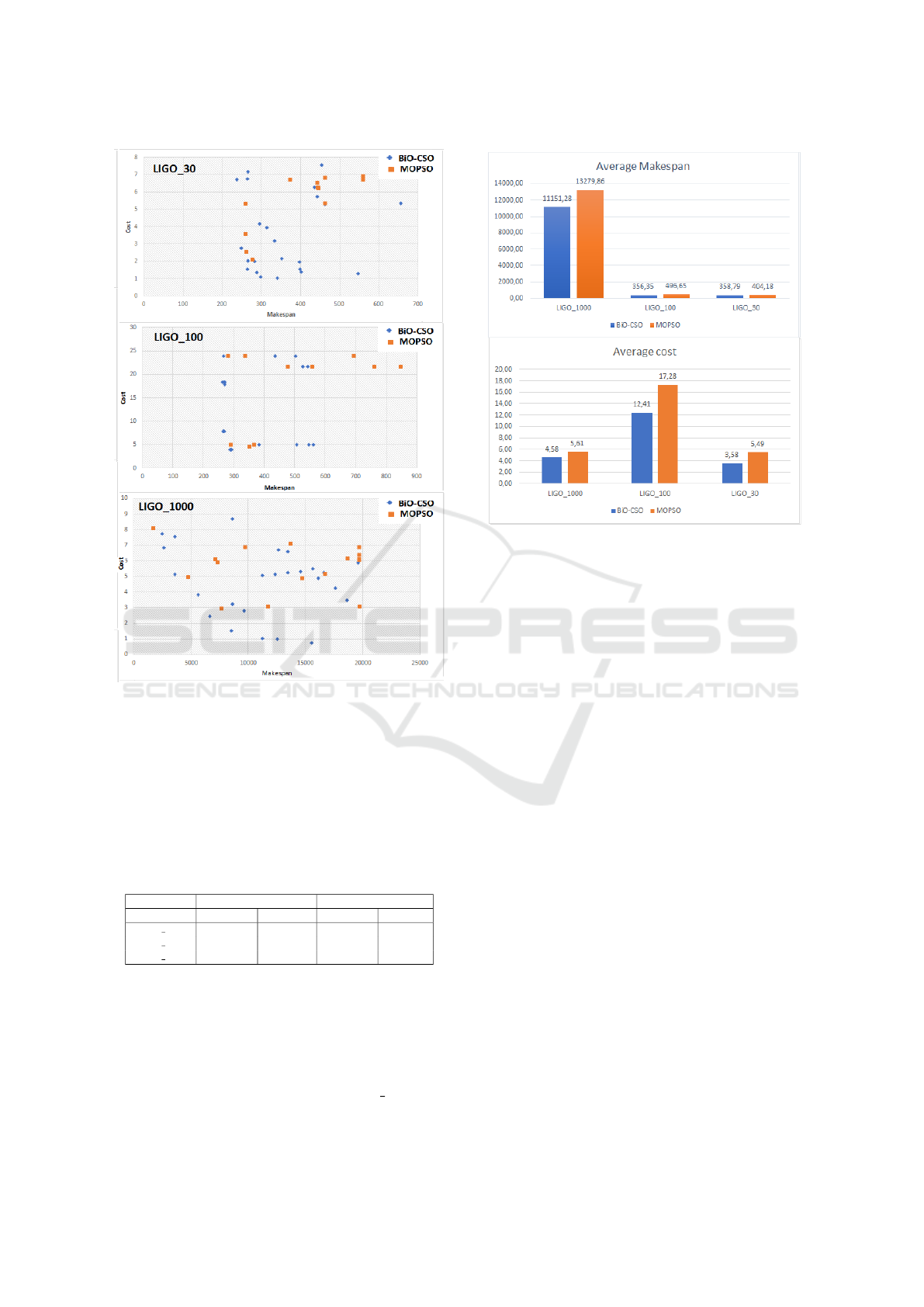
Figure 2: Non-Dominated solution sets generated by BiO-
CSO and MOPSO for LIGO workflow.
to gain an improvement of 16, 03%, 47, 21%, and
11, 23% compared to the MOPSO algorithm for the
different scaled of LIGO workflow. The cost of BiO-
CSO was better by 18, 41%, 27, 75%, and 34, 82%
over the MOPSO algorithm for the LIGO workflow
with 30, 100 and 1000 tasks respectively.
Table 5: Average values for computation and data transfer
time.
Data transfer time Computation time
Workflow BiO-CSO MOPSO BiO-CSO MOPSO
LIGO 30 261,91 295,05 96,87 109,13
LIGO 100 274,39 382,42 81,96 114,23
LIGO 1000 9255,56 11022,28 1895,72 2257,58
The table 5 illustrates the average values for com-
putation and data transfer time obtained by BiO-CSO
and MOPSO for the LIGO workflow with 30, 100 and
1000 tasks. It shows that our algorithm BiO-CSO
achieves better average values than MOPSO for all
the LIGO workflow scales with a gain ranging from
11% to 28%. For example, for the LIGO 1000, the
BiO-CSO data transfer time is 16% better the the
Figure 3: Cost and makespan average values obtained by
BiO-CSO and MOPSO for LIGO workflow.
MOPSO one. It can be seen also that the data transfer
time represents roughly 75% of the workflow execu-
tion time due to the huge amount of data treated.
8 CONCLUSION
In this paper, we addressed the problem of Big Data
Scientific workflow scheduling in the Cloud. We
started by formulating the problem as a bi-objective
optimization problem minimizing both the makespan
and the cost of the workflow. We then proposed the
BiO-CSO algorithm which is an extension of the CSO
one to deal with bi-objective optimization. The ob-
jectives conflict is resolved using the Pareto analysis.
The experiments were conducted on the LIGO work-
flow and discussed in comparison to the current al-
gorithm frequently used for workflow scheduling e.g.
PSO. From the experimental results we conclude that
BiO-CSO is able to produce better schedules based
on multiple objectives. Future work will investigate
the extension of BiO-CSO to deal with further objec-
tives such as minimizing energy consumption and its
application on different types of Big Data scientific
workflows.
Bi-Objective CSO for Big Data Scientific Workflows Scheduling in the Cloud: Case of LIGO Workflow
623

REFERENCES
Bahrami, M., Bozorg-Haddad, O., and Chu, X. (2018). Cat
swarm optimization (cso) algorithm. In Advanced Op-
timization by Nature-Inspired Algorithms, pages 9–
18. Springer.
Berriman, G. B., Juve, G., Deelman, E., Regelson, M., and
Plavchan, P. (2010). The application of cloud comput-
ing to astronomy: A study of cost and performance.
In 2010 Sixth IEEE International Conference on e-
Science Workshops, pages 1–7. IEEE.
Bousselmi, K., Brahmi, Z., and Gammoudi, M. M. (2016a).
Energy efficient partitioning and scheduling approach
for scientific workflows in the cloud. In 2016
IEEE International Conference on Services Comput-
ing (SCC), pages 146–154. IEEE.
Bousselmi, K., Brahmi, Z., and Gammoudi, M. M. (2016b).
Qos-aware scheduling of workflows in cloud comput-
ing environments. In 2016 IEEE 30th International
Conference on Advanced Information Networking and
Applications (AINA), pages 737–745. IEEE.
Bouzidi, A. and Riffi, M. E. (2013). Discrete cat swarm op-
timization to resolve the traveling salesman problem.
International Journal, 3(9).
Brewer, E. A. (2000). Towards robust distributed systems.
In PODC, volume 7.
Calheiros, R. N., Ranjan, R., Beloglazov, A., De Rose,
C. A., and Buyya, R. (2011). Cloudsim: a toolkit for
modeling and simulation of cloud computing environ-
ments and evaluation of resource provisioning algo-
rithms. Software: Practice and experience, 41(1):23–
50.
Casas, I., Taheri, J., Ranjan, R., Wang, L., and Zomaya,
A. Y. (2017). A balanced scheduler with data reuse
and replication for scientific workflows in cloud com-
puting systems. Future Generation Computer Sys-
tems, 74:168–178.
Chen, W. and Deelman, E. (2012). Workflowsim: A toolkit
for simulating scientific workflows in distributed envi-
ronments. In 2012 IEEE 8th International Conference
on E-Science, pages 1–8. IEEE.
Chu, S.-C., Tsai, P.-W., et al. (2007). Computational in-
telligence based on the behavior of cats. Interna-
tional Journal of Innovative Computing, Information
and Control, 3(1):163–173.
Das, S., Abraham, A., and Konar, A. (2008). Swarm in-
telligence algorithms in bioinformatics. In Computa-
tional Intelligence in Bioinformatics, pages 113–147.
Springer.
Deelman, E. (2010). Grids and clouds: Making workflow
applications work in heterogeneous distributed envi-
ronments. The International Journal of High Perfor-
mance Computing Applications, 24(3):284–298.
Deelman, E., Kesselman, C., Mehta, G., Meshkat, L., Pearl-
man, L., Blackburn, K., Ehrens, P., Lazzarini, A.,
Williams, R., and Koranda, S. (2002). Griphyn and
ligo, building a virtual data grid for gravitational wave
scientists. In Proceedings 11th IEEE International
Symposium on High Performance Distributed Com-
puting, pages 225–234. IEEE.
Dillon, T., Wu, C., and Chang, E. (2010). Cloud comput-
ing: issues and challenges. In 2010 24th IEEE in-
ternational conference on advanced information net-
working and applications, pages 27–33. Ieee.
Durillo, J. J. and Prodan, R. (2014). Multi-objective work-
flow scheduling in amazon ec2. Cluster computing,
17(2):169–189.
Guo, L., Zhao, S., Shen, S., and Jiang, C. (2012). Task
scheduling optimization in cloud computing based on
heuristic algorithm. Journal of networks, 7(3):547.
Juve, G., Chervenak, A., Deelman, E., Bharathi, S., Mehta,
G., and Vahi, K. (2013). Characterizing and profiling
scientific workflows. Future Generation Computer
Systems, 29(3):682–692.
Poola, D., Garg, S. K., Buyya, R., Yang, Y., and Ra-
mamohanarao, K. (2014). Robust scheduling of scien-
tific workflows with deadline and budget constraints
in clouds. In 2014 IEEE 28th international confer-
ence on advanced information networking and appli-
cations, pages 858–865. IEEE.
Reyes-Sierra, M., Coello, C. C., et al. (2006). Multi-
objective particle swarm optimizers: A survey of the
state-of-the-art. International journal of computa-
tional intelligence research, 2(3):287–308.
Singh, S. and Chana, I. (2015). Qrsf: Qos-aware resource
scheduling framework in cloud computing. The Jour-
nal of Supercomputing, 71(1):241–292.
Tripathi, P. K., Bandyopadhyay, S., and Pal, S. K. (2007).
Multi-objective particle swarm optimization with time
variant inertia and acceleration coefficients. Informa-
tion sciences, 177(22):5033–5049.
Wangsom, P., Lavangnananda, K., and Bouvry, P. (2019).
Multi-objective scheduling for scientific workflows on
cloud with peer-to-peer clustering. In 2019 11th Inter-
national Conference on Knowledge and Smart Tech-
nology (KST), pages 175–180. IEEE.
Wu, F., Wu, Q., and Tan, Y. (2015). Workflow scheduling
in cloud: a survey. The Journal of Supercomputing,
71(9):3373–3418.
Xu, H., Yang, B., Qi, W., and Ahene, E. (2016). A multi-
objective optimization approach to workflow schedul-
ing in clouds considering fault recovery. KSII Trans-
actions on Internet & Information Systems, 10(3).
Yao, G.-s., Ding, Y.-s., and Hao, K.-r. (2017). Multi-
objective workflow scheduling in cloud system based
on cooperative multi-swarm optimization algorithm.
Journal of Central South University, 24(5):1050–
1062.
Yu, J., Kirley, M., and Buyya, R. (2007). Multi-objective
planning for workflow execution on grids. In Proceed-
ings of the 8th IEEE/ACM International conference on
Grid Computing, pages 10–17. IEEE Computer Soci-
ety.
Yuan, D., Yang, Y., Liu, X., Zhang, G., and Chen, J.
(2012). A data dependency based strategy for inter-
mediate data storage in scientific cloud workflow sys-
tems. Concurrency and Computation: Practice and
Experience, 24(9):956–976.
ICSOFT 2020 - 15th International Conference on Software Technologies
624
