Improving Statistical Reporting Data Explainability via Principal

Component Analysis

Shengkun Xie and Clare Chua-Chow

Global Management Studies, Ted Rogers School of Management, Ryerson University, Toronto, Canada

Keywords:

Explainable Data Analysis, Data Visualization, Principal Component Analysis, Size of Loss Frequency,

Business Analytics.

Abstract:

The study of high dimensional data for decision-making is rapidly growing since it often leads to more accu-

rate information that is needed to make reliable decision. To better understand the natural variation and the

pattern of statistical reporting data, visualization and interpretability of data have been an on-going challeng-

ing problem, mainly, in the area of complex statistical data analysis. In this work, we propose an approach of

dimension reduction and feature extraction using principal component analysis, in a novel way, for analyzing

the statistical reporting data of auto insurance. We investigate the functionality of loss relative frequency, to

the size-of-loss as well as the pattern and variability of extracted features, for a better understanding of the

nature of auto insurance loss data. The proposed method helps improve the data explainability and gives an

in-depth analysis of the overall pattern of the size-of-loss relative frequency. The ﬁndings in our study will

help the insurance regulators to make a better rate ﬁlling decision in the auto insurance that would beneﬁt

both the insurers and their clients. It is also applicable to similar data analysis problems in other business

applications.

1 INTRODUCTION

The study of high dimensional data for decision-

making is rapidly growing since it often leads to more

accurate information, which is needed to make reli-

able decision. (Elgendy and Elragal, 2014; Goodman

and Flaxman, 2017; Hong et al., 2019). Also, global

businesses have entered a new era of decision mak-

ing using big data, and it has posed a new challenge

to most companies. Statistical analysis provides man-

agers with tools for making a better decision. How-

ever, it is always a challenge to pick a better tool to

analyze the data to give a better picture necessary to

make even smarter and better business decisions. In

insurance rate regulation, the statistical data report-

ing is a big data application. It involves many dis-

tributed computer systems to implement data collec-

tions and data summaries, regularly, and the amounts

of data collected are massive (Wickman, 1999). For

example, to study the loss behaviour by the forward

sortation area (FSA) in Ontario, Canada, around 10

Gigabytes of loss data were collected from all auto

insurance companies during the period from 2010 to

2012. Processing this signiﬁcant amount of data to

extract useful information is extremely difﬁcult and

required speciﬁc statistical approaches that can help

reduce the dimensionality and complexity of the data.

This is why the insurance regulators are focusing on

the analysis of statistical reporting, which contains

the aggregate loss information from the industry. On

the other hand, big data is not just about a large vol-

ume of data being collected; it also implies the high

level of complexity of the frequently updated data

(Lin et al., 2017; Bologa et al., 2013). In the regu-

lation process, insurance loss data is continuously be-

ing collected. The collected data are then further ag-

gregated and summarized using some necessary sta-

tistical measures such as count, total and mean. The

data organizations are separated by different factors

of interest. For instance, in statistical data report-

ing of large-loss analysis, claim counts and claim loss

amounts are reported by coverage, territory, accident

year and reporting year (McClenahan, 2014). These

data, which are organized as exhibits, are then used by

insurance regulators for a better understanding of the

insurance risk and uncertainty, through suitable sta-

tistical analysis, both quantitatively and qualitatively.

The obtained results from statistical analysis are used

as guidelines for decision-making of rate ﬁling re-

views. Because of the need for understanding the na-

Xie, S. and Chua-Chow, C.

Improving Statistical Reporting Data Explainability via Principal Component Analysis.

DOI: 10.5220/0009805901850192

In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 185-192

ISBN: 978-989-758-440-4

185

ture of the aggregated loss data, it calls for suitable

data analytics that can be used for processing statis-

tical data reporting. (Xie and Lawniczak, 2018; Xie,

2019).

As a multivariate statistical approach, the conven-

tional Principal Component Analysis (PCA) is often

used to reduce the dimension of multivariate data or

to reconstruct the multidimensional data matrix us-

ing only the selected PCs. However, within the PCA

approach, the functionality between the multivariate

data and other variables is not considered (Bakshi,

1998). Application using PCA may become problem-

atic when multivariate data are interconnected. From

the data visualization perspective, it could be mis-

leading if the frequency value at a given size-of-loss

interval is visualized without incorporating the size-

of-loss in the plot. In statistical data reporting, the

incurred losses are grouped as intervals. Each size-

of-loss interval is not even, and with the increase of

the incurred loss, the width of the intervals dramati-

cally increases. To overcome the potential mistakes

that can be caused by the visualization of loss data,

PCA is used to extract key information from the data

matrix so that the main pattern functionality between

the relative frequency and the size-of-loss can be vi-

sualized properly. By doing so, we signiﬁcantly im-

prove data explainability. In this work, PCA is used

for both low-rank approximations and feature extrac-

tions, with the consideration of the functionality of

relative frequency values and the size-of-loss.

Our contribution to this research area is using

PCA in a novel way, to extract its key features of auto

insurance loss to improve the data visualization for a

better decision-making process. To our best knowl-

edge, the proposed method appears for the ﬁrst time

in literature to consider the data explainability prob-

lem of statistical data reporting in insurance sector.

The proposed method helps to improve the data ex-

plainability as well as a better understanding of the

overall pattern of the size-of-loss relative frequency

at the industry level. Also, feature extraction by PCA

facilitates the understanding of loss count data vari-

ability, both the overall and the local behaviour, and

its natural functionality between the frequency values

and the size-of-loss. The analysis conducted in this

work illustrates the application of a suitable multi-

variate statistical approach to dimension reduction of

statistical data in auto insurance to have a higher data

interpretability. This paper is organized as follows.

In Section 2, the data and its collection are brieﬂy in-

troduced. In Section 3, the proposed methods, includ-

ing feature extraction and low-rank approximation via

PCA, are discussed. In Section 4, analysis of auto in-

surance size-of-loss data and the summary of the main

results are presented. Finally, we conclude our ﬁnd-

ings and provide further remarks in Section 5.

2 DATA

In this work, we focus on the study of the size-of-loss

relative frequency of auto insurance using datasets

from the Insurance Bureau of Canada (IBC), which

is a Canadian organization responsible for insurance

data collections and their statistical data reporting

problems in the area of property and casualty in-

surance. During the data collection process, insur-

ance companies report the loss information, includ-

ing the number of claims, number of exposures, loss

amounts, as well as other key information such as

territories of loss, coverages, driving records associ-

ated with loss, and accident years. These statistical

data are reported regularly (i.e., weekly, biweekly or

monthly). At the end of each half-year, the total claim

amounts and claim counts reported by all insurance

companies are aggregated by territories, coverages,

accident years, etc. The statistical data reporting is

then used for insurance rate regulation to ensure the

premiums charged by insurance companies are fair

and exact. The dataset used in this work consists of

summarized claim counts by different sizes of loss,

which are represented by a set of non-overlapping in-

tervals. The claim counts are aggregated by major

coverages, i.e. Bodily Injuries (BI) and Accident Ben-

eﬁts (AB). Also, the data were summarized by differ-

ent accident years, by different report years and by

different territories, i.e. Urban (U) and Rural (R).

To carry out the study, we organize data by cov-

erages (AB and BI) and by territories (U and R). We

consider the data from different reporting years and

accident years as repeated observations. There are

two reporting years, 2013 and 2014, respectively. For

each reporting year, there is a set of rolling most re-

cent ﬁve years of data corresponding to ﬁve accident

years. Therefore, for this study, we have in total ten

years of observation. Also, since we have both Acci-

dent Beneﬁts and Bodily Injuries as the coverage type

and Urban and Rural as the territory, we consider the

following four different combinations, Accident Ben-

eﬁts and Urban ( ABU), Accident Beneﬁts and Rural

(ABR), Bodily Injuries and Urban (BIU), and Bodily

Injuries and Rural (BIR). These data are then formed

into a data matrix with a 40 × 24 dimension, where

40 is the total number of observations, and 24 is the

number of total intervals of the size-of-loss.

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

186

3 METHODS

3.1 Deﬁning Size of Loss Relative

Frequency Distribution

Since the claim count data was pre-grouped, we must

ﬁrst give a deﬁnition to the empirical size-of-loss rela-

tive frequency distribution based on the aggregate ob-

servations of claim counts. Let f (x) be the true size-

of-loss relative frequency distribution, where x ∈ R

is the ultimate loss. Ideally, to study the size-of-loss

relative frequency distribution function, we would ex-

pect to have a set of raw data pairs of loss frequency

values and the ultimate loss, so that we can estimate

the distribution function by some parametric mod-

elling approaches. However, in statistical data report-

ing, we are only able to analyze the grouped data be-

cause the raw data is usually not available to insur-

ance regulators. For the grouped data, the estimated

size-of-loss relative frequency distribution is deﬁned

as follows

f (x) =

∑

i=1

if x ∈ [l

, l

i+1

), (1)

where C

is the total claim counts associated with the

ith interval. [l

, l

i+1

) is the ith size-of-loss interval.

Note that, the function of

f (x) is an empirical estimate

of its true size-of-loss relative frequency distribution.

In this work, we use the PCA approach to approxi-

mate the function f (x) by retaining only a small num-

ber of principal components. Since we have grouped

data, the function

f (x) is replaced by a vector.

3.2 Feature Extraction by Principal

Component Analysis

Feature extraction is a dimension reduction method in

machine learning. It aims at extracting important and

key features from data so that further analysis can be

facilitated. Assume that we have n observations of

f (x), the function of f (x) is replaced by a p-variate

vector, denoted by Y

=[y

, y

, . . . y

], where i=1,2,. . .,

n. Here n is the number of observations and p is the

number of variables, which corresponds to the num-

ber of size-of-loss intervals. These observation data

can be organized by the following n × p data matrix

Y = (Y

, Y

, . . . , Y

)







. . . y







where y

i j

corresponds to the observed relative fre-

quency value at the ith observation and the jth inter-

val. We assume that each column of Y is centred,

and we will explore both cases with and without scal-

ing on the data matrix Y. Using PCA, we map the

data matrix Y onto a low-dimensional data matrix Z,

which will be deﬁned later. This mapping is achieved

by retaining only a selected number of components,

called principal components. These principal compo-

nents explain the majority of the data variation of the

underlying variables. Speciﬁcally, the ﬁrst principal

component is the normalized linear combination of

variables that lead to the following form:

= φ

+ φ

+ . . . , +φ

, i = 1, . . . , n, (2)

which has the maximum variance, subject to the

constraint

∑

j=1

= 1. The ﬁrst principal com-

ponent loading vector φ

= [φ

, φ

, . . . , φ

]

indi-

cates the direction in the principal component fea-

ture space, and the ﬁrst principal component score

vector Z

= [z

, . . . , z

]

is the projected values of

Y onto the feature subspace φ

. The subsequent

principal components are obtained by following the

same step as the ﬁrst principal component, which

maximizes the variance of the linear combination of

the underlying variables after removing the varia-

tion that has been explained by the previous compo-

nents and they are orthogonal to the previous princi-

pal components. Through this process, we can obtain

the principal component loading matrix, denoted by

φ=[φ

, φ

, . . . , φ

], and the principal component score

matrix, denoted by Z=[Z

, Z

, . . . , Z

]. Also, we have

Z=Yφ

. Once we compute these principal compo-

nents, we can reduce the dimension of our data by

solely focusing on the major principal components.

These low-dimensional projected feature vectors can

be visualized if the dimension is not higher than three.

If we retain only M principal components, then the

principal components scores matrix in the feature sub-

space is given as follows:

∗

= [Z

, Z

, . . . , Z

] =







. . . z







Note that, by retaining only M components, we can

reduce the dimension of data matrix Y from n × p to

n × M, where M  p. This is how we improve the

data explainability using a feature domain, instead of

the original domain. Mapping data matrix Y onto a

feature matrix Z is referred to as feature extraction in

the machine learning literature (Khalid et al., 2014).

Improving Statistical Reporting Data Explainability via Principal Component Analysis

187

3.3 Low Rank Approximation of

Relative Frequency Distribution by

Principal Component Analysis

The relative frequency distribution is considered to be

a function of the size-of-loss, as shown in Equation

(1). By taking a linear combination of observations

with a suitable choice of weight values, one can ex-

tract the major patterns of the size-of-loss relative fre-

quency distribution. The extracted major pattern re-

ﬂects the functionality between the relative frequency

value and the size-of-loss. This function approxima-

tion uses only M principal components to reconstruct

the data matrix Y. Reducing the dimension from p to

M to reconstruct the data matrix Y is called a low-rank

approximation of Y (Clarkson and Woodruff, 2017),

and it can be expressed as follows

Y ≈ Zφ

, (3)

where φ is the p × M loading matrix, and Z is the

n × M score matrix. When M = p, the data matrix is

fully restored by the score and loading matrices. An-

other common approach related to low rank approx-

imation is to ﬁnd principal components through the

Singular Value Decomposition (SVD) of the data ma-

trix Y (Golub and Reinsch, 1971; Alter et al., 2000).

Mathematically, it means that the data matrix Y can

be decomposed into the following equation

Y = UΣV

, (4)

where U is an n × n unitary matrix, Σ is n × p diag-

onal matrix and V is a p × p unitary matrix. For a

given new observation Y with a dimension 1 × p , the

projected value becomes Y V, which is the feature ex-

traction using PCA discussed in section 3.2. If we use

only the ﬁrst M eigenvectors, the dimension of the ex-

tracted feature vector is M.

On the other hand, based on Equation (4), we can

derive the spectral decomposition of Y

Y as shown

below in Equation (5)

Y = VΣ

UΣV

, (5)

where Y

Y can be interpreted as the p × p sample

covariance matrix. Since U is an unitary matrix, we

have U

U= 1, which is an identity matrix. This im-

plies that

Y = VΣ

ΣV

= (VΣ)(VΣ)

. (6)

This is a cholesky decomposition of YY

. Note that,

the following solution of Y solves the above Equation

∗

= ΣV

. (7)

Using Equations (4) and (7), we can obtain Y = UY

∗

This result implies that any orthogonal decomposition

of Y

∗

will solve Equation (6). This is the reason why

the principal component is not unique.

Orignal ABU

0.00 0.08

L0 L3 L6 L9 L12 L15 L18 L21

Approximation ABU

0.00 0.08

Orignal ABR

0.00 0.15

L0 L3 L6 L9 L12 L15 L18 L21

Approximation ABR

0.00 0.15

Orignal BIU

0.00 0.20

L0 L3 L6 L9 L12 L15 L18 L21

Approximation BIU

0.00 0.20

Orignal BIR

0.0 0.3

L0 L3 L6 L9 L12 L15 L18 L21

Approximation BIR

0.0 0.3

Figure 1: The barplots of loss relative frequency by differ-

ent combinations of major coverages and territories, before

and after reconstruction using the ﬁrst ﬁve principal com-

ponents.

Orignal ABU

0.00 0.08

L0 L3 L6 L9 L12 L15 L18 L21

Approximation ABU

0.00 0.08

Orignal ABR

0.00 0.15

L0 L3 L6 L9 L12 L15 L18 L21

Approximation ABR

0.00 0.15

Orignal BIU

0.00 0.20

L0 L3 L6 L9 L12 L15 L18 L21

Approximation BIU

0.00 0.25

Orignal BIR

0.0 0.3

L0 L3 L6 L9 L12 L15 L18 L21

Approximation BIR

0.0 0.3

Figure 2: The barplots of loss relative frequency by differ-

ent combinations of major coverages and territories, before

and after reconstruction using only the ﬁrst two principal

components.

4 RESULTS

First, we illustrate that the visualization of the size-of-

loss distribution could be misleading when the func-

tionality between relative frequency values and the

size-of-loss is not considered. Figures 1 and 2 show

the relative frequency values for all combinations of

major coverages and territories. It is mistaken if one

tries to comment on the shape of the distribution since

the intervals of the size-of-loss are not the same. The

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

188

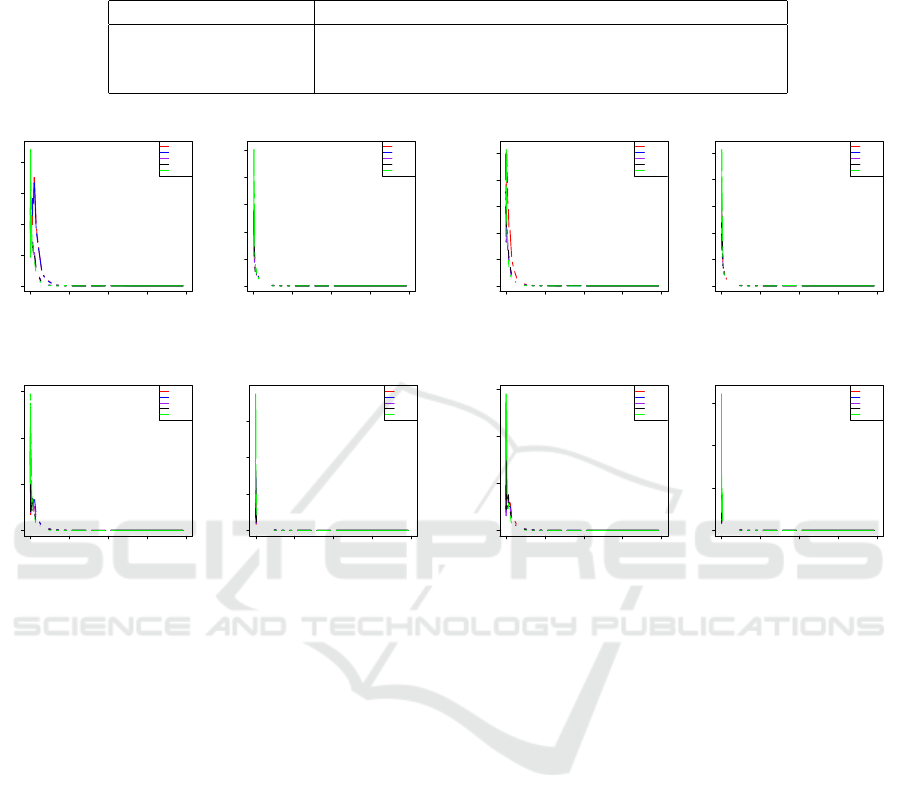
Table 1: Results of the ﬁrst 6 PCs of loss relative frequency, including the standard deviation of principal component, the

proportion of variation explained by each principal component and the cumulative proportion of variation explained by the

ﬁrst few PCs.

PC1 PC2 PC3 PC4 PC5 PC6

Standard deviation 3.8051 2.2667 1.2818 0.8789 0.7836 0.6426

Proportion of Variance 0.6033 0.2141 0.0684 0.0321 0.0255 0.0172

Cumulative Proportion 0.6033 0.8174 0.8858 0.9180 0.9436 0.9608

●

0 500000 1000000 1500000 2000000

0.00 0.02 0.04 0.06 0.08

AB−Ubran−2013 Report Year

Size of Loss

Frequency

●

● ●

●

AY2009

AY2010

AY2011

AY2012

AY2013

(a) ABU

●

0 500000 1000000 1500000 2000000

0.00 0.02 0.04 0.06 0.08 0.10

AB−Rural−2013 Report Year

Size of Loss

Frequency

●

AY2009

AY2010

AY2011

AY2012

AY2013

(b) ABR

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

BI−Ubran−2013 Report Year

Size of Loss

Frequency

●

AY2009

AY2010

AY2011

AY2012

AY2013

●

● ●

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

BI−Rural−2013 Report Year

Size of Loss Level

Frequency

●

● ●

●

● ●

●

● ●

●

AY2009

AY2010

AY2011

AY2012

AY2013

(d) BIR

Figure 3: The loss relative frequency patterns for different

accident years and different combinations of coverage and

territory for 2013 reporting year, with respect to the size-of-

loss.

interval width is dramatically increased with the in-

crease of the size-of-loss. The shape of the distribu-

tion heavily depends on the size-of-loss. This result

implies that when visualizing the relative frequency

values, they must be presented with respect to the

size-of-loss. When this is the case, the tail of the dis-

tribution is much heavier as the bars located at right

side of the distribution are stretched out, and the bars

located at the left-hand side will be combined and be-

come more dominant than other size-of-loss. In addi-

tion, Figures 1 and 2 summarized the results using the

PCA to reconstruct the data matrix stated in Equation

(3). In Figure 1, ﬁve PCs were used, while in Figure

2, only two PCs were used. The results show the more

PCs used the better approximation of the original data

pattern. However, if only the major PCs were used,

one can observe a similar tendency of the loss relative

frequency within the same coverage, which leads to

a better data interpretability. In Figures 3 and 4, the

relative frequency values of different accident years

●

● ●

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15 0.20 0.25

AB−Ubran−2014 Report Year

Size of Loss

Frequency

●

● ●

●

AY2010

AY2011

AY2012

AY2013

AY2014

(a) ABU

●

● ●

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15 0.20 0.25

AB−Rural−2014 Report Year

Size of Loss

Frequency

●

● ●

●

AY2010

AY2011

AY2012

AY2013

AY2014

(b) ABR

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

BI−Ubran−2014 Report Year

Size of Loss

Frequency

●

AY2010

AY2011

AY2012

AY2013

AY2014

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

BI−Rural−2014 Report Year

Size of Loss

Frequency

●

● ●

●

AY2010

AY2011

AY2012

AY2013

AY2014

(d) BIR

Figure 4: The loss relative frequency patterns for different

accident years and different combinations of coverage and

territory for 2014 reporting year, with respect to the size-of-

loss.

with respect to the size-of-loss for different combina-

tions of coverage and territory of the reporting years

of 2013 and 2014 are presented. The results shown in

Figures 3 and 4 are more interpretable as they show

clearly the similar loss patten for different accident

years.

The results shown in Figures 3 and 4 reveal that

the size-of-loss relative frequency values do not heav-

ily depend on the reporting years. The result implies

that the claim counts were mainly developed within

the accident year. We also observe that within the

same coverage, either AB or BI, the size-of-loss rela-

tive frequency appears to have high similarity among

different accident years. For both coverages, the

zero claim amount has the most dominant frequency.

This fact implies that many reported claims cause

zero loss, which may be due to the insurance de-

ductible. This result suggests that the loss amount

associated with zero size-of-loss is mainly due to the

expenses that occurred during the claim reporting pro-

Improving Statistical Reporting Data Explainability via Principal Component Analysis

189

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

AB−Ubran−2013 Report Year

Size of Loss

Frequency

●

AY2009

AY2010

AY2011

AY2012

AY2013

(a) ABU

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

AB−Rural−2013 Report Year

Size of Loss

Frequency

●

AY2009

AY2010

AY2011

AY2012

AY2013

(b) ABR

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35

BI−Ubran−2013 Report Year

Size of Loss

Frequency

●

AY2009

AY2010

AY2011

AY2012

AY2013

●

0 500000 1000000 1500000 2000000

0.0 0.1 0.2 0.3 0.4

BI−Rural−2013 Report Year

Size of Loss

Frequency

●

AY2009

AY2010

AY2011

AY2012

AY2013

(d) BIR

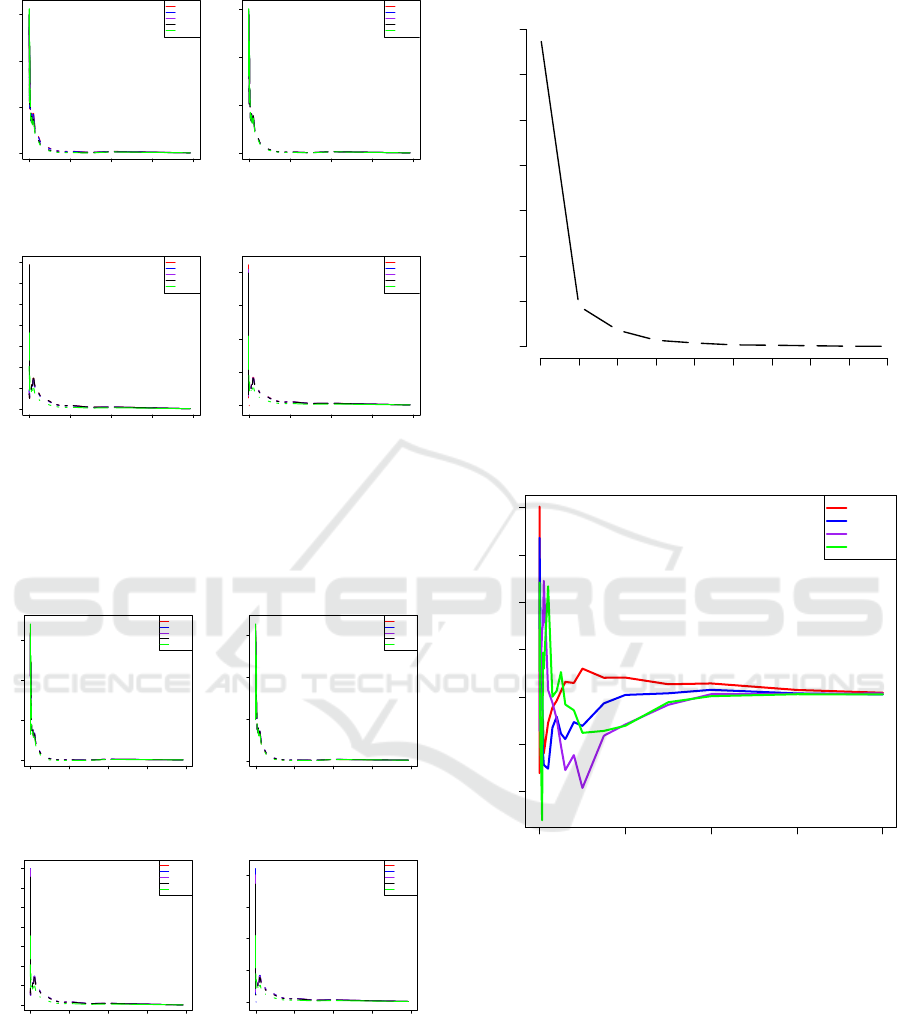
Figure 5: The ﬁrst principal component approximation of

loss relative frequency patterns of different accident years

and different combinations of coverage and territory for

2013 reporting year, with respect to the size-of-loss.

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

AB−Ubran−2014 Report Year

Size of Loss Level

Frequency

●

AY2010

AY2011

AY2012

AY2013

AY2014

(a) ABU

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15

AB−Rural−2014 Report Year

Size of Loss

Frequency

●

AY2010

AY2011

AY2012

AY2013

AY2014

(b)ABR

●

0 500000 1000000 1500000 2000000

0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35

BI−Ubran−2014 Report Year

Size of Loss

Frequency

●

AY2010

AY2011

AY2012

AY2013

AY2014

●

0 500000 1000000 1500000 2000000

0.0 0.1 0.2 0.3 0.4

BI−Rural−2014 Report Year

Size of Loss

Frequency

●

AY2010

AY2011

AY2012

AY2013

AY2014

(d) BIR

Figure 6: The ﬁrst principal component approximation of

loss relative frequency patterns of different accident years

and different combinations of coverage and territory for

2014 reporting year, with respect to the size-of-loss.

cess. From the management perspective, reducing

the processing of claims with zero loss is necessary

●

Claim Counts Scree Plot

Variances

0.000 0.005 0.010 0.015 0.020 0.025 0.030 0.035

1 2 3 4 5 6 7 8 9 10

Figure 7: The Scree plot, which shows the distribution of

eigenvalues with respect to their principal components.

0e+00 1e+05 2e+05 3e+05 4e+05

−0.4 −0.2 0.0 0.2 0.4 0.6 0.8

Principal Component Vector Plot

Size of Loss

Harmonic

●

1st PC

2nd PC

3rd PC

4th PC

Figure 8: The plot of principal component loadings with

respect to the size-of-loss for the ﬁrst four PCs.

for auto insurance companies to signiﬁcantly reduce

the total expenses. On the other hand, in Figures 3

and 4, the overall pattern of AB coverage shows that

as the size-of-loss increases, the claim frequency de-

creases. For BI coverage, the overall pattern of loss

relative frequency shows that as the size-of-loss in-

creases, the claim frequency decreases ﬁrst, then it

increases again. It reaches the local maximum at the

size-of-loss around $5,000 to $75,000. In Figures 5

and 6 show the approximation of size-of-loss relative

frequency using only the ﬁrst PC to reconstruct the

data matrix. From these results, we observe that the

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

190

●

−2.5

0.0

2.5

−4 0 4 8

PC1 (60.3% explained var.)

PC2 (21.4% explained var.)

● ● ● ●

ABR ABU BIR BIU

Figure 9: The extracted two dimensional features, which

are the ﬁrst two principal components, with the input data

being scaled.

●

−0.1

0.0

0.1

−0.2 0.0 0.2

PC1 (81.5% explained var.)

PC2 (10.6% explained var.)

● ● ● ●

ABR ABU BIR BIU

Figure 10: The extracted two dimensional features, which

are the ﬁrst two principal components, without the input

data being scaled.

overall relative frequency pattern was picked up by

the ﬁrst PC, although there are some small differences

when comparing to the original observations shown

in Figures 3 and 4. The beneﬁt of having these ma-

jor patterns recognized by the ﬁrst PC is to enhance a

understanding of driving forces for insurance claims.

Coverages and Territories might share some common-

ality in claim frequency distribution.

Figure 7 displays the results of eigenvalues for

their principal components. From the results shown

in 7, we can see that the ﬁrst four PCs can explain the

signiﬁcant amount of data variation. These four PCs

have explained more than 95% of the total variation,

which can be seen from Table 1. In particular, the ﬁrst

principal component and the second principal compo-

nents have explained about 60% and 21% of the total

variation, respectively. That is to say, the ﬁrst two

PCs have been able to explain 81% of the total varia-

tion. In Figure 8, the harmonic pattern as a function

of the size-of-loss is displayed. The result shows that

the main harmonic patterns are signiﬁcant only be-

tween zero and $250,000 as the harmonic approaches

to zero when the size-of-loss is greater than $250,000.

Also, this result implies that the primary insurance un-

certainty in terms of loss relative frequency is mainly

concentrated in between zero and $250,000. The ﬂuc-

tuation of loss relative frequency from different acci-

dent years and different reporting years starts to be-

come small when an individual size-of-loss is higher

than $250,000. This result provides us with valuable

information on the estimate of the cut-off value of the

large size-of-loss, which is an important aspect that

leads to reinsurance or determination of the large size-

of-loss loading factor. On the other hand, the ﬁrst two

principal component loading vectors, share a similar

functionality with respect to the size-of-loss. In con-

trast, the third and fourth principal component load-

ing behaves similarly and go in the opposite direction

from the ﬁrst two PCs. This fact may suggest that dif-

ferent principal components could explain the diverse

nature of variation. To extract the major pattern of the

loss data is to see if there is anything in common, one

should focus on either the ﬁrst or ﬁrst two PCs.

Figures 9 and 10 show the extraction of two-

dimensional features, respectively, for both cases of

input data with and without scaling. In practice, It

is critical to see if there is an effect from the scaling

of the data because the variation of each underlying

variable may be different, because the separation of

extracted features may be affected by the scales of the

variables. Figure 9 shows the results with scaling be-

fore applying PCA. The result reveals that the two-

dimensional features can be separated by the type of

data with a slight overlapping part on AB coverage

(ABR and ABU). The BI coverage is well separated

by different territories. The result suggests that PCA

could form each type of claim count data into clusters,

which facilitates the understanding of their similari-

ties and differences. Furthermore, the extracted fea-

tures of the BI coverage appear to be more linear than

the features extracted from the AB coverage. This re-

sult implies that the extracted features of the BI cov-

erage are more correlated within the same territory.

Based on this result, we can further infer that the low-

rank approximation of original data enhance the level

of similarity within the same territory. This result co-

incides with the observation we found in both Figures

5 and 6, which suggests a high level of similarity of

relative frequency distribution among different com-

binations of territory. However, PCA can only capture

the similarity within the BI coverage, but not the AB

coverage. Similarly, Figure 10 displays the extracted

features from the ﬁrst two PCs, using the input data

without scaling. We can observe that without scaling,

the separability of the extracted features is lower than

Improving Statistical Reporting Data Explainability via Principal Component Analysis

191

the one associated with the scaled input data. From

the result, we can conclude that it is crucial to scale

the data when using the PCA approach.

5 CONCLUDING REMARKS

Data visualization and data interpretability improve-

ment have been an on-going challenging problem in

the complex statistical analysis. Importantly our re-

search has shown that breaking down the grouped

data using PCA will give more detailed information

for the insurance regulators to make better decision.

In this work, we proposed PCA as feature extraction

and low-rank approximation methods, and we applied

it to the auto insurance size-of-loss data. We illustrate

that PCA is a suitable technique to improve data visu-

alization and the interpretability of data. First, we use

principal component analysis to extract data features

from the size-of-loss relative frequency distributions

for a better understanding of their natural ﬂuctuation

and functionality to the size-of-loss. We also use PCA

to reconstruct the input data matrix so that the major

pattern of the size-of-loss relative frequency distribu-

tion can be obtained for data from a combination of

major coverages and territories. By doing these, we

capture the common functionality of data so that the

result can be used as a baseline of the size-of-loss rel-

ative frequency distribution. Our study shows that the

size-of-loss distributions share some common statis-

tical property within the same major coverage or the

same territory. It is necessary to further study this

commonality by relating the size-of-loss relative fre-

quency pattern to some potential risk factors, includ-

ing coverages, territories, accident years and report-

ing years. It is interesting to estimate these factor

effects and to test their statistical signiﬁcance in the

future research.

REFERENCES

Alter, O., Brown, P. O., and Botstein, D. (2000). Singu-

lar value decomposition for genome-wide expression

data processing and modeling. Proceedings of the Na-

tional Academy of Sciences, 97(18):10101–10106.

Bakshi, B. R. (1998). Multiscale pca with application to

multivariate statistical process monitoring. AIChE

journal, 44(7):1596–1610.

Bologa, A.-R., Bologa, R., Florea, A., et al. (2013). Big

data and speciﬁc analysis methods for insurance fraud

detection. Database Systems Journal, 4(4):30–39.

Clarkson, K. L. and Woodruff, D. P. (2017). Low-rank

approximation and regression in input sparsity time.

Journal of the ACM (JACM), 63(6):54.

Elgendy, N. and Elragal, A. (2014). Big data analytics: a

literature review paper. In Industrial Conference on

Data Mining, pages 214–227. Springer.

Golub, G. H. and Reinsch, C. (1971). Singular value de-

composition and least squares solutions. In Linear Al-

gebra, pages 134–151. Springer.

Goodman, B. and Flaxman, S. (2017). European union reg-

ulations on algorithmic decision-making and a “right

to explanation”. AI Magazine, 38(3):50–57.

Hong, S., Hyoung Kim, S., Kim, Y., and Park, J. (2019).

Big data and government: Evidence of the role of

big data for smart cities. Big Data & Society,

6(1):2053951719842543.

Khalid, S., Khalil, T., and Nasreen, S. (2014). A survey of

feature selection and feature extraction techniques in

machine learning. In 2014 Science and Information

Conference, pages 372–378. IEEE.

Lin, W., Wu, Z., Lin, L., Wen, A., and Li, J. (2017). An

ensemble random forest algorithm for insurance big

data analysis. Ieee Access, 5:16568–16575.

McClenahan, C. L. (2014). Ratemaking. Wiley StatsRef:

Statistics Reference Online.

Wickman, A. E. (1999). Insurance data and intellectual

property issues. In CASUALTY ACTUARIAL SOCI-

ETY FORUM Winter 1999 Including the Ratemaking

Discussion Papers, page 309. Citeseer.

Xie, S. (2019). Deﬁning geographical rating territories

in auto insurance regulation by spatially constrained

clustering. Risks, 7(2):42.

Xie, S. and Lawniczak, A. (2018). Estimating major risk

factor relativities in rate ﬁlings using generalized lin-

ear models. International Journal of Financial Stud-

ies, 6(4):84.

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

192