A Parallel Many-core CUDA-based Graph Labeling Computation
Stefano Quer
a
Department of Control and Computer Engineering (DAUIN), Politecnico di Torino, Turin, Italy
Keywords:
Graph Theory, Graph Algorithms, Algorithm Design and Analysis, Parallel Algorithms, Graphics Processors.
Abstract:
When working on graphs, reachability is among the most common problems to address, since it is the base
for many other algorithms. As with the advent of distributed systems, which process large amounts of data,
many applications must quickly explore graphs with millions of vertices, scalable solutions have become
of paramount importance. Modern GPUs provide highly parallel systems based on many-core architectures
and have gained popularity in parallelizing algorithms that run on large data sets. In this paper, we extend
a very efficient state-of-the-art graph-labeling method, namely the GRAIL algorithm, to architectures which
exhibit a great amount of data parallelism, i.e., many-core CUDA-based GPUs. GRAIL creates a scalable
index for answering reachability queries, and it heavily relies on depth-first searches. As depth-first visits are
intrinsically recursive and they cannot be efficiently implemented on parallel systems, we devise an alternative
approach based on a sequence of breadth-first visits. The paper explores our efforts in this direction, and it
analyzes the difficulties encountered and the solutions chosen to overcome them. It also presents a comparison
(in terms of times to create the index and to use it for reachability queries) between the CPU and the GPU-
based versions.
1 INTRODUCTION
Given a directed graph, the basic reachability query
answers whether there is a simple path leading from a
vertex u to another vertex v. Reachability plays an
important role in several modern applications such
as office systems, software management, geograph-
ical navigation, Internet routing, and XML index-
ing. As one of the most fundamental graph opera-
tors, it has also drawn much research interest in re-
cent years (Chen and Chen, 2011; Zhang et al., 2012;
Ruoming and Guan, 2013; Su et al., 2017).
Standard approaches to solve reachability queries
rely either on graph traversal algorithms or on the
computation of the Transitive Closure of the graph.
Unfortunately, breadth-first (BFS) and depth-first
(DFS) searches have linear time complexity (in the
graph size) for each query. At the same time, stor-
ing the list of all reachable nodes for every vertex
implies a quadratic memory occupation (in the graph
size). As a consequence, both of these direct ap-
proaches do not scale well for large graphs, and most
practical reachability algorithms lie somewhere in be-
tween them. Current approaches usually involve a
pre-processing phase which creates an “index”, and
a
https://orcid.org/0000-0001-6835-8277
then they use this index to achieve efficient traversal
times for each query. An index essentially consists in
some sort of graph labeling, i.e., it associates extra in-
formation items with the vertices, while keeping their
amount within reasonable limits. These data struc-
tures are then used to develop efficient queries, result-
ing in a speed-up of the query resolution time at the
expense of requiring more space to store the labeling.
Existing algorithms differentiate themselves accord-
ing to several factors, but the trade-off between the in-
dexing space and the querying time often constitutes
their basic characteristic. In recent times their biggest
limitation lies in their capacity to process large graphs
efficiently, and so scalability has become one of the
most significant metrics for analyzing reachability
methods.
Interestingly, recently there has also been an
emerging trend to develop applications that scale
gracefully by exploiting the increasing number of
processors provided by parallel systems. The ad-
vent of NVIDIA’s general purpose GPU (Graphi-
cal Processing Unit) architecture, commonly known
as CUDA, has transformed mainstream computers
into highly-parallel systems with significant compu-
tational power. Since the release of CUDA’s first
version in 2006, there has been a continued effort
to redesign algorithms in order for them to exhibit a
Quer, S.
A Parallel Many-core CUDA-based Graph Labeling Computation.
DOI: 10.5220/0009780205970605
In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 597-605
ISBN: 978-989-758-443-5
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
597

large degree of data parallelism and benefit from the
ever-increasing number of processors and bandwidth
available on GPUs. Specifically, GPUs are especially
designed to concurrently and efficiently execute the
same program over different data. For that reason,
there has been a recent boost in producing graph-
processing software in CUDA, both from NVIDIA,
with its NVIDIA Graph Analytic library, and from in-
dependent projects, such as the recent GUNROCK li-
brary.
In this context, we propose an analysis, and
a many-core CUDA-based implementation, of the
indexing method called GRAIL (Yildirim et al.,
2010). GRAIL (Graph Reachability Indexing via
RAndomized Interval Labeling) was designed with
particular emphasis on scalability as it has linear in-
dex creation time and linear space occupation. More-
over, it is able to solve reachability queries with time
costs ranging from constant to linear in the graph size.
The core of this work is to study how to redesign its
entire work-flow such that it exhibits a higher degree
of data parallelism, and it can benefit from execution
on Single Instruction, Multiple Threads (SIMT) sys-
tems.
GRAIL is essentially based on the DFS procedure.
DFS is intrinsically recursive and it essentially pro-
ceeds sequentially on the graph, as it recursively visits
single paths in-depth. Unfortunately, CUDA (even us-
ing Dynamic Parallelism) does not support more than
24 in-depth recursion levels, and it is still only suit-
able to manage small graphs. For this reason, the first
step necessary to adapt the algorithm to CUDA, is to
modify its execution structure in order to formally re-
move recursion and to increase parallelism. As ex-
plicitly substituting recursion adopting a “user” stack
would not satisfy our requirements in terms of effi-
ciency and memory usage, we resort to Naumov et
al. (Naumov et al., 2017) in order to exploit specific
properties of Direct Acyclic Graphs (DAGs). In this
way, we replace one single DFS run with three BFS
executions able to partially label all graph vertices as
desired. As BFS is by definition not recursive, and
it iteratively expands set of states (the frontier set),
it enables a much higher degree of data parallelism.
Partial labels will then be completed into label pairs
(suited to perform interval inclusion checks) by us-
ing one more BFS visit. As a consequence, as the
final algorithm will perform four BFS traversals in-
stead of one DFS of its CPU-based counterpart, it
will be fundamental to rely on a very work-efficient
BFS on CUDA. Thus, we will devote a considerable
effort on adapting state-of-the-art BFS algorithms to
suit our needs, following other works in the area, such
as (Luo et al., 2010; Liu and Howie Huang, 2015; Shi
et al., 2018). Our experimental results will prove that
the CUDA-based GPU implementation is faster, or at
least competitive, with the original CPU one. This re-
sult also open new fields of research, where heteroge-
neous computational units may work together to solve
complex tasks.
The paper is organized as follow. Section 2 intro-
duces the related works and the required background.
Section 3 describes our methodology while Section 4
reports our experimental results. Finally, Section 5
draws some conclusions and reports some hints on fu-
ture works.
2 BACKGROUND
2.1 Related Works
The majority of the existing reachability computation
approaches belong to three main categories.
The first category (Su et al., 2017) includes on-
line searches. Instead of materializing the transi-
tive closure, these methods use auxiliary labeling in-
formation for each vertex. This information is pre-
computed and used for pruning the search space.
These approaches can usually be applicable to very
large graphs but their query performance is not always
appealing as they can be one or two orders of magni-
tude slower than the ones belonging to the other two
categories.
The second category (Ruoming and Guan, 2013)
includes reachability oracles, more commonly known
as hop labeling. Each vertex v is labeled with two
sets: L
out(v)
, which contains hops (vertices) v can
reach, and L
in(v)
, which contains hops that can reach v.
Given those two sets for each vertex v, it is possible to
compute whether u reaches v by determining whether
there is at least a common hop, L
out(u)
∩ L
in(v)
6=
/
0.
These methods lie in between the first and the third
category, thus, they should be able to deliver more
compact indices and also offer fast query perfor-
mance.
The third category (Jin et al., 2008; Chen and
Chen, 2011) includes transitive closure compression
approaches. These methods compress the transitive
closure, i.e., they store for each vertex v a compact
representation of all vertices reachable from v, i.e.,
TC(v). The reachability from vertex v to u is then
verified by checking vertex u against TC(v). Exist-
ing studies show how these approaches are the fastest
in terms of query answering even if representing the
transitive closure, despite compression, is still expen-
sive. For that reason, these approaches do not scale
well enough on large graphs.
ICSOFT 2020 - 15th International Conference on Software Technologies
598

To sum up, after more than two decades since first
proposals and a long list of worthy attempts, many
adopted techniques fail to meet general expectations,
are exceedingly complex, or do not scale well enough.
2.2 Notation
Let G = (V, E) be a directed graph with V being the
set of vertices and E the set of directed edges. We
shall refer to the cardinality of V and E, respectively,
with n and m. Our implementations adopt the Com-
pressed Sparse Row (CSR) representation for a graph,
which is able to offer fast row access while avoid-
ing useless overhead for very sparse matrices. CSR is
particularly well suited to represent very large graphs
since it is basically a matrix-based representation that
stores only non-zero elements of every row and, as
such, is able to offer fast row access while avoiding
useless overhead for very sparse matrices.
We use the notation u →
?
v to indicate the reacha-
bility query to check whether there is a path that goes
from node u to node v. Moreover, we write u → v to
indicate that such a path exists, and u 6→ v if it does
not exist.
As a last comment, let us remember that reachabil-
ity on directed graphs can be reduced to reachability
on Directed Acyclic Graphs (DAGs), since for every
directed graph it is possible to construct a condensa-
tion graph finding all strongly connected components
of the original graph. Henceforth, it will be assumed
that all following graphs are directed and acyclic.
2.3 GPUs and CUDA
Modern GPU processors consist of a SIMT (Single
Instruction, Multiple Threads) architecture. SIMT
processors may manage thousand of threads, where
threads are divided into blocks of threads belonging
to different SIMD (Single Instruction, Multiple Data)
core processors. Within the same block, synchroniza-
tion is basically free, but divergent control flow can
significantly reduce the efficiency within the block.
Memory access patterns can also affect the perfor-
mance and typically each SIMD processor in a SIMT
machine is designed to access data from the same
cache.
Nowadays, CUDA and OpenCL are the leading
GPU frameworks. CUDA is a proprietary framework
created by NVIDIA, whilst OpenCL is open source.
Even if OpenCL is supported in more applications
than CUDA, the general consensus is that CUDA gen-
erates better performance results as NVIDIA provides
extremely good integration. For that reason, we will
explicitly refer to CUDA in the sequel.
2.4 The GRAIL Approach
Interval labeling consists in assigning to each node a
label representing an interval. Intervals are usually
generated using either a pre-post or a min-post label-
ing scheme. GRAIL (Yildirim et al., 2010) uses the
min-post labeling, and it assigns to each graph vertex
v an interval label L
v
such that L
v
= [s
v
, e
v
], where:
• e
v
(or outer rank) is defined as the rank of vertex
v in a post-order traversal.
• s
v
(or inner rank) is equal to e
v
, if the vertex is a
leaf, and it is the minimum e
v
among the descen-
dants of v if the vertex is an internal node.
Then, based on the observations that for Direct Trees
(DTs) every node has a single parent, GRAIL checks
reachability verifying interval containment, i.e., given
two nodes u and v and their labels, respectively L
u
and
L
v
, u → v ⇔ L
v
⊆ L
u
.
For example, for the DT of Fig. 1(a) the labeling
can be constructed through a simple DFS, with a con-
struction time which is linear in the number of ver-
tices. Then, it can be used to verify that E 6→ L, since
[2, 2] 6⊆ [5, 5], and that D → L, since [2, 2] ⊆ [1, 4].
D
H
E
[5,5]
[7,9]
[7,8]
[1,3]
[2,2]
[1,6]
[7,7]
[1,4]
[1,10]
A
B
C
G
I
L
F
[1,1]
(a)
E
D
C
H
G
A
[1,9]
[1,8]
[2,2]
[1,3]
[1,5]
[1,4]
[1,10]
B
F
I
L
[1,1]
[1,6]
[1,7]
(b)
E
D
H
G
[2,2]
[1,3]
[1,8]
[1,9]
[1,5][1,8]
[1,7]
[1,3]
[1,5]
[4,4]
[1,1]
[1,1]
[1,10]
[1,10]
[1,6]
[1,9]
[1,6]
[1,7]
[1,2]
[1,4]
A
B
C
F
I
L
(c)
Figure 1: A DT (a) and a DAG (b) with a single label pair,
and the same DAG (c) with two label pairs.
For DAGs, that are a generalization of DTs, min-
post labeling correctly detects all reachable pairs. Un-
fortunately, is may also falsely detect as reachable
pairs that are actually unreachable. This effect can
be seen in Fig. 1(b), where as node I has vertices E,
G and H as parents, its inner rank will propagate to
all of them. This entails that two nodes that do not
reach each other but have a common descendant, such
as E and F, could be marked as reachable. In fact,
[1, 5] ⊆ [1, 8] and this would result in concluding that
F → E, which is not true.
To avoid exceptions as long as possible, GRAIL’s
approach randomizes multiple interval labeling, i.e.,
instead of using a unique label, it performs many
traversals following random orders, creating multi-
ple intervals for every vertex. The result of this pro-
A Parallel Many-core CUDA-based Graph Labeling Computation
599

cess is represented in Fig. 1(c) for two label pairs. In
this case, we can see that F 6→ E as [1, 5] ⊆ [1, 8] but
[1, 8] 6⊆ [1, 3].
Usually, a small number of labels is sufficient
to drastically reduce the number of exceptions. By
adding just one label, one can notice that the num-
ber of exceptions in the graph of Fig. 1b decreased
from 15 to just 3. All remaining false positives must
be dealt with by creating exception lists, which may
be expensive, or by resorting to extra DFS queries,
that are anyhow much faster than the original DFSs as
they use interval comparison to prune the tree at every
level. Maintaining d intervals per node implies that
the amount of memory to store the index is O(d · n),
and the construction algorithm runs in O(d · (n + m)),
both still linear in the graph size. Since the number
of possible labelings is exponential, usual values for
d go from 2 to 5, regardless of the graph’s size.
3 GRAPH EXPLORATION
Despite their high computing throughput, GPUs can
be particularly sensitive to several computational is-
sues. In particular, GPUs are poorly suited for graph
computation and BFS is representative of a class of
algorithms for which it is hard to obtain significantly
better performance from parallelization. Memory us-
age optimization is also non-trivial because memory
access patterns are determined by the structure of
the input graph. Moreover, parallelization introduces
contention, memory and control flow divergence, load
imbalance, and under-utilization on multi-threaded
architectures.
As reported by Merrill et al. (Merrill et al., 2012),
previous works on parallel graph algorithms relied
on two key architectural features for performance.
The first focuses on hiding memory latency, adopt-
ing multi-threading and overlapped computations.
The second concentrates on fine-grained synchroniza-
tion, adopting specific atomic read-write operations.
Atomicity is especially useful to coordinate dynamic
shared data manipulation and to arbitrate contended
status updates.
However, even if modern GPU architectures pro-
vide both mechanisms, serialization from atomic syn-
chronization is particularly expensive for GPUs in
terms of efficiency and performance. Moreover, mu-
tual exclusion does not scale to thousands of threads.
3.1 The Labeling Strategy in CUDA
Standard DFS-based labeling approaches traverse
graphs recursively following a specific vertex order
for each node. Moreover, they update global variables
(which need to be protected and accessed in mutual
exclusion in parallel environments) representing in-
ner and outer ranks during the visit. These character-
istics are conspicuous limitations for parallelization.
However, while DFS explores single paths in-depth
until all vertices have been reached, BFS expands the
current set of vertices (i.e., the current frontier) in par-
allel. In other words, BFS has no restrictions against
the number of vertices being processed concurrently,
and it allows a higher degree of data parallelism.
The key to substitute DFSs with BFSs for graph
labeling is to realize that finding the post-order of a
node in a directed tree DT is equivalent to computing
an offset based on the number of nodes to the left and
below the node itself. Following Naumov et al. (Nau-
mov et al., 2017), we will substitute a single DFS with
three BFSs able to compute in parallel the number of
nodes that every vertex can reach. This process pro-
duces a complete label pair for each node, but this
labeling, which uses separate counters for the pre and
post-order ranks, is not suited to check for label in-
clusion. Thus, for each graph vertex v, we retain only
its outer rank e
v
and we adopt an extra breadth-first
visit to recompute the inner rank and to build the en-
tire min-post labels L
v
= [s
v
, e
v
] for each vertex. The
entire process (including four BFSs) is described by
Algorithm 1, and illustrated by the running example
of Fig. 2. Pseudo-codes are not reported for the sake
of space.
COMPUTELABELS (G)
1: DT = DAGTODT (G)
2: COMPUTESUBGRAPHSIZE (DT)
3: COMPUTEPOSTORDER (DT)
4: COMPUTEMINPOSTLABELING (DT)
Algorithm 1: GRAIL labels computation through four
BFSs.
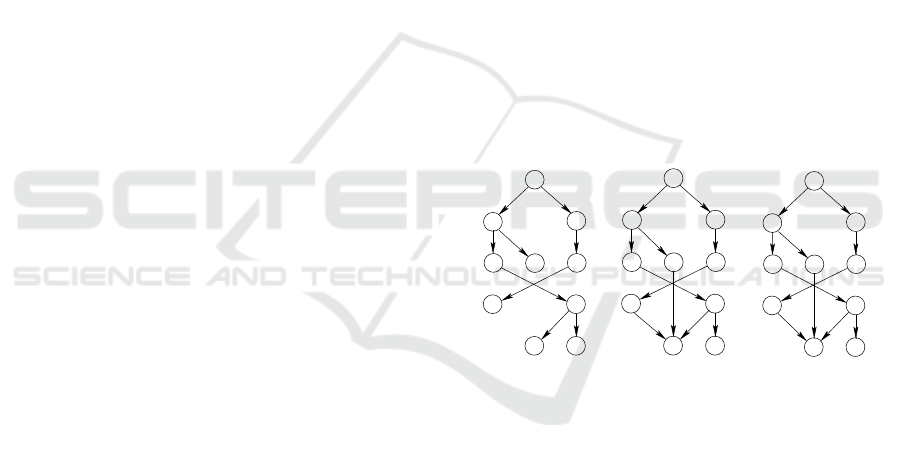
Fig. 2a shows the initial graph G, i.e., a very sim-
ple DAG, composed by only 7 nodes for the sake of
simplicity.
Fig. 2b shows the DT derived from the graph of
Fig. 2a by function DAGTODT of line 2 of Algo-
rithm 2. Generally speaking, there are many methods
to select a parent for each vertex and transform a DAG
into a DT. The so called “path based method” follows
an intuitive approach, as it iterates over the graph’s
nodes through a top-down BFS and it assigns to each
child its parent’s path, unless the children has already
been provided with a path. In that case a node-by-
node comparison of the two paths takes place, until
a decision point is found and solved by selecting the
path with the “smaller” node according to the order-
ing relationship in the graph.
ICSOFT 2020 - 15th International Conference on Software Technologies
600

A
G
E
F
C
B
D
(a) G.
B
A
D
G
E
F
C
(b) DT.
A
D
G
E
F
C
B
1 2
4
7
2
1
1
ζ
v
(c) ζ
v
.
ζ
,
~
v
τ
v
B
A
D
G
E
C
0,0
0,0
4,4
1,1
0,1
0,4
F
0,0
(d)
˜
ζ
v
, τ
v
.
B
A
G
E
F
C
E
(7−1)+0=6
(4−1)+0=3
(1−1)+0=0
(2−1)+1=2 (1−1)+4=4
(2−1)+4=5
(1−1)+1=1
ζ
v
−1) + τ
v
post−order = (
v
(e) (ζ
v
− 1) + τ
v
.
L =[s ,e ]
v v v
B
A
G
E
F
C
E
[1,7]
[1,4] [2,6]
[2,5]
[2,2]
[2,3]
[1,1]
(f) L
v
= [s
v
, e
v
].
Figure 2: GRAIL labels computation through four BFSs.
(a) Initial graph. (b) The corresponding DT, i.e., the same
graph after the selection of a single parent for each vertex.
(c) The DT with the subgraph size. (d) The original graph
with
˜
ζ
v
and τ
v
reported for each vertex v. (e) The post-order
times as computed by the first three breadth-first visits. (f)
The final min-post labeling L
v
= [s
v
, e
v
] obtained by the pro-
cedure COMPUTELABELS of Algorithm 1.
In Fig. 2c we represent the subgraph size for every
node of the DT of Fig. 2(b). The algorithm to compute
these values is implemented by function COMPUTE-
SUBGRAPHSIZE of Algorithm 1. It basically explores
the set of nodes following a bottom-up traversal in
which every time a node i is encountered the node’s
subgraph size is propagated to its parent p. At every
iteration a node i is extracted from a queue Q
1
stor-
ing all nodes to be visited. Moreover, the edge (p, i),
where p is the parent of node i, is marked as already
visited. The algorithm then checks if parent p has
been visited by all of its children and, if so, it is in-
serted on a secondary queue Q
2
storing nodes which
will be visited during the next iteration, after a pre-
fix sum
1
on the children subgraph sizes is performed.
Notice that, since the algorithm proceeds bottom-up,
1
The prefix sum, or cumulative sum, of a sequence of
numbers {x
0
, x
1
, x
2
, . . .} is a second sequence of numbers
{y
0
, y
1
, y
2
, . . .} such that each y
i
is the sums of prefixes, i.e.,
y
0
= x
0
, y
1
= x
0
+ x
1
, y
2
= x
0
+ x
1
+ x
2
, etc.
it is necessary to wait until a parent has been visited
by all of its children in order to compute the prefix
sum, given that the children’s subgraph sizes would
not be available otherwise. As a result, the algorithm
produces the subgraph size ζ
v
for every node v, and
the prefix sum of the subgraph sizes for every pair
(v, p).
Fig. 2d and 2e show the computation of the post-
order times for all nodes, as performed by function
COMPUTEPOSTORDER. The algorithm proceeds in a
breadth-first manner, visiting the DT top-down. Let
us consider a vertex p and refer to its children with
C
p
. Among these children there is an ordering re-
lationship given by the original DFS visit. For each
vertex v ∈ C
p
, we define
˜
ζ
v
=
∑
i<v,i∈C
p
ζ
i
(1)
which indicates the number of nodes that can be
reached from all the children of the parent p of vertex
v, coming before v in the ordering relationship given
by a DFS. After that, as in a DT there is a unique path
that goes from the root r to a node v, i.e., r → v, we
define τ
v
as the sum of all the
˜
ζ
u
along the path, i.e.,
τ
v
=
∑
u∈{r→v}
˜
ζ
u
(2)
Given
˜
ζ
v
and τ
v
(as computed by Equations 1 and 2)
for each vertex v, we can compute the post-order time
as follows:
post-order
v
= (ζ
v
− 1) + τ
v
(3)
Fig. 2d indicates for each node v the values of
˜
ζ
v
and
τ
v
as computed by Equations 1 and 2. Fig. 2e reports
for all vertex v the computations represented by Equa-
tion 3 to evaluate the final post-order raking times.
Finally, function COMPUTEMINPOSTLABELING
computes all node’s actual label pair, i.e., L
v
= [s
v
, e
v
].
It essentially proceeds breadth-first on the DT, visit-
ing it bottom-up. Each outer-rank e
v
is increased by
1 to obtain its final value. Each inner rank s
v
is com-
puted in the following way. If the vertex is a leaf, then
s
v
= e
v
. If the vertex is not a leaf, s
v
is equal to the
minimum value of the post-order rank e
v
among the
descendants of v. The final labels are represented in
Fig. 2f.
3.2 CUDA Code Optimizations
To properly design the procedure COMPUTELABELS
on CUDA-based architectures, it is necessary to effi-
ciently implement the required queues and to limit the
overhead caused by threads’ divergence.
To represent frontier nodes, usually CPU-based
parallel versions rely on a unique queue which is com-
plemented by a synchronization mechanism to realize
A Parallel Many-core CUDA-based Graph Labeling Computation
601

accesses in mutual exclusions. Nonetheless, this ap-
proach is of no use for porting BFS on CUDA as a
lock and a queue may work fine for threads in the or-
der of tens, but will never guarantee acceptable per-
formances for thousands of threads. As other CUDA-
based BFS implementations, we replace our queues
with a “frontier”, or “status”, array, i.e., an array with
n elements, one for every vertex v ∈ V . The value of
each element indicates whether v will be part of the
frontier set on the next iteration or not. Henceforth,
all our queues are actually implemented through sta-
tus arrays and several mechanisms built on top. Then,
at every iteration one thread will be assigned to each
node, and it will process the vertex depending on its
value on the status array, finally updating the status
array for all of the vertex’s children.
Following previous works (Su et al., 2017), this
manipulation strategy implies huge levels of thread
divergence slowing down the entire process. In fact,
even when only few vertices belong to the frontier set,
the status array requires a full array scan at every it-
eration. The different number of children that each
node may have, can force threads to behave differ-
ently, i.e., to diverge, since some threads will process
thousands of children vertices while others none. To
reduce divergence by concurrently processing nodes
that have similar out-degrees at the same time, we fol-
low Luo et al. and Liu et al. (Luo et al., 2010; Liu and
Howie Huang, 2015). Thus, we divide the frontier set
into three distinct queues. Nodes are inserted in the
small queue if they have less than 32 children, in the
large queue if they have more than 256 children, and
in the medium queue in all other cases. Subsequently
each queue is processed by a number of threads be-
fitting the amount of work that has to be performed.
Nodes belonging to the small queue will be handled
by a single thread, whereas a warp of threads will be
assigned to each node in the medium queue, and a
block of threads to each vertex of the large one. To
implement this strategy, three different kernels will
be launched, each optimized to handle its own queue.
This approach will result in having approximately the
same amount of work for each thread in each ker-
nel, as well as in assigning resources proportionally
to each node’s processing requirements.
3.3 The Searching Strategy on CUDA
Once labels have been computed, they can be used to
verify reachability queries. Following the Enterprise
BFS (Liu and Howie Huang, 2015), we try to develop
our searching algorithm to maximize the number of
queries, i.e., concurrent graph explorations, that can
be managed in parallel. Unfortunately, the Enterprise
BFS algorithm parallelizes breadth-first visits belong-
ing to the same traversal. On the contrary, our query
search strategy must parallelize in-depth queries be-
longing to distinct traversal procedures. In general,
this implies that a significant number of threads will
visit a large number of nodes at the same time. As
a consequence, during each algorithmic step, many
visited nodes will be logically associated to distinct
explorations making hard to keep track of what each
thread is doing.
More specifically, when we process a query
u →
?
v, we start a BFS on the subtree rooted at u, and
we use labels to prune the set of nodes that have to be
visited in order to discover whether v is reachable or
not. Vertices are visited concurrently for each BFS
traversal level. Since we want to proceed in parallel
on all the nodes with several visits, we must imple-
ment a mechanism to singularly identify the frontier
set for each query. To do this, we use a status array
of integer values rather than Boolean values, and we
rely on bit-wise operators to manipulate single bits
of these values. In other words, the set of queries is
divided in groups of k queries, where k is the high-
est number of bits that can be efficiently stored (and
retrieved) on a single CUDA data-type. Groups are
then processed one at a time, and queries within the
same group are managed in parallel. Within each
group, a query is identified through an index value
included between 1 and k and corresponding to a bit
field. Therefore, during the bin generation phase the
status array is scanned and a node is inserted into a
bin if its value is different than zero. Similarly, dur-
ing the traversal, the status array’s value are modi-
fied through bit-wise atomic operations. We use func-
tions such as the CUDA API ATOMICOR(ADDRESS,
VALUE), which allows us to set the i-th bit of vertex v
to represent that this vertex has to be explored during
the next iteration, and that its exploration is associated
with the i-th search.
Furthermore, given the high number of expected
label comparisons, these arrays will be accessed con-
tinuously, and it is important to limit the number of
global accesses related to these requests. Thus, at the
beginning of each kernel execution all threads coop-
eratively load the labels of the searched nodes from
the global memory array into a shared memory cache.
4 EXPERIMENTAL RESULTS
Tests have been performed on a machine initially
configured for gaming purposes and equipped with a
CPU Intel Core i7 7770HQ (with a quad-core proces-
sor running at 2.8 GHz, and 16 GB of RAM), and a
ICSOFT 2020 - 15th International Conference on Software Technologies
602

GPU NVIDIA GTX 980 over-clocked to 1, 300 MHz
(with 4 GB of dedicated fast memory, and 2, 048
CUDA cores belonging to Compute Level 5.2). All
software runs under Ubuntu 18.04.
We conducted our experiments on three different
data sets, varying in size and edge density, gener-
ated from real applications, and used to verify the
original GRAIL algorithm (Yildirim et al., 2010)
2
.
Given the different architectures of our machine com-
pared to the one of Yildirim et al. (Yildirim et al.,
2010), our tests produced index construction times
and reachability query times from one to two order
of magnitudes smaller than those of the original pa-
per. For that reason, we avoid considering small and
medium size graphs, and we only concentrate on the
large set. Table 1 reports its characteristics. The
set includes graphs up to 25 M vertices and 46 M
edges, and many older algorithms are unable to run
on some of them. Among the graphs, Citeseer is sig-
nificantly smaller, the Uniprot family ranges from rel-
atively large to huge graphs, and the Cit-Patents is a
large dense graph. The Uniprot subset has a distinct
topology, as these DAGs have a very large set of roots
that are all connected to a single sink through very
short paths, which will have significant implications
for reachability testing.
Table 1: The large data set.
Benchmark # Vertices (n) # Edges (m) Avg. Degree
Citeseer 693948 925779 1.33
Cit-Patents 3774769 17034732 4.5
Uniprot
22
1595445 3151600 1.97
Uniprot
100
16087296 30686253 1.91
Uniprot
150
25037601 46687655 1.86
4.1 GPU Labeling
Our GPU algorithm was carefully designed to avoid
constant calls to memory allocation and data transfer
functions in order to maximize continuous GPU ex-
ecution time. We exploited the fact that the input of
each breadth-first visit is the output of the preceding
one to pre-allocate and keep most of the data struc-
tures in the GPU’s global memory until no further use
is required. However, given the limited size of the
GPU’s global memory (i.e., 4 GB), and the size of the
larger graphs that we analyzed, it was not possible to
pre-allocate all data structures beforehand and some
of them were necessarily freed, reallocated, and re-
initialized when needed. This factor, along with the
time required to transfer the data structures between
the CPU and the GPU, added a significant overhead
to the total GPU times.
2
The data set was obtained from https://code.google.
com\-/archive/p/grail.
Results, to create a single label pair, are re-
ported in Table 2. The columns indicate the to-
tal time demanded by the CPU to build the la-
beling (column CPU Time), the times required
by all main phases of the GPU (the ones re-
ported in Algorithm. 1, namely DAGTODT, COM-
PUTESUBGRAPHSIZE, COMPUTEPOSTORDER, and
COMPUTEMINPOSTLABELING), and the total time
needed by the GPU (column GPU Time, which is the
sum of the previous partial times).
Table 2: Labeling times for one label and large-real graphs.
All times are in milliseconds.
Benchmark
CPU
DAGtoDT
Subgraph Post Min-Post GPU
Time Size Order Labeling Time
Citeseer 33 38 20 10 8 76
Cit-Patents 1048 189 210 28 57 479
Uniprot
22
772 36 24 11 7 78
Uniprot
100
1270 301 228 70 68 667
Uniprot
150
67 470 344 108 106 1028
Generally speaking, the indexing times range
from 100 milliseconds for the smaller graphs in the
data set, to 1000 milliseconds for the larger. The algo-
rithm spends considerable time on the first two phases
of the algorithm (i.e., DAGTODT and COMPUTE-
SUBGRAPHSIZE), especially on the larger instances
of the data set. This can be explained by consider-
ing the large amount of edges that are discarded by
the first procedure. Notice again, that all times refer
to create a single label pair, i.e, L
v
= [s
v
, e
v
] for each
graph vertex v. This is somehow a disadvantages for
the GPU. In fact, CPU times increase linearly to build
more labels, whereas for the GPU functions DAG-
TODT and COMPUTESUBGRAPHSIZE can be called
only once when computing multi-dimensional labels
(as represented in Fig. 1(c)), thus the GPU times grow
less than linearly. It is worth noticing that our results
share many similarities with those presented in the
original GRAIL paper (Yildirim et al., 2010) (even
if, as previously stated, we are from one to two orders
of magnitude faster). GPU and CPU present contrast-
ing results, where the winner strongly depends on the
topology of the graph. It is finally useful to note that
one of the major limits of the GPU approach is its in-
herently sequential nature. In fact, each one of the
four algorithmic phases (i.e., each BFS) produces the
data structures required by the following phase. This
inevitably prevents the GPU from concurrently run-
ning different parts of the algorithm at the same time,
or from sharing tasks between the CPU and the GPU
adopting a cooperative approach.
4.2 GPU Search
Given the labeling computed in the previous section,
we now present our data on reachability queries, com-
A Parallel Many-core CUDA-based Graph Labeling Computation
603

paring again our GPU results with the standard CPU
ones. Each run consists in testing reachability for
100,000 randomly generated query pairs. All reported
results are averages over twenty runs. As described
in Section 3.3, we divide our queries in groups of k
queries, managed in parallel. Unfortunately, our ar-
chitecture limited the parallelism to k = 64.
During the testing phase of the CPU-based algo-
rithms, we noticed that the GRAIL algorithm solves
from 75% to 90% of all the queries (depending on
the graph’s density) with the first label comparison.
As a consequence, the search algorithm was modified
in order to avoid assigning GPU resources to those
queries for which an answer can be provided with a
single label comparison. Thus, the search procedure
performs a preliminary CPU filtering of all queries,
which consists in a single label comparison. If this
comparison is inconclusive, we transfer the problem
on the GPU. Considering this initial CPU side screen-
ing, the metrics for measuring the search algorithm’s
performances are reported in Table 3. They include
the time spent to perform the first label comparison of
every query on CPU (CPU Filter), and the time spent
analyzing queries on the GPU (GPU Search). Col-
umn GPU Queries indicates the number of queries
assigned to the GPU for testing reachability. Addi-
tionally, we also report the original search times using
only the CPU (CPU Time).
Table 3: Search times for one label and large-real graphs.
All times are in milliseconds.
Benchmark
CPU
CPU Filter GPU Search GPU Queries
Time
Citeseer 20 6 26 7324
Cit-Patents 2747 8 530 19112
Uniprot
22
37 10 710 26551
Uniprot
100
38 11 1045 25030
Uniprot
150
31 9 156 48582
Compared with the results presented by Yildirim
et al. (Yildirim et al., 2010), the amount of queries that
resulted in a positive answer (positive queries) were
practically identical, and the graph instances that re-
quired larger processing times, both for querying and
indexing, are the same in most cases. The only sig-
nificant difference between the two studies regarded
the times of the unguided DFS search compare to the
label-guided DFS search for testing reachability. In
particular, in the original work the unguided DFS pro-
vided similar results to the guided DFS, whereas in
our framework unguided DFS is consistently slower
than guided DFS. Moreover, our unguided DFS per-
formed relatively better on the small sparse data set
than on the most critical instances.
Interestingly, both experimental investigations
confirmed that the topography of the standard graph
set is so peculiar to be meaningless in many cases, as
a significant amount of queries is directly explored by
the CPU, and it needs no further investigation. For
example, for Uniprot
150
only 50% of the queries are
analyzed by the GPU, and in average very few of
them contain reachable pairs. As a consequence, the
original CPU-based DFS exploration is extremely ef-
ficient, and it is really hard to beat. This is again due
to the particular topography of the considered graphs,
which are quite shallow. Moreover (see the Uniprot
family), these graphs are often characterized by short
paths that connect many roots to a single sink. As a
consequence, we need some extra analysis to inves-
tigate results on more critical, e.g., deeper, instances.
Another implicit problem of our GPU approach is the
low level of parallelism due to the adopted hardware
configuration, with data types limited to 64 bits. Any-
how, this last limitation may be easily overcome by
using GPU architectures allowing efficient manipula-
tion of longer data types.
5 CONCLUSIONS
In this work we design a data-parallel version of the
graph labeling approach named GRAIL, and we im-
plement it on a GPU CUDA-based architecture. Ex-
perimental results, for both the labeling and the search
procedure, show that our implementation presents re-
sults in the same order of magnitude of the CPU-base
version although it must deal with the intrinsic com-
plexity of avoiding recursion, transforming DFS into
several BFSs, and transferring data between compu-
tational units. In general, the CPU implementations
may be preferred when working on small graphs,
while the GPU implementations become attractive on
larger graphs or cooperative approaches. In these
cases, the main limitation lies in the amount of mem-
ory available, which in turn may become a major is-
sue.
Future works will include experimenting on more
heterogeneous and circuit-oriented graph sets. Re-
garding the labeling algorithm, it should be possi-
ble to explore some alternative to obtain higher de-
gree of concurrency among the subsequent algorith-
mic phases, eventually adopting CPU-GPU coopera-
tive approaches. Concerning the searching approach,
future work should concentrate on hardware architec-
tures or methodologies to increase the amount of par-
allel queries answered at each run.
ICSOFT 2020 - 15th International Conference on Software Technologies
604

ACKNOWLEDGMENTS
The author wish to thank Antonio Caiazza for imple-
menting the first version of the tool and performing
the initial experimental evaluation.
REFERENCES
Chen, Y. and Chen, Y. (2011). Decomposing DAGs into
Spanning Trees: A new way to Compress Transitive
Closures. In 2011 IEEE 27th International Confer-
ence on Data Engineering, pages 1007–1018.
Jin, R., Xiang, Y., Ruan, N., and Wang, H. (2008). Ef-
ficiently Answering Reachability Queries on Very
Large Directed Graphs. In Proceedings of the 2008
ACM SIGMOD International Conference on Manage-
ment of Data, SIGMOD ’08, pages 595–608, New
York, NY, USA. ACM.
Liu, H. and Howie Huang, H. (2015). Enterprise: Breadth-
first graph traversal on GPUs. In International Confer-
ence for High Performance Computing, Networking,
Storage and Analysis, pages 1–12.
Luo, L., Wong, M., and Hwu, W.-m. (2010). An effective
gpu implementation of breadth-first search. In 47th
Design Automation Conference, DAC ’10, pages 52–
55, New York, NY, USA. ACM.
Merrill, D., Garland, M., and Grimshaw, A. (2012). Scal-
able gpu graph traversal. In Proceedings of the
17th ACM SIGPLAN Symposium on Principles and
Practice of Parallel Programming, PPoPP ’12, page
117–128, New York, NY, USA. Association for Com-
puting Machinery.
Naumov, M., Vrielink, A., and Garland, M. (2017). Parallel
Depth-First Search for Directed Acyclic Graphs. In
Nvidia Technical Report NVR-2017-001.
Ruoming, J. and Guan, W. (2013). Simple, fast, and scal-
able reachability oracle. CoRR, abs/1305.0502.
Shi, X., Zheng, Z., Zhou, Y., Jin, H., He, L., Liu, B., and
Hua, Q.-S. (2018). Graph processing on gpus: A sur-
vey. ACM Comput. Surv., 50(6).
Su, J., Zhu, Q., Wei, H., and Yu, J. X. (2017). Reachability
querying: Can it be even faster? IEEE Transactions
on Knowledge and Data Engineering, 29(3):683–697.
Yildirim, H., Chaoji, V., and Zaki, M. J. (2010). GRAIL:
Scalable Reachability Index for Large Graphs. Proc.
VLDB Endow., 3(1-2):276–284.
Zhang, Z., Yu, J. X., Qin, L., Zhu, Q., and Zhou, X.
(2012). I/o cost minimization: Reachability queries
processing over massive graphs. In Proceedings of the
15th International Conference on Extending Database
Technology, EDBT ’12, page 468–479, New York,
NY, USA. Association for Computing Machinery.
A Parallel Many-core CUDA-based Graph Labeling Computation
605