Some Considerations on the Use of Digital Environments in Learning

Numerical Sets

Maria Cristina Carrisi

Dipartimento di Matematica e Informatica, Università degli Studi di Cagliari, Via Ospedale 72, Cagliari, Italy

Keywords: Numerical Sets, Arithmetic Operations, Digital Environments, Data Types.

Abstract: Teachers are nowadays encouraged to use technological tools to engage students more and transmit topics in

a simpler way. In addition, information science has become part of many curricula as a separate topic or as a

part of other subjects like mathematics. This article will discuss how choosing a particular technological

environment can reinforce misconceptions or ideas and how important the role of the teacher is in building a

learning environment effective and epistemologically relevant. In particular, the focus will be on the impact

that some technological environments have on learning numerical sets and arithmetic operations such as

division, because these are studied in all school systems and levels, even if with different approaches and

degrees of detail. The topic will be contextualized referring to the Italian school system (degree 10), but

conclusions are general.

1 INTRODUCTION

Since the second half of the 20th century, global

society has been experiencing a digital revolution that

has a strong impact on the productive, economic and

social system. This transformation is accelerating and

in this context the so called STEM skills are essential

for countries and companies, in order to remain

competitive, and for individual citizens, in their

profession but also in everyday life, to be able to

understand the complex economic and social

processes in which we are all inevitably involved.

This led many countries, all over the word, to

modify school curricula in order to introduce digital

skills and computational thinking in the different

grades of instruction. Nations are carrying out this

process variously and substantial differences are

observed also between European countries. In Italy

Computer Science has been introduced in all grades,

since 2013. Digital competences are addressed both

as a separate subject and as a part of other subjects

like Mathematics or Technologies, depending on the

grade of instruction and, only for high schools,

depending on the educational path. Moreover, in

order to develop digital citizenship, teachers of all

subjects should make students use digital

https://orcid.org/0000-0002-2837-3971

environments, at school or at home, for the analysis

of data, the production of reports, projects or

presentations.

The relationship between the use of digital

environments and learning effectiveness has been

widely studied in the literature, as well as the

knowledge interchange between Computer Science

and the other STEM subjects, particularly

mathematics. This paper aims to contribute to this

debate by analysing some digital environments that

process numerical data in order to study whether they

can give rise, reinforce or solve misconceptions on

mathematical topics and in particular on the division

operation. We focus on the behaviour of the division

into different numerical sets because this topic is of

general interest, it is studied all over the world in the

different degrees of education and has being

recognized in the literature as one of the main

mathematical concepts used in real life problems.

2 BACKGROUND AND

MOTIVATION

We live in an increasingly digitalized world where

technology is pervasive and knowledge is growing

480

Carrisi, M.

Some Considerations on the Use of Digital Environments in Learning Numerical Sets.

DOI: 10.5220/0009566504800487

In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 1, pages 480-487

ISBN: 978-989-758-417-6

day by day. In this context, educational systems must

necessarily modify their paradigms, in order to train

at their best the citizens of the future. For this reason,

in 2006 the European Commission released a

document addressed to member states (European

Commission, 2006) containing recommendations on

educational systems and in which they identified

eight key citizenship skills, among which

“Mathematical competence and basic competences

in science and technology” and “Digital

competence”. Based on the results of international

surveys such as the OECD (Organisation for

Economic Cooperation and Development) PISA

(Programme for International Student Assessment)

and PIAAC (Programme for the International

Assessment of Adult Competencies), which indicate

that teenagers and adults still have insufficient basic

skills and that the 44% of the Union population have

low or no (19%) digital skills, in 2018 the European

Commission released a new document (European

Commission, 2018) highlighting the necessity to

work more on issues like “problem solving, critical

thinking, ability to cooperate, creativity,

computational thinking” and to promote the

acquisition of STEM and digital competences.

2.1 Digital Competences in Italian

School

The different nations of the Union have implemented

these indications with different time and modes

(Heinz et al, 2016; Partanen et al, 2017).

In Italy, since September 2010, new high schools

(educational paths) have been introduced. This

promoted a reorganization of the old school curricula

and the creation of new guidelines (MIUR, 2010;

MIUR 2013; MIUR, 2018) with the aim to guide

teachers in devising learning situations that allow

students to acquire knowledge and skills, according

to the European Commission recommendations. The

use of digital environments and coding has been

introduced into all levels’ school programs:

Primary School: “The conscious and motivated use

of calculators and computers must be suitably

encouraged from the early years of primary school,

for example, in order to verify the correctness of

mental and written calculations and to explore the

world of numbers and shapes”. Students must

become able to “search data to obtain information

and build representations (tables and graphics) […]

get information from data represented in tabular and

graphic way”.

Middle School: “Whenever possible, students can be

introduced to some particularly simple and versatile

programming languages that bring them to develop a

taste for ideation and realization of projects

(interactive websites, exercises, games, utilities) and

for understanding the relationship between source

code and visible result”. Students must become able

to “program and create simple instructions to control

the behaviour of a robot”.

Secondary School: It divides in Liceo, Technical and

Professional schools. High school specializes and

curricula diversify. Every teacher is encouraged to

use digital environments and students are driven to

increase their technological skills to search, organize

and present information in an appealing way and to

use specific application programs (Computer-Aided

Design and Drafting, Image Manipulation Program,

accounting software, specific database, ecc.),

especially in technical schools. STEM teachers are

more involved in this process and Math teachers in

particular, because the Italian Ministry of Education,

University and Research ruled that Math teaching

includes also elements of computer science. For

example, according to Liceo (MIUR, 2010) we read

“The acquisition of digital skills […] is certainly a

theme developed in the first two years of each path

within the Mathematics discipline”. Math teaching is

divided in Mathematics and Elements of Computer

Science. Students are supposed to be “able to use

digital tools for geometric representation and

calculus. […] The use of IT tools is an important

resource that will be introduced critically, without

creating the illusion that it can solve problems

automatically and without compromising the

necessary acquisition of mental calculation skills.

[…] A fundamental topic will be the concept of

algorithm and the development of algorithmic

resolution strategies for simple and easy modelling

problems”.

As in other European countries (Partanen, 2017),

also in Italy the development of digital competences

is largely entrusted to Math teachers, who have the

heavy burden to choose the best way to transmit them

together with the mathematical contents, so that each

subject benefits from the other. Literature exhibits

contradictory results on the successful integration

between Mathematics and computer science,

according to learning the specific contents of the two

disciplines (Niess, 2005; OECD, 2015), and while it

is clear that computer skills, particularly computer

programming, benefit of a good understanding of

math contents, the reverse is not so obvious and, in

the author’s knowledge, it seems not to have

sufficiently discussed yet in the literature.

In my previous working experience as a high

school teacher I had the opportunity to observe on the

Some Considerations on the Use of Digital Environments in Learning Numerical Sets

481

field students facing problems in the deep learning of

mathematical concepts that arose while building an

algorithm and writing a program. This led me to

deepen the issue, in order to analyse if, and in which

way, the most diffused digital environments in Italian

schools interfere in learning mathematics.

In the following we present an overview on how

some digital environments treat numerical data and

the division operation, and which pros and cons there

are in using such environment to treat a division with

remainder problem. The choice of the mathematical

topic, inspired by my observations during classroom

activities and reinforced by the scientific debate on

mathematics for the future (Gravemeijer, 2017;

Dogan, 2019), will be properly motivated in section

3. The digital tools analysed in section 4 have been

chosen referring to their presence in the most used

Italian mathematics’ textbooks and in pre-service and

in-service teacher training courses.

3 WHICH MATHEMATICS IN

THE DIGITAL ERA?

Scientific community is wondering about which

direction mathematical education should take to

prepare properly the citizens of the digital age. It is

now commonly recognized that math teaching should

focus on problem solving procedure more than

computation, and this implies to develop the ability of

analyse the domain of data, the presence of eventual

constraints, and to interpret results. The blended

teaching of Math and Computer Science surely help

teachers to create learning situations appropriate to

develop such skills. But what about mathematical

contents?

In 2017 Gravemeijer et al. suggested that Math

curricula should focus on topics that (1) are useful in

everyday life, in order to be able to understand and

interpret the data conveyed by the different

information media about health, economy, etc.; (2)

are required in workplaces; (3) complement

computers’ “abilities”. In particular, the authors

underlined the importance of numbering and

quantifying (Gravemeijer, 2017).

Problems dealing with the division with

remainder fall within this context. This type of

problems has been widely studied in the literature

(see for example Dogan, 2019) because, despite their

apparent simplicity (they deal with natural numbers

and arithmetic operations), they are very delicate.

Indeed, they treat epistemologically relevant issues,

like: the transition from the division with remainder

to the decimal division, hence the passage from

natural numbers to rational numbers; the ability to

recognize when to operate in each of the two sets; the

analysis of the opportunity and modalities of

approximating partial results in order to obtain a final

result compatible with the context of the problem.

3.1 Numerical Sets in Italian School

From the analysis of the indications given by the

Italian Ministry of Education (MIUR, 2010; MIUR,

2013; MIUR, 2018), we see that in Italy numbers and

operations are studied in all the three educational

cycles, with various approaches and different levels

of detail. It represents what institutionally is asked to

students, regardless of the differences that clearly

arise in the scholastic activity.

Primary School: Students face natural numbers and

they learn how to operate with them. Pupils become

able to perform division, finding quotient and

remainder. Decimal numbers and fractions are

introduced immediately after. From this point on, the

remainder seams to disappear from students’

background and they consider the division with a

decimal result the right way to operate, that replaces

the “wrong” or “outdated” method of the division

with remainder.

Middle School: The work on Integers is focused on

factorization and on the research of multiples and

submultiples, therefore only on cases in which the

division gives zero remainder. Students use to say that

the division gives no reminder. This linguistic

inaccuracy may hide a misconception: the absence of

the remainder, in many students’ mind, means that

such operation isn’t a division with remainder but it

is another type of operation.

High Schools: Numerical sets are studied in terms of

their algebraic structure. Arithmetic is given for

known and acquired and students are considered to be

capable to understand to which numerical set the

solution of a problem belongs. The focus is on real

numbers and their approximation and this may lead

students to see Integers or Rational numbers only as

an approximation of Real numbers, without an

independent essence.

Almost all problems presented in middle and high

schoolbooks deal with Real solutions, reinforcing

such kind of approach. Students are not induced to

analyse the domain of data and of expected solutions,

even if it is a fundamental step in problem solving.

However, there are problems, like that involving the

division with remainder, that can be solved only in the

context of Integers. Arithmetic and Integers have ever

been of great interest for mathematicians and today

CSEDU 2020 - 12th International Conference on Computer Supported Education

482

have a new life, been fundamental for many computer

security methods (see for example Rivest et al.,

1987), but it seems that their treatment, in Italian

Math curricula, is unappropriated to overcome those

critical points that makes learning effective.

3.2 A Case Study

A classroom observation has been conducted in

academic years 2017-2018 and 2018-2019 in 5

second classes (degree 10) of a “Liceo Scientifico

opzione Scienze Applicate”, in which I observed

about ninety 15-16 years old students facing the

following problem:

In a supermarket, the following sales promotion on a

certain product is active: if you buy three products of

the same kind, only two have to be paid. If the number

of product bought and the price of the single product

are known, what is the total price of the purchase?

The above is an example of a problem framed

almost entirely in the context of Integers (data and

operations). Only the price of the product could have

a Rational value and this data has a secondary role in

the solving process. Such kind of problems can be

proposed in different classes and in all school levels,

having the foresight to adapt it to students’ level of

competence.

In primary schools it is appropriate to fix the value

of N, the number of the purchased products. Students

may proceed by trials and errors, starting from

particular cases and using a graphical approach to

find the solution, like the following:

Case N=5 Case N=8

Using a graphical representation and different cases

the teacher should bring the students to generalize the

method by using the division with the remainder,

conveying to a more formal approach.

In high school the graphical approach can be also

used but in addition we expect that students are able

to consider the number N as a variable and that they

reach by themselves an algebraic formulation, like the

following:

Let N be the number of products bought and p be the

price of the single product. Let’s divide N times 3

obtaining the quotient q and the remainder r. The

quotient represents the quantity of groups of three

products. For each group, only two products have to

be paid. The number of remaining products, identified

by the remainder, have to be paid entirely. Thereby,

the final price, considering the sale promotion, is

(2*q + r)*p.

During the observation the above problem has been

presented to students, asking them to create the

resolution algorithm and subsequently a program in

C++ language. The objective of the observation

wasn’t to collect data about the number of students

that succeed or fail, but rather to observe which

strategies and prior mathematical knowledge they

would have used to face the problem resolution.

Moreover, I was interested in students’ reactions

when using a digital environment that treats data

differently from their previous experiences. At the

time of observation, students were able to use

spreadsheets and to search autonomously for suitable

predefined functions, almost all them learned Scratch

in middle school, and they were experiencing for the

first few time C++ language (declaration of variables

of different type and arithmetical operations).

I focused on the following questions:

 Students deal with division with remainder

problems with ease?

 High school students are able to understand when

to operate with quotient and remainder or with

decimal results? They show the misconception of

the division between integers?

 The prior knowledge of digital environments

eases or complicates the resolution of such kind of

problems?

 The most used digital instruments may route

informally mathematical notions?

 It is possible to identify digital tools that behave

properly with respect to above question?

I briefly summarize my observations. Almost all

students approached the problem by considering a

particular case and fixing the number of products N

and the price of the single product.; they hold the

calculator and tried to divide N by 3, finding,

obviously, a decimal number. Most of the students

realized that the decimal result was not correct but,

except for some attempts to obtain the right solution

by approximation, rounding up the result, they were

unable to proceed. I suggested to represent

graphically the problem this helped students to realize

that truncation was a better approach rather than

rounding up, but something still was missing.

Students searched it in the decimal part of the result,

vainly trying to convert it in an Integer number. The

remainder of the division, necessary to obtain the

right solution, was still lacking because in their mind

the division always produces a decimal result. When

I tried to suggest to use the division with remainder

they say “That thing that we did in lower school?”. It

is evident that students conceive that knowledge

Some Considerations on the Use of Digital Environments in Learning Numerical Sets

483

confined in space and time. This suggestive is

strengthened by the analysis of curricula in the

previous section and by the functioning of the main

hardware and software instruments the students deal

with, starting from the calculator.

Subsequently I proposed to students to implement

the algorithm in C++ language. Although the

functioning of the division operator had already been

explained, strongly highlighting the different

behaviour of such operator with respect to the type of

data on which it works, and it had recently been

brought back to memory in the context of binary

numbering, students expected that the division

between integers would have produced a decimal

result and they inferred that computer was showing

an approximated result. This make us understand how

deeply rooted such misunderstanding is and how,

over time, even involuntarily, it has been enforced

during their schooling.

4 ANALYSIS OF SOME DIGITAL

ENVIRONMENTS

Any modern digital instrument is programmed in

order to perform different types of operations on

different types of data. Data are represented through

variables whose values belong to a particular domain

and in this set operations are defined. Regardless of

the particular instrument or programming language,

according to numerical data it is important to

underline that, because of its space limits, any device

can store a finite number of digits and therefore it

always works with a limited range of numbers that

can be represented with a finite number of decimal

digits. Nowadays, programming languages use

mainly two ways to represent numerical data

(Rodriguez, 2008), that corresponds to different data

types:

 Two’s complement, that allows to represent

a subset of mathematical Integers;

 Floating point, that allows to represent a

subset of Rational numbers including 0.

Data type defines the set of possible values assumed

by the variable, the operations that can be done on

data and their result, the meaning of the data, and the

way values of that type will be stored into the

hardware.

A strongly typed programming language has strict

typing rules in variables declaration and assignment,

in return values and function calling, and this implies

that errors and exceptions may appears in compiling

and executing (Liskov et al, 1974). The implicit type

conversion at runtime is not allowed and it prevents

the possibility of producing unpredictable results. In

a strongly typed programming languages the

programmer has to declare explicitly data type before

using a variable and such type can’t change

unexpectedly during execution. Such kind of

languages force the programmer to take continuously

into account data type and its implication on the

operations’ results.

In weakly typed programming languages and in

informal environments this doesn’t happen. To

simplify users’ use, only floating point are generally

usable in a simple and immediate way, and arithmetic

operations are defined in this numerical set.

In school activities teachers are free to choose the

digital environment they consider more suitable,

depending to the school level, to the type of school,

to the subject or to the particular topic they want to

address. This choice is not simple at all because of the

large amount of factors involved in the decision. In

high schools the choice could be inspired by the

desire to offer students an instrument immediately

expendable in the work market or during the

academic studies. In this context languages like

C/C++ or Python take place. In lower degrees, or

when the digital skill is used to support the acquisition

of other subjects’ knowledge, informal environments

are generally preferred, like spreadsheets or Scratch

(Resnick et al, 2009). They are widespread in Italian

schools and are proposed in most school books

because of their strengths, like the possibility to focus

on the algorithm building process, being released

from the syntax of a particular language and for this

reason they can be used for different subjects and in

all school levels. But to achieve this simplicity, such

environments must keep hidden important aspects of

the management of variables, like the types of data

(variables domain) and the functioning of operations,

relations and functions, all relevant aspects from

mathematical point of view. Teachers have to be

aware of this in order to make their choice appropriate

(Chevallard, 1985) and intervene in order to prevent

misconceptions (Shaughnessy, 1985; Maurer, 1987;

Zan, 2000; Zan, 2007).

4.1 Calculators

Calculator is the first digital instrument students deal

with and in such sense it is the most important

according to what knowledge it can implicitly route.

In Italy, its use is promoted since from the early years

of primary school (see section 3.1), when Math

studying is focused on Natural numbers but

calculators operate on floating point data. The

CSEDU 2020 - 12th International Conference on Computer Supported Education

484

division between two integers always produces a

decimal number. In order to obtain the quotient of the

division students must truncate the decimal result and

only few calculators provide for an operator to

calculate the remainder of a division. The early use of

an instrument quick and easy to use, but that gives

results different from that obtained by students using

the classical division algorithm is certainly

destabilizing as observed in the classroom experience

described in section 3.2.

4.2 Spreadsheet

Spreadsheet allows to treat various types of data but

regarding numbers it makes available only floating

point numbers. All arithmetical operations are

allowed and they are represented trough the classical

symbols + - * and /. Integers can be represented as

decimal numbers without decimal ciphers, activating

an approximation that rounds up or down, as

appropriate, and not simply truncates. It is possible to

properly represent integers only using the predefined

INT function that converts any decimal number in its

integer part by truncating the decimal part of the

number, but this implies a more advanced

competence in the use of this digital environment.

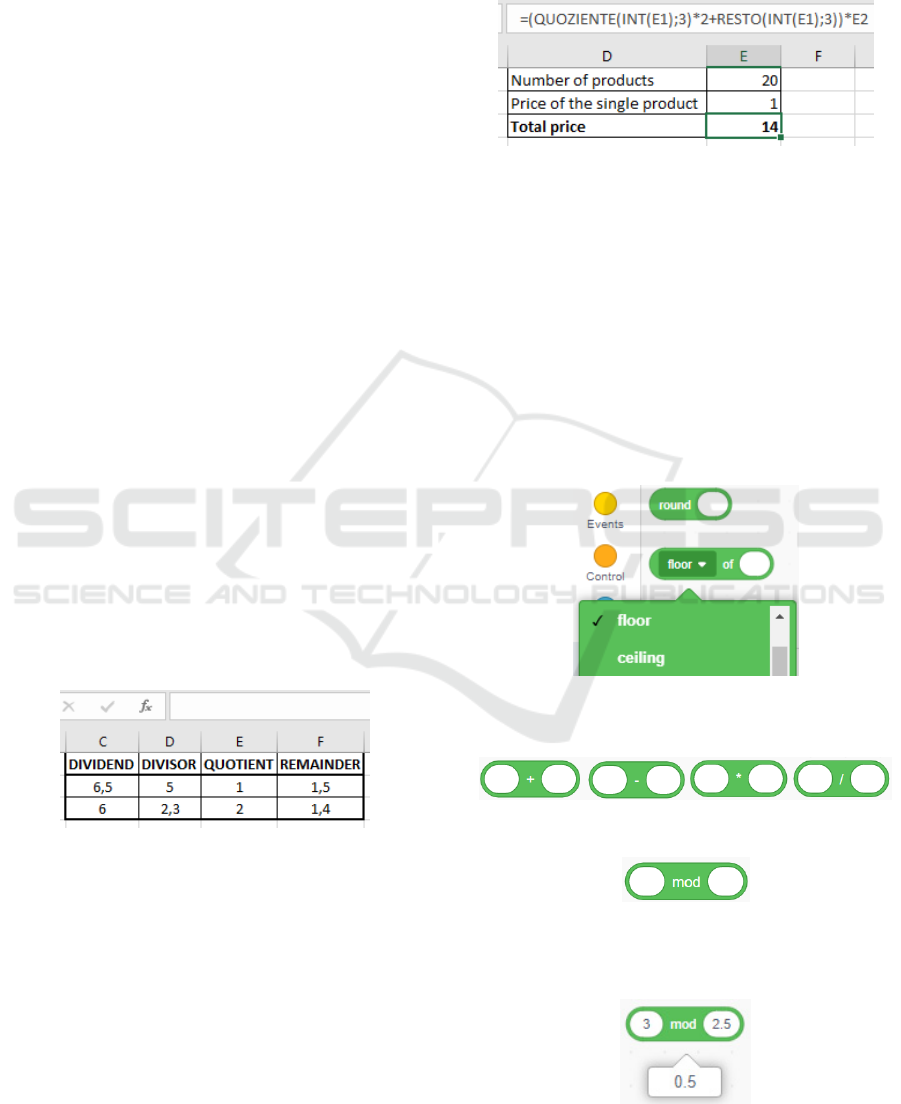
According to division, spreadsheets furnish the

operator / that gives the decimal result of a division,

and the functions QUOTIENT and REMAINDER

that should receive two integers and return an integer

but they work also when the dividend, the divisor, or

both are decimal without returning any error message,

therefore, don’t behaving exactly like the

corresponding mathematical operations.

Figure 1: Functions Quotient and Remainder working on

rational values.

In order to solve properly the problem discussed in

sec. 3.2, teachers should encourage students to use the

INT function (see Figure 2) in order to cast the data

and make the QUOTIENT and REMAINDER

functions work properly even in case of incorrect data

entry. In such way a reflection is induced on the

domain of data and results, allowing to give to the

activity a deeper meaning from the mathematical

point of view. Despite Figure 2 shows a very compact

formulation, used for opportunity reasons, during the

work in classroom it is preferable to use auxiliary

cells to receive the results of the INT, QUOTIENT

and REMAINDER functions so that students can

clearly see the various steps of the solving procedure.

Figure 2: Solution of the problem described in sec. 3.2.

4.3 Scratch

According to numbers, Scratch behave as spreadsheet

and calculators, allowing to treat only floating point

numbers. The only way to obtain an integer number

is by approximation. Scratch allows to approximate

in three different ways by using blocks in the

“Operators” category (green colour): ‘Floor’

performs a truncation, ‘ceiling’ an upper

approximation, ‘round’ behave as ‘floor’ when the

decimal part of the number is less than 0.5 and as

‘ceiling’ otherwise.

The “Operators” category provides blocks for

arithmetical operations

defined in floating point set, and to calculate the

remainder of a division via the ‘mod’ operator

Unfortunately, as in spreadsheets, it works differently

from the division defined in Integers, giving a

decimal result when operating on rational data.

Figure 3: Scratch ‘mod’ block working on rational data.

Some Considerations on the Use of Digital Environments in Learning Numerical Sets

485

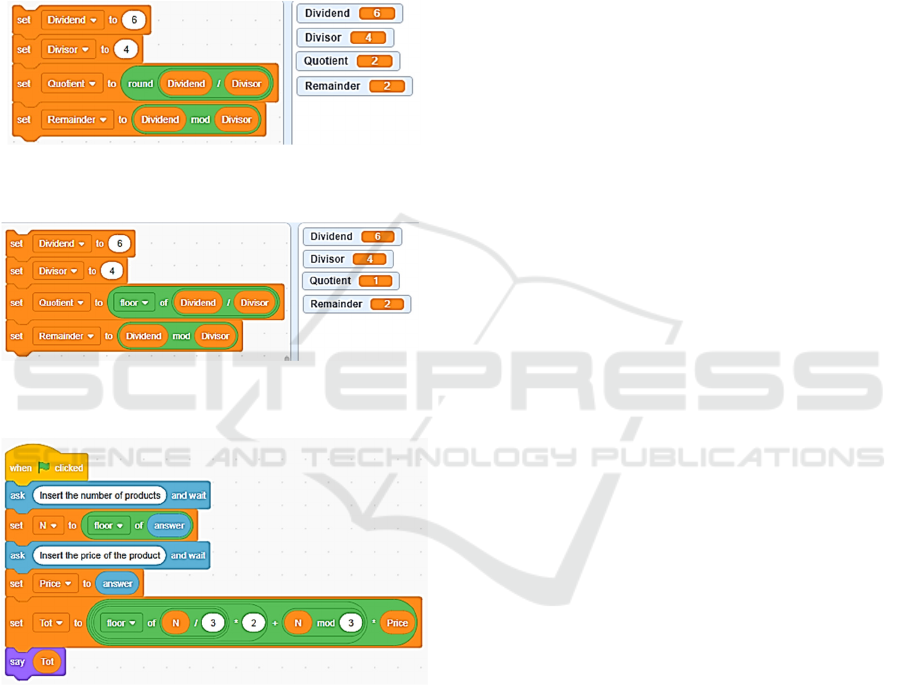
Scratch blocks are organized in sections and, in each

section they are grouped, generally by scope. It

happens for arithmetical operations, for relations (<,

>, =) but also for blocks ‘mod’ and ‘round’. This

induce the user to think that they are logically related

and referred respectively to remainder and quotient of

a division but it is not correct. Instead it is necessary

to act as in the use of calculators, namely truncating

the decimal result of a division, by using the ‘floor’

block.

Figure 4: Incorrect use of Scratch blocks ‘mod’ and ‘round’

to calculate a division with remainder.

Figure 5: Correct use of Scratch blocks ‘mod’ and ‘floor’ to

calculate a division with remainder.

Figure 6: Scratch solution of the problem presented in sec.

3.2.

In view of the above, the Scratch solution of the

problem presented in sect. 3.2 is presented in Figure

6. Also in this case it is necessary to cast the data to

prevent that incorrect data entry makes the functions

work improperly. This makes the development rather

cumbersome, despite of the apparent simplicity of the

environment.

4.4 C/C++ Language

C/C++ is a strongly typed programming language.

Variables must be declared before use, providing

name and type and they cannot unexpectedly change

type during execution. Integers and floating point

numbers are allowed and the programming language

provides 5 arithmetic operations: + - * / %. All

operations are closed with respect to the set they act

on. In particular, the division adapts, working

differently depending on operands’ type. When it

works on at least one floating point number it returns

a floating point result. When it acts on two Integer

numbers it returns an integer result, i.e. the quotient

of the division. There is no way to obtain a decimal

result from a division between integers, except by

explicitly forcing the interpretation of one of the

operands as a floating point number. The fifth

arithmetical operation, indicated by the symbol %, is

defined only on integers and returns the integer

remainder of a division. In case of incorrect use an

error is reported during program compiling, for

example if the programmer tries to use the operator %

on floating point numbers.

According to C++ language the development of

the problem presented in section 3.2 is:

int N;

float p,tot;

cin >> N >> p;

tot =((N/3)*2+N%3)*p;

cout << tot;

where only the content of the main function is

reported. The development is more compact and

extremely more adherent to the algebraic formulation

that students should have found. Incorrect data entry

is prevented by typing, in fact even if the user inserts

a decimal number it will be automatically truncated

and the algorithm will work properly. It is however

evident that such solution is well suited only for high

school paths and unthinkable in primary school.

5 DISCUSSION AND FUTURE

WORK

In this paper some of the most popular digital

environments used in Italian schools have been

analysed, with respect to their functioning about the

division between Integer numbers. It has been shown

that, behind the friendly and ready to use interface,

environments, like Scratch or spreadsheets, hide

delicate aspects in the management of data and their

CSEDU 2020 - 12th International Conference on Computer Supported Education

486

operations, that can be properly faced only by a

shrewd and qualified user. On the other hand, more

rigorous environments seem to be not affordable for

lower level students. This doesn’t mean that such

environments mustn’t be used in school but rather

that teachers have to choose them carefully,

depending on the activity they propose to students

and to the grade of instruction. Math teachers can take

advantage on the above mentioned weakness, in order

to make the activity epistemologically relevant from

the mathematical point, aimed at overcoming the

misconception on the division between Integers.

Who produce or promote digital environments for

learning, especially if they are addressed for

elementary or middle school students, who are

building their linguistic and mathematical

knowledge, should be careful not to introduce

excessive, and sometimes only apparent,

simplifications that may strengthen misconceptions.

It may be interesting, as a future work, to build a

calculator for elementary students or a personalized

version of Scratch, using its extension BYOB

(Harvey & Monig, 2010) that can overcome the

problems underlined in the present paper.

In the future the author would like to extend the

results of the present paper to other mathematical

topics like the division between signed number,

analysing the behaviour of the most used digital

environments with respect to this.

REFERENCES

Chevallard, 1985. La transposition didactique. Du savoir

savant au savoir enseigné. La Pensée Sauvage,

Grenoble.

Dogan Coskun, S., Ev Cimen, E. (2019). Pre-service

elementary teachers’ difficulties in solving realistic

division problems. Acta Didattica Napocensia, 12(2),

183-194. DOI:10.24193/and.12.2.14

European Commission, 2006. Recommendation of the

European Parliament and of Council of 18 December

2006 on key competences for lifelong learning. Official

Journal of the European Union, L 394/10 (https://eur-

lex.europa.eu/legal-content/EN/TXT/PDF/?uri=

CELEX:32006H0962&from=IT accessed 18.3.2020)

European Commission, 2018. Council Recommendation of

22 May 2018 on key competences for lifelong learning.

Official Journal of the European Union, C 189/1

(https://eur-lex.europa.eu/legal-content/ EN/

TXT/PDF/?uri=CELEX:32018H0604(01)&qid=15844

84557047&from=IT accessed 18.3.2020)

Gravemeijer, K., Stephan, M., Julie, C., Lin, F., Ohtani, M.,

2017. What Mathematics Education May prepare

Students for the society of the Future?. Int. J. of Sci. and

Math. Educ. Suppl 1, S105-S123.

Harvey, B., Monig, J., 2010. Bringing 'No Ceiling' to

Scratch: Can One Language Serve Kids and Computer

Scientists? In proceedings of Constructionism 2010.

Heintz, F., Mannila, L., Färnqvist, T., 2016. A Review of

Models for Introducing Computational Thinking,

Computer Science and Computing in K-12 Education.

Frontiers in Education October.

Liskov, B, Zilles, S., 1974. Programming with abstract data

types. doi:10.1145/942572.807045.

Maurer, S.B., 1987. New knowledge about errors and new

views about learners: what they mean to educators and

more educators would like to know. Cognitive Science

and Mathematics Education, Lawrence Erlbaum

Associates.

Ministero dell’Istruzione, Università e Ricerca, 2010. I

Regolamenti - Le indicazioni Nazionali.

https://archivio.pubblica.istruzione.it/riforma_superior

i/nuovesuperiori/index.html accessed 18.3.2020.

Ministero dell’Istruzione Università e Ricerca, 2013.

Indicazioni nazionali per il curricolo della scuola

dell’infanzia e del primo ciclo d’istruzione, Gazzetta

Ufficiale della Repubblica Italiana, serie generale n.30,

5-2-2013.

Ministero dell’istruzione, Università e Ricerca, 2018.

Indicazioni Nazionali e Nuovi Scenari,

https://www.miur.gov.it/documents/20182/0/Indicazio

ni+nazionali+e+nuovi+scenari/ accessed 18.3.2020

Niess, M. J., 2005. Preparing teachers to teach science and

mathematics with technology: Developing a technology

pedagogical content knowledge. Teaching and Teacher

Education 21 (5), 509-523.

OECD, 2015. Students, Computers and Learning.

Partanen, T., Niemelä, P., Mannilla. L., Poranen, T., 2017.

Educating Computer Science Educators Online-A

Racket MOOC for Elementary Math Teachers of

Finland, In Proceedings of the 9

International

Conference on Computer Supported Education

(CSEDU 2017).

Rivest, R., Shamir, A., Adleman, L., 1987. A method for

obtaining digital signatures and public-key

cryptosystems, Communications ACM, 21, 120-128.

Resnick, M., Maloney, J., Monroy-Hernández, A., Rusk,

N., Eastmond, E., Brennan, K., Millner, A.,

Rosenbaum, E., Silver, J., Silverman, B., Kafai, Y.,

2009. Scratch: Programming for All. Communications

of ACM, 11. http://scratch.mit.edu/

Rodriguez, G., 2008. Algoritmi Numerici. Pitagora

Editrice, Bologna. ISBN: 88-371-1714-0.

Shaughnessy, J.M., 1985. Problem-Solving Derailers: The

Influence of misconceptions on Problem-Solving

performance. Teaching and Learning Mathematical

Problem Solving. Lawrence Erlbaum associates.

Zan R., 2000. ‘Misconceptions’ e difficoltà in Matematica,

L’insegnamento della Matematica e delle scienze

Integrate, vol. 23, Centro di ricerca in didattica Ugo

Morin.

Zan, R., 2007, Difficoltà in matematica. Osservare,

interpretare, intervenire. Springer.

Some Considerations on the Use of Digital Environments in Learning Numerical Sets

487