
Estimating Problem Instance Difficulty
Hermann Kaindl, Ralph Hoch and Roman Popp
Institute of Computer Technology, TU Wien, Austria
Keywords:
Case-based Reasoning, Similarity Metric, Heuristic Search, Admissible Heuristic, Problem Difficulty.
Abstract:
Even though for solving concrete problem instances, e.g., through case-based reasoning (CBR) or heuristic
search, estimating their difficulty really matters, there is not much theory available. In a prototypical real-
world application of CBR for reuse of hardware/software interfaces (HSIs) in automotive systems, where the
problem adaptation has been done through heuristic search, we have been facing this problem. Hence, this
work compares different approaches to estimating problem instance difficulty (similarity metrics, heuristic
functions). It also shows that even measuring problem instance difficulty depends on the ground truth available
and used. A few different approaches are investigated on how they statistically correlate. Overall, this paper
compares different approaches to both estimating and measuring problem instance difficulty with respect to
CBR and heuristic search. In addition to the given real-world domain, experiments were made using sliding-
tile puzzles. As a consequence, this paper points out that admissible heuristic functions h guiding search
(normally used for estimating minimal costs to a given goal state or condition) may be used for retrieving
cases for CBR as well.
Notation
s,t Start node and goal node, respectively
c(m, n) Cost of the direct arc from m to n
k(m, n) Cost of an optimal path from m to n
g
∗
(n) Cost of an optimal path from s to n
h
∗
(n) Cost of an optimal path from n to t
g(n), h(n) Estimates of g
∗
(n) and h
∗
(n), respectively
f (n) Static evaluation function: g(n) + h(n)
C
∗
Cost of an optimal path from s to t
N# Number of nodes generated
1 INTRODUCTION
There is a lot of theory on complexity classes of
problems, e.g., the famous issue of P vs. NP, but
not much on the difficulty of solving concrete prob-
lem instances of the same problem class (e.g., the
well-known Fifteen Puzzle, see http://kociemba.org/
themen/fifteen/fifteensolver.html). For solving con-
crete problem instances, e.g., through heuristic search
(Edelkamp and Schroedl, 2012; Pearl, 1984), how-
ever, estimating their difficulty really matters. Often,
this is done there through heuristic functions h(n),
which estimate the cost from this particular instance
n to a goal. In case-based reasoning (CBR) (see,
e.g., (Goel and Diaz-Agudo, 2017)), estimating the
effort for adapting some stored solution of a previ-
ously solved problem instance to a solution of a new
problem instance is often indirectly addressed by re-
trieving the nearest neighbor determined through sim-
ilarity metrics. The underlying assumption is that
the relative effort for solution adaptation of stored in-
stances (cases) correlates with the similarity of these
instances with the given problem instance.
In fact, there are two different views of problem
difficulty involved here:
• The cost of the solution, and
• The effort of finding a solution.
Depending on the view taken, C
∗
(the cost of an op-
timal path from the start node s to a goal node t) is
a good measure of problem difficulty in terms of the
cost of a solution (for its execution by a robot, for in-
stance), while the number of nodes generated and the
time needed for finding a solution are good measures
for the difficulty in terms of the effort for finding a so-
lution. (Korf et al., 2001) provide an excellent study
of the relation between the two for IDA* and opti-
mal solutions. For finding error-bounded solutions,
there is a trade-off, and finding any solution usually
requires much less effort, of course.
For both heuristic search and CBR, this paper
compares different approaches to estimating prob-
lem instance difficulty. Originally, the motivation
for this investigation came from a prototypical real-
world application of CBR, where the problem adap-
Kaindl, H., Hoch, R. and Popp, R.
Estimating Problem Instance Difficulty.
DOI: 10.5220/0009390003590369
In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 359-369
ISBN: 978-989-758-423-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
359

Figure 1: Terminology Clarification.
tation has been done through heuristic search, see
(Rathfux et al., 2019a; Rathfux et al., 2019b). More
specifically, this heuristic search uses A* (Hart et al.,
1968), so that the solutions have guaranteed minimal
cost (actually, a minimum number of steps), which
was desired in this domain. The overall theme of
this work was reusing hardware/software interfaces
(HSIs) in automotive systems. After having a stored
most similar one selected and retrieved, its config-
uration is transformed to another one that fulfils all
the new requirements. The number of transformation
steps is desired to be minimal in order to avoid hav-
ing to create new hardware. Since we defined an ad-
missible heuristic h, A* guarantees optimal solutions.
An interesting question was then, whether to use this
heuristic h instead of similarity metrics for selecting a
stored HSI.
In order to avoid potential misunderstandings of
certain key notions (such as “solution”) in this combi-
nation of heuristic search and CBR, Figure 1 provides
an overview. It distinguishes a problem-description
space and a solution space. Each stored case in the
repository has a representation in both spaces. In the
problem-description space, the requirements on a new
HSI are specified, and in the solution space the inter-
nal configuration of the HSI fulfilling them is stored.
Heuristic search is used here for finding a solution
in the sense of a sequence of transformations from a
given HSI to another one that fulfills the requirements
(which define the goal conditions for the search). In
CBR, a major step is the selection of the “best” case
in the repository for adaptation of its stored solution
(here in the sense of a given HSI) to a solution of
the new case (an HSI fulfilling the new requirements).
While this selection is usually done through similar-
ity metrics, in the special case of automatic adaption
using heuristic search, there is the additional possibil-
ity to estimate the adaptation effort using its heuristic
function.
For studying different estimation techniques (in
the sense of heuristic functions and similarity metrics)
more generally, we also employed the well-known
Fifteen Puzzle. In contrast to the real-world domain,
it is widely known and was often used in the litera-
ture on heuristic search. All the results can be eas-
ily replicated publicly. This version of the sliding-
tile puzzle is only used here as a vehicle for compar-
ing such estimates (including simpler and less precise
ones) and not for presenting a new search algorithm
that would be faster than any other before (by using
the best heuristic estimate known), when the Twenty-
four Puzzle would have to be the choice today, such
as in (Bu and Korf, 2019).
Comparing different estimates needs to refer to
“real” problem instance difficulty, whatever this may
mean precisely. However, this raises yet another is-
sue, how that can be measured. For the Fifteen Puz-
zle, usually the instances are ordered according to the
lengths of their minimal solution paths C
∗
(due to unit
costs, the length is the same here as the cost of an
optimal path). But how well do they correlate with
the numbers of nodes explored by some algorithm for
solving them? And how do the numbers of nodes
explored by, e.g., A* correlate with those of IDA*
(Korf, 1985)? In addition, it makes a (theoretically
understood) difference of whether optimal solutions
are to be found, or solutions with a bounded error,
or just any solutions. For our experiment, we deal
here with finding optimal solutions through heuristic
search, since it provides a well-defined case for com-
paring the search effort with estimates.
Hence, this paper actually compares different ap-
proaches to both estimating and measuring problem
(instance) difficulty with respect to CBR and heuris-
tic search. For estimating, we employ both various
similarity metrics and different h functions. For mea-
suring problem instance difficulty, we employ mini-
mum solution length (cost), the number of nodes gen-
erated for solving them by some algorithm, and two
new measures very recently defined by us in (Rathfux
et al., 2019b).
The remainder of this paper is organized in the fol-
lowing manner. First, we present some background
material and discuss related work, in order to make
this paper self-contained. Then we explain several
approaches to measuring problem instance difficulty,
followed by explaining several approaches to estimat-
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
360

ing it. Based on all that, we present our experimental
results and interpret them. Finally, we provide a con-
clusion based on our experimental results.
2 BACKGROUND AND RELATED
WORK
2.1 CBR in a Nutshell
Case-based Reasoning (CBR) is an approach to solve
problem instances based on previously solved prob-
lem instances (Kolodner, 1993). It is assumed to
be closely related to the way a person solves prob-
lems: by recalling past experiences and applying that
knowledge to the new problem, or in other words,
mapping the new problem to previous experiences.
For the cognitive science foundations of CBR see
(Lopez de Mantaras et al., 2005).
The first CBR systems have been developed in the
early 1980s and were based on the work of (Schank,
1983). Essentially, CBR is a cyclic process for solv-
ing problems (Aamodt and Plaza, 1994) and consists
of four major process steps. First, a fitting problem
instance for a new problem instance is retrieved from
the repository. This step is typically performed us-
ing similarity metrics. Next, the solution of the re-
trieved problem instance is reused by adapting it to
the new problem instance. Note, that his step may be
supported by an automatic adaption of the given prob-
lem instance to the new one by using, e.g., heuristic
search. The resulting solution is then tested and, if
necessary, revised. Finally, the resulting solution is
stored, together with the new problem instance, in the
repository, i.e., the new knowledge is retained in the
repository.
CBR has been applied in a variety of domains,
see, e.g., (Burke et al., 2006; Bulitko et al., 2010;
Kaindl et al., 2010). Search techniques have been
used to help optimize a CBR system for predicting
software project effort in (Kirsopp et al., 2002). An
early combination of CBR with minimax search for
game-playing can be found in (Reiser and Kaindl,
1995).
2.2 Similarity Metrics
Similarity metrics (Cha, 2007) are used to determine
how similar two objects are to each other, e.g., in
CBR. It is an approach commonly used in informa-
tion retrieval systems, e.g., to compare text docu-
ments, or for clustering of data in data mining appli-
cations (Bandyopadhyay and Saha, 2012). For each
object, a similarity value can be calculated in relation
to another object, i.e., each pair of objects has a simi-
larity score assigned. Thus, attributes of objects need
to be quantified so that they can be used in similarity
metrics. Typically, similarity scores are normalized
values in the interval [0, 1], where 0 indicates no sim-
ilarity at all and 1 indicates maximum similarity. A
popular similarity metric, among others, is the Cosine
Similarity (Sohangir and Wang, 2017).
2.3 A* and IDA*
The traditional best-first search algorithm A* (Hart
et al., 1968) maintains a list of so-called open nodes
that have been generated but not yet expanded, i.e.,
the frontier nodes. It always selects a node from this
list with minimum estimated cost, one of those it con-
siders “best”. This node is expanded by generating
all its successor nodes and removed from this list. A*
specifically estimates the cost of some node n with an
evaluation function of the form f (n) = g(n) + h(n),
where g(n) is the (sum) cost of a path found from s to
n, and h(n) is a heuristic estimate of the cost of reach-
ing a goal from n, i.e., the cost of an optimal path
from s to some goal t. If h(n) never overestimates this
cost for all nodes n (it is said to be admissible) and
if a solution exists, then A* is guaranteed to return an
optimal solution with minimum cost C
∗
(it is also said
to be admissible). Under certain conditions, A* is op-
timal over admissible unidirectional heuristic search
algorithms using the same information, in the sense
that it never expands more nodes than any of these
(Dechter and Pearl, 1985). The major limitation of
A* is its memory requirement, which is proportional
to the number of nodes stored and, therefore, in most
practical cases exponential.
IDA* (Korf, 1985) was designed to address this
memory problem, while using the same heuristic eval-
uation function f (n) as A*. IDA* performs iterations
of depth-first searches. Consequently, it has linear-
space requirements only. IDA*’s depth-first searches
are guided by a threshold that is initially set to the
estimated cost of s; the threshold for each succeed-
ing iteration is the minimum f -value that exceeded
the threshold on the previous iteration. While IDA*
shows its best performance on trees, one of its major
problems is that in its pure form it cannot utilize du-
plicate nodes in the sense of transpositions. A trans-
position arises, when several paths lead to the same
node, and such a search space is represented by a di-
rected acyclic graph (DAG). IDA* “treeifies” DAGs,
and this disadvantage of IDA* relates to its advantage
of requiring only linear space.
In principle, we could have used for this research
Estimating Problem Instance Difficulty
361

other search algorithms as well, e.g., with limited
memory (Kaindl et al., 1995) or for bidirectional
search. (Kaindl and Kainz, 1997), but experiments
using A* and IDA* were sufficient.
2.4 HSI Domain
We use the real-world domain of Electronic Control
Units (ECUs) and HSIs in automotive vehicles for
our experiment. In this domain, each ECU provides
an HSI through which external hardware components
can communicate with internal software functions.
The software of these ECUs runs on a microcontroller
with internal resources, and the external hardware
components require some of them for functioning as
needed. In addition, hardware components may be
placed on the ECU to pre-process signals from exter-
nal hardware, so that they can be mapped to or access
resources. The external hardware is connected to the
ECU via pins, and the ECU-pins are routed through
hardware components on the ECU to pins of the mi-
crocontroller (µC-pin). Each µC-pin is internally con-
nected to several resources, e.g., an Analog-Digital-
Converter (ADC). The hardware components together
with selected resources on connected µC-pins provide
a specific interface type on an ECU-Pin, which an ex-
ternal hardware can use. All the selected interface
types together specify the HSI.
External hardware requires certain functionality
on ECU-pins for its own functioning as needed.
Therefore, requirements are specified that an ECU
and its HSI have to fulfill. An ECU is only satisfac-
tory for the customer if all requirements of all exter-
nal hardware are met. To fulfill requirements, spe-
cific types of resources in the microcontroller (µC-
Resources) have to be made available to ECU-pins via
hardware components. The connections of ECU-pins
to hardware components and from hardware compo-
nents to µC-pins are fixed. Each µC-pin is connected
to several µC-Resources, but only one of them can be
used at the same time. However, which µC-Resource
is selected on a specific ECU is variable and can be
configured. Hence, this variability provides options
to fulfill requirements. In essence, this variability de-
fines the search space for finding optimal solutions.
This domain knowledge is captured in the meta-
model published in our previous work (Rathfux et al.,
2019a), where also HSI problem instances and so-
lutions are included. We employ design-space ex-
ploration using the VIATRA2 tool (Hegedus et al.,
2011), which provides an infra-structure for heuris-
tic search based on model-transformations, which im-
plement activating or deactivating a connection to a
µC-Resource on the model, until all the goal condi-
tions are fulfilled as specified by the requirements.
VIATRA2 also provides an implementation of A*,
for which we defined an admissible heuristic function
in (Rathfux et al., 2019b).
Note, that that the overhead of A* for maintaining
its priority queue does not matter in such a model-
driven implementation, since it can only visit about
1,000 nodes per second for our application on a state-
of-the-art laptop. In a very efficient implementation
of the Fifteen Puzzle in C, A* can visit on the same
hardware three orders of magnitude more nodes per
second, and IDA* even four.
3 MEASURING AND
ESTIMATING PROBLEM
INSTANCE DIFFICULTY
We provide here the definitions of measures and esti-
mates used in our experiment. Two of them are actu-
ally hybrids in the sense that a measure is combined
with an estimate.
3.1 Measuring
For measuring the difficulty of some problem instance
in some domain (as compared to the difficulty of other
problem instances), the question arises, what “prob-
lem instance difficulty” really means. Another ques-
tion is what ground truth is available and used for
measuring it. Of course, all of these measures are only
available after the fact, so that estimating is necessary
in practice (see below). However, our experiment had
them available, of course. For getting a better theoret-
ical understanding, it is still useful to study relations
between measures and estimates, see also (Korf et al.,
2001) for the number of nodes explored by IDA* us-
ing a given heuristic h, based on knowledge about its
distribution over the problem space.
According to one view, the difficulty of a prob-
lem instance is the running time it takes to solve it
(and indirectly also the size of memory used). This
time is usually proportional to the number of nodes
explored for a given algorithm like IDA* (with only
linear memory requirements). This depends on the
algorithm used, however! In particular, this is differ-
ent for A*, even though IDA* is conceptually derived
from A*. However, the memory need of A* grows
with the number of nodes explored, and maintaining
the stored nodes for fast access incurs additional over-
head.
According to the other view, which is independent
from a specific algorithm, is C
∗
, the cost of an opti-
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
362

mal path from s to t (for unit costs, its length). The
assumption is that C
∗
of a given problem instance cor-
relates with the time it takes for solving it. How strong
is this correlation actually?
3.2 Estimating
For estimating problem instance difficulty, let us dis-
tinguish here admissible heuristics from similarity
metrics, where the former are employed for heuristic
search and the latter for CBR.
3.2.1 Admissible Heuristics
Such heuristics fully depend, of course, on the prob-
lem domain. For the real-world HSI domain, we
had to develop an admissible heuristic on our own
before, which is sketched in (Rathfux et al., 2019a)
and more formally defined in (Rathfux et al., 2019b).
Let us denote it as h
HSI
here. Since we followed the
constraint relaxation meta-heuristic (given already in
(Pearl, 1984)) for its development, h
HSI
is actually
consistent, but this is only relevant for our purposes
here for implying admissibility of h
HSI
.
For the Fifteen Puzzle domain previously stud-
ied in-depth, all the heuristics we include in our ex-
periment of estimating problem instance difficulty
are well-known, published and their admissibility is
proven. In fact, already in (Pearl, 1984) the constraint
relaxation meta-heuristic was illustrated for two such
heuristic functions:
• h
T R
, simply counting the number of tiles that are
positioned “right”, i.e., in the position as defined
by the target configuration t,
• h
M
, the so-called Manhattan Distance heuristic.
Both of them obviously return estimated numbers of
steps that are at least needed to arrive at the target
node t. While h
T R
provides only very rough esti-
mates, h
M
is obviously more accurate. Both, how-
ever, cannot compare with specifically pre-compiled
pattern databases, see (Felner et al., 2004). Essen-
tially, these cache heuristic values from breadth-first
searches from the target node t backwards. In con-
trast to computing heuristic values on demand like
h
M
, pattern databases are pre-computed for later use
in heuristic search for some given problem instance.
They may largely differ in their sizes, e.g., a static
5-5-5 partitioning version requires about 3MB, 6-6-3
partitioning about 33MB, and 7-8 partitioning more
than half a GB. The heuristic function using these
small, medium-sized and large versions are denoted
below as h
P555
, h
P663
and h
P78
, respectively.
3.2.2 Similarity Metrics
One possibility to calculate similarity metrics is using
vectors encoding information. We studied different
variations on how to create such vectors.
In the HSI domain, we used bit-vectors. A bit-
vector is a vector where each entry is either true (1)
or false (0). We constructed the vectors using the re-
quirements given for each pin. A vector has n × i en-
tries, where n is the number of ECU-Pins and i is the
number of interface types. Each entry in the vector
corresponds to interface type it on ECU-Pin p and is
1 if his particular interface type is required on this pin.
Using these vectors, the heuristic value for s
H BIT
can
be calculated by counting the entries that are the same
in both the original vector and the vector to be com-
pared to. s
RR BIT
is defined analogously, but instead of
counting the matching entries the differing entries are
counted. Hence, this is actually a dissimilarity metric.
Additionally, we constructed vectors using the in-
terface types of requirements at each ECU-Pin. In
contrast to the vectors described above, we used the
interface types directly (as a string representation) in
the vector. Hence, these vectors have a maximum of
n entries, where n is the number of ECU-Pins. It
is a maximum of n, since we did not include ECU-
Pins without interface types. Using such vectors, we
defined a similarity metric s
R
where we counted the
conformance of interface types on ECU-Pins of two
HSIs. To normalize these similarity values, they are
divided by the number of rows of the larger vector.
A more usual approach to calculating similarity
metrics is using Cosine similarity, which essentially
calculates the angle between two vectors. Two vec-
tors that have the same orientation have a similarity
score of 1, where two vectors that are orthogonal to
each other have a similarity score of 0. This similarity
metric is not dependent on the domain and, thus, we
employed it in the HSI as well as the Puzzle domain.
The calculation of the cosine similarity is shown in
Equation 1.
s
Cos
(s) = cos(θ) =
A · B
kAk · kBk
=
∑
N
i=1
A
i
· B
i
q
∑
N
i=1
A
2
i
·
q
∑
N
i=1
B
2
i
(1)
In the HSI domain, we defined the cosine similar-
ity s
COS BIT
using the same bit-vectors as for s
H BIT
.
By including the interface types of each requirement,
we defined two interface similarity metrics s
IT
and
s
IT R
. These metrics construct their vectors based on
all available interface types and count their occur-
rences. In s
IT R
, we additionally took the requirements
into account.
Estimating Problem Instance Difficulty
363

For the puzzle domain, we defined the cosine sim-
ilarity s
COS
as well. We used the values of the tiles
and their positions for the construction of the vector
and compared it with the vector of the goal state.
For defining another metric s
h
(s), we used the
count of all tiles that are already positioned correctly,
i.e., are in the same position they have to be in the
target state t, and divideed it by the number of tiles,
making it normalized in the interval [0, 1]. This metric
is shown in Equation 2.
s
h
(s) =
∑
15
n=0
TilePosCorrect
n
15
(2)
The same metric can also be defined using the heuris-
tic h
T R
from above as shown in Equation 3.
s
h
(s) =
h
tr
15
(3)
This approach is the same as the one for the Russel-
Rao Dissimilarity s
RR
, where the tiles that are not in
the right position are used for its calculation.
3.3 Hybrids of Measuring and
Estimating
Since “blind” algorithms like Dijkstra’s famous
shortest-path algorithm cannot solve “difficult” prob-
lem instances, algorithms like A* and IDA* employ
heuristic estimates h and still guarantee that a solution
found is optimal, if h is admissible (see also above).
The time they take for that heavily depends on the
quality of h used (see, e.g., (Pearl, 1984)). Hence, we
found it interesting to combine h with a measure into
a hybrid, for getting yet another view.
In fact, (Korf et al., 2001) showed that the ef-
fect of a heuristic function is to reduce the effective
depth of search by a constant, relative to a brute-force
search, rather than reducing the effective branching
factor. And especially for distinguishing “easy” prob-
lems in the HSI domain from the others, d
abs
turned
out to be very useful in (Rathfux et al., 2019b):
d
abs
(s) = C
∗
− h(s) (4)
d
rel
(s) =
d
abs
(s)
C
∗
(5)
For using d
rel
before, however, we did not yet gain
any experience. Still, it provides yet another view,
since d
abs
is most likely not very useful when com-
paring solutions with a large difference in cost.
Below, we use these formulas in the category of
measures, since by including C
∗
they cannot be used
for estimating in the course of a search for a newly
given problem instance.
4 EXPERIMENT
The experiment is designed to explore how these dif-
ferent approaches to estimating problem instance dif-
ficulty relate to measuring problem instance difficulty,
where also for the latter different approaches are com-
pared as listed above. Results on this relationship are
presented both using Pearson correlation coefficients,
and how many selection errors the different estimates
make, as counted with respect to the various measur-
ing approaches. All this has been done in two do-
mains, the proprietary HSIs and the widely known
Fifteen Puzzle.
4.1 Experiment Design
First, we created a repository of problem instances
for both domains by running A* and for the Fifteen
Puzzle also IDA*, and with a variety of admissible
heuristics to find optimal solutions. We stored for
each problem instance the values C
∗
, d
abs
, d
rel
and N#
(the number of nodes generated by A* and IDA*, re-
spectively). Since d
abs
, d
rel
also depend on the heuris-
tic used, we stored these values for each of them, and
the values calculated by the various heuristic func-
tions separately as well. In addition, we calculated the
values of a variety of similarity metrics (as explained
above) and stored them.
For studying the correlation between the values
of heuristic functions, similarity metrics and the
different measures of the ground truth, we calculated
Pearson correlation coefficients:
r =
∑
n
i=1
(x
i
− ¯x) · (y
i
− ¯y)
p
∑
n
i=1
(x
i
− ¯x)
2
·
p
∑
n
i=1
(y
i
− ¯y)
2
(6)
If the absolute value of a correlation coefficient is
higher than the absolute value of another one, the first
one indicates a stronger relationship. In fact, we ac-
tually calculated these coefficients between all these
values, since we were interested in the correlations
among the estimates and also among the measures as
well.
However, Pearson correlation coefficients are de-
fined for linear correlations. h-values as estimates of
C
∗
, however, are usually exponentially related to the
number of explored nodes in searches by A*, IDA*
and the like, for finding optimal solutions. That is
why we determine Pearson correlation coefficients
between h-values and the logarithm of the number of
nodes.
In addition, for each Pearson correlation coeffi-
cient we determined its significance as the probabil-
ity p that it could be the result of random fluctuation.
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
364

All the calculations of Pearson correlation coefficients
and their significance were run using Matlab.
In addition, we were interested in the respective
numbers of selection errors that each of the estimates
would make when being used for selecting a case
from a case base. An error means to select a case that
is worse than another one with respect to the problem
instance difficulty. Since we have different measures
for that, we were interested in the numbers of errors
for each of them. However, executing an experiment
directly with a case base and then finding optimal so-
lutions for each of its cases stored and the given goal
(state or condition, respectively) would be very ex-
pensive.
Instead, we used the repository initially created as
follows. For each of its entries, we defined all the tu-
ples (est, di f f ) where for each est through a heuris-
tic function or similarity metric, respectively, and for
each measure of problem instance difficulty di f f , one
of the latter is assigned to the former. For each tu-
ple, we calculated how many errors it induces. To
calculate these errors, we ordered all tuples by their
similarity or heuristic values, respectively, in a vector,
and then checked it against the vector of the corre-
sponding measure. The assumption is that a higher
similarity value or a lower heuristic value, respec-
tively, indicates a case with lower problem instance
difficulty than another case with lower similarity or
higher heuristic value, respectively. Hence, the order
defined by the respective measure should be the same,
e.g., the number of nodes generated N#. Given that,
an error is defined to occur for a given tuple, if the
orders in the corresponding vectors are different.
As an example, let us consider two entries (15, 4)
and (16, 3), which are ordered in the sequence <
(15, 4), (16, 3) > based on their estimate. Since the
second tuple (16, 3) has a higher estimate but lower
difficulty measure, e.g., C
∗
, than the previous one,
then it is counted as an error.
As some values of the tuples in a given vector may
have the same similarity or heuristic value, respec-
tively, we shuffled all tuples and then ordered them,
introducing a different order of tuples with the same
estimate each time. We ran these process 100 times
for each measure and calculated the mean and median
values of the numbers of errors.
Of course, we included for both domains prob-
lem instances with varying difficulty. The C
∗
values
varied from 3 to 17 for the HSI domain, and from
41 to 66 for the Fifteen Puzzle. Since N# depends
on the algorithm used, we attempted to perform the
searches with both A* and IDA*, in order to investi-
gate the correlation between their respective N# val-
ues. Unfortunately, using IDA* is infeasible for the
more difficult HSI problem instances due to the very
high number of DAGs in this search space. (There are
known means to address this, but then it would be-
come some variant of IDA*.) For the Fifteen Puzzle,
it was possible to solve all the 100 random instances
listed in (Korf, 1985) running A* on a state-of-the-art
laptop with 32GB of memory.
More precisely, we executed the experiment runs
on a standard Windows laptop computer with an In-
tel Core i7-8750H Processor (9MB Cache, up to 4.1
GHz, 6 Cores). It has a DDR4-2666MHz memory of
32GB. The disk does not matter, since all the experi-
mental data were gathered using the internal memory
only.
4.2 Experimental Results
After having run the experiment as designed above for
both the HSI domain and the Fifteen Puzzle, we got
the results as presented below.
4.2.1 HSI Domain
In the HSI domain, we used more than 1,000 HSI
specifications for our experiment. These specifica-
tions have been randomly adapted from ten base con-
figurations and are spread across three categories:
Base5, Base7 and Base9. These categories indicate
the number of requirements that are already config-
ured and fulfilled by the HSI.
Each of the 1,000 cases has between three and
seventeen randomly selected requirements. For each
of these cases, their h
HSI
and their similarity values
(using a variety of metrics as defined above) were
calculated with regard to fitting base models, e.g.,
models using the same ECU. An automatic adapta-
tion from each of the 1,000 HSI specifications to ones
that satisfy the new requirements (as goal specifica-
tions) has been performed through heuristic search
using A
∗
with our admissible heuristic function h
HSI
.
This guarantees an optimal solution C
∗
each, i.e., one
with a minimal number of adaptation steps.
For these data, all correlation coefficients between
the measures of the ground truth and the heuris-
tic functions and similarity metrics, respectively, are
given in Table 1. All the data in this table are highly
statistically significant with p < 0.01. A higher (ab-
solute) value indicates a stronger correlation with C
∗
and thus a better estimate. Some of these correlation
coefficients are extremely high, such as the one be-
tween h
HSI
and C
∗
. That is, this heuristic function
is very good at estimating the number of steps mini-
mally required for solution adaptation. The reason is
that the vast majority of problem instances is “easy”
in the sense that they require no reconfigurations, and
Estimating Problem Instance Difficulty
365
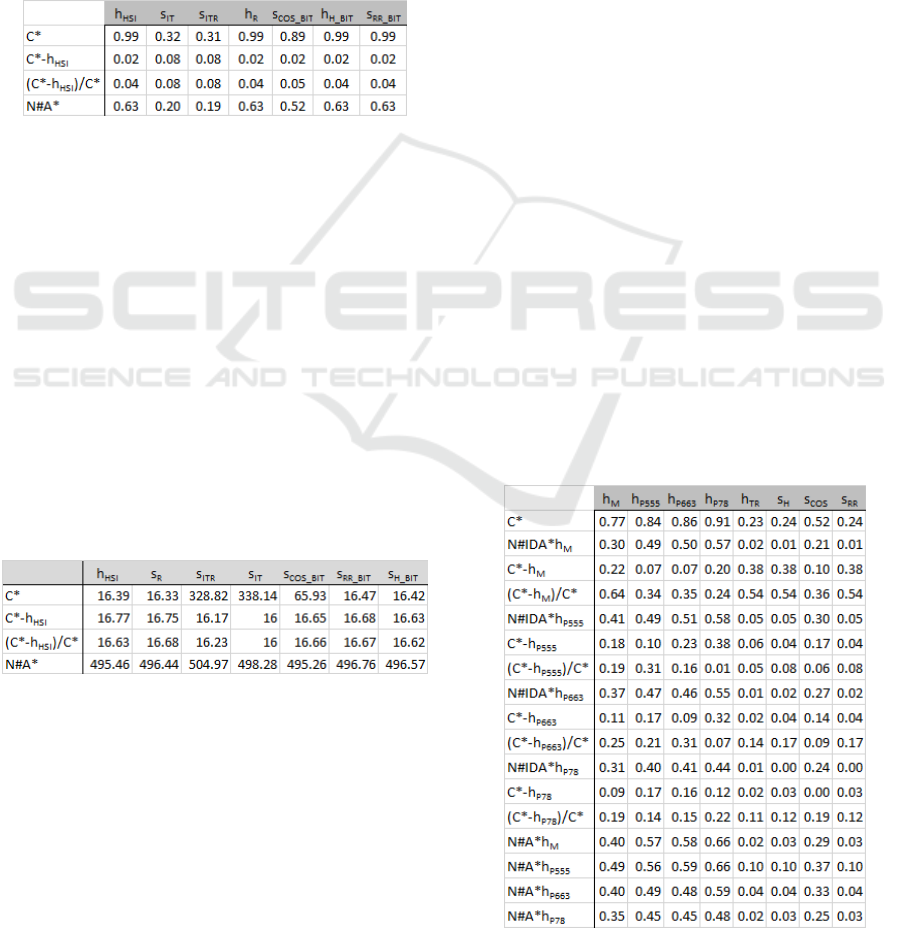
only a few problem instances actually require a few
reconfigurations, see (Rathfux et al., 2019b). Apart
from that, h
HSI
captures the knowledge for estimation
very well. It is actually because of this distribution
of problem instances that also some of the similar-
ity metrics correlate with C
∗
so strongly. The differ-
ence in the knowledge involved only matters for very
few problem instances here. For the absolute and the
relative error measures of the ground truth, however,
the correlation is very weak. The reason is that both
d
abs
= d
rel
= 0 for the majority of problem instances
here.
Table 1: Correlation coefficients — HSI.
Even for the numbers of nodes generated by A*, more
precisely ln(N#A)*, the correlations with some of the
estimates are fairly high. For the given problem in-
stances, where only a few problem instances actually
require a few reconfigurations, these numbers can be
predicted well.
We also calculated the numbers of errors for the
heuristic function and each similarity metric. Table 2
shows the numbers of selection errors in the HSI do-
main. (More precisely these are the mean values as
explained above, and we omit the median values since
they are consistent with the mean values, i.e., outliers
do not play a role here.) In fact, the numbers of er-
rors of predicting N#A* are very high. The selection
results of predicting the other measures of the ground
truth are much better.
Table 2: Numbers of selection errors — HSI.
4.2.2 Fifteen Puzzle
As indicated above, we ran the set of 100 random Fif-
teen Puzzle instances published in (Korf, 1985) for
gathering their data on the different heuristics h
T R
,
h
M
, h
P555
, h
P663
and h
P78
, as well as the C
∗
, d
abs
and
d
rel
data (for the latter with all these heuristics). Since
both IDA* and A* were able to solve all those in-
stances even when using h
M
(but not with h
T R
), we
were also able to get the data on N#IDA* and N#A*,
more precisely the various numbers when using the
different heuristic functions (except h
T R
).
For these data, all correlation coefficients between
the measures of the ground truth and the heuris-
tic functions and similarity metrics, respectively, are
given in Table 3. Note again, that we determined Pear-
son correlation coefficients between each h-value and
the logarithm of the number of nodes. As a base, we
took the value 2.1304 from (Korf et al., 2001), since
it was determined there as the asymptotic branching
factor for the Fifteen Puzzle. Most of the data in this
table are highly statistically significant with p < 0.01,
while especially those related to N#IDA* are only sta-
tistically significant with p < 0.05, which is due to
the fluctuation of the N#IDA* data. For the heuristic
functions used here, their respective domain knowl-
edge involved and their corresponding accuracy are
known. In fact, it is exactly reflected here in their
correlation with C
∗
. Estimates with more knowledge
correlate more strongly with C
∗
than the ones with
less knowledge. The similarity metric corresponding
to h
T R
in this regard, Hamming, has more or less the
same correlation coefficient. In contrast, Cosine cor-
responds much better with C
∗
than Hamming. Still, its
(absolute) correlation coefficient is much lower than
the ones of the heuristic functions incorporating more
domain knowledge. For the absolute and the relative
error measures of the ground truth, however, this pat-
tern is less clearly pronounced. d
abs
is very hard to
estimate for similarity metrics, which makes sense,
since a heuristic function is actually part of its calcu-
lation. However, also for heuristic functions estimat-
ing d
abs
is difficult. The same applies to d
rel
.
Table 3: Correlation coefficients — Fifteen Puzzle.
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
366

For the numbers of nodes generated by IDA* and
A*, respectively, more precisely their logarithm, the
correlations are lower than in the HSI domain. This
can be explained by the fact that the problem in-
stances in the HSI domain are much less difficult,
both with respect to their solutions lengths and the
effort to determine optimal solutions (in terms of the
numbers of nodes explored). In addition, IDA* shows
stronger fluctuations of these numbers than A*, when
both use the same admissible heuristic. This can also
be seen in Figure 2 (generated by a clustering algo-
rithm), where all the correlations are visualized as dis-
tances between nodes. If the distance between two
nodes is small then this indicates a strong correlation
and vice versa a larger distance indicates a weak cor-
relation. The distances in the picture between C
∗
and
the data points corresponding to the numbers of nodes
generated are not smaller than those between C
∗
and
most of the heuristic functions. The distance from C
∗
to the cluster of similarity metrics, however, is clearly
larger, and this corresponds well with the observation
made above, of course. In fact, all the heuristic func-
tions attempt to estimate C
∗
somehow, especially the
ones based on pattern databases and to a lesser extent
h
M
.
Figure 2: Two-dimensional clustering of correlations —
Fifteen Puzzle.
Overall, Figure 2 actually illustrates clusters. There
are two distinct clusters among the ground truth val-
ues. The first one contains all N# values. Although
Table 4: Numbers of selection errors — Fifteen Puzzle.
these values vary strongly in the number of nodes,
they correlate well with each other. The second clus-
ter contains the variations of d
rel
and d
abs
. They do
not correlate well with estimating functions, but with
each other.
Finally, we also checked the number of errors dur-
ing selection, see Table 4. The somewhat surprising
result is, that a higher correlation coefficient does not
necessarily carry over to a reduction of the number of
errors. As pointed out above, N# are hard to estimate
and even higher correlation coefficients do not yield
lower error values when selecting. The best selections
results are accomplished in terms of C
∗
. In this case, a
higher correlation coefficient also means fewer errors
during selection. Also, heuristics with more knowl-
edge provide better results, and the heuristic functions
lead to fewer selection errors than the similarity met-
rics in this regard.
5 CONCLUSION
In CBR, an underlying assumption is that the rela-
tive effort for solution adaptation of stored instances
(cases) correlates with the similarity of these in-
stances with the given problem instance. In our pro-
totypical real-world HSI application, heuristic search
is used for automatic solution adaptation. Hence,
we conjectured that admissible heuristic functions h
guiding search (normally used for estimating minimal
costs to a given goal state or condition) may be used
for retrieving cases for CBR as well. As a result of our
experiment, we actually conclude that the numbers of
selection errors can be reduced with regard to the opti-
mal solution length by using such heuristic functions,
Estimating Problem Instance Difficulty
367

if they have more knowledge incorporated than the
similarity metrics, and if the problem instances are
difficult (as shown for the Fifteen Puzzle instances).
ACKNOWLEDGMENTS
The InteReUse project (No. 855399) has been funded
by the Austrian Federal Ministry of Transport, In-
novation and Technology (BMVIT) under the pro-
gram “ICT of the Future” between September 2016
and August 2019. More information can be found at
https://iktderzukunft.at/en/.
The VIATRA team provided us with their VIA-
TRA2 tool. Our implementations of Fifteen Puzzle
are based on the very efficient C code of IDA* and
A* made available by Richard Korf and an efficient
hashing schema by Jonathan Shaeffer. Ariel Felner
and Shahaf Shperberg provided us with hints about
the availability of code for the Fifteen Puzzle pattern
databases.
Last but not least, Alexander Seiler and Lukas
Schr
¨
oer helped us with getting all the C code running
under Windows for our Fifteen Puzzle experiment.
REFERENCES
Aamodt, A. and Plaza, E. (1994). Case-based Reasoning:
Foundational Issues, Methodological Variations, and
System Approaches. AI Commun., 7(1):39–59.
Bandyopadhyay, S. and Saha, S. (2012). Unsuper-
vised Classification: Similarity Measures, Classi-
cal and Metaheuristic Approaches, and Applications.
Springer Publishing Company, Incorporated.
Bu, Z. and Korf, R. E. (2019). A*+IDA*: A simple hy-
brid search algorithm. In Proceedings of the Twenty-
Eighth International Joint Conference on Artificial In-
telligence, IJCAI-19, pages 1206–1212. International
Joint Conferences on Artificial Intelligence Organiza-
tion.
Bulitko, V., Bj
¨
ornsson, Y., and Lawrence, R. (2010). Case-
based subgoaling in real-time heuristic search for
video game pathfinding. J. Artif. Int. Res., 39(1):269–
300.
Burke, E. K., Petrovic, S., and Qu, R. (2006). Case-based
heuristic selection for timetabling problems. Journal
of Scheduling, 9(2):115–132.
Cha, S.-H. (2007). Comprehensive Survey on Dis-
tance/Similarity Measures between Probability Den-
sity Functions. International Journal of Mathematical
Models and Methods in Applied Sciences, 1(4):300–
307.
Dechter, R. and Pearl, J. (1985). Generalized best-
first strategies and the optimality of a*. J. ACM,
32(3):505–536.
Edelkamp, S. and Schroedl, S. (2012). Heuristic
Search: Theory and Applications. Morgan Kaufmann,
Waltham, MA.
Felner, A., Korf, R. E., and Hanan, S. (2004). Additive pat-
tern database heuristics. J. Artif. Int. Res., 22(1):279–
318.
Goel, A. K. and Diaz-Agudo, B. (2017). What’s hot in case-
based reasoning. In Proc. Thirty-First AAAI Confer-
ence on Artificial Intelligence (AAAI-17), pages 5067–
5069, Menlo Park, CA. AAAI Press / The MIT Press.
Hart, P., Nilsson, N., and Raphael, B. (1968). A formal
basis for the heuristic determination of minimum cost
paths. IEEE Transactions on Systems Science and Cy-
bernetics (SSC), SSC-4(2):100–107.
Hegedus, A., Horvath, A., Rath, I., and Varro, D.
(2011). A Model-driven Framework for Guided De-
sign Space Exploration. In Proceedings of the 2011
26th IEEE/ACM International Conference on Auto-
mated Software Engineering, ASE ’11, pages 173–
182, Washington, DC, USA. IEEE Computer Society.
Kaindl, H. and Kainz, G. (1997). Bidirectional heuristic
search reconsidered. Journal of Artificial Intelligence
Research (JAIR), 7:283–317.
Kaindl, H., Kainz, G., Leeb, A., and Smetana, H. (1995).
How to use limited memory in heuristic search. In
Proc. Fourteenth International Joint Conference on
Artificial Intelligence (IJCAI-95), pages 236–242. San
Francisco, CA: Morgan Kaufmann Publishers.
Kaindl, H., Smialek, M., and Nowakowski, W. (2010).
Case-based reuse with partial requirements speci-
fications. In Proceedings of the 18th IEEE In-
ternational Requirements Engineering Conference
(RE’10), pages 399–400.
Kirsopp, C., Shepperd, M., and Hart, J. (2002). Search
heuristics, case-based reasoning and software project
effort prediction. In Proceedings of the 4th Annual
Conference on Genetic and Evolutionary Computa-
tion, GECCO’02, pages 1367–1374, San Francisco,
CA, USA. Morgan Kaufmann Publishers Inc.
Kolodner, J. (1993). Case-Based Reasoning. Morgan Kauf-
mann Publishers Inc., San Francisco, CA, USA.
Korf, R. (1985). Depth-first iterative deepening: An op-
timal admissible tree search. Artificial Intelligence,
27(1):97–109.
Korf, R. E., Reid, M., and Edelkamp, S. (2001). Time
complexity of iterative-deepening-A*. Artificial In-
telligence, 129(1):199 – 218.
Lopez de Mantaras, R., McSherry, D., Bridge, D., Leake,
D., Smyth, B., Craw, S., Faltings, B., Maher, M. L.,
Cox, M. T., Forbus, K., and et al. (2005). Retrieval,
reuse, revision and retention in case-based reasoning.
The Knowledge Engineering Review, 20(3):215–240.
Pearl, J. (1984). Heuristics: Intelligent Search Strate-
gies for Computer Problem Solving. Addison-Wesley,
Reading, MA.
Rathfux, T., Kaindl, H., Hoch, R., and Lukasch, F. (2019a).
An Experimental Evaluation of Design Space Explo-
ration of Hardware/Software Interfaces. In Proceed-
ings of the 14th International Conference on Evalu-
ation of Novel Approaches to Software Engineering,
ENASE 2019, pages 289–296. INSTICC, SciTePress.
Rathfux, T., Kaindl, H., Hoch, R., and Lukasch, F. (2019b).
Efficiently finding optimal solutions to easy problems
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
368

in design space exploration: A* tie-breaking. In van
Sinderen, M. and Maciaszek, L. A., editors, Proceed-
ings of the 14th International Conference on Software
Technologies, ICSOFT 2019, Prague, Czech Republic,
July 26-28, 2019., pages 595–604. SciTePress.
Reiser, C. and Kaindl, H. (1995). Case-based reasoning for
multi-step problems and its integration with heuristic
search. In Haton, J.-P., Keane, M., and Manago, M.,
editors, Advances in Case-Based Reasoning, pages
113–125, Berlin, Heidelberg. Springer Berlin Heidel-
berg.
Schank, R. C. (1983). Dynamic Memory: A Theory of
Reminding and Learning in Computers and People.
Cambridge University Press, New York, NY, USA.
Sohangir, S. and Wang, D. (2017). Improved sqrt-cosine
similarity measurement. Journal of Big Data, 4(1):25.
Estimating Problem Instance Difficulty
369
