
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object
Classification
Sameera Ramasinghe
1 a
, Salman Khan
2,1
and Nick Barnes
1
1
Australian National University, Australia
2
Inception Institute of Artificial Intelligence, U.A.E.
Keywords:
Convolution Neural Networks, Volumetric Convolution, Zernike Polynomials, Deep Learning.
Abstract:
Convolution is an effective technique that can be used to obtain abstract feature representations using hierarchical
layers in deep networks. However, performing convolution in non-Euclidean topological spaces such as the unit
ball (
B
3
) is still an under-explored problem. In this paper, we propose a light-weight experimental architecture
for 3D object classification, that operates in
B
3
. The proposed network utilizes both hand-crafted and learned
features, and uses capsules in the penultimate layer to disentangle 3D shape features through pose and view
equivariance. It simultaneously maintains an intrinsic co-ordinate frame, where mutual relationships between
object parts are preserved. Furthermore, we show that the optimal view angles for extracting patterns from 3D
objects depend on its shape and achieve compelling results with a relatively shallow network, compared to the
state-of-the-art.
1 INTRODUCTION
Convolution is an extremely effective technique that
can be used to extract useful features from spatially
correlated data structures, with minimal supervision
((Krizhevsky et al., 2012; He et al., 2016)). Interest-
ingly, extending convolution to topological data struc-
tures other than Euclidean spaces, such as spheres,
is beneficial to many research areas such as robotics,
geoscience and medical imaging, as real-world 3D
data naturally lie on a non-Euclidean manifold. The
aforementioned extension, however, is not straightfor-
ward due to the non-uniform grid structures of non-
Euclidean spaces, and is an open research problem.
Recently, there have been some key efforts to ex-
tend traditional convolution to spherical space. A pre-
liminary study of this was presented by (Boomsma
and Frellsen, 2017), where they apply a cube-sphere
transformation on 3D data, and add padding prior to
perform 2D convolution on the transformed data. The
work by (Cohen et al., 2018) recently received much at-
tention as they used spherical harmonics to efficiently
perform convolution on the surface of the sphere (
S
2
),
while achieving 3D rotational equivariance. A key
limitation of their work, however, is that the proposed
convolution operation is limited to polar shapes, as the
a
https://orcid.org/0000-0002-3200-9291
objects are represented in (
S
2
). In a slightly different
approach, (Weiler et al., 2018) proposed a method to
achieve SE(3) equivariance by modeling 3D data as
dense vector fields in 3D Euclidean space.
On the contrary, (Ramasinghe et al., 2019) pre-
sented a novel convolution operation that can perform
convolution in
B
3
. In this work, we adapt their derived
formulas and present a novel experimental architecture
which can be used to classify 3D objects. Our architec-
ture can handle non-polar shapes, and capture both 2D
texture and 3D shape features simultaneously. We use
a capsule network after the convolution layer as it al-
lows us to directly compare feature discriminability of
spherical convolution and volumetric convolution with-
out any bias. In other words, the optimum deep archi-
tecture for spherical convolution may not be the same
for volumetric convolution. Capsules, however, do not
deteriorate extracted features and the final accuracy
only depends on the richness of input shape features.
Therefore, a fair comparison between spherical and
volumetric convolutions can be done by simply replac-
ing the convolution layer. Additionally, the proposed
architecture exploits both hand-crafted and learned fea-
tures and demonstrates that fusing these feature types
results in an improved performance. We show that the
optimum view-angles for extracting features from a 3D
object depends on its shape. We also demonstrate that
different learning models such as convolution and cap-
Ramasinghe, S., Khan, S. and Barnes, N.
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object Classification.
DOI: 10.5220/0009344801150125
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 115-125
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
115

sule networks can work in unison towards a common
goal. Furthermore, our network achieves competitive
results with a significantly shallow design, compared
to the state-of-the-art.
It is important to note that the proposed experimen-
tal architecture is only a one possible example out of
many possible designs, and is focused on three factors:
1) Capture useful features with a relatively shallow
network compared to state-of-the-art. 2) Show rich-
ness of computed features through clear improvements
over spherical convolution. 3) Demonstrate the useful-
ness of the volumetric convolution and axial symmetry
feature layers as fully differentiable and easily plug-
gable layers, which can be used as building blocks for
end-to-end deep architectures.
The rest of the paper is structured as follows. In
Sec. 2 we introduce the overall problem and our pro-
posed solution. Sec. 3 presents an overview of the
necessary theoretical background. Sec. 4.2 presents
our experimental architecture, and in Sec. 5 we show
the effectiveness of the derived operators through ex-
tensive experiments. Finally, we conclude the paper in
Sec. 6.
2 PROBLEM DEFINITION
Convolution is an effective method to capture useful
features from uniformly spaced grids in
R
n
, within
each dimension of
n
, such as gray scale images (
R
2
),
RGB images (
R
3
), spatio-temporal data (
R
3
) and
stacked planar feature maps (
R
n
). In such cases, uni-
formity of the grid within each dimension ensures the
translation equivariance of the convolution. However,
for topological spaces such as
S
2
and
B
3
, it is not pos-
sible to construct such a grid due to non-linearity. A
naive approach to perform convolution in
B
3
would
be to create a uniformly spaced three dimensional grid
in
(r,θ,φ)
coordinates (with necessary padding) and
perform 3D convolution. However, the spaces between
adjacent points in each axis are dependant on their ab-
solute position and hence, modeling such a space as a
uniformly spaced grid is not accurate.
To overcome these limitations, we propose a novel
experimental architecture which can effectively oper-
ate on functions in
B
3
. It is important to note that
ideally, the convolution in
B
3
should be a signal on
both 3D rotation group and 3D translation. However,
since Zernike polynomials do not have the necessary
properties to automatically achieve translation equiv-
ariance, we stick to 3D rotation group in this work.
In Sec. 3, we present an overview of the theoretical
background that is relevant to the context of this paper.
3 THEORETICAL BACKGROUND
3.1 3D Zernike Polynomials
3D Zernike polynomials are a complete and orthogo-
nal set of basis functions in
B
3
, that exhibits a ‘form
invariance’ property under 3D rotation ((Canterakis,
1999)). A
(n,l,m)
th
order 3D Zernike basis function
is defined as,
Z
n,l,m
= R
n,l
(r)Y
l,m
(θ,φ) (1)
where
R
n,l
is the Zernike radial polynomial,
Y
l,m
(θ,φ)
is the spherical harmonics function,
n ∈ Z
+
,
l ∈ [0,n]
,
m ∈ [−l,l]
and
n − l
is even. Since 3D
Zernike polynomials are orthogonal and complete in
B
3
, an arbitrary function
f (r, θ,φ)
in
B
3
can be approx-
imated using Zernike polynomials as follows.
f (θ, φ,r) =
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Z
n,l,m
(θ,φ, r) (2)
where Ω
n,l,m
( f ) could be obtained using,
Ω
n,l,m
( f ) =
Z
1
0
Z
2π
0
Z
π
0
f (θ, φ,r)Z
†
n,l,m
r
2
sinφdrdφdθ
(3)
where
†
denotes the complex conjugate. In Sec. 3.2,
we will derive the proposed volumetric convolution.
3.2 Volumetric Convolution
Consider a 3D rotation operation, which moves a point
p
on the surface of the unit sphere to another point
p
0
. If we decompose the rotation using Eular angles
as
R(θ,φ) = R(θ)
y
R(φ)
z
R(θ)
y
, the first rotation
R(θ)
y
can differ while mapping
p
to
p
0
(if
y
is the north pole).
In another words, there is no unique rotation operation
which can map
p
to
p
0
. However, enforcing the kernel
to be symmetric around the north pole (
y
-axis) makes
the rotated kernel function depend only on
p
and
p
0
,
since then the initial rotation around
y
does not affect
the kernel function. Following this observation, we are
able to define a 3D rotation kernel which only depends
on azimuth and polar angles, as shown in upcoming
derivations.
Let the kernel be symmetric around
y
and
f (θ, φ,r)
,
g(θ,φ, r)
be the functions of object and kernel respec-
tively. Then we define volumetric convolution as,
f ∗ g(α,β)
:
= h f (θ, φ,r), τ
(α,β)
(g(θ,φ,r))i
(4)
=
Z
1
0
Z
2π
0
Z
π
0
f (θ,φ,r),τ
(α,β)
(g(θ,φ,r))sin φ dφdθdr,
(5)
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
116

where
τ
(α,β)
is an arbitrary rotation, that aligns the
north pole with the axis towards
(α,β)
direction (
α
and
β
are azimuth and polar angles respectively). Eq. 4
is able to capture more complex patterns compared
to spherical convolution due to two reasons: 1) the
inner product integrates along the radius and 2) the
projection onto spherical harmonics forces the function
into a polar function, that can result in information
loss.
(Ramasinghe et al., 2019) present the following
theorem to present volumetric convolution. A short
version of the proof is then provided. Please see Ap-
pendix 6 for the complete derivation.
Theorem 1:
Suppose
f ,g : X −→ R
3
are square
integrable complex functions defined in
B
3
so that
h f , f i < ∞
and
hg,gi < ∞
. Further, suppose
g
is sym-
metric around north pole and
τ(α,β) = R
y
(α)R
z
(β)
where R ∈ SO(3). Then,
Z
1
0
Z
2π
0
Z
π
0
f (θ, φ,r),τ
(α,β)
(g(θ,φ, r)) sinφ dφdθdr
≡
4π
3
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n,l,0
(g)Y
l,m
(α,β),
(6)
where
Ω
n,l,m
( f ),Ω
n,l,0
(g)
and
Y
l,m
(θ,φ)
are
(n,l,m)
th
3D Zernike moment of
f
,
(n,l,0)
th
3D Zernike moment
of g, and spherical harmonics function respectively.
Proof:
Completeness property of 3D Zernike Poly-
nomials ensures that it can approximate an arbitrary
function in
B
3
, as shown in Eq. 2. Leveraging this
property, Eq. 4 can be rewritten as,
f ∗ g(α,β) = h
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Z
n,l,m
,
τ
(α,β)
(
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m
0
=−l
Ω
n
0
,l
0
,m
0
(g)Z
n
0
,l
0
,m
0
)i.
(7)
However, since
g(θ,φ, r)
is symmetric around
y
,
the rotation around
y
should not change the function.
This ensures,
g(r,θ, φ) = g(r,θ − α,φ) (8)
and hence,
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m
0
=−l
Ω
n
0
,l
0
,m
0
(g)R
n
0
,l
0
(r)Y
l
0
,m
0
(θ,φ)
=
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m
0
=−l
Ω
n
0
,l
0
,m
0
(g)R
n
0
,l
0
(r)Y
l
0
,m
0
(θ,φ)e
−im
0
α
.
(9)
This is true, if and only if
m
0
= 0
. Therefore, a symmet-
ric function around
y
, defined inside the unit sphere
can be rewritten as,
∞
∑
n
0
=0
n
0
∑
l
0
=0
Ω
n
0
,l
0
,0
(g)Z
n
0
,l
0
,0
(10)
which simplifies Eq. 7 to,
f ∗ g(α,β) = h
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Z
n,l,m
,
τ
(α,β)
(
∞
∑
n
0
=0
n
0
∑
l
0
=0
Ω
n
0
,l
0
,0
(g)Z
n
0
,l
0
,0
)i
(11)
Using the properties of inner product, Eq. 11 can be
rearranged as,
f ∗ g(α,β) =
∞
∑
n=0
n
∑
l=0
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n
0
,l
0
,0
(g)
hZ
n,l,m
,τ
(α,β)
(Z
n
0
,l
0
,0
)i. (12)
Using the rotational properties of Zernike polynomials,
we obtain (see Appendix 6 for our full derivation),
f ∗ g(θ,φ) =
4π
3
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n,l,0
(g)Y
l,m
(θ,φ)
(13)
Since we can calculate
Ω
n,l,m
( f )
and
Ω
n,l,0
(g)
eas-
ily using an iterative method ((Ramasinghe et al.,
2019)),
f ∗ g(θ,φ)
can be found using a simple ma-
trix multiplication. It is interesting to note that,
since the convolution kernel does not translate, the
convolution produces a polar shape, which can be
further convolved–if needed–using the relationship
f ∗ g(θ,φ) =
q
4π
2l+1
∑
l
l
∑
m=−l
ˆ
f (l,m) ˆg(l, m)Y
(l,m)
(θ,φ)
where,
ˆ
f (l,m)
and
ˆg(l, m)
are the
(l, m)
th
frequency
components of f and g in spherical harmonics space.
3.3 Equivariance to 3D Rotation Group
The equivariance of the volumetric convolution to 3D
rotation group can be shown using the following theo-
rem.
Theorem 1:
Suppose
f ,g : X −→ R
3
are square
integrable complex functions defined in
B
3
so that
h f , f i < ∞
and
hg,gi < ∞
. Also, let
η
α,β,γ
be a
3D rotation operator that can be decomposed into
three Eular rotations
R
y
(α)R
z
(β)R
y
(γ)
and
τ
α,β
an-
other rotation operator that can be decomposed into
R
y
(α)R
z
(β)
. Suppose
η
α,β,γ
(g) = τ
α,β
(g)
. Then,
η
(α,β,γ)
( f ) ∗ g(θ,φ) = τ
(α,β)
( f ∗ g)(θ,φ)
, where
∗
is
the volumetric convolution operator.
The proof to above theorem can be found in Ap-
pendix 6.
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object Classification
117
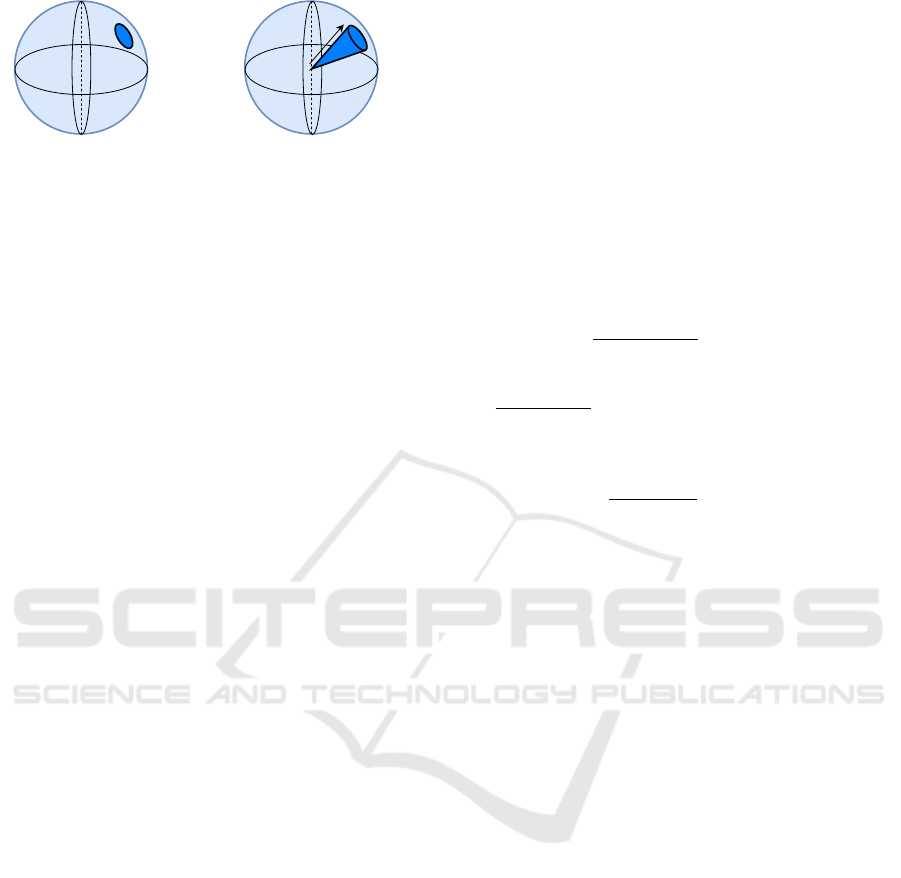
r
(θ ,ϕ )(θ ,ϕ )
Figure 1: Difference between spherical convolution (left) and
volumetric convolution (right). In volumetric convolution,
inner product between kernel and the shape is taken in
B
3
and in spherical convolution, it is taken in
S
2
. Modeling and
convolving in
B
3
allows encoding non-polar 3D shapes with
texture.
3.4 Axial Symmetry of Functions in B
3
Axial symmetry of a function in
B
3
around an arbitrary
axis can be found using the following formula.
Proposition:
Suppose
g : X −→ R
3
is a square
integrable complex function defined in
B
3
such that
hg,gi < ∞
. Then, the power of projection of
g
in to
S =
{Z
i
}
where
S
is the set of Zernike basis functions that
are symmetric around an axis towards
(α,β)
direction
is given by,
||sym
(α,β)
||=
∑
n
n
∑
l=0
||
l
∑
m=−l
Ω
n,l,m
Y
m,l
(α,β)||
2
(14)
where
α
and
β
are azimuth and polar angles respec-
tively.
The proof the above proposition is given in Ap-
pendix 6.
4 A CASE STUDY: 3D OBJECT
RECOGNITION
4.1 3D Objects as Functions in B
3
A polar 3D object can be expressed as a single val-
ued function on the
S
2
. Performing convolution on
S
2
can be considered as moving the kernel on
S
2
and
then calculating inner product with the shape func-
tion. However, representing non-polar shapes as polar
objects can lead to critical information loss. Further-
more, since the inner produce happens on
S
2
, it is not
possible to capture patterns across radius.
The aforementioned limitations can be avoided
by performing convolution inside the unit ball (
B
3
).
Modeling the shape functions inside
B
3
allows us to
represent non-polar shapes without loss of informa-
tion and it allows encoding 2D texture information, as
each point inside
B
3
can be allocated a scalar value.
Figure 1 illustrates the difference between volumetric
and spherical convolutions. However, we experiment
only on uniform textured 3D objects in this work, and
therefore, apply an artificial surface function to the
objects as follows:
f (θ, φ,r) =
(
r, if surface exists at (θ,φ, r)
0, otherwise
(15)
4.2 An Experimental Architecture
We implement an experimental architecture to demon-
strate the usefulness of the proposed operations. While
these operations can be used as building-tools to con-
struct any deep network, we focus on three key fac-
tors while developing the presented experimental ar-
chitecture: 1)
Shallowness:
Volumetric convolution
should be able to capture useful features compared
to other methodologies with less number of layers.
2)
Modularity:
The architecture should have a mod-
ular nature so that a fair comparison can be made
between volumetric and spherical convolution. We
use a capsule network after the convolution layer for
this purpose. 3)
Flexibility:
It should clearly exhibit
the usefulness of axial symmetry features as a hand-
crafted and fully differentiable layer. The motivation
is to demonstrate one possible use case of axial sym-
metry measurements in 3D shape analysis.
The proposed architecture consists of four compo-
nents.
First
, we obtain three view angles, and later
generate features for each view angle separately. We
optimize the view angles to capture complimentary
shape details such that the total information content is
maximized. For each viewing angle ‘
k
’, we obtain two
point sets P
+
k
and P
−
k
consisting of tuples denoted as:
P
+
k
= {(x
i
,y
i
,z
i
) : y
i
> 0}, and
P
−
k
= {(x
i
,y
i
,z
i
) : y
i
< 0}, (16)
such that
y
denotes the horizontal axis.
Second
, the six
point sets are volumetrically convolved with kernels
to capture local patterns of the object. The generated
features for each point set are then combined using
compact bilinear pooling.
Third
, we use axial sym-
metry measurements to generate additional features.
The features that represent each point set are then com-
bined using compact bilinear pooling.
Fourth
, we
feed features from second and third components of
the overall architecture to two independent capsule
networks and combine the outputs at decision level to
obtain the final prediction. The overall architecture of
the proposed scheme is shown in Fig. 2.
4.3 Optimum View Angles
We use three view angles to generate features for bet-
ter representation of the object. First, we translate
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
118
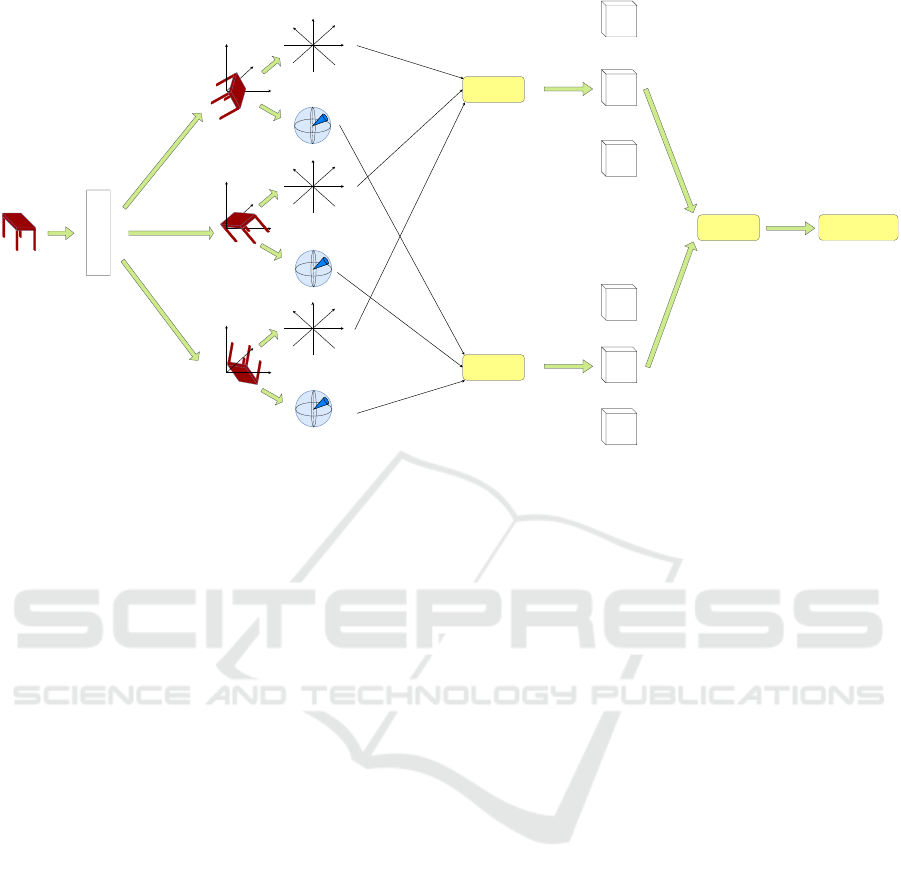
CBP
CBP
Max-Pool
Classification
1-D ConvNet
Figure 2: Experimental architecture: An object is first mapped to three view angles. For each angle, axial symmetry and
volumetric convolution features are generated for
P
+
and
P
−
. These two features are then separately combined using compact
bilinear pooling. Finally, the features are fed to two individual capsule networks, and the decisions are max-pooled.
the center of mass of the set of
(x,y, z)
points to the
origin. The goal of this step is to achieve a general
translational invariance, which allows us to free the
convolution operation from the burden of detecting
translated local patterns. Subsequently, the point set is
rearranged as an ordered set on
x
and
z
and a 1D convo-
lution net is applied on
y
values of the points. Here, the
objective is to capture local variations of points along
the
y
axis, since later we analyze point sets
P
+
and
P
−
independently. The trained filters can be assumed
to capture properties similar to
∂
n
y/∂x
n
and
∂
n
y/∂z
n
,
where
n
is the order of derivative. The output of the 1D
convolution net is rotation parameters represented by a
1 × 9
vector
~r = {r
1
,r
2
,· ·· ,r
9
}
. Then, we compute
R
1
= R
x
(r
1
)R
y
(r
2
)R
z
(r
3
)
,
R
2
= R
x
(r
4
)R
y
(r
5
)R
z
(r
6
)
and
R
3
= R
x
(r
7
)R
y
(r
8
)R
z
(r
9
)
where
R
1
,R
2
and
R
3
are
the rotations that map the points to three different view
angles.
After mapping the original point set to three view
angles, we extract the
P
+
k
and
P
−
k
point sets from each
angle
k
that gives us six point sets. These sets are
then fed to the volumetric convolution layer to obtain
feature maps for each point set. We then measure the
symmetry around four equi-angular axes using Eq. 14,
and concatenate these measurement values to form a
feature vector for the same point sets.
4.4 Feature Fusion using Compact
Bilinear Pooling
Compact bilinear pooling (CBP) provides a compact
representation of the full bilinear representation, but
has the same discriminative power. The key advantage
of compact bilinear pooling is the significantly reduced
dimensionality of the pooled feature vector.
We first concatenate the obtained volumetric con-
volution features of the three angles, for
P
+
and
P
−
separately to establish two feature vectors. These two
features are then fused using compact bilinear pooling
((Gao et al., 2016)). The same approach is used to
combine the axial symmetry features. These fused
vectors are fed to two independent capsule nets.
Furthermore, we experiment with several other fea-
ture fusion techniques and present results in Sec. 5.2.
4.5 Capsule Network
Capsule Network (CapsNet) ((Sabour et al., 2017))
brings a new paradigm to deep learning by modeling
input domain variations through vector based repre-
sentations. CapsNets are inspired by so-called inverse
graphics, i.e., the opposite operation of image render-
ing. Given a feature representation, CapsNets attempt
to generate the corresponding geometrical representa-
tion. The motivation for using CapsNets in the network
are twofold: 1) CapsNet promotes a dynamic ‘routing-
by-agreement’ approach where only the features that
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object Classification
119

are in agreement with high-level detectors are routed
forward. This property of CapsNets does not deteri-
orate extracted features and the final accuracy only
depends on the richness of original shape features. It
allows us to directly compare feature discriminability
of spherical and volumetric convolution without any
bias. For example, using multiple layers of volumetric
or spherical convolution hampers a fair comparison
since it can be argued that the optimum architecture
may vary for two different operations. 2) CapsNet pro-
vides an ideal mechanism for disentangling 3D shape
features through pose and view equivariance while
maintaining an intrinsic co-ordinate frame where mu-
tual relationships between object parts are preserved.
Inspired by these intuitions, we employ two in-
dependent CapsNets in our network for volumetric
convolution features and axial symmetry features. In
this layer, we rearrange the input feature vectors as
two sets of primary capsules—for each capsule net—
and use the dynamic routing technique proposed by
(Sabour et al., 2017) to predict the classification results.
The outputs are then combined using max-pooling, to
obtain the final classification result. For volumetric
convolution features, our architecture uses
1000
pri-
mary capsules with
10
dimensions each. For axial
symmetry features, we use
2500
capsules, each with
10
dimensions. In both networks, decision layer con-
sist of 12 dimensional capsules.
4.6 Hyperparameters
We use
n = 5
to implement Eq. 13 and use a decaying
learning rate
lr = 0.1 × 0.9
g
step
3000
, where
g
step
is incre-
mented by one per each iteration. For training, we use
the Adam optimizer with
β
1
= 0.9, β
2
= 0.999, ε =
1 × 10
−8
where parameters refer to the usual notation.
All these values are chosen empirically. Since we have
decomposed the theoretical derivations into sets of
low-cost matrix multiplications, specifically aiming to
reduce the computational complexity, the GPU imple-
mentation is highly efficient. For example, the model
takes less than 15 minutes for an epoch during the
training phase for ModelNet10, with a batchsize 2, on
a single GTX 1080Ti GPU.
5 EXPERIMENTS
In this section, we discuss and evaluate the perfor-
mance of the proposed approach. We first compare the
accuracy of our model with relevant state-of-the-art
work, and then present a thorough ablation study of
our model, that highlights the importance of several
architectural aspects. We use ModelNet10 and Model-
Net40 datasets in our experiments. Next, we evaluate
the robustness of our approach against loss of informa-
tion and finally show that the proposed approach for
computing 3D Zernike moments produce richer repre-
sentations of 3D shapes, compared to the conventional
approach.
5.1 Comparison with the
State-of-the-art
Table 1 illustrates the performance comparison of our
model with state-of-the-art. The model attains an over-
all accuracy of
92.17%
on ModelNet10 and
86.5%
accuracy on ModelNet40, which is on par with state-
of-the-art. We do not compare with other recent work,
such as (Kanezaki et al., 2016), (Qi et al., 2016),
(Sedaghat et al., 2016), (Wu et al., 2016), (Qi et al.,
2016) and (Bai et al., 2016), (Maturana and Scherer,
2015) that show impressive performance on Model-
Net10 and ModelNet40. These are not comparable
with our proposed approach, as we propose a shallow,
single model without any data augmentation, with a
relatively low number of parameters. Furthermore,
our model reports these results by using only a sin-
gle volumetric convolution layer for learning features.
Fig. 3 demonstrates effectiveness of our architecture
by comparing accuracy against the number of trainable
parameters in state-of-the-art models.
5.2 Ablation Study
Table 2 depicts the performance comparison between
several variants of our model. To highlight the ef-
fectiveness of the learned optimum view points, we
replace the optimum view point layer with three fixed
orthogonal view points. This modification causes an
accuracy drop of 6.57%, emphasizing that the opti-
mum view points indeed depends on the shape. An-
other interesting—perhaps the most important—aspect
to study is the performance of the proposed volumet-
ric convolution against spherical convolution. To this
end, we replace the volumetric convolution layer of
our model with spherical convolution and compare
the results. It can be seen that our volumetric convo-
lution scheme outperforms spherical convolution by
a significant margin of 12.56%, indicating that vol-
umetric convolution captures shape properties more
effectively.
Furthermore, using mean-pooling instead of max-
pooling, at the decision layer drops the accuracy to
87.27%
. We also evaluate performance of using a sin-
gle capsule net. In this scenario, we combine axial
symmetry features with volumetric convolution fea-
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
120

Table 1: Comparison with state-of-the-art methods on ModelNet10 and ModelNet40 datasets (ranked according to performance).
Ours achieve a competitive performance with the least network depth.
Method Trainable layers # Params M10 M40
SO-Net ((Li et al., 2018)) 11FC 60M 95.7% 93.4%
Kd-Networks ((Klokov and Lempitsky, 2017)) 15KD - 94.0% 91.8%
VRN ((Brock et al., 2016)) 45Conv 90M 93.11% 90.8%
Pairwise ((Johns et al., 2016)) 23Conv 143M 92.8% 90.7%
MVCNN ((Su et al., 2015)) 60Conv + 36FC 200M - 90.1%
Ours 3Conv + 2Caps 4.4M 92.17% 86.5%
PointNet ((Qi et al., 2017)) 2ST + 5Conv 80M - 86.2%
ECC ((Simonovsky and Komodakis, 2017)) 4Conv + 1FC - - 83.2%
DeepPano ((Shi et al., 2015)) 4Conv + 3FC - 85.45% 77,63%
3DShapeNets ((Wu et al., 2015)) 4-3DConv + 2FC 38M 83.5% 77%
PointNet ((Garcia-Garcia et al., 2016)) 2Conv + 2FC 80M 77.6% -
Table 2: Ablation study of the proposed architecture on
ModelNet10 dataset.
Method Accuracy
Final Architecture (FA) 92.17%
FA + Orthogonal Rotation 85.60%
FA - VolCNN + SphCNN 79.53%
FA -MaxPool + MeanPool 87.27%
FA + Feature Fusion (Axial + Conv) 86.53%
Axial Symmetry Features 66.73%
VolConv Features 85.3%
SphConv Features 71.6%
FA - CapsNet + FC layers 87.3 %
FA - CBP + Feature concat 90.7%
FA - CBP + MaxPool 90.3%
FA - CBP + Average-pooling 85.3 %
20 40 60 80 100 120 140 160 180 200
80
90
100
SO-Net
VRN
Pairwise
MVCNN
Ours
PointNet
3DShapeNet
Accuracy
Number of trainable parameters
Figure 3: Accuracy vs number of trainable params (in mil-
lions) trend (ModelNet40).
tures using compact bilinear pooling (CBP), and feed
it a single capsule network. This variant achieves an
overall accuracy of
86.53%
, is a
5.64%
reduction in
accuracy compared to the model with two capsule net-
works.
Moreover, we compare the performance of two
feature categories—volumetric convolution features
and axial symmetry features—individually. Axial sym-
metry features alone are able to obtain an accuracy of
66.73%
, while volumetric convolution features reach a
significant
85.3%
accuracy. On the contrary, spherical
convolution attains an accuracy of
71.6%
, which again
highlights the effectiveness of volumetric convolution.
Then we compare between different choices that
can be applied to the experimental architecture. We
first replace the capsule network with a fully connected
layer and achieve an accuracy of 87.3%. This is per-
haps because capsules are superior to a simple fully
connected layer in modeling view-point invariant rep-
resentations. Then we try different substitutions for
compact bilinear pooling and achieve 90.7%, 90.3%
and 85.3% accuracies respectively for feature concate-
nation, max-pooling and average-pooling. This justi-
fies the choice of compact bilinear pooling as a feature
fusion tool. However, it should be noted that these
choices may differ depending on the architecture.
5.3 Rotation Parameters
The optimum view-angles for learning features in 3D
space depend on the geometric features of a particular
3D object. Therefore, allowing the network to learn
these optimum view-angles, in contrast to using fixed
angles for every shape, improves the performance, as
discussed in Section 5.2. Table 3 depicts the final
rotation parameters learned by the network, which
are then used for rotating the object. As it is clearly
evident, each shape category corresponds to different
rotation parameters, which empirically proves that the
optimum view-angles indeed depend on the object
class.
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object Classification
121

Table 3: Average rotation parameter values across classes of ModelNet10. The values are reformatted to be positive angles
between 0 and 360.
Class r
1
r
2
r
3
r
4
r
5
r
6
r
7
r
8
r
9
Bathtub Bathtub 319.2 100.5 57.8 185.2 223.4 98.3 350.6 167.4 14.2
Bed 264.3 196.3 103.7 208.5 186.2 194.4 267.9 246.3 81.2
Chair 198.6 91.2 243.7 47.4 161.2 87.9 240.5 47.3 203.4
Desk 88.4 80.2 130.9 206.6 86.5 112.8 291.7 233.2 351.4
Dresser 58.0 145.7 353.1 148.4 346.4 125.3 47.0 2.2 35.4
Monitor 218.9 279.0 58.1 10.4 30.3 331.4 90.7 285.6 346.1
Night stand 85.3 336.1 175.9 246.4 169.4 278.7 317.0 137.6 302.9
Sofa 306.1 86.9 109.2 311.1 22.5 321.4 96.9 47.0 76.2
Table 299.8 85.2 126.5 215.1 221.9 245.5 237.1 50.6 128.4
Toilet 277.0 325.3 215.5 255.6 192.2 19.8 278.4 193.4 348.2
Average 211.6 172.6 157.4 183.4 164.1 182.4 221.8 141.1 189.7
6 CONCLUSION
In this work, we present a novel experimental archi-
tecture, which can learn feature representations in
B
3
.
We utilize the underlying theoretical foundations for
volumetric convolution and demonstrate how it can
be efficiently computed and implemented using low-
cost matrix multiplications. Moreover, we show that
our experimental architecture gives competitive results
to state-of-the-art with a relatively shallow design, in
3D object recognition task. Finally, we empirically
demonstrate that fusing learned and hand-crafted fea-
tures results in improved performance, as they provide
complementary information.
REFERENCES
Bai, S., Bai, X., Zhou, Z., Zhang, Z., and Latecki, L. J.
(2016). Gift: A real-time and scalable 3d shape search
engine. In Computer Vision and Pattern Recognition
(CVPR), 2016 IEEE Conference on, pages 5023–5032.
IEEE.
Boomsma, W. and Frellsen, J. (2017). Spherical convolu-
tions and their application in molecular modelling. In
Advances in Neural Information Processing Systems,
pages 3436–3446.
Brock, A., Lim, T., Ritchie, J. M., and Weston, N.
(2016). Generative and discriminative voxel modeling
with convolutional neural networks. arXiv preprint
arXiv:1608.04236.
Canterakis, N. (1999). 3d zernike moments and zernike
affine invariants for 3d image analysis and recogni-
tion. In In 11th Scandinavian Conf. on Image Analysis.
Citeseer.
Cohen, T. S., Geiger, M., Koehler, J., and Welling, M. (2018).
Spherical cnns. International Conference on Learning
representations (ICLR).
Gao, Y., Beijbom, O., Zhang, N., and Darrell, T. (2016).
Compact bilinear pooling. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 317–326.
Garcia-Garcia, A., Gomez-Donoso, F., Garcia-Rodriguez, J.,
Orts-Escolano, S., Cazorla, M., and Azorin-Lopez, J.
(2016). Pointnet: A 3d convolutional neural network
for real-time object class recognition. In Neural Net-
works (IJCNN), 2016 International Joint Conference
on, pages 1578–1584. IEEE.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Johns, E., Leutenegger, S., and Davison, A. J. (2016). Pair-
wise decomposition of image sequences for active
multi-view recognition. In Computer Vision and Pat-
tern Recognition (CVPR), 2016 IEEE Conference on,
pages 3813–3822. IEEE.
Kanezaki, A., Matsushita, Y., and Nishida, Y. (2016). Rota-
tionnet: Joint object categorization and pose estimation
using multiviews from unsupervised viewpoints. arXiv
preprint arXiv:1603.06208.
Klokov, R. and Lempitsky, V. (2017). Escape from cells:
Deep kd-networks for the recognition of 3d point cloud
models. In 2017 IEEE International Conference on
Computer Vision (ICCV), pages 863–872. IEEE.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Li, J., Chen, B. M., and Lee, G. H. (2018). So-net: Self-
organizing network for point cloud analysis. arXiv
preprint arXiv:1803.04249.
Maturana, D. and Scherer, S. (2015). Voxnet: A 3d convo-
lutional neural network for real-time object recogni-
tion. In Intelligent Robots and Systems (IROS), 2015
IEEE/RSJ International Conference on, pages 922–928.
IEEE.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Point-
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
122

net: Deep learning on point sets for 3d classification
and segmentation. Proc. Computer Vision and Pattern
Recognition (CVPR), IEEE, 1(2):4.
Qi, C. R., Su, H., Nießner, M., Dai, A., Yan, M., and Guibas,
L. J. (2016). Volumetric and multi-view cnns for object
classification on 3d data. In Proceedings of the IEEE
conference on computer vision and pattern recognition,
pages 5648–5656.
Ramasinghe, S., Khan, S., Barnes, N., and Gould, S.
(2019). Representation learning on unit ball with
3d roto-translational equivariance. arXiv preprint
arXiv:1912.01454.
Sabour, S., Frosst, N., and Hinton, G. E. (2017). Dynamic
routing between capsules. In Advances in Neural In-
formation Processing Systems, pages 3859–3869.
Sedaghat, N., Zolfaghari, M., Amiri, E., and Brox, T. (2016).
Orientation-boosted voxel nets for 3d object recogni-
tion. arXiv preprint arXiv:1604.03351.
Shi, B., Bai, S., Zhou, Z., and Bai, X. (2015). Deeppano:
Deep panoramic representation for 3-d shape recog-
nition. IEEE Signal Processing Letters, 22(12):2339–
2343.
Simonovsky, M. and Komodakis, N. (2017). Dynamic edge-
conditioned filters in convolutional neural networks on
graphs. In Proc. CVPR.
Su, H., Maji, S., Kalogerakis, E., and Learned-Miller, E.
(2015). Multi-view convolutional neural networks for
3d shape recognition. In Proceedings of the IEEE
international conference on computer vision, pages
945–953.
Weiler, M., Geiger, M., Welling, M., Boomsma, W., and Co-
hen, T. (2018). 3d steerable cnns: Learning rotationally
equivariant features in volumetric data. arXiv preprint
arXiv:1807.02547.
Wu, J., Zhang, C., Xue, T., Freeman, B., and Tenenbaum,
J. (2016). Learning a probabilistic latent space of ob-
ject shapes via 3d generative-adversarial modeling. In
Advances in Neural Information Processing Systems,
pages 82–90.
Wu, Z., Song, S., Khosla, A., Yu, F., Zhang, L., Tang, X., and
Xiao, J. (2015). 3d shapenets: A deep representation
for volumetric shapes. In Proceedings of the IEEE
conference on computer vision and pattern recognition,
pages 1912–1920.
APPENDIX
Convolution within Unit Sphere using 3D
Zernike Polynomials
Theorem 1:
Suppose
f ,g : X −→ R
3
are square
integrable complex functions defined in
B
3
so that
h f , f i < ∞
and
hg,gi < ∞
. Further, suppose
g
is sym-
metric around north pole and
τ(α,β) = R
y
(α)R
z
(β)
where R ∈ SO(3). Then,
Z
1
0
Z
2π
0
Z
π
0
f (θ, φ,r),τ
(α,β)
(g(θ,φ, r)) sinφ dφdθdr
≡
4π
3
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n,l,0
(g)Y
l,m
(α,β),
(17)
where
Ω
n,l,m
( f ),Ω
n,l,0
(g)
and
Y
l,m
(θ,φ)
are
(n,l,m)
th
3D Zernike moment of
f
,
(n,l,0)
th
3D Zernike moment
of g, and spherical harmonics function respectively.
Proof:
Since 3D Zernike polynomials are orthog-
onal and complete in
B
3
, an arbitrary function
f (r, θ,φ)
in
B
3
can be approximated using Zernike polynomials
as follows.
f (θ, φ,r) =
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Z
n,l,m
(θ,φ, r) (18)
where Ω
n,l,m
( f ) could be obtained using,
Ω
n,l,m
( f ) =
Z
1
0
Z
2π
0
Z
π
0
f (θ, φ,r)Z
†
n,l,m
r
2
sinφdrdφdθ
(19)
where
†
denotes the complex conjugate.
Leveraging this property (Eq. 18) of 3D Zernike
polynomials Eq. 4 can be rewritten as,
f ∗ g(α,β) = h
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Z
n,l,m
,
τ
(α,β)
(
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m
0
=−l
Ω
n
0
,l
0
,m
0
(g)Z
n
0
,l
0
,m
0
)i.
(20)
But since
g(θ,φ, r)
is symmetric around
y
, the rota-
tion around
y
should not change the function. Which
ensures,
g(r,θ, φ) = g(r,θ − α,φ) (21)
and hence,
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m
0
=−l
Ω
n
0
,l
0
,m
0
(g)R
n
0
,l
0
(r)Y
l
0
,m
0
(θ,φ)
=
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m
0
=−l
Ω
n
0
,l
0
,m
0
(g)R
n
0
,l
0
(r)Y
l
0
,m
0
(θ,φ)e
−im
0
α
.
(22)
This is true, if and only if
m
0
= 0
. Therefore, a
symmetric function around
y
, defined inside the unit
sphere can be rewritten as,
∞
∑
n
0
=0
n
0
∑
l
0
=0
Ω
n
0
,l
0
,0
(g)Z
n
0
,l
0
,0
(23)
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object Classification
123

which simplifies Eq. 20 to,
f ∗ g(α,β) = h
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Z
n,l,m
,
τ
(α,β)
(
∞
∑
n
0
=0
n
0
∑
l
0
=0
Ω
n
0
,l
0
,0
(g)Z
n
0
,l
0
,0
)i
(24)
Using the properties of inner product, Eq. 24 can
be rearranged as,
f ∗ g(α,β) =
∞
∑
n=0
n
∑
l=0
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n
0
,l
0
,0
(g)
hZ
n,l,m
,τ
(α,β)
(Z
n
0
,l
0
,0
)i. (25)
Consider the term τ
(α,β)
(Z
n
0
,l
0
,0
). Then,
τ
(α,β)
(Z
n
0
,l
0
,0
(θ,φ,r)) = τ
(α,β)
(R
n
0
,l
0
(r)Y
l
0
,0
(θ,φ))
= R
n
0
,l
0
(r)τ
(α,β)
(Y
l
0
,0
(θ,φ))
= R
n
0
,l
0
(r)
l
0
∑
m
00
=−l
0
Y
l
0
,m
00
(θ,φ)D
l
0
m
00
,0
(α,β,·),
(26)
where
D
l
m,m
0
is the Wigner-D matrix. But we know
that D
l
0
m
00
,0
(θ,φ) = Y
l
0
,m
00
(θ,φ). Then Eq. 25 becomes,
f ∗ g(α,β) =
∞
∑
n=0
n
∑
l=0
∞
∑
n
0
=0
n
0
∑
l
0
=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n
0
,l
0
,0
(g)
l
0
∑
m
00
=−l
0
Y
l
0
,m
00
(α,β)hZ
n,l,m
,Z
n
0
,l
0
,m
00
i, (27)
f ∗ g(α,β) =
4π
3
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n,l,0
(g)Y
l,m
(α,β),
(28)
Equivariance of Volumetric Convolution
to 3D Rotation Group
Theorem 2:
Suppose
f ,g : B
3
−→ R
are square in-
tegrable complex functions defined in
B
3
such that
h f , f i < ∞
and
hg,gi < ∞
. Also, let
η
α,β,γ
be a 3D rota-
tion operator that can be decomposed into three Euler
rotations
R
y
(α)R
z
(β)R
y
(γ)
and
τ
α,β
another rotation
operator that can be decomposed into
R
y
(α)R
z
(β)
.
Suppose η
α,β,γ
(g) = τ
α,β
(g). Then,
η
(α,β,γ)
( f ) ∗ g(θ,φ) = τ
(α,β)
( f ∗ g)(θ, φ), (29)
where ∗ is the volumetric convolution operator.
Proof:
Since
η
(α,β,γ)
∈ SO(3)
, we know that
η
(α,β,γ)
( f (x)) = f (η
−1
(α,β,γ)
(x))
. Also we know that
η
(α,β,γ)
: R
3
→ R
3
is an isometry. We define,
hη
(α,β,γ)
f ,η
(α,β,γ)
gi =
Z
B
3
f (η
−1
(α,β,γ)
(x))g(η
−1
(α,β,γ)
(x))dx.
(30)
Consider the Lebesgue measure
λ(B
3
) =
R
B
3
dx
. It
can be proven that a Lebesgue measure is invariant un-
der the isometries, which gives us
dx = dη
(α,β,γ)
(x) =
dη
−1
(α,β,γ)
(x),∀x ∈ B
3
. Therefore,
hη
(α,β,γ)
f ,η
(α,β,γ)
gi = h f , gi
=
Z
S
3
f (η
−1
(α,β,γ)
(x))g(η
−1
(α,β,γ)
(x))d(η
−1
(α,β,γ)
x).
(31)
Let
f (θ, φ,r)
and
g(θ,φ, r)
be the object function
and kernel function (symmetric around north pole)
respectively. Then volumetric convolution is defined
as
f ∗ g(θ,φ) = h f , τ
(θ,φ)
gi. (32)
Applying the rotation η
(α,β,γ)
to f , we get
η
(α,β,γ)
( f ) ∗ g(θ,φ) = hη
(α,β,γ)
( f ),τ
(θ,φ)
gi (33)
Using the result in Eq. 31, we have
η
(α,β,γ)
( f ) ∗ g(θ,φ) = h f ,η
−1
(α,β,γ)
(τ
(θ,φ)
g)i. (34)
However, since η
α,β,γ
(g) = τ
α,β
(g), we get
η
(α,β,γ)
( f ) ∗ g(θ,φ) = h f ,τ
(θ−α,φ−β,)
gi. (35)
We know that,
f ∗ g(θ,φ) = h f , τ
(θ,φ)
gi
=
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n,l,0
(g)Y
l,m
(θ,φ).
(36)
Then,
η
(α,β,γ)
( f ) ∗ g(θ,φ) = h f ,τ
(θ−α,φ−β)
gi
=
∞
∑
n=0
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
( f )Ω
n,l,0
(g)Y
l,m
(θ − α, φ − β)
= ( f ∗ g)(θ − α,φ − β) = τ
(α,β)
( f ∗ g)(θ, φ).
(37)
Hence, we achieve equivariance over 3D rotations.
Axial Symmetry Measure of a Function
in B
3
around an Arbitrary Axis
Proposition:
Suppose
g : B
3
−→ R
3
is a square
integrable complex function defined in
B
3
such that
hg,gi < ∞
. Then, the power of projection of
g
in to
S = {Z
i
}
where
S
is the set of Zernike basis functions
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
124

that are symmetric around an axis towards
(α,β)
di-
rection is given by
k sym
(α,β)
g(θ,φ,r)
k=
∑
n
n
∑
l=0
k
l
∑
m=−l
Ω
n,l,m
Y
l,m
(α,β) k
2
,
(38)
where
α
and
β
are azimuth and polar angles respec-
tively.
Proof:
The subset of complex functions which are
symmetric around north pole is
S =
{
Z
n,l,0
}
. There-
fore, projection of the function into S gives
sym
y
g(θ,φ, r)
=
∑
n
n
∑
l=0
h f ,Z
n,l,0
iZ
n,l,0
(θ,φ, r).
(39)
To obtain the symmetry function around any axis
which is defined by
(α,β)
, we rotate the function
by
(−α,−β)
, project into
S
, and finally compute the
power of the projection
sym
(α,β)
g(θ,φ,r)
=
∑
n,l
hτ
(−α,−β)
( f ),Z
n,l,0
iZ
n,l,0
(θ,φ,r).
(40)
For any rotation operator
τ
, and for any two points
defined on a complex Hilbert space, x and y,
hτ(x),τ(y)i
H
= hx,yi
H
. (41)
Applying this property to Eq. 40 gives
sym
(α,β)
g(θ,φ,r)
=
∑
n,l
h f ,τ
(α,β)
(Z
n,l,0
)iZ
n,l,0
(θ,φ,r).
(42)
Using Eq. 18 we get
sym
(α,β)
g(θ,φ,r)
=
∑
n
n
∑
l=0
h
∑
n
0
n
0
∑
l
0
=0
l
0
∑
m
0
=−l
0
Ω
n
0
l
0
m
0
Z
n
0
,l
0
,m
0
,
τ
(α,β)
(Z
n,l,0
)iZ
n,l,0
(θ,φ,r).
(43)
Using properties of inner product Eq. 43 further sim-
plifies to
sym
(α,β)
g(θ,φ,r)
=
∑
n
n
∑
l=0
∑
n
0
n
0
∑
l
0
=0
l
0
∑
m
0
=−l
0
Ω
n
0
l
0
m
0
hZ
n
0
,l
0
,m
0
,
τ
(α,β)
(Z
n,l,0
)iZ
n,l,0
(θ,φ,r). (44)
Using the same derivation as in Eq. 26,
sym
(α,β)
g(θ,φ,r)
=
∑
n
n
∑
l=0
∑
n
0
n
0
∑
l
0
=0
l
0
∑
m
0
=−l
0
Ω
n
0
l
0
m
0
l
∑
m
00
=−l
Y
l,m
00
(α,β)hZ
n
0
,l
0
,m
0
,Z
n,l,m
00
iZ
n,l,0
(θ,φ,r).
(45)
Since 3D Zernike Polynomials are orthogonal we get
sym
(α,β)
g(θ,φ,r)
=
4π
3
∑
n
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
Y
l,m
(α,β)Z
n,l,0
(θ,φ,r).
(46)
In signal theory the power of a function is taken as
the integral of the squared function divided by the size
of its domain. Following this we get
ksym
(α,β)
g(θ,φ,r)
k
= h(
∑
n
n
∑
l=0
l
∑
m=−l
Ω
n,l,m
Y
l,m
(α,β))Z
n,l,0
(θ,φ,r),
(
∑
n
0
n
0
∑
l
0
=0
l
0
∑
m
0
=−l
0
Ω
n
0
,l
0
,m
0
Y
l
0
,m
0
(α,β)Z
n
0
,l
0
,0
(θ,φ,r))
†
i.
(47)
We drop the constants here since they do not depend
on the frequency. Simplifying Eq. 47 gives
k sym
(α,β)
g(θ,φ,r)
k=
∑
n
n
∑
l=0
l
∑
m=−l
l
∑
m
0
=−l
Ω
n,l,m
Y
l,m
(α,β)
Ω
n,l,m
0
Y
l
0
,m
(α,β),
(48)
which leads to
k sym
(α,β)
g(θ,φ,r)
k=
∑
n
n
∑
l=0
k
l
∑
m=−l
Ω
n,l,m
Y
l,m
(α,β) k
2
.
(49)
which completes our proof.
Learned and Hand-crafted Feature Fusion in Unit Ball for 3D Object Classification
125
